A theoretical study of aqueous solvation of K⁺ comparing ab initio, polarizable, and fixed-charge models

Abstract

The hydration of K⁺ is studied using a hierarchy of theoretical approaches, including ab initio Born-Oppenheimer molecular dynamics and Car-Parrinello molecular dynamics, a polarizable force field model based on classical Drude oscillators, and a nonpolarizable fixed-charge potential based on the TIP3P water model. While models based more directly on quantum mechanics offer the possibility to account for complex electronic effects, polarizable and fixed-charges force fields allow for simulations of large systems and the calculation of thermodynamic observables with relatively modest computational costs. A particular emphasis is placed on investigating the sensitivity of the polarizable model to reproduce key aspects of aqueous K⁺, such as the coordination structure, the bulk hydration free energy, and the self diffusion of K⁺. It is generally found that, while the simple functional form of the polarizable Drude model imposes some restrictions on the range of properties that can simultaneously be fitted, the resulting hydration structure for aqueous K⁺ agrees well with experiment and with more sophisticated computational models. A counterintuitive result, seen in Car-Parrinello molecular dynamics and in simulations with the Drude polarizable force field, is that the average induced molecular dipole of the water molecules within the first hydration shell around K⁺ is slightly smaller than the corresponding value in the bulk. In final analysis, the perspective of K⁺ hydration emerging from the various computational models is broadly consistent with experimental data, though at a finer level there remain a number of issues that should be resolved to further our ability in modeling ion hydration accurately.

I. INTRODUCTION

Small ions such as K⁺ and Na⁺ play a ubiquitous role in biology. For this reason, understanding how they are solvated by water molecules remains an issue of great relevance. A powerful approach to investigate ion solvation is to rely on computer simulations of atomic models based on potential functions^1–5. For meaningful simulation studies it is important to use models that represent the microscopic interactions as accurately as possible. In the past few decades, a number of fixed-charge nonpolarizable force fields have been parameterized to model ion solvation^6–9, and are now used on a regular basis to investigate diverse problems. Induced electronic polarization, which is generally neglected in standard molecular dynamics simulations of biomolecular systems, remains of particular concern in the case of ionic systems where non-additive many-body effects could be important. In principle, accurate computational models can be developed, validated, and refined by comparing with experimental data (gas and bulk phase), as well as high level ab initio computations. In practice, however, this presents a difficult challenge for a number of reasons.

The individual microscopic interactions that are involved in ion hydration are most directly probed by single-ion thermochemical gas phase experimental data on small water clusters^10–12. Nonetheless, how this information must be extrapolated to the bulk phase is uncertain because the properties of small clusters can be both similar and different from their bulk counterparts. Interpretation of experimental data about ions in the bulk phase is also not without any difficulties. Analysis of the neutron scattering data used to measure the coordination structure of Na⁺ and K⁺ in liquid water must rely on simulation models to determine the partial radial distribution functions¹⁴. These problems are reflected in the lack of consensus concerning the structural properties of hydrated ions, especially their hydration numbers¹⁵. An additional piece of information in developing meaningful ion solvation models is the experimentally measured hydration free energies. Experimental determination of the hydration free energies of charged species is a challenging problem that has been revisited numerous times over the years^{4,5,12,16–19,25,26}. Single ion solvation properties in the infinite dilution limit must be extracted from electrochemical data using extra-thermodynamic assumptions, which are uncertain⁵. These difficulties are further compounded by the fact that, in a real physical system, the total reversible work to take an ion from the gas phase and transfer it into a bulk liquid phase includes a contribution from the electrostatic potential associated with the vacuum/liquid interface. The currently available experimental data is, by itself, insufficient to establish a definitive picture of the solvation of simple ions such as K⁺ and Na⁺ in water.

Computations can be used to extend the information extracted from experiments. Because they can account for a wide range of complex electronic effects, simulations based on quantum mechanical ab initio methods offer an important source of information to deepen and extend our knowledge of ion solvation. However, bulk phase ab initio simulations are computationally intensive and can be burdened by finite size effects, short sampling time, and any approximations inherent to the treatment of electron correlation. In the particular case of density functional theory (DFT), approximations in available exchange-correlation functionals and the neglect of van der Waals dispersive attraction must also be kept in mind^20–22. Alternatively, simulations based on physically realistic classical potential functions offer a path for estimating statistically converged thermodynamic averages, in terms of size and configurational sampling, although the validity of the simplifying assumptions upon which these potential functions are constructed must be assessed. In spite of these difficulties, it is our hope that a well-defined (if not definitive) perspective on the aqueous solvation of small ions can emerge by critically examining and contrasting all the available data from simulations and experiments.

In the present effort, aqueous solvation of K⁺ is investigated using a hierarchy of computational approaches. This includes two quantum mechanical ab initio simulation methods, Born-Oppenheimer molecular dynamics (BOMD), and Car-Parrinello molecular dynamics (CPMD), as well as two classical force field methods, TIP3P, a widely used nonpolarizable effective fixed charge model^8,23, and SWM4-NDP, a polarizable model based on classical Drude oscillators²⁴. The polarizable model of ion solvation presented here is based upon the classical Drude oscillator^27–32. In this model, electronic induction is represented by the displacement of a charge-carrying auxiliary particle attached to a polarizable atom under the influence of the local electric field. The familiar self-consistent field (SCF) regime of induced polarization is reproduced in molecular dynamics simulations if the classical Drude oscillators are kept near their local energy minima for a given configuration of the atoms in the system³².

In the following, the ability of the models to reproduce the single-ion thermochemical gas phase data in small clusters is examined. In addition, a particular emphasis is placed on examining the sensitivity in the Drude model of key aspects of aqueous solvation of K⁺, such as the coordination structure, the hydration free energy, and the coefficient of self-diffusion. It is found that, while the simple functional form of potential functions imposes some restrictions on the range of properties that can simultaneously be fitted, the resulting hydration structure for aqueous K⁺ is in broad accord with experiment and with ab initio simulations. In conclusion, MD studies based on properly parameterized models can yield meaningful results, although there remain a number of small discrepancies that shall be critically examined.

II. METHODS

The hydration of K⁺ was studied using four distinct computational models, the details of which are outlined below. The four computational models are: (i) a fixed charge model based upon the TIP3P²³ water model, (ii) a Drude polarizable model based upon the SWM4-NDP water model²⁴, (iii) a density functional theory (DFT) model based upon the gradient-corrected PW91 approximate density functional^33,34 and (iv) a second DFT model using the gradient-corrected BLYP approximate density functional^35,36. In all periodic simulations with a net charge, a uniform cancelling background charge is assumed.

A. Fixed charge model

The fixed charge model of aqueous K⁺ is based on the Lennard-Jones parameters that were previously optimized⁸ to give reasonable monohydrate energy and hydration free energies for K⁺ when used in conjunction with the TIP3P water model²³; the parameters for K⁺ are E_min = 0.0870 kcal/mol, and σ = 2.142645 Å assuming a Lorentz-Berthelot combination rule with the TIP3P parameters. A system consisting of a box of 500 TIP3P water molecules and a single K⁺ ion was simulated with periodic boundary conditions. Long range electrostatic interactions were computed using Ewald summation³⁷. The canonical ensemble was simulated using Nosé-Hoover thermostats³⁸ and a 1 fs time-step. The internal geometry of the TIP3P water molecule was fixed using the SHAKE³⁹ algorithm. After an initial equilibration of 100 ps, equilibrium properties were averaged over a 1 ns molecular dynamics simulation.

B. Drude polarizable model

The model for K⁺ is consistent with the recently developed SWM4-NDP polarizable water model with a negatively charged Drude oscillator bound to its oxygen site²⁴. The SWM4-NDP potential reproduces most properties of bulk water under ambient conditions. In particular, the model yields a correct static dielectric constant, which makes it appropriate to study systems dominated by water-mediated electrostatic interactions. Accordingly, polarization of the cation is represented with a negatively charged particle bound to its nucleus. All atomic dispersion and electronic overlap effects are represented in a pairwise additive way using the Lennard-Jones potential.

The interaction energy of a single ion of charge q_ion with N water molecules is

$$U_{\text{iw}}({\mathbf{r}}_{is},\mathbf{r},{\mathbf{r}}_D)=\frac{1}{2}{k}_{\text{D}}{\mid \mathbf{r}-{\mathbf{r}}_{\text{D}}\mid }^2+\sum _{i=1}^N\sum _{s=1}^4\left[\frac{(q_{\text{ion}}-q_{\text{D}})q_s}{\mid \mathbf{r}-{\mathbf{r}}_{is}\mid }+\frac{q_{\text{D}}{q}_s}{\mid {\mathbf{r}}_{\text{D}}-{\mathbf{r}}_{is}\mid }\right]+\sum _{i=1}^{N}4{\epsilon }_{\text{ion}-\text{O}}\left[{\left(\frac{{\sigma }_{\text{ion}-\text{O}}}{\mid \mathbf{r}-{\mathbf{r}}_{i\text{O}}\mid }\right)}^{12}-{\left(\frac{{\sigma }_{\text{ion}-\text{O}}}{\mid \mathbf{r}-{\mathbf{r}}_{i\text{O}}\mid }\right)}^6\right],$$ (1)

where the vectors r and r_D are the positions of the ionic core and the ionic Drude particle, respectively. The ionic core has a charge (q_ion − q_D) and the Drude particle has a charge q_D. The spring constant k_D is set to 1000 kcal/mol/Ų for all Drude oscillators in the system. This value dictates the magnitude of the charge the Drude particle should carry to produce an ionic polarizability α, i.e., $q_{\text{D}}=-\sqrt{\alpha k_{\text{D}}}$²⁴. In Eq. (1), the vector r_is is the position of the interaction site σ of water molecule i. The SWM4-NDP water model comprises five sites: the oxygen atom “O” (charge -q_D), the hydrogen atoms “H₁” and “H₂” (charged), a massless site “M” (charged), and a Drude particle “D” attached to the oxygen atom (negatively charged). The Lennard-Jones parameters for the ion-water oxygen interaction are determined via the Lorentz-Berthelot combination rule⁴⁰, ${\epsilon }_{\text{ion}-\text{O}}=\sqrt{{\epsilon }_{\text{ion}}{\epsilon }_{\text{O}}}$ and σ_ion-O = (σ_ion + σ_O)/2.

The Drude polarizable model for aqueous K⁺ is based upon the recently published SWM4-NDP polarizable model for water²⁴. The parameters for K⁺ were chosen to give agreement with experimental monohydrate properties¹⁰ and an hydration free energy for the cation that was consistent with published values^5,41,42.

The simulation protocol for studying the bulk hydration structure of the polarizable Drude model is identical to that of the fixed charge model, except that a dual thermostat scheme was used to keep the Drude particles at a low temperature (1 Kelvin) and therefore close to the (self-consistent field) ground state³².

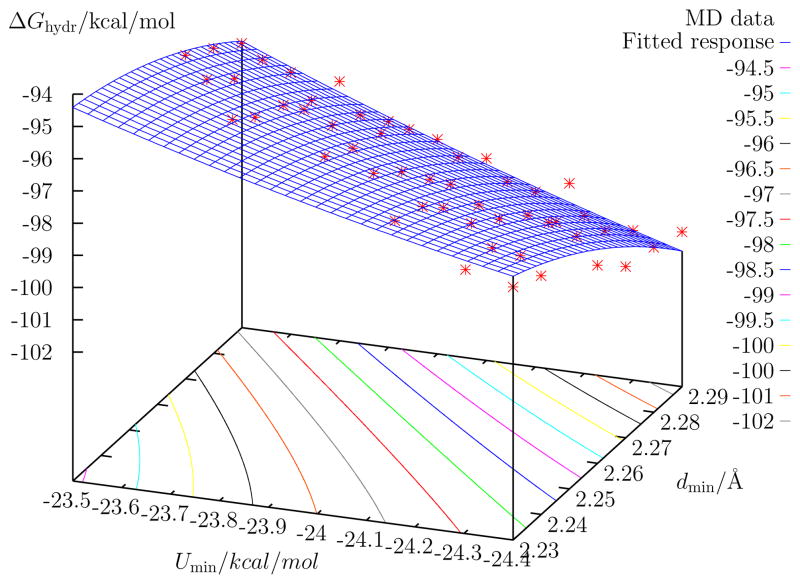
The adjustable parameters for monatomic ions within the classical Drude scheme to build a polarizable biomolecular force field are the Lennard-Jones parameters of the ion, σ_ion and ε_ion. Rather than try to determine these parameters by scanning in the space of {σ_ion, ε_ion}, it has proved more convenient to explore the space of monohydrate interaction energies and minimum-energy ion-oxygen distances {U_min, d_min}⁵. Furthermore, quadratic response functions are fitted to the data from explicit computations, defined by coordinates in {U_min, d_min}, to interpolate predicted properties between simulated models^5,24. A set of polarizable models for K⁺ were thus constructed by determining the Lennard-Jones parameters spanning a regular grid in the {U_min, d_min} coordinates. For each model on the grid, MD simulations were then carried out to compute the aqueous bulk hydration number, n(r_c), and the bulk hydration free energy, ΔG_hydr. These properties were then fitted to a polynomial response function with a quadratic dependence on {U_min, d_min}. The results of these computations are summarized in Figs. 1 and 2. To monitor consistency between K⁺ and Na⁺ models, the hydration free energy of Na⁺ is also reported in Fig. 3 for a set of Na⁺ polarizable Drude models.

FIG. 1.

Coordination number, n(r_c = 3.5Å), for a family of putative K⁺ ions as a function of monohydrate properties for the polarizable model. The open square (□) indicates the location of the D_6.8 model, while the filled square (■) indicates that of the D_6.5 model.

FIG. 2.

Computed hydration free energy for a family of putative K⁺ ions as a function of monohydrate properties for the polarizable model. The open square (□) indicates the location of the D_6.8 model, while the filled square (■) indicates that of the D_6.5 model.

FIG. 3.

Computed hydration free energy of Na⁺ as a function of monohydrate properties for the polarizable model.

The hydration free energy of the ions was decomposed into three contributions⁵⁹,

$$\mathrm{\Delta }{G}_{\text{hydr}}=\mathrm{\Delta }{G}_{\text{hydr}}^{\text{rep}}+\mathrm{\Delta }{G}_{\text{hydr}}^{\text{disp}}+\mathrm{\Delta }{G}_{\text{hydr}}^{\text{elec}},$$ (2)

where $\mathrm{\Delta }{G}_{\text{hydr}}^{\text{rep}}$ and $\mathrm{\Delta }{G}_{\text{hydr}}^{\text{disp}}$ are the repulsive and attractive (dispersive) components, respectively, of the Lennard-Jones interaction in Eq. (1). The electrostatic component of the hydration free energy is $\mathrm{\Delta }{G}_{\text{hydr}}^{\text{elec}}$. Each component of the total hydration free energy was computed from independent simulations in which an ion was placed at the center of a droplet of 250 explicit SWM4-NDP water molecules, contained by the reactive spherical solvent boundary potential (SSBP)⁸. The repulsive contribution, $\mathrm{\Delta }{G}_{\text{hydr}}^{\text{rep}}$, was computed using a soft-core scheme as described elsewhere⁵⁹ and was unbiased using the weighted histogram analysis method (WHAM)⁶⁰, while $\mathrm{\Delta }{G}_{\text{hydr}}^{\text{disp}}$ and $\mathrm{\Delta }{G}_{\text{hydr}}^{\text{elec}}$ were computed using thermodynamic integration (TI). In discussions of the hydration free energies of ionic species, one may consider the real physical value, which includes the contribution of the phase potential arising from crossing the physical air/water interface, and the intrinsic bulk phase value, which is independent of any interfacial potential^5,19. Because the interfacial potential in SSBP is nearly identical to the one from a simulation of a vacuum-liquid interface⁵, the charging free energy computed with SSBP effectively includes the interfacial potential contribution that an ion gains by crossing the physical interface from the gas phase to the bulk water. It follows that the results from those SSBP computations can readily be interpreted as real hydration free energies. Unless specificied otherwise, real hydration free energies are discussed in the rest of the paper.

For convenience, the upper bound on the radial integral used throughout to define the hydration number was set to r_c = 3.5Å. While this choice for r_c may not coincide with the conventional definition that r_c is the position of the first minimum in the radial distribution function for the O-K⁺ contact in all of the models of aqueous K⁺ studied here, it is necessary when comparing so many different models. As it turns out, r_c = 3.5 Å is a good approximation for the position of the first minimum in g_OK+(r) for all of the Drude models, the fixed charge model and the PW91/pw representation of the system. Since the only radial distribution function examined here is for the O-K⁺ contact, the definitions g_OK+(r) ≡ g(r) and n_OK+(r) ≡ n(r) are employed in the remainder of the text.

C. Ab initio models

The fixed charge and Drude polarizable models of aqueous K⁺ are compared with two different ab initio density functional theory (DFT) models of the same system, each using a different gradient-corrected approximate density functional: BLYP^35,36 and PW91^33,34. Although both ab initio simulations were performed at the Γ-point, there are many methodological differences between the two computations. Simulations with the PW91 exchange-correlation functional were performed within a Born-Oppenheimer molecular dynamics (BOMD) scheme using the VASP software package^43,44, while simulations using the BLYP functional were performed within the Car-Parrinello molecular dynamics scheme⁴⁵ using the PINY MD software package^46,47. Some results from this BOMD simulation have previously been published elsewhere^15,48. The simulation details are given below.

In the BOMD simulation of aqueous K⁺, core-valence interactions are described using the projector augmented-wave (PAW) method^49,50. Convergence was accepted for the electronic structure calculation when the energy difference between successive self-consistent iterations is less than 10⁻⁶ eV and the valence orbitals are expanded in plane waves with a kinetic energy cutoff of 36.75 Ry (500 eV). This model of the aqueous K⁺ system is henceforth referred to as PW91/pw.

The system consisted of 64 water molecules and one K⁺ ion in a cubic box of length 12.4171 Å with periodic boundary conditions. The fixed volume was chosen such that the water density matches the experimental density of liquid water at standard conditions. Initial conditions come from a well-equilibrated classical MD run of pure liquid water at standard conditions using SPC/E⁵¹ water for 20 ps, followed by a 10 ps BOMD simulation of pure water. In the BOMD simulation of pure water, a Nosé-Hoover thermostat was applied to constrain the temperature to 375 K, after which a K⁺ ion was inserted into the box of pure water and all hydrogens were deuterated. The 3p semicore electrons were explicitly included in the valence orbitals for K⁺ ion. During the equilibration phase, constant temperature was maintained at T = 330 K with velocity scaling and the equations of motion were integrated using a 1 fs time-step for 14.5 ps. The equilibrated system was then simulated in the microcanonical ensemble with a 0.5 fs time-step for 40 ps of production. During the course of the BOMD simulation, the temperature was 313 ± 21 Kelvin.

The CPMD simulations of aqueous K⁺ used the gradient-corrected BLYP approximate density functional^35,36 and a plane-wave basis set. Calculations were performed with a 70 Ry energy cutoff and norm-conserving pseudopotentials⁵². Following the prescription of the initial fully ab initio simulations carried out on this system⁵³, the semicore 3σ and 3p states of potassium have been included with the valence electrons. A baseline fictitious electronic mass of 475 a.u. was used with mass preconditioning⁵⁴. The canonical ensemble was sampled using Nosé-Hoover chain thermostats^38,55–58 and a 0.125 fs time-step. In order to ensure adiabaticity, the hydrogen masses were substituted with oxygen masses. The temperature over the course of the CPMD simulation was 296 ± 15 Kelvin. This model of the aqueous K⁺ system is henceforth referred to as BLYP/pw.

The BLYP/pw system consisted of the same equilibrated BOMD simulation box as above, containing 64 water molecules with a single potassium cation and with periodic boundary conditions. The system was further equilibrated for 5 ps of CP molecular dynamics. Results were collected during a subsequent 50 ps CPMD simulation. An error analysis and finite system size study for this small system and the relatively short simulation times of the ab initio systems presented in the Appendix indicate that the simulations are statistically accurate and representative of the properties of a system with a large number of water molecules (no significant finite size effect on the ion-water radial distribution function).

III. RESULTS AND DISCUSSION

A. Monohydrate and cluster energy

The interaction energy of the K⁺ monohydrate was computed with various methods. The geometry of the monohydrate was optimized for the fixed charge and polarizable Drude models using the CHARMM⁶¹ software package and also quantum mechanically at the Hartree-Fock level with the 6–31G^* basis set. In each case the K⁺ ion was coplanar with the plane of the water molecule, coordinated with the oxygen atom (that is, had C_2v symmetry). As a furthur comparison, interaction energies have also been computed for DFT optimized geometries (see Tables I and II). The resulting geometries are summarized in Table II. The monohydrate interaction energies for these geometries, at various levels of theory⁶², are presented in Table I, with and without the Boys-Bernardi counterpoise correction to basis set superposition error⁶³. The experimental gas phase enthalpy for this system has been measured to be −17.9 kcal/mol¹⁰ (see Table III and footnote to Table I).

TABLE I.

Interaction energy, ΔE, for K⁺ ···OH₂ binding in kcal/mol. Interaction energies are compared from quantum chemical basis set computations, classical force fields and experiment. Unless otherwise noted, the quantum chemical interaction energies are presented for geometries optimized at the HF/6–31G^* level. Data are presented both with and without counterpoise corrections (CPC) to the basis set superposition error (BSSE).

Geometry	Basis	Method	ΔE	ΔE (CPC)
HF/6–31G*	6–31G*	HF	−20.29	−18.76
HF/6–31G*	6–311++G(3df,3pd)	MP2	−17.47	−17.18
HF/6–31G*	6–311++G(3df,3pd)	CCSD	−17.31	−17.03
HF/6–31G*	6–311++G(3df,3pd)	BLYP	−16.57	−16.44
BLYP/6-311++G(3df,3pd)	6-311++G(3df,3pd)	BLYP	−16.68	−16.56
HF/6-31G*	pw (70 Ry)	BLYP	−16.50	N/A
HF/6-31G*	pw (140 Ry)	BLYP	−16.62	N/A
HF/6-31G*	pw (280 Ry)	BLYP	−16.62	N/A
HF/6-31G*	6-311++G(3df,3pd)	PW91	−17.69	−17.55
PW91/6-311++G(3df,3pd)	6-311++G(3df,3pd)	PW91	−17.82	−17.68
HF/6-31G*	pw (70 Ry)	PW91	−17.25	N/A
HF/6-31G*	pw (140 Ry)	PW91	−17.37	N/A
HF/6-31G*	pw (280 Ry)	PW91	−17.37	N/A
Fixed charge		Fixed charge	−18.9
D6.5		Drude model	−17.7
D6.8		Drude model	−17.9
Expt.a		Drude model	−18.3 b

^aRef.¹⁰

^bInteraction energy estimated from an experimentally measured enthalpy, −17.9 kcal/mol plus −0.4 kcal/mol taken from Drude model computations of the monohydrate enthalpy (see Table III).

TABLE II.

Optimized geometries for K⁺ ···OH₂.

Theory level	rOK+/Å	rOH/Å	θHOH/degree
HF/6-31G*	2.6481	0.9511	105.03
BLYP/6-311++G(3df,3pd)	2.6395	0.9736	104.16
PW91/6-311++G(3df,3pd)	2.6116	0.9709	104.06
Fixed Charge	2.6243	0.9572	104.52
Drude (D6.8)	2.6196	0.9572	104.52

TABLE III.

Hydration enthalpy, ΔH, for gas phase K⁺(H₂O)_n clusters in kcal/mol.

n	Fixed Charge	Drude D6.8	Exp.a	Exp.b
1	−18.5 ± 0.02	−17.5 ± 0.04	−17.9	−18.1
2	−35.6 ± 0.03	−33.0 ± 0.04	−34.0	−34.2
3	−51.2 ± 0.05	−46.2 ± 0.05	−47.2	−47.4
4	−64.3 ± 0.06	−57.7 ± 0.05	−59.0	−59.2
5	−74.6 ± 0.07	−67.0 ± 0.06	−69.7	−69.9
6	−84.4 ± 0.08	−76.0 ± 0.08	−79.7	−79.9

^aRef.¹⁰

^bRef.¹²

The interaction energies presented in Table I demonstrate the variability and accuracy of the various quantum chemical approaches that have subsequently been applied to larger aqueous K⁺ clusters. The interaction energies in Table I are all roughly in good accord with the experimental estimate of −18.3 kcal/mol (see footnote to Table I), though there are small differences that deserve to be noted. Nearly all of the quantum chemical interaction energies appear to be slightly less negative than the experimental estimate. The Hartree-Fock calculation, which overestimates the binding by as much as ~2.5 kcal/mol, is the lone exception to this rule. Previous analysis showed that the larger binding energy is directly related to the overestimated dipole of the water molecule, due to neglect of electron correlation³. The fixed charge K⁺ monohydrate, which was originally parameterized to give a reasonable bulk hydration free energy in TIP3P⁸, also overestimates the monohydrate binding energy. As expected, the counterpoise corrections become smaller for larger basis sets.

In order to assess both the magnitude of the fluctuations in the potential energy within the first hydration shell of K⁺ and the level of consistency with which these are represented by various computational models, a series of K⁺(H₂O)_n clusters were examined and compared. First, the enthalpy of hydration, ΔH, is reported in Table III for a series of K⁺(H₂O)_n clusters with 1 ≤ n ≤ 6 using simulations based on the fixed charge TIP3P and Drude polarizable force fields (model D_6.8). The enthalpy of the small clusters of one K⁺ ion and n water molecules were calculated as, ΔH = nk_BT − (〈U_n〉 + k_BT ), where 〈U_n〉 is the average potential energy of the cluster estimated from a 1 ns trajectory at a temperature of 300 K. Examination of Table III indicate that the trend is reproduced by both models (more accurately by the polarizable model), although neither model reproduces the experimental gas phase data exactly.

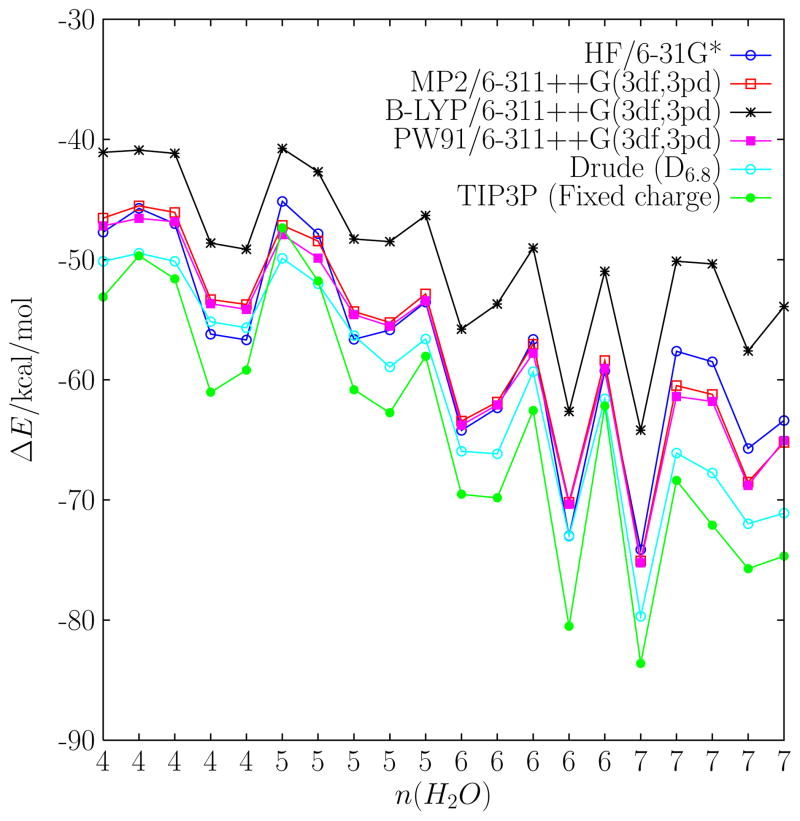
In addition, the energy of instantaneous snapshots of water molecules surrounding K⁺ extracted from a simulation generated using the polarizable force field with model D_6.8 were calculated and compared for the various models. Configurations with 4 ≤ n ≤ 7 were extracted. For each configuration, all the O-K⁺ distances were within a 3.5 Å radius from the K⁺, serving here as the standard definition of the first hydration shell of the ion (see above). The ranking of cluster interaction energies for the instantaneous configurations, shown in Fig. 4, follows that for the K⁺ monohydrates, with a few variations. Interestingly, both the polarizable (D_6.8) and the fixed charge model closely follow the trends of the quantum chemical interaction energies. While both models yield similar bulk hydration free energies, the polarizable D_6.8 model is in closer agreement to the MP2 and PW91 (with an atom-centered basis set) interaction energies for this set of configurations. Despite the difference in magnitude, the energy of the instantaneous snapshots are highly correlated. A normalized correlation coefficient can be defined as,

FIG. 4.

Interaction energies for a series of K⁺(H₂O)_n clusters at various levels of ab initio theory and for a fixed charge and Drude polarizable model. Each cluster was extracted from MD simulation of aqueous K⁺. The x-axis indexes the number of water molecules, n, coordinating the cation.

$$C_{ij}=\frac{\langle \mathrm{\Delta }{E}_i\mathrm{\Delta }{E}_j\rangle }{\sqrt{\langle \mathrm{\Delta }{E}_i^2\rangle \langle \mathrm{\Delta }{E}_j^2\rangle }}$$ (3)

where ΔE_i = E_i − 〈E_i〉. The C_ij vary between 0.94 (e.g., Drude with HF/6-31G*) to 0.99 (e.g., Drude with MP2, or Drude with PW91) for all the models. The high correlations suggest that, while the magnitude of the energies are different, the structure of the potential energy surface is similar in all the models.

B. Hydration free energy

The hydration free energy provides an important reference to assess the validity of various models. The Lennard-Jones parameters of K⁺ were explored to ascertain the sensitivity of the polarizable potential energy function. Lennard-Jones parameters could not be found to generate polarizable models of K⁺ which had both very small O-K⁺ monohydrate distances and lower interaction energies. As is evident in Fig. 1, it was nevertheless possible to find polarizable models for K⁺ that had hydration numbers of ~ 6.5. Looking at both Figs. 1 and 2, it is observed that polarizable models for K⁺ that have a hydration number of ~ 6.5 also have hydration free energies of about −75 kcal/mol. The hydration free energy of a set of Na⁺ models was also calculated to assess the consistency, or lack thereof, with the putative K⁺ models. The absolute Na⁺ hydration free energies are shown in Fig. 3. This consistency is important because, while there are inherent uncertainties concerning the absolute scale of single-ion hydration free energy, the relative hydration free energy between monovalent cations is known from experiment very accurately¹². The relative hydration free energy between K⁺ and Na⁺ from experiments is 17.2 kcal/mol. In order to reproduce this value, a K⁺ model with a hydration free energy of −75 kcal/mol would require a corresponding Na⁺ hydration energy of −92.2 kcal/mol.

From an exploration of the {U_min, d_min} space for aqueous hydration of K⁺, two models were selected for further study: one which accurately captures the monohydrate geometry and interaction energy, (U_min, d_min) =(−17.9 kcal/mol, 2.62 Å), and another which sacrifices some of this accuracy in order to yield a hydration number that is in closer accord with that predicted by a recent analysis of neutron scattering experiments, (U_min, d_min) =(−17.7 kcal/mol, 2.59 Å). The first model has a hydration number of 6.8, while the second model has a coordination number of 6.5 (integrating the radial distribution functions up to a distance of 3.5 Å). These two polarizable models are referred to as D_6.8 and D_6.5, respectively. They are indicated in Figs. 1 and 2. As an example of how these Drude models must work in conjunction with other Drude polarizable ions, consider a Drude model of Na⁺ that can be matched with the D_6.8 model of K⁺: D_6.8 has an hydration free energy of ΔG_hydr = −80.15 kcal/mol. Any Drude model for Na⁺ that has an hydration free energy of ΔG_hydr = −97.35 kcal/mol (representable as a contour in Fig. 3) might be suitable. The best choice, however, would also accurately reproduce the monohydrate properties⁵. In this case, a Drude Na⁺ model with (U_min, d_min) =(−24.0 kcal/mol, 2.252 Å) is an optimal choice. For the D_6.5 model of K⁺, with an hydration free energy of ΔG_hydr = −76.60 kcal/mol, a Drude model for Na⁺ would be found along the ΔG_hydr = −93.80 kcal/mol contour of Fig. 3. If such a model Drude could be found for Na⁺, it would lie outside of the boundaries of Fig. 3.

The hydration free energy for the PW91 and BLYP models are estimated to be −74.3 and −66.1 kcal/mol using a computational scheme based on the quasi-chemical theory²⁶. In this computational scheme, the K⁺ ion and the 4 nearest water molecules (within ~ 3.0 Å, see Fig. 6 below) are modeled explicitly with the exchange-correlation density functional, while the influence of the remaining liquid is incorporated via a far-field treatment. Dispersion interactions and packing effects have been neglected in these particular estimates. These effects are expected to contribute with opposite signs and yield an overall slightly less favorable hydration free energy. It is also worth noting that the quasi-chemical estimates for the BLYP and PW91 density functionals are based on ab initio computations including all electrons, differing slightly with the models of the BOMD and CPMD simulations which represented the core electrons using a pseudo-potential. Superficially, the estimates for PW91 and BLYP appear to differ from the molecular dynamics based free energy perturbation (FEP/MD) calculations based on the potential functions by as much as 14 kcal/mol, but this is deceptively incorrect. The FEP/MD calculations with SSBP include the phase potential arising from the vacuum-liquid interface (e.g., they are real hydration free energies)⁵, whereas the calculations carried out according to the quasi-chemical theory report intrinsic hydration free energy. In calculations based on potential functions, the phase potential is on the order of −500 mV in the liquid, thus contributing favorably to the solvation of a cation by about 12 kcal/mol⁵. Adding this contribution from potential functions to the estimated intrinsic hydration free energy based on the quasi-chemical theory yields a real hydration free energy on the order of about −86 kcal/mol for the PW91 approximate exchange-correlation functional, or a little less if packing and dispersion effects are incorporated. While further work would be required to ascertain the validity of this comparison, the present analysis suggests that the hydration free energy from the D_6.8 polarizable model is consistent with the value obtained from the quasi-chemical treatment.

FIG. 6.

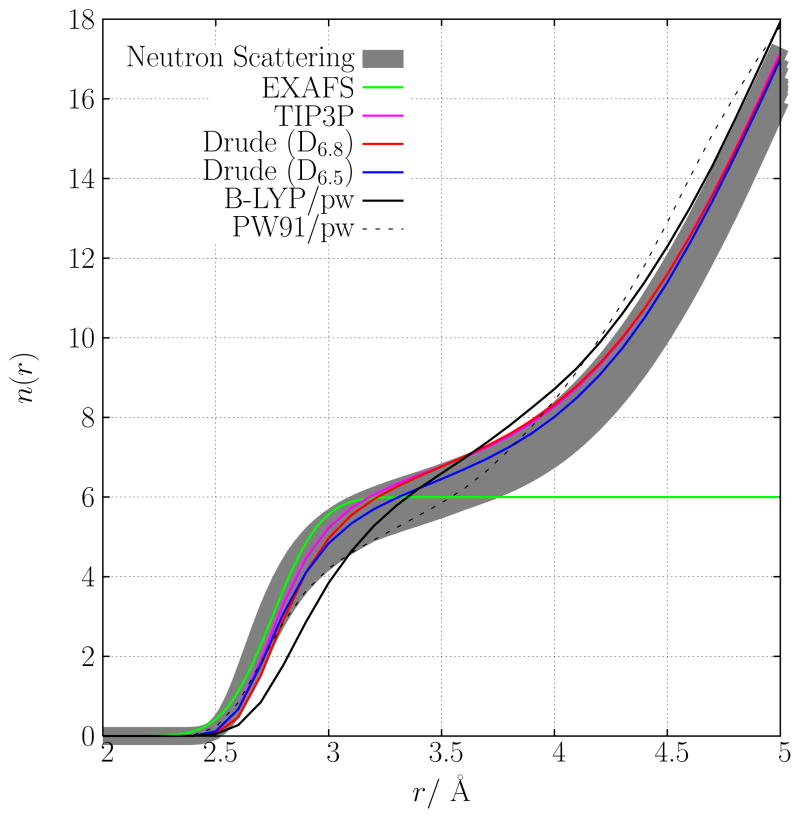
Hydration number, n(r) of K⁺ contact from several different models: the fixed charge model, two polarizable models, the BLYP/pw and PW91/pw models. The coordination number is: neutron data, 5.5–6.4; TIP3P, 6.77; D_6.8, 6.8; D_6.5, 6.5; BLYP, 6.6; PW91, 5.86 (all integrated up to a distance of 3.5 Å). The hydration number n(r) estimated from EXAFS is also shown⁷¹.

C. Hydration structure in the bulk liquid

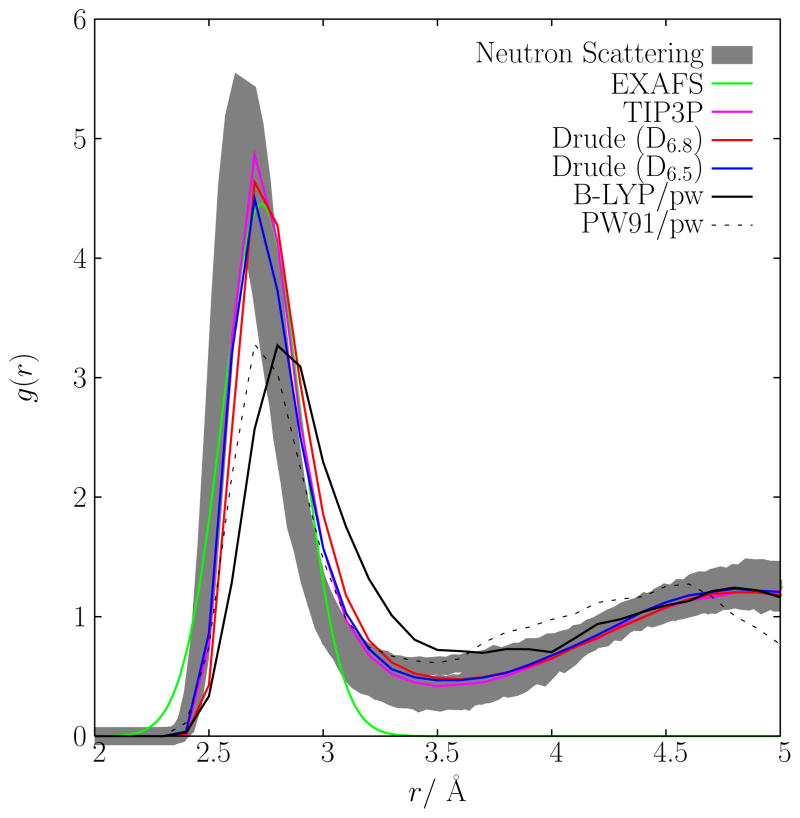
The radial distribution functions, g(r), for the O-K⁺ contact, for each of the computational models studied here, are presented in Fig. 5, along with recently reported experimental radial distributions¹⁴. In order to gauge the spread in the experimental data, they are presented as a set of overlapping distributions, each one deduced from neutron scattering measurements on K⁺ solutions made with different salts (KF, KCl, KBr and KI) and of different concentrations (data for a total of 12 different solutions are shown). The radial distribution of the fixed charge model, based upon TIP3P water, agrees closely with that of the D_6.8 model. Assuming a 3.5 Å cutoff, the coordination numbers are 6.77 and 6.8, for TIP3P and D_6.8, respectively. The D_6.5 model, adjusted to yield a slightly lower coordination number, remains within the range of the experimentally refined distributions. All the radial distribution functions are peaked around 2.7 to 2.8 Å, though the distributions from the two ab initio simulations (BLYP and PW91) are clearly more diffuse and less sharply peaked than those from classical simulations (TIP3P and Drude polarizable models). It is worth noting that the distribution functions extracted from neutron scattering were also obtained from classical simulations, which were constrained to fit the experimental data¹⁴. An estimate of the first peak (represented as a Gaussian) based on an analysis of the anomalous diffraction of K⁺ by X-ray absorption fine structure (EXAFS) spectra is also shown⁷¹.

FIG. 5.

Radial distribution function extracted from the analysis of neutron scattering experimental data¹⁴ and different simulations based on the fixed charge model, two polarizable models, the BLYP/pw and PW91/pw models. The position of the main peak is: neutron data, 2.65; TIP3P, 2.71; D_6.8, 2.71; D_6.5, 2.71; BLYP, 2.83; PW91, 2.73 (in Å). The Gaussian radial distribution function extracted from EXAFS (mean at 2.73 Å and width 0.1712 Å), normalized to a coordination number of 6 is also shown⁷¹.

The hydration numbers for K⁺ in each of the computational models, as well as those deduced from experiments, are presented in Fig. 6. A 3.5 Å radial cutoff, which is near the minimum between the first and second peaks in g(r), is used throughout to define a unique standard for comparing the calculated coordination number of aqueous K⁺ (see earlier discussion). It is found that recently reported hydration numbers deduced from neutron diffraction experiments¹⁴ range from 5.5 ≤ n(r_c = 3.5Å)≤ 6.4. Earlier experiments had estimated this number anywhere from 4 to 8 molecules in the first shell¹⁵. Density functional models estimate the hydration number to be slightly below (PW91) or above 6 (BLYP). Although the computational models studied here all differ in their details, the calculated number of water molecules in the first hydration shell consistently lies within the range of what can within the range of what can currently be be estimated from experiment.

In Fig. 7, the probability distribution, P (N; r_c = 3.5Å), of finding N water molecules that have their oxygen atoms within 3.5 Å from the ion is presented for the different models. In BLYP/pw ab initio simulation, the number of water molecules found with the highest probability within the first hydration shell is 5, while it is 6 for the PW91/pw simulation. For the polarizable model D_6.8, the probability distribution has a maximum at 6, while it is 7 for the fixed charge model. The maximum of 5 for the BLYP/pw simulation is partly due to the use of the r_c = 3.5 Å cutoff. As can be seen from Fig. 5, a r_c = 3.75 Å cutoff would be closer to the minimum and, indeed this larger cutoff was previously determined by Ramaniah et al.⁵³ in their simulation using the same BLYP approximate exchange-correlation functional and semi-core K⁺ pseudopotential that has been employed here. If a cutoff of r_c = 3.75 Å is used, the maximum in P (N) becomes 6 for the BLYP/pw simulation.

FIG. 7.

The probability distributions, P(N; r_c = 3.5 Å), for the hydration number of aqueous K ⁺in the(a) fixed charge, (b) Drude polarizable (D_6.8), (c) BLYP/pw and (d) PW91/pw descriptions of the system.

The fluctuations about the mean hydration number offer a measure of the dynamics within the coordination shell of solvent surrounding K⁺. Remarkably, all of the distributions is Fig. 7 are well described by Gaussian distributions with similar variances. The standard deviation for the fixed charge model is σ_N = 0.86, for the D_6.8 model it is σ_N = 0.86, while for the ab initio models it is σ_N = 0.87 and σ_N = 0.96 for BLYP/pw and PW91/pw, respectively. Thus, while the mean coordination number varies slightly among the different models, coordination states within ±1 about the mean occur approximately 70% of the time in all the models. The significant fluctuations in coordination suggests that the hydration structure around K⁺ is quite dynamic. This is expected, as the density at the minimum between the first and second hydration shell (r = 3.5 Å) is about 50–60% of the bulk solvent density.

A useful way to characterize the hydration structure of an ion is to examine “partial” radial distribution functions. For example, the radial distribution function of whichever oxygen atom is closer to the K⁺ ion than is any of the other oxygen atoms in the system, or whichever oxygen is the second closest, and so on. For each such partial radial distribution function, the radial integral converges to 1 at some finite distance, by construction. In Fig. 8, the partial radial distribution functions for each of the first 8 nearest oxygen atoms are presented. The differences between the various descriptions of aqueous K⁺ that were apparent in the g(r) are also seen in the partial radial distribution functions. The BLYP/pw description tends to have the loosest first solvation shell. This is especially noticeable for the 1st to 4th-nearest contacts, where the O-K⁺ distances are further, on average than for the PW91/pw description. The fixed charge partial radial distributions are closely matched with those of the D_6.8 and D_6.5 polarizable models. The partial radial distribution functions from the BLYP/pw and PW91/pw simulations are similar to one another for the 5 nearest water molecules around K⁺. For the the 6th-, 7th- and 8th-nearest O-K⁺ contacts, the PW91/pw coordination structure is looser compared with that of BLYP/pw—that is, the oxygen atoms of these three partial radial distributions are further from the K⁺ ion in the PW91/pw representation of this system than they are in the BLYP/pw representation.

FIG. 8.

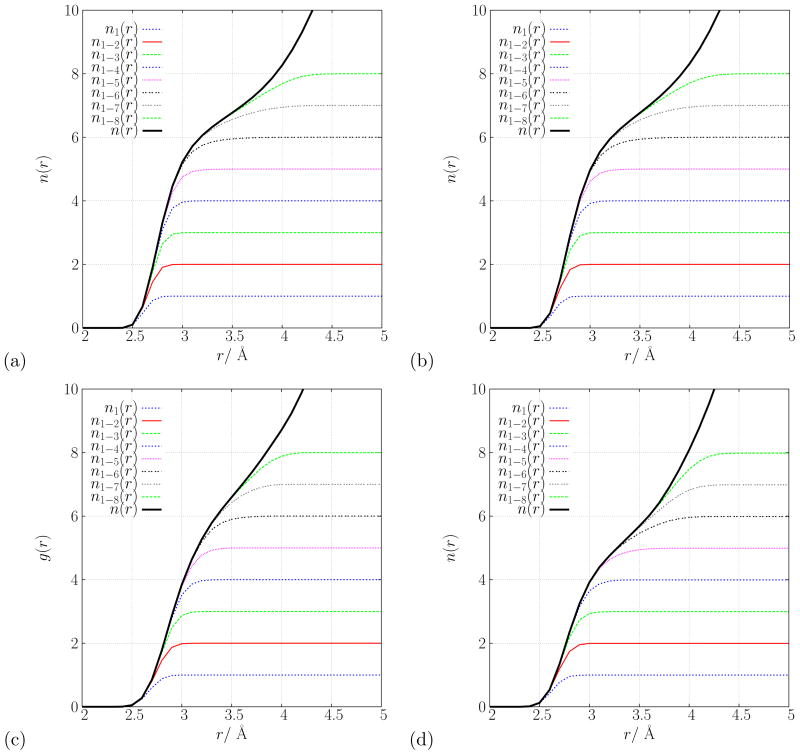
Partial radial distribution functions of the O-K⁺ contact for the fixed charge, Drude (D_6.8) polarizable, BLYP/pw and PW91/pw descriptions of the system. The panels contain partial radial distribution functions for the (1) nearest contact, (2) next nearest, (3) third nearest, (4) fourth, (5) fifth, (6) sixth, (7) seventh and (8) eighth nearest contact.

In addition, Fig. 9 displays the cumulative partial hydration numbers for each of the models studied here. From Fig. 9, it can easily be seen which of the nearby water molecules is contributing significant density to the radial distribution function features within r_c = 3.5 Å. For example, with the fixed charge model, there are essentially 6 oxygen atoms entirely within the 3.5 Å cutoff; the remainder of the n(r_c) = 6.77 coordination number is contributed by both the 7th- and 8th-nearest water molecules. In the PW91/pw simulation, 5 oxygens lie within the 3.5 Å cutoff, while the 6th- and 7th-nearest water molecules also contribute to the density within the first hydration shell.

FIG. 9.

Cumulative partial hydration numbers, n_1−α(r), of aqueous K⁺ in the (a) fixed charge, (b) Drude polarizable (D_6.8), (c) BLYP/pw and (d) PW91/pw descriptions of the system.

D. Self-diffusion of K⁺

The diffusion constant of K⁺ has been computed for the D_6.5 and D_6.8 polarizable Drude models from the mean-square displacement. Because there is only a single ion in the system, relatively long simulations are required to obtain well converged estimates. Accordingly, 5 independent simulations of 1 ns length were averaged together for each polarizable model. The diffusion constant of the D_6.5 model was 1.71 ± 0.2 × 10⁻⁵cm²/s and for the D_6.8 model it was 1.83 ± 0.2 × 10⁻⁵cm²/s. Both of these values are in excellent agreement with the experimental value of 1.96 ×10⁻⁵cm²/s⁶⁵. One may note that, in this particular case, the model with the lower hydration number actually diffuses slightly more slowly (though the difference is very small). However, a systematic analysis of a family of models shows that the diffusion coefficient does tend to decrease when the hydration number increases (by about −0.092 × 10⁻⁵cm²/s), in accord with the expected hydrodynamic trend).

E. Electronic polarization near and far from K⁺

The induction effects of the K⁺ ion on its first hydration shell were compared between the polarizable model and the ab initio models by computing the respective distributions of molecular dipole magnitudes. For models of neutral molecules based on point charges, calculating the molecular dipole amounts to a straightforward sum over molecular charges. The situation is more ambiguous for ab initio simulations of condensed phase systems, where the electronic charge density is continuously distributed. One approach that has been used in the past^66–68,72 is to transform from the Kohn-Sham orbitals to the basis of maximally localized Wannier functions^73–75. In the localized basis, the Wannier function centers (WFCs) allow for an assignment of molecular dipoles. In the present study, analysis of the WFCs allows for comparison between the water dipole distributions in the bulk and in the nearest solvation shell, as well as between computational models for K⁺ hydration.

F. Electronic polarization near and far from K⁺

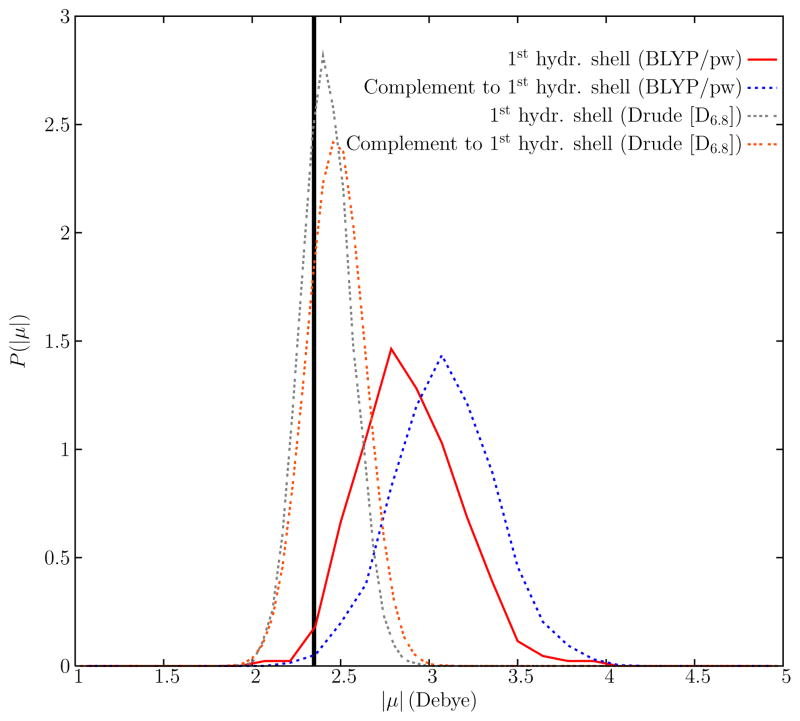
The effects of polarization within the first hydration shell of K⁺ were studied by computing the distribution of molecular dipole magnitudes for water molecules within the first hydration shell and those outside. The molecular dipoles in the CPMD simulation were assigned using the WFCs, and the distributions are shown in Fig. 10. In total, WFCs were computed for 58 different configurations of the equilibrated BLYP/pw system. These configurations were taken from the final 29 ps of the production run, and each was 500 fs apart from the next. The average dipole magnitude for water molecules outside of the first hydration shell is consistent with previously reported pure liquid water values for both the SWM4-NDP²⁴ and BLYP/pw⁶⁷. Of particular interest, there is a small but net downward shift in the average dipole magnitude for water molecules within the first hydration shell for both the BLYP/pw and Drude polarizable models, The shift is 0.2 Debye and 0.05 Debye for the BLYP/pw and the D_6.8 polarizable models, respectively. Relative to the value of the average molecular dipole magnitude in the bulk, δ〈|μ|〉/〈|μ|〉, the shifts are 6.5% in the BLYP/pw simulation, and 2% in the polarizable force field simulation.

FIG. 10.

Probability distributions of molecular dipole magnitudes, P(|μ|), for water molecules in the aqueous K⁺ system. Distributions are shown for water molecules in the first hydration shell, defined by a 3.5 Å O-K⁺ distance, and for water molecules outside of the first hydration shell, for the Drude polarizable and BLPY/pw descriptions, respectively. For reference, the vertical line at |μ| = 2.35 Debye indicates the magnitude of the TIP3P molecular dipole.

The observation that the molecular dipole of water within the first hydration shell of K⁺ has a slightly smaller average value than that in bulk water is rather counterintuitive. A water molecule in the the first hydration shell would be expected to be polarized by the electric field from the ion. This is certainly observed for a K⁺ monohydrate, but the situation is more complex in the bulk phase. But the surprising electrostatic properties revealed by Fig. 10 result from a balance of competing factors. There is a net benefit to align the water molecules and induce dipoles within the first hydration shell. But there is also an unfavorable energy cost arising from the interaction between those dipoles pointing toward a central point. Furthermore, the molecular dipole of water increases from the vapor to the liquid phases due to the hydrogen bonding network structure of liquid water^76–78. As this network is disrupted in the neighborhood of K⁺, the average magnitude of the molecular dipole decreases⁶⁸. Finally, it is worth noting that, because the shift in the 〈|μ|〉 is small, fixed charged models like TIP3P closely approximate the hydration structure of the polarizable models near K⁺. This may partly explain the surprising ability of nonpolarizable models to represent bulk hydration of ions.

G. On differences and similarities

The present study shows that our present knowledge of K⁺ hydration is satisfactory, with different models being in broad agreement with the available experimental data. The interaction energy of the monohydrate is about −18 kcal/mol, near the experimental gas phase estimate. The hydration structure in the bulk is consistent with a coordination number on the order of 6–7 and with a first peak around 2.7 Å, as indicated by the analysis of neutron scattering from solutions. The total solvation free energy is about −80 kcal/mol, consistent with a variety of thermodynamic estimates from experiments^{12,16,17,41,42} or computations^4–9. In comparison, the AMOEBA model of Grossfield and Ponder yield a real hydration free energy for K⁺ that is roughly 4–5 kcal/mol larger than the present estimate, and a coordination number of 7.0⁴. Such differences appear to be within acceptable bounds.

Nevertheless, at a finer level, there remains some discrepancies that should be better understood to further refine our models of ion hydration. For example, there are notable differences between the position and the shape of the main peak extracted from the neutron scattering data and the results from the two ab initio simulations (Fig. 5). The average radial distribution function extracted from neutron scattering for 12 solutions is sharply peaked at 2.65 Å, whereas the peak from the two ab initio simulations are more diffuse. In the case of the simulation based on BLYP, the peak is also slightly shifted toward larger distances. What is puzzling is the fact that the two classical models (including the nonpolarizable force field) are in closer agreement with the results from neutron scattering experiments than the two ab initio simulations. Normally, the average cooordination structure from ab initio is quite reliable. However, it is important to keep in mind that the radial distribution functions are extracted from the neutron scattering data using a refinement procedure, which relies on a set of simulations biased to fit the experiments¹⁴. Those simulations are not not exempt from assumptions. For example, the K⁺-oxygen minimum distance is set to 2.6 Å (Alan Soper, personal communication), based on an earlier estimate from Herdman and Neilson⁶⁹. Furthermore, the ion-water repulsion is modeled after a Lennard-Jones potential, which is normally steeper than the core repulsion calculated from ab initio. In spite of these caveats, the g(r) extracted from the neutron scattering data shown in Fig. 5 is in reasonable accord with a variety of experimental x-ray and neutron scattering data indicating that the peak in the K⁺-oxygen distribution function should be somewhere between 2.60 and 2.80 Å (though some older estimates were as high as 2.92 Å) ⁷⁰. Furthermore, the coordination number extracted from the neutron scattering data via the refinement procedure, ranging from 5.5 to 6.4, appears to be nearly reproduced by all the models (Fig. 6). In excellent accord with the current results, a recent estimate based on an analysis of the anomalous diffraction of K⁺ by X-ray absorption fine structure (EXAFS) spectra estimates the average distance between the K⁺ and the water oxygen in the first shell at 2.730±0.05 Å, and the coordination number at 6 ± 1⁷¹.

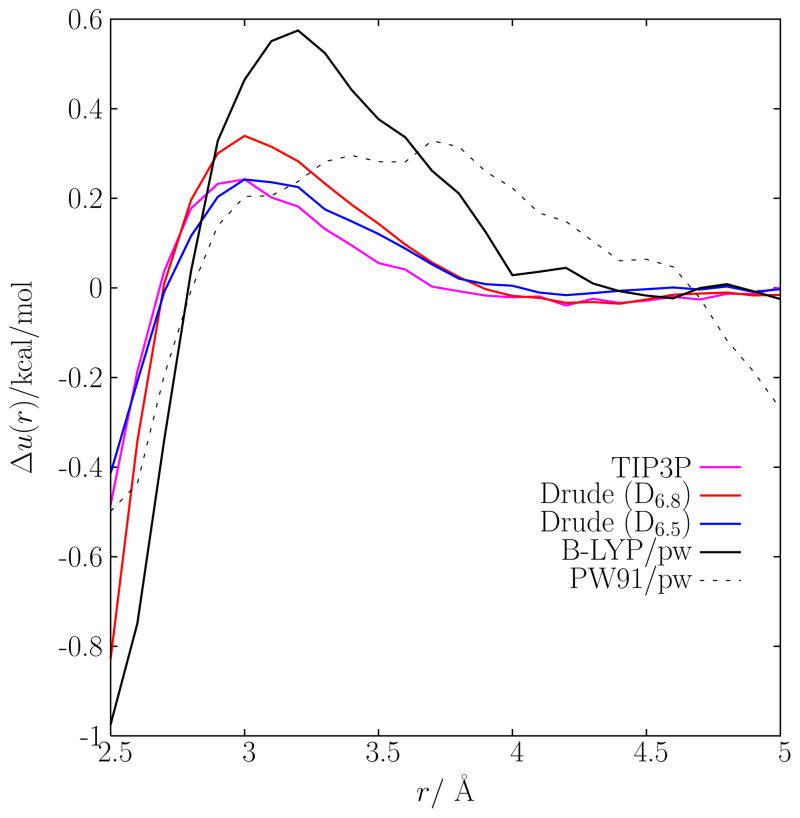
While an assessment of the sensitivity of the results extracted from neutron scattering data to all input assumptions would be required to ascertain the accuracy of the different computational models, an important question remains whether the observed differences in the radial distribution functions signal some fundamental underlying problems in our understanding of K⁺ hydration. At the simplest level, differences in the radial distribution of K⁺-water oxygen observed in Fig. 5 could be caused simply by differences in the direct ion-water interaction. Such small differences, on the order of ~ 0.5 kcal/mol, can already be noted in Table I. In fact, nearly all the ab initio calculations yield a K⁺-water binding energy that is slightly weaker than the experimental estimate (the exception being the HF/6-31G* calculation). By a low order perturbative treatment, one can express the small differences observed between the various radial distribution functions from the various models in terms of a putative difference in the direct ion-water interaction. Taking the average radial distribution function extracted from the neutron scattering data as a reference g_ref(r), we define the potential u_i(r),

$$\mathrm{\Delta }{u}_i(r)=-k_{\text{B}}Tln\left[\frac{g_{\text{ref}}(r)}{g_i(r)}\right]$$ (4)

To lowest order, Δu_i(r) is the potential that needs to be added to the ion-water interaction of a model i in order to recover g_ref(r). Of course, such analysis is valid only if the perturbation is small. At higher order, the ability of a liquid to coordinate an ion is also related to the amount of cohesion that exists in the pure liquid, e.g., hydration of an ion would be reduced in a water model that attributes more internal cohesion to the liquid, and it should be increased in a model that attributes less cohesion to the liquid. Nonetheless, an analysis based on Eq. (4) is informative. The results for Δu_i(r) are plotted in Fig. 11. According to this perturbative analysis, it appears that all the models (except the ab initio simulations from BLYP), would require a fairly small perturbation in the ion-water interaction to yield g_ref (r). At near-contact (r ≈ 2.6–2.7 Å), the perturbation amount to a fraction of kcal/mol, which is consistent with the magnitude of the variations observed in the binding energy of the monohydrates given in Table I. From this perspective, it is possible that the differences observed between the various models might reflect the relatively small differences in the direct ion-water interaction.

FIG. 11.

Perturbative analysis of the K⁺-water oxygen interaction using the average radial distribution function extracted from the neutron scattering data as a reference.

IV. CONCLUSION

A hierarchy of computational models have been used to study the properties of aqueous K⁺, including two ab initio models, a fixed charge model and a polarizable model based on classical Drude oscillators. The O-K⁺ radial distribution functions of the models have been compared with those derived from neutron scattering experiments¹⁴. Among the different computational representations of the system, the polarizable model and fixed charge model appear to agree more closely with the shape of the radial distribution functions deduced from experiments. All the computational models yield hydration number between 5.86 (PW91/pw) and 6.8 (D_6.8), in good accord with the experimental estimates (Fig. 6), and yield a reasonable monohydrate binding energy as well as hydration free energy.

A somewhat counterintuitive observation made on the basis of the D_6.8 and CPMD simulations concerns the induced dipolar of water molecules nearest to the K⁺. The electronic polarization effects of the K⁺ ion on the water molecules in the first hydration shell have been examined using a BLYP/pw ab initio simulation and a polarizable force field simulation of aqueous K⁺. In both cases, a slight shift to lower average dipole magnitudes for molecules in the first hydration shell, compared to the bulk liquid, has been observed. This observation contradicts the intuitive notion that water molecules in direct contact with a cation must be over-polarized compared to bulk value. In fact, it appears that in the case of K⁺ they are, if anything, slightly less polarized than the water molecules in the bulk. This is, perhaps, one reason for the relative success of simple fixed charged models^6–9. It may be that K⁺ has a size that renders it similar to water in its “polarizing strength”, suggesting that only smaller ions require a treatment of induced polarization. In view of this result, one might be tempted to suggest that a polarizable force field is not really needed for K⁺. In the context of a homogeneous bulk liquid phase, this is partly true. However, one must be careful in over-extending this conclusion to inhomogeneous environments such as interfaces, or the interior of narrow pores. In those systems, the limitations of nonpolarizable force fields in the case of K⁺ have been clearly documented⁷⁹.

Although a fairly consistent perspective of K⁺ hydration emerges from the current study, resolving a number of issues could further our ability in modeling ion hydration accurately. In particular, a sensitivity analysis of the hydration structure properties extracted from scattering experimental data would be very useful. Contrasting the results from different computational models also helps delineate the limits of present knowledge about K⁺ hydration. Simulations based on quantum mechanical ab initio methods can account for a wide range of complex electronic effects. But the complete information about the thermodynamic properties in the bulk phase of those ab initio models is not easily accessible to ascertain the implications of the results. The properties in the bulk phase can be fully explored for computationally simpler models based on a potential function, such as the polarizable force field based on Drude oscillator. But such models use parameterized mathematical functional forms to represent complex microscopic interactions. While those parameters can be freely adjusted to reproduce various properties for any cation, the structure of the potential function places internal constraints on the range of possible models that can be constructed. This is illustrated in Figs. 1–3. In the present study, the coordination numbers of K⁺ and Na⁺ are strongly correletated with the monohydrate binding energies, and thus with the bulk hydration free energies. This was illustrated here by considering two different polarizable models for K⁺. One model, referred to as D_6.8, was fitted to agree with the K⁺ monohydrate properties. The other model, referred to as D_6.5, was adjusted to interact less strongly with water, in order to yield a lower hydration number in closer accord with the ab initio simulations. However, the hydration free energy of the D_6.5 model of K⁺ is decreased, and it is not possible to parameterize a model of Na⁺ with a relative hydration free energy that is consistent with the experiment^12,41,42. Thus, in the context of the po-larizable potential function based on classical Drude oscillators, the relative hydration free energy of K⁺ and Na⁺ (or any other ion) limits the range of accessible coordination numbers. Such internal constraints deduced from simulations based on a given functional form of force field are model-specific. Nonethelesss, qualitatively similar observations are made from the AMOEBA model of K⁺, where a slightly larger coordination number is correlated with a slightly larger hydration free energy⁴. This suggests that such internal constraints qualitatively reflect inherent trends (e.g., one cannot arbitrarily shift the first peak in g(r) to larger distances and expect to lower the hydration number while reproducing the monohydrate properties and achieving a reasonable hydration free energy), though particular results could change quantitatively if a different functional form was used. Thus, development of a microscopic perspective on K⁺ hydration, integrating all the available information provided by experiments and computational models, remains partly subjective at this point.

Appendix: Analysis of statistical error and finite size effects

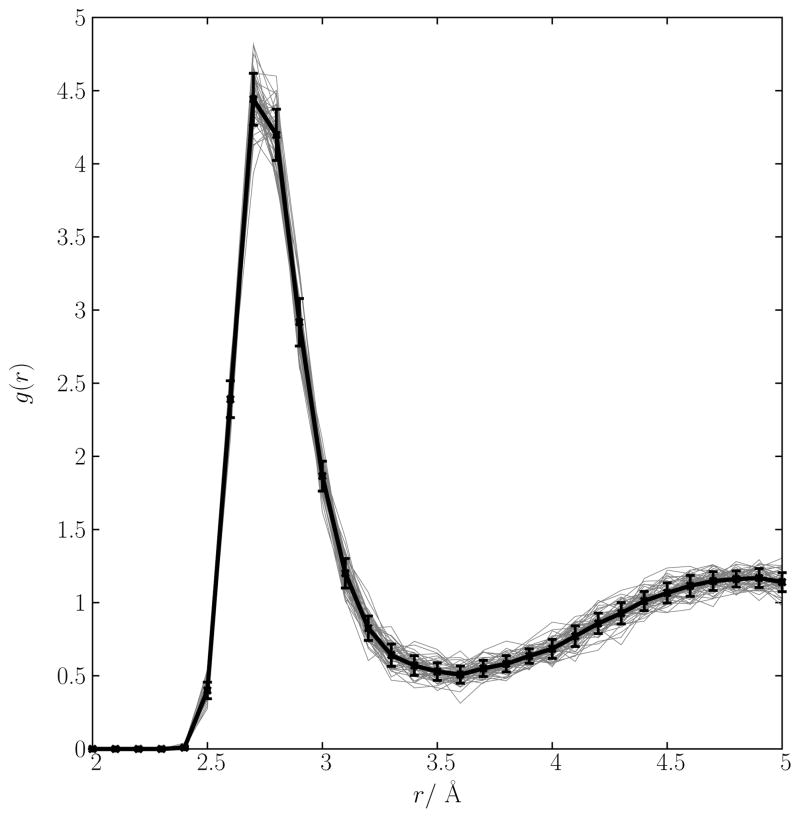
The statistical error in the radial distribution functions calculated from the BLYP/pw simulation was determined by dividing the 50 ps trajectory into 16 2 ps parts and calculating the error in the mean of each histogram window, r, to generate $\mathrm{\Delta }(r)=\sigma (r)/\sqrt{25}$, the r-dependent error in g(r). This estimate compares well with a more accurate one obtained by performing 50 simulations of length 40 ps (the same length as the BOMD simulation) using the Drude force field and computing Δ(r) = Σ_kσ^(κ)(r)/50. In Fig. 12, the radial distribution function computed from each of the 50 independent 40 ps simulations is plotted along with the average g(r). The spread in the distributions in Fig. 12 gives an excellent estimate of the statistical uncertainty from a short simulation (also shown are the error bars resulting from the above analysis of the Drude model trajectories).

FIG. 12.

Statistical spread in g(r) of the O-K⁺ contact taken from 40 ps of molecular dynamics. The Drude polarizable model was used simulate the system. The black line is the average g(r).

In order to assess the significance of finite size effects in the relatively small system containing 64 water molecules, the radial distribution function for the O-K+ contact is compared, in Fig. 13, with that generated from a much larger system containing 500 water molecules. In both cases, it is a polarizable model system that is being simulated. It is evident that finite size effects are not significant for this property of aqueous K⁺.

FIG. 13.

Radial distribution function of the O-K⁺ contact taken from two different system sizes: a smaller system with 64 water molecules and a larger system containing 500 water molecules. Both system sizes were modeled using the Drude D_6.8 polarizable force field.