Biomimetic ratcheting motion of a soft, slender, sessile gel

Abstract

Inspired by the locomotion of terrestrial limbless animals, we study the motion of a lubricated rod of a hydrogel on a soft substrate. We show that it is possible to mimic observed biological gaits by vibrating the substrate and by using a variety of mechanisms to break longitudinal and lateral symmetry. Our simple theory and experiments provide a unified view of the creeping, undulating, and inchworming gaits observed in limbless locomotion on land, all of which originate as symmetry-breaking bifurcations of a simple base state associated with periodic longitudinal oscillations of a slender gel. These ideas are therefore also applicable to technological situations that involve moving small, soft solids on substrates.

The creeping, crawling, and slithering gaits of worms, snails, and snakes show how organisms are able to adapt to and exploit certain environmental and ecological niches. Because these gaits involve the continuous interaction of long flexible bodies with a solid substrate, they are qualitatively different from the more commonly studied modes of animal locomotion such as walking, swimming, and flying (1). In these gaits, periodic pulses of muscular deformation are rectified by one or more symmetry-breaking mechanisms, just as in a mechanical ratchet. Worms use a combination of unidirectional waves and the inequality of static and dynamic friction (1–3); snails glide on a secreted bed of mucus that undergoes a yield–heal cycle in response to periodic unidirectional pulses producing a material ratchet (1, 4); snakes use bending waves and the asymmetric friction associated with their scales to undulate or sidewind (1, 5), whereas inchworms move in and out of the plane (1). Robotic engineers have mimicked these gaits (5) by building arrays of simple motor elements wired together by a complex actuator/controller. An alternative scheme closer to biology is to use a simple periodic pattern generator and let the gait be determined by the internal and external dynamics of the system. For example, externally or internally induced periodic deformation waves lead to the generation of periodic pulses in a soft, slender gel rod on a substrate. Motion results when this elastic deformation is rectified by using the asymmetry in (i) the shape of the pulses, (ii) the material properties of the interface, or (iii) the body shape. As an example, consider a snail that glides on a thin layer of mucus by generating direct or retrograde muscular waves of contraction. In the neighborhood of the contractile pulse, a large shear stress is generated in the thin mucus layer, so that it yields and flows (4). As the pulse propagates from one end of the snail to another, a localized region of slip moves and leads to motion. In such a situation, the snail moves by pulling/pushing on those parts of the mucus that are not flowing. Here, the asymmetry arises from two causes: the unidirectional propagation of contractile pulses and the material behavior that switches between flow and no-flow. However, either one of these mechanisms should be sufficient.

Snail-Like Motion: Theory and Scaling

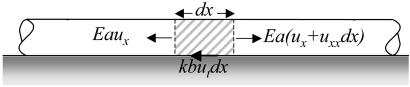
Motivated by the above, we consider the mechanics of a long cylindrical filament (length, l, and area of cross-section, a) on a substrate, with a thin film of intercalating liquid at the interface. When the deformations in the filament can be characterized by a purely axial displacement field, u(x, t), the local strain is ∂u/∂x ≡ u_x, and the local velocity is ∂u/∂t ≡ u_t. For small displacements, the behavior of the filament can be well approximated by a linear Hookean constitutive law so that the stress σ = Eu_x, where E is Young's modulus of the gel. The interaction of the gel with the substrate is modeled by means of a simple dynamic friction law so that the resisting force per unit area is ku_t, where k is the coefficient of kinetic friction (for a liquid layer of thickness, h, and k ≈ μ/h, where μ is the shear viscosity and h is the nominal thickness of the liquid film). In the absence of inertia and any other body forces (due to muscular movement, etc.), balancing the elastic force in an infinitesimal axial segment of the gel with the frictional force (see Fig. 1) leads to the following equation of motion:

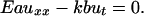[1]

Here b is the nominal width of the contact zone between the cylindrical gel and the substrate. If a localized pulse is suddenly applied to a part of the filament far from the boundary, the diffusion equation (Eq. 1) shows that, after a short time, t, the effects of the contraction are felt locally over a distance (Eat/kb)^1/2. If the pulse moves with a constant velocity, V, in the positive x direction, solving Eq. 1 for the displacement field in the comoving frame yields

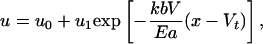[2]

where u₀ and u₁ are constants of integration. The effects of the pulse therefore remain localized over a characteristic healing length, l_c ≈ Ea/kbV (defined as the axial range of the influence of the pulse). If the spatial periodicity of the pulses is larger than l_c, they do not interact and their combined effect is simply additive. In this scenario, if each contractile pulse generates a strain ε localized over a width w « l_c, ṅ is the number of pulses generated per unit time, and α ∈ [0,1] is the rectification efficiency, the typical velocity of the filament is

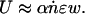[3]

If the rate of pulse generation is on the order of ṅ_m ≈ V/l_c, the scenario can become more complicated than the cases that we will consider here.

Fig. 1.

A schematic illustration of the elastic and frictional forces on an infinitesimal axial segment of the gel dx that leads to the equation of motion (Eq. 1). The axial displacement of the filament at location, x, at an instant of time, t, is denoted u(x,t). The filament has an area of cross section, a, and is made of an elastic material with a Young's modulus, E. The area of contact with the substrate is b, and the coefficient of dynamic friction is k. In this article, a_b ≡ ∂a/∂b.

Experiment

To test these ideas experimentally, we prepared an “artificial snail,” which is nothing more than a long cylindrical hydrogel rod with a radius of 2 mm and a length of 2 cm lying on a thin film of silicon rubber bonded to a glass plate. The hydrogel is prepared by crosslinking acrylamide in water with a typical liquid-volume fraction of 80%. This preparation leads naturally to the presence of an intercalating liquid layer that separates the hydrogel from the elastic substrate, otherwise the soft gel will adhere strongly to the substrate.

To mimic the muscular contractions of a real snail in our artificial gel-snail, we induce periodic vibrations of the soft filament by using an external source; the glass plate itself is clamped to a vibrating table driven by a pattern generator. When the hydrogel rod is aligned with the direction of vibration and the table is subject to asymmetric vibrations, the gel rod glides on the thin water film, consistent with a simple ratchet driven by an asymmetric waveform (the various gaits together with detailed descriptions can be seen in Movies 1–6, which are published as supporting information on the PNAS web site).

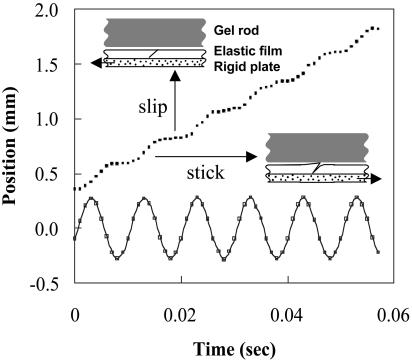
However, it is also possible to use externally generated periodic pulses that may be rectified by an asymmetric interfacial interaction between the filament and the substrate; these mimic the yield–heal cycle in the real snail. To bring this about, we introduce a series of straight incisions (scales) in the thin film of rubber. Like scales, the incisions are tilted with respect to the axis of the gel rod. This geometric asymmetry causes the incisions to open only when the fluid in the contact region is sheared in one direction, leading to an asymmetric coefficient of kinetic friction that arises from the biased hydrodynamic lubrication forces in a wedge-like geometry (L.M., S.D., and M.K.C., unpublished work). Thus, when the substrate is subject to a periodic excitation, the scales dynamically rectify the motion. In Fig. 2a, we show a sequence of images of two “snails,” each sitting on a single slanted incision with opposite orientation subject to vibration; they move toward each other slowly. In Fig. 2b, we show that if the number of scales is increased, the filament speeds up. In Fig. 3, we show the kinetics of motion; during half the cycle of vibration, the scale is closed so that the gel slips relative to the substrate, whereas during the other half, the scale opens in response to the hydrodynamic forces, and the gel is dragged along with the substrate. Based on the elastic modulus of the gel (E ≈ 40 kPa), its cross-sectional area (a ≈ 10^–5 m²), interfacial friction (kb ≈ 5 Pa/s), and a typical velocity (U ≈ 1 cm/s), we find that the healing length l_c ≈ 10 m, i.e., the entire gel slips on the surface as a single entity. In such a situation, the velocity of the gel

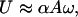[4]

where A is the amplitude, and ω is the frequency of the vibration. The formula (Eq. 4) is simple and intuitive, and all the complexity involved with the elastohydrodynamics is buried in the prefactor α, which characterizes the efficiency of rectification. This factor depends on a number of parameters, including the amount of liquid in the contact zone and its viscosity, the elastic properties of the gel and of the substrate, and the number of incisions and the angle they make with the free surface of the substrate. When the healing length is longer than the system size, α ≈ 1. If the stiff gel is replaced by a very soft one (E ≈ 1 kPa) obtained by weak crosslinking and the intercalating water is replaced by the much more viscous glycerine with a much higher interfacial friction (kb ≈ 1500 Pa.s), for a typical velocity (U ≈ 0.5 cm/s), we find that the healing length l_c ≈ 1 mm, i.e., multiple pulses occur along the gel (see Movies 1–6). In such a situation, although Eq. 4 is still qualitatively valid, the ratcheting efficiency is α ≈ 0.05 « 1.

Fig. 2.

Snapshots of a polyacrylamide hydrogel rod (≈2-mm radius and ≈2-cm length) on a thin elastomeric film of polydimethylsiloxane, which is subject to harmonic longitudinal vibrations (frequency, 100 Hz; amplitude, 0.27 mm). (a) Two “scales” or incisions are scored on the elastic layer, with opposite orientations making an angle of 60° with the vertical, which serve to rectify the motion of the gel as it is preferentially lubricated only in one direction. Thus, the two gel rods move toward each other even though the applied wave form is symmetric. (b) As the number of scales is increased, the velocity of the gel increases.

Fig. 3.

The kinetics of motion as resolved by using videoscopy. In response to a symmetric waveform (shown as a solid line), the gel moves by a stick–slip mechanism. Movement arises because of a dynamical asymmetry induced by fluid flow; the gel slips on the substrate during half the cycle and is dragged along during the other half because of the asymmetric opening of the slanted incisions. When almost perfect stick–slip exists, as here, the rectification efficiency is α ≈ 1. With partially dried hydrogels, α < 1.

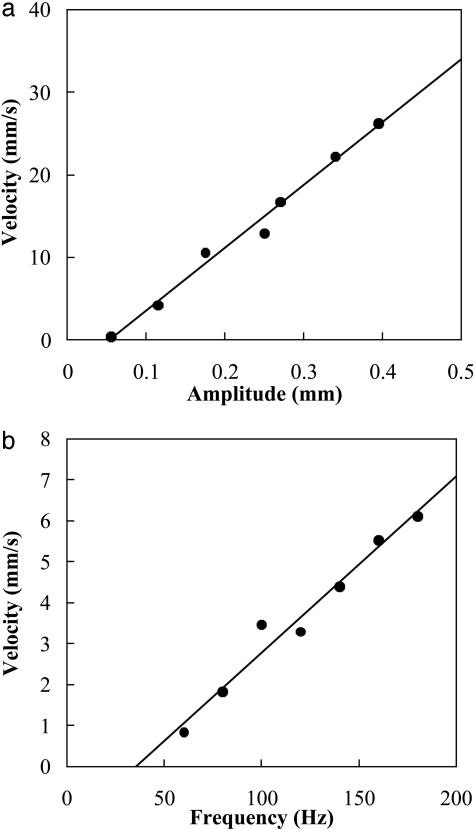
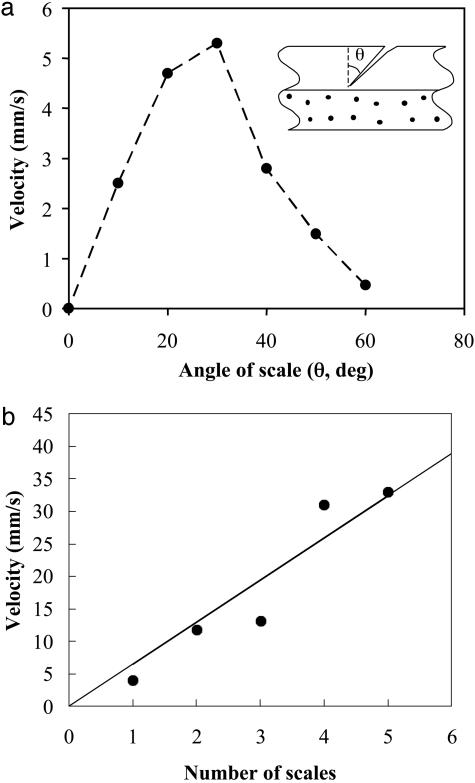
Here, we limit ourselves to exploring the dependence of the gel velocity on the kinematic parameters in the problem that have biological analogs and are common to all of the rectification mechanisms. In Fig. 4a we show that velocity of the gel depends linearly on the amplitude of vibration, whereas Fig. 4b shows that velocity is linearly proportional to the frequency of vibration, consistent with Eq. 3; in both these situations, the number of scales is relatively small, so that they act independently. In Fig. 5a, we show the dependence of the velocity of the gel on the angle θ, which the scales make with the vertical. As the angle is increased from zero, the velocity first increases with θ but then decreases for large values of θ. This behavior has its origins in the geometry of the scales; for small angles, symmetry dictates that the velocity must increase linearly with θ, whereas for large angles, as the scales become more and more horizontal, the incision opening decreases, so that the velocity must decrease. Thus, an optimal scale angle exists that maximizes the velocity, as seen in Fig. 5a. Finally, we consider the effect of increasing the number of incisions. Because the healing length is much larger than the system size, the scales act independently, and the gel velocity will be proportional to the number of incisions. In Fig. 5b, we show our experimental results indicating that the velocity scales linearly with the number of incisions.

Fig. 4.

The dependence of the velocity on the driving parameters. (a) At constant frequency, the gel velocity is linearly proportional to the amplitude of vibrations. (b) At constant amplitude, the velocity is proportional to the frequency of vibrations.

Fig. 5.

The dependence of the velocity of the filament on the geometry and number of incisions. (a) The velocity of the scales first increases with the angle made by the incisions with the vertical and then decreases as the incisions become more and more horizontal, so that they do not open as much. (b) The velocity of the gel increases linearly with the number of incisions that are equally spaced and oriented at 30° to the vertical (the gel length is 2 cm).

Gait Transitions: Snake and Inchworm-Like Gaits

The snail-like gait is only one of the gaits observed in slender, land-based, limbless organisms. Two other relatively common modes of slender organisms moving on substrates are the snake-like undulatory gait and the inchworm-like gait. In the serpentine gait, the body bends laterally and moves tangential to itself everywhere, deriving its traction by pushing in a direction transversely by relying on the effects of anisotropic friction that favor forward tangential motion over lateral and backward tangential motions. In the inchworm gait, the body bends out of the plane of the substrate, lifting itself partially and using the fore–aft friction/adhesion asymmetry to propel itself.

From a kinematic viewpoint, the snail gait involves purely axial deformations, whereas the snake and inchworm gaits involve bending deformations. A natural transition between the snail gait and the snake/inchworm gait arises if the compressive stresses generated by the muscular contraction exceed the buckling threshold for the filament. Assuming that the typical pulsatile contraction has a length, w, the buckling stress for one such segment scales as Ea/w². Thus, if the muscular strain ε ≥ a/w², the filament will buckle locally. If the buckled filament bends only laterally, remaining in continuous contact with the substrate, the filament slithers. In the presence of anisotropic frictional interactions as described above, the slithering will lead to serpentine undulation. On the other hand, if the filament buckles out of the plane, forming one or more loops, it starts to inchworm in the presence of any differential friction between the anterior and posterior ends. Whether or not the snake or the inchworm gait is chosen depends on a number of factors, such as the geometry of the cross-section (which might favor one mode over the other), the weight per unit length of the body (which might again favor one mode over another), and the details of the frictional inhomogeneity and anisotropy. Postponing the quantitative analysis of these transitions, we consider a simple experimental realization of the gaits themselves by using a slight variant of the hydrogel/elastomer system discussed earlier.

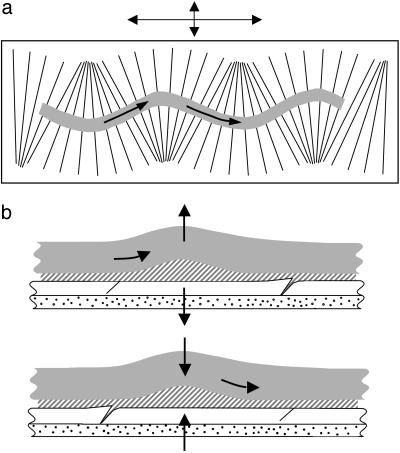
If the incisions or scales are at a periodically varying lateral angle to the gel (Fig. 6a), a combination of longitudinal and small lateral vibrations of the plate lead to a sinuous snake-like gait that arises from the effects of spatially varying anisotropic kinetic friction (Movies 1–6). Similarly, if the plate is subject to purely transverse vibrations, we see an inchworm-like gait as the gel buckles out of the plane periodically (Fig. 6b).

Fig. 6.

The axial snail-like motion loses stability to snake-like and inchworm-like motions when the geometry of the scales and/or vibration is varied. (a) In-plane bending deformations arise when the scales are inclined at a varying angle to the axis of the filament. These deformations lead to an anisotropic friction; thus, sideways oscillations cause the filament to bend and slither along (see Movies 1–6). (b) Out-of plane bending deformations arise when the filament is subjected to small-amplitude vertical oscillations. These deformations cause the filament to buckle out of the plane and then slip in one direction due to the presence of the scales, as shown.

Conclusions

By considering the dynamical interaction of a soft, slender filament with a substrate, we have shown that it is possible to mimic a number of different modes of motion seen in biological locomotion at interfaces such as creeping, crawling, inching, reptating, and slithering. At a purely physical level, this leads to a unified view wherein these modes arise naturally as symmetry-breaking bifurcation transitions of slender bodies when the muscular forces exceed the buckling load. By using a soft, sessile gel filament on an elastic substrate as a model system, we have shown that these gaits can all be easily realized experimentally by using an external source of vibration coupled to the asymmetric interfacial interaction between the gel and the substrate. An important aspect of these biomimetic gaits is that the motion of the gel is not prescribed a priori; instead, it arises from the interaction between the body and the environment once a periodic forcing is applied and is thus similar to biological reality.

However, in contrast to biological locomotion, in our model system, the engine is not onboard because we drive the gel externally. Furthermore, the interaction is not active in that no feedback loop exists that allows the engine, i.e., the external vibration, to respond to the deformations of the gel. This feedback is crucial in the animal world, because the organism can respond to external stimuli by changing its gait. Thus, from both a biological and physical perspective, many questions remain for further study. These questions include a quantitative study of the gait transitions, the optimal gaits associated with each mode, and the exploration of additional gaits such as side-winding, slide-pushing, and concertina motion (1). On the technological side, the externally applied vibration that we have focused on is but one way to generate periodic pulses; artificially actuated gels that respond to various stimuli such as electromagnetic fields, temperature, and chemical oscillations point toward applications to situations requiring the autonomous motion of soft solids on surfaces.