Abstract
Traditional deformable image registration imposes a uniform smoothness constraint on the deformation field. This is not appropriate when registering images visualizing organs that slide relative to each other, and therefore leads to registration inaccuracies. In this paper, we present a deformation field regularization term that is based on anisotropic diffusion and accommodates the deformation field discontinuities that are expected when considering sliding motion. The registration algorithm was assessed first using artificial images of geometric objects. In a second validation, monomodal chest images depicting both respiratory and cardiac motion were generated using an anatomically-realistic software phantom and then registered. Registration accuracy was assessed based on the distances between corresponding segmented organ surfaces. Compared to an established diffusive regularization approach, the anisotropic diffusive regularization gave deformation fields that represented more plausible image correspondences, while giving rise to similar transformed moving images and comparable registration accuracy.
Index Terms: Deformable image registration, regularization, sliding organs, medical imaging
1. Introduction
Registration problems involving sliding organs are ubiquitous in medical imaging applications, such as image-guided surgery, image-guided radiation therapy, atlas-based image segmentation, and longitudinal analysis involving multiple organs. Common examples of organ slides in these applications includes the brain sliding against the skull due to intraoperative brain shift, the heart sliding against the lungs throughout the cardiac cycle, and respiration-induced sliding of the lungs against the chest wall or the abdominal organs against each other. In these and other examples, mis-registrations will impact clinical decisions and patient outcomes, causing surgical tools to be ineffectively guided or incorrectly positioned, or correspondences needed to quantify change to be incorrectly estimated. Furthermore, other applications rely on the accurate estimation of deformation fields, such as when estimating brain morphology changes due to aging or disease progression. Inappropriate deformation fields can reduce the sensitivity and specificity of such studies. In this paper, we present and evaluate a novel method for deformable image registration in which the images contain multiple organs that may have slid with respect to each other, inducing discontinuities in the inter-image deformation field.
Deformable image registration generates a deformation field u that transforms a moving image (IM) to better match a fixed image (IF), i.e. if Tu is the transformation associated with u, then IF ≈ Tu (IM) [1]. This is often performed by iteratively optimizing a cost function C(u) of the current estimation of u, which typically incorporates an intensity-based distance measure D (IF, Tu(IM)) that captures the intensity differences between the fixed image and the transformed moving image. However, for general deformation registration methods, where dense displacement fields or time-dependent vector fields are estimated, finding the transformation based on a similarity-measure only is ill-posed. Therefore regularization of the displacement field (or velocity fields) is necessary [2]. A regularization term S(u) is introduced into the cost function to penalize unrealistic deformation fields, such that:
| (1) |
Typical regularizations enforce a smoothly-varying deformation field. For example, one may penalize gradients in any of the three components of the deformation field u (the “diffusive regularization”) [3].
However, enforcing a smooth deformation field is not appropriate when registering images of sliding organs, since discontinuities in the deformation field are expected. If a smooth motion field is enforced and one object remains stationary while another slides along it, the moving object's deformation vectors will be incorrectly applied to the stationary organ, making it appear to move. Similarly, if a smooth motion field is enforced when two structures slide against each other in opposite directions, the opposing vectors near the boundary will be averaged and the motion at the interface will not be recovered.
Non-parametric image registration algorithms that accomodate deformation field discontinuities include that of Risholm et al. [4], who developed models of resection and retraction to register pre- and intra-operative brain MRI images. Schmidt-Richberg et al. [5] registered end-inspiration and end-expiration lung CT images by using organ segmentations to ensure that the component of the deformation field tangential to the organ boundary was smoothed only within individual organs and not across organ boundaries. Yin et al. [6] focused on registration accuracy near lung lobe fissures, where deformation field discontinuities are allowed in any direction. They added an additional weighting term to the diffusive regularization that increases with distance to the organ boundary, so that discontinuities near the organ boundary are not penalized.
In this paper, we present a regularization approach based on anisotropic diffusion that enables more accurate registration of images of sliding organs. Our regularization formulation was validated in the context of monomodal image registration using (1) artificial images of simple objects and (2) images derived from an anatomically-realistic software phantom. Both of these assessments demonstrated the advantages of the regularization presented here compared to the diffusive regularization.
2. Sliding Organ Registration Algorithm
2.1. Overview
The sliding organ registration algorithm presented here proposes a deformation field regularization that is appropriate for sliding organs. The regularization is based on decomposing the deformation field u into normal and tangential components, which are defined with respect to a given organ boundary along which sliding motion is expected to occur (Figure 1a). These two components are handled differently to enforce a realistic deformation field that considers physiological sliding motion:
Fig. 1.

Schematic illustrating the underlying concepts of the anisotropic diffusive regularization.
Motion normal to the organ boundary should be smooth both across organ boundaries and deep within organs. The motion normal to the organ boundary must be smooth in both the normal and tangential directions. The former condition enforces coupling between neighboring organs under the assumption that objects do not pull apart (an appropriate assumption within images of the human body) (Figure 1b, panel (i)). The later forces smooth motion of individual organs (Figure 1b, panel (ii)).
Motion tangential to the organ boundary should be smooth in the tangential direction within each individual organ, avoiding sharp discontinuities in its motion (Figure 1b, panel (iii)). However, smoothness is not required across organ boundaries (Figure 1b, panel (iv)). Thus, the sliding transformations to be captured are not penalized.
Throughout the remainder of this paper, we use the sum of squared intensity difference for the intensity-based distance measure D (IF, Tu(IM)), which is appropriate since we are focusing on monomodal image registration.
2.2. Anisotropic diffusive regularization for sliding organ registration
The diffusive regularization is a good example of typical regularizers that penalize any sharp discontinuities in the deformation field and are therefore inappropriate when considering sliding organs. It is equivalent to smoothing the deformation field with a Gaussian kernel and is defined as follows:
| (2) |
Ω is the domain of the deformation field and ▽ul(x) is the gradient of the l-th component of u at position x = (x, y, z), determined by extracting the l-th component of u and calculating the gradient around x.
Our proposed alternative is to formalize the conditions described in Section 2.1 by applying separate nonlinear anisotropic smoothing filters to the normal and tangential components of the deformation field u. Anisotropic diffusion models the diffusion of particles against a concentration gradient when diffusion in particular directions is favoured [7]. The diffusion equations are:
| (3) |
| (4) |
| (5) |
where ▽u(x) is the gradient of the concentration u at the position x, j(x) is the flux that counteracts the concentration gradient, D is the diffusion tensor that steers the diffusion process, and div represents the divergence operator. The eigenvectors and eigenvalues of the diffusion tensor D dictate the magnitude and directionality of the diffusion.
In image processing, concentrations are modeled by voxel intensity, concentration gradients are caused by intensity discontinuities (i.e. edges), and diffusion results in local image smoothing. A common application of anisotropic diffusion is anisotropic filtering, in which D ≠ I and images can be smoothed only in certain directions in order to smooth while maintaining edges. When D = I, traditional Gaussian smoothing results. The approach presented in this paper can be thought of as anisotropic filtering performed on deformation fields rather than intensity images.
The proposed anisotropic diffusive regularizer is as follows:
| (6) |
where
| (7) |
and n is the normal of the organ boundary in the vicinity of x, ▽ul(x) is the gradient of the l-th component of u(x), is the component of ul (x) in the normal direction, and w is a weighting term which decays exponentially from 1 to 0 as a function of distance to the organ boundary. ‖P▽ul(x)‖2 and both represent the squared magnitude of a flux (equation 3), where D = P and D = [n, 03, 03]T, respectively (03 = [0, 0, 0]). The eigenvectors of P specify that diffusion should occur the tangential plane but not in the normal direction, while nT dictates diffusion in the normal direction only.
Close to organ boundaries, where w is close to 1:
‖P▽ul(x)‖2 penalizes any discontinuities within the deformation field that are in the plane tangential to the organ boundary. This anisotropically smooths the discontinuities depicted in panels (ii) and (iii) of Figure 1b.
penalizes any discontinuities in the normal component of the deformation field that are in the direction normal to the organ boundary. This anisotropically smooths the discontinuities depicted in panel (i) of Figure 1b.
Discontinuities in the tangential component of the deformation field that are in the direction normal to the organ boundary are not penalized in the vicinity of organ boundaries (panel (iv) of Figure 1b). Therefore sliding motions are preserved.
Further away from organ boundaries, w approximates zero and equation 6 tends to the diffusive regularization (equation 2). The deformation field u is smoothed isotropically, enforcing smooth motion in all directions within each individual organ.
The optimal registration cost function C(u) has and can be found using finite differences:
| (8) |
The update term can be decomposed into the update terms associated with the intensity-based distance measure and the regularization term:
| (9) |
The gradient of equation 6 with respect to u can be found using the calculus of variations, leading to the update term for the anisotropic regularization:
| (10) |
where el is the lth canonical unit vector, i.e. ex = [1, 0, 0]T.
2.3. Implementation
This effort is part of the Tube Toolkit (TubeTK), a new toolkit providing software for registration, segmentation, analysis and quantification of images depicting tubular structures, such as vessels, bronchi and neurons. All software is open-source and freely available at http://public.kitware.com/Wiki/TubeTK. The sliding organ registration algorithm was implemented using the iterative finite difference solver framework provided by the Insight Toolkit (ITK) [8, 9], an open-source software toolkit for image processing, segmentation and registration (www.itk.org).
Organ boundaries were defined as VTK polydata (The Visualization Toolkit, www.vtk.org.) [10]. The normal n assigned to each voxel equaled that of the closest boundary point within this data representation, and the weighting w for each voxel was calculated as a function of the distance between the voxel and this point. Discrete image gradient and divergence were calculated within the 3×3×3 neighborhood surrounding each voxel of interest. Image registration progressed according a user-specified timestep and number of iterations. The resulting deformation field was applied to the original moving image using linear interpolation to generate the transformed moving image. Data was visualized using using ParaView, an open-source application for data analysis and visualization (www.paraview.org) [11].
3. Validation
3.1. Demonstration using artificial data
Figure 2 illustrates the properties of the anisotropic diffusive regularization using images of simple objects sliding against each other. Figure 2a shows a slice through the three-dimensional fixed image. The image shows two tubes, one bright and one of medium intensity, that are square in cross section and suspended within a dark background. From left to right in Figure 2a, each tube's intensity is uniform, then increasing/decreasing, and then uniform once again. To mimic sliding motion in the moving image (Figure 2b), the subset of the bright tube with increasing intensity was translated four pixels to the right, and the subset of the medium-intensity tube with decreasing intensity was translated four pixels to the left.
Fig. 2.

Demonstration of sliding organ registration with artificial data using the diffusive regularization and the anisotropic diffusive regularization. Deformation fields visualize the registration results, with intensity proportional to vector magnitude, and show deformations from the fixed image to the moving image. The transformed moving images ideally match the original fixed image.
The organ boundaries (including the interface between the bright and medium-intensity tubes and between each tube and the background) and the boundary normal vectors were determined analytically using geometrical knowledge of the object surfaces (Figure 2c). All registrations were performed over 500 iterations with a time step of 0.125s.
Figures 2d and 2e show the result of registration using the diffusive regularization. Although the original fixed image is almost perfectly recreated, the resulting deformation field is incorrect close to the organ boundaries. This is because the very different motions occurring on either side of the boundary are averaged together. As shown in Figures 2f and 2g, the deformation field resulting from the anisotropic diffusive regularization better recreates the applied transformation. Motion near the surface boundary is better preserved, as are motion vectors indicating compression and expansion in the regions neighboring the translated subsets. This is a much more realistic deformation field considering the dynamics of sliding motion. The RMS absolute intensity difference between the original fixed and moving images was 1.97 (mean ± standard deviation: 0.34 ± 1.94). Following registration, the RMS absolute intensity difference was reduced to 0.73 using the diffusive regularization (mean ± standard deviation: 0.058 ± 0.73) and 0.75 using the anisotropic diffusive regularization (mean ± standard deviation: 0.069 ± 0.75).
3.2. Validation using the XCAT software phantom
A second validation study involved registering chest images depicting the heart, lungs and liver that were generated using the 4D extended cardio-torso (XCAT) software phantom [12]. Based on images from the Visible Human Project, the XCAT phantom is a realistic and flexible model of human anatomy and physiology. The organ shapes within the phantom are constructed using a non-uniform rational B-splines (NURBS) surfaces, and the phantom incorporates cardiac and respiratory motion based on models constructed from gated high-resolution CT patient datasets.
Two “activity” images visualizing each organ's attenuation coefficient were created using parameters corresponding to a typical healthy patient, including a 5s respiratory period and a 1s cardiac cycle. The images were generated at 0s and 2.5s, representing approximately full-exhale + end-diastole (the moving image) and full-inhale + end-systole (the fixed image). Voxels were 3.125mm3. Voxel intensities were adjusted from the eight activity levels provided by the XCAT phantom to six gray levels approximately matching those of a typical CT (computed tomography) scan (Figures 3 and 4). The organ boundary was defined by the lung surface. A surface model of the lungs was extracted from the fixed image using 3D Slicer (www.slicer.org) [13] using threshold-based segmentation followed by manual removal of the smaller bronchi, model extraction using Marching Cubes, model smoothing, and model decimation by 50%. Image registration was performed using the diffusive and anisotropic diffusive regularizations over 2000 iterations with a time step of 0.125.
Fig. 3.
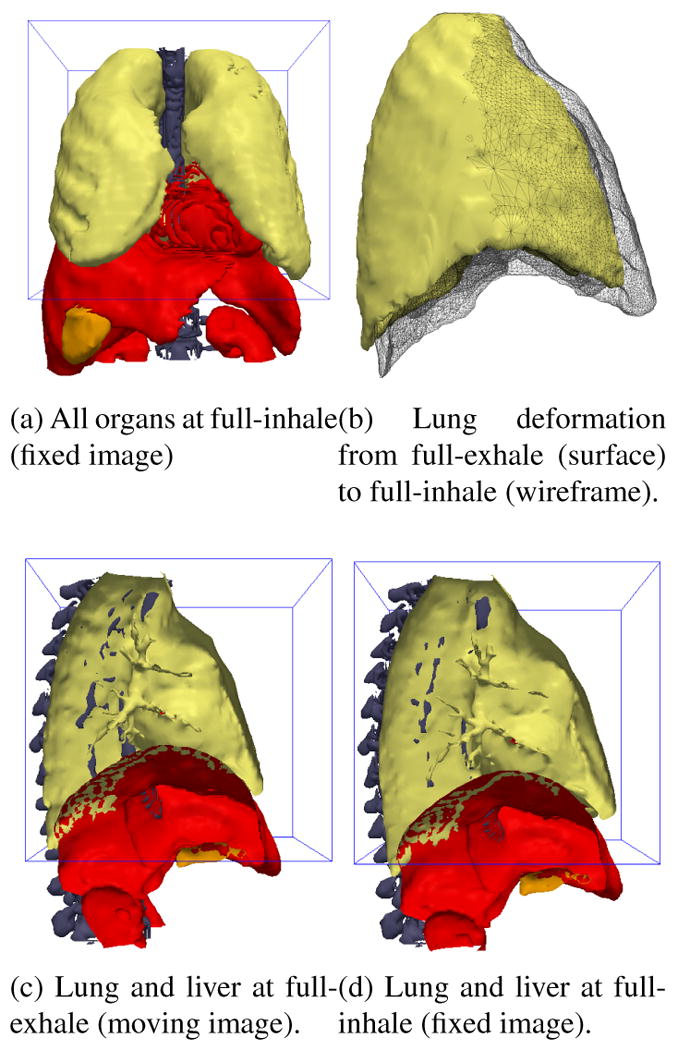
Surfaces extracted from the fixed and moving XCAT phantom images. The 3D box outline indicates the domain of the fixed and moving images to be registered.
Fig. 4.
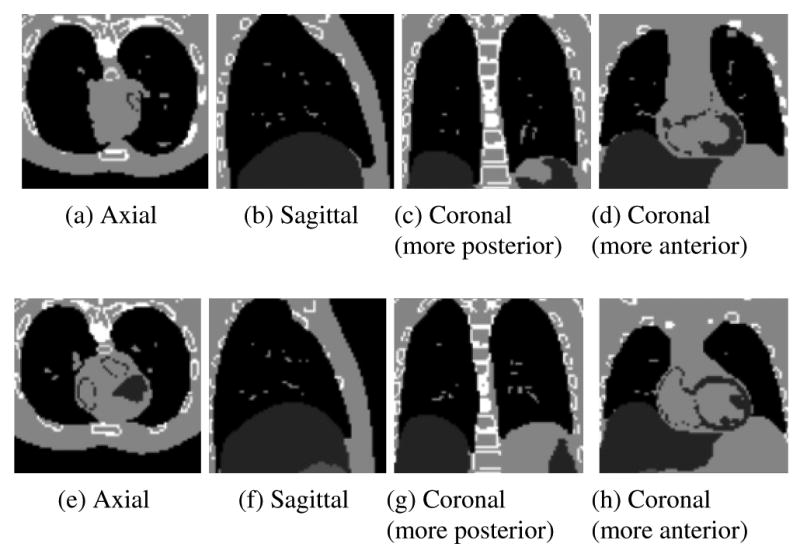
Slices through the original fixed (a-d) and moving (e-h) images created using the XCAT software phantom.
Applying the deformation fields yielded by image registration using the diffusive and anisotropic diffusive regularizations gives the transformed moving images shown in Figure 5. Many of the substantial deformations between the original moving and fixed images were recovered, including the expansion of the chest and lungs, the movement of the liver downwards, and the heart's contraction and anterior/inferior translation. Before registration, the RMS absolute intensity difference between the fixed and moving images was 62.43 (mean ± standard deviation: 27.61 ± 55.99). This was reduced to 30.69 (mean ± standard deviation: 10.82 ± 28.72) following registration using the diffusive regularization and to 33.41 (mean ± standard deviation: 12.12 ± 31.13) following registration with the anisotropic diffusive regularization.
Fig. 5.
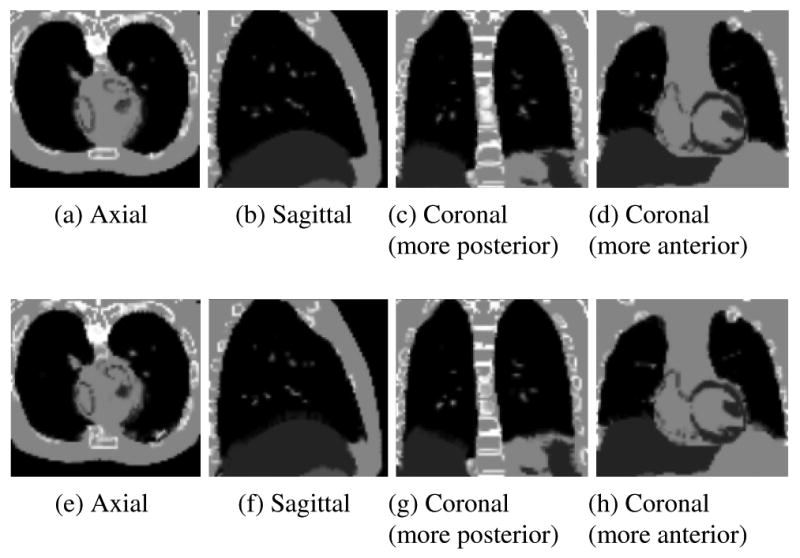
Slices through the transformed moving images following registration using the diffusive (a-d) and anisotropic diffusive (e-h) regularizations. The transformed moving images ideally match the original fixed images in Figure 4.
Figure 6 shows a sagittal slice through the registration deformation fields and illustrates the advantages of the anisotropic diffusion regularization term presented here. The images to be registered exhibit sliding motion between the lungs and the liver (note that the diaphragm is not visualized in the XCAT images). This sliding motion is especially noticeable in the anterior/inferior part of the lung. Figure 6a demonstrates the overall motion field smoothness that is enforced by the diffusive regularization, which generates improbably complex deformations throughout the anterior liver. In contrast, the anisotropic regularization effectively decouples the motion of the lungs and liver in this area (Figure 6b). The resulting deformation field clearly depicts the liver moving upwards while the lung slides in the anterior-posterior direction along it.
Fig. 6.
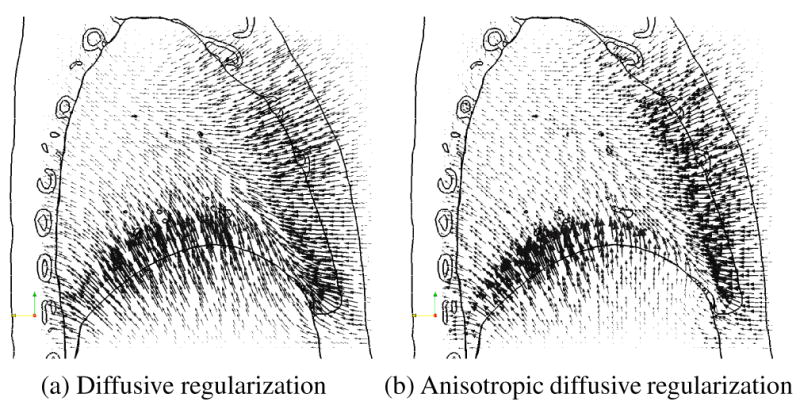
Sagittal slice through the deformation field resulting from registering the XCAT phantom images, overlaid onto an outline of the original fixed image. Motion vectors indicate deformations from the fixed image (full-inhale, shown by outlines) to the moving image (full-exhale).
A quantitative validation was performed by calculating the distances between organ surfaces extracted from the original fixed image with those from (1) the original moving image; (2) the transformed moving image under the diffusive regularization; and (3) the transformed moving image under the anisotropic diffusive regularization. Label maps segmenting “lungs + background”, “liver + heart”, “bone” and “muscle” were created for each image using intensity thresholding (allowing ±15 from the original images' constant gray levels when segmenting the transformed moving images). Surface models were created using the Marching Cubes algorithm followed by model smoothing (no decimation). Note that the image “background” label map created a surface representing the patient's chest, the heart surface model represents the dark areas within the heart and not the entire cardiac surface, and that the “muscle” class represents all structures of light intensity in Figures 5, including the chest wall, heart and stomach. When more than one surface was generated from the same intensity (ex. lung/chest surface and liver/heart), each structure's surface was extracted using surface connectivity based on manually-defined fiducial points. This had the beneficial side effect of removing small floating polydata that survived the threshold criteria but did not correspond to an organ of interest.
Surface to surface distances were determined using Mesh-Valmet 2.1 (http://www.ia.unc.edu/dev/download/MeshValmet/MeshValmet.html). Summary statistics of the distance between surface A and surface B were calculated based on the distances from each point in A to the closest point in B combined with the distances from each point in B to the closest point in A.
Results are shown in Table 1. The large distance errors between the surfaces segmented from the original fixed image and those from the original moving images illustrate the substantial deformations that we are attempting to find here. Following image registration, error decreased for all organs except for the “bone” and “heart” surfaces. These were the two smallest and most diffuse tissue types, more likely to be influenced by their neighborhood than to drive the registration themselves. Distance errors were typically slightly greater for registration using the anisotropic diffusive regularization compared to registration with the diffusive regularization.
Table 1.
Surface to surface distances between surfaces segmented from the original fixed image with those from the original moving image and from the transformed moving images. All values in millimetres (mm).
| Organ | Before Registration | Registered (Anisotropic) |
Registered (Diffusive) |
|---|---|---|---|
| Signed vertex distance (mean ± standard deviation): | |||
| Lungs | 1.69 ± 8.34 | 0.35 ± 5.95 | -0.03 ± 4.86 |
| Liver | 1.38 ± 13.05 | 0.15 ± 8.41 | -0.51 ± 7.47 |
| Chest | 0.01 ± 9.02 | 0.25 ± 1.65 | 0.25 ± 1.65 |
| Muscle | -0.27 ± 5.19 | -0.19 ± 3.28 | -0.17 ± 3.23 |
| Bone | 1.68 ± 3.88 | -0.00 ± 5.08 | 0.05 ± 4.92 |
| Heart | 5.75 ± 8.24 | 7.00 ± 11.14 | 6.79 ± 11.00 |
| Absolute vertex distance (mean): | |||
| Lungs | 6.63 | 3.71 | 2.94 |
| Liver | 10.87 | 5.03 | 3.79 |
| Chest | 8.82 | 0.72 | 0.73 |
| Muscle | 3.44 | 1.86 | 1.81 |
| Bone | 2.43 | 3.34 | 3.28 |
| Heart | 8.24 | 8.87 | 8.60 |
| Absolute vertex distance (histogram central 68th percentile): | |||
| Lungs | [3.29, 7.84] | [0.52, 4.08] | [0.45, 2.95] |
| Liver | [9.52, 19.48] | [1.77, 8.64] | [0.89, 5.76] |
| Chest | [9.08, 12.33] | [0.08, 0.61] | [0.08, 0.68] |
| Muscle | [0.70, 5.56] | [0.35, 2.09] | [0.35, 2.09] |
| Bone | [0.08, 2.55] | [0.50, 4.40] | [0.69, 4.42] |
| Heart | [4.57, 10.91] | [4.36, 14.11] | [4.33, 14.95] |
4. Discussion and Conclusions
This paper has presented a novel deformation field regularization term based on anisotropic diffusion for deformable registration between images depicting sliding organs. Anisotropic regularization is more appropriate than uniform regularization whenever discontinuities in the deformation field are expected, as is the case whenever objects move independently. Our validation studies have illustrated that the anisotropic diffusive regularization does allow sliding motions to be recovered, a step towards effective registration of such images.
Fundamentally, the goal of image registration is to establish correspondence. The transformation resulting from image registration encapsulates this correspondence, and the deformation field is the entity that is used when deformable image registration is applied to practical problems in image-guided therapy, physiological modeling and atlas building, and image-based anatomical studies. Developing regularization terms based on physiological constraints increases the probability that image registration will yield the correct deformation field, out of the many deformation fields that map the intensities of the moving image onto those of the fixed image. In the validation study registering the XCAT images, the anisotropic diffusive regularization did give slightly greater errors compared to the diffusive regularization. However, its deformation field was much more realistic and therefore ultimately more useful. Here, we argue that a slight decrease in registration accuracy as measured by the similarity between the fixed image and the transformed moving image is acceptable if it leads to an increase in registration accuracy as measured by the plausibility of the resulting deformation field.
Within this paper, comparing our method to the diffusive regularization allowed for a straightforward assessment of the benefits of anisotropic regularization. However, the concept itself is more general, and can be applied in future to regularize velocities in fluid-based deformable registration.
In future, we would like to investigate alternatives to segmented organ surface models for determination of the organ boundary normals and the weightings between the anisotropic diffusive and diffusive regularizations. These values could be derived from local intensity information within the fixed image, for example using the structure tensor or a local edge detector. Future work also includes determining the ideal weighting between the intensity-based distance measure and the regularization term in equation 9.
Finally, the XCAT software phantom provided idealized yet anatomically-realistic imagery with which to evaluate our registration algorithm, and a quantitative assessment must be performed using clinical images. Validation based on segmented organ boundaries gives one measure of registration accuracy, but does not evaluate the accuracy with which internal structures are related. This will be addressed in future by determining target registration error in clinical images.
Acknowledgments
This project was supported, in-part, by (1) NIH/NCI sponsored 1R01CA138419-01; (2) NIH/NIBIB sponsored 2U54EB005149-06; (3) NIH/NCI sponsored 1R41CA153488-01; (4) NSF sponsored EECS-0925875; (5) NIH/NIMH sponsored 1R01MH091645-01A1; and (6) NIH/NIBIB sponsored 5P41EB002025-27. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health. Thanks also to Dr. Paul Segars for providing the XCAT phantom software.
Contributor Information
Danielle F. Pace, Kitware Inc., Clifton Park, NY and Carrboro, NC, USA
Andinet Enquobahrie, Kitware Inc., Clifton Park, NY and Carrboro, NC, USA.
Hua Yang, Kitware Inc., Clifton Park, NY and Carrboro, NC, USA.
Stephen R. Aylward, Kitware Inc., Clifton Park, NY and Carrboro, NC, USA
Marc Niethammer, University of North Carolina at Chapel Hill, Department of Computer Science, Chapel Hill, NC, USA.
References
- 1.Crum WR, Hartkens T, Hill DLG. Non-rigid image registration: theory and practice. The British Journal of Radiology. 2004;77:S140–S153. doi: 10.1259/bjr/25329214. [DOI] [PubMed] [Google Scholar]
- 2.Nagel HH, Enkelmann W. An investigation of smoothness constraints for the estimation of displacement vector fields from image sequences. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1986;8(no. 5):565–593. doi: 10.1109/tpami.1986.4767833. [DOI] [PubMed] [Google Scholar]
- 3.Modersitzki J. Numerical methods for image registration. Oxford University Press; 2004. [Google Scholar]
- 4.Risholm P, Samset E, Talos IF, Wells W. Information Processing in Medical Imaging, Lecture Notes in Computer Science. 2009. A non-rigid registration framework that accomodates resection and retraction; pp. 447–458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schmidt-Richberg A, Ehrhardt J, Werner R, Handels H. Medical Image Computing and Computer-Assisted Intervention, vol 5761 of Lecture Notes in Computer Science. 2009. Slipping objects in image registration: Improved motion field estimation with direction-dependent regularization; pp. 755–762. [DOI] [PubMed] [Google Scholar]
- 6.Youbing Y, Hoffman EA, Lin CL. Medical Image Computing and Computer-Assisted Intervention, Lecture Notes in Computer Science. 2010. Lung lobar slippage assessed with the aid of image registration; pp. 578–585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Weickert J. Scale-Space Theory in Computer Vision, vol 1252 of Lecture Notes in Computer Science. 1997. A review of nonlinear diffusion filtering; pp. 3–28. [Google Scholar]
- 8.Ibanez L, Schroeder W, Ng L, Cates J. The ITK Software Guide. Second. Kitware, Inc.; 2005. [Google Scholar]
- 9.Enquobahrie A, Yang H, Aylward S. Implementation of local structure tensor and enhancement anisotropic diffusion filters in ITK. The Insight Journal. 2010 http://hdl.handle.net/10380/3199.
- 10.Schroeder W, Martin K, Lorensen B. The Visualization Toolkit: An object-oriented approach to 3D graphics. Fourth. Kitware Inc.; 2006. [Google Scholar]
- 11.Squillacote A Henderson. The ParaView Guide. Third. Kitware Inc.; 2008. [Google Scholar]
- 12.Segars WP, Sturgeon G, Mendonca S, Grimes J, Tsui BMW. 4D XCAT phantom for multimodality imaging research. Medical Physics. 2010;37:4902–4915. doi: 10.1118/1.3480985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pieper S, Halle M, Kikinis R. 3D Slicer. IEEE International Symposium on Biomedical Engineering; 2004. pp. 632–635. [Google Scholar]


