Abstract
The free energy governing K+ conduction through gramicidin A channels is characterized by using over 0.1 μs of all-atom molecular dynamics simulations with explicit solvent and membrane. The results provide encouraging agreement with experiments and insights into the permeation mechanism. The free energy surface of K+, as a function of both axial and radial coordinates, is calculated. Correcting for simulation artifacts due to periodicity and the lack of hydrocarbon polarizability, the calculated single-channel conductance for K+ ions is 0.8 pS, closer to experiment than any previous calculation. In addition, the estimated single ion dissociation constants are within the range of experimental determinations. The relatively small free energy barrier to ion translocation arises from a balance of large opposing contributions from protein, single-file water, bulk electrolyte, and membrane. Mean force decomposition reveals a remarkable ability of the single-file water molecules to stabilize K+ by –40 kcal/mol, roughly half the bulk solvation free energy. The importance of the single-file water confirms the conjecture of Mackay et al. [Mackay, D. H. J., Berens, P. H., Wilson, K. R. & Hagler, A. T. (1984) Biophys. J. 46, 229–248]. Ion association with the channel involves gradual dehydration from approximately six to seven water molecules in the first shell, to just two inside the narrow pore. Ion permeation is influenced by the orientation of the single-file water column, which can present a barrier to conduction and give rise to long-range coupling of ions on either side of the pore. Small changes in the potential function, including contributions from electronic polarization, are likely to be sufficient to obtain quantitative agreement with experiments.
Molecular dynamics (MD) simulation has become an essential tool for investigating a wide range of chemical and biological systems. Greater computational resources, improvements in simulation methodologies, and refinement of interaction potentials have made it possible to model increasingly complex processes that previously were intractable (1). It is important that the approach be thoroughly tested on systems that are small and yet possess the same ingredients and challenges as much larger and more complex biomolecular systems. These benchmarks serve to set standards on which studies of more complex problems can find foundation. For example, a single key protein secondary structure, the β hairpin, has been used as a benchmark test in protein-folding studies (2). In the present study, we tackle the problem of ion permeation with a similar mindset. Ion permeation involves a seemingly straightforward process of an ion passing across the membrane through a molecular pore. However, this process is difficult to model because it entails the accurate representation of intermolecular interactions in vastly different environments (aqueous solution and narrow protein pore) for which there is little direct experimental data (3). As a rigorous examination of an all-atom force field to model ion permeation, we combine free energy methods with fully atomistic, dynamical simulations on a benchmark system.
Atomic structures have been reported for many ion channels, but none is structurally and functionally as well characterized (4), or as amenable to computer simulation, as the gramicidin A (gA) channel. gA channels form by transmembrane dimerization of single-stranded, right-handed β6.3-helices (5) with the sequence (underlined residues are d-amino acids): formyl-Val-Gly-Ala-Leu-Ala-Val-Val-Val-Trp-Leu-Trp-Leu-Trp-Leu-Trp-ethanolamine (6). High resolution structures have been obtained for gA embedded in detergent micelles by using liquid-state NMR (7, 8) and oriented dimyristoylphosphatidylcholine bilayers by using solid-state NMR (9), and refined with MD simulation (10). The depth of experimental knowledge and the simplicity of this protein also have lent it to numerous computational models (11) and make it the system of choice for investigating ion conduction.
Since the first MD simulations on a fully flexible atomic model of gA were carried out 20 yr ago (12), system sizes and simulation times have grown by orders of magnitude, yet quantitative agreement with ion-flux experimental measurements has remained a difficult task (11, 13). A direct connection between the atomic structure and the observed conductance properties cannot easily be obtained via a “brute force” MD simulation approach because ionic fluxes correspond to transit times of 10–100 ns, such that statistically accurate conductance measurements are beyond the capabilities of present day computers. A better computational strategy is to first determine the equilibrium free energy landscape, as described by the potential of mean force (PMF), which governs the systematic forces acting on the permeating ions in the system, and then invoke an appropriate macroscopic or semimicroscopic formalism to calculate the ionic current. Successful application of this computational strategy in calculating ion conductances in the KcsA potassium channel (14, 15) prompts us to return to the problem of ion permeation through the gA channel and assess how close we are to obtaining quantitative agreement with experiment. Although the microscopic force field still requires further refinements to describe accurately the permeation of ions across the gA channel, the current model does a surprisingly good job of predicting experimental conductances.
Theory and Methods
To focus our computational effort on the calculation of the free energy landscape governing ion conduction, we separate the system into “pore” and “bulk” regions (16). The equilibrium properties of the system then can be reconstructed from a hierarchy of PMFs 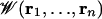 , representing the pore region occupied by n ions. In the case of the gA channel, at moderately low alkali metal cation concentration (<100 mM), ion conduction is governed primarily by the 1-ion PMF,
, representing the pore region occupied by n ions. In the case of the gA channel, at moderately low alkali metal cation concentration (<100 mM), ion conduction is governed primarily by the 1-ion PMF, 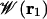 , which can be expressed in terms of the total potential energy U of the system as a function of ionic coordinates ri (i = 1, N) and remaining degrees of freedom X (water, protein, lipids)
, which can be expressed in terms of the total potential energy U of the system as a function of ionic coordinates ri (i = 1, N) and remaining degrees of freedom X (water, protein, lipids)
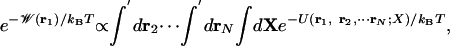 |
[1] |
where the primes indicate that ions 2 to N reside in the bulk, kB is Boltzmann's constant, and T the temperature. Normalization is chosen such that 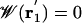 at any point
at any point 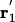 far away in the bulk. By choosing a suitable pore region, we can calculate
far away in the bulk. By choosing a suitable pore region, we can calculate 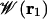 that will provide a meaningful representation of single occupancy. Analysis of trajectories indicates that a sphere of radius 14 Å (relative to the center of mass of the dimer) best defines this pore region. During the simulations used to calculate
that will provide a meaningful representation of single occupancy. Analysis of trajectories indicates that a sphere of radius 14 Å (relative to the center of mass of the dimer) best defines this pore region. During the simulations used to calculate 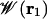 , other ions were excluded from this sphere.
, other ions were excluded from this sphere.
The reaction coordinate for ion permeation is the z component (parallel to the membrane normal) of the distance of the ion to the center of mass of the gA dimer. A PMF also can be defined relative to the instantaneous channel axis, but it is the absolute lab-frame z that is the most pertinent because ion conduction corresponds to a displacement of charge parallel to an applied transmembrane electric field. The ion is confined in a narrow region in the xy plane as it moves through the channel, and it may be assumed that motions perpendicular to z reach equilibrium rapidly and thus may be integrated away (16),
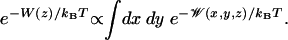 |
[2] |
This 1D PMF W(z), or “free energy profile,” has limited significance outside the channel because the lateral displacement in the xy plane is unbounded. In the present calculations, the lateral displacement of the ion was restricted to ensure good sampling in a well defined region of configurational space by using a flat-bottom cylindrical restraint with radius 8 Å (relative to the center of mass of the dimer). The influence of this potential can then be removed rigorously after the simulation.
We calculated the 1D PMF W(z), as well as a 2D PMF as a function of axial and radial coordinates, W(z, r), with umbrella sampling (17), for a system that consists of a gA helical dimer [Protein Data Bank, PDB ID code 1JNO (8)] embedded in a dimyristoylphosphatidylcholine bilayer solvated by 1 M KCl (Fig. 1). The choice of starting structure is based on recent evidence (10) that dynamical trajectories based on the PDB:1JNO structure reproduces experimental solid-state NMR measurements (18) better than the solid-state NMR PDB:1MAG structure (9). Specific simulation parameters are provided in Simulation Details, which is published in the supporting information on the PNAS web site.
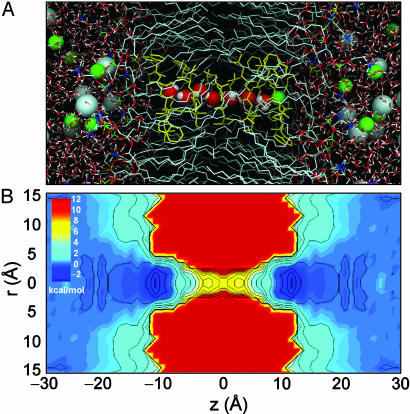
Fig. 1.
gA in the bilayer. (A) gA dimer (yellow); dimyristoylphosphatidylcholine bilayer atoms C (gray), O (red), N (blue), and P (green); K+ (green spheres) and Cl– (gray spheres); water O (red) and H (white). Within the channel, seven single-file water molecules are drawn as spheres adjacent to a single K+ ion at the channel entrance. (B) The 2D PMF of a single K+ ion as a function of axial (z) and radial (r) positions. Contours are drawn at 1-kcal/mol intervals.
Umbrella sampling entails simulations that generate distributions of ion position, biased by a series of window functions wi(z) that hold the ion near regular positions along the z axis. A total of 101 windows, defined by harmonic potential functions, positioned in 0.5-Å increments from z = –20 to +30 Å, were carried out concurrently on different CPUs with initial configurations selected from an unbiased MD trajectory. To ensure convergence, 1 ns of trajectory generation was performed for each window. Symmetrized ionic distributions were unbiased with the weighted histogram analysis method (19). An additional 4-ns simulation, in the absence of a window function, was used to calculate the bulk limit 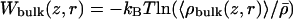 , where
, where 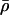 is the K+ density far from the channel. Wbulk(z, r) and W(z, r) were then matched far from the channel to set the correct bulk reference for the 2D PMF.
is the K+ density far from the channel. Wbulk(z, r) and W(z, r) were then matched far from the channel to set the correct bulk reference for the 2D PMF.
An independent check of the barrier height in W(z, r) was obtained by free energy perturbation (FEP) calculations, where an ion at the center of the channel was interchanged alchemically with a water in the bulk. The alchemical ion–water exchange process carried out during the FEP calculation corresponds to the total work required to move a K+ from the bulk to the center of the channel and, in addition, the work to move a water molecule from the center of the channel to the bulk. The free energy for the complete exchange process is
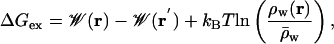 |
[3] |
where 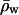 is the mean water density far from the channel. The weighted histogram analysis method was used to obtain the free energy change ΔGex for the perturbation (20); the relative local density of water is obtained from the 80-ns MD trajectory.
is the mean water density far from the channel. The weighted histogram analysis method was used to obtain the free energy change ΔGex for the perturbation (20); the relative local density of water is obtained from the 80-ns MD trajectory.
Results and Discussion
Potential of Mean Force. We begin with the 2D PMF, Fig. 1B, because it offers the most complete description of the free energy surface governing ion conduction. It reveals a flat landscape in the bulk, the depth and position of binding sites at the channel entrances, the scale of the free energy barrier that must be surmounted by the permeating ion, and the extent of lateral ion motion. The value of the 2D PMF far from the channel is used to set the absolute reference for the free energy surface. Because the 2D PMF is determined in the laboratory frame, lateral movement of the ion relative to the channel, and channel tilting (12° on average) lead to fairly broad free energy wells near the channel entrances. There is a well at z = 11.3 Å (outer binding site), where the PMF drops to –3.2 kcal/mol relative to the bulk. In the narrowest part of the channel, an ion experiences a barrier of 10.4 kcal/mol relative to the binding site (or 7.2 kcal/mol relative to the bulk). The independent estimate obtained from FEP calculations resulted in a barrier height 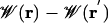 of Eq. 3 of 8.6 kcal/mol, consistent with the 2D PMF.
of Eq. 3 of 8.6 kcal/mol, consistent with the 2D PMF.
The 1D PMF W(z) of an ion along the channel axis, is a fundamental concept in classical models of ion permeation (21). It is defined by integrating out the lateral motions of the ion (see Eq. 2). This assumption is reasonable for a narrow channel; however, the 2D PMF (Fig. 1B) shows that the ion is confined laterally only in the range –15 to 15 Å. Outside this region, the ion may be displaced to any extent in the xy plane, and the concept of a free energy profile W(z) is not meaningful. To avoid these problems, the 1D PMF was calculated with the cylindrical restraint. The large effective width of the channel entrance near the binding site, relative to the center of the channel, leads to a higher barrier of ≈12 kcal/mol with respect to the binding site. There is a deep outer binding site at z = 11.3 Å and a less deep inner binding site at 9.7 Å that was not obvious in the 2D PMF. In addition there are three local free energy minima inside each subunit of the gA dimer. It should be stressed that, by virtue of Eq. 2, W(z) cannot be set with respect to some absolute reference; it is incorrect to assume that W(z) is equal to zero for large z. Consequently, the true depth of the binding sites relative to the bulk can be defined only via the free energy surface provide by the 2D PMF.
Maximum Conductance. To ascertain the magnitude of the current that can pass through the channel, the net stationary flux (J) of ions across the channel can be calculated by using a 1D Nernst–Planck equation (22)
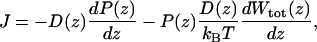 |
[4] |
where D(z) is the K+ diffusion coefficient as a function of z, and P(z) is the probability density per unit length of finding a K+. Wtot can be expressed as a sum of the equilibrium PMF W, dominated by local molecular interactions, and the interaction of atomic charges with the transmembrane potential (23). As the potential difference increases, contributions from the coupling to the dipole moment of the system, dominated by the single file of water, become significant (Supporting Text). To gauge the ability of MD to reproduce experiment, we consider only the maximum single channel conductance gmax. This analysis provides a rough estimate because we ignore changes in ion conduction that could be associated with multiple ion occupancy at high concentration. In addition, this model assumes that only the ionic z coordinate is a rate-determining coordinate. Later, we discuss the significance of this assumption when we examine the role of the flipping of the single-file water column. Under symmetric concentration baths and low membrane potential, the maximum conductance is (24)
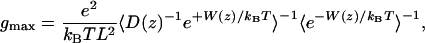 |
[5] |
where the brackets signify spatial averaging over the length L of the pore region. L is equal to the diameter of the sphere defining the single ion region (28 Å) and is within the range where the 1D PMF is meaningful (|z| < 15 Å). The diffusion coefficient D(z) is extracted from the Laplace transform of the velocity autocorrelation function by using an analysis based on the generalized Langevin equation for a harmonic oscillator (25). Such an analysis is required to separate the local dissipative forces that give rise to random diffusional motion of the ions from the average systematic forces arising from the PMF. D(z) thus determined is ≈2/3 of bulk diffusion coefficient within the channel (Supporting Text). The maximum conductance, calculated by using Eq. 5, is 4.7 × 10–3 pS, ≈5 orders of magnitude less than the experimental value of 21 pS [in DPhPC bilayers with 1 M KCl at 100 mV (26)], indicating that the barrier is several kcal/mol too high.
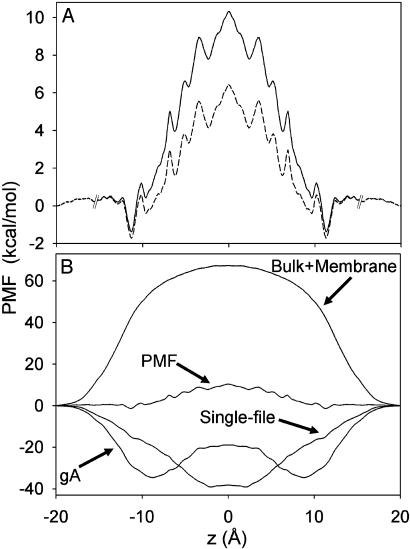
An artifact is introduced by the periodic boundary conditions, which cause a spurious destabilization of the ion in the membrane, caused by the finite size and the periodicity of the system. In addition, the hydrocarbon chains of the lipid molecules in the current model are nonpolarizable, with an effective dielectric constant of 1 (27) that, in reality, should be closer to the value for bulk hydrocarbons of ≈2 (28). These artifacts can be corrected by using a continuum electrostatic approximation (29) using trajectories to average over protein and single-file water configurations. Estimates, obtained from 1-ns MD trajectories show that correcting for the spurious destabilization leads to a –1.6 kcal/mol correction (at the channel center, relative to the bulk). Correcting for the effect of the dielectric constant of the hydrocarbon chains leads to a further –2.1 kcal/mol stabilization, in accord with calculations incorporating electronic polarizability (Supporting Text). It is also possible to estimate the effect of high electrolyte concentration (30) by approximating the effect of reducing it from 1 M to a more appropriate level of 0.1 M. This result leads to a small additional stabilization of –0.2 kcal/mol. When all of these corrections are made, the barrier in the 1D PMF is reduced to just 8.1 kcal/mol with respect to the binding site (dashed curve, Fig. 2A). This result leads to a maximum conductance of 0.8 pS, approaching the experimental value better than any previous MD study of gA. The agreement is encouraging because the discrepancy can be accounted for by only small changes to the PMF.
Fig. 2.
(A) One-dimensional PMF. Broken lines at |z| = 15 Å indicate that the 1D PMF is not rigorously defined beyond those points. The dashed curve is the PMF corrected for simulation artifacts. (B) Mean force decomposition. Average forces have been antisymmetrized before integration with Eq. 7.
Equilibrium Dissociation Constants
The single ion dissociation constant, KD, can be calculated from the single ion equilibrium PMF 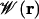 (16)
(16)
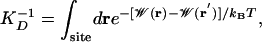 |
[6] |
where r′ is a reference position in the bulk. This quantity can also be conveniently expressed in terms of the 1D PMF calculated with a cylindrical restraint (Supporting Text). The dissociation constant for the entire channel (–12.5 < z < 12.5 Å), obtained from the corrected PMF, is 0.34 M. This result is within the range of experimental values determined from NMR and conductance studies: 0.017 M (31) and 0.019–0.73 M (32). Integrals over individual energy wells indicate that ions will bind only to the outer (10.2 < z < 12.5 Å) and inner (6.9 < z < 10.2 Å) sites with dissociation constants of 0.83 M and 3.6 M, respectively. At 1 M, the outer binding site is likely to be occupied whereas the inner binding site is not. Experimentally, however, the major cation binding site is the inner site (31, 33). The relative depth of the inner and outer cation-binding sites near the entrance of the gA channel is very sensitive to the details of the potential function, previous studies finding alternatively that the inner (34, 35) or outer (36) binding site can be the most stable position. One important factor is clearly the choice of ion-carbonyl Lennard–Jones parameter (3). Data for liquid amides suggest that the free energy of solvation of K+ in liquid n-methyl-acetymide (NMA) (a quantity not known experimentally) is similar to the free energy of hydration of K+ in liquid water (37). The PARAM27 force field gives a K+-bulk NMA free energy ≈7 kcal/mol less than the K+-bulk water free energy (3). Instead, if the parameter was chosen to reproduce the K+-single NMA molecule interaction energy in vacuum [28–32 kcal/mol experimentally (38)] more closely, the barrier in the 1D PMF would be considerably reduced and depths of the binding sites increased (favoring the inner binding site due to increased solvation by protein).
Mean Force Decomposition. By virtue of the relationship between the PMF and the thermodynamic reversible work, the contribution from any microscopic force Fα to the total free energy profile can be computed independently (23),
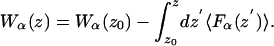 |
[7] |
The decomposition of the force can be accomplished in any number of ways, yet we consider the protein and water within the pore region (single-file) to be the most relevant to ion permeation. These contributions are shown in Fig. 2B. The relatively flat PMF arises from the cancellation of very large opposing contributions from protein, single-file water, and the remaining bulk electrolyte and membrane, and it is easy to understand how the PMF can be in error by a few kcal/mol. The contribution from the membrane and bulk electrolyte is 67.4 kcal/mol as expected for a Born energy barrier due to a low dielectric membrane slab (39, 40). This barrier is eliminated, almost completely, by interactions with the protein and single-file water. The water column provides an attractive contribution that corresponds to a fairly constant force that vanishes near the channel center as the water dipoles become symmetric around the ion. Surprisingly, the single-file water itself accounts for –39.2 kcal/mol stabilization; i.e., nearly half the –80 kcal/mol solvation free energy of K+ in bulk water (37) is obtained with just two water molecules in contact with the ion. For comparison, a FEP calculation (with the same potential function) shows that the solvation free energy of K+ surrounded by its first hydration shell of eight water molecules is approximately –46 kcal/mol (41). This result is made possible by the large gas-phase interaction of –18.9 kcal/mol (3) between K+ and a TIP3P water molecule, and the significantly anisotropic orientation of the single-file water, as conjectured 20 yr ago by Wilson and coworkers (12).
The large stabilization arising from the single-file water molecules raises questions about the ability of a nonpolarizable force field to represent a strongly anisotropic system. To examine the importance of induced polarization on the ability of single-file water molecules to solvate a cation, we calculated the charging free energy of a K+ at the center of a model system comprising only eight water molecules in single file by using nonpolarizable TIP3P (42) as well as the recently developed polarizable SWM4-DP (43) water model based on Drude oscillators (Supporting Text). For both water models, the cation parameters were previously optimized to reproduce the experimental solvation free energy of K+ in bulk water. By using nonpolarizable TIP3P, the charging free energy was –42.0 kcal/mol, similar to the contribution of the single file to the PMF of K+ in gA. The charging free energy with the polarizable water model is –41.5 kcal/mol, essentially the same as the nonpolarizable result. Including the influence of a cavity reaction field representing bulk water does not affect this conclusion; the charging free energies become –52.2 and –52.3 kcal/mol, for TIP3P and SWM4-DP water, respectively. We conclude that the nonpolarizable TIP3P water model (42) adequately describes both extremes in ion solvation, the bulk phase as well as the strongly anisotropic single file.
The binding sites in the PMF arise from a delicate interplay between water and protein interactions. It has in the past been assumed that the binding sites owe their existence to a superposition of a long-range electrostatic image repulsion (“Bulk + Membrane” in Fig. 2B) and a short-range attractive interaction (44). In contrast, Fig. 2B shows that the inner binding site (the dominant binding site experimentally) arises from the mean force exerted by the protein. There is a broad attractive free energy contribution from the protein near the channel entrances, reaching a minimum of –34.6 kcal/mol at |z| = 8.8 Å, responsible for this binding site. At z = 11.3 Å, a small dip in the single-file water contribution corresponds to the location of the outer binding site, which, as a consequence of the greater role of water outside of the channel, is not determined solely by protein interactions.
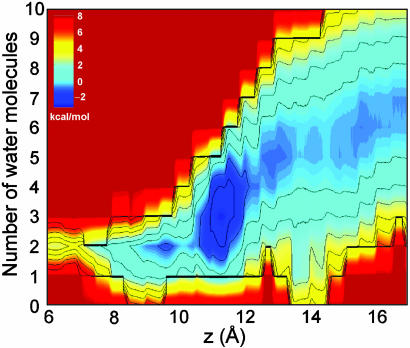
Energetics of Ion Dehydration. The importance of hydration in the single file observed in the mean force decomposition led us to study more closely the mechanism of ion dehydration on entry into the channel. Sudden changes in solvation at a particular position could cause difficulties in revealing the free energy of ion permeation as a function of a single coordinate z (45). The 2D unbiasing of histograms (Supporting Text) leads to an expression for the free energy as a function of ion position z and a secondary parameter n, the hydration number, such that we may examine the role played by solvation in ion permeation across the gA channel. The 2D PMF W(z,n) of Fig. 3 shows the free energy of an ion at position z, hydrated by n water molecules, relative to an ion in the bulk with 6 to 7 solvating water molecules. This bulk hydration number is in agreement with the number 6.46 obtained for bulk 1 M KCl in TIP3P water (46). As noted previously (34), dehydration occurs progressively over 6–7 Å, and this number drops to just 2 inside the single-file column within the channel. By focusing on the entry region, Fig. 3 shows that an ion in the inner binding site is solvated predominantly by two water molecules whereas the outer binding site involves solvation by three water molecules. Dehydration varies more abruptly as the ion enters the narrow pore from the outer binding site but seems to remain a continuous function of z and is not opposed by a free energy barrier (34).
Fig. 3.
PMF W(z, n) as a function of ion z and hydration number n (Supporting Text).
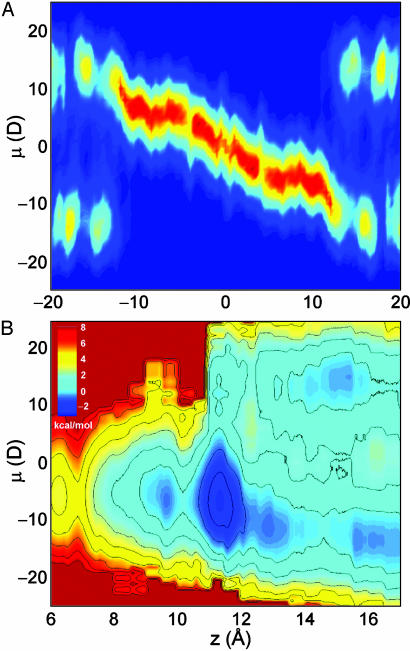
The Single-File Water Dipole. The single-file column of water is particularly interesting because the pore imposes a preferred alignment of water dipoles that can influence conduction. Fig. 4A shows the 2D histogram of the net dipole moment of the single-file water molecules as a function of ion position. When the ion is outside the channel, there are two possible dipole moments for the single file, ±15 D, corresponding to the water molecule dipoles running almost parallel or antiparallel to the z axis. As the ion enters the channel, the net dipole changes linearly, being zero on average when the ion is at the center of the pore, corresponding to a linear chain of dipoles with equal numbers of waters on either side of the ion oriented in opposite directions.
Fig. 4.
Histogram of single-file water dipole moment μ (A) with corresponding 2D PMF W(z, μ) (B).
The PMF W(z, μ) of Fig. 4B reveals the two possible dipole moments when the ion is in the bulk, and also when the ion resides in the outer binding site. When the ion occupies this site, the preferred state has the water at the end of the single-file column, with its oxygen pointing toward the cation. A steady flow of ions through the channel must, at some point, require a complete flip of the single-file water molecules. Unless the water chain is directed correctly, an approaching ion would simply bounce off the channel entrance. There is a 2- to 3-kcal/mol barrier to this process, in agreement with a previous estimate of 2.2 kcal/mol (47). An alternative pathway for permeation is for the ion to enter the outer binding site and then overcome a smaller barrier of <1 kcal/mol to flip the single-file waters before moving into the inner binding site. However, at moderately high potential difference, the coupling of the single-file water dipole to the transmembrane potential may lead to almost order of magnitude changes in the conductance. Because of the large dipole moment of the single-file water, which changes with ion position, the effect of the applied voltage difference on the ion will be nontrivial (Supporting Text).
Fig. 4A suggests complexities associated with multiple ion permeation, which will be important at high concentration. As an ion approaches from the right, it requires that the dipole moment be –15 D before it enters the pore. Once it reaches the left hand side of the channel, the dipole moment will be +15 D, making it difficult for another ion to enter from the right. Freeing the passage for a second incoming ion on the right would require the left-hand ion to move into the left-hand outer binding site, or further away from the channel. This finding suggests the existence of structural long-range coupling across the pore that would be absent in continuum solvent models. However, because double occupancy perturbs the single-file column significantly (35), no conclusion about the likely positions of the ions in the doubly occupied state can be conjectured without further calculations.
The abrupt change in μ at the outer binding site has implications for free energy calculations of ion permeation because it reveals the presence of a free energy barrier opposing ion permeation that is not a function of the ionic coordinate z. The magnitude of the free energy barrier indicates that a complete flipping of the single-file water molecules will occur on a long time scale, requiring many ns of sampling (explaining the poor sampling in the bulk regions of Fig. 4). Consequently, PMFs based on a single z coordinate, with short umbrella sampling simulations are likely to be inaccurate. From a more fundamental point of view, such a reorientation process cannot easily be incorporated into the simple picture embodied by the Nernst–Planck Eq. 4 theory discussed above. A more complete description of ion conduction should involve not only the ion position z, but also a water dipole moment coordinate (48).
Conclusion
One objective of present-day computer simulations of biological systems is to obtain an accurate quantitative description of function from structure. Ion permeation presents a challenge because of the need to accurately model the strong interactions of ion with bulk water, and with protein in a state of almost complete dehydration. Recent calculations of the PMF of K+ permeation through the gA channel (13) suggested that modern MD force fields fall short of describing the interactions of the ion with the protein and confined water adequately for studies of ion permeation. We show here that improved free energy techniques, and accounting for spurious simulation artifacts, lead to encouraging semiquantitative agreement with experiment and new insights into the permeation mechanism. For the first time, a 2D PMF that is a function of both axial and radial coordinates was calculated to characterize the complete free energy surface governing the permeation of K+ across the gA channel embedded in a phospholipid bilayer membrane. Analysis of the 2D PMF reveals that the classical concept of free energy profile W(z) is meaningful only when the ion is <15 Å away from the center of the channel where its lateral displacements are bounded.
The process of ion association with the channel has been observed to be one of gradual dehydration from approximately seven water molecules in the first hydration shell, to three at the outer binding site and two at the inner binding site. Mean force decomposition demonstrates the striking ability of the single-file water to stabilize an ion by almost half the bulk free energy of solvation in the center of the channel. Although the hydration number of the ion varies monotonically as the ion moves into the single-file region (Fig. 3), the dipole of the single-file water column experiences a transition when 11 < z < 12 (Fig. 4B). The process of flipping the water chain represents a rate-limiting process to ion permeation that is not a function of ion position, suggesting that the dynamics of the ion, together with the orientation of the single-file water, should be considered to describe the mechanism of ion permeation. More generally, this finding reveals a fundamental limitation in permeation models that are based on the assumption that the ion position is the only “relevant” variable. In future studies, it will be important to use computational techniques, such as the Transition Path Sampling (TPS) algorithm (45), to seek a more complete description of ion permeation.
From a technical point of view, vast improvements in PMF calculations have arisen from the availability of inexpensive computer clusters. To exploit this architecture, uncorrelated starting configurations were constructed for each biased window simulation, required in the umbrella sampling calculation, by placing the ion at regular positions along the reaction coordinate. These initial configurations were then equilibrated and simulated concurrently until good convergence of the PMF was achieved. One important advantage of this “placing” procedure is to avoid the inaccuracies observed in previous PMF calculations where the ion was dragged through the different simulation windows sequentially (13, 34). Those errors are caused mainly by slow configurational relaxations in the system, which give rise to nonequilibrium hysteresis growing systematically through the sequential window simulations. In particular, the orientation of the single-file water molecules inside the long and narrow gA channel may be difficult to sample accurately because its transitions are opposed by a significant free energy barrier.
Although gA is the simplest channel, the calculated conductance displays a larger discrepancy with experiment than previous calculations for KcsA (15). A comparison reveals that the β-helical backbone hydrogen bonds must be perturbed for the carbonyl groups to stabilize a permeating cation in gA whereas the carbonyl groups of the selectivity filter point toward the center of the pore and are readily available to coordinate a permeating K+ in KcsA. Modeling this process requires a very accurate representation of not only intermolecular ion–channel and ion–water interactions, but also intramolecular channel interactions. Furthermore, neglect of induced electronic polarizability for those molecular moieties that do not carry a permanent dipole, such as lipid acyl chains and nonpolar side chains, becomes all of the more important. Nonetheless, the agreement with experimental dissociation and conductance measurements is promising and indicative of the overall correctness of the computational method. Beyond these encouraging numerical results, we emphasize that an important strength of the present PMF strategy is to help provide a rigorous conceptual framework to characterize the mechanism of ion conduction at the microscopic level.
Supplementary Material
Acknowledgments
We thank Guillaume Lamoureux for his help with polarizable water and Prof. David Chandler for insightful discussions on reaction coordinates for ion permeation. This work was supported by the Revson and Keck Foundations (T.W.A.) and National Institutes of Health Grants GM21342 (to O.S.A.) and GM62342 (to B.R.).
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: gA, gramicidin A; MD, molecular dynamics; PMF, potential of mean force; NMR, nuclear magnetic resonance; FEP, free energy perturbation.
References
- 1.Karplus, M. (2002) Acc. Chem. Res. 35, 321–323. [DOI] [PubMed] [Google Scholar]
- 2.Zhou, R., Berne, B. J. & Germain, R. (2001) Proc. Natl. Acad. Sci. USA 98, 14931–14936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Roux, B. & Bernèche, S. (2002) Biophys. J. 82, 1681–1684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Andersen, O. & Koeppe, R. (1992) Physiol. Rev. 72, S89–S158. [DOI] [PubMed] [Google Scholar]
- 5.Urry, D. W. (1971) Proc. Natl. Acad. Sci. USA 68, 672–676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sarges, R. & Witcop, B. (1965) J. Am. Chem. Soc. 87, 2011–2020. [DOI] [PubMed] [Google Scholar]
- 7.Arseniev, A. S., Lomize, A. L., Barsukov, I. L. & Bystrov, V. F. (1986) Biol. Membr. (Russia) 3, 1077–1104. [Google Scholar]
- 8.Townsley, L. E., Tucker, W. A., Sham, S. & Hinton, J. F. (2001) Biochemistry 40, 11676–11686. [DOI] [PubMed] [Google Scholar]
- 9.Ketchem, R. R., Roux, B. & Cross, T. A. (1997) Structure 5, 1655–11669. [DOI] [PubMed] [Google Scholar]
- 10.Allen, T. W., Andersen, O. S. & Roux, B. (2003) J. Am. Chem. Soc. 125, 9868–9877. [DOI] [PubMed] [Google Scholar]
- 11.Roux, B. (2002) Acc. Chem. Res. 35, 366–375. [DOI] [PubMed] [Google Scholar]
- 12.Mackay, D. H. J., Berens, P. H., Wilson, K. R. & Hagler, A. T. (1984) Biophys. J. 46, 229–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Allen, T. W., Bastug, T., Kuyucak, S. & Chung, S. H. (2003) Biophys. J. 84, 2159–2168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bernèche, S. & Roux, B. (2001) Nature 414, 73–77. [DOI] [PubMed] [Google Scholar]
- 15.Bernèche, S. & Roux, B. (2003) Proc. Natl. Acad. Sci. USA 100, 8644–8648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Roux, B. (1999) Biophys. J. 77, 139–153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Torrie, G. M & Valleau, J. P. (1977) J. Comp. Phys. 23, 187–199. [Google Scholar]
- 18.Ketchem, R. R., Hu, W. & Cross, T. A. (1993) Science 261, 1457–1460. [DOI] [PubMed] [Google Scholar]
- 19.Kumar, S., Bouzida, D., Swendsen, R. H., Kollman, P. A. & Rosenberg, J. M. (1992) J. Comp. Chem. 13, 1011–1021. [Google Scholar]
- 20.Souaille, M. & Roux, B. (2001) Comput. Phys. Commun. 135, 40–57. [Google Scholar]
- 21.Hille, B. (2001) Ionic Channels of Excitable Membranes (Sinauer, Sunderland MA), 3rd Ed.
- 22.Levitt, D. (1986) Annu. Rev. Biophys. Chem. 15, 29–57. [DOI] [PubMed] [Google Scholar]
- 23.Roux, B. & Karplus, M. (1991) Biophys J. 59, 961–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Roux, B. & Karplus, M. (1991) J. Phys. Chem. 95, 4856–4868. [Google Scholar]
- 25.Berne, B. J., Borkovec, M. & Straub, J. E. (1988) J. Phys. Chem. 92, 3711–3725. [Google Scholar]
- 26.Busath, D. D., Thulin, C. D., Hendershot, R. W., Phillips, L. R., Maughan, P., Cole, C. D., Bingham, N. C., Morrison, S., Baird, L. C., Hendershot, R. J., et al. (2003) Biophys. J. 75, 2830–2844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Stern, H. A. & Feller, S. E. (2003) J. Chem. Phys. 118, 3401–3412. [Google Scholar]
- 28.Lide, D. R. (1992) CRC Handbook of Chemistry and Physics (1991–1992) (CRC, Boston), 72nd Ed.
- 29.Hunenberger, P. H. & McCammon, J. A. (1999) J. Chem. Phys. 110, 1856–1872. [Google Scholar]
- 30.Jordan, P. C., Bacquet, R. J., McCammon, J. A. & Tran, P. (1989) Biophys. J. 55, 1041–1052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Jing, N., Prasad, K. U. & Urry, D. W. (1995) Biochim. Biophys. Acta 1238, 1–11. [DOI] [PubMed] [Google Scholar]
- 32.Hinton, J. F., Whaley, W. L., Shungu, D. C., Koeppe, R. E., 2nd, & Millett, F. S. (1986) Biophys. J. 50, 539–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Olah, G. A., Huang, H. W., Liu, W. H. & Wu, Y. L. (1991) J. Mol. Biol. 218, 847–858. [DOI] [PubMed] [Google Scholar]
- 34.Roux, B. & Karplus, M. (1993) J. Am. Chem. Soc. 115, 3250–3262. [Google Scholar]
- 35.Roux, B., Prod'hom, B. & Karplus, M. (1995) Biophys. J. 68, 876–892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Woolf, T. & Roux, B. (1997) Biophys. J. 72, 1930–1945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Cox, B. G., Hedwig, G. R., Parker, A. J. & Watts, D. W. (1974) Aust. J. Chem. 27, 477–501. [Google Scholar]
- 38.Dzidic, I. & Kebarle, P. (1970) J. Phys. Chem. 74, 1466–1474. [Google Scholar]
- 39.Parsegian, A. (1969) Nature 221, 844–846. [DOI] [PubMed] [Google Scholar]
- 40.Levitt, D. (1978) Biophys. J. 22, 209–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Roux, B., Bernèche, S. & Im, W. (2000) Biochemistry 39, 13295–13306. [DOI] [PubMed] [Google Scholar]
- 42.Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W. & Klein, M. L. (1983) J. Chem. Phys. 79, 926–935. [Google Scholar]
- 43.Lamoureux, G., MacKerell, A. D. & Roux, B. (2003) J. Chem. Phys. 119, 5185–5197. [Google Scholar]
- 44.Andersen, O. S & Procopio, J. (1980) Acta Physiol. Suppl. 481, 27–35. [PubMed] [Google Scholar]
- 45.Bolhuis, P. G., Dellago, C. & Chandler, D. (2000) Proc. Natl. Acad. Sci. USA 97, 5877–5882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Im, W. & Roux., B. (2002) J. Mol. Biol. 391, 1177–1197. [DOI] [PubMed] [Google Scholar]
- 47.Pomès, R. & Roux, B. (2002) Biophys. J. 82, 2304–2316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Schumaker, M. F., Pomes, R. & Roux, B. (2001) Biophys. J., 80, 12–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.