Residual-QSAR. Implications for genotoxic carcinogenesis

Abstract

Introduction

Both main types of carcinogenesis, genotoxic and epigenetic, were examined in the context of non-congenericity and similarity, respectively, for the structure of ligand molecules, emphasizing the role of quantitative structure-activity relationship ((Q)SAR) studies in accordance with OECD (Organization for Economic and Cooperation Development) regulations. The main purpose of this report involves electrophilic theory and the need for meaningful physicochemical parameters to describe genotoxicity by a general mechanism.

Residual-QSAR Method

The double or looping multiple linear correlation was examined by comparing the direct and residual structural information against the observed activity. A self-consistent equation of observed-computed activity was assumed to give maximum correlation efficiency for those situations in which the direct correlations gave non-significant statistical information. Alternatively, it was also suited to describe slow and apparently non-noticeable cancer phenomenology, with special application to non-congeneric molecules involved in genotoxic carcinogenesis.

Application and Discussions

The QSAR principles were systematically applied to a given pool of molecules with genotoxic activity in rats to elucidate their carcinogenic mechanisms. Once defined, the endpoint associated with ligand-DNA interaction was used to select variables that retained the main Hansch physicochemical parameters of hydrophobicity, polarizability and stericity, computed by the custom PM3 semiempirical quantum method. The trial and test sets of working molecules were established by implementing the normal Gaussian principle of activities that applies when the applicability domain is not restrained to the congeneric compounds, as in the present study. The application of the residual, self-consistent QSAR method and the factor (or average) method yielded results characterized by extremely high and low correlations, respectively, with the latter resembling the direct activity to parameter QSARs. Nevertheless, such contrasted correlations were further incorporated into the advanced statistical minimum paths principle, which selects the minimum hierarchy from Euclidean distances between all considered QSAR models for all combinations and considered molecular sets (i.e., school and validation). This ultimately led to a mechanistic picture based on the identified alpha, beta and gamma paths connecting structural indicators (i.e., the causes) to the global endpoint, with all included causes. The molecular mechanism preserved the self-consistent feature of the residual QSAR, with each descriptor appearing twice in the course of one cycle of ligand-DNA interaction through inter-and intra-cellular stages.

Conclusions

Both basal features of the residual-QSAR principle of self-consistency and suitability for non-congeneric molecules make it appropriate for conceptually assessing the mechanistic description of genotoxic carcinogenesis. Additionally, it could be extended to enriched physicochemical structural indices by considering the molecular fragments or structural alerts (or other molecular residues), providing more detailed maps of chemical-biological interactions and pathways.

Introduction

It is widely recognized that cancer and carcinogenesis are the main challenges facing 21st Century medicinal chemistry [1,2], particularly in the area of preventative toxicology [3-6] as it assumes an idealized toxicity against organisms and acts through a subtle, undiscovered molecular mechanism. The basic mechanism in cancer cell proliferation is through a variety of compounds, making it difficult to assess specific ligand-receptor interaction patterns [7,8].

There is a reasonable basis for cancer apoptosis in the electrophilic theory of Miller and Miller [9,10], which assumes a positively charged or polarized nature of the ligand (carcinogenic alkylating agents, originally). Currently, there is a more integrated and general view of genotoxic carcinogenicity [11] that is closely related to mutagenic phenomena through a covalent binding to DNA, followed by direct damage by means of a unified (or by reactive intermediates) electrophilic mechanism of action. In contrast, epigenetic carcinogenesis [12] activates through a variety of specific and different mechanisms that do not involve covalent binding to DNA but to more congeneric (or similar) molecules, with a specific (or local) mechanism of action for each particular set of compounds.

Even though epigenetic carcinogenesis has typically been treated with the structure-activity relationship (QSAR) principle of congenericity [13], the present report will focus on genotoxic carcinogenesis because of its chemical bonding at the DNA level. In addition, the statistical physicochemical combination analysis for a variety of toxicants produces a molecular mechanistic model of action with a comprehensive physicochemical interpretation.

With the ever-increasing costs of traditional animal testing and the large number of industrial chemicals that need toxicological evaluation, international programs like Europe's REACH (Registration, Evaluation and Authorization of Chemicals) expressly endorse in silico (computational) ecotoxicological studies as alternative approaches to reduce experimental hazard, especially when "testing does not appear necessary" [14]. This strategy is particularly useful in the first phases of validation for a new compound, before entering the industrial mainstream. This process primarily consists of preliminary screening based on models of literature and their extrapolations (Phase I), followed by the read-across, grouping and construction of new models employing the available commercial or non-commercial models, such as OncoLogic [15], HazardExpert [16], Derek [17], ToxTree [18], Multicase [19], and CAESAR [20,21] (Phase II), and eventually concluding with in vitro or in vivo assays (Phase III).

Phases I and II are theoretical-computational and, when approached through statistical or multivariate methods, the OECD (Organization for Economic Cooperation and Development) principles for a QSAR study must include the following information [22,23]: "(i) a defined endpoint, (ii) an unambiguous algorithm, (iii) a defined domain of applicability, (iv) appropriate measures of goodness-of-fit, robustness and predictivity, and (v) a mechanistic interpretation."

In this context, the goal of the present work was to advance a general QSAR modeling approach employing the residues of direct correlation with definite physico-chemical descriptors to a second (or looping) correlation with the residual QSAR method. This was then applied to a non-congeneric series of rat toxicants to discover a general mechanism for genotoxic carcinogenesis in accordance with OECD-QSAR principles.

Residual-QSAR Method

Assuming there is a structure-activity multi-linear correlation problem with the parameters and observed endpoint set as 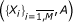, the standard QSAR corresponds to the ordinary regression equation producing the following computed activity [24]:

(1)

However, in carcinogenic modeling, it is difficult to find a proper set of structural parameters with significant correlation to the observed activity, especially when considering compounds having highly diverse molecular structures (i.e., being non-congeners) yet producing similar carcinogenic endpoints. Even by applying the available commercial or academic software to compute thousands of structural parameters and their non-linear combinations [25], the obtained significant correlation relies on structural parameters or combinations thereof with little physical or chemical meaning. This makes QSAR analysis an artifact outside of reality [26]. Such studies may not include the hydrophobic feature (LogP) within the correlation equation (Tarko L, Putz MV: On Quantitative Structure-Toxicity Relationships (QSTR) using High Chemical Diversity Molecules Group, submitted), which has less physico-chemical meaning, especially with respect to cellular toxicity.

In such circumstances, it is preferable to test the induced influence of a given set of structural parameters with established significance over the cancer genotoxicity correlation (Eq. (1)). Hypothetically, this shows the direct, scarce correlation with the observed activity. The residual correlation follows (Eq. (2)):

(2)

From this point forward, one may use the various residual-QSAR (res-QSAR) models to obtain the correlation equation of the computed activity in terms of the original structural parameters.

Self-Consistent res-QSAR Model

One may insert equation (1) into equation (2), while preserving the observed activity by the rule of computed activity:

(3)

This model has the conceptual advantage of containing looping or self-consistent QSAR information that is in line with the recursive evolution of cancer at the cellular level. It has also an apparent weakness in that it requires prior knowledge of the observed activity, even for the untested compounds or those that are designed in silico. However, such a drawback may now be avoided with the advent of unified databases with the aid of software to presumptively assess the "observed" activity of any common molecular-species couples [27].

Asymptotic res-QSAR Model

The obtained residual-QSAR matches were assumed with the observed activity,

(4)

yielding the following asymptotic residual-model from Equations (1) and (2):

(5)

This model illustrates the residual QSAR method to amplify asymptotically the computed toxicity towards the observed carcinogenicity (Figure 1). This considers the limitation of no use when considering the case of b₁ → 1, which produces the asymptotic (infinite) expressed activity Y_A→ ∞ with residual correlation. This difficult computation can be removed by reconsidering the residual equation (2) within different computational activity frameworks that are suited to assess the carcinogenic molecular mechanisms.

Figure 1.

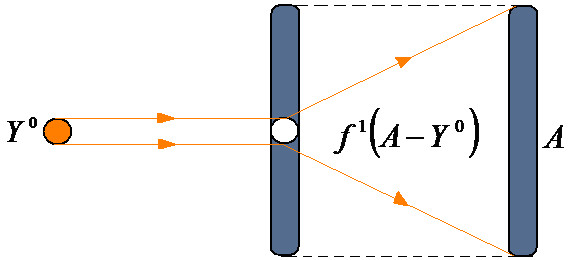
Representation of the residual-QSAR algorithm from a given computed activity (Y⁰) to the observed one (A) through the "diffracting" process of the residual A-Y⁰ activity.

Factor res-QSAR Model

If the observed, computational activity is proportionality confirmed by the following residual correlation factor,

(6)

then equation (5) can be modified to the following workable model (Eq. 7).

(7)

This model will eventually "diverge" when the residual correlation factor approaches unity (R₁→ 1), along with the asymptotic condition, b₁→ 1, noting the same asymptotic feature of this model as its ancestor, Eq. (5). This model is still identical to that obtained from replacing the residual factor with its complement, R₁→ 1-R₁, because of the scale multiplication operation with the same correlation efficiency.

Averaged res-QSAR Model

When the presence of the observed activity dependency is replaced by its average within the self-consistent equation (Eq. (3)) over the entire N-molecular series, the averaged residual-QSAR model is changed to the following:

(8)

where the average activity may be computed either as a simple statistical mean,

(9)

or as the interpolation function, A = f_A(N), which is averaged as the integral,

(10)

Conceptually, the residual QSAR features correlation performances complementary to the direct QSAR analysis. This is effective in assessing the molecular phenomenology of cancer genotoxicity, as the direct structural parameters show little correlation. In addition, they apparently have no direct influence on observed activity, and slow-acting carcinogenesis does not have a significant, direct influence on physicochemical, structural parameters. However, for congeneric molecular species, significant direct correlation is expected, with low residual-QSAR influence as its statistical-information complement. Therefore, the present residual-QSAR approach is best suited for non-congeneric compounds, such as those involved in genotoxic carcinogenesis. The present study will provide concrete illustration of the direct and residual QSAR models and their interpretation towards assessing a molecular mechanism for the observed genotoxic carcinogenesis, in accordance with OECD principles.

Application and Discussion

This application and analysis will parallel the OECD-QSAR principles discussed in the introduction. However, the OECD principles of QSAR modeling are not regarded as separate, but they are linked as much as the practical-computational context is unfolded.

(i) The actual defined endpoint is defined as the excessive apoptosis with the TD50 rate (in mg/kg body wt/day) of carcinogenic potency in rats derived from the Carcinogenic Potency Database [28]. This refers to the (half) probability that tumor cells develop through ingestion in each positive experiment with the species. Therefore, the present residual-QSAR study provides a mechanistic interpretation of how the extrinsic inducers (i.e., the toxins in the molecular trial or testing-predicting series, see Tables 1 and 2[29], respectively) cross the cellular plasma membrane and/or transduce/induce a positive signal trigger of DNA binding and subsequent genotoxic carcinogenesis.

Table 1.

The molecules listed with their effect on rat TD50 activity [28] and the semi-empirical PM3 (Hyperchem [29]) computed structural parameters of hydrophobicity (LogP), polarizability (POL, in ų) and total optimized energy (Etot, in kcal/mol) belonging to the Gaussian training set illustrated in Figure 2.

No.	Chemical Compound	Formula	CASRN	TD50_Rat(a)	A(b)	logP	POL	Etot
1	3,3'-Dimethoxy-4,4'-biphenylene diisocyanate	C16H12N2O4	91-93-0	1630	2.79	2.07	30.03	-82478.58594
2	Chrysazin (Danthron)	C14H8O4	117-10-2	245	3.61	1.87	24.44	-68162.28125
3	Acetaldehyde	C2H4O	75-07-0	153	3.82	-0.58	4.53	-13662.00781
4	Allyl isothiocyanate	C4H5NS	57-06-7	96	4.02	1.17	11.74	-20700.27344
5	Isobutyl nitrite	C4H9NO2	542-56-3	54.1	4.27	1.63	9.96	-31363
6	Urethane	C3H7NO2	51-79-6	41.3	4.38	-0.06	8.35	-27989.58203
7	Ethylene oxide	C2H4O	75-21-8	21.3	4.67	-0.16	4.31	-13626.54297
8	Hexa(hydroxymethyl)melamine	C9H18N6O6	531-18-0	10.2	4.99	1.96	27.19	-108827.0859
9	1,2-Dichloroethane	C2H4Cl2	107-06-2	8.04	5.09	1.59	8.3	-21506.41406
10	Tris(2,3-dibromopropyl) phosphate	C9H15Br6O4P	126-72-7	3.83	5.42	5.37	35.91	-108827.0859
11	Beta-Propiolactone	C3H4O2	57-57-8	1.46	5.84	-0.25	6.23	-23148.73047
12	Chlorambucil	C14H19Cl2NO2	305-03-3	0.896	6.048	4.14	31.04	-76933.42969
13	Azaserine	C5H7N3O4	115-02-6	0.793	6.10	-1.03	14.25	-54439.625
14	Dacarbazine	C6H10N6O	4342-03-4	0.71	6.15	-0.92	17.95	-49126.58594
15	Thiotepa (Tris(aziridinyl)-phosphine sulfide)	C6H12N3PS	52-24-4	0.164	6.789	0.54	17.63	-38905.46484
16	Aflatoxin-B1	C17H12O6	1162-65-8	0.0032	8.49	0.99	29.86	-91307.82331
17	2,3,7,8-Tetrachlorodibenzo-p-dioxin	C12H4 Cl4 O2	1746-01-6	0.0000457	10.34	4.93	28.31	-76933.75
18	Aflatoxicol	C17H14O6	29611-03-8	0.00247	8.61	0.46	30.41	-91979.58594
19	1-(2-Hydroxyethyl)-1-nitrosourea	C3H7N3O3	13743-07-2	0.244	6.61	-0.95	10.92	-42184.19141
20	N'-Nitrosonornicotine-1-N-oxide	C9H11N3O2	78246-24-9	0.876	6.06	0.25	19.48	-53174.95313
21	Benzo(a)pyrene	C20H12	50-32-8	0.956	6.02	5.37	36.04	-58881.02734
22	2-Acetylaminofluorene	C15H13NO	53-96-3	1.22	5.91	2.61	26.26	-56110.60547
23	1,2-Dibromoethane	C2H4Br2	106-93-4	1.52	5.82	1.71	9.7	-28203.0625
24	Hydrazobenzene	C12H12N2	122-66-7	5.59	5.25	3.8	19.85	-67801.28125
25	Ethylene thiourea (ETU)	C3H6N2S	96-45-7	8.13	5.09	0.33	11.45	-22095.42578
26	Thioacetamide	C2H5NS	62-55-5	11.5	4.94	-0.21	9.04	-15263.96289
27	o-Nitroanisole	C7H7NO3	91-23-6	15.6	4.81	-0.18	14.75	-45613.03906
28	2-Aminodipyrido[1,2-a:3',2'-d]imidazole	C10H8N4	67730-10-3	42.3	4.37	2.35	20.73	-45103.06641
29	Dichlorodiphenyltrichloroethane (DDT)	C14H9Cl5	50-29-3	84.7	4.07	6.39	33.4	-77956.60156
30	p-Cresidine	C8H11NO	120-71-8	98	4.01	1.48	16.09	-36280.75391
31	Ethyl 2-(4-chlorophenoxy)-2-methylpropionate	C12H15ClO3	637-07-0	169	3.77	2.97	24.73	-65740.6875
32	Vinyl acetate	C4H6O2	108-05-4	341	3.47	-0.01	8.65	-26598.12305
33	Salicylazosulfapyridine	C18H14N4O5S	599-79-1	1590	2.799	4.54	36.79	-107222.1719

^(a) in [mg/kg body wt/day]; ^(b) computed as Log[1/TD₅₀]

Table 2.

The molecules belonging to the quasi-Gaussian test set, as illustrated in Figure 2, with the same type of activity and structural parameters as those reported in Table 1.

No.	Chemical Compound	Formula	CASRN	TD50_Rat(a)	A(b)	logP	POL	Etot
34	Phenacetin	C10H13NO2	62-44-2	1250	2.90	0.99	19.85	-49230.08203
35	Dimethylvinyl chloride (DMVC)	C4H7Cl	513-37-1	31.8	4.498	1.51	9.85	-20725.60325
36	Sulfallate	C8H14ClNS2	95-06-7	26.1	4.58	2.73	24.79	-46435.69922
37	beta-Butyrolactone	C4H6O2	3068-88-0	13.8	4.86	0.17	8.06	-26599.55273
38	Vinyl Chloride	C2H3Cl	75-01-4	6.11	5.21	1.01	6.18	-13820.70898
39	Acrylamide	C3H5NO	79-06-1	3.75	5.43	-0.28	7.52	-20478.92578
40	Mirex	C10Cl12	2385-85-5	1.77	5.75	6.41	38.39	-114919.4688
41	Dimethylnitramine	C2H6N2O2	4164-28-7	0.547	6.26	0.97	7.64	-28551.91406
42	N-Nitrosodimethylamine	C2H6N2O	62-75-9	0.0959	7.02	0.01	7.01	-21802.08203
43	N-Methyl-N'-nitro-N-nitrosoguanidine	C2H5N5O3	70-25-7	0.803	6.1	1.5	11.13	-46112.81641
44	1-Phenyl-3,3-dimethyltriazene	C8H11N3	7227-91-0	2.31	5.64	2.53	17.51	-36944.65625
45	Michler's ketone	C17H20N2O	90-94-8	5.64	5.25	3.4	22.8	-44481.07422
46	1'-Acetoxysafrole	C12H12 O4	34627-78-6	25	4.6	-0.11	22.47	-64108.48047
47	o-Nitrosotoluene	C7H7NO	611-23-4	50.7	4.29	2.29	13.48	-32074.53516
48	p-Nitrosodiphenylamine	C12H10 N2O	156-10-5	201	3.7	3.07	22.66	-50526.36328
49	1,4-Dichlorobenzene (p-dichlorobenzene)	C6H4Cl2	106-46-7	644	3.19	3.08	14.29	-32415.54297

^(a) in [mg/kg body wt/day]; ^(b) computed as Log[1/TD₅₀]

(ii) The unambiguous algorithm is addressed by four stages:

• The first is the hypothesis-driven selection of variables, as suggested by Hansch [30], with clear physicochemical interpretation. Because genotoxicity implies that the electrophilic effects of compound-DNA binding, the basic influences of hydrophobicity (LogP, modeling the traversing of the host cellular membrane) and polarizability (POL, modeling the charge deformation of the molecule while approaching and binding, as electrophilic theory prescribes) along the optimal total energy (Etot, modeling the stereochemistry and optimal 3D molecular conformation approaching DNA biding) are separately explored and combined to assess the synergetic translation-, vibration-and rotation-based mechanisms, respectively. Clear physical and chemical meaning is maintained with this approach by offset, and this has also recently been confirmed by several ecotoxicological studies [31-34].

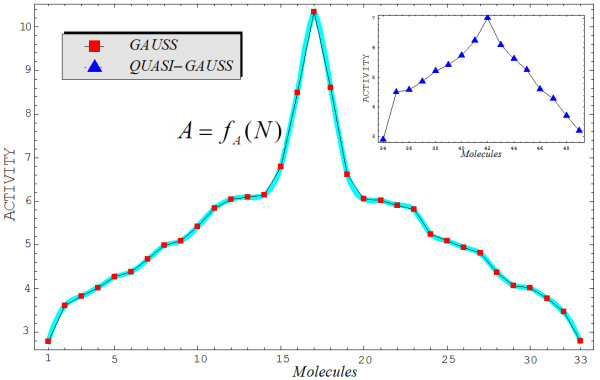
• The selection of a trial (school) and test (for prediction) set of molecules from a pool of available molecules does not necessarily set the domain of applicability, but once such a domain is available or defined, certain molecules are assessed in the trial and test series. In this respect, this part of the OECD Second QSAR Principle includes the Third QSAR Principle. Although many statistically-or logically-based screening methods are available [35,36], we chose other principles that are included in the normal ordering of observed activities, despite the degree of similarity of the molecules in the available domain of selection. The method used was quite general. If the domain contained congeneric molecules, then the best-fitting activity with a Gaussian curve was selected first, leaving the rest for the test set (i.e., in an ideal case, this should represent another Gaussian set of molecular activities). If the available molecules were not congeneric and the similarity rule did not apply (i.e., the present study), then we applied a natural principle to the trial and test molecules. The application of this principle of normal activities (presumed to be more general than the principle of congenericity in the selection of a QSAR school and predicting molecules) is shown in Figure 2, with reference to the trial and test molecules of Tables 1 and 2, respectively.

Figure 2.

Graphical representation of the working activities for the molecules in Tables 1 and 2, classified to build up the "Gaussian" and "quasi-Gaussian" series that are specific to the training and testing QSAR purposes, respectively. The interpolating function, A = f_A(N), to be used in Equation (10) is also shown as the contour of the Gaussian set of trial molecules.

• The computational stage of variables assigns numbers to all structural descriptors considered for each molecule in the trial and test sets and yields quantum accuracy values for selected physicochemical variables. In the present study, the particular values of the LogP, POL, and Etot indices are given in Tables 1 and 2, reported using the semiempirical PM3 method for each molecule considered in the trial and test series, respectively. At this point, worth noting that the so called "equal stericity" (and energy) degree of freedom was considered for molecules 8 and 10 of Table 1, permitted for about 10% of the total pool of molecules, for those compounds closely laying on the Gaussian graph of Figure 2 as well as having identical carcinogenic characteristics as damage factor, disease-specific part of the effect factor, or the same uncertainty factor of the combined damage and effect factor [37]; such conditions allow similar information in a series with high diverse molecules in order to make the analysis a step closer to the traditional QSAR dogma of "congeneric molecules" [13].

• The analytical stage of the QSAR model yielded the regression equations and their correlation factors and allied statistical descriptors. Table 3 gives the direct and residual QSAR models for all descriptor combinations considered for the trial molecules of Table 1 according to Equations (1) and (2), respectively. As anticipated, while the direct QSAR provided very low correlations, the residual-QSAR was characterized by the limiting case of unity factors of residuals, which raised the residual correlation factor as much as the complementary direct QSAR was lowered. The direct and residual QSAR complementary nature was, in this way, advanced. In particular, the lowest direct correlation, the LogP mechanism, corresponded to the highest residual QSAR. At the same time, when LogP was further synergistically combined with other structural influences like POL and Etot, the direct potency increased by a factor of one hundred, whereas the residual QSAR correlations decreased by only a few units. This proves the utility of the direct QSAR principle in assessing a statistical model that could be supplemented with further considerations, as with residual QSAR and other validity measures, to provide the best understanding of the analyzed phenomenon. Table 4 compares the detailed self-consistent principle with the factor and averaged versions of the residual QSAR modeling of Equation (3). If Equation (3) is amended with the residual correlation factor or its complement to yield the observed-to-QSAR activity proportionality or if the averaged activity in Equation (8) is replaced with expressions of Equations (9) (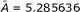) and (10) (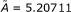), then the results are systematically the same or very close to those reported in Table 3. In other words, whenever the model resembles the direct molecular variables' dependency, the direct QSAR statistical efficiency will be systematically reached.

Table 3.

The parameters and statistical correlation coefficients for the residual-QSAR algorithm of Equations (1) and (2), as applied to the molecules of Table 1 in all possible combinations of variables.

STRUCTURAL VARIABLES	a0	bi0			R0	a1	b1	R1
LogP	5.297587	-0.007280			0.0091	5.285636	1	0.9999
POL	4.712835	0.029613			0.1832	5.285636	1	0.9831
Etot	4.676954	-0.000011			0.2033	5.285636	1	0.9791
LogP, POL	4.339331	-0.279746		0.072662	0.2925	5.285636	1	0.9563
LogP, Etot	4.578059	-0.162902		-0.000018	0.2608	5.285636	1	0.9654
POL, Etot	4.679442	-0.000978		-0.000012	0.2033	5.285636	1	0.9791
LogP, POL, Etot	4.341697	-0.273668	0.06646	-0.000002	0.2929	5.285636	1	0.9562

Table 4.

Residual-QSAR self-consistent (SC), factor (F1), averaged (AV, with 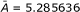) models of Equations (3), (7), and (8) for the Hansch parameters of Table 3, with the modeling and predictive powers for the "Gaussian" and "Quasi-Gaussian" molecules of Tables 1 and 2 represented by their associated correlation factors, respectively.

Structural Variables	Activity Model
	Type	Equation	RGauss	RQ-Gauss
Ia: LogP	SC	A-0.011951 + 0.00728[LogP]	0.99996	0.99994
	F1	-119.51 + 72.8[LogP]	0.0091	0.1240
	AV		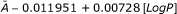0.0091	0.1240
Ib: POL	SC	A + 0.572801-0.029613[POL]	0.98307	0.97713
	F1	33.8936-1.75225[POL]	0.1832	0.23179
	AV		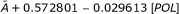0.1832	0.23179
Ic: Etot	SC	A + 0.608682 + 1.1 × 10-5[Etot]	0.98362	0.97238
	F1	29.1235 + 5.26316 × 10-4[Etot]	0.2033	0.04250
	AV		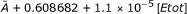0.2033	0.04250
IIa: LogP, POL	SC	A + 0.946305 + 0.279746[LogP]-0.072662[POL]	0.95626	0.94916
	F1	21.6546 + 6.40151[LogP]-1.66275[POL]	0.2925	0.21906
	AV		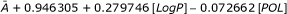0.2925	0.21906
IIb: LogP, Etot	SC	A + 0.707577 + 0.162902[LogP] + 1.8 × 10-5[Etot]	0.96686	0.96164
	F1	20.4502 + 4.70815[LogP] + 5.20231 × 10-4 [Etot]	0.2608	0.0524
	AV		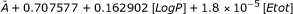0.2608	0.0524
IIc: POL, Etot	SC	A + 0.606194 + 0.000978[POL] + 1.2 × 10-5 [Etot]	0.97838	0.97017
	F1	29.0045 + 0.046793[POL] + 5.74163 × 10-4 [Etot]	0.2033	0.03654
	AV		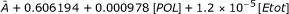0.2033	0.03654
III: LogP, POL, Etot	SC	A + 0.943939 + 0.273668[LogP]-0.06646[POL] + 2. × 10-6[Etot]	0.95628	0.94927
	F1	21.5511 + 6.24813[LogP]-1.51735[POL] + 4.56621 × 10-5[Etot]	0.2929	0.19871
	AV		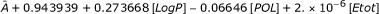0.2929	0.19871

(iii) The defined domain of applicability, although conceptually included in one of the above stages of the unambiguous algorithm framework, is customarily specified separately for clarity. However, because the present application focused on modeling genotoxic carcinogenesis, this principle is redundant because of its implicit non-congeneric approach features. As such, the molecules in Tables 1 and 2 span many organic classes and derivatives, including amides, amines, aromatic systems, lactones, nitrites, quinines, cyanides, urethanes, ketones, and cycloalkanes. The QSAR analysis and mechanistic model was, therefore, expected to have non-local character (i.e., not depending on the series of toxicants involved) susceptible of general behavior.

(iv) The validity and predictivity principle is considered to be one of the most important stages of QSAR analysis. Although internal and external validation statistical procedures exist, the former is often overestimated. This has been confirmed in situations when the external validation sets were well predicted, even with poor cross-validated performance [38]. As a general rule, external validation tests are considered the true standard to assess prediction in QSAR modeling. Focusing on the special case of genotoxicity, one must consider all residual QSAR models obtained within previous QSAR principles (i.e., the self-consistent and factor/averaged residual QSAR models of Table 4, in particular) while remembering that the last ones resemble the direct QSAR statistical performances. The external validation set is presented in Table 2 and was identified through the quasi-Gaussian shape of the Figure 2 inset. The testing set and associated statistical performances are reported in the last column of Table 4. These need to be interpreted in light of the searched mechanistic model, or the predictive power lies only in the range of the residual QSARs, with no real information contained therein. This will be realized by applying the final principle of the OECD-QSAR framework.

(v) The possibility of advancing a mechanistic interpretation may be achieved by applying the statistical information from all trial and test sets and residual-QSAR modeling levels. If uniform criteria are implemented, one may specialize this principle by the minimum (statistical) path principle. Like all natural optimum principles, it assumes the shortest statistical path selected among all possible paths connecting the QSAR models. In all trial and test cases, it synergistically includes the primary path of action in terms of the physicochemical descriptors. Consequently, this principle also provides the second and third paths and the entire hierarchy of structural causes successively triggering the investigated endpoint effect with the observed actions. The minimum path principle ultimately reveals the structural causes and corresponding mechanistic picture, linking them to the observed action and providing the described biological effect. Depending on the QSAR model and statistical information to be processed, the statistical paths can be computed in various forms. For example, with the aid of Euclidean measure, similar studies recently presented the Spectral-SAR algebraic version of the consecrated QSAR applied to various ecotoxicological scenarios [31,34,39]. Accordingly, the correlation factors of Table 4 were combined through all statistical path combinations [40]:

(11)

with

(12)

The numbers of paths built from connected, distinct models were indexed with k orders (dimension of correlation space or the number of structural variables included in a given model) from k = 1 to k = M. Each path was then computed by the Euclidean formula,

(13)

with

(14)

being the number of combinations of structural indicators potentially considered. Then the minimum principle can be written as

(15)

with l₁,...,l_k,...,l_Mrepresenting the endpoint residual-QSAR regression models computed with 1, 2,..., M structural parameters, respectively.

The results are collected in Table 5, where the first (alpha), second (beta), and third (gamma) statistical paths are indicated. They were computed by the described optimal procedure with the amendment that, in the case of equal correlation paths, the minimum path was considered to cover the QSAR model with the highest correlation factor. Once a path was selected, the next hierarchical path was chosen as the minimum among the remaining ones, such that all considered endpoints were involved only once (except for all variables containing endpoint-the model III-that is a common horizon to all other combinations). With this method, the correlation information was combined and employed in the most general and natural manner, providing suitable structural paths to cause the observed activity. This also assured unity/specificity along the ergodicity of the paths' maps. Similar rules apply in deciding the overall models of Table 5, which is most representative to the alpha, beta and gamma paths. The path that is reached the most times throughout all the residual-QSARs was considered adjudicated for a given path type. In particular, the procedure started with the alpha path, which corresponds to the following chain of models (Table 5):

(16a)

Table 5.

Synopsis of the statistical paths connecting the correlation factors for the models of Table 4.

Statistical Path	Self-Consistent res-QSARs		Factor and Averaged res-QSARs
	Gauss	Q-Gauss	Gauss	Q-Gauss
Ia-IIa-III	0.04372γ	0.05089γ	0.2838γ	0.11541
Ia-IIb-III	0.04368	0.05067	0.2838	0.21791
Ia-IIc-III	0.04368	0.05067	0.2838	0.24963γ
Ib-IIa-III	0.02683	0.02808	0.1097	0.03308α
Ib-IIb-III	0.02679	0.02786β	0.1097β	0.3257
Ib-IIc-III	0.02679α	0.02786	0.1097	0.35742
Ic-IIa-III	0.02738	0.02333	0.0896	0.19691
Ic-IIb-III	0.02734β	0.02311	0.0896	0.15621β
Ic-IIc-III	0.02734	0.02311α	0.0896α	0.16813

It is then followed by the beta path identified by the models' sequence

(16b)

and, finally, by the gamma path's progression

(16c)

All these paths were selected more than once from all of the computed residual-QSARs in Table 5. In addition, part of the alpha path is identified first, and the rest should fulfill the ergodicity rule invoked above at this level (i.e., characterizing the models' sequence not previously consumed).

By analyzing the results of Equations (16a-c) to understand the molecular mechanics from inter-to intracellular space, we can see that the intermediate residual-QSARs that approximate the interaction of structures with the environment can be retained. This method was inspired by the Husserl phenomenology method [41], which puts the core of the event in parenthesis and excludes the very incipient moments (i.e., the initial, transient stage does not decisively count in evolution) and those of the very final recordings (i.e., when all causes are mixed) to understand properly the evolutionary causes of some event. As a result, the molecular mechanism of genotoxic carcinogenesis may be a result of the succession of several linked structural causes,

(17)

beginning with the associated scenario (Figure 3[42]). A molecule is first polarized (POL) upon entering intercellular space due to the plasmatic environment's solvent effects. It then rotates to the optimal steric position (Etot) to realize cellular membrane transduction by activating its hydrophobicity (LogP). It may travel this way though the cellular space while binding to DNA elements via further steric interactions (Etot) and while remaining polarized. It may eventually break some parts of DNA residues and carry them in the extra-cellular space (LogP), where the enriched molecule will suffer further polarization (POL) from solvent interactions with the new molecular structure. The mechanism then enters a new ligand-DNA cycle, while the remaining DNA will enter mutagenesis. Remarkably, each considered structural (causal) indicator acted twice at the level of one interaction cycle in the obtained mechanism (17) in accordance with the self-consistent nature of the present residual-QSAR analysis (Eq. (3)).

Figure 3.

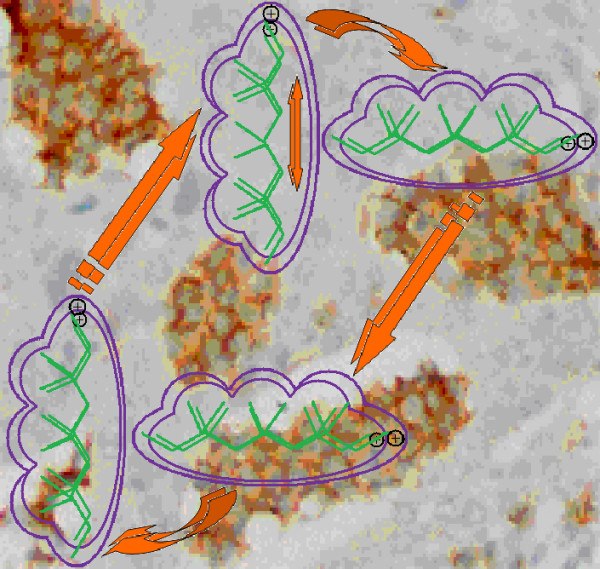
Illustration of the molecular mechanism for genotoxic carcinogenesis according to the present residual-QSAR correlation-path hierarchy superimposed over an immunohistochemcial analysis of paraffin-embedded sections of rat intestinal cancer using the Caspase-2 antibody [42].

More detailed mechanisms of action may describe genotoxic carcinogenesis if additional physicochemical information is considered, but the steps of analysis would be the same. Additional, detailed intermediate steps would need to be added, while preserving the mechanisms' self-consistency and cyclic character through the statistical paths. The electrophilic influence (through polarization) should also be included as a natural generalization of Millers' theory.

Conclusions

Cancer is often called "the disease of the 21st Century," and its phenomenology still resists conceptual clarifications, despite continuous laboratory and clinical efforts through trial-and-error attempts to design suitable drugs and vaccines against its various forms of action [43,44]. The quantitative structure-activity relationship (QSAR) is recognized for the modeling and prediction of complex ligand-receptor interactions at bio-, eco-, or pharmacological levels, and can further our understanding of mutagenesis and carcinogenesis. In this context, the present work advanced a complementary form of QSAR under its residual version. It specifically applies to the modeling of genotoxic interactions, where toxicants covalently bind to DNA by a mechanism that involves an electrophilic stage (i.e., polarization). Residual QSAR methods have the following features:

• Self-consistency (i.e., looping or cyclicity) of the computed activity that respects the observed one, with both contained in the same multilinear equation;

• They are suited for non-congeneric series that display low-direct-correlation-models to almost all common physicochemical descriptors. Complementary high-correlation factors cause the residual QSAR to induce remaining effects that slowly grow over many cycles, producing cancer cells as an exacerbated apoptosis.

The presented application clearly illustrates these basic residual-QSAR properties, implemented in close agreement with the regulatory OECD principles on multi-regression models. It also advances the principle of normal activities in the screening stage of selecting the trial from the test sets of compounds. This is presumed to have more power than the consecrated QSAR dogma of congenericity, which is not applicable for genotoxic effects. The principle of minimum paths across the computed endpoints was reloaded at the statistical level of only correlation factors, leading to a complete ergodic-hierarchical framework that permits the identification of the structural dynamics triggering carcinogenesis. The structural causes entered a single cycle of inter-and intracellular interactions twice overall, resembling the self-consistency or looping specificity of the employed residual QSAR modeling. The present analysis may be naturally extended to include more structural descriptors to enrich the detailed interaction scheme of the toxicant-DNA binding and growing cancer cells. It may also consider the influence of molecular fragments, especially through structural alerts [45]. Such studies are currently in progress and will be the subject of forthcoming communications targeting a conceptual understanding of genotoxic carcinogenesis by means of QSAR modeling and its associated principles.

Competing interests

The author declares that he has no competing interests.

Acknowledgements

Author thanks Romanian Ministry of Education and Research for supporting the present work through the CNCS-UEFISCDI (former CNCSIS-UEFISCSU) project < Quantification of The Chemical Bond within Orthogonal Spaces of Reactivity. Applications on Molecules of Bio-, Eco-and Pharmaco-Logical Interest>, Code PN II-RU-TE-2009-1 grant no. TE-16/2010-2011.