Analysis of Functional Responses at G Protein-Coupled Receptors: Estimation of Relative Affinity Constants for the Inactive Receptor State

Abstract

We describe a modification of receptor theory that enables the estimation of relative affinity constants for the inactive state of a G protein-coupled receptor. Our approach includes the traditional parameters of observed affinity (K_obs) and efficacy (fraction of ligand-receptor complex in the active state, ε) and introduces the concept of the fraction of the ligand-receptor complex in the inactive state (intrinsic inactivity, ε_i). The relationship between receptor activation and the ligand concentration is known as the stimulus, and the operational model expresses the response as a logistic function of the stimulus. The latter function includes K_obs and the parameter τ, which is proportional to ε. We introduce the parameter τ_i, which is proportional to ε_i. We have previously shown that the product, K_obsτ, of one agonist, expressed relative to that of another (intrinsic relative activity, RA_i), is a relative measure of the affinity constant for the active state of the receptor. In this report, we show that the product, K_obsτ_i, of one agonist, expressed relative to that of another (intrinsic relative inactivity, RI_i), is a relative measure of the affinity constant for the inactive state of the receptor. We use computer simulation techniques to verify our analysis and apply our method to the analysis of published data on agonist activity at the M₃ muscarinic receptor. Our method should have widespread application in the analysis of agonist bias in drug discovery programs and in the estimation of a more fundamental relative measure of efficacy (RA_i/RI_i).

Introduction

An abundance of evidence indicates that receptors evolved to act as molecular switches that undergo a conformational change into an active state when occupied by an endogenous agonist. Some of the strongest evidence for this view comes from the results of single-channel recordings at ligand-gated ion channels, which show an abrupt quantal increase in conductance upon binding of agonist with no evidence of gradual conductance changes (Colquhoun and Sakmann, 1985). At G protein-coupled receptors, the active state of the receptor presumably interacts with a conformation of the heterotrimeric G protein that has the guanine nucleotide-binding pocket on the ras domain of Gα opened up for rapid GDP-GTP exchange (Oldham and Hamm, 2008).

The existence of quantal receptor states is not inconsistent with an agonist having a continuum of observed affinities for a G protein-coupled receptor, depending upon the concentration of G protein in the plasma membrane, the type of G protein with which the receptor interacts, and the concentration of guanine nucleotide. These factors can change the observed affinity of the agonist-receptor complex over a broad interval bounded on the high and low ends by the microscopic affinity constants of the agonist for the active and inactive states of the receptor, respectively (Ehlert, 2008). Thus, two states of the receptor can give rise to a continuum of observed affinities and efficacies. There may also be multiple active receptor states that exhibit differential selectivity for signaling proteins (i.e., G proteins or G protein-coupled receptor kinases), giving rise to biased agonism (Kenakin, 2011).

Although the estimation of observed affinity and relative efficacy provides an accurate estimate of how an agonist interacts with the receptor population, these macroscopic constants can vary for the same agonist-receptor complex as just described. However, the affinity constants of the agonist for the ground (K_a) and active (K_b) states of the receptor are invariant and represent a more fundamental estimate of the agonist-receptor interaction because a change in the equilibrium between these states gives rise to variation in observed affinity and efficacy and not a change in the affinity of the states themselves. We have previously described how to estimate the product of observed affinity and efficacy of an agonist through analysis of the concentration-response curve (Ehlert et al., 1999; Ehlert, 2008) and have recently shown that this estimate is proportional to the microscopic affinity constant of the active state of the receptor (Tran et al., 2009).

Given the inherent symmetry of ligand-receptor interactions, we reasoned that if the product of observed affinity (K_obs) and the fraction of the agonist-receptor complex in the active state (i.e., efficacy) is proportional to K_b, then it seems likely that the product of observed affinity and the fraction of the agonist-receptor complex in the inactive state (1 − efficacy) should be proportional to the microscopic affinity constant of the agonist for the inactive state (K_a). In the present report, we present analytical proof and computer simulation analysis showing that this postulate is correct and analyze published agonist concentration-response curves from the literature to illustrate our method for determining a relative estimate of the affinity constant of the agonist for the ground state of the receptor. We also show how to estimate the affinity constant of the agonist for the inactive state of the receptor in units of inverse molarity (M⁻¹) from functional data.

Materials and Methods

Simulation of Agonist Concentration-Response Curves.

We generated theoretical agonist concentration-response curves and analyzed them using the method describe under Results to determine whether it were possible to estimate the relative values of the agonist affinity constants for active and inactive states of the receptor that were used to generate the data in the first place.

Our approach for the simulations is based on two assumptions: 1) activation of a G protein-coupled receptor by an agonist is equivalent to the fraction of the agonist-receptor complex in the active state associated with the G protein-guanine nucleotide complex (DR_s*GX) (Ehlert and Rathbun, 1990; Ehlert, 2000) and 2) the operational model accurately describes the relationship between receptor activation and the measured response (Black and Leff, 1983). Thus, we used the following equation to generate agonist concentration-response curves:

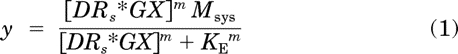In this equation, m represents the transducer slope factor, M_sys represents the maximal response of the system, K_E represents the sensitivity constant of the transduction mechanism, and [DR_s*GX] represents the amount of the active state of the agonist receptor complex (DR_s*) in a quaternary complex with G protein (G) bound with guanine nucleotide (X). The model is essentially equivalent to that described by Black and Leff (1983), but with the concentration of agonist-receptor complex replaced with [DR_s*GX]. In addition, we have used the variable M_sys instead of E_m.

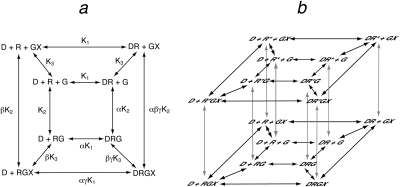
The model used to simulate the formation of the quaternary complex (DRGX) is shown in Fig. 1. The central square of equilibrium expressions in Fig. 1a represents the ternary complex model of De Lean et al. (1980), and the outer square incorporates a guanine nucleotide-binding step. Each receptor complex shown in Fig. 1a represents the summation of active and inactive states. For example, the DRGX complex is equivalent to the sum of the active (DR_s*GX) and inactive (DR_sGX) states. Thus, the complete model includes two layers of equilibrium expressions, each like that shown in Fig. 1a but undergoing an interconversion between active (R_s*) and inactive (R_s) states of the receptor complex as shown in Fig. 1b. A complete description of the constants in the model is given under Appendix as well as the equation used to generate the active state of the quaternary complex (eq. 30).

Fig. 1.

Quaternary complex model for the interaction of orthosteric ligand (D) with a receptor (R) and G protein (G) that binds guanine nucleotide (X). a, equilibrium between the various ligand-receptor-G protein-guanine nucleotide complexes of the quaternary complex model. b, in this scheme, the active (R*) and inactive (R) states of each receptor complex in the quaternary complex model are shown. The microscopic affinity constants of D for the active (K_b) and inactive (K_a) states of the receptor are defined by eqs. 45 and 44, respectively.

The model shown in Fig. 1b also enables the calculation of the amount of free active receptor in a complex with the G protein and guanine nucleotide (R_s*GX) (eq. 51). This species represents constitutive receptor activity. In all of our simulations, we used parameter estimates that yielded insignificant constitutive activity such that the response in the absence of agonist was less than 0.65% of the maximal response of the system.

Analysis of Theoretical and Experimental Data.

We used a modification of the operational model to analyze both theoretical and experimental agonist concentration-response curves. For estimation of the RA_i and K_obs values of agonist, we used global nonlinear regression analysis to fit eq. 2 to the concentration-response curve of the most efficacious agonist while simultaneously fitting eq. 3 to the concentration-response curves of the other agonists:

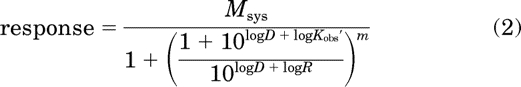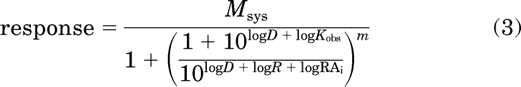In these equations, M_sys represents the maximal response of the system, m represents the transducer slope factor, D represents the concentration of agonist, and K_obs represents the affinity constant of the agonist. The symbol, ′, is used to denote the parameters of the standard agonist. R represents the product of K_obs′ and τ′, and τ is defined by eq. 20. RA_i is a relative estimate of the product of affinity and efficacy of the agonist and its definition is given by eq. 24. All of the agonist concentration-response curves were fitted simultaneously, sharing the estimates of M_sys and m among the curves and obtaining a unique estimate of R for the most efficacious agonist and unique estimates of K_obs and RA_i for the other agonists. The details of the fitting procedure have been described previously (Ehlert, 2008).

For the estimation of RI_i and K_a values, each agonist concentration-response curve was fitted to the following equation by nonlinear regression analysis:

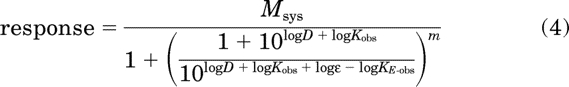In this equation, ε represents efficacy, and K_E-obs is a measure of the sensitivity of the signaling pathway as described below in connection with eq. 20. Equation 4 was derived by taking the operational model (eq. 18), substituting in eq. 20 for τ, and expressing the parameters in logarithmic form. During regression analysis, the values of M_sys, K_obs, and m were constrained to the estimates obtained from the RA_i analysis. Repetitive regression analyses were done, each time constraining K_E-obs to a constant so that the upper limit of the domain of K_E-obs values that yielded a least-squares fit was identified. The estimate of log ε was obtained for each agonist by regression analysis with K_E-obs constrained to the maximal value within the domain of K_E-obs values that yielded a least-squares fit for the most efficacious agonist. More specific details of the analysis are described under Results. Having an estimate of ε enabled the estimation of RI_i and K_a using eqs. 8, 21, 23, and 26 as described under Results.

Results

Receptor Theory

A Relative Estimate of Agonist Affinity for the Inactive State of the Receptor.

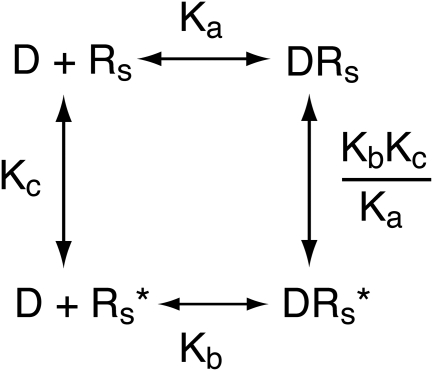
Our thesis is that the product of K_obs and the fraction of the agonist-receptor complex in the active state is proportional to the microscopic affinity constant of the agonist for the inactive state of the receptor. If correct, this hypothesis should be easy to prove for a simple system, consisting of a receptor in equilibrium between active (R_s*) and inactive states (R_s). This simple model is shown in Scheme 1, in which the affinity constants of the agonist (D) for the active and inactive states are denoted by K_b and K_a, respectively, and K_c denotes the unimolecular constant describing the equilibrium between the receptor states. Our analysis applies to the condition in which there is little constitutive receptor activity (K_c ≪ 1).

Scheme 1.

Model for the interaction of an orthosteric ligand (D) with active (R_s*) and inactive (R_s) states of the receptor. K_b and K_a denote the microscopic affinity constants of the ligand for the active and inactive states, respectively. The constant describing the spontaneous interconversion of R_s and R_s* is denoted by K_c (K_c = R_s*/R_s).

To prove our hypothesis for the model in Scheme 1, we first derive expressions for observed affinity and the fraction of the agonist-receptor complex in the active state (observed efficacy, ε). It has been shown that the function describing the amount of agonist-receptor complex in the active state (DR_s*) is given by Tran et al. (2009):

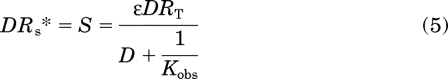In this equation D denotes the concentration of agonist, R_T denotes the total concentration of receptors, ε denotes the efficacy of the agonist, and K_obs denotes the observed affinity constant of the agonist (reciprocal of the observed dissociation constant). This function is also known as the stimulus (S) as described by Furchgott (1966) and Stephenson (1956) in nearly equivalent forms. K_obs for the receptor is given by the following equation as described previously (Tran et al., 2009):

Efficacy is equivalent to the fraction of the agonist-receptor complex in the active state. This can be determined at 100% receptor occupancy by taking the limit of the receptor activation function as the agonist concentrations approaches saturating levels as described previously (Tran et al., 2009):

The fraction of the agonist-receptor complex in the inactive state (ε_i) is equivalent to

We define ε_i as the intrinsic inactivity of the agonist-receptor complex. Substituting in eq. 7 for ε in eq. 8 followed by simplification yields

The product of K_obs and ε_i of one agonist expressed relative to that of another standard agonist is equivalent to

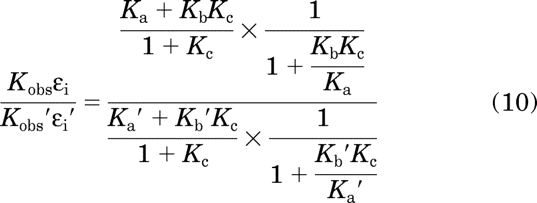in which the parameters of the standard agonist are denoted with ′. The right side of this equation was derived by taking the expression on the left side and substituting in eqs. 6 and 9 for K_obs and ε_i, respectively. Further simplification yields

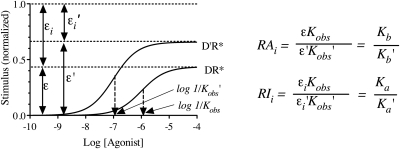
This equation shows that if a receptor conforms to Scheme 1, then the product of observed affinity and intrinsic inactivity of one agonist expressed relative to that of another is equivalent to the corresponding ratio of microscopic affinity constants for the inactive state of the receptor. We define this term as the intrinsic relative inactivity of the agonist (RI_i). Figure 2 illustrates the relationship between RI_i and the product K_obsε_i for two agonists. Also shown is the relationship between RA_i and the product of K_obsε, which is described by eq. 24.

Fig. 2.

Relationship between the stimulus and efficacy (ε), intrinsic inactivity (ε_i), the observed affinity constant (K_obs), and the affinity constants of the active (K_b) and inactive (K_a) states of the receptor. The theoretical plots show the amount of agonist bound to the active state of the receptor (DR*) for two agonists, D and D′. The curves are based on the model shown in Scheme 1 and were derived using eqs. 5 to 7. The maximal amounts of the active and inactive states of the agonist-receptor complexes are denoted ε and ε_i, respectively. RA_i is a relative measure of the product of affinity and efficacy of one agonist (D) expressed relative to that of another (D′), whereas RI_i is a relative measure of the product of affinity and intrinsic inactivity. The mathematics described by eqs. 24 and 11 show that RA_i and RI_i are relative measures of the microscopic affinity constants of the active (K_b/K_b′) and inactive (K_a/K_a′) states of the receptor, respectively.

Estimation of the K_a Value in Units of Inverse Molarity.

If the receptor lacks appreciable constitutive activity, then it is usually possible to obtain an accurate estimate of the K_a value. In such instances, the K_a value is approximately equal to the product of K_obs and ε_i as shown by eqs. 12 to 15:

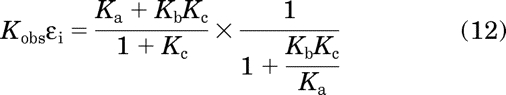The right side of this equation was derived by substituting in eqs. 6 and 9 for K_obs and ε_i on the left side, respectively. Rearrangement yields

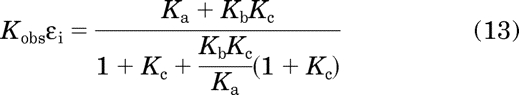When there is little constitutive activity, K_c ≪ 1, and, consequently, eq. 13 can be approximated by

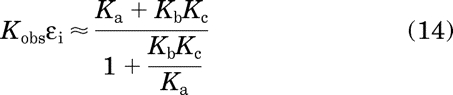This equation reduces to

Modification of the Operational Model for Estimation of RI_i and K_a.

Most assays for agonist activity at G protein-coupled receptors involve the measurement of a response downstream from receptor activation and not receptor activation itself. To estimate RI_i or K_a, therefore, it is necessary to incorporate the theory described above into an equation that expresses the response as a function of the parameters K_obs and ε. We use the reverse engineering approach described by Black and Leff (1983). These investigators showed that if the initial input to a receptor transduction mechanism is consistent with the receptor activation function (eq. 5) and the output (response, y) is a logistic function similar to

then the equation that expresses the response (y) as a function of the stimulus (eq. 5) is

In eq. 16, n represents the slope factor of the concentration-response curve, E_max represents the maximal response, and EC₅₀ represents the concentration of agonist eliciting a half-maximal response. In eq. 17, S denotes the active agonist-receptor complex (DR*), M_sys denotes the maximal response of the system, K_E denotes the sensitivity constant of the system, and m denotes the transducer-slope factor. Substituting in eq. 5 for S in eq. 17 yields the following equation after simplification:

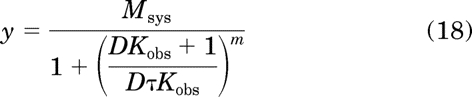in which

This equation for τ can be written in a simpler form by substituting in K_E-obs for the ratio K_E/R_T:

We define τ_i as

It follows that the product of K_obsτ_i of one agonist expressed relative to that of a standard agonist is equivalent to the corresponding ratio of products of observed affinity and intrinsic inactivity:

Again, the ′ is used to designate the parameters of the standard agonist. From eq. 11, it follows that

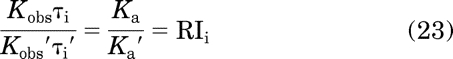We have previously shown an analogous relationship between the product of observed affinity and efficacy and the ratio of microscopic affinity constants of the active state of the receptor (Tran et al., 2009):

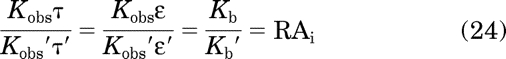This ratio is known as the intrinsic relative activity of the agonist (RA_i).

When there is little constitutive activity, it is possible to estimate the K_a value of the agonist from the parameters of the operational model as shown by the next two equations:

The right side of eq. 25 was generated from the left side by substituting in eq. 21 for τ_i and simplifying. When there is little constitutive activity, the right side of the equation can be replaced with K_a as shown by eq. 15:

Analysis of Simulated Agonist Concentration-Response Curves.

Another approach for proving that the product K_obsε_i is proportional to the microscopic affinity constant of the agonist for the inactive state of the receptor is to generate theoretical agonist concentration-response curves using the operational model and to determine whether it is possible to obtain accurate estimates for the RI_i and K_a values from the theoretical data. A robust way to simulate the data is to generate the receptor-activation function using the ternary complex model with guanine nucleotide (quaternary complex model) defined at the level of receptor states. We have previously explained that the fraction of the agonist-receptor complex in the active state associated with the heterotrimeric G protein bound with guanine nucleotide (DR_s*GX, active quaternary complex) is proportional to receptor activation (Ehlert and Rathbun, 1990; Ehlert, 2000). Thus, we have used this model to generate the theoretical stimulus for the operational model as described under Appendix. The resulting output (agonist concentration-response curve) was submitted to nonlinear regression analysis to obtain estimates of K_obsε_i for each agonist. A random error with a range of ±5% was added to the theoretical data to ensure that our estimation procedure was feasible. The remainder of this section describes how to estimate RI_i (relative estimate of K_obsε_i) and K_a from agonist concentration-response curves.

Analysis of Agonist Concentration-Response Curves When the Intracellular Concentration of GTP Is High and the Transducer Slope Factor Equals One (m = 1).

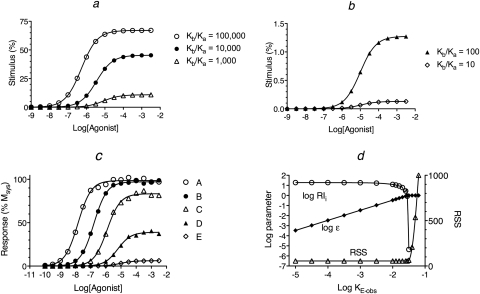
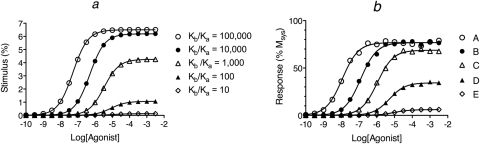
We simulated curves for agonist receptor activation (DR_s*GX) under conditions in which the concentration of guanine nucleotide is high (X = 10⁻³ M), because GTP is often present in cells at concentrations that saturate G proteins. For these simulations, the affinity constant of each agonist for the inactive state (K_a) was set to a constant value (K_a = 10⁵ M⁻¹) and that for the active state (K_b) was varied to yield K_b/K_a ratios of 100,000, 10,000, 1000, 100, and 10 for agonists A to E, respectively. The amount of agonist bound in the form of quaternary complex was estimated using eq. 30 as described under Appendix. The resulting receptor activation curves (stimulus function) are shown in Fig. 3, a and b. The complete set of parameters for the simulations is listed in the legend to Fig. 3. With these parameters, the amount of spontaneous receptor activation was very low in the absence of agonist (R_s*GX = 0.013%), which yielded a basal response of only 0.65%. The maximal fractional amount of the DR_s*GX complex is equivalent to ε, and the reciprocal of the concentration of agonist causing a half-maximal formation of DR_s*GX is equivalent to K_obs. The values of K_a, K_b, K_b/K_b′, K_obs, and a relative estimate of ε are listed for each agonist in Table 1.

Fig. 3.

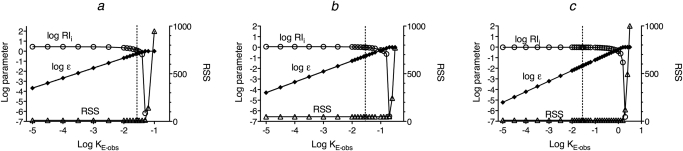
Analysis of simulated agonist concentration-response curves. Agonist concentration-response curves were generated by first calculating the stimulus (a and b) using eq. 30 under Appendix with the concentration of guanine nucleotide high (X = 1.0 mM). This stimulus was used as input to the operational model (eq. 1) to yield the response as a function of the agonist concentration (c). d, nonlinear regression analysis of the concentration-response curve of agonist A using eq. 4. The points show the estimates of log RI_i, log ε, and the RSS plotted against the value to which K_E-obs was constrained during regression analysis. A least-squares fit was obtained whenever log K_E-obs ≤ −1.55. The affinity constants of the agonists (A–E) for the inactive state of the receptor were the same (K_a = 10⁵ M⁻¹). Those for the active state (K_b) were 10¹⁰, 10⁹, 10⁸, 10⁷, and 10⁶, respectively, as indicated by the K_b/K_a ratios in a and b. The microscopic state constants for the quaternary complex model were log K_e, −2.15; log K_g, 2.85; log K_k, 8.00; log K_m, 4.60; and log K_c, −4.30. The ratio of G protein to receptor was 10, and the receptor concentration was 1.0 unit. The parameters of the operational model were M_sys, 100; m, 1.0; and log K_E, −1.7.

TABLE 1.

Theoretical and estimated parameters for the agonist concentration-response curves shown in Fig. 3

Agonist	Theoretical Parameters					Estimated Parameters
	Log Ka	Log Kb	Log Kb/Kb′	Log Kobsa	Relative Efficacyb	Log Ka	Log RIic	Log RAic	Log Kobs	Relative τd
A	5.0	10.0	4.0	6.28	1.00	4.93	−0.077	3.99	N.D.	1.00
B	5.0	9.0	3.0	5.45	0.68	5.07	−0.059	2.95	N.D.	0.62
C	5.0	8.0	2.0	5.08	0.16	5.01	−0.013	2.01	5.10	0.15
D	5.0	7.0	1.0	5.01	0.019	5.00	−0.019	0.98	5.00	0.018
E	5.0	6.0	0.00	5.00	0.0019	5.00	0.00	0.00	5.00	0.0017

N.D., not determined.

^a Represents the log reciprocal of the agonist concentration required for half-maximal formation of the DR_s*GX complex.

^b Represents the maximal amount of DR_s*GX complex formed by the agonist, expressed relative to that of agonist A.

^c Expressed relative to that of agonist E.

^d Expressed relative to that of agonist A.

The simulated stimulus curves were used as input to the operational model, and theoretical agonist concentration-response curves were generated using eq. 1, with M_sys = 100%, K_E-obs = 0.02, and m = 1. A random error (±5%) was added to the simulated data, and the resulting curves are illustrated in Fig. 3c. The EC₅₀ and E_max values of the agonists were estimated by nonlinear regression analysis of the data using eq. 16, and these estimates are listed in Table 2.

TABLE 2.

Estimation of RA_i, K_obs, and relative efficacy using eqs. 27 to 29, respectively

The parameters were estimated from the EC₅₀ and E_max values of the concentration-response curves shown in Fig. 3. For the calculations, it was assumed that the E_max of agonist A was a good estimate of M_sys.

Agonist	Log EC50	Emaxa	Log RAib	Log Kobs	Relative Efficacyc
A	−7.83	1.00	4.00	N.D.	N.D.
B	−6.79	0.99	2.95	N.D.	N.D.
C	−5.91	0.85	2.01	5.10	1.00
D	−5.21	0.40	0.98	4.99	0.12
E	−5.03	0.063	0.00	5.01	0.012

N.D., not determined.

^a The estimate of E_max is expressed relative to that of agonist A.

^b Expressed relative to that of agonist E.

^c Expressed relative to that of agonist C.

The first step in the analysis of the simulated data involves estimation of the agonist RA_i values by global nonlinear regression analysis using eqs. 2 and 3 as described previously (Ehlert, 2008). This analysis also yields estimates of the K_obs values of the partial agonists. The log RA_i values were first estimated relative to the most efficacious agonist (0.00, −1.05, −1.99, −3.01, and −3.99 for agonists A to E, respectively). These values are listed in Table 1, normalized to the least efficacious agonist. For each agonist, there is reasonable agreement between log RA_i and the log ratio of its K_b value expressed relative to that of the least efficacious agonist (K_b′). This regression analysis also yielded estimates of M_sys (98.6%) and m (1.00).

The estimation of RI_i and K_a requires estimates of the K_obs values of the full agonists. We used the theoretical values for the full agonists A and B, but with real experimental data, it would be necessary to estimate K_obs using the method of partial receptor inactivation.

The first step in the estimation of RI_i and K_a involves determination of the maximal value of K_E-obs that yields a least-squares fit of eq. 4 to the concentration-response curve of the most efficacious agonist (agonist A). Equation 4 is essentially the operational model with τ expressed as the ratio ε/K_E-obs. Regression analysis is done with the log K_obs value of agonist A constrained to its estimated value (theoretical value of 5.0 in this case). The parameters M_sys and m are constrained to the values estimated in the RA_i analysis described above. The parameter log K_E-obs is constrained to an arbitrarily low value (e.g., −4). The parameter ε is constrained to the range 0 < ε < 1.0 (i.e., log ε < 0), because for a real receptor, ε can only assume values between 0 and 1. Regression analysis is initiated, and the estimate of log ε that yields a least-squares fit is determined. This process is repeated iteratively, constraining log K_E-obs to higher values for each regression until the maximal value of log K_E-obs that yields a least-squares fit is determined.

A summary of this iterative procedure is shown in Fig. 3d for agonist A. The plot shows that the residual sum of squares (RSS) for the regression is at a minimum whenever log K_E-obs is constrained to a value less than −1.55.

This process was also done for agonists B to D, and the results are shown in Fig. 4. The vertical dashed lines in Fig. 4, a to c, correspond to the maximal value of log K_E-obs that yields a least-squares fit for agonist A (log K_E-obs = −1.55). The estimates of log ε when log K_E-obs is constrained to its upper limit (−1.55) were −0.02, −0.23, −0.84, −1.77, and −2.78 for agonists A to E, respectively.

Fig. 4.

Summary of nonlinear regression analysis of the concentration-response curves of agonists B (a), C (b), and D (c) from Fig. 3c. The plots show the estimates of log RI_i, log ε, and the RSS when nonlinear regression analysis was done with the value of log K_E-obs constrained to various values shown on the abscissa. The vertical dashed line indicates log K_E-obs = −1.55.

With these estimates of ε, it is possible to estimate ε_i using eq. 8. Then, τ_i is estimated from ε_i using eq. 21. Finally, RI_i and K_a are estimated from τ_i and K_obs using eqs. 23 and 26, respectively. The relationship between log RI_i and log K_E-obs is also shown in Fig. 3d (agonist A) and Fig. 4 (agonists B to D). For agonists B to D, the estimate of log RI_i is approximately equal to the true value (log RI_i = 0) when log K_E-obs = −1.55. For agonists C and D, the estimate of log RI_i is constant over the range log K_E-obs ≤ −1.55. For all the agonists, the estimate of log RI_i is equivalent to the corresponding ratio of K_obs values when log K_E-obs is very low.

The estimates of log RI_i and log K_a are listed in Table 1. There is general agreement between these estimates and the theoretical values used to generate the data (i.e., log RI_i = 0 and log K_a = 5). Although the estimates of log RI_i and log K_a are accurate, the values of log K_E-obs, ε, and ε_i are unreliable.

The lengthy iteration procedure summarized in Figs. 3d and 4 was described to verify and explain the relationship between log K_E-obs and the estimates of log RI_i and log K_a. However, the maximal estimate of log K_E-obs for the most efficacious agonist can be determined more quickly by regression analysis with eq. 4 with the parameters constrained as described above except that ε is constrained to 1.0 (log ε = 0) and log K_E-obs is unconstrained. The resulting estimate of log K_E-obs is a little larger than the maximal value that yields a least-squares fit (−1.55). The latter can be determined by constraining log K_E-obs to nearby smaller values as described above in connection with Fig. 3d. It is unnecessary to do the regression with the less efficacious agonists.

When the transducer slope factor in the operational model (m) is equivalent to one, the slope factor of the agonist concentration-response curve (n) is also equivalent to one, and there are simple relationships among the EC₅₀ and E_max values of agonists and the parameters RA_i, K_obs, and relative efficacy (eqs. 27–39). Under this condition (i.e., m = 1), RA_i is described by the following equation (Ehlert et al., 1999):

The ′ is used to designate the parameters of the standard agonist. It can also be shown that the K_obs value of an agonist can be estimated by (see Appendix, eq. 56):

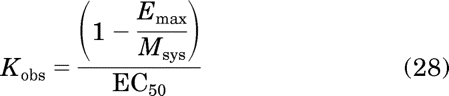Finally, the relative efficacy of agonists can be estimated by (see Appendix, eqs. 57–59):

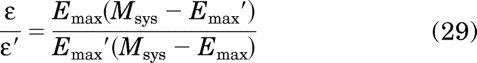Practically speaking, eqs. 28 and 29 can only be applied to the analysis of partial agonists, because there is little difference between E_max and M_sys for full agonists. These equations yielded reasonably accurate estimates of the corresponding parameters for the partial agonists as illustrated in Table 2.

Analysis of Agonist Concentration-Response Curves When the Intracellular Concentration of GTP is Low and the Transducer Slope Factor Equals One (m = 1).

We also considered the condition in which the concentration of guanine nucleotide is low. These simulations were performed as described above for the data in Fig. 3 except that the concentration of guanine nucleotide (X) was set to a lower value of 1.8 μM. Figure 5 shows the results of these simulations. The reduction in X caused an increase in the value of K_obs and a decrease in the maximal amount of DR_s*GX for each agonist (Fig. 5a; Table 3). The reduction in efficacy was offset by the increase in affinity such that there was little change in the agonist concentration-response curves except for an overall decrease in E_max (Fig. 5b). The EC₅₀ and E_max values of the curves are listed in Table 4. The RA_i values of the agonists were estimated by global nonlinear regression analysis using eqs. 2 and 3, and these estimates are listed in Table 3.

Fig. 5.

Simulated stimuli (a) and agonist concentration-response curves (b) for the condition of a low concentration (1.8 μM) of guanine nucleotide. The stimuli were generated using eq. 30 under Appendix with the concentration of guanine nucleotide set to a low value (X = 1.8 μM). The stimulus was then used as input to the operational model (eq. 1) to yield the response as a function of the agonist concentration. The affinity constants of the agonists (A–E) for the inactive state of the receptor were the same (K_a = 10⁵ M⁻¹). Those for the active state (K_b) were 10¹⁰, 10⁹, 10⁸, 10⁷, and 10⁶, respectively, as indicated by the K_b/K_a ratios in a. The other parameters were the same as those given in the legend to Fig. 3. The basal response caused by constitutive receptor activity was only 0.64% for this simulation.

TABLE 3.

Theoretical and estimated parameters for the agonist concentration-response curves shown in Fig. 5

Agonist	Theoretical Parameters					Estimated Parameters
	Log Ka	Log Kb	Log Kb/Kb′	Log Kobsa	Relative Efficacyb	Log Ka	Log RIic	Log RAic	Log Kobs	Relative τd
A	5.0	10.0	4.0	7.28	1.00	4.95	−0.028	4.10	N.D.	1.00
B	5.0	9.0	3.0	6.30	0.95	4.95	−0.034	3.06	N.D.	0.96
C	5.0	8.0	2.0	5.47	0.66	5.01	0.013	2.07	5.39	0.66
D	5.0	7.0	1.0	5.08	0.16	5.01	0.008	1.06	5.00	0.16
E	5.0	6.0	0.0	5.01	0.020	5.00	0.00	0.00	5.00	0.018

N.D., not determined.

^a Represents the log reciprocal of the agonist concentration required for half-maximal formation of the DR_s*GX complex.

^b Represents the maximal amount of DR_s*GX complex formed by the agonist, expressed relative to that of agonist A.

^c Expressed relative to that of agonist E.

^d Expressed relative to that of agonist A.

TABLE 4.

Estimation of RA_i, K_obs, and relative efficacy using eqs. 27 to 29, respectively

The parameters were estimated from the EC₅₀ and E_max values of the concentration-response curves shown in Fig. 5. For the calculations, it was assumed that the E_max of agonist A was a good estimate of M_sys.

Agonist	Log EC50	Emaxa	Log RAib	Log Kobs	Relative Efficacyc
A	−7.95	1.00	4.02	N.D.	N.D.
B	−6.91	1.00	2.98	N.D.	N.D.
C	−5.98	0.90	2.00	5.00	1.00
D	−5.29	0.45	1.02	5.03	0.096
E	−5.03	0.079	0.00	4.99	0.010

N.D., not determined.

^a The estimate of E_max is expressed relative to that of agonist A.

^b Expressed relative to that of agonist E.

^c Expressed relative to that of agonist C.

The agonist-concentration response curves were also analyzed by regression analysis using eq. 4 to estimate the RI_i and K_a values of the agonists using the procedure described above. A least-squares fit was obtained for the most efficacious agonist when the estimate of K_E-obs was constrained over the domain K_E-obs ≤ −0.50. The concentration-response curves of the less efficacious agonists were analyzed by eq. 4 with K_E-obs constrained to −0.50. The resulting estimates of ε for each agonist were used to estimate RI_i and K_a as described above. These values are listed in Table 3. There is general agreement between the RA_i, RI_i, and K_a estimates and the corresponding theoretical values (K_b/K_b′, K_a/K_a′, and K_a) used to generate the data. For the partial agonists, there was also good agreement between the theoretical values of RA_i, K_obs, and relative efficacy and the corresponding estimates determined from the EC₅₀ and E_max values using eqs. 27 to 29 (Table 4).

Analysis of Agonist Concentration-Response Curves When the Intracellular Concentration of GTP Is High and the Transducer Slope Factor Greater Than One.

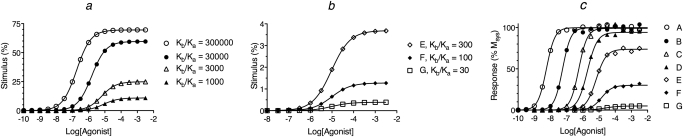
We also considered theoretical data derived from the operational model with a transducer slope factor greater than one (i.e., m = 1.8). The theoretical microscopic constants for these simulations are listed in Table 5, and the corresponding receptor activation functions are shown in Fig. 6, a and b. The theoretical concentration-response curves were generated using the operational model with a K_E-obs value of 0.02, and the resulting curves are shown in Fig. 6c. The EC₅₀, E_max, and slope factors (n) of the agonists were estimated from the theoretical concentration-response curves, and these values are listed in Table 6. The K_obs, RA_i, RI_i, and K_a values were estimated by nonlinear regression analysis using the approach described above for the analysis of the data in Fig. 3, and the resulting parameter estimates are listed in Table 5. There was general agreement between these estimates and the corresponding theoretical values that were used to generate the theoretical data. The largest error (approximately 3-fold) was in the estimate of K_a and RI_i for the most efficacious agonist.

TABLE 5.

Theoretical and estimated parameters for the agonist concentration-response curves shown in Fig. 6

Agonist	Theoretical Parameters					Estimated Parameters
	Log Ka	Log Kb	Log Kb/Kb′	Log Kobsa	Relative Efficacyb	Log Ka	Log RIic	Log RAic	Log Kobs	Relative τd
A	5.0	10.48	4.0	6.74	1.00	4.43	−0.52	4.06	N.D.	1.00
B	5.0	9.48	3.0	5.81	0.86	4.98	0.025	3.07	N.D.	0.86
C	5.0	8.48	2.0	5.19	0.36	4.99	0.038	2.07	N.D.	0.37
D	5.0	8.0	1.52	5.08	0.16	5.00	0.050	1.59	5.08	0.15
E	5.0	7.48	1.0	5.02	0.053	5.00	0.043	1.09	5.02	0.054
F	5.0	7.0	0.52	5.01	0.018	4.99	0.038	0.60	5.00	0.019
G	5.0	6.48	0	5.00	0.0056	4.95	0.00	0.00	4.96	0.0058

N.D., not determined.

^a Represents the log reciprocal of the agonist concentration required for half-maximal formation of the DR_s*GX complex.

^b Represents the maximal amount of DR_s*GX complex formed by the agonist, expressed relative to that of agonist A.

^c Expressed relative to that of agonist G.

^d Expressed relative to that of agonist A.

Fig. 6.

Simulated stimuli (a and b) and agonist concentration-response curves (c) for the condition of a transducer slope factor greater than 1 (m = 1.8). The stimuli were generated using eq. 30 under Appendix with the concentration of guanine nucleotide set to a high value (X = 1.0 mM). The stimulus was then used as input to the operational model (eq. 1) to yield the response as a function of the agonist concentration. The affinity constants of the agonists (A–G) for the inactive state of the receptor were the same (K_a = 10⁵ M⁻¹). Those for the active state (K_b) were 3 × 10¹⁰, 3 × 10⁹, 3 × 10⁸, 10⁸, 3 × 10⁷, 10⁷, and 3 × 10⁶, respectively, as indicated by the K_b/K_a ratios in a and b. The other parameters were the same as those given in the legend to Fig. 3 except that the value of the transducer slope factor in the operational model (m) was 1.8. The basal response caused by constitutive receptor activity was only 0.011% for this simulation.

TABLE 6.

Estimated parameters for the agonist concentration-response curves shown in Fig. 6

Agonist	Estimated Parameters
	Emaxa	log EC50	Slope Factor (n)
A	1.00	−8.25	1.66
B	0.998	−7.25	1.70
C	0.992	−6.25	1.65
D	0.94	−5.72	1.43
E	0.74	−5.18	1.39
F	0.30	−4.84	1.33
G	0.050	−4.62	1.05

^a E_max is normalized relative to that of agonist A.

Other Simulations.

We also examined a variety of other conditions including a change in the ratio of G protein to receptor and a variation in the sensitivity constant of the transducer function (K_E). In each case, we obtained reliable estimates of RA_i, RI_i, and K_a of all but the most efficacious agonist in a series.

Analysis of Experimental Data

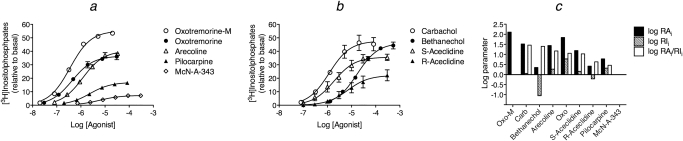
We analyzed some of our prior data on muscarinic agonist stimulation of phosphoinositide hydrolysis in Chinese hamster ovary cells transfected with the human M₃ muscarinic receptor (Ehlert et al., 1999) (Fig. 7a). The EC₅₀ and E_max values of the agonists were estimated by nonlinear regression analysis using eq. 16 with the slope factor constrained to a value of one (Table 8). There was no significant reduction in residual error when the slope factors of the agonists were allowed to differ from one during regression analysis (F_{9, 155} = 0.35; P = 0.96).

Fig. 7.

Muscarinic agonist stimulated phosphoinositide hydrolysis in CHO cells expressing the human M₃ muscarinic receptor. a and b, concentration-response curves of various muscarinic agonists. c, corresponding estimates of log RA_i, log RI_i, and their ratio, log RA_i/log RI_i. The data in a and b are from Ehlert et al. (1999) and represent the mean increase in [³H]inositol phosphates, expressed relative to basal accumulation in the absence of agonist. Mean values ± S.E.M. from four experiments are shown.

TABLE 8.

Estimation of RA_i, K_obs, and relative efficacy using eqs. 27 to 29, respectively

The parameters were estimated from the EC₅₀ and E_max values of the concentration-response curves shown in Fig. 7.

Agonist	Log EC50	Emaxa	Log RAib	Log Kobs	Relative Efficacyc
Oxotremorine-M	−6.45	0.93	2.11	5.32	1.00
Oxotremorine	−6.36	0.61	1.84	5.95	0.13
Carbachol	−5.93	0.80	1.52	5.23	0.32
Arecoline	−5.93	0.68	1.44	5.44	0.17
S-Aceclidine	−5.73	0.60	1.19	5.33	0.12
Pilocarpine	−5.64	0.29	0.78	5.49	0.031
R-Aceclidine	−5.16	0.37	0.42	4.96	0.047
Bethanechol	−4.77	0.78	0.35	4.12	0.27
McN-A-343	−5.23	0.12	0.00	5.17	0.010

^a Expressed relative to M_sys.

^b Expressed relative to that of McN-A-343.

^c Expressed relative to that of oxotremorine-M.

We used global nonlinear regression analysis to estimate the K_obs and RA_i values of the agonists using eqs. 2 and 3 with oxotremorine-M used as the standard agonist. These values were subsequently normalized relative to the least efficacious agonist as listed in Table 7. Next, we fitted eq. 4 to each agonist concentration-response curve with the values of M_sys and m constrained to the values obtained from the RA_i analysis (i.e., 59.5-fold increase in [³H]inositol phosphates and 1.08, respectively) and the value of K_E-obs constrained to the maximal value that yielded a least-squares fit for the most efficacious agonist, oxotremorine-M (log K_E-obs = −1.0). From this regression, the values of RI_i and K_a were estimated for each agonist as described above, and the estimates are listed in Table 7. The estimate of the K_a of oxotremorine-M was highly dependent on the value of K_E-obs. When log K_E-obs was reduced from the maximal value that yielded a least-squares fit (−1.0) to −1.3, the estimate of the log K_a of oxotremorine-M increased from 4.09 to 5.18. At lower values of K_E-obs, the estimate of log K_a changed very little and approached the limiting value of K_obs (5.46). Thus, it was impossible to estimate the K_a of oxotremorine-M accurately.

TABLE 7.

Estimated parameters for the agonist concentration-response curves shown in Fig. 7

Agonist	Estimated Parameters
	Log Ka	Log RIia	Log RAia	Log Kobs	Relative τb
Oxotremorine-M	N.D.	N.D.	2.01	5.46	1.00
Oxotremorine	5.96	0.74	1.77	6.02	0.16
Carbachol	5.17	−0.05	1.43	5.31	0.37
Arecoline	5.44	0.22	1.37	5.51	0.20
S-Aceclidine	5.35	0.13	1.13	5.40	0.15
Pilocarpine	5.54	0.32	0.75	5.55	0.044
R-Aceclidine	5.01	−0.21	0.38	5.03	0.063
Bethanechol	4.09	−1.13	0.27	4.21	0.32
McN-A-343	5.22	0.00	0.00	5.23	0.017

N.D., not determined.

^a Expressed relative to that of McN-A-343.

^b Expressed relative to that of oxotremorine-M.

We also used eqs. 27 to 29 to estimate the RA_i, K_obs, and relative efficacy values of the agonists because these equations are applicable when the slope factors of the concentration-response curves are equivalent to one. These estimates are listed in Table 8 for all of the agonists. There was little difference between the parameter values when estimated using the latter method or by regression analysis using eq. 4 (Table 7).

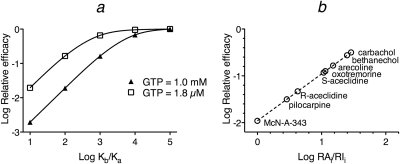
A plot of the log RA_i, RI_i, and RA_i/RI_i ratios of each agonist expressed relative to that of the least efficacious agonist [4-(m-chlorophenyl-carbamoyloxy)-2-butynyltrimethylammonium (McN-A-343)] is shown in Fig. 7c. For oxotremorine-M, the log K_a and RI_i are not given, because of the error in the estimation of K_a. There was much greater variation in the RA_i compared with the RI_i. The ratio RA_i/RI_i is a relative measure of the selectivity of the agonist for the active state relative to the inactive state. This estimate for the most efficacious agonist oxotremorine-M was at least 200-fold greater than that for McN-A-343. Whereas bethanechol has approximately 10-fold lower affinity for the active and inactive states of the M₃ receptor compared with carbachol, it maintains a comparable degree of selectivity for the active state.

Discussion

In this report, we introduce the concept of the fraction of the agonist-receptor complex in the inactive state (intrinsic inactivity, ε_i) and show that the product of ε_i and K_obs is proportional to the microscopic affinity constant of an orthosteric ligand for the inactive state of the receptor (K_a) when there is little constitutive activity. We also show that, among a group of agonists, it is possible to estimate the K_a value of any agonist having an efficacy less than one-third that of the most efficacious agonist.

We have assumed that the fraction of the agonist-receptor complex in the active state coupled with the guanine nucleotide-bound form of the G protein (DR_s*GX) is an accurate measure of receptor activation for responses mediated through G proteins. The maximal amount of this quaternary complex can be substantially less than the amount of receptor, depending on the concentration of GTP, the relative amount of G protein to receptor, and the nature of their interaction. For the example shown in Fig. 3, the theoretical maximal amount of DR_s*GX that could be formed by an agonist having a very large K_b/K_a ratio is only 71% of the total amount of receptor. For the example in Fig. 5, in which the concentration of GTP is only 1.8 μM, the maximum possible amount of DR_s*GX is only approximately 6% of the amount of receptor. Thus, at G protein-coupled receptors, the maximal value that ε can attain is probably substantially less than one.

When agonist receptor activation approaches the maximal limit of the system, then our method for estimating the parameter K_E-obs in eq. 4 provides an accurate means of estimating the K_a value of any agonist. For example, the maximal amount of receptor activation caused by agonist A (67%) in the simulation shown in Fig. 3 is almost equivalent to the maximal limit of this theoretical simulation (71%). Using the approach described in the text, it was possible to obtain a reasonable estimate of K_a through regression analysis of the concentration-response curve using eq. 4 with the value of log K_E-obs constrained to the maximal value that yields a least-squares fit (i.e., log K_E-obs = −1.55). Accurate estimates of the K_a values of the less efficacious agonists were also obtained when log K_E-obs was constrained to −1.55.

However, with real data, it could be possible that the most efficacious agonist in a series might behave like agonist C, for example, which only causes 11% receptor activation. When its concentration-response curve was analyzed, the maximal value of log K_E-obs that yielded a least-squares fit was much larger (−0.8). With log K_E-obs constrained to −0.8, the corresponding estimate of log K_a (4.32) is substantially different from the true value (5.00), although the estimates of the log K_a values of the less efficacious agonists (D and E) are accurate. Thus, without knowledge of the level of receptor activation caused by an agonist, we would be uncertain whether our estimate of the K_a of the most efficacious agonist is accurate.

A possible solution is to examine the activity of agonists in a broken cell preparation with low concentrations of GTP and GDP (e.g., agonist-induced [³⁵S]GTPγS binding). Under this condition, highly efficacious agonists might cause full receptor activation as shown for the theoretical example in Fig. 5 even though the same agonists exhibit substantially different relative efficacies when the concentration of GTP is high (e.g., compare the relative efficacies of agonists A–C for the concentration-response curves in Figs. 3c and 5b). Thus, for a given receptor-G protein pair, if efficacious agonists exhibit different relative efficacies in an intact cell assay, but the same efficacy in a [³⁵S]GTPγS binding assay with a low concentration of guanine nucleotides (GDP + GTP), then this result suggests that the estimate of the K_a of the most efficacious agonist in the [³⁵S]GTPγS assay would be accurate. This information could then be used to assign an appropriate K_a value for the most efficacious agonist in the intact cell assay.

Our inability to estimate the K_a value of oxotremorine-M in the phosphoinositide assay on CHO cells expressing the M₃ muscarinic receptor illustrates the problem of estimating K_a for the most efficacious agonist in a series. Given the colossal ratio of K_b/K_a that is required for agonist A to elicit a near maximal formation of DR_s*GX in the simulation shown in Fig. 3, it seems likely that highly efficacious agonists with more reasonable (i.e., smaller) K_b/K_a ratios would not cause substantial receptor activation in the presence of the normally high concentration of GTP in the cytosol. Under this condition, the K_a would be approximately equal to K_obs. Strange (2008) has also suggested that the K_a value of an agonist at a G protein-coupled receptor is probably approximately equivalent to K_obs because of the high concentration of cytosolic GTP. Nonetheless, our demonstration that it is only possible to estimate a range of K_a values for the most efficacious agonist in a series indicates the uncertainty in assuming that K_a is equivalent to K_obs. We have noted that the functional estimates of the K_obs values of efficacious muscarinic agonists for M₂ and M₃ receptors expressed in CHO cells and the mouse ileum, respectively, are unusually high, suggesting a substantial deviation of K_obs from K_a (Tran et al., 2009).

The observed affinity and efficacy of an agonist-receptor complex can change, depending on the concentration of GTP and how the G protein interacts with the receptor (Ehlert and Rathbun, 1990; Ehlert, 2000). When a given agonist-receptor complex is compared across systems, a reduction in the concentration of GTP has the effect of reducing agonist efficacy, because the maximal amount of DR_s*GX formed is less. When an agonist is compared with other agonists in a series, however, reducing the concentration of GTP has the effect of increasing the efficacy of agonists relative to the most efficacious agonist. In addition, a decrease in GTP causes the efficacy of the most efficacious agonist to achieve, or to come closer to achieving, the maximal level of receptor activation for the system. A plot of relative efficacy against the ratio of K_b/K_a illustrates this relationship for the theoretical examples shown in Figs. 3 and 5 (Fig. 8a). Even though agonists A to E have the same microscopic affinity constants for the active (K_b) and inactive (K_a) states of the receptors in the two simulations, more of the agonists exhibit maximal relative efficacy for the system when the concentration of GTP is low. Figure 8b shows the corresponding plot for the experimental data shown in Fig. 7, a and b.

Fig. 8.

Relationship between relative efficacy and the selectivity of agonists for the active state of the receptor. a, relative efficacy is plotted against K_b/K_a for the data shown in Figs. 3 (GTP = 1.0 mM) and 5 (GTP = 1.8 μM). b, relative efficacy is plotted against log RA_i/RI_i for the data in Fig. 7, a and b.

To summarize, we have developed a method of analysis to estimate the K_a value of any agonist, full or partial, having an efficacy less than one-third that of the most efficacious agonist in a series. The analysis depends on having accurate estimates of the K_obs values of full agonists, which can be determined using the method of partial receptor inactivation. The analysis provides accurate estimates of K_a even if K_obs > K_a. This condition can occur with a low concentration of GTP in assays on cellular homogenate, and, perhaps, in some intact cell preparations and tissues. Finally, we also show how to estimate the K_obs and relative efficacies of partial agonists from their EC₅₀ and E_max values when the Hill slopes of their concentration-response curves are equal to one.

Appendix

Simulation of the DR_s*GX Complex.

We used the model described in Fig. 1 to simulate the amount of agonist (D) bound in the form of an active quaternary complex (DR_s*GX) consisting of the active state of the receptor (R_s*), the G protein (G), and guanine nucleotide (X). The equation describing the amount of DR_s*GX as a function of the agonist concentration is as follows:

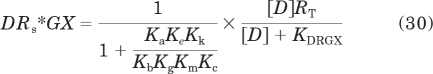in which R_T denotes the total amount of receptors. The affinity constants with lettered subscripts refer to the properties of the receptor states, and these are defined below by eqs. 44 to 50. The derivation of eq. 30 has been described previously (Ehlert and Rathbun, 1990; Ehlert, 2000). K_DRGX is given by

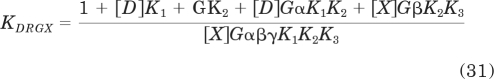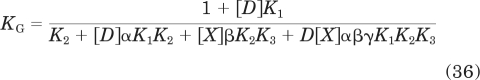In these equations, G_T and G denote the total and free concentrations of G protein. The cooperativity constants and microscopic constants for the receptor complexes are defined in Fig. 1a. As described previously (Ehlert, 2000, 2008), these are defined at the level of receptor states by the following equations:

The fundamental affinity constants for the receptor states are

Simulation of the R_s*GX Complex.

The model in Fig. 1a was also used to simulate constitutive receptor activity, that is, the amount of the active state of the unoccupied receptor in a complex with G protein and guanine nucleotide (R_s*GX). The equation describing the amount of this complex as a function of the agonist concentration is as follows:

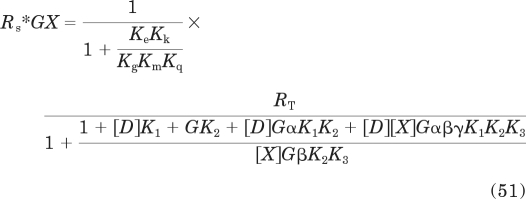In this equation, G is defined as described above.

Estimation of K_obs and Relative Efficacy When the Slope Factor of the Agonist Concentration-Response Curve Is Equal to One (n = 1).

When the agonist concentration-response curve has a slope factor of 1, then the transducer slope factor in the operational model is also equal to one (m = 1), and there are simple relationships between observed affinity (K_obs) and relative efficacy and the EC₅₀ and E_max values of agonists. To derive these relationships, we begin by expressing E_max and EC₅₀ in terms of the parameters of the operational model. E_max can be derived by solving the limit of the operational model (eq. 18) as D approaches infinity when m = 1:

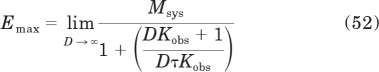Solving this limit yields

The EC₅₀ value can be solved from the following relationship:

The left side of the equation represents the E_max multiplied by 0.5, with the E_max value defined by eq. 53. The right side of the equation represents the operational model with the agonist concentration replaced with by EC₅₀. This equation communicates the idea that the response is half-maximal when the drug concentration equals the EC₅₀. Simplification yields

Having expressions for E_max and EC₅₀ enables the proof of the equations for K_obs and relative efficacy (eqs. 28 and 29, respectively) described under Results. K_obs can be estimated from the expression

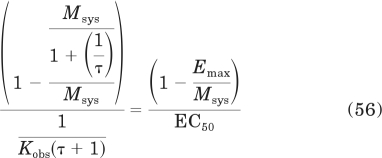The left side of this equation was derived from the right side by substituting in eqs. 53 and 55 for E_max and EC₅₀, respectively. Simplification yields eq. 28 under Results.

The efficacy of one agonist (ε), expressed relative to that of another (ε′), can be estimated from the equation

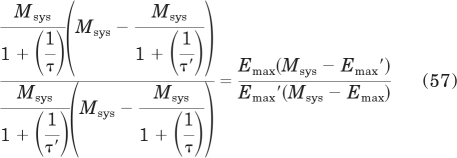The left side of this equation was derived from the right side by substituting in eq. 53 for E_max. The parameters of the agonist to which the efficacy of the other agonist is normalized are indicated with ′. Simplification yields

Substituting in eq. 19 for τ yields

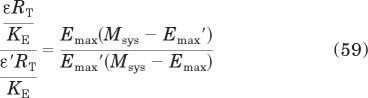Simplification yields eq. 29 under Results.

Authorship Contributions

Participated in research design: Ehlert, Griffin, and Suga.

Conducted experiments: Ehlert, Griffin, and Suga.

Performed data analysis: Ehlert, Griffin, and Suga.

Wrote or contributed to the writing of the manuscript: Ehlert.