Analysis of Agonism and Inverse Agonism in Functional Assays with Constitutive Activity: Estimation of Orthosteric Ligand Affinity Constants for Active and Inactive Receptor States

Abstract

We describe a modification of receptor theory for the estimation of observed affinities (K_obs) and relative efficacies of orthosteric ligands in functional assays that exhibit constitutive activity. Our theory includes parameters for the fractions of the occupied receptor population in the active (intrinsic efficacy, ε) and inactive (ε_i) states and analogous parameters for the fractions of the free receptor population in the active (ε_sys) and inactive (ε_i-sys) states. The total stimulus represents the summation of the active states of the free and occupied receptor populations. A modified operational model is developed that expresses the response as a logistic function of the total stimulus. This function includes the standard parameters related to affinity and efficacy (K_obs and τ) as well as a parameter proportional to the activity of the free receptor complex, τ_sys. Two related parameters are proportional to the fraction of the free (τ_i-sys) and occupied (τ_i) receptor populations in the inactive state. We show that the estimates of the affinity constants of orthosteric ligands for the active (K_b) and inactive (K_a) states of the receptor are equivalent to τK_obs/τ_sys and τ_iK_obs/τ_i-sys, respectively. We verify our method with computer simulation techniques and apply it to the analysis of M₂ and M₃ muscarinic receptors. Our method is applicable in the analysis of ligand bias in drug discovery programs.

Introduction

Constitutive activity is an inevitable property of any ligand-sensitive molecular switch that evolved to be off (R) in the absence of endogenous ligand and on (R*) in its presence. For whether by conformational selection,

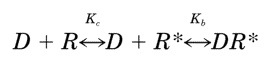or conformational induction,

activation of the receptor by the ligand (D) cannot occur unless there is some spontaneous activation of the receptor in the absence of ligand (K_c > 0; Fig. 1a). It is now clear that many G protein-coupled receptors exhibit constitutive activity, particularly when overexpressed or when the appropriate G protein is overexpressed (Seifert and Wenzel-Seifert, 2002).

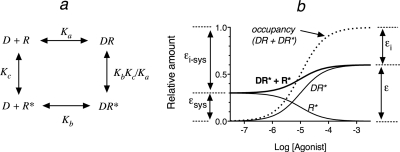
Fig. 1.

The simple two-state model for receptor activation and the components of the total stimulus for an orthosteric agonist. a, the equilibrium of an orthosteric ligand (D) with a receptor having active (R*) and inactive states (R) is shown. K_b and K_a denote the affinity constants of D for the active and inactive states, respectively. The equilibrium constant for the relative amounts of active and inactive states in the absence of D is denoted by K_c. b, The relative amounts of receptor occupancy (DR* + DR), the stimulus (DR*), the constitutive stimulus (R*), and the total stimulus (DR* + R*) are shown as a function of the agonist concentration. The fraction of the orthosteric ligand-receptor complex in the active and inactive states is denoted by intrinsic efficacy (ε) and intrinsic inactivity (ε_i), and the fraction of the free receptor in the active and inactive states is denoted by the intrinsic efficacy of the system (ε_sys) and the intrinsic inactivity of the system (ε_i-sys), respectively.

Different mechanisms have evolved to minimize receptor activation in the absence of endogenous ligand. Ligand-gated ion channels, for example, often incorporate at least two ligand-binding sites per channel (Hille, 2001), which increases ligand induction of the active state by the nth power of the ratio of affinity constants for active and inactive states (K_b/K_a)ⁿ, where n denotes the number of linked binding sites (Monod et al., 1965; Ehlert, 2008). This greater capacity of the ligand to induce the open state allows the channel to exhibit a lower probability of opening in the absence of ligand. One of the most unique solutions to the problem minimizing constitutive activity is exhibited by opsin. Its covalently attached ligand, 11-cis-retinal, behaves as an inverse agonist, whereas the light-induced all-trans form behaves as an agonist (Surya et al., 1995).

Current methods for deducing the receptor-activation function of a population of G protein-coupled receptors involve analyzing a downstream response using a null equation (Stephenson, 1956; Furchgott, 1966) or the operational model (Black and Leff, 1983). These innovative techniques enable the estimation of the observed affinity constant (K_obs) of a ligand and the intrinsic efficacy (ε) of one agonist expressed relative to that of another, provided that there is little constitutive response in the absence of orthosteric ligand. It is also possible to obtain relative estimates of the affinity constants of agonists for the active and inactive states of the receptor (Tran et al., 2009; Ehlert et al., 2011) using modifications of these methods.

Although constitutive activity may often seem like a novelty of overexpressed recombinant receptors, this type of experimental system is often used in pharmacological research and drug development (Chen et al., 1999), and appropriate methods for analyzing drug action in these systems would be useful. In the present article, therefore, we describe an extension of receptor theory that enables the estimation of the observed affinities and relative efficacies of orthosteric ligands, including agonists, neutral antagonists, and inverse agonists, in receptor systems exhibiting constitutive activity. We also show how to estimate the affinity constants of orthosteric ligands for active and inactive states of the receptor, in units of inverse molarity (M⁻¹), whenever there is constitutive activity for a simple two-state receptor system. The method enables the estimation of K_b for all orthosteric ligands except full inverse agonists and the K_a of all ligands having an efficacy less than one-third that of the most efficacious agonist in a series. Finally, we describe how these calculations relate to a more complicated system having multiple active receptor states.

Materials and Methods

Cell Culture.

Human embryonic kidney 293 cells stably expressing G_α15 (HEK 293 G_α15; provided by Dr. Olivier Civelli, University of California, Irvine, CA) were cultured in Dulbecco's modified Eagle medium with high glucose plus l-glutamine supplemented with 10% fetal calf serum, 3.7 g/l sodium bicarbonate, penicillin-streptomycin (100 units/ml and 100 μg/ml, respectively), puromycin (0.625 μg/ml), and (2R,3S,4R,5R,6S)-5-amino-6-[(1R,2S,3S,4R,6S)-4,6-diamino-3-[(2R,3R,4R,5R)-3,5-dihydroxy-5-methyl-4-methylaminooxan-2-yl]oxy-2-hydroxycyclohexyl]oxy-2-(1-hydroxyethyl)oxane-3,4-diol (G418) (0.4 mg/ml) at 37°C in a humidified atmosphere of 5% CO₂/95% air. The plasmid encoding the human M₃ muscarinic receptor (provided by Dr. Tom Bonner, National Institutes of Health, Bethesda, MD) was transfected into HEK 293 G_α15 cells grown in 100-mm culture plates using GeneJammer (Agilent Technologies, Santa Clara, CA) following the manufacturer's protocols. After 24 h, the cells were seeded into 24-well culture plates coated with poly-d-lysine (BD Biosciences, San Jose, CA) and incubated an additional 24 h before labeling with [³H]inositol for the phosphoinositide assay described next.

Agonist-Stimulated Phosphoinositide Hydrolysis.

Agonist-stimulated [³H]inositolphosphate accumulation was measured in adherent HEK G_α15 cells prelabeled with [³H]inositol using a modification of the methods described by Griffin et al. (2007). Cells were grown in 24-well plates and incubated with [³H]inositol (2 μCi) for approximately 18 h. The cells were washed, and agonist-stimulated phosphoinositide hydrolysis was measured in the presence of lithium in Dulbecco's modified Eagle's medium. The incubation with agonist lasted 2 h, and the reaction was stopped by the addition of perchlorate. Other details of the assay are described by Griffin et al. (2007).

Simulation of Agonist Concentration-Response Curves.

We generated theoretical ligand concentration-response curves exhibiting constitutive activity to verify that our methods of analysis were accurate in estimating the theoretical microscopic parameters that were used to simulate the data in the first place. Our approach has been described previously (Ehlert, 2000, 2011; Tran et al., 2009). It is based on the assumption that the active state of the ligand-receptor complex bound with G protein and guanine nucleotide (DR_s*GX) is proportional to ligand-induced receptor activation and the amount of free active receptor complex bound with G protein and guanine nucleotide (R_s*GX) is proportional to constitutive receptor activity. We substituted an equation for the summation of these two components of receptor activation into the operational model to simulate a functional response downstream from receptor activation:

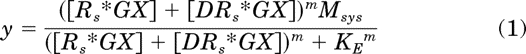In this equation, m represents the transducer slope factor, M_sys is the maximum response of the system, and K_E is the sensitivity constant of the transduction mechanism. The model is essentially equivalent to that described by Black and Leff (1983), but with receptor occupancy replaced with the summation of [R_s*GX] and [DR_s*GX]. A complete description of the model and the equations used to generate the active states of the RGX and DRGX complexes is described in Ehlert et al. (2011).

Analysis of Ligand Concentration-Response Curves.

Both simulated and experimental concentration-response curves were analyzed by global nonlinear regression analysis using Prism (GraphPad Software, Inc., San Diego, CA) and eqs. 28, 43, 44, and 51 as described under Results. A description of how to estimate the initial parameter estimates for these regression equations is given in Appendix.

Results

Receptor Theory

The thesis of this article is that it is possible to estimate the affinity constants of an orthosteric ligand for active (K_b) and inactive (K_a) states of the receptor through analysis of its concentration-response curve whenever a receptor exhibits a detectable level of constitutive activity. In this section, we develop a model for constitutive receptor activity and illustrate how the K_b and K_a values of an orthosteric ligand are related to the receptor activation function. We also apply this theory to develop an operational model that can be used to estimate K_b and K_a from the concentration-response curve of an orthosteric ligand for eliciting a downstream response at a G protein-coupled receptor. Finally, we also develop the requisite theory for estimating the observed affinity constant and relative efficacy of an orthosteric ligand when there is constitutive receptor activity.

Model for Constitutive Activity.

Using the model shown in Fig. 1a, it is possible to develop a mathematical expression for receptor activation as a function of the orthosteric ligand concentration when there is constitutive activity. The level of constitutive receptor activation is determined by the constant K_c, which is equivalent to the ratio of active (R*) to inactive (R) states of the unoccupied receptor. Normally, the value of K_c is very low, but for the example shown in Fig. 1, it has been set to an arbitrarily high value (0.43) so that it is easy to illustrate the various receptor species as a function of the agonist concentration (Fig. 1b). The affinity constants of the orthosteric ligand (D) for the active (R*) and inactive (R) states of the receptor are denoted by K_b and K_a. The concentration of agonist required for half-maximal formation of the active (DR*) and inactive (DR) receptor complexes is equivalent to the reciprocal of the observed dissociation constant (K_obs), which is defined by eq. 8.

Fig. 1b tracks the various receptor species as a function of the agonist concentration. The fraction of the unoccupied receptor population in the active state (R*) is denoted by the intrinsic efficacy of the system (ε_sys). The value of ε_sys is constant, and in the absence of agonist, it is equivalent to the fraction of the total receptor population in the active state (0.3). As the concentration of agonist increases, receptor occupancy of the active (DR*) and inactive states (DR) of the receptor increases. The fraction of the agonist-receptor population in the active state is denoted by intrinsic efficacy (ε), and at 100% receptor occupancy, it is equivalent to the fraction of the total receptor population in the active state.

There are two useful terms that describe the fraction of receptor complex in the inactive state. The intrinsic inactivity of the system (ε_i-sys) denotes the fraction of the free receptor population in the inactive state, and intrinsic inactivity (ε_i) denotes the fraction of the ligand-receptor population in the inactive state. The relationship between these latter terms and the intrinsic efficacy terms are:

As receptor occupancy increases, the amount of constitutive activity (R*) decreases because the latter is defined as the fraction of the free receptor in the active state, and the free receptor population decreases with an increase in receptor occupancy. The total amount of receptor in the active state is denoted by the summation of R* and DR* in Fig. 1b.

Using the model in Fig. 1a it is possible to express the affinity constants of the active and inactive states of the receptor in terms of the parameters of the receptor population:

These equations can be proved by deriving equations for ε, ε_i, ε_sys, ε_i-sys, and K_obs and then substituting these equations into eqs. 4 to 6 to determine whether the latter are equalities. It has been shown that ε and K_obs are defined by Tran et al. (2009):

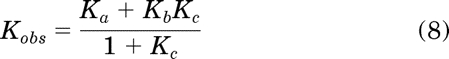Solving eq. 2 for ε and substituting the result into eq. 7 and simplifying yields:

The efficacy of the system (ε_sys) can be derived from K_c:

Solving eq. 3 for ε_sys, substituting the result into eq. 10 and simplifying yields:

Substituting in eqs. 7 to 11 for the corresponding parameters in eqs. 4 to 6 yields:

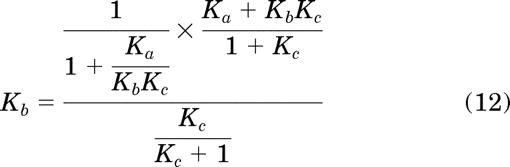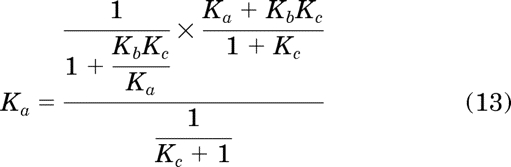Simplification of eqs. 12 to 14 yields the equalities K_b = K_b, K_a = K_a, and K_c = K_c, respectively, which proves the original equations (4–6) from which they were derived.

The implications of this theory for neutral antagonists and inverse agonists are shown in Fig. 2, a and b, respectively. Because ligand receptor occupancy decreases the amount of unoccupied receptor in the active state (R*), neutral antagonists inhibit constitutive activity and replace it with an equivalent amount of ligand-receptor complex in the active state (DR*), so that there is no change in the total level of receptor activation (DR* + R*). Thus, neutral antagonists have intrinsic efficacy, but its value (ε) is equivalent to that of the system (ε_sys). Likewise, the intrinsic inactivity of a neutral antagonist (ε_i) is equivalent to that of the system (ε_i-sys).

Fig. 2.

The components of the total stimulus for a neutral antagonist (a) and an inverse agonist (b) and the stimulus component for the different types of orthosteric ligands (c). The various receptor species and efficacy components in a and b are defined in the legend to Fig. 1. In c, the stimulus represents the fraction of the orthosteric ligand-receptor complex in the active state (DR*).

It can also be shown that an inverse agonist has intrinsic efficacy, but its value is less than that of the system, and its intrinsic inactivity is greater than that of the system (Fig. 2b).

The amounts of active ligand-receptor complex (DR*) generated by an agonist, neutral antagonist, and inverse agonist are illustrated in Fig. 2c. Although the concept that a neutral antagonist and an inverse agonist have intrinsic efficacy may seem counterintuitive, these properties follow directly from the definition of efficacy established by Stephenson (1956) and Furchgott (1966). These concepts also yield the somewhat more intuitive conclusions that the ε value of a neutral antagonist is equivalent to that of the system and that the ε_i value of an inverse agonist is greater than that of the system. Regardless, eqs. 4 and 5 also apply to the estimation of the K_b and K_a values of neutral antagonists and inverse agonists.

Operational Model for Constitutive Activity.

The theory described above applies to the activation of an isolated receptor. G protein-coupled receptors, however, interact with G proteins and other effector proteins to elicit a response, and the response that is usually measured is downstream from receptor activation. To analyze such data, the theory can be incorporated into the operational model of Black and Leff (1983) so that K_b and K_a can be estimated through the analysis of functional responses downstream from receptor activation.

Our strategy involves 1) developing an equation that describes total receptor activation (DR* + R*) as a function of the orthosteric ligand concentration (total stimulus) and 2) substituting this function for the stimulus in the logistic-transducer function described by Black and Leff (1983). This transducer function is given by:

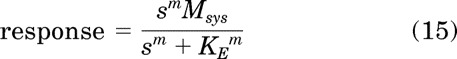in which s denotes the stimulus (agonist-receptor activation), M_sys is the maximum response of the system, m is the transducer-slope factor, and K_E is a constant reflecting the sensitivity of the system. M_sys is equivalent to the parameter E_m of Black and Leff (1983). Below we describe how to develop an equation for the total stimulus, which can be substituted for s in eq. 15.

The total stimulus (T) of a receptor system generated in the presence of an orthosteric ligand is defined as:

in which ca and s denote constitutive activity (R*) and the amount of orthosteric ligand receptor complex in the active state (DR*), respectively.

Constitutive receptor activity represents a constant fraction (ε_sys) of the unoccupied receptor population. The relative amount of unoccupied receptors (R/R_T) decreases as the concentration of the orthosteric ligand (D) increases:

This equation shows that the fractional amount of unoccupied receptors decreases proportionally with receptor occupancy by the orthosteric ligand. The fractional amount of constitutively active receptor (ca) is equivalent to the product of the right side of eq. 17 and ε_sys, which represents the fraction of active, unoccupied receptors.

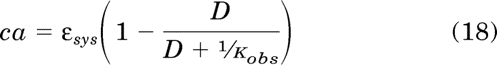The parameter ε_sys can be expressed in terms of measurable parameters of the operational model by substituting in ε_sys for s in eq. 15:

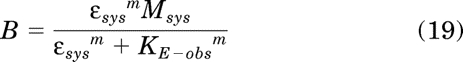In this equation, B is defined as the basal response elicited by a constitutively active receptor in the absence of orthosteric ligand, and K_E-obs is defined as:

Rearrangement of eq. 19 yields:

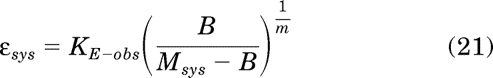This equation can be substituted back into eq. 18 to yield an equation for constitutive receptor activity in the presence of orthosteric ligand:

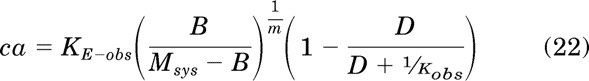Simplification yields:

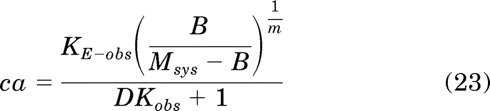The stimulus elicited by the orthosteric ligand-receptor complex (DR*) is simply equivalent to the product of intrinsic efficacy (ε) and receptor occupancy:

Substituting eqs. 23 and 24 for ca and s in eq. 16 yields an equation for the total stimulus (T):

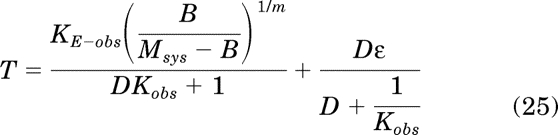Simplification yields:

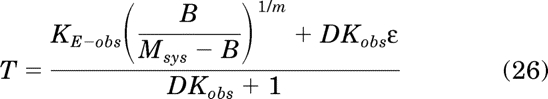To derive an equation for the response, the stimulus (s) in the transducer function of the operational model (eq. 15) is replaced by the total stimulus:

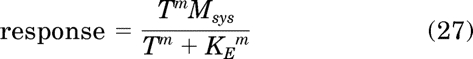Substituting eq. 26 for T and simplifying yields:

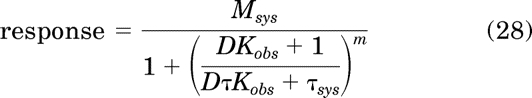in which τ and τ_sys are defined by:

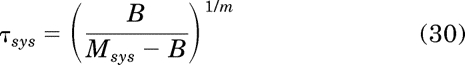It follows from eq. 21 that:

Equation 28 represents the operational model for a constitutively active receptor. There are additional parameters related to this model, which are described next. The parameter τ_i is defined as:

We define τ_i-sys as:

Using eqs. 4, 5, 29, 31, 32, and 33, it is possible to define the affinity constants of orthosteric ligands for active and inactive states of the receptor and the constant, K_c, for the isomerization of the free receptor:

The operational model for constitutive activity (eq. 28) can be rewritten in a form that includes K_b by making the appropriate substitution with eq. 34:

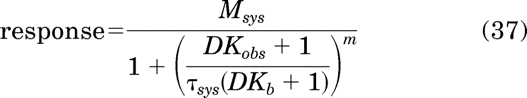Estimation of the K_obs of Orthosteric Ligands When There Is Constitutive Activity.

There is insufficient information in the concentration-response curve of a single orthosteric ligand to estimate its observed affinity constant K_obs, but it is possible to do so if responses are measured before and after inactivation of a fraction of the receptor population (Furchgott, 1966) or in different cells transiently expressing different levels of receptor. It is also possible to estimate the K_obs of a partial agonist if its concentration-response curve is analyzed with that of a full agonist (Stephenson, 1956).

First, we develop an equation based on the operational model (eq. 28) assuming that an irreversible neutral antagonist is used to inactive part of the receptor population. Such an agent has no effect on constitutive receptor activity (τ_sys). The equation for the constitutively active (ca) component of the total stimulus is derived from eq. 18 by multiplying the receptor occupancy component by the scalar q, which represents the fraction of the receptor population remaining after treatment with an irreversible neutral antagonist:

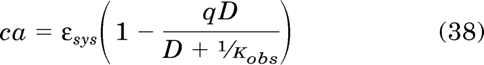Substituting eq. 21 for ε_sys yields:

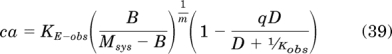The equation for the orthosteric ligand component of the stimulus (s) is derived from eq. 24 by multiplying the receptor occupancy expression by q:

Adding eqs. 39 and 40 yields the total stimulus as defined by eq. 16:

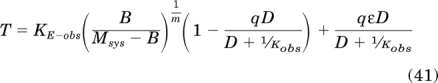Simplification yields:

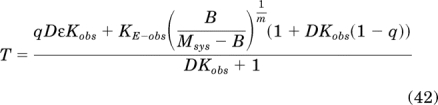Substituting eq. 42 for T in the logistic transducer function of the operational model (eq. 27) yields:

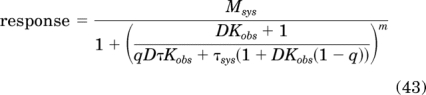This equation is used to estimate the K_obs value of an orthosteric ligand by the method of partial receptor inactivation with an irreversible neutral antagonist as described below.

It is also possible to rearrange eq. 43 into the following form for estimation of the K_b value of the orthosteric ligand:

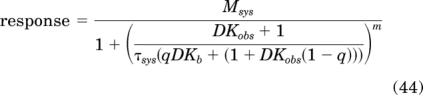The corresponding equation for an irreversible full inverse agonist is developed using the following rationale. After receptor inactivation, constitutive receptor activity is reduced to a fraction of the original value (q), and this effect is adequately reflected by a reduction in the basal response of the system (B) or in the τ_sys value. Alkylation of the receptor population also reduces the orthosteric ligand component of the stimulus to the same fraction (q) of the original stimulus. The total stimulus, therefore, is given by the following equation:

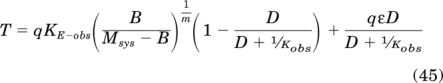Simplification yields:

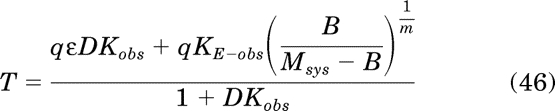Substituting eq. 46 for T in the transducer-response function of the operational model (eq. 27) yields an equation describing the response after partial receptor inactivation with an irreversible inverse agonist:

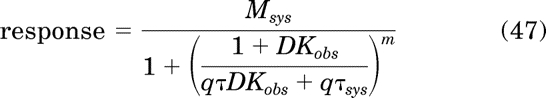To estimate K_obs and τ, global nonlinear regression analysis is used to fit eq. 47 to the concentration-response curves measured before and after receptor inactivation sharing the estimates of K_obs, τ, τ_sys, M_sys, and m between the curves. The parameter q is constrained to 1.0 for the control curve and a unique estimate is obtained for the curve measured after receptor inactivation.

Equation 47 can also be expressed in the following form for the estimation of K_b:

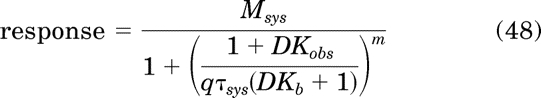The analysis is done sharing the estimates K_obs, K_b, M_sys, τ_sys, and m between the control and “inactivated” curves and obtaining a unique estimate of q for the inactivated curve (q constrained to 1.0 for control).

Equations 47 and 48 can also be used to estimate K_obs and K_b of orthosteric ligands from their concentration-response curves measured in cells transiently expressing high and low levels of a receptor. The data from high and low receptor-expressing cells are analyzed as described above for the control and inactivated conditions, respectively.

Estimation of Relative Efficacy.

Using the method of partial receptor inactivation, it is possible to estimate the observed affinity constant of an orthosteric ligand using eqs. 43 or 47, depending on the nature of the irreversible antagonist. This analysis also provides an estimate of the τ value of the orthosteric ligand. The relative efficacy of one orthosteric ligand (ε) expressed relative to that of another (ε′) is simply equal to the corresponding ratio of τ values:

Substituting in eq. 29 for τ and simplifying proves this equation.

Analysis of Simulated Orthosteric Ligand Concentration-Response Curves

In this section, we generate theoretical concentration-response curves and analyze the simulated data with the operational model for constitutive receptor activity to determine whether it is possible to estimate the K_b and K_a values that were used to simulate the data.

The concentration-response curves were generated as described under Materials and Methods. A theoretical total stimulus was generated assuming that the constitutive stimulus is proportional to the active state of the free receptor associated with the G protein bound with guanine nucleotide (R_s*GX) and that the orthosteric ligand-induced stimulus is proportional to the corresponding active state of the quaternary complex (DR_s*GX). The summation of the constitutive and ligand-induced stimuli was defined as the total stimulus (T) and used as input to the operational model (eq. 1). A random error with a range of ± 5% was added to the theoretical data to ensure that our estimation procedure was feasible. In the remainder of this section, we illustrate how to estimate K_obs, relative efficacy, K_b, and K_a.

Estimation of the K_obs and K_b Values of an Orthosteric Ligand Using the Method of Partial Receptor Inactivation.

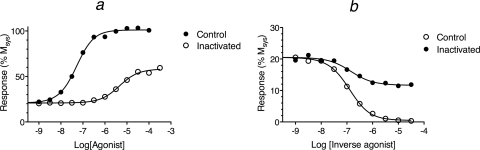
Figure 3a illustrates the theoretical concentration-response curve of a full agonist in a system with constitutive receptor activity. The curves have been simulated under control conditions and after a fraction of the receptor population has been bound with an irreversible neutral antagonist. Receptor inactivation was simulated by multiplying the ligand-receptor component of the stimulus by the scalar, 0.005 (q). A random error (±5%) was also added to the data. The parameters for the simulation are given in the legend to Fig. 3. The “control” and “inactivated” curves were analyzed simultaneously using global nonlinear regression analysis with eq. 43. In the analysis, the estimates of M_sys, m, K_obs, τ_sys, and τ were shared between the two concentration-response curves, and a unique estimate of q was obtained for the inactivated curve. The estimate of q was constrained to a constant value of 1.0 for the control curve. Regression analysis yielded estimates of 5.12 ± 0.08, 101.4 ± 1.0, 1.16 ± 0.13, and 0.0060 ± 0.0005 for log K_obs, M_sys, m, and q, respectively, and these were similar to those used to generate the theoretical data (5.08, 100, 1.0, and 0.005, respectively). The estimates of log τ and log τ_sys were 2.22 ± 0.10 and −0.51 ± 0.11.

Fig. 3.

Simulation of the effects of partial inactivation of the receptor population with an irreversible neutral antagonist on the response to an agonist (a) and an inverse agonist (b). The theoretical curves were generated using the operational model for the total stimulus (eq. 27) with the latter defined as the summation of the active states of the quaternary (DR_s*GX) and ternary (R_s*GX) complexes. These were simulated using the quaternary complex model described in Ehlert et al. (2011). The values of log K_a and log K_b for the orthosteric ligands were: agonist, 5.0 and 8.0; inverse agonist, 7.0 and 5.0, respectively. The microscopic state constants for the quaternary complex model were: log K_e, −2.15; log K_g, 2.85; log K_k, 8.00; log K_m, 4.60, and log K_c, −4.30. The ratio of G protein to receptor was 10, and the receptor concentration was 40 units. These parameters yield a quaternary complex (DR_s*GX) function with a log K_obs of 5.08. The parameters of the operational model were M_sys, 100; m, 1.0; and log K_E, −1.7.

From the values of K_obs, τ, and τ_sys it is possible to estimate the K_b value of the orthosteric agonist using eq. 34. This calculation yielded an estimate of 7.84 for log K_b, which is similar to the theoretical value used for the simulation (8.0). K_b can also be estimated by global nonlinear regression analysis of the data in Fig. 3a using eq. 44. When this was done sharing the estimate of M_sys, m, K_obs, K_b, and τ_sys between the two curves and obtaining a unique estimate of q for the control (constrained to one) and “inactivated” curves, a value of 7.84 ± 0.10 was obtained for log K_b.

We also simulated data for an inverse agonist under control conditions and after partial inactivation of 50% of the receptor population (q = 0.5, fraction of residual receptors) (Fig. 3b). The simulated data were analyzed by global nonlinear regression analysis as described above using eq. 43. In this situation, it is impossible to get a reliable estimate of M_sys unless the data are analyzed simultaneously with those of an efficacious agonist. For the regression in Fig. 3b we constrained the estimate of M_sys to the theoretical value (100%), which is nearly the same as that estimated in Fig. 3a for the efficacious agonist. The estimates of log K_obs, m, and q (6.86 ± 0.09, 1.34 ± 0.28, and 0.42 ± 0.04, respectively) were similar to those used to simulate the data (7.00, 1.0, and 0.5, respectively). The microscopic constants used to simulate the data are given in the legend to Fig. 3.

The value of K_b can be estimated using eq. 34, but in the case of a full inverse agonist, the calculation has substantial error as indicated by the log estimate of 5.56 for the simulated data in Fig. 3b. This estimate differs somewhat from the theoretical value used for the simulation (5.0). The K_b value was also estimated by regression analysis using eq. 44 as described above, which yielded the same unreliable estimate of 5.56 ± 0.34. As described below, more reliable estimates can be made for partial inverse agonists.

Can the agonist data be analyzed using the standard operational model after subtracting the basal response from the total response? Likewise, can the response of the inverse agonist be expressed as percentage of inhibition of basal activity and analyzed with the standard operational model? In the case of the inverse agonist (Fig. 3b), fitting the standard operational model:

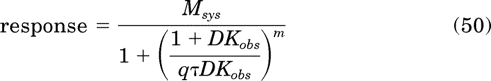to the data with the estimate of M_sys constrained so that it cannot exceed complete inhibition of basal activity (i.e., M_sys ≤ 20% inhibition) yielded the following estimates of log K_obs (6.45 ± 0.20), m (1.68 ± 0.36), and q (0.19 ± 0.2). These estimates have substantial error compared with the theoretical values (7.0, 1.0, and 0.5), and the increase in the residual sum of squares (RSS) was colossal (10-fold). The reason for the poor fit is that partial receptor inactivation increases the potency of an inverse agonist and reduces the potency of agonists when the transducer slope factor is equal to or greater than one. Thus, the standard operational model does not adequately describe the behavior of inverse agonists. In the case of the full agonist (Fig. 3a), there was little error in the estimate of K_obs and q when eq. 50 was used to analyze the data, but with partial agonists, the error in K_obs can be substantial (3-fold).

Estimation of the K_b Values of a Series of Orthosteric Ligands.

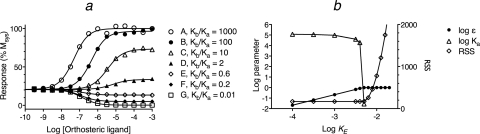
We simulated concentration-response curves for a series of agonists and inverse agonists in a system having constitutive activity to determine whether it were possible to estimate their K_b and K_a values (Fig. 4). The K_a value of each theoretical agonist was 10⁵ M⁻¹ and that of the inverse agonists was 10⁷ M⁻¹. The ratio of K_b/K_a varied from 10³ for the most efficacious agonist (A) to 10⁻² for the full inverse agonist (G). The complete list of parameters for the simulations is given in the legend to Fig. 4. The theoretical total stimuli were generated using the approach described under Materials and Methods. These were used as input to the logistic-transducer function of the operational model (eq. 1) to generate the simulated concentration-response curves shown in Fig. 4a.

Fig. 4.

Simulation and analysis of the response of orthosteric ligands at a constitutively active receptor. a, the theoretical curves were generated using the operational model for the total stimulus (eq. 27) with the latter defined as the summation of the active states of the quaternary (DR_s*GX) and ternary (R_s*GX) complexes. These were simulated using the quaternary complex model described in Ehlert et al. (2011). The log affinity constant of the agonists A to D for the inactive state was 5.0, and that for the inverse agonists (E–G) was 7.0. The K_b value expressed relative to K_a is given in the symbol key. The parameters of the model were the same as those given in the legend to Fig. 3. b, nonlinear regression analysis of the concentration-response curve of agonist A according to eq. 52. During regression analysis, K_E was constrained to a range of values shown on the abscissa. The corresponding estimates of log ε and the residual sum of squares are plotted against the constrained value of log K_E.

To estimate K_b values, all of the concentration-response curves in Fig. 4a were analyzed simultaneously using global nonlinear regression analysis with a form of eq. 37 in which some of the parameters are expressed as logarithms:

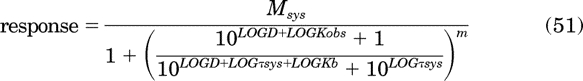In this equation, LOGD, LOGτsys LOGKb, and LOGKobs denote the logarithms of D, τ_sys K_b and K_obs, respectively. The curves were analyzed simultaneously sharing the estimates of M_sys, m, and log τ_sys among the curves and obtaining unique estimates of log K_obs and log K_b for each orthosteric ligand. Regression analysis will not yield an accurate estimate of the K_obs of a full agonist, and the nonlinear regression algorithm used might not converge on a solution. This is not a problem because the error in the estimate of the K_obs of a full agonist is inversely correlated with τ such that the product of the two (τK_obs) is constant over the domain that yields a least-squares fit. Thus, K_obs can be constrained to an arbitrarily low value (lower than the true value) during regression analysis, and the resulting estimate of K_b or the product, τK_obs, is accurate (see eq. 34; K_b = τK_obs/τ_sys). In our case, we simply constrained the K_obs value of agonist A to its theoretical value (i.e., 5.08; log reciprocal of the EC₅₀ value for half-maximal formation of DR_s*GX). Regression analysis yielded the following estimates of the log K_obs values of the orthosteric ligands B to G: 5.17 ± 0.03, 5.07 ± 0.01, 5.12 ± 0.03, 6.90 ± 0.04, 6.97 ± 0.01 and 6.89 ± 0.01, respectively. These values are nearly identical to those used to simulate the data (5.01, 5.001, 5.001, 7.00, 7.00 and 7.00, respectively). The corresponding estimates of the log K_b values for agonists A to G (7.88 ± 0.02, 6.91 ± 0.01, 5.96 ± 0.01, 5.38 ± 0.03, 6.71 ± 0.04, 6.37 ± 0.01, and 5.16 ± 0.09, respectively) were also similar to their theoretical values (8.0, 7.0, 6.0, 5.301, 6.78, 6.301, and 5.0, respectively). The K_obs and K_b values are listed in Table 1. Regression analysis also yielded estimates of M_sys (100.3 ± 0.50), m (1.15 ± 0.10), and log τ_sys (−0.51 ± 0.005).

TABLE 1.

Theoretical and estimated parameters for the orthosteric ligand concentration-response curves shown in Fig. 4

Ligand	Theoretical Parameters				Estimated Parameters
	Log Kb	Log Ka	Log Kobsa	Log Relative Efficacyb	Log Kb	Log Ka	Log Kobs	Log Relative τc
A	8.00	5.00	5.08	0.00	7.88 ± 0.02	4.29	N.D.	0.00
B	7.00	5.00	5.01	−0.93	6.91 ± 0.01	5.14	5.17 ± 0.03	−1.08
C	6.00	5.00	5.00	−1.93	5.96 ± 0.01	5.06	5.07 ± 0.01	−1.92
D	5.30	5.00	5.00	−2.62	5.38 ± 0.03	5.10	5.12 ± 0.03	−2.56
E	6.78	7.00	7.00	−3.15	6.71 ± 0.004	6.94	6.90 ± 0.04	−3.01
F	6.30	7.00	7.00	−3.62	6.37 ± 0.01	6.99	6.97 ± 0.01	−3.41
G	5.00	7.00	7.00	−4.92	5.16 ± 0.09	6.91	6.89 ± 0.01	−4.53

N.D., not determined.

^a The log reciprocal of the orthosteric ligand concentration required for half-maximal formation of the DR_s*GX complex.

^b The maximal amount of DR_s*GX complex formed by the orthosteric ligand, expressed relative to that of agonist A.

^c Expressed relative to that of agonist A.

Estimation of the K_a Values of a Series of Orthosteric Ligands.

The estimation of K_a is more complicated than that of K_b. It is impossible, for example, to estimate the K_a of a single orthosteric ligand if the only information available is its concentration-response curve measured before and after partial receptor inactivation. In this section, therefore, a method for estimating the K_a values of the series of orthosteric ligands illustrated in Fig. 4 is described. The method is accurate for those ligands with relative efficacies less than one-third that of the most efficacious ligand in the series.

The process of estimating K_a consists of the following steps:

1. Determining the maximal estimate of K_E-obs that yields a least-squares fit of eq. 52 to the concentration-response curve of the most efficacious agonist.

2. Estimating a provisional value of ε for each orthosteric ligand by regression analysis with eq. 52 with K_E-obs constrained to the maximal estimate for the most efficacious agonist.

3. Estimating K_a from the provisional ε values of the agonists through a series of calculations using eqs. 2, 3, 32, and 35.

4. For those agonists having an efficacy value less than one-third that of the most efficacious agonist, the estimate of K_a is valid.

5. For the most efficacious agonist and agonists with an efficacy not less than one-third that of the most efficacious agonist, the value of K_a represents a minimal, limiting estimate.

The first step involves nonlinear regression analysis of the concentration-response curve of the most efficacious agonist (agonist A; Fig. 4) using the following equation:

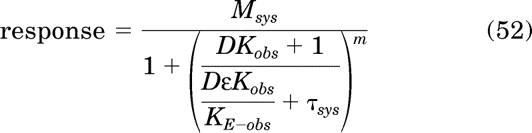This equation represents the operational model for constitutive activity (eq. 28) with τ replaced with ε/K_E-obs. The goal is to identify the maximal estimate of K_E-obs that yields a least-squares fit. Regression analysis is done iteratively with M_sys, m, and K_obs constrained as constants equivalent to those estimated in the K_b analysis described above. An approximate estimate of K_E-obs is obtained in the first regression by constraining ε to 1.0 and estimating K_E-obs. In the second and subsequent regressions, K_E-obs is constrained to a constant 0.1 log unit less than that of the prior regression. For each of these subsequent regressions, log ε is constrained to the range log ε < 0 (1 > ε > 0), and regression analysis yields an estimate of log ε. This stepwise process is continued until the RSS no longer decreases. This occurs when the RSS of a regression is equivalent to that of the prior regression. That the RSS is at a minimum can be verified by doing the regression with log K_E-obs constrained to arbitrarily low value (e.g., −4.0) and verifying that the RSS is the same. The maximum value of log K_E-obs that yields a minimum value of the RSS is recorded as well as the provisional estimate of log ε for this value of log K_E-obs. For agonist A in Fig. 4, these values were −0.03 and −2.4, for log ε and log K_E-obs, respectively.

An example of how the RSS changes with a change in the value to which K_E-obs is constrained during nonlinear regression is shown in Fig. 4b for agonist A. The plot shows the results of regression analysis using eq. 52 with the parameters M_sys, m, and K_obs constrained to constants as described above and K_E-obs constrained to various values indicated on the abscissa. A vertical line through each set of points shows the results of a single nonlinear regression step. As the value to which log K_E-obs is constrained decreases from a high value (−1.8), the RSS decreases and reaches a stable minimum value when log K_E-obs ≤ −2.4. The estimate of log ε is a little less than 0 (ε slightly less than 1.0) when log K_E-obs is equivalent to its maximal value for generating a least-squares fit.

Having identified the maximal, limiting estimate for the domain of log K_E-obs for agonist A and its associated provisional log ε value, the concentration-response curves of the less efficacious orthosteric ligands are analyzed by nonlinear regression analysis with eq. 52 with M_sys, m, and K_obs constrained as described above and log K_E-obs constrained to its maximal limiting estimate (−2.4 for the data in Fig. 4). Regression analysis yields the provisional log ε values of the orthosteric ligands. From these estimates of ε, ε_i values are estimated using eq. 2. Then, estimates of τ_i are calculated using eq. 32, and finally, K_a is estimated using eq. 35 and the estimates of K_obs, τ_i, and τ_sys. These values are listed in Table 1. There was good agreement between these log K_a estimates for ligands B to G (5.14, 5.06, 5.10, 6.94, 6.99, and 6.91, respectively) and those used to simulate the data (5.0, 5.0, 5.0, 7.0, 7.0, and 7.0, respectively). The exception is in the estimation of K_a of the most efficacious agonist (A), which exhibited a log difference of approximately 0.71 in its estimation (log estimate, 4.29; log theoretical estimate, 5.0).

It can be shown that the estimate of K_a approaches K_obs when K_E-obs is constrained to an arbitrarily low value during regression analysis with eq. 52. Constraining log K_E-obs to an arbitrarily low value also yields a least-squares fit as shown in Fig. 4b. For agonist A in Fig. 4, the true value of K_a lies somewhere between the limiting value of K_a estimated above and the K_obs value. The same can be said of any agonist analyzed that has an efficacy not less than one-third that of the most efficacious agonist in a series.

It is possible to estimate the limiting minimal value of log K_a by the method of partial receptor inactivation using an approach analogous to that illustrated in Fig. 4b. The data in Fig. 3a were analyzed in this manner using a modified form of eq. 43 in which τ was replaced with ε/K_E-obs. The ligand and system parameters for the agonist in Fig. 3a are identical to those of agonist A in Fig. 4. This analysis yielded a minimum estimate of log K_a of 4.35, which is similar to that estimated above for agonist A in Fig. 4 (4.29).

If the most efficacious orthosteric ligand in a series is an inverse agonist, the nonlinear regression analysis is done as described above but with the regression equation modified:

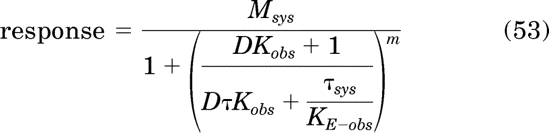This equation is analogous to the operational model for constitutive receptor activity (eq. 28, but with τ_sys replaced with ε_sys/K_E-obs). The regression analysis requires an estimate of M_sys, which can only be determined by the method of partial receptor inactivation with an efficacious agonist or by assuming that the E_max of a full agonist is equivalent to M_sys. Thus, it seems unlikely that an experimenter would know M_sys without also having the concentration-response curve of an efficacious agonist. Regardless, if M_sys is known and the most efficacious ligand is an inverse agonist, a limiting estimate of log K_E-obs can be estimated using eq. 53 as in a manner analogous to that described above for the most efficacious agonist. This estimate can be used to calculate the provisional ε values of the inverse agonists from their corresponding τ values. Ultimately, K_a values can be estimated using eqs. 3, 32, and 35 as described above.

Estimation of the Relative Efficacy Values of a Series of Orthosteric Ligands.

It is possible to estimate the relative efficacy of the orthosteric ligands in various ways based on the parameter values estimated so far. For example, the intrinsic relative activity (RA_i) of the orthosteric ligand is defined as the product of its observed affinity and efficacy expressed relative to that of a reference orthosteric ligand (Ehlert et al., 1999; Griffin et al., 2007). From eq. 4, it follows that:

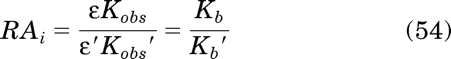in which ′ denotes the parameters of the reference orthosteric ligand. Rearranging eq. 54 yields:

Thus, the parameter estimates (K_b and K_obs) from the initial regression with eq. 51 could be used to estimate relative efficacy using eq. 51 provided that the K_obs value of any full agonist was previously determined. The relative efficacy values of the ligands were determined in this way and there was good agreement between the estimates and the theoretical values (see Table 1). Alternatively, the concentration-response curves could be analyzed with eq. 28 using global nonlinear regression analysis, sharing the estimates of M_sys, m, and τ_sys among the curves and obtaining unique estimates of K_obs and τ for each orthosteric ligand. Again, the K_obs of any full agonist needs to be determined previously and constrained as a constant during regression analysis. The relative efficacy values of the orthosteric ligands could then be estimated from the τ values using eq. 49.

Estimation of the K_b Values of Orthosteric Ligands and the K_obs and Relative Efficacy Values of Partial Agonists Is Easy When the Hill Slope Is Equal to One.

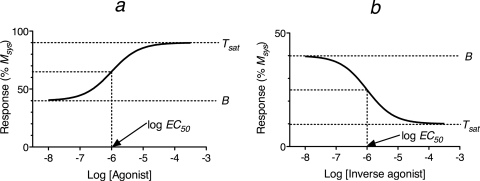
When the Hill slope of the ligand concentration-response curve is equivalent to one, the transducer-slope factor in the operational model is also equal to one, and there are simple relationships between the parameters of the concentration-response curve and K_b, K_obs, and relative efficacy. For these relationships, we define the EC₅₀ value as the concentration of orthosteric ligand that elicits a half-maximal change in response from the basal level caused by constitutive receptor activity (B) to that observed at maximally effective concentrations of the ligand. We define the effect at maximally effective concentrations of the ligand as T_sat (total response at a saturating ligand concentration). For an agonist, this value is equal to the maximum total response above background level without constitutive activity. For an inverse agonist, T_sat represents the difference between the response measured at saturating concentration of inverse agonist and the level of response measured in the absence of constitutive activity. Figure 5 illustrates these terms for an agonist (a) and inverse agonist (b).

Fig. 5.

The definitions of EC₅₀, the basal response of a constitutively active receptor (B), and the total response of the receptor at a maximally effective concentration of the orthosteric ligand (T_sat) are shown for an agonist (a) and an inverse agonist (b).

When the Hill slope of the concentration-response curve is equivalent to one, the K_b value of an orthosteric ligand relative to that of a reference orthosteric ligand can be expressed in terms of the empirical parameters of the concentration-response curve:

In this equation the parameters of the standard orthosteric ligand are denoted by ′. We have previously defined the RA_i value as a relative measure of the affinity constant of an agonist for the active state of the receptor (Tran et al., 2009). It can also be shown that the K_b and K_obs values of an orthosteric ligand are described by:

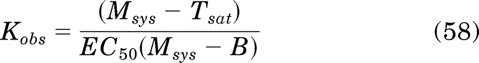Finally, the efficacy of one orthosteric ligand expressed relative to a reference ligand is equivalent to:

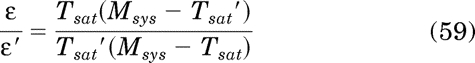where the parameters of the reference orthosteric ligand are denoted by ′. The derivation of eqs. 56 to 59 is given in Appendix. The equations for K_obs and relative efficacy can only be applied in the analysis of partial agonists and inverse agonists, because there is little difference between M_sys and the T_sat of a full agonist. In fact, the T_sat of a full agonist could be used as an estimate of M_sys in the estimation of K_obs and relative efficacy of partial agonist.

The T_sat and EC₅₀ values of all of orthosteric ligands A to G can be estimated from the parameters of the operational model for constitutive activity (eq. 28) as described in Appendix (see eqs. 61 and 70) or by nonlinear regression analysis using a four-parameter logistic equation:

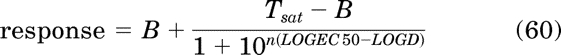In this equation, n denotes the Hill slope of the concentration-response curve and LOGEC₅₀ and LOGD denote the log values of EC₅₀ and D, respectively.

These estimates of T_sat and log EC₅₀ for the data in Fig. 4 are listed in Table 2. The estimates of K_b, K_obs, and relative efficacy were also estimated from the T_sat and EC₅₀ values using eqs. 57 to 59, and these estimates are also listed in Table 2 for ligands B to G. The log efficacy values have been normalized relative to that of agonist B. There is agreement between these estimates of K_b, K_obs, and relative efficacy and the theoretical values listed in Table 1 after normalizing the theoretical efficacy values to that of agonist B. This is expected because the transducer slope factor for this simulation was equal to one (m = 1; see legend to Fig. 4).

TABLE 2.

Estimation of K_b, K_obs, and relative efficacy using equations 57, 58, and 59, respectively

The parameters were estimated from the T_sat and EC₅₀ values of the concentration-response curves shown in Fig. 4. For the calculations, it was assumed that the T_sat of agonist A was a good estimate of M_sys. The estimate of the basal response was 20.6%.

Agonist	Tsat	Log EC50	Log Kb	Log Kobs	Log Relative Efficacya
	% Msys
A	100	−7.32	8.00	N.D.	N.D.
B	96.6	−6.33	7.00	4.97	0.00
C	73.4	−5.46	6.02	4.99	−1.01
D	34.0	−5.08	5.37	5.07	−1.74
E	13.5	−6.96	6.72	6.95	−2.26
F	5.05	−6.92	6.32	7.01	−2.72
G	0.28	−6.90	5.03	6.99	−4.00

N.D., not determined.

^a Expressed relative to that of agonist B.

Additional Simulations.

We also simulated concentration-response curves with random error for orthosteric ligands under conditions of constitutive activity with different concentrations of guanine nucleotide and with transducer slope factors (m) that differed from one. In each case, we were able to obtain reasonable estimates of K_b and K_a as well as the receptor population parameters (K_obs and relative efficacy) except for the K_a value of the most efficacious agonist and the K_b value of full inverse agonists. This analysis was done based on the regression eqs. 28, 37, and 52 as described above. With the most efficacious agonist, the limiting minimal estimate of K_a was accurate when the concentration of guanine nucleotide was low, but with real data there is uncertainty in knowing whether the estimate is accurate as described in Ehlert et al. (2011).

We also considered the possibility of two active states of the receptor and a summary of the results of these simulations is given in Appendix.

Analysis of Experimental Data

M₂ Muscarinic Receptor-Mediated Phosphoinositide Hydrolysis in HEK 293 Cells Overexpressing G_α15.

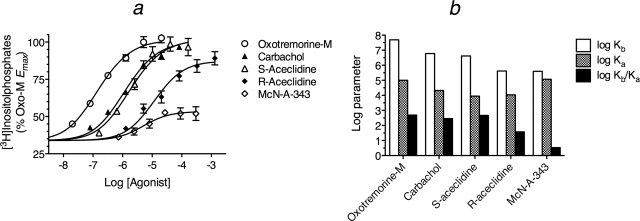
We previously investigated the activity of a group of muscarinic agonists for eliciting [³H]phosphoinositide hydrolysis in HEK 293 cells prelabeled with [³H]inositol and expressing G_α15 and the M₂ muscarinic receptor (Griffin et al., 2007). The cells were treated with pertussis toxin and 4-DAMP mustard to inhibit signaling through G_i and to block a small response elicited by an endogenous M₃ receptor, respectively. In that study, we analyzed the component of the response above constitutive M₂ receptor activity using the standard operational model and a null equation. The background level of [³H]inositolphosphate accumulation in HEK 293 G_α15 cells was approximately 1500 to 2000 cpm. After transient transfection of the M₂ receptor, inositolphosphate accumulation in the absence of orthosteric ligand increased to 3500 to 4000 cpm. Thus, approximately 2000 cpm of [³H]inositolphosphates could be attributed to constitutive activity of the M₂ receptor. Figure 6a shows the results of our prior study plotted as the total response (constitutive and ligand induced activity) normalized relative to the T_sat of oxotremorine-M (approximately 6000 cpm). The T_sat and log EC₅₀ values (mean ± S.E.M.) of oxotremorine-M, carbachol, S-aceclidine, R-aceclidine, and 4-(m-chlorophenyl-carbamoyloxy)-2-butynyltrimethylammonium (McN-A-343) were 100 ± 0.7, 94.9 ± 0.6, 99.7 ± 1.0, 86.1 ± 0.9, and 53.5 ± 1.0 for T_sat and −6.79 ± 0.02, −6.02 ± 0.02, −5.76 ± 0.03, −4.93 ± 0.04, and −5.24 ± 0.11 for log EC₅₀, respectively.

Fig. 6.

M₂ muscarinic receptor-mediated stimulation of phosphoinositide hydrolysis in HEK 293 cells expressing G_α15. a, the effects of muscarinic agonists on [³H]inositolphosphate accumulation are shown. The [³H]inositolphosphate level measured in cells not transfected with the M₂ receptor was subtracted from the measurements made in cells transfected with the M₂ receptor and normalized relative to the E_max of oxotremorine-M. The data are from Griffin et al. (2007) and represent the mean ± S.E.M. of four to six experiments, each done in triplicate. b, analysis of the data in a yielded estimates of the affinity constants of the agonists for the active (K_b) and inactive (K_a) states of the receptor. The K_a value was assumed to be approximately equal to K_obs.

The observed affinity constants of carbachol and oxotremorine-M were determined in competitive binding assays with [³H]N-methylscopolamine on intact HEK cells overexpressing G_α15. The data in Fig. 6a were analyzed as described above to estimate the K_b, the minimum value of K_a, K_obs, and relative efficacy, and these results are given in Table 3. During regression analysis, the log K_obs values of oxotremorine-M and carbachol were constrained to the values determined in the competitive binding experiments with [³H]N-methylscopolamine (5.0 and 4.3, respectively). Regression analysis yielded estimates of M_sys (106 ± 2), log τ_sys (−0.52 ± 0.03), and m (0.63 ± 0.08). Relative efficacy was calculated as the agonist τ value expressed relative to that of oxotremorine-M. The estimates of K_b, K_a, and their ratio are illustrated in the histogram shown in Fig. 6b. Because there is potential ambiguity in the estimate of the K_a value of the most efficacious agonists (oxotremorine-M, carbachol, and S-aceclidine), we assumed that their K_a values were similar to K_obs for the illustration in Fig. 6b.

TABLE 3.

M₂ receptor-mediated stimulation of [³H]inositolphosphate accumulation in HEK 293 cells expressing G_α15

The parameters were estimated from the agonist concentration-response curves shown in Fig. 6.

Agonist	Log Kb	Log Kaa	Log Kobsb	Log Kb/Kac	Log Relative Efficacyd
Oxotremorine-M	7.69 ± 0.03	3.76	5.01 ± 0.08	2.7–3.9	0.00
Carbachol	6.78 ± 0.02	3.46	4.32 ± 0.10	2.5–3.3	−0.24
S-Aceclidine	6.62 ± 0.04	3.00	3.95 ± 0.29	2.7–3.6	−0.03
R-Aceclidine	5.62 ± 0.04	4.01	4.04 ± 0.04	1.6	−1.11
McN-A-343	5.60 ± 0.11	5.06	5.07 ± 0.11	0.54	−2.16

^a A minimum estimate of log K_a.

^b The K_obs values of oxotremorine-M and carbachol were estimated in competitive binding experiments on intact HEK 293 cells expressing G_α15 and the M₂ muscarinic receptor, and the K_obs values of the remaining agonists were estimated by nonlinear regression analysis using eq. 37.

^c The range of values represents log K_b/K_obs − log K_b/K_a.

^d The log τ value of the agonist expressed relative to that of oxotremorine-M.

M₃ Muscarinic Receptor-Mediated Phosphoinositide Hydrolysis in HEK G_α15 Cells.

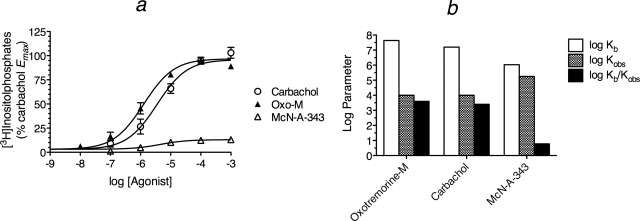
We also transiently expressed the M₃ receptor in HEK 293 G_α15 cells and measured phosphoinositide hydrolysis elicited by oxotremorine-M, carbachol, and McN-A-343. The data are plotted as total response (constitutive and ligand induced activity) normalized relative to the T_sat of oxotremorine-M (Fig. 7a). In these experiments, the background level of [³H]inositolphosphate accumulation was similar to that observed in our prior studies on the M₂ receptor, but the constitutive activity elicited by transient transfection of the M₃ receptor was only approximately 600 to 1000 cpm, and T_sat values of oxotremorine-M and carbachol were much greater (40,000–60,000 cpm of [³H]inositolphosphates). The T_sat and log EC₅₀ values (mean ± S.E.M.) of oxotremorine-M, carbachol, and McN-A-343 were 100 ± 1.3, 110 ± 2.0, and 14.3 ± 0.8 for T_sat and −5.97 ± 0.04, −5.33 ± 0.06, and −5.21 ± 0.23 for log EC₅₀, respectively.

Fig. 7.

M₃ muscarinic receptor-mediated stimulation of phosphoinositide hydrolysis in HEK 293 cells expressing G_α15. a, the effects of muscarinic agonists on [³H]inositolphosphate accumulation are shown. The [³H]inositolphosphate level measured in cells not transfected with the M₃ receptor was subtracted from the measurements made in cells transfected with the M₃ receptor and normalized relative to the E_max of carbachol. The data represent the mean ± S.E.M. of three experiments, each done in triplicate. b, analysis of the data in a yielded estimates of the affinity constants of the agonists for the active (K_b) and inactive (K_a) states of the receptor. The K_a value was assumed to be approximately equal to K_obs.

The K_obs values of carbachol and oxotremorine-M were estimated by the method of partial receptor inactivation using a 5-min incubation with the aziridinium ion of 4-DAMP mustard (1.0 μM) as a means of inactivating a fraction of the receptor population. Treatment with 4-DAMP mustard had little effect on the basal [³H]inositolphosphate response in HEK 293 G_α15 cells transfected with the M₃ receptor. The data were analyzed as described above in connection with Fig. 3 to yield a log K_obs value for carbachol and oxotremorine-M of 3.74 ± 0.14 and 4.00 ± 0.13, respectively.

The data in Fig. 7a were analyzed for estimation of K_b, K_obs, relative efficacy, and the minimum estimate of K_a as described above, and the corresponding parameter estimates are listed in Table 4. Regression analysis yielded estimates of M_sys (99.1 ± 2.03), log τ_sys (−1.74 ± 0.25), and m (0.85 ± 0.08). During the analysis, the log K_obs values of carbachol and oxtremorine-M were constrained to those estimated by the method of partial receptor inactivation. The K_b, K_a, and K_b/K_a values of the agonists are illustrated in Fig. 7b and listed in Table 4. For the histogram, it was assumed that the K_a values of oxotremorine-M and carbachol were approximately equal to K_obs. Although the E_max value of carbachol was greater than that of oxotremorine-M, a reasonable fit of eq. 28 was obtained sharing the estimate of M_sys. The parameters yielded a lower estimate for the efficacy of carbachol (0.66) relative to oxotremorine-M (see Table 4).

TABLE 4.

M₃ receptor-mediated stimulation of [³H]inositolphosphate accumulation in HEK 293 cells expressing G_α15

The parameters were estimated from the agonist concentration-response curves shown in Fig. 7.

Agonist	Log Kb	Log Kaa	Log Kobsb	Log Kb/Kac	Log Relative Efficacyd
Oxotremorine-M	7.64 ± 0.27	2.68	4.00 ± 0.13	3.6–4.9	0.00
Carbachol	7.20 ± 0.27	3.31	3.74 ± 0.14	3.4–3.9	−0.18
McN-A-343	6.03 ± 0.21	5.25	5.25 ± 0.20	0.78	−2.85

^a A minimum estimate of log K_a.

^b The K_obs values of carbachol and oxotremorine-M were estimated by the method of partial receptor inactivation as described in the text, and that of McN-A-343 by regression analysis of the data in Fig. 7 using eq. 37.

^c The range of values represents log K_b/K_obs − log K_b/K_a.

^d The log τ value of each agonist normalized relative to that of oxotremorine-M.

Discussion

Most receptors evolved to be active when occupied by an endogenous ligand and inactive when unoccupied. Because high activity is associated with an optimum structure, multiple active states would reduce activity from the optimum, and multiple inactive states with variable affinity would engender ligand induction of an inactive state over an active one. Thus, discrete active and inactive states with high and low affinity for the endogenous ligand, respectively, are likely properties of an efficient, ligand-dependent molecular switch. That evolution has selected efficient receptors can be seen in the uniform quantal currents of single ligand-gated ion channels (Colquhoun and Sakmann, 1985). The ensemble average of their individual random behaviors yields a continuum of predictable, ligand-dependent activity at the level of the receptor population. The methods of this article describe how to estimate orthosteric ligand affinity constants for active and inactive states of a constitutively active G protein-coupled receptor by analyzing a response downstream from receptor activation.

We have previously shown that the product of affinity and efficacy is proportional to the affinity constant of the agonist for the active state of the receptor (Tran et al., 2009). When an agonist concentration-response curve is analyzed with the operational model, it is always possible to estimate the product of the parameters, K_obs and τ (Griffin et al., 2007; Ehlert, 2008). This product is proportional to both the product of affinity and efficacy (Ehlert et al., 1999) and the affinity constant of the active state (Tran et al., 2009). The proportionality constant for the latter (τ_sys) is a function of the inherent activity of the free receptor (K_c) and the sensitivity of the downstream signaling pathway (K_E-obs), and it can be estimated from the basal response of the system using the operational model (see eqs. 28 and 30). Thus, by dividing the product, τK_obs, by τ_sys, it is possible to estimate the affinity constant of an agonist for the active state of the receptor. Analogous reasoning shows that it is possible to estimate the affinity constant of the inactive state by dividing the product, τ_iK_obs, by τ_i-sys. It is impossible, however, to obtain a reliable estimate of τ_iK_obs for the most efficacious agonist in a series unless additional information is obtained. Likewise, it is difficult to estimate τK_obs for a full inverse agonist.

An advantage of estimating the microscopic affinity constants of orthosteric ligands for receptor states is that the latter are purely receptor-dependent properties. Although the nature of the G protein, other effectors that come in contact with the receptor, and the concentration of GTP can change the activation state and observed affinity of the receptor population, these have no effect on the structure of receptor states, per se, nor on the estimation of K_b and K_a. Thus, a unique set of receptor states can give rise to a continuum of observed affinities and efficacies (Ehlert, 2000).

Although the existence of agonist bias in receptor signaling (Kenakin, 2011) may seem to conflict with the simple picture given above, it implies a set of discrete receptor states that differentially signal through different effectors (e.g., G proteins, G protein-coupled receptor kinases). It follows that the different effectors report the activity of different receptor states. Thus, the G protein is not so much a determinant of drug-receptor activity so much as a window onto the different receptor states that generate unique activities. Using our approach it is possible to estimate the affinity constants of these states by analyzing responses elicited through different G proteins. Even if the estimate of the affinity constant of the active state represents a weighted average of multiple active states, it would still represent a receptor-dependent property characteristic of the particular response.

Constitutive receptor systems offer an advantage for drug discovery in that these systems enable the detection of inverse agonist activity and are more sensitive to agonist activity (Chen et al., 1999). Because most potent antagonists are likely to exhibit selectivity for the inactive state of the receptor, constitutively active receptor systems are useful for the direct detection of antagonist activity (Chen et al., 2000). We show that constitutively active systems are also useful in the estimation of microscopic affinity constants for active and inactive states of the receptor. Constitutive activity can be achieved by overexpression of the receptor or by increasing the sensitivity of the transduction mechanism. The latter can be accomplished by overexpressing the G protein, which has been described for several receptors including the D₂ dopamine (Senogles et al., 1990) and M₃ muscarinic (Burstein et al., 1997) receptors. Although overexpression of receptors and G proteins may lead to nonphysiological signaling and a change in the parameters of the receptor population (i.e., K_obs and ε), the estimation of K_b for the receptor state that interacts with the overexpressed G protein should be unaffected.

The observed affinity constants (K_obs) of carbachol and oxotremorine-M were approximately 10-fold higher at the M₂ receptor compared with the M₃. There was little difference between M₂ and M₃ receptors with regard to the K_b and K_a values of the agonists, however, although the range of the K_a estimate was large (0.7 and 1.3 log units for carbachol and oxotremorine-M, respectively). The increase in observed affinity at the M₂ receptor can be attributed to the greater constitutive activity of the M₂ receptor relative to the M₃ in HEK 293 cells expressing G_α15. When expressed relative to the τ value of oxotremorine-M, the τ_sys value of the M₂ receptor (0.21%) was 10-fold greater than that of the M₃ receptor (0.023%). The consequences of eq. 8 suggest a comparable difference in the K_obs value of a highly efficacious agonist.

Analysis of single-channel recordings of the neuromuscular nicotinic acetylcholine receptor of the adult mouse yielded estimates of 5.0 × 10⁷ and 7.1 × 10³ M⁻¹ for the affinity constants of acetylcholine for the open and closed states (Auerbach, 2010). The difference in affinity (7000-fold) corresponds to approximately 5.2 kcal · mol⁻¹ of available energy for inducing the open state of the channel. We estimated affinity constants of 1.6 × 10⁷ and 2.0 to 5.5 × 10³ M⁻¹ for carbachol at the active and inactive states of the M₃ receptor, which corresponds to a 2900- to 7800-fold difference in affinity (4.7–5.3 kcal · mol⁻¹). The agreement between the microscopic affinity constants of acetylcholine and its carbamate analog at nicotinic and muscarinic receptors suggest that natural selection has sculpted optimal binding pockets for acetylcholine on these proteins (see also Jackson, 1989).

The estimate of the K_b/K_a ratios of McN-A-343 at M₂ and M₃ receptors was very low (approximately 3.5- to 6.0-fold, 0.15–0.37 kcal · mol⁻¹), indicating that this M₁ and M₄ selective muscarinic agonist has little selectivity for the active states of M₂ and M₃ receptors and that it would be unlikely for this agonist to elicit a response at these receptors unless there were significant constitutive activity or a highly sensitive system to amplify low constitutive activity. These results have implications for native systems, such as the guinea pig ileum, where the compound exhibits an E_max of approximately 30% that of carbachol through activation of the M₃ receptor. Perhaps there is substantial constitutive activity in ileal smooth muscle that is prevented from eliciting contraction by inhibitory K⁺ currents (e.g., Ca²⁺-activated K⁺ channels). Inhibition of K_Ca channels with charybdotoxin elicits spontaneous contraction of guinea pig ileum (Hong et al., 1997). A small 3- to 5-fold selectivity for the active state could generate a substantial contraction in a smooth muscle with a moderate threshold for the response caused by K⁺ channel activity that is almost satisfied by constitutive receptor activity.

Our method for the estimation of K_a is limited in the sense that it is never possible to estimate the K_a of the most efficacious agonist in a series, only agonists with K_b/K_a ratios less than one-third that of the most efficacious agonist. Ehlert et al. (2011) describe this limitation in detail with regard to the estimation of RI_i. Our estimates of the K_b values of agonists for the M₃ receptor were more variable than those of the M₂ receptor. This can be attributed to 1) the greater relative error in the estimation of the very low constitutive activity of the M₃ receptor, 2) the limited number of agonists run in the M₃ receptor assay, and 3) the wider spacing of the agonist concentrations in the M₃ assay. Accurate estimation of K_b depends on an accurate estimate of constitutive activity (τ_sys) and the transducer slope factor (m) in the operational model. The error in the estimate of the latter parameter is greatly reduced with more agonists having a range of efficacies and a tighter geometric spacing of agonist concentrations.

Our method of estimating the receptor-dependent K_b and K_a values of orthosteric ligands through the analysis of downstream responses at G protein-coupled receptors has widespread application in drug discovery, particularly when defined receptor-effector systems are used (Stewart et al., 2010).

Appendix

Summary of the Analysis of Simulations Involving Two Active States of the Receptor

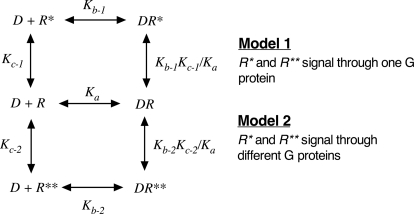
Using techniques described previously (Ehlert, 2008; Tran et al., 2009), we also investigated a model having two active states that signal through the same G protein (model 1) and another having two active states that signal through two different G protein to elicit two different responses (model 2) (see Fig. 8).

Fig. 8.

Model for a receptor with two active states (R* and R**). In model 1, both active states signal through the same G protein to elicit the same response. In model 2, each active state signals through a different G protein to elicit a different response.

The results of our analysis showed that the behavior of the first model depends on the activity of the two states, their relative abundances in the absence of orthosteric ligand, and the selectivity of the orthosteric ligand for the two states. If the relative abundances (K_c-1 = K_c-2) and the activities of the two active states are the same, then the estimate of the K_b value of an orthosteric agonist is approximately equal to that of the state for which it has higher affinity, particularly when K_b-1/K_b-2 or K_b-2/K_b-1 is more than 10. At lower ratios, there is more discrepancy, but the difference is never large because of the lack of a large difference between K_b-1 and K_b-2 under this condition. If there is a difference in the abundance (K_c-1 ≠ K_c-2) or the activity of the two states, however, then the estimate of K_b could range from K_b-1 to K_b-2, even when K_b-1 > K_b-2. For example, if an active state with much lower affinity is much more abundant or has much greater activity, then the estimate of K_b could approximate K_b-2 even if K_b-1 > K_b-2.

When there are different states that differentially couple to different G proteins to elicit different measurable responses, then the estimate of K_b-1 or K_b-2 is accurate, provided that it is possible to measure the constitutive activity associated with each active state. If not, it is possible to obtain a reliable estimate of RA_i as described previously (Ehlert, 2008; Tran et al., 2009).

Derivation of Equations 56 to 59

Our strategy involves first deriving equations for T_sat, B, and EC₅₀ in terms of the parameters of the operational model for constitutive activity when the transducer slope factor is equivalent to one (m = 1). These expressions can then be substituted into eqs. 56 to 59 under Results to determine whether the latter are equalities.

T_sat can be determined by evaluating the limit of the operational model for constitutive activity (eq. 28) with m = 1 as D approaches infinity:

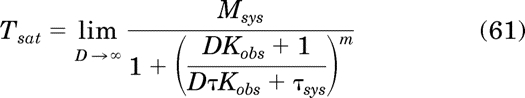Taking the limit yields:

When m = 1, eq. 62 reduces to:

The equation for the basal response elicited by constitutive activity (B) in the absence of an orthosteric ligand can be derived by evaluating the operational model for constitutive activity (eq. 28) when D = 0:

When m = 1, eq. 64 reduces to:

The expression for EC₅₀ can be derived by first considering the range of responses elicited by an orthosteric ligand in the presence of constitutive receptor activity. For an orthosteric agonist, this range spans from B to T_sat and is equivalent to T_sat − B. An EC₅₀ response for an agonist occurs when the total response is equivalent to half of this dynamic range plus the basal response:

In this equation, response₅₀ denotes the total response observed at the EC₅₀ concentration of orthosteric agonist. For an orthosteric inverse agonist, the dynamic range is B − T_sat, and an EC₅₀ response occurs when half of this dynamic range is subtracted from the basal response:

Both eqs. 66 and 67 reduce to the following form:

If the term, response₅₀, in eq. 68 is substituted with the operational model for constitutive activity (eq. 28) with EC₅₀ substituted for D, the following equation is generated:

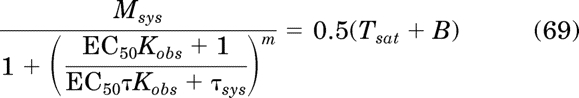Substituting eqs. 62 and 64 for T_sat and B and solving for EC₅₀ yields:

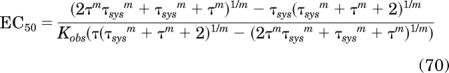When m = 1, eq. 70 reduces to:

Now it is possible to substitute eqs. 63, 65, and 71 for T_sat, B, and EC₅₀, respectively, into eqs. 56 to 59 to determine whether the latter are equalities. Beginning with eq. 56, making the appropriate substitutions yields:

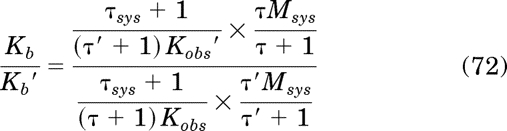Simplification yields:

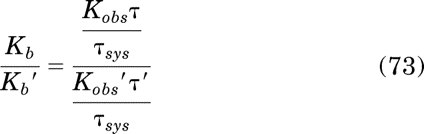Substitution of eq. 34 for τK_obs/τ_sys yields the equality K_b/K_b′ = K_b/K_b′, which verifies eq. 56. Substituting eqs. 65 and 71 for T_sat and EC₅₀ in eq. 57 yields:

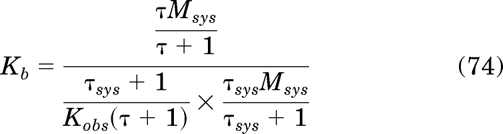Simplification yields the equality K_b = K_b, which verifies eq. 57. Substituting in eqs. 63, 65, and 71 for T_sat, B, and EC₅₀, respectively, in eq. 58 yields the following expression:

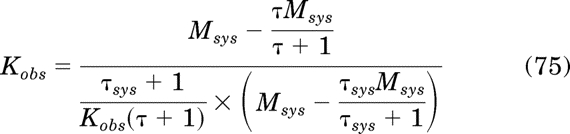Simplification yields the equality K_obs = K_obs, which proves eq. 58. Finally, eq. 56 can be rewritten in the following form because it has been shown the RA_i is equivalent to the product of the observed affinity and efficacy of one orthosteric ligand, expressed relative to that of another:

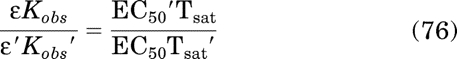Substituting in eq. 58 for K_obs yields:

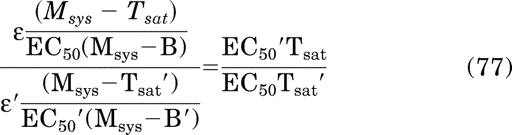This equation reduces to eq. 59, which proves the latter.

Estimation of Initial Parameter Values for Nonlinear Regression Analysis

Below, we describe equations for estimating the initial parameter values for nonlinear regression analysis of concentration-response curves using eq. 51 and the log forms of eqs. 28, 43, and 44. The parameter estimates are denoted by ″ and expressed in terms of the empirical parameters of the concentration-response curve. The definitions of the variables are given under Results.

Initial Parameter Estimates for Equation 43.

Equation 43 is first modified so that the independent variable D and the parameters τ, τ_sys, and K_obs are expressed as logarithms:

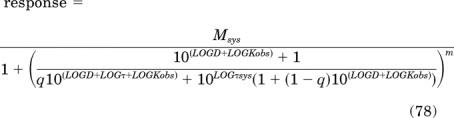In this equation, LOGD, LOGτ, LOGτsys, and LOGKobs denote the log values of D, τ, τ_sys, and K_obs.

If the orthosteric ligand is an agonist, the initial parameter estimates of M_sys, q, and LOGτ are calculated as:

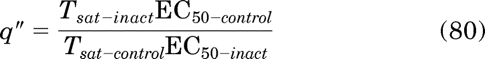in which, T_sat-full denotes the T_sat of a full agonist, and the subscripts “control” and “inact” denote parameters of the concentration-response curves measured before and after partial receptor inactivation, respectively. If the orthosteric ligand is an inverse agonist, M_sys must be constrained to a constant value previously estimated from the analysis of agonist data. The initial estimates of q and LOGτ for an inverse agonist are calculated as:

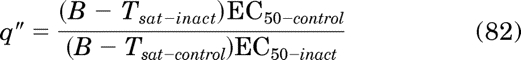The remaining initial parameter values are estimated in the same manner for both agonists and inverse agonists:

Initial Parameter Estimates for Equations 28, 44, and 51.

Equations 28 and 44 are first modified by expressing the independent variable D and the parameters τ, τ_sys, and K_b as logarithms as in eqs. 87 and 88, respectively:

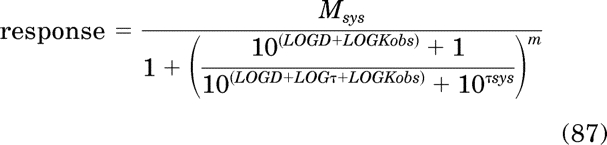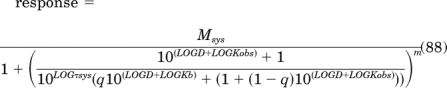in which LOGKb denotes the log affinity constant of the active state of the receptor. The initial value of LOGKb (LOGKb″) is estimated as:

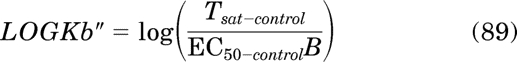The initial values of the other parameters in eq. 87 and all of the other parameters in eqs. 88 and 51 are estimated as described above.

Authorship Contributions

Participated in research design: Ehlert, Suga, and Griffin.

Conducted experiments: Ehlert, Suga, and Griffin.

Performed data analysis: Ehlert, Suga, and Griffin.

Wrote or contributed to the writing of the manuscript: Ehlert.