Localization of electrons due to orbitally ordered bi-stripes in the bilayer manganite La_2-2xSr_1+2xMn₂O₇ (x ∼ 0.59)

Abstract

Electronic phases with stripe patterns have been intensively investigated for their vital roles in unique properties of correlated electronic materials. How these real-space patterns affect the conductivity and other properties of materials (which are usually described in momentum space) is one of the major challenges of modern condensed matter physics. By studying the electronic structure of La_2-2xSr_1+2xMn₂O₇ (x ∼ 0.59) and in combination with earlier scattering measurements, we demonstrate the variation of electronic properties accompanying the melting of so-called bi-stripes in this material. The static bi-stripes can strongly localize the electrons in the insulating phase above T_c ∼ 160 K, while the fraction of mobile electrons grows, coexisting with a significant portion of localized electrons when the static bi-stripes melt below T_c. The presence of localized electrons below T_c suggests that the melting bi-stripes exist as a disordered or fluctuating counterpart. From static to melting, the bi-stripes act as an atomic-scale electronic valve, leading to a “colossal” metal-insulator transition in this material.

In correlated electron materials, electrons can self-organize and form a variety of stripe patterns with potential ordering of charges, spins, and orbitals, which are believed to be closely connected to many unique properties of these materials including superconductivity (1–3), metal-insulator transitions (4), and the colossal magnetoresistive or CMR effect (5). Moreover, although the presence of static stripes is indisputable, the existence (and potential impacts) of dynamic or fluctuating (or nematic) counterparts in such compounds is a subject of great debate (6–9). However, how electronic properties in momentum space are altered by these self-organized electronic phases in real-space lacks direct experimental demonstrations. Here we have an opportunity to address this issue by studying the electronic band structure in the stripe patterns of manganites.

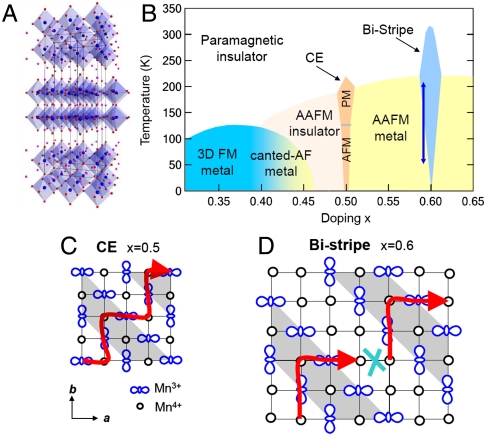
Manganites are famous for the CMR effect, metal-insulator transitions, and magnetic and orbital ordering (10–14). In the bilayer family La_2-2xSr_1+2xMn₂O₇ (see Fig. 1A for the crystal structure), it is believed that the main physics occurs in the MnO₂ layers with the other layers supporting the crystal structure and doping holes or electrons into the MnO₂ layers, analogous to the role the CuO₂ layers play in the physics of high-T_c superconductors. With a variation of hole doping x into the MnO₂ planes, the ground state of the material changes drastically and many different phases emerge (Fig. 1B) (15, 16). Most previous efforts to understand the electronic structure of La_2-2xSr_1+2xMn₂O₇ have focused on the lower doped regimes (for example x = 0.4) in which the ferromagnetic ground state and associated colossal magnetoresistance occur (17–21). Here we focus on the higher doping regimes in which the orbital-ordered stripe phases are more stable (gold and blue “ice-cream cone” regions at and near x = 0.50 and 0.60), realizing that the stripe and orbital ordering are potentially relevant for many families of compounds besides the manganites.

Fig. 1.

Long-range stripe structure in real-space. (A) Crystal structure of bilayer manganite La_2-2xSr_1+2xMn₂O₇ with La/Sr (purple) atoms between MnO₆ octahedra (Mn: blue, O: red). (B) Phase diagram of La_2-2xSr_1+2xMn₂O₇, from refs. 15, 16. (C) CE ordering at x = 0.50 and (D) Bistripe ordering at x = 0.60. Red arrows indicate electron hopping paths, which are broken in the x = 0.60 bi-stripe phase. The doping and temperature of our study is indicated by the blue arrow in box B, with x ∼ 0.59 and T_c ∼ 160 K.

The yellow portion covering most of the low-temperature high-doping range of the phase diagram is an A-type antiferromagnetic (AAFM) metal consisting of ferromagnetically ordered MnO₂ planes stacked in an antiferromagnetic sequence (15). Very near the commensurate doping levels of x = 0.50 and 0.60, charge/orbital ordering is the stable state, as indicated by the gold and blue regions (15, 22). At x = 0.50 the ordering is of the famous CE type first proposed by Goodenough (12), and schematically illustrated in Fig. 1C. Each Mn site is drawn as having a charge of either 3+ or 4+ with these charges arranged in a checkerboard fashion, though in actuality the charge disproportionation can be much smaller than a full electron charge (23). On the Mn³⁺ sites, the extra charge is believed to occupy a specific quantum orbital (e.g., an in-plane d_3x²-r² or d_3y²-r² orbital), with these orbitals arranged in a zigzag fashion as shown in the schematic picture. This arrangement forms a stripe-like state as illustrated by the diagonal gray-shaded regions. For x = 0.60, a variant of the CE ordering, so-called bi-stripes, has been proposed in which the additional doped holes introduce extra Mn⁴⁺ sites between the stripes (Fig. 1D) (24, 25). These manganite stripe states show somewhat different behavior from the stripes in cuprates (1, 2) and enrich the variety of self-organized electronic phases.

Earlier scattering measurements have shown that the static bi-stripes disappear or melt below a critical temperature T_c ∼ 160 K (24, 26), accompanying a “colossal” change in conductivity as a function of temperature (15, 26). This unique behavior inspires the current study of electronic structure associated with the bi-stripes. Using angle-resolved photoemission spectroscopy (ARPES), we investigated the temperature-dependent electronic excitations of the layered manganite perovskite La_2-2xSr_1+2xMn₂O₇ (x ∼ 0.59). At x ∼ 0.59, we are able to access both the static bi-stripe region as well as the region near it simply by changing temperature (vertical blue arrow in Fig. 1B). For our particular samples the low-temperature state is thus an A-type antiferromagnetic metal with a transition at T_c ∼ 160 K to the higher temperature bi-stripe-ordered insulator. Here we note that we usually expect ordering to occur at lower temperatures instead of higher temperatures; the “backwards” behavior observed here is usually considered to be a consequence of the competition of the ordering phenomena which localizes electrons, with the double-exchange interaction which favors delocalization of electrons in ferromagnetically ordered MnO₂ planes.

One of our main hypotheses is illustrated by the heavy red lines superimposed on Fig. 1 C and D: a hopping path for electrons is drawn which follows a natural overlap of orbitals—though insulating with a gap at the Fermi energy E_F, this hopping path nonetheless allows for Bloch-like electron states which, as evidenced by clear band dispersion in our measurements, sample multiple crystalline sites in the material. On the other hand, as will be shown later, we experimentally find that in the bi-stripe phase (blue region in Fig. 1B) this hopping path is destroyed due to the static bi-stripe order (see Fig. 1D), for we have observed almost completely nondispersive/localized electron states. A consequence of this localization is a colossal (∼5 orders of magnitude for the x ∼ 0.59 compound) and sudden change of conductivity upon entering the static bi-stripe phase from the AAFM phase below (26). In particular, the insulation of the bi-stripe phase is significantly larger than other phases in La_2-2xSr_1+2xMn₂O₇, suggesting exotic electronic properties in these bi-stripes.

By studying the electronic structure of La_2-2xSr_1+2xMn₂O₇ (x ∼ 0.59) and in combination with earlier scattering measurements, we are able to demonstrate the variation of electronic properties accompanying the melting of bi-stripes in this material. The static bi-stripe state shows remarkable incoherent spectral weight above T_c ∼ 160 K, owing to a strong localization of electrons in this special insulating phase. When the static bi-stripes melt below T_c, the incoherent spectral weight persists and coexists with the dispersive weight of mobile electrons, and it diminishes as the dispersive weight grows up with decreasing temperature. The presence of incoherent spectral weight below T_c is indicative of bi-stripe patches, which may exist as a fluctuating counterpart after the melting of the static bi-stripes.

Results and Discussion

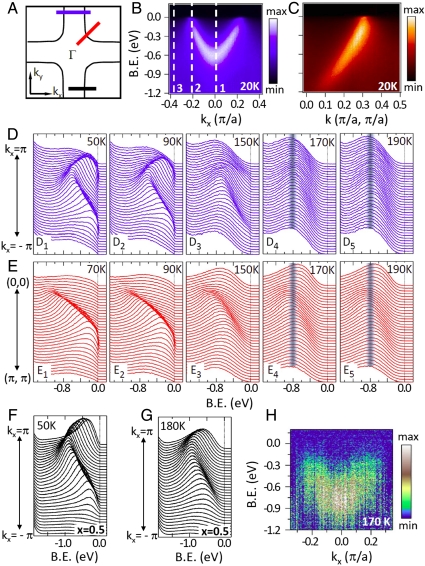
Fig. 2A is the schematic plot of the Fermi surface of La_2-2xSr_1+2xMn₂O₇ (x ∼ 0.59) in the AAFM metallic state (27). Contrary to the bilayer split band structure we reported for the x = 0.36 and 0.38 compounds (28), the Fermi surface of the x ∼ 0.59 compound consists of only one hole pocket (primarily of in-plane d_x²-y² states) around the zone corner, owing to its AAFM spin and orbital ordering which blocks the coupling between neighboring MnO₂ planes (27). Fig. 2 B and C show the near-E_F band dispersion along the blue and red cuts in Fig. 2A, respectively. The variation of these bands with temperature (see Fig. 2 D and E) sheds light on the influence of bi-stripes on the electronic excitations. Near the zone boundary, as shown in Fig. 2D, the dispersive d_x²-y² band is very clear at low temperature. With increasing temperature, the dispersive d_x²-y² states diminish and some nondispersive weight continuously increases and eventually a nondispersive feature around -0.8 eV (indicated by the shaded area) becomes dominant when static bi-stripes prevail above T_c ∼ 160 K. The dominance of the nondispersive feature and the weakness of the dispersive band in the static bi-stripe phase (boxes D₅ and E₅) can be naturally understood as a localization of the electrons (the delocalization of electrons in a solid is what gives rise to the dispersion). Similar behavior also occurs along the zone diagonal (see Fig. 2E), indicating that the static bi-stripes localize the electrons in all directions. It is worth noting that such nondispersive spectral weight has not been observed in other La_2-2xSr_1+2xMn₂O₇ compounds and that it emerges only at the region near x = 0.60, suggesting a close connection between the nondispersive spectral weight and the static bi-stripe phase. Indeed, transport and neutron scattering measurements suggest that the insulating behavior is determined by the static bi-stripe state (15, 26), the collapse of which leads to the emergence of AAFM metallic state and results in a dramatic change of conductivity. This behavior stresses the importance of the statice bi-stripe state (ice-cream cone region near x = 0.60) for conductivity.

Fig. 2.

Electronic structure measurements of La_2-2xSr_1+2xMn₂O₇ (x ∼ 0.59). (A) A schematic Fermi surface plot. (B,C) Energy vs. momentum dispersive band taken at T ∼ 20 K along the blue and red cuts in box A. (D, E) Stacked EDCs from the two cuts at various temperatures. (F, G) Stacked EDCs of x = 0.5 compound, along the black cut in box A and taken at 50 K (AFM-CE state) and 180 K (PM-CE state), respectively. (H) Bloch-like dispersive band derived from box D₄ by subtracting an empirical k-independent “background” represented by EDC cut 3 in box B.

Though the static bi-stripes are found to localize the electrons, the related CE ordering observed in the x = 0.50 sample does not strongly localize the electrons, as shown in Fig. 2 F and G. In this case the sample transitions from an antiferromagnetic (AF) CE stripe-ordered state at low temperature ∼50 K to a paramagnetic (PM) CE stripe-ordered state at intermediate temperature ∼180 K (22), with a weak but noticeable change in the spectral weight (see Fig. S1). Though the high temperature state is insulating with no states at the Fermi energy consistent with theory (29), the hopping path nonetheless allows for Bloch-like electron states which, as evidenced by the clear band dispersion, sample multiple crystalline sites in the material. The difference between CE stripes and bi-stripes on the localization of the electrons can be understood by the schematics of Fig. 1 C and D. In these schematics we draw in the zigzag conduction paths. A long hopping path is allowed for the x = 0.50 sample, giving a Bloch-like dispersive band, while these paths are destroyed for the x ∼ 0.59 sample due to the extra Mn⁴⁺ sites embedded between the stripes. This blocked hopping path gives rise to the localized states we observe in the static bi-stripe phase. Here we also note the influence of the spin order on the electronic structure is not dominant—Fig. 2 F and G show a clear but weak modification upon the change of magnetic order which is qualitatively consistent with what has been observed in x = 0.40 samples upon transitioning from the low temperature ferromagnetic state to the higher temperature paramagnetic state (18, 20). These pieces together indicate that in this study the charge and orbital stripe order impacts the electronic properties much more strongly than does the spin order.

A slight bit of remnant dispersive d_x²-y² weight persists above T_c for the x ∼ 0.59 sample (see Fig. 2H), which can be empirically resolved by removing a nondispersive weight represented by an energy distribution curve (EDC) along the cut 3 in Fig. 2B. Though dispersive, these weak states above T_c are not metallic, i.e., they do not cross E_F. Compared to the perfect bi-stripe pattern that possesses 60% hole doping, the extra electrons in x ∼ 0.59 compound may contribute to the remnant dispersive weight. On the other hand, thermal fluctuations may also disturb the static bi-stripes and lead to a dispersive weight.

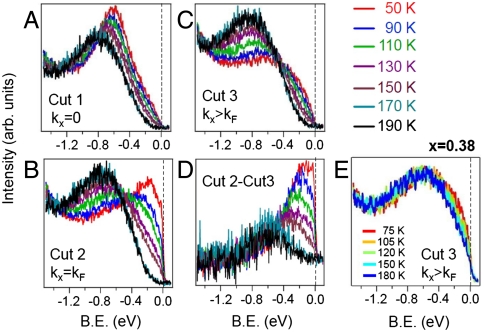
Fig. 3 quantitatively reveals the evolution of spectral weight with increasing temperature. Fig. 3 A–C show EDCs taken at representative momentum positions (EDC cuts 1, 2, and 3) in Fig. 2B. EDC 1 runs across the band bottom, EDC 2 is taken at k_F, and EDC 3 is in the unoccupied k range. All spectra (as well as those on all individual boxes throughout the paper) were normalized by incident photon flux only. As the temperature increases and the long-range bi-stripe structure is approached, the near-E_F spectral weight diminishes and extra spectral weight grows around -0.8 eV. Fig. 3D shows “differential” EDCs, obtained by subtracting EDC cut 3 from EDC cut 2, giving an emphasis on the dispersive d_x²-y² states (similar to what was done to make the plot of Fig. 2H). Here, the dispersive spectral weight continuously diminishes with increasing temperature and a gap of ∼100 meV opens just above T_c. Near the zone center, along the red cut in Fig. 2A, a similar loss of the spectral weight has also been observed (see Fig. S2). It is evident that the drastic increase of spectral weight at -0.8 eV is dominated by the nondispersive weight, while the dispersive states from the itinerant electrons weaken in intensity when approaching the static bi-stripe region. This behavior of the spectral weight naturally indicates two-component behavior in our ARPES data, with one being the Bloch-like states and the other being the nondispersive or localized state at -0.8 eV from static localized electrons. Here we note that the very strong temperature dependence of the deep and nondispersive weight appears to be unique to these samples near the bi-stripe regime. For instance, Fig. 3E shows EDCs at k > k_F taken from an x = 0.38 sample, showing only a minimal temperature dependence to the weight at ∼-0.8 eV.

Fig. 3.

Temperature dependence of electronic structure. (A–C) EDC cuts 1, 2, and 3, indicated by the white dashed lines in Fig. 2B, taken at various temperatures. (D) Differential EDCs obtained by subtracting EDC cut 3 from EDC cut 2. (E) EDCs taken at a position similar to cut 3 from an x = 0.38 sample.

Fig. 4 plots the variation of spectral weight of these data as a function of temperature. The red squares show the dispersive spectral weight, i.e., the integral of the weight across the entire band of Fig. 2H, while the blue squares show the near-E_F portion of this data (within 100 meV of E_F). The black dots show the temperature-induced change in the integrated weight from -1.4 eV to -0.4 eV of EDCs in Fig. 3C, which to a good approximation depicts the temperature-dependent behavior of the localized/nondispersive spectral weight. The plot shows that the near-E_F weight and the dispersive band weight possess a distinct break at T_c ∼ 160 K—they both approximately linearly decrease when approaching T_c from below, and eventually the former drops to zero and the latter weakens more rapidly above T_c. The behavior of the near-E_F weight is in accord with the electronic conductivity measurements (26). On the other hand, the localized weight grows with increasing temperature, becoming dominant in the insulating region of the static bi-stripe phase.

Fig. 4.

Temperature-dependent spectral weight from ARPES and superlattice counts from X-ray scattering (ref. 26) of La_2-2xSr_1+2xMn₂O₇ (x ∼ 0.59). Red and blue squares represent the total (entire occupied band) and the near-E_F (-0.1 eV to +0.05 eV) spectral weight respectively. Black dots show the temperature-induced change in the nondispersive/localized weight, obtained by integrating the EDCs of Fig. 3C from -1.4 eV to -0.4 eV and scaling such that it extrapolates to zero at 0 K. All curves are scaled independently so that the change in weight can be qualitatively estimated.

In this system, the band width W (∼3 eV) of the dispersive component (gold diamonds in Fig. 4) is much larger than the energy scale (-0.8 eV) of the localized component (see SI Text for more details). This comparison sets a strong constraint on theoretical models of the behavior and rules out some alternative underlying mechanisms such as Mott physics and small polaronic interactions. Instead, our data naturally lead to a picture of dynamic electronic phase separation due to the bi-stripes: the dispersive states come from itinerant electrons in stripe-free regions, while the nondispersive/localized weight arises from bi-stripes, with the ratio of the two changing with temperature. As discussed in the SI Text, Mott or small polaron interactions do appear to become relevant as a secondary interaction once the bi-stripes have localized the electrons.

We emphasize that in Fig. 2 D and E the nondispersive spectral weight above T_c is a signature of bi-stripes, as also observed above T_c in X-ray scattering measurements [green diamonds in Fig. 4 (26)]. It is then somewhat surprising that our ARPES data show a clear localized signal below T_c indicating a significant population of bi-stripe states, while the scattering measurements indicate the correlation of bi-stripes quickly disappears below T_c. However, we note that scattering does not actually measure the presence of individual stripes, but rather measures the correlations between them, i.e., it measures the periodicity in the spacing of the stripes. Therefore, a collection of disordered or fluctuating stripes existing below T_c can be invisible to scattering experiments, while still localizing the electrons which live within the stripe regions, giving rise to the localized ARPES signal. With the stripes disordered or fluctuating, there will always be some regions of the material absent of stripes, and these regions will contribute to the dispersive portions of electronic structure. As we approach the region of static ordered stripes at higher temperature, the proportion of localized weight grows until finally at T_c static stripe correlations appear, the electrons become almost fully localized within the stripes, and the colossal change in conductivity appears. This concept is also highly relevant for studies of fluctuating or disordered stripes in many other materials—the absence of a clear stripe signal in scattering experiments implies the loss of order between the stripes rather than the actual destruction of the stripes. Finding another clear measure for the presence of the stripes, especially when they are disordered or fluctuating in time, requires other experimental methods which may or may not be straightforward to apply or interpret. This difficulty is responsible for the great amount of debate within the condensed matter physics community about the presence of such fluctuating stripes. In the present case, the localization of the electrons, which is clearly detectable via ARPES, can be regarded as a clear signal of the bi-stripes.

Alternatively, when bi-stripes melt, strain fields or quenched disorder can localize nanoscale stripe-like patches which would lead to a persistence of incoherent signal in the measurements. This finding appears similar to the observations in cuprate superconductors, which reveal the stripe-like electronic pattern with a disordered fashion (30, 31).

Unlike the charge stripes in cuprates, which are electrically conductive, the electron hopping is jammed between the stripes in the bi-stripe phase. Combined with transport and scattering measurements (26), our data indicate that these stripes behave like electronic valves—the fluctuating bi-stripe components (which occur below T_c) do not significantly impair the overall electronic conductance; however, when they become stable and form long-range patterns (above T_c), the electric conductivity is heavily suppressed. These properties may suggest some approaches to tune physical properties of materials by manipulating the stripe structure.

Materials and Methods

The single crystals were grown using the traveling solvent floating zone method. The x ∼ 0.59 samples were carefully selected and characterized as reported in ref. 27. The x = 0.50 samples were individually selected for this study on the basis of a low temperature insulating state in transport measurements. ARPES were performed at Beamlines 12.0.1 and 10.0.1 of the Advanced Light Source (ALS), Berkeley, using Scienta electron analyzers under a vacuum of ∼2–3 × 10^-11 torr, with 56 eV photons. The combined instrumental energy resolution was better than 20 meV, and the momentum resolution was about 0.02 π/a. In order to assure that any changes in our data are intrinsic, all spectra within any one panel were normalized by incident photon flux only.