Quantitative dissection of the simple repression input–output function

Abstract

We present a quantitative case study of transcriptional regulation in which we carry out a systematic dialogue between theory and measurement for an important and ubiquitous regulatory motif in bacteria, namely, that of simple repression. This architecture is realized by a single repressor binding site overlapping the promoter. From the theory point of view, this motif is described by a single gene regulation function based upon only a few parameters that are convenient theoretically and accessible experimentally. The usual approach is turned on its side by using the mathematical description of these regulatory motifs as a predictive tool to determine the number of repressors in a collection of strains with a large variation in repressor copy number. The predictions and corresponding measurements are carried out over a large dynamic range in both expression fold change (spanning nearly four orders of magnitude) and repressor copy number (spanning about two orders of magnitude). The predictions are tested by measuring the resulting level of gene expression and are then validated by using quantitative immunoblots. The key outcomes of this study include a systematic quantitative analysis of the limits and validity of the input–output relation for simple repression, a precise determination of the in vivo binding energies for DNA–repressor interactions for several distinct repressor binding sites, and a repressor census for Lac repressor in Escherichia coli.

It is now possible not only to make quantitative, precise, and reproducible measurements on the response of a variety of different genetic regulatory architectures, but also to synthesize novel architectures de novo. These successes have engendered hopeful analogies between the circuits found in cells and those that are the basis of many familiar electronic devices (1, 2). However, in many cases, unlike the situation with the electronic circuit analogy, our understanding of these circuits is based upon enlightened empiricism rather than systematic, quantitative knowledge of the input–output relations of the underlying genetic circuits.

Regulatory biology has shed light on the space–time response of a wide variety of these genetic circuits. Examples range from the complex regulatory networks that govern processes such as embryonic development (3, 4) to the synthetic biology setting of building completely new regulatory circuits in living cells (5). In particular, the dissection of genetic regulatory networks is resulting in the elucidation of ever more complex wiring diagrams (see, as an example, ref. 6). With these advances it is becoming increasingly difficult to develop intuition for the behavior of these networks in space and time. In addition, often, the diagrams used to depict these regulatory architectures make no reference to the census of the various molecular actors (the intracellular number of polymerases, activators, repressors, inducers, etc.) or to the quantitative details of their interactions that dictate their response. As a result, there is a growing need to put the description of these networks on a firm quantitative footing.

Often, the default description of regulatory response is offered by phenomenological Hill functions (7–12), which in the case of repression have the form

where n is the Hill coefficient that determines the sensitivity of the gene regulatory function, K_d is a dissociation constant, and α and β are constants that determine the maximum and basal levels of expression, respectively. Although such descriptions might provide a satisfactory fit of the data, they can deprive us of insights into the mechanistic underpinnings of a given regulatory response or, worse, can force us into thinking about the behavior of a given circuit in a way that is not faithful to the known architecture.

Alternatively, using thermodynamic models, it has been shown for a wide class of regulatory architectures that for each and every circuit, one can derive a corresponding “governing equation” that provides the fold change in gene expression as a function of the relevant regulatory tuning variables (13–15). The goal of our work is to carry out a detailed experimental characterization of the predictions posed by one such governing equation for the regulatory motif describing simple repression (Fig. 1A) in which a repressor can bind to a site overlapping the promoter, resulting in the shutting down of expression of the associated gene. This is a particularly fundamental case study because in Escherichia coli alone, there are >400 circuits that are regulated by different transcription factors that repress by binding to a single site in the vicinity of the promoter (16). Indeed, simple repression and activation are often thought of as the elementary ingredients of a much more diverse range of real regulatory circuits (17, 18).

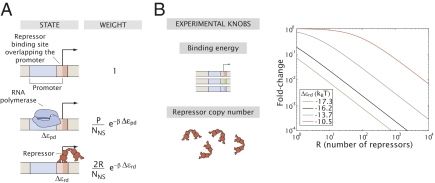
Fig. 1.

The simple repression motif. (A) States and weights of the thermodynamic model describing this regulatory motif. We assume that Lac repressor sterically excludes RNA polymerase from the promoter, although that assumption is not critical to our analysis. P and R are the numbers of RNA polymerase and Lac repressor molecules inside the cell, respectively. N_NS is the number of nonspecific sites, which we assume to be the size of the genome. Δε_pd and Δε_rd are the difference in energy between being specifically and nonspecifically bound for RNA polymerase and Lac repressor, respectively. The difference in color in the repressor binding site denotes an overlap of the binding site with the promoter. (B) The tuning variables that can be varied in the model and controlled experimentally are the binding strength (by changing the Lac repressor operator sequence) and the number of Lac repressors (by changing its mRNA ribosomal binding site). The effect of tuning these parameters on the fold change in gene expression is shown in the graphs. Note that stronger repressor binding corresponds to a larger fold change. For a detailed derivation of the expression and discussion of the assumptions used see SI Text and Fig. S2.

As seen in Fig. 1, the level of expression in circuits governed by simple repression can be tuned by several different parameters. One of the key tuning variables in nearly all regulatory and signaling networks is the numbers (or concentrations) of the relevant molecular players in the process of interest. We use the repressor number as one of the main tunable parameters in the experiments described below, with a 100-fold range of different repressor counts considered. To explore our understanding of how this parameter dictates regulatory response, we need to know how many repressors our strains of interest harbor. A series of beautiful recent experiments has made important progress in carrying out the molecular census, using a variety of clever methods. These molecular counts include the census of all actin-related proteins in Schizosaccharomyces pombe cells (19), a count of essentially all the proteins in Saccharomyces cerevisiae cells (20), a determination of the distribution of both lipids and proteins in synaptic vesicles (21), and several counts of the proteins in E. coli (22, 23) and other cell types as well (24). Most relevant to the current work is a recent experiment using a fluctuation-based counting method to determine the number of transcription factors in E. coli that control a synthetic circuit of interest (10). Our work adds a twist to protein census taking by using thermodynamic models as a way to count the number of repressors in a simple regulatory motif.

Quantitative control of the absolute number of transcription factors is seldom used in experiments that aim to dissect regulatory architectures even though it is one of the main strategies to verify the predictions from thermodynamic models (13–15). Previous work has usually relied on the control of an external inducer to vary the regulatory response of a genetic circuit (5, 9, 11, 12, 25, 26). However, the use of inducer molecules, although experimentally convenient, adds another layer of complexity to the modeling approach and has been systematically characterized in only a few cases (11).

Recent measurements (10, 23, 27–31,) have also often focused on the variability or “noise” associated with transcriptional regulation. Although there has been great recent interest in this gene expression variability, we argue that a crucial quantitative prerequisite to fully dissecting the properties of genetic networks is a viable description of their mean response, and any conceptual frameworks used to describe the noise must first be consistent with these mean responses.

In this work we test these thermodynamic models of transcriptional regulation by generating parameter-free predictions for the level of gene expression as a function of the regulatory tuning variables of the simple repression architecture. We show significant agreement between the theoretical description and the measurements over multiple orders of magnitudes of the inputs and outputs of the system. We conclude that through thermodynamic models we can accurately predict the level of regulation due to simple repression, opening the door to the design of synthetic genetic circuits where the level of gene expression can be tuned theoretically and to the better interpretation of the transcriptional response of naturally occurring circuits.

Theory and Experimental Design

Although our analysis should be relevant generically for simple repression, the reasoning behind our experiments is based upon a series of earlier measurements and calculations on the level of repression in the specific case of the lac operon (32, 33). In particular, we consider the case where there is only a single specific binding site for the Lac repressor (Fig. 1). The wild-type lac operon was rewired such that only the main operator was present and then, in turn, different strains were constructed in which the strength of that main operator was systematically weakened according to the progression Oid to O1 to O2 to O3 shown in Fig. S1.

Thermodynamic models assume that the processes leading to transcription initiation by RNA polymerase (RNAP) are in quasi-equilibrium. This assumption means that we can use the tools of statistical mechanics to describe the binding of RNA polymerase and transcription factors (TFs) to DNA. Further, the level of gene expression is assumed to be proportional to the probability that RNA polymerase is bound to the promoter of interest (13, 34). This probability is determined, in turn, by the interactions between polymerase and the promoter and competition for those binding sites by repressors. In Fig. 1A we show the thermodynamic states and weights corresponding to a minimal model of the simple repression regulatory motif. In this simplified model the promoter can be found in only one of three states: (i) empty, (ii) occupied by RNA polymerase, and (iii) occupied by Lac repressor. The partition function for this system is obtained by summing over the statistical weights of each of these states and is given by

where P is the number of RNA polymerase molecules, R is the number of Lac repressor tetramers, and N_NS ∼ 5 × 10⁶ is the number of nonspecific DNA sites (the length of the genome), corresponding to the reservoir for both molecules. β = (k_BT)⁻¹ with k_B being the Boltzmann constant and T the absolute temperature. The energies Δε_pd (RNA polymerase–DNA) and Δε_rd (repressor–DNA) correspond to the difference between specific and nonspecific binding for RNA polymerase and Lac repressor, respectively, where we make the simplifying assumption of a homogeneous nonspecific background. The factor of 2 in front of the number of Lac repressors stems from the fact that this molecule is a tetramer, a dimer of dimers, with two binding heads. Therefore, 2R corresponds to the number of binding heads inside the cell. For a complete derivation of these terms, please refer to refs. 14 and 35, SI Text and Fig. S2.

The probability of finding RNA polymerase bound to the promoter is then given by

where Z is the partition function defined in Eq. 2. A much more convenient quantity to measure is the fold change or relative change in gene expression due to the presence of the transcription factor; namely,

The great advantage of this quantity is that it is easily accessible both theoretically and experimentally. It is unitless and can be measured by comparing the levels of gene expression (in any arbitrary or absolute units) when Lac repressor is present and absent. We define this fold change in gene expression with respect to the absence of transcription factor and not with respect to a state where the transcription factor is fully induced such as in the presence of saturating concentrations of Isopropyl β-d-1-thiogalactopyranoside (IPTG). Using inducers would require us to consider the induction process explicitly (11). In the case of a weak promoter such as lacUV5 used in this work (ref. 15 and SI Text) the term << 1. This outcome results in the fold change collapsing to the simpler form,

This last expression serves as the basis of our experimental design where we identify two tuning variables that can be controlled experimentally in a systematic fashion: the binding energy and the number of Lac repressors. In Fig. 1B we show the predicted fold change as a function of these two experimentally accessible parameters. Alternatively, the binding of Lac repressor can be described by a dissociation constant, the concentration of Lac repressor for which the fold change in gene expression is 1/2. This approach is explained in SI Text. Throughout the text we report both binding energies and approximate dissociation constants, although all of our measurements and analysis are built around binding energies and repressor numbers. Approximate concentrations and dissociation constants are provided merely as rough estimates for the purposes of comparison with literature values in which sometimes these quantities are favored. For details of the estimation of the concentrations and dissociation constants, see SI Text, Connecting Δε_rd to K_d.

Earlier hints as to how simple repression plays out quantitatively were offered by Oehler et al. (32, 33) who measured the fold change in gene expression for constructs bearing each one of the four operators and for two different numbers of Lac repressor per cell. Using Eq. 5 or equivalent expressions (15, 36), the binding energy of Lac repressor to each one of the operators can be estimated. It must be noted, though, that these original measurements were not performed with the intention of the kind of quantitative dissection advocated here and that therefore the uncertainties in the parameters are substantial. In SI Text, Figs. S3 and S4, and Table S1, we give a detailed analysis of the extent to which these earlier results are consistent with our own data. Additionally, in SI Text and Fig. S5 we show that our results do not depend on the particular choice of quantification protocol for our enzymatic reporter. Finally, as shown in SI Text and Table S2, even if we replace our reporter with a fluorescent protein the results are essentially unaltered.

For the measurements reported here, we created ∼30 strains of bacteria where we systematically tuned the number of repressors, using a recently developed scheme for controlling ribosomal binding strength (37). Although this scheme provides a rough expectation for the number of repressors in each one of those strains, we had no precise or accurate a priori knowledge of the actual intracellular numbers of Lac repressors. These strains bear reporter constructs regulated by simple repression such as those shown in Fig. S1, for which we measure the fold change in gene expression. If we are to believe the input–output function from Eq. 5, once we know the binding energy of the operator in question there is a direct and unequivocal relation between the fold change in gene expression and the number of repressor molecules. Testing these predictions requires an accurate and precise quantification of the absolute levels of repressor inside the cell. In fact, we view this approach as a way to count molecules by inference by looking at levels of gene expression and passing these levels of expression through the theoretical filter of Eq. 5.

In the following sections we test these parameter-free predictions over a wide range of both expression and repressor numbers and show that they largely jibe with our experimental observations. The logic advocated here is that if Eq. 5 is shown to be predictive, it will open the door to creating synthetic gene regulatory circuits whose level of gene expression can be precisely tuned a priori and to being able to predict the regulation of a particular promoter by just looking at its regulatory sequence. In addition, a predictive understanding of the input–output relation of these architectures will serve as a jumping-off point for the design and understanding of more complex circuits such as those involving DNA looping, cooperative repression, etc. (15).

Results

Eq. 5 represents a provocatively simple expression purporting to describe the response of a bacterial cell to a wide variety of perturbations such as altering the DNA target sites (with the K_ds changing by three orders of magnitude or, equivalently, Δε_rd changing by 7 K_BT) (15, 36, 38, 39) and repressor copy numbers (with the copy numbers changing by several orders of magnitude). If we take this equation seriously, it implies that once we have determined the parameter Δε_rd, there is a quantitative relation between the fold change in gene expression and the corresponding number of Lac repressors. Namely, once we know one quantity we can predict the other.

To exploit Eq. 5 we designed lacUV5 promoters with a single binding site for Lac repressor at the wild-type position of O1. These promoters bore Oid, O1, O2, or O3 and controlled the expression of the enzymatic reporter gene lacZ (Materials and Methods and Fig. S1), although as reported in SI Text, we also examined many of the same constructs using fluorescence as well, resulting in nearly identical results. We integrated each one of these simple repression constructs such as the one shown in in Fig. 1A in the chromosome of a strain bearing no Lac repressor and in six different strains that we systematically designed to express different constitutive levels of Lac repressor. As mentioned above, although we had a qualitative expectation about the number of Lac repressors present in each strain, we had no previous quantitative information about that magnitude.

Taking the Repressor Census Through Thermodynamic Models.

We measured the fold change in gene expression of our simple repression constructs bearing the operators Oid, O1, O2, or O3 in the six different strain backgrounds we created. There are several different ways to explore the results in conjunction with Eq. 5. As noted above, one scheme is to determine the absolute number of repressor molecules within one strain and to combine this with the measured fold change to obtain the in vivo binding energy for each of the different operators through Eq. 5. With these binding energies in hand, a way to put the predictability of the thermodynamic model on the stand is to predict the number of repressors in the other strains. An alternative concept is simply to use all of the fold-change and repressor count measurements and to see how well they agree with the functional form provided by Eq. 5 by making one global fit to the in vivo binding energy for each operator.

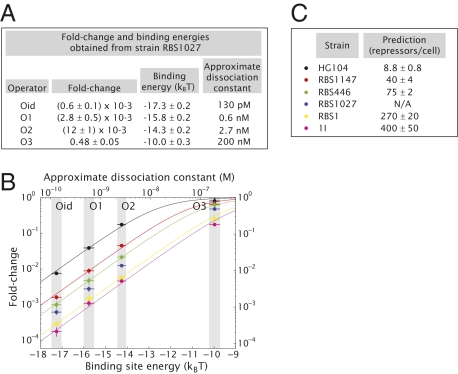
Regardless of the scheme chosen it is necessary to possess an absolute count of the repressor number in each one of our strain backgrounds. Details of this determination are given below. To carry out the first scheme presented above we used strain RBS1027 as the basis of the calculation of the binding energies. The resulting fold change in gene expression for each operator in this strain background and the calculated binding energies are shown in Fig. 2A. Using these binding energies we plot the fold change in gene expression as a function of binding energy for all strains and choices of operators in Fig. 2B (the corresponding absolute values of gene expression measured for each strain are shown in Fig. S6). The data in Fig. 2B are fitted to Eq. 5 to generate a prediction for the number of repressors within each one of the five remaining strains. These predictions are shown in Fig. 2C.

Fig. 2.

Single-site binding energies and prediction of the number of repressors for different strains. (A) The operator binding energies and approximate dissociation constants are deduced from the measurement of the fold change for the different operators in strain RBS1027 combined with our knowledge of its intracellular number of repressors, using Eq. 5. (B) The fold change in gene expression is measured for all four operators in six different strain backgrounds (including RBS1027). Using the binding energies from A, we fit the data to Eq. 5 to make a parameter-free prediction of the number of repressors present in each strain shown in C. Errors in the predictions represent the SE of the corresponding fit. The errors in the binding energies are here denoted as gray shaded regions. Estimated dissociation constants are shown for convenience for comparison with literature values. The basis for these estimates is explained in SI Text.

Because the majority of our strains were created for this particular work, the resulting predicted cellular numbers cannot be compared with any external standard. However, strain HG104 expresses wild-type levels of repressor from the native lacI gene. Indeed, for this strain we predict 8.8 ± 0.8 repressor tetramers per cell, comparable to the previous and, to our knowledge, only available absolute measurement (40).

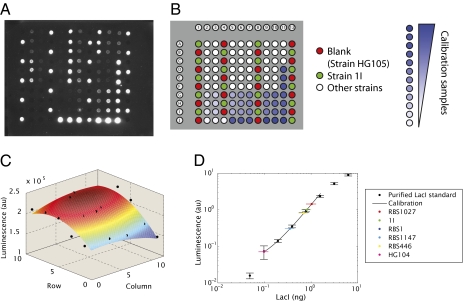
To bring the predictions of the model for simple repression to fruition we need to directly measure the number of repressors in each one of our six strains. We measured the in vivo number of Lac repressors in these six strains by performing quantitative immunoblots (19, 41, 42) from cell lysates such as those shown in Fig. 3A. To get an absolute count of the amount of Lac repressor in each strain a series of dilutions of a purified Lac repressor standard of a known concentration was used (Fig. 3B). Quantification of the luminescence of the immunoblots was performed using a cooled CCD camera. Care was taken to account for spatial nonuniformities in the light collection as depicted in Fig. 3C. We can reliably detect a wide range of purified Lac repressor standards using our immunoblots (as low as 50 pg, corresponding to around five repressors per cell). This result increases our confidence in the method as a way of precisely quantifying protein counts in bulk even at very low levels (Materials and Methods and Fig. 3D). It is important to note, however, that counting methods based on purification, such as immunoblots, have the inherent caveat that some proteins might have stayed behind in the different fractions. Although we took action to reduce this effect, the results from immunoblots should be viewed as a lower bound on the actual number of proteins in vivo.

Fig. 3.

Immunoblots for the measurement of the in vivo number of Lac repressors. (A) Typical luminescence image obtained from an immunoblot. (B) Map of the samples loaded on the membrane shown in A. The blank (HG105) and 1I samples are used to create a normalization map by subtracting the blank luminescence from all samples and dividing by 1I. White spots correspond to the cell lysates measured and the blue spots correspond to the different concentrations of purified Lac repressor standard. (C) Normalization map generated by fitting a 2D polynomial to 1I samples scattered around the membrane (black dots) after removing the blank. This map was used to account for nonuniformities in the collection of luminescence from the membrane. (D) Luminescence vs. quantity of LacI loaded. The calibration samples are used to construct a power law fit. The luminescence of the measured samples is shown as well. The unknown amounts of repressor loaded are determined by using the calibration curve. Samples 1I and RBS1 have been diluted 1:8 to match them to the dynamic range of the assay and therefore appear to have less signal within a spot (SI Text).

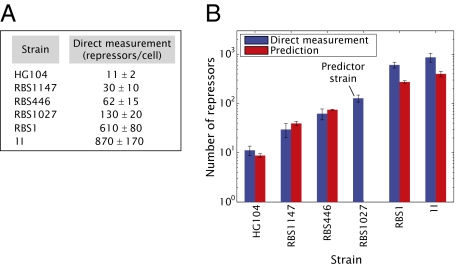
Our predictions for the number of Lac repressors in each strain can now be compared with the direct measurements of this quantity, which are shown in Fig. 4A. In Fig. 4B we compare the predictions and direct measurements explicitly. The direct measurements are comparable to the predictions within experimental error, giving us confidence that the proposed input–output function from Eq. 5 appropriately describes the input–output properties of the simple repression regulatory motif. This result suggests in turn that once we know the binding energy for an operator, we have predictive power. Although this analysis yielded results that are largely consistent between theory and experiment, it appears that we systematically underestimate the number of repressors in the two strains with the highest repressor number. The reader is referred to SI Text for a further discussion of these two strains.

Fig. 4.

Experimental and theoretical characterization of repressor copy number. (A) Immunoblots were used to measure the number of Lac repressors in six strains with different constitutive levels of Lac repressor. Each value corresponds to an average of cultures grown on at least 3 different days. The error bars are the SD of these measurements. (B) The fold-change measurements in Fig. 2B were combined with the binding energies obtained from Fig. 2A (derived from strain RBS1027) to predict the number of Lac repressors per cell in each one of the six strains used in this work. These predictions were examined experimentally by counting the number of Lac repressors using quantitative immunoblots.

Direct Determination of the in Vivo Lac Repressor Binding Energies.

The scheme for exploring the limits and validity of the thermodynamic model advocated in the previous section is based on using one strain to determine the binding energy of Lac repressor to its operator DNA. However, as noted earlier, an alternative approach is to simply use the entirety of our data to evaluate global fits of Eq. 5 to the data corresponding to a given operator. Implementation of this concept is shown in Fig. S7B, where we combine all of our measurements to determine the best values of the different in vivo binding energies. On the other hand, one might choose to use the information about fold change and repressor copy number for one particular strain to derive the different binding energies. This analysis can be done, in turn, for all strains created for this work in an analogous way to what we did with strain RBS1027 in the previous section. In Fig. 5 we compare such fits with the binding energies that can be obtained from analyzing a single strain. Additionally, we show the energies obtained from the Oehler et al. data (33) (SI Text and Fig. S8) and from Fig. S7B for comparison. These multiple approaches for obtaining the binding energies, all leading to essentially comparable results (for example, Fig. S7A), increase our confidence in the simple model of Eq. 5 and in the minimalist modeling philosophy used to obtain it as a quantitative and predictive tool.

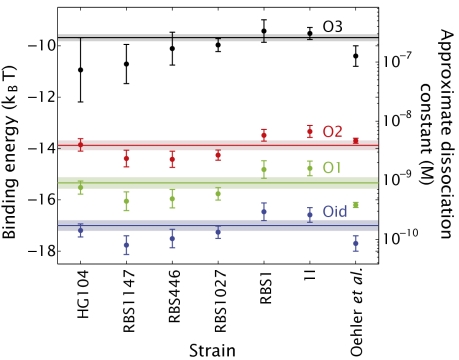
Fig. 5.

Determination of the in vivo binding energies. For each strain we combine the measurements of the fold change in gene expression with the corresponding number of repressors and solve Eq. 5 to obtain an estimate of the binding energies (dots). The energies obtained from the Oehler et al. data (33) are also shown. The lines correspond to using all measurements of the fold change in gene expression with their corresponding repressor numbers to fit Eq. 5 to obtain the best possible estimate for the binding energies. This fit is shown in Fig. S7B. The results of this approach are shown as horizontal lines and the shaded region captures the uncertainty.

Finally, it is common in the theoretical treatment of experiments on transcriptional regulation to include a constant level of expression dubbed the “leakiness”. Such leakiness is usually understood as a low level of activity that is independent of any regulation. The reader is referred to SI Text and Fig. S9 for a more detailed description of leakiness where we show that the values obtained for the binding energies do not change significantly for reasonable values of the leakiness.

Discussion

Theoretical models of gene expression, especially in bacteria, have reached a very high level of sophistication. Similarly, measurements of gene expression have come to the point where they are both reproducible and quantitative enough to serve as the basis for explicit attempts at confronting theory and experiment and to explore the merits of these theoretical perspectives as a conceptual framework for describing regulatory response. Indeed, such measurements have now reached the point where in our view it is no longer appropriate to use just words to describe them—they call for a theoretical response that is commensurate with the level of quantitative detail in the experiments themselves. To that end, we have undertaken a detailed study of one of the most important and fundamental regulatory building blocks found in living organisms from all three domains of life, namely, simple repression. Simple repression and its positive regulation counterpart, namely simple activation, serve as the paradigmatic building blocks of the much richer regulatory strategies that are used in the growing list of both natural and synthetic networks now being explored.

In recent years, the governing equations characterizing the transcriptional response of these elementary regulatory building blocks and much more complicated assemblies of them have been worked out in detail using the ideas of statistical mechanics. The work described here provides a template for the kind of rich interplay between theory and experiment that should be demanded of these other networks as well. In particular, the governing equations describing regulatory architectures feature certain key tuning variables that serve to elicit different biological responses. In the experiments described here, we have explored two of the elementary tuning parameters that govern the simple repression motif, namely, the strength of the transcription factor binding sites and the molecular counts of the repressors themselves. We have shown that an input–output function for simple repression obtained from thermodynamic assumptions, which depends on those two tuning parameters, can indeed predict in a parameter-free manner the regulatory outcome over roughly four orders of magnitude in the transcriptional output.

Using the thermodynamic model approach coupled tightly with precise measurements we have been able to perform a systematic quantitative dissection of the input–output relation for simple repression and believe that similar analyses should be carried out for each of the other governing equations describing key regulatory motifs. As a by-product of these measurements, we have been able to make a precise determination of the in vivo binding energies for DNA–repressor interactions. In addition, these results provide a census of the repressor content for Lac repressor in E. coli over a large dynamic range (roughly two orders of magnitude in repressor counts). The predictive power revealed by this model on the basis of a few parameters is one of the first steps toward having a standardized description of a regulatory architecture on the basis of its microscopic parameters (1, 2). Harkening back to the electronic circuit analogy, the results presented here are analogous to illustrating that for a resistor there is a value for the resistance that is necessary and sufficient to predict the current given the voltage. In our case specification of the binding energy Δε_rd is necessary and sufficient to predict the fold change in gene expression given the number of repressors.

Further characterization of this architecture should explore the role of promoter copy number and operator position as these architectural features are known to alter the expression profile as well (43–45). In addition, with these insights in hand for the case of simple repression in the lac operon, it is now important to examine a suite of similar architectures in E. coli and other bacteria with the idea being to explore the extent to which the successes found in this case can be expected to apply to other genes.

Materials and Methods

DNA Constructs and Strains.

The construction of all plasmids and strains is described in detail in SI Text.

In short, plasmids pZS25O1+11, pZS25O2+11, pZS25O3+11, and pZS25Oid+11 have a lacUV5 promoter controlling the expression of a LacZ reporter as shown schematically in Fig. S1.

Plasmid pZS3*1-lacI expresses Lac repressor off of a p_LtetO-1 promoter (46). The ribosomal binding site of this construct was weakened following ref. 37, using site-directed mutagenesis (Quikchange II; Stratagene) in order to generate constructs expressing LacI at different levels as described in SI Text and Table S3.

The E. coli strains used in this experiment are shown in Table S4. HG105 is wild-type E. coli (MG1655) with a complete deletion of the lacIZYA genes. HG104 is also wild-type E. coli with a deletion of the lacZYA genes. We therefore expect strain HG104 to express wild-type levels of Lac repressor.

Reporter constructs and Lac repressor constructs were integrated into the galK and ybcN regions, respectively, using recombineering (47) and combined using P1 transduction. Please refer to SI Text for details.

Growth Conditions and Gene Expression Measurements.

Strains to be assayed were grown in M9 minimal medium plus 0.5% glucose and harvested during exponential growth. Our protocol for measuring LacZ activity is basically a slightly modified version of the one described in refs. 48 and 49. Details are given in SI Text.

Measuring in Vivo Lac Repressor Number.

Cell lysates of our different strains bearing Lac repressor were obtained as described in SI Text. Calibration samples using a known concentration of purified Lac repressor (courtesy of Stephanie Johnson, California Institute of Technology, Pasadena, CA) diluted in a lysate of HG105 strain (strain without Lac repressor) were used.

A nitrocellulose membrane was prepared for sample loading and afterward blocked and treated with anti-LacI primary monoclonal antibody and HRP-linked secondary antibody as discussed in SI Text. Two microliters of each sample was spotted on the membrane in a pattern similar to that of a 96-well plate. The resulting drops had a typical size of 3 mm. All samples were loaded in triplicate with the exception of samples 1I and HG105. Both of them were loaded on the order of 20 times on different positions of the membrane to obtain a spatial standard that would allow for corrections of nonuniformities in the light collection (see below).

The membrane was dried and developed with Thermo Scientific SuperSignal West Femto Substrate and imaged in a Bio-Rad VersaDoc 3000 system with an exposure of 5 min. A typical raw image of one of the membranes is shown in Fig. 3A and the corresponding loading map can be seen in Fig. 3B. Custom Matlab code was written to detect the spots and calculate their total luminescence. The luminescence coming from the HG105 blank samples was fitted to a second-degree polynomial, which was in turn subtracted from all other luminescence values. After this procedure another second-degree polynomial was fitted to the 1I samples, resulting in a typical surface such as the one shown in Fig. 3C. Note that differences of up to 25% could be observed between different positions on the membrane. This last polynomial was used to normalize the intensity of all other samples.

The luminescence corresponding to the calibration samples was overlaid with the luminescence from the strains. The calibration samples were fitted to a power law using only the calibration data points in the range of the samples that were to be measured. An example of this calibration is shown in Fig. 3C. For additional details please refer to SI Text.

Finally, the amount of Lac repressor found in a spot was related to the number of Lac repressor molecules per cell by calibration of the OD readings of the original cultures to cell density as described in SI Text.