Entropy and the driving force for the filling of carbon nanotubes with water

Abstract

The spontaneous filling of hydrophobic carbon nanotubes (CNTs) by water observed both experimentally and from simulations is counterintuitive because confinement is generally expected to decrease both entropy and bonding, and remains largely unexplained. Here we report the entropy, enthalpy, and free energy extracted from molecular dynamics simulations of water confined in CNTs from 0.8 to 2.7-nm diameters. We find for all sizes that water inside the CNTs is more stable than in the bulk, but the nature of the favorable confinement of water changes dramatically with CNT diameter. Thus we find (i) an entropy (both rotational and translational) stabilized, vapor-like phase of water for small CNTs (0.8–1.0 nm), (ii) an enthalpy stabilized, ice-like phase for medium-sized CNTs (1.1–1.2 nm), and (iii) a bulk-like liquid phase for tubes larger than 1.4 nm, stabilized by the increased translational entropy as the waters sample a larger configurational space. Simulations with structureless coarse-grained water models further reveal that the observed free energies and sequence of transitions arise from the tetrahedral structure of liquid water. These results offer a broad theoretical basis for understanding water transport through CNTs and other nanostructures important in nanofluidics, nanofiltrations, and desalination.

Nanofluidics and nanofiltration have emerged quite recently as an intriguing interdisciplinary science, with applications to sensing (1), desalination (2, 3), and efficient energy storage and conversion technologies (4). Water confined in carbon nanotubes (CNTs) exhibits unexpected properties, such as fast conduction rates (5, 6) and a variety of structural (7) and phase transitions (8, 9). Future progress and technological advances for utilizing confined water in various nanostructures would undoubtedly depend on obtaining a basic understanding of the fundamental driving forces in these systems. In particular, both experimental and theoretical studies have shown that CNTs spontaneously fill with water (5, 8–10), a counterintuitive proposition because hydrophobic confinement is generally expected to decrease both entropy and bonding due to breaking water–water hydrogen bonds (HB) upon creating a surface. Although there have been numerous studies (11–14) on the structural and mechanical properties of water confined in CNTs, the thermodynamic signatures and origins of this wetting phenomenon have been only sparingly explored—for example, only for a single-file water chain (5)—and thus remain unexplained for CNTs of general sizes. Here, we report the entropy, enthalpy, and free energy extracted from molecular dynamics (MD) simulations of water confined in CNTs with diameters between 0.8 and 2.7 nm.

Results and Discussion

To assess the role of thermodynamics on the behavior of water under one-dimensional confinement, we inserted 10-nm-long armchair CNTs with a diameter from 0.8 to 2.7 nm (Fig. S1 and Table S1) into a box of preequilibrated simple point charge-extended (SPC-E) (15) water molecules and performed constant pressure (1 atm, 300 K) MD simulations for 5 ns (Fig. S2). We calculated the absolute entropy and enthalpy components of the free energy (including diffusional and quantum effects) every 1.0 ns along the trajectory using the two-phase thermodynamics (16) (2PT) free energy method. These thermodynamic observables converged within 5 ns and the reported thermodynamics were obtained by statistical averaging over the final 25 ns.

For all sized tubes, we find that water molecules inside the CNTs have lower free energies than bulk water, consistent with the spontaneous filling of the hydrophobic internal space of CNTs observed experimentally (17, 18). However, as shown in Fig. 1A, the trend is not monotonic: The 0.8-nm CNT has the lowest free energy (ΔA⁰ = -3.9 ± 1.2 kJ/mol) but there is a second minimum for the 1.2-nm CNT (ΔA⁰ = -1.5 ± 0.7 kJ/mol) with smooth convergence to the bulk value beyond 1.4 nm. From the relative contributions of the enthalpy and entropy to the free energy (Fig. 1B), we find that the entropy dominates for tube diameters less than 1.0 nm (gas phase), the enthalpy dominates for tubes between 1.1 and 1.2 nm (ice phase), and both energies compensate for tubes larger than 1.4 nm (liquid phase). In these larger CNTs, the enthalpy is unfavorable (ΔU⁰ > 0) but the entropy is always favorable and dominant (TΔS⁰ > ΔU⁰ > 0).

Fig. 1.

Relative thermodynamics of water confined in infinite CNTs. The CNTs are labeled (x, y) according to their chirality as shown in Fig. S1. In this study, x = y indicates armchair nanotubes. (A) Relative Helmholtz free energy as a function of CNT diameter, referenced to a bulk water box of 14,000 molecules: , , . The error bars indicate the statistical errors. The vertical dashed line indicates the point of convergence to the bulk. (B) Percentage of the free energy ΔA⁰ arising from the enthalpy 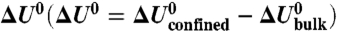or entropy .

These free energy results contradict the general expectation that depletion of HB at the hydrophobic interface (19) would lead to unfavorable free energies. We note that this reasoning considers only the enthalpic penalty of confinement, and ignores entropic and structural effects that can be important on the nanoscale, which we elaborate below. An increase in enthalpy, nonetheless, is indeed observed and shows excellent correlation to the average number of HB per water molecule (Fig. 2). Water inside the 0.8-nm CNT loses an average of two HB, has a density of one-half the bulk value (Table S2), and enthalpically is most disfavored, whereas water in the 1.0-nm CNT loses an average of one HB until the 1.6-nm CNT and beyond, which has about 3.5 HB, the same as the bulk. This simple picture of unfavorable enthalpy due to confinement breaks down for the 1.1- and 1.2-nm CNTs, where water molecules form ice-like stacked pentagons and hexagons, respectively (8, 9). In these CNTs, the pore sizes are commensurate with the H-bonded structure of ice, leading to a radial density profile with little to no probability of water molecules near the center of the CNT throughout the entire 50 ns of dynamics (Fig. S3). The hexagonal and pentagonal water–ice structures have, on average, 3.6 HB, slightly larger than the bulk value. Including the weak yet favorable van der Waals (vdW) interactions of water with the CNT walls, we calculate a net decreased enthalpy of -3.1 ± 0.5 and -2.6 ± 0.4 kJ/mol for 1.1- and 1.2-nm CNTs, respectively, relative to the bulk. Although the exact magnitude of the energy will depend on the interaction potentials, we verified that the decreased enthalpy in these systems is unique to these tubes regardless of force field used.

Fig. 2.

Correlation of the average number of HB/molecule with ΔU⁰. We define an HB to exist only when the inter-oxygen distance is less than 3.5 Å and simultaneously the O-H….O angle is less than 30° (34). Statistics are collected by scanning the 50-ns NPT trajectory every 5 ps.

On the other hand, the ice-like water inside the 1.1- and 1.2-nm CNTs loses on average 7.4 and 4.1 eu (1 eu = 1 J·mol^-1·K^-1) of entropy relative to the bulk (or 11% and 6% of the bulk value) (Fig. 3A). Pentagonal ice-like water molecules inside the 1.1-nm CNT form slightly more rigid and entropically less stable frameworks than the hexagonal ice-like molecules inside the 1.2-nm CNT (Fig. 4B). Interestingly, while maintaining the ice-like structure by having little to no lateral (in-plane) diffusion, we find that the water molecules in these intermediate CNTs exhibit axial diffusions similar to the bulk, meaning that these water molecules can best be thought of as a highly diffusing solid.

Fig. 3.

(A) Relative entropy ΔS⁰ for water inside the various CNTs. The 0.8-nm CNT with single-file water molecules inside has the largest entropic gain (42.7 eu/H₂O) relative to the bulk, followed by the 1.0-nm CNT (19.9 eu/H₂O). The 1.1- and 1.2-nm CNTs have lower entropy (-7.4 and -4.1 eu/H₂O) relative to the bulk due to the formation of rigid ice-like motifs (1 eu = 1 J·mol^-1·K^-1). (B) Decomposition of ΔS⁰ in terms of rotational (S_rot, red squares) and translations (S_trans, blue circles) atomic motions. Both rotational and translational entropy are the dominant contributors for water inside subnanometer CNTs, whereas the translational entropy accounts for all of the entropic gain beyond 1.2 nm. (C) Rotational density of states (power spectrum) for water molecules confined in CNTs with diameters of 0.8 (red), 1.2 (blue), and 2.7 nm (green) compared to bulk water (black). The spectra are the average of 25 individual calculations every 1 ns, computed as the Fourier transform of the atomic velocity autocorrelation function. The rotational spectrum of waters inside all 10 CNTs in this study is shown in Fig. S4 and compared to that of ice and water vapor.

Fig. 4.

Thermodynamics of water inside 10 CNTs using the SPC-E (black squares), single-particle two-body M3B (blue triangles), and the single-particle three-body mW (red circles) water potentials. All three water models have been fitted to reproduce the cohesive energy and density of water at 300 K and 1 atm. We adjusted the water–carbon interactions of the mW and M3B water potentials to have the same interaction as the SPC-E. (A) Free energy profile. The coarse-grained mW water model tracks the SPC-E expect for the single-file 0.8-nm CNT. The M3B water model has unfavorable free energies for all CNT sizes. (B) Enthalpy profile. The tetrahedral H bonding in mW captures the profile of the SPC-E, whereas the loss of H bonding in the M3B leads to unfavorable enthalpies for all sized CNTs. (C) Entropy profile. The mW tracks the SPC-E except for the 0.8- and 1.0-nm CNTs where rotational entropy is found to contribute to the total entropy as much as 40–60% in the real water, SPC-E.

In contrast, the water molecules inside subnanometer CNTs have dramatically different character: For the enthalpically disfavored single-file 0.8-nm CNT, we calculate an entropy gain of 42.7 eu, which is 68% more than the bulk value but 26% less than the gas-phase value, whereas waters inside the 1.0-nm CNT gain 19.9 eu (32% more than the bulk). Physically, the entropic gain of water in these subnanometer CNTs arises from the “liberation” of water molecules from the tetrahedral frameworks in the bulk, allowing for greater phase space sampling inside the CNTs and therefore greater configurational entropy (20). More generally, for every CNT considered in this study, other than 1.1- and 1.2-nm CNTs, entropic gain from the less constrained water molecules near the wall dominates any enthalpic loss due to a reduced HB, leading to decreased free energies.

We gain further insight into the nature of these confined waters by expressing the total entropy of water as a sum of translational, rotational, and internal vibrational components (16): S_tot = S_trans + S_rot + S_vib. Due to the rigid water model used in this study, S_vib = 0. We find that the water molecules inside subnanometer CNTs have increased rotational entropy, with ΔS_rot accounting for 60% and 40% of the entropic gain for the 0.8- and 1.0-nm CNTs, respectively, which is due to the loss of in-plane HB neighbors (5). The rotational density of states (RDOS; Fig. 3C) shows a red shift with enhancement of the low-frequency modes for water inside these CNTs compared to the bulk, particularly in the 170 to 170–220 cm^-1, which is prominent in the RDOS of water vapor (Fig. S4A). For the 1.1- and 1.2-nm CNTs, however, we find more restricted rotations, which account for 50% and 95%, respectively, of the entropic loss. There is a blue shift with enhancement of the high-frequency rotational modes in these systems, producing rotational spectra resembling a combination of ice and bulk water (Fig. S4B). This blue shift corresponds to increased high-frequency rattling as occurs in a solid, whereas the red shift corresponds toward the free rotations of a gas. Beyond 1.2 nm, ΔS_rot is almost converged and behaves similarly to the bulk.

The other component of the entropy, ΔS_trans, results from increased diffusional motions and enhanced low-frequency oscillations. In sharp contrast to the conventional textbook picture that the confinement would cause decreased translational entropy, we instead find increased translational entropy for confined water for all sized CNTs except for 1.1- and 1.2-nm CNTs. This translational entropic gain is primarily attributable to the water molecules closest to the CNT walls, which have lower effective density and smaller number of HB compared to bulk (Fig. 3B). The in-plane translational motions of these water molecules are enhanced due to the low density, whereas the axial diffusion and rattling motions are found to be similar to the bulk. Therefore, ΔS_trans correlates with the surface-area-to-volume ratio of the CNT, leading to a 1/d convergence of the overall entropy to the bulk value. Due to this density-dependent nature and structural rigidity, ΔS_trans is largest and favorable for small CNTs (0.8 and 1.0 nm), unfavorable for medium-sized ice-like CNTs (1.1 and 1.2 nm), and responsible for all the entropic gain for CNTs larger than 1.2 nm.

To gain further insights into this unique structure-thermodynamics relationship of confined water, we repeated our simulations replacing the SPC-E water model with either the single-particle M3B (21) or monotonic water model (mW) (22) water model, modified to have the same water-CNT interaction energy as SPC-E. Both potentials were parameterized to reproduce the average density and cohesive energy of bulk water but differ in their inability (M3B) or ability (mW) to form a tetrahedral H-bonded water network. Because of the character of single-particle water models, ΔS_tot is equal to ΔS_trans because ΔS_vib = ΔS_rot = 0.

We find that the M3B waters have unfavorable free energies inside all sizes of CNTs (Fig. 4A), with a maximum at the 0.8-nm CNT and then a monotonic convergence to the bulk value, as expected for a Lennard–Jones (LJ) fluid. Indeed, for finite CNTs inside a M3B water box, we observed spontaneous emptying of the CNTs. The coarse-grained M3B waters without H-bonding ability suffer entropic loss and significantly increased enthalpy compared to the real water molecule. In contrast, the mW water model, which does have a tetrahedral H-bonding structure, is 83% more enthalpically stable inside the CNTs than M3B (Fig. 4B) and has an entropy profile which closely tracks the real water model (Fig. 4C), except for the subnanometer CNTs. In the subnanometer CNTs, both coarse-grained water models significantly underestimate the entropy gained in the real water model due to the lack of rotational entropy inherent in single particles. Taken together, we conclude that the observed spontaneous filling of CNTs with water arises because of the tetrahedral H-bonding network in the bulk. In particular, this tetrahedral bonding character is responsible for a surprising increase, rather than decrease, in translational entropy of water under confinement, a phenomenon perhaps unique to water.

There have been some suggestions that the fast conduction rates of water through CNTs observed experimentally are related to the atomic smoothness of nanopores (13) or the structure of water and depletion layer at the interface with the CNT walls (14). The diameter-dependent thermodynamic driving force revealed here, as well as a sequence of structural transitions, may be a key to understanding diameter-dependent flow rates recently predicted (5). The results presented here can also be helpful in designing various geometries of nanopores that utilize the unusual properties of confined water and its flow in water treatment.

Conclusions

We have shown that the counterintuitive wetting of internal space of hydrophobic CNTs by water results from favorable free energies inside the CNT for all sizes, but the nature of confinement changes considerably with CNT diameter. This favorable free energy under confinement is due primarily to increased entropy—i.e., increased rotational and translational entropy for small CNTs but mainly increased translational entropy for larger CNTs, except in the case of the 1.1- and 1.2-nm CNTs where the rigid H-bonded water framework leads to favorable enthalpy. The increased rotational entropy of water within the CNT pore as compared to bulk water is expected because there are broken HB upon creating a surface inside the CNT, whereas the bulk water is rotationally more hindered due to a tetrahedral bonding. However, the increased translational entropy under confinement is unexpected, and we also find that it arises from the tetrahedral structure of bulk water using coarse-grained simulations. Thus the thermodynamics of water under confinement are intimately connected to the structure of water and its commensurability with the pore sizes. One possible consequence of this study relates to using CNT as membranes for water desalination (2) and filtration (23). Our results using the coarse-grained structureless water potentials (effectively an LJ fluid) suggest that there may be an additional thermodynamic barrier for the flow of gas molecules, ions, or other liquids through CNTs, even if they were to have interactions with the CNT walls similar to water, due to the lack of tetrahedral motifs or entropic gain in those gases or liquids without structures. Explicit calculation of the entropy presented here would allow for predictions of the effect of temperature on these systems, which can be tested and utilized to affect flow in nanofluidic applications.

Methods

Interaction Potentials.

The carbon–carbon interactions were described using the quantum-mechanics-based force field for carbon (24), whereas the water–carbon interactions were modeled with explicit LJ 12-6 potentials , with ε_O–C = 0.474 and ε_H–C = 0.133 kJ/mol, σ_O–C = 2.95 and σ_C–H = 2.80 Å, fitted to reproduce the rotational dynamics of water on graphene from quantum mechanics. To test the sensitivity of our thermodynamic results to the force field parameters, we repeated our simulations using the AMBER95 (25) parameters and the TIP3P (26) water model widely used in CNT-water systems (5) and found quantitatively similar results (Fig. S5).

MD Simulations.

Finite nanotubes of 10 nm in length and diameters from 0.82 (6,6) to 2.72 nm (20,20) (see Fig. S1 B–F) were aligned along the z axis and inserted in the center of a preequilibrated box of 14,000 SPC-E water molecules (Fig. S1A). We evacuated the internal volume and performed the 10-ns constant temperature and constant pressure (NPT) dynamics (27–29) at 1 atm and 300 K, using temperature and barostat coupling constants of 0.1 and 2.0 ps, respectively. A 10-Å cutoff was used for vdW and real space electrostatics, with the vdW energies and forces tapered smoothly to zero from 9 Å. The long-range electrostatics were evaluated using the particle–particle particle–mesh (30) with a convergence tolerance of 10^-5 kcal/mol. All simulations were performed using the LAMMPS (31) 2010 software package. The initially empty CNTs fill with water in just 1 ns (Fig. S2). Snapshots of the system were saved every 10 ps, and the snapshot in which the number of water molecules is closest to the average (Table S1) was selected as input for a further 50 ns of NPT dynamics using an infinite nanotube, shown to better represent the experimental system (32) than calculations using open-ended, finite nanotubes (33).

Free Energy Calculations.

Short, 20-ps constant-temperature constant-volume trajectories were generated starting at 50 snapshots from the MD trajectory (1-ns apart over the 50-ns simulation) with the coordinates and velocities saved every 4 fs. Absolute molar entropies and zero-point energy corrections to the enthalpy^* were obtained using the 2PT method (16). The 2PT method extracts the total density of states from the Fourier transform of the atomic velocity autocorrelation function. We separately extracted the thermodynamics of the waters interior and exterior to the CNT and then separated out gas- and solid-phase contributions. In addition, we partitioned the entropy into rotation and translational components as described in ref.  16. The relative free energy of water inside the 0.8-nm (6,6) CNT (-3.98 kJ/mol) compared to bulk calculated using the 2PT method in this work agrees well with the value of -3.34 kJ/mol in ref. 5 from potential of mean force calculations, justifying the 2PT method as an effective and very fast way (16) of calculating free energies.

To complement the simulations using the SPC-E water model, we carried out simulations with two structureless water models, M3B (two-body potential) and mW (three-body potential), each starting with the same configuration. In all cases, the reference was the thermodynamics of a bulk water box of 14,000 molecules.