Abstract
Background
Anopheles sinensis is a competent malaria vector in China. An understanding of vector population structure is important to the vector-based malaria control programs. However, there is no adequate data of A. sinensis population genetics available yet.
Methodology/Principal Findings
This study used 5 microsatellite loci to estimate population genetic diversity, genetic differentiation and demographic history of A. sinensis from 14 representative localities in China. All 5 microsatellite loci were highly polymorphic across populations, with high allelic richness and heterozygosity. Hardy–Weinberg disequilibrium was found in 12 populations associated with heterozygote deficits, which was likely caused by the presence of null allele and the Wahlund effect. Bayesian clustering analysis revealed two gene pools, grouping samples into two population clusters; one includes six and the other includes eight populations. Out of 14 samples, six samples were mixed with individuals from both gene pools, indicating the coexistence of two genetic units in the areas sampled. The overall differentiation between two genetic pools was moderate (F ST = 0.156). Pairwise differentiation between populations were lower within clusters (F ST = 0.008–0.028 in cluster I and F ST = 0.004–0.048 in cluster II) than between clusters (F ST = 0.120–0.201). A reduced gene flow (Nm = 1–1.7) was detected between clusters. No evidence of isolation by distance was detected among populations neither within nor between the two clusters. There are differences in effective population size (Ne = 14.3-infinite) across sampled populations.
Conclusions/Significance
Two genetic pools with moderate genetic differentiation were identified in the A. sinensis populations in China. The population divergence was not correlated with geographic distance or barrier in the range. Variable effective population size and other demographic effects of historical population perturbations could be the factors affecting the population differentiation. The structured populations may limit the migration of genes under pressures/selections, such as insecticides and immune genes against malaria.
Introduction
Anopheles sinensis Wiedemann 1828 is a widely distributed Oriental species [1], [2], [3]. In China, A. sinensis was incriminated as a competent malaria vector and was responsible for the transmission during the recurrence of vivax malaria in recent years [4]. Genetically based methods have been proposed for malaria vector control. These methods focus mainly in altering vectorial capacity through the genetic modification of natural vector populations by means of introducing refractoriness genes or by sterile insect technologies [5]. Knowledge of the genetic structure of vector species is, therefore, an essential requirement as it should contribute not only to predict the spread of genes of interest, such as insecticide resistance or refractory genes, but also to identify heterogeneities in disease transmission due to distinct vector populations [6]. A complete understanding of vector population structure and the processes responsible for the distribution of differentiation is important to vector-based malaria control programs and for identifying heterogeneity in disease transmission as a result of discrete vector populations [7]. Susceptibility to Plasmodium infection, survival and reproductive rates, degree of anthropophily, and the epidemiology of malaria in the human host may all be affected by genetic variation in vector populations [8].
A. sinensis exhibits variation in ecology [9], morphology [9], [10], chromosomes [9], [11], isozymes [9], mtDNA [12], random amplified polymorphic DNA (RAPDs) [13], and rDNA second internal transcribed spacer (ITS2) sequences [14]. Cytogenetic studies have revealed two karyotypic forms, A (XY1) and B (XY2), in A. sinensis [11], which have distinct ITS2 sequences [14]. Both forms exist in Thailand [11], and only form B occurs in China and Korea [14], [15]. The susceptibility to malaria varies in different geographic areas. In Thailand, wild A. sinensis was poorly susceptible to Plasmodium vivax [16], so were the laboratory lines of forms A and B [17]. In China, A. sinensis is more susceptible to P. vivax than to P. falciparum, and therefore it is an important vector in the areas where no other vector species exist [22], [23]. In Korea, A. sinensis was incriminated as a competent malaria vector [18], [19] and was responsible for the transmission during the recurrence of vivax malaria in recent years [20], [21]. In Japan, due to its abundance A. sinensis has long been suspected to be the most important vector of malaria in temperate Japan, including Okinawa and Hokkaido Islands [2], [3].
Despite its significance in malaria transmission, only a few studies on population genetics have been conducted [12], [13]. Microsatellites are highly polymorphic genetic markers that evolve much faster than mitochondrial or nuclear genes, and are particularly useful for resolving the structure of populations at a finer geographical and evolutionary scale. They have been extensively used for population studies of anophelines, such as A. darlingi [24], [25], [26], A. moucheti [27], A. gambiae [28] and A. nili [29]. Microsatellite DNA markers have been isolated from A. sinenesis [30], [31]. In this study, we have used microsatellite markers to estimate levels of genetic differentiation among populations of A. sinensis to determine the population structure across its range in China.
Results
Population sampling and species identification
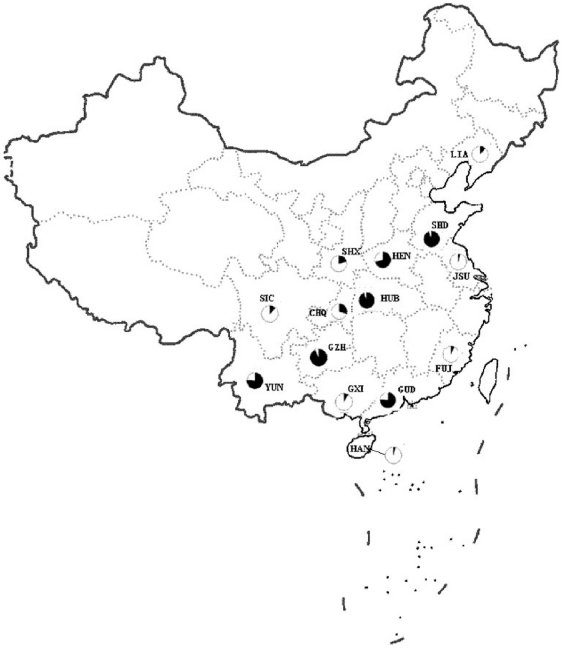
Fourteen samples of wild mosquitoes were collected from 20 locations in China (Figure 1, Table 1). A total of 327 female A. sinensis were identified by a species diagnostic PCR assay [32]. Five samples, YUN, HUB, LIA, SHD and SIC, consisted of specimen pooled from two or three collections, as stated in Table 1.
Figure 1. A schematic map of China showing sampling sites for A. sinensis.
The population genetic affiliation to the two clusters in each locality was displayed by a pie chart with black as cluster I and white as cluster II (see Table 3 for details).
Table 1. Anopheles sinensis collections in China.
| Code | Collection site | Latitude/Longitude Coordinates | Sample size | Date |
| YUN | Yanjin, YunnanPuer, Yunnan | 104°13′ E, 28°06′ N101°11′ E, 23°06′ N | 309 | 7/068/05 |
| HUB | Guangshui, HubeiSuizhou, Hubei | 113°47′ E, 31°41′ N113°15′ E, 31°52′ N | 237 | 7/077/07 |
| GZH | Congjiang, Guizhou | 108°41′ E, 25°43′ N | 27 | 8/07 |
| HEN | Tongbai, Henan | 113°23′ E, 32°29′ N | 26 | 8/07 |
| GUD | Zhuhai, Guangdong | 113°30′ E, 22°17′ N | 30 | 10/07 |
| SHX | Ningshan, Shaanxi | 108°25′ E, 33°31′ N | 418 | 7/077/97 |
| LIA | Xingchen, LiaoningSuizhong, Liaoning | 120°25′ E, 40°33′ N119°58′ E, 40°16′ N | 65 | 7/089/08 |
| SHD | Donge, ShandongYutai, ShangdongWeishan, Shangdong | 116°15′ E, 36°18′ N116°33′ E, 34°59′ N116°58′ E, 34°52′ N | 11114 | 7/067/067/06 |
| CHQ | Wanxian, Chongqing | 108°22′ E, 31°15′ N | 25 | 8/08 |
| GXI | Tiane, Guangxi | 106°59′ E, 25°01′ N | 16 | 7/05 |
| SIC | Pujiang, SichuanPixian, Sichuan | 103°29′ E, 30°14′ N103°53′ E, 30°50′ N | 128 | 7/967/97 |
| FUJ | Jiangyang, Fujian | 118°02′ E, 27°24′ N | 20 | 9/97 |
| HAN | Chengmai, Hainan | 109°58′ E, 19°39′ N | 15 | 7/96 |
| JSU | Wujin, Jiangsu | 119°54′ E, 31°44′ N | 20 | 7/97 |
Genetic variability within populations
Polymorphism at five microsatellite loci varied, with number of alleles (A) as 12 (ANS15), 17 (ANS1 and ANS6), 18 (ANS11) and 19 (ANS5), respectively (Table 2). The average number of alleles per locus was in a range between 6.5 (ANS5) and 10.4 (ANS11). The minimum mean number of alleles of all loci was in LIA population (6.2), and the maximum in YUN (10.2). Allele distributions across populations were depicted in Figure S1. The average observed heterozygosity (HO) across all samples ranged from 0.398 (ANS5) to 0.757 (ANS11), the minimum Ho was in GUD (0.433), the maximum Ho in SIC (0.760). To determine if the null alleles impacted the population genetic analyses, we performed these analyses both before and after the dataset were adjusted for estimated null allele frequencies. The effect of this treatment was minimal and did not significantly change the degree or statistical significance of the estimated parameters.
Table 2. Summary of microsatellite variation at 5 loci for A. sinensis in China.
| Locus | HEN | YUN | GUD | SHX | GZH | HUB | SHD | CHQ | LIA | FUJ | GXI | HAN | JSU | SIC | all samples | |
| (n) | N = 26 | N = 39 | N = 30 | N = 22 | N = 27 | N = 30 | N = 26 | N = 25 | N = 11 | N = 20 | N = 16 | N = 15 | N = 20 | N = 20 | N = 327 | |
| ANS1 | A | 10 | 9 | 12 | 10 | 11 | 13 | 10 | 9 | 8 | 9 | 7 | 8 | 11 | 10 | 9.786 |
| RS | 3.328 | 3.027 | 2.772 | 2.69 | 3.092 | 3.337 | 3.207 | 2.946 | 3.391 | 2.856 | 2.899 | 3.167 | 3.383 | 2.908 | 3.072 | |
| H E | 0.877 | 0.812 | 0.729 | 0.701 | 0.818 | 0.877 | 0.849 | 0.786 | 0.892 | 0.75 | 0.777 | 0.844 | 0.888 | 0.767 | 0.812 | |
| H O | 0.391 | 0.486 | 0.500 | 0.650 | 0.630 | 0.586 | 0.714 | 0.417 | 0.273 | 0.500 | 0.667 | 0.733 | 0.789 | 0.700 | 0.574 | |
| r | 0.251 | 0.175 | 0.127 | 0.020 | 0.096 | 0.132 | 0.063 | 0.199 | 0.313 | 0.134 | 0.048 | 0.045 | 0.040 | 0.027 | 0.119 | |
| F IS | 0.560* | 0.406* | 0.318* | 0.075 | 0.233* | 0.335* | 0.162 | 0.475* | 0.704* | 0.339 | 0.146 | 0.135 | 0.113 | 0.089 | 0.151 | |
| ANS5 | A | 6 | 13 | 8 | 7 | 6 | 5 | 3 | 6 | 3 | 6 | 6 | 8 | 7 | 7 | 6.500 |
| RS | 2.616 | 3.143 | 2.482 | 2.737 | 2.345 | 2.093 | 1.547 | 2.498 | 1.675 | 2.258 | 2.062 | 2.155 | 2.099 | 2.918 | 2.331 | |
| H E | 0.695 | 0.829 | 0.654 | 0.736 | 0.624 | 0.520 | 0.28 | 0.658 | 0.329 | 0.585 | 0.480 | 0.510 | 0.514 | 0.789 | 0.586 | |
| H O | 0.333 | 0.447 | 0.300 | 0.476 | 0.346 | 0.393 | 0.273 | 0.333 | 0.182 | 0.400 | 0.250 | 0.533 | 0.550 | 0.750 | 0.398 | |
| r | 0.207 | 0.181 | 0.209 | 0.141 | 0.165 | 0.078 | 0.001 | 0.189 | 0.101 | 0.108 | 0.147 | - | - | 0.011 | 0.110 | |
| F IS | 0.526* | 0.464* | 0.546* | 0.359* | 0.451* | 0.248 | 0.027 | 0.499* | 0.459 | 0.321 | 0.487 | -0.047 | -0.072 | 0.050* | 0.203 | |
| ANS11 | A | 10 | 12 | 11 | 10 | 12 | 12 | 10 | 11 | 6 | 11 | 12 | 8 | 10 | 10 | 10.357 |
| RS | 3.308 | 3.434 | 3.334 | 3.276 | 3.387 | 3.482 | 3.018 | 3.295 | 3.153 | 3.383 | 3.282 | 3.116 | 3.372 | 3.152 | 3.285 | |
| H E | 0.870 | 0.899 | 0.875 | 0.862 | 0.887 | 0.907 | 0.796 | 0.868 | 0.844 | 0.887 | 0.859 | 0.825 | 0.886 | 0.836 | 0.864 | |
| H O | 0.640 | 0.714 | 0.800 | 0.857 | 0.800 | 0.828 | 0.783 | 0.739 | 0.636 | 0.850 | 0.813 | 0.533 | 0.750 | 0.850 | 0.757 | |
| r | 0.115 | 0.091 | 0.032 | - | 0.037 | 0.034 | - | 0.059 | 0.094 | - | 0.011 | 0.147 | 0.061 | - | 0.049 | |
| F IS | 0.269* | 0.207* | 0.087 | 0.006 | 0.100 | 0.089 | 0.017 | 0.151 | 0.255 | 0.043 | 0.056 | 0.362 | 0.157 | -0.017 | 0.109 | |
| ANS15 | A | 6 | 7 | 5 | 6 | 7 | 6 | 6 | 6 | 5 | 7 | 5 | 8 | 8 | 10 | 6.571 |
| RS | 2.841 | 2.806 | 2.356 | 2.831 | 2.605 | 2.855 | 2.788 | 2.809 | 2.535 | 3.043 | 2.510 | 3.344 | 3.061 | 3.030 | 2.815 | |
| H E | 0.766 | 0.757 | 0.639 | 0.762 | 0.697 | 0.775 | 0.759 | 0.766 | 0.668 | 0.817 | 0.686 | 0.883 | 0.819 | 0.805 | 0.757 | |
| H O | 0.308 | 0.500 | 0.100 | 0.476 | 0.444 | 0.321 | 0.550 | 0.067 | 0.400 | 0.900 | 0.688 | 0.733 | 0.950 | 0.950 | 0.528 | |
| r | 0.253 | 0.141 | 0.325 | 0.153 | 0.142 | 0.250 | 0.109 | 0.387 | 0.144 | - | - | 0.065 | - | - | 0.141 | |
| F IS | 0.603* | 0.343 | 0.846* | 0.381 | 0.366* | 0.590* | 0.281 | 0.916* | 0.415 | -0.105 | -0.003 | 0.174 | -0.165 | -0.186 | 0.126 | |
| ANS6 | A | 7 | 10 | 7 | 9 | 10 | 9 | 9 | 9 | 9 | 8 | 6 | 9 | 12 | 7 | 8.643 |
| RS | 3.063 | 3.056 | 2.964 | 3.28 | 3.315 | 3.027 | 3.251 | 3.191 | 3.417 | 3.224 | 2.749 | 3.156 | 3.222 | 2.892 | 3.129 | |
| H E | 0.822 | 0.808 | 0.797 | 0.868 | 0.874 | 0.810 | 0.859 | 0.848 | 0.896 | 0.858 | 0.735 | 0.839 | 0.851 | 0.774 | 0.831 | |
| H O | 0.583 | 0.519 | 0.467 | 0.765 | 0.500 | 0.522 | 0.500 | 0.652 | 0. 909 | 0.900 | 0.429 | 0.467 | 0.650 | 0.550 | 0.577 | |
| r | 0.123 | 0.153 | 0.178 | 0.042 | 0.192 | 0.151 | 0.185 | 0.097 | - | - | 0.164 | 0.190 | 0.049 | 0.117 | 0.117 | |
| F IS | 0.295 | 0.363* | 0.419* | 0.122 | 0.433* | 0.361 | 0.423* | 0.235 | -0.015 | -0.051 | 0.426 | 0.453* | 0.241 | 0.295 | 0.212 | |
| All loci | A | 7.800 | 10.200 | 8.600 | 8.400 | 9.200 | 9.000 | 7.600 | 8.200 | 6.200 | 8.200 | 7.200 | 8.200 | 9.600 | 8.800 | 8.371 |
| RS | 3.048 | 3.093 | 2.792 | 2.972 | 2.949 | 2.959 | 2.762 | 2.948 | 2.834 | 2.959 | 2.700 | 2.988 | 3.027 | 2.980 | 2.929 | |
| H E | 0.806 | 0.821 | 0.739 | 0.786 | 0.780 | 0.778 | 0.709 | 0.785 | 0.726 | 0.779 | 0.707 | 0.780 | 0.792 | 0.794 | 0.770 | |
| H O | 0.451 | 0.533 | 0.433 | 0.645 | 0.544 | 0.530 | 0.564 | 0.442 | 0.480 | 0.701 | 0.569 | 0.600 | 0.738 | 0.760 | 0.571 | |
| r | 0.190 | 0.148 | 0.174 | 0.071 | 0.127 | 0.129 | 0.072 | 0.186 | 0.130 | 0.048 | 0.074 | 0.089 | 0.030 | 0.031 | 0.107 | |
| F IS | 0.445 | 0.354 | 0.418 | 0.183 | 0.307 | 0.323 | 0.208 | 0.444 | 0.350 | 0.091 | 0.201 | 0.237 | 0.070 | 0.044 | 0.263 | |
First row indicates collection sites and sample size in parenthesis; A, number of alleles; RS, allelic richness; H E, expected heterozygosity; H O, observed heterozygosity; r, estimated frequency of null alleles; F IS, inbreeding coefficient; All loci/samples, mean values over loci or populations; -, no significant heterozygote deficiency;
*, Probability test against Hardy- Weinberg proportions (P<0.001).
The Hardy-Weinberg exact tests were performed for five loci. No locus was in Hardy-Weinberg equilibrium (HWE) for all the samples assayed. At the population level, 26 out of 70 (37.14%) comparisons did not conform to Hardy-Weinberg expectations after sequential Bonferroni correction, and the deviations were associated with positive inbreeding coefficient (F IS), reflecting heterozygosity deficits (Table 2). Significant deviation from HWE varied across loci in a population -dependent manner. The YUN, HEN, GUD and GZH populations had the highest number of loci in departure from HWE (4 of 5), while the SHD, SHX, LIA, HAN and SIC populations had the fewest (1 of 5). The FUJ, GXI and JSU populations had no loci in departure from HWE (Table 2). In all samples, some specimen failed to amplify at one locus while succeeded at the remaining loci, suggesting the presence of null alleles. Estimates of the frequency of null alleles are given in Table 2. The locus ANS15, for example, showed both high F IS values and high frequencies of null alleles in samples CHQ, GUD, HEN and HUB.
Fisher's exact tests were conducted for linkage disequilibrium (LD) within each of the 14 collections. Out of 140 comparisons only five pairs (3.57%) were at LD (P<0.05). Two pairs were detected in HAN (ANS5/ANS15, ANS1/ANS5) and the other three pairs were in SHD (ANS6/ANS15), HUB (ANS1/ANS6), GUD (ANS6/ANS11), respectively (Table 2). No pair of loci appeared in LD in more than one population, suggesting genetic independence between loci. When the test was performed in the pooled populations, no pairs of loci out of 10 possible combinations showed significant P values (P>0.05).
Genetic differentiation among populations
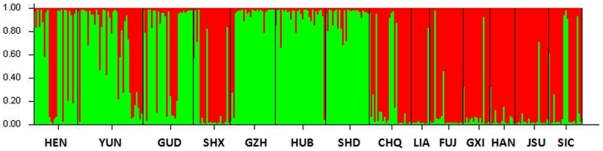
The significant deviations from HWE with heterozygote deficiency and the presence of LD suggest the presence of population subdivision within samples (the Wahlund effect). We therefore examined if there were different gene pools in these samples. The Bayesian cluster analysis divided populations into two main subgroups (posterior probability of Bayesian clustering Ln(D) likelihood score optimal for k = 2 clusters) (Figure 2). One gene pool (cluster I) was composed of GZH, HUB, SHD, HEN, GUD and YUN, and the other (cluster II) was composed of LIA, CHQ, FUJ, GXI, HAN, JSU, SIC and SHX. Allele composition varied to a limited extent among populations within the clusters but varied considerably between the clusters. For example, 3 alleles at locus ANS1, 4 alleles at ANS5 and 3 alleles at ANS6 were differentially distributed among populations between the clusters (Figure S2). In different localities, there are different proportions of individuals from different gene pools (Table 3). For example, in the HEN 70% of individuals were assigned to the cluster I and the remaining 30% to the cluster II; an opposite occurred in CHQ, in which 69.8% of individuals belong to the cluster II and 30.2% to the cluster I. In total, six samples (three in each cluster) were mixed with at least 15% of individuals assigned to the other cluster (Figure 1 and Table 3), indicating the coexistence of two gene pools in these localities.
Figure 2. Bayesian cluster analysis using STUCTURE.
Graphical representation of the data set for the most likely K (K = 2), where each color corresponds to a suggested cluster and each individual is represented by a vertical bar. The X-axis corresponds to population codes. The Y-axis presents the probability of assignment of an individual to each cluster.
Table 3. Probability of assignment of individuals to each population cluster.
| Cluster | Populations | Probability of assignment of individuals to each cluster | Number of loci in departure from HWE | |
| I | II | |||
| I | SHD | 0.939 | 0.061 | 1 |
| HUB | 0.929 | 0.071 | 2 | |
| GZH | 0.882 | 0.118 | 4 | |
| YUN | 0.774 | 0.226 | 4 | |
| GUD | 0.756 | 0.244 | 4 | |
| HEN | 0.700 | 0.300 | 4 | |
| II | JSU | 0.039 | 0.961 | 0 |
| HAN | 0.046 | 0.954 | 1 | |
| FUJ | 0.073 | 0.927 | 0 | |
| GXI | 0.082 | 0.918 | 0 | |
| LIA | 0.121 | 0.879 | 2 | |
| SIC | 0.166 | 0.834 | 1 | |
| SHX | 0.213 | 0.787 | 1 | |
| CHQ | 0.302 | 0.698 | 3 | |
Overall genetic divergence between two gene pools was assessed. First, specimens were assigned to the cluster I or II at greater than 80% probabilities, which resulted in 126 individuals in the cluster I and 135 individuals in the cluster II. Then the two pools of individuals were analyzed by the Wright's F statistics (Table 4). The overall value of F IT (0.379) showed significant heterozygote deficits at the total population level, most likely due to the presence of null alleles. Individually, three loci, ASN1, ASN6 and ASN11, presented significant heterozygote reduction at the population level (P<0.05). The average value of F IS (0.264) showed heterozygote reduction at the subpopulation level. These results corroborated the homozygote excess detected with the individual HWE tests (Table 2). Locus ANS5 had the highest F ST value (0.545) while other loci ranged between 0.020–0.086. The average F ST = 0.156, indicating a moderate genetic heterogeneity between the two gene pools. An AMOVA analysis using the two clusters found that 15.6% of the variance was attributed to between populations and 84.4% to within populations.
Table 4. Wright's F statistics values per locus between two clusters.
| Locus | F IT | F ST | F IS | ||
| P1 | P2 | ||||
| ANS1 | 0.344; P = 0.041 | 0.047 | 0.259 | 0.259 | 0.312; P = 0.571 |
| ANS5 | 0.626; P = 0.543 | 0.545 | 0.08 | 0.08 | 0.177; P = 0.373 |
| ANS11 | 0.156; P = 0.018 | 0.020 | 0.124 | 0.124 | 0.138; P = 0.772 |
| ANS15 | 0.402; P = 0.072 | 0.086 | 0.266 | 0.266 | 0.346; P = 0.504 |
| ANS6 | 0.345; P = 0.032 | 0.036 | 0.277 | 0.277 | 0.321; P = 0.586 |
| Total | 0.379; P = 0.707 | 0.156 | 1.006 | 1.006 | 0.264; P = 2.807 |
| CI | 0.229–0.574 | 0.026–0.452 | 0.148–0.335 | ||
CI = 99% confidence internal. P1 = assuming non-random breeding; P2 = assuming random breeding.
Then we tested genetic heterogeneity among populations within and between the two gene pools. We chose populations in which more than 85% individuals were assigned to the cluster I or II for the analysis. The resultant populations included three (GZH, HUB and SHD) from the cluster I and five (LIA, FUJ, GXI, HAN and JSU) from the cluster II. Table 5 shows F ST estimates for pairwise comparisons among populations. Within the clusters, paiwise F ST was low, 0.008 (HUB-GZI) to 0.028 (GZH-SHD) in the cluster I, and 0.004 (JSU-LIA) to 0.048 (HAN-GXI) in the cluster II. Between the clusters, higher level of differentiation was demonstrated with F ST from 0.120 (FUJ-GZH) to 0.201 (SHD-GXI). Of 28 pairwise comparisons, 17 were significant including all 15 comparisons between clusters (P<0.05). Nm estimates among populations were higher (4.93 to 65.54) within the clusters, and much lower (0.99 to 1.84) between the clusters (Table 5).
Table 5. Pairwise genetic distance (F ST) and gene flow (Nm) for populations of A. sinensis.
| Cluster Population | I | II | |||||||
| GZH | HUB | SHD | LIA | FUJ | GXI | HAN | JSU | ||
| I | GZH | 30.614 | 8.616 | 1.389 | 1.833 | 1.471 | 1.656 | 1.684 | |
| HUB | 0.008(827) | 12.839 | 1.377 | 1.726 | 1.373 | 1.475 | 1.656 | ||
| SHD | 0.028(1372) | 0.019(558)* | 1.088 | 1.292 | 0.993 | 1.083 | 1.193 | ||
| II | LIA | 0.153(1966) * | 0.154(1131) * | 0.187(585) * | 6.277 | 5.381 | 5.537 | 65.539 | |
| FUJ | 0.120(963) * | 0.127(629) * | 0.162(1004) * | 0.038(1451) | 6.434 | 5.564 | 27.528 | ||
| GXI | 0.145(194) * | 0.154(1007) * | 0.201(1541) * | 0.044(2126) | 0.037(1166)* | 4.926 | 9.256 | ||
| HAN | 0.131(720) * | 0.145(1418) * | 0.188(1984) * | 0.043(2533) | 0.043(1233) | 0.048(709) | 13.263 | ||
| JSU | 0.129(1292) * | 0.131(572) * | 0.173(600) * | 0.004(964) | 0.009(510) | 0.026(1484) | 0.019(1703) | ||
The pairwise Nm values are above diagonal; pairwise F ST values below diagonal and within population along the diagonal.
*, P<0.05 after sequential Bonferroni correction. The bold values are comparison between clusters. Approximate geographical distances in km are in parentheses. Abbreviations of localities are in Table 1.
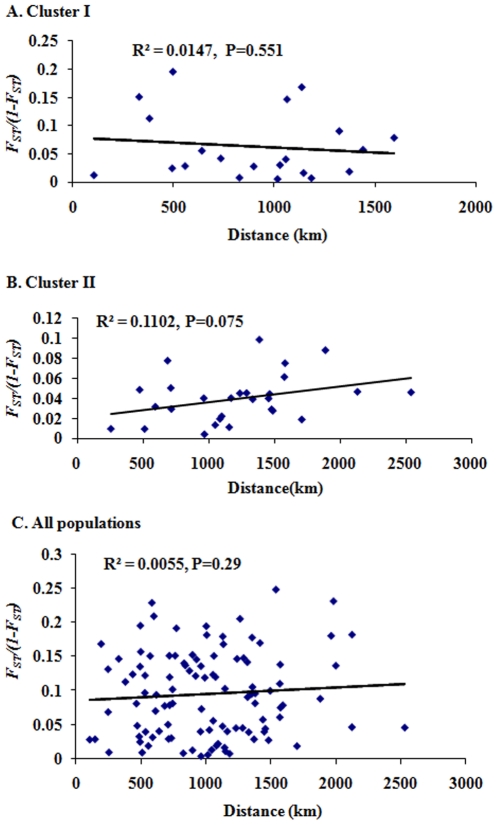
Tests of isolation by distance were performed for each population cluster and for all of the populations together. No statistically significant correlations were detected between genetic differentiation and geographic distances based on the Mantel test in all cases (Figure 3). The results suggest that geographic distance does not significantly contribute to the genetic differentiation observed in A. sinensis populations.
Figure 3. Correlation between average F ST estimates and geographic distance between collection sites for pairwise comparisons of A. sinensis populations.
A, populations of cluster I; B, populations of cluster II; C, all populations.
Effective population size and demographic stability
Estimates of expected heterozygosity under mutation-drift equilibrium (MDE) were calculated for detecting demographic instability. These statistics are expected to be equal in a neutral locus at MDE. Results of the heterozygosity tests (Table 6) did not reveal any evidence for departure from MDE in two models (SMM and TMP) in any of the 14 populations. However, a consistent trend for lower-than-expected heterozygosity (i.e., He<Heq) was detected in the GXI and SIC populations under SMM model (P<0.05), suggesting a recent demographic expansion.
Table 6. P-value for the heterozygosity tests for each A. sinensis population.
| Cluster | Population | TPM | SMM | |||
| 70%a | 80% a | 90% a | ||||
| I | HEN | He>Heq | 4 | 4 | 4 | 4 |
| Sign test | 0.333 | 0.329 | 0.322 | 0.324 | ||
| Wilcoxon test | 0.063 | 0.063 | 0.063 | 0.063 | ||
| YUN | He>Heq | 3 | 3 | 3 | 1 | |
| Sign test | 0.666 | 0.681 | 0.67 | 0.097 | ||
| Wilcoxon test | 0.813 | 1 | 1 | 0.156 | ||
| GUD | He>Heq | 3 | 3 | 2 | 2 | |
| Sign test | 0.673 | 0.67 | 0.34 | 0.35 | ||
| Wilcoxon test | 0.813 | 0.813 | 0.625 | 0.156 | ||
| GZH | He>Heq | 2 | 2 | 2 | 1 | |
| Sign test | 0.325 | 0.33 | 0.342 | 0.094 | ||
| Wilcoxon test | 1 | 0.813 | 0.156 | 0.094 | ||
| HUB | He>Heq | 3 | 2 | 2 | 2 | |
| Sign test | 0.678 | 0.33 | 0.328 | 0.333 | ||
| Wilcoxon test | 0.625 | 1 | 1 | 0.625 | ||
| SHD | He>Heq | 3 | 3 | 2 | 2 | |
| Sign test | 0.666 | 0.66 | 0.329 | 0.34 | ||
| Wilcoxon test | 1 | 0.813 | 0.625 | 0.156 | ||
| II | CHQ | He>Heq | 3 | 3 | 3 | 1 |
| Sign test | 0.661 | 0.677 | 0.678 | 0.094 | ||
| Wilcoxon test | 0.625 | 1 | 0.813 | 0.063 | ||
| LIA | He>Heq | 3 | 3 | 3 | 3 | |
| Sign test | 0.66 | 0.661 | 0.659 | 0.681 | ||
| Wilcoxon test | 0.219 | 0.813 | 0.813 | 1 | ||
| FUJ | He>Heq | 3 | 3 | 3 | 3 | |
| Sign test | 0.671 | 0.673 | 0.663 | 0.676 | ||
| Wilcoxon test | 0.813 | 0.813 | 0.813 | 0.813 | ||
| GXI | He>Heq | 1 | 1 | 1 | 0 | |
| Sign test | 0.086 | 0.094 | 0.087 | 0.010* | ||
| Wilcoxon test | 0.156 | 0.094 | 0.063 | 0.031* | ||
| HAN | He>Heq | 3 | 3 | 2 | 2 | |
| Sign test | 0.675 | 0.68 | 0.329 | 0.336 | ||
| Wilcoxon test | 0.813 | 1 | 1 | 0.625 | ||
| JSU | He>Heq | 3 | 3 | 3 | 2 | |
| Sign test | 0.657 | 0.66 | 0.674 | 0.332 | ||
| Wilcoxon test | 1 | 0.813 | 0.813 | 0.219 | ||
| SIC | He>Heq | 2 | 2 | 1 | 0 | |
| Sign test | 0.323 | 0.325 | 0.99 | 0.013* | ||
| Wilcoxon test | 0.625 | 0.219 | 0.094 | 0.031* | ||
| SHX | He>Heq | 3 | 3 | 3 | 2 | |
| Sign test | 0.647 | 0.677 | 0.659 | 0.332 | ||
| Wilcoxon test | 0.813 | 0.813 | 1 | 0.219 | ||
TMP, two-phase mutation model with (indels larger than one repeat of 30%, 20% and 10%, respectively);
, single step mutation; SMM, stepwise mutation model. He>Heq, number of loci showing a heterozygote excess (out of 5 loci tested in each samples).
*,P<0.05 (two tails P-value for deviation from MDE).
Estimates of long-term Ne varied considerably depending on the model used. Under the heterozygote excess model all of the Ne estimates were infinity. Under the linkage disequilibrium model, diverse Ne values were detected across populations (Table 7). The two clusters showed similar variability of Ne, from ∞ (CHQ) to 18.4 (SHD) in the cluster I and ∞ (HUB) to 14.2 (LIA) in the cluster II, respectively.
Table 7. Estimated Ne based on the linkage disequilibrium model.
| Cluster | Population | Ne | 95%CI |
| I | HEN | 48.4 | 25.3–210.9 |
| HUB | ∞ | 166.9-∞ | |
| YUN | 250.4 | 73.9-∞ | |
| GUD | 117.8 | 48.5-∞ | |
| SHD | 18.4 | 12.3–31.7 | |
| GZH | 60.6 | 32.8–226.7 | |
| II | CHQ | ∞ | 61.3-∞ |
| FUJ | 105.8 | 35.6-∞ | |
| JSU | 27.7 | 18.2–50.3 | |
| LIA | 14.3 | 7.9–41.3 | |
| GXI | 35.3 | 16.8–446.8 | |
| SHX | 29.3 | 17.8–65.7 | |
| SIC | 63.4 | 29.7–2739.5 | |
| HAN | 91.6 | 28.2-∞ |
CI, confidence intervals; ∞, infinity.
Discussion
Sampling strategy and geographic coverage greatly influence the analysis and interpretation of the data generated from the samples. A. sinensis occur in most parts of China, a range as from 100° E to 120° E, and from 19° N to 54° N [22]. In this study, A. sinensis mosquitoes were collected from most localities across its range in China. The LIA was at the most northern limit, and HAN was at the most southern limit of the distribution.
The five microsatellites in A. sinensis [30] are highly polymorphic in the populations, and thus are useful for exploring A. sinensis population genetic structure. Theses microsatellite loci have not been physically mapped to A. sinensis polygene chromosomes. Therefore, their location with respect to polymorphic chromosome forms is unknown, but linkage disequilibrium between loci was detected only in 3.6% of 140 comparisons suggests that they are at least statistically independent and might distribute across the genome. The high allelic diversity and expected heterozygosity were observed in most of populations, which was similar to the level of diversity in the A. darlingi in Peru and Brazil (HO = 0.742, 0.457) [24], A. albimanus in Latin America (HO = 0.73) [33], African vectors A. gambiae (HO = 0.59) [34] and A. funestus (HO = 0.672, 0.529) [35], [36]. In China, A. sinensis occurs in the temperate climate zones, populations undergo marked seasonal variations in abundance, reaching high densities only during the summer months. The high level of genetic diversity suggests that A. sinensis are able to maintain a relatively large effective population size in spite of the seasonality of low temperature in cold winter.
In this study, significant deviations from HWE due to the heterozygote deficits were detected in most samples. These could be attributed to the Wahlund effect, inbreeding, selection or null alleles. Selection was not considered because it usually occurs in one locus, not systemically in multiple loci as detected in this study. Inbreeding has genome-wide effect. If inbreeding were important in our case, we would expect a similar heterozygosity deficiencies in all markers with each population studied, which we did not detect. The reduction of heterozygotes at several loci detected in this study is likely the results of presence of null alleles that are not amplified because of the mutations at the primer annealing sites. In this study, there were specimens that failed to amplify some alleles at certain loci, but efficiently amplified at other loci. The Wahlund effect, referring to subpopulations in a sample, is likely another cause for the heterozygote deficits. Indeed, the Bayesian analysis revealed two gene pools across the locations sampled (Figure 2), and the two gene pools coexist in at least six collections (Table 3). Thus, a part of the heterozygote deficits detected in these samples could be the result of the Wahlund effect.
The two genetic divisions of A. sinensis were represented by two population clusters. There is substantial differentiation between two gene pools, demonstrated by mean F ST = 0.156 between the two clusters (Table 4) and pairwise comparisons (F ST = 0.120–0.201) among populations between the two clusters (Table 5). The gene flow was remarkably limited between the clusters (Nm = 1–1.7). The level of differentiation is comparable to that detected previously between A. sinensis populations in China using isozymes and RAPD markers (F ST = 0.069–0.111) [13], [28], between A. albimanus populations from Central and South America (F ST = 0.114) [33], among A. gambiae populations in west Africa separated by >200 km (F ST = 0.034–0.167) [37], and among A. darlingi populations from Brazil and Peru [24] as well as between A. funestus populations from west, central, and eastern Africa (F ST = 0.110) [7]. The distribution of two clusters appears no noticeable geographic patterns, and no correlation between genetic and geographic distance was detected by the Mantel test (Figure 3). In addition, the sympatric occurrence of two gene pools was found in 6 of 14 collections (Table 3). Therefore, the differentiation between the two population clusters probably was not influenced by geographic distance and barriers (e.g., Yangtze River, Yellow River and Qinling Mountains).
Within the population clusters, pairwise differentiation was little or low (F ST = 0.004–0.048). No isolation by distance was detected (Figure 3). However, a large amount of variability in Ne among the populations (14.4-∞ in the cluster I and 18.4-∞ in the cluster II, Table 7) suggests that ecological and/or historical heterogeneity may contribute to the differentiation observed among these populations. Similarly, Ne heterogeneity has been reported to be associated with the population differentiation for A. darling [24] and A. albimanus [38]. In the cluster II, there is some evidence of a population expansion in SIC and GXI (Table 7). Taken together, the population diversity in the form of two clusters may be caused largely by the differences in Ne among the populations and/or different demographic [8].
This study revealed that A. sinensis populations across China are primarily structured with two major genetic units. The distribution pattern could not be attributed to the isolation by distance. The wide range and sympatric distribution of the two genetic pools suggest that these two gene pools may have been segregating in the A. sinensis populations for a relative long time. Our findings emphasize the need for further investigation with deeper sampling (especially in the areas both gene pools exist) and more genetic loci in order to thoroughly elucidate the forces that shape and maintain the population structure. More studies are required to characterize the two gene pools of A. sinensis regarding ecology and malaria susceptibility. The population structure of A. sinensis implies that the expansion and spread of genes responsible for immunity against malaria or insecticide resistance would be easier within than between the genetic units. Moreover, the estimate of effective population size would help to evaluate the effectiveness of mosquito control measurements [8].
Materials and Methods
Mosquito collections and species identification
Wild adult A. sinensis were collected from 1996 to 2008, by using indoor light traps at livestock corrals. Human landing catches at human living room were tried in 1996 in Sichuan (SIC) and Hainan (HAN). Only two specimens were caught by human bait in SIC. A. sinensis is zoophilic, therefore, the human bait was no longer used in later collections. The 20 collection sites in 14 provinces in China were located from 109°58′ N to 120°25′ N, and 23°60′ E to 31°44′ E (Table 1, Figure 1). Five samples, YUN, HUB, LIA, SHD and SIC, consisted of specimens pooled from two or three sites in proximity to each other, as stated in Table 1. The distances between sites were 25–100 km.
Mosquitoes of A. hyrcanus group were identified by morphology using the identification keys of Lu et al. [22]. Specimens were kept individually in silica gel filled tubes at 4°C, until DNA extraction was performed according to Collins et al. [39]. A. sinensis species identification was done by a PCR assay based on ribosomal DNA ITS2 markers previously described in Ma et al. [32].
Genotyping and data analysis
Five microsatellite loci, ANS1, ANS5, ANS6, ANS11 and ANS15 [30], were used for genotyping. Each locus was amplified by PCR using fluorescently labeled (FAM, NED, or HEX) forward primers. Amplified fragments were separated by capillary electrophoresis in an automatic sequencer (ABI 3770, Applied Biosystems, Foster City, CA) and size scored using GENOTYPER 3.7 software (Applied Biosystems, Foster City, CA).
Genetic diversity within samples and overall was measured at each locus by estimates of allele frequencies, number of alleles A, allele richness Rs, inbreeding coefficient F IS, expected heterozygosity H E, and observed heterozygosity Ho [40], using the software FSTAT 2.9.3.2 [41]. Within each locality the frequency of null alleles was determined using the Brookfield 2 estimate [42], and the allele and genotype frequencies were then adjusted accordingly in MICRO-CHECKER 2.2.3 [43]. The null allele-adjusted dataset was compared to the original dataset to investigate the impact of null alleles on estimations of genetic differentiation. Genotypic frequencies were tested against Hardy-Weinberg equilibrium (HWE) for each locus in the pooled population and in each sample. Statistical significance was assessed by the exact probability test available in GENEPOP 3.2 [44]. Linkage disequilibrium between loci was tested by exact tests on contingency tables, also available in GENEPOP.
Genetic differentiation was estimated by calculating Wright's F statistics (F ST, F IS, F IT) values per locus between clusters and pairs of populations using ARLEQUIN 2.001 [45] and GENEPOP. The number of migrants per population per generation (Nm) between localities was estimated from pairwise F ST [46]. An analysis of molecular variance (AMOVA) was used to examine the distribution of genetic variation in Arlequin using F ST. We focused on estimates of F ST performed under the infinite alleles model (IAM) because this model is considered more reliable when fewer than 20 microsatellites are used [47]. The significance for all calculations was assessed by 10,000 permutations and the P-values. The isolation by distance model was investigated as a potential explanation for the observed population differentiation. The significance of the regression of genetic differences on geographic distance between sample pairs was tested using a Mantel test [48] with 100,000 permutations using GENEPOP.
A Bayesian approach was used to infer the number of clusters (K) in the data set without prior information of the sampling locations, implemented with STRUCTURE 2.2 [49]. A model where the allele frequencies were correlated within populations was assumed (λ was set at 1, the default value). The software was run with the option of admixture, allowing for some mixed ancestry within individuals, and α was allowed to vary. Twenty independent runs were done for each value of K (K = 1 to 9), with a burn-in period of 100,000 iterations and 100,000 replications. The method of Evanno et al. [50] was used to determine the most likely number of clusters. This approach uses an ad hoc quantity, ΔK, based on the second order rate of change of the likelihood function between successive values of K.
Because demographic instability such as recent population bottleneck and/or expansion might bias genetic differentiation estimates to a significant extent [51], [52], heterozygosity tests [53] were used to detect deviations from mutation-drift equilibrium (MDE). These tests compare two estimates of expected heterozygosity, one based on allele frequencies (He), assuming Hardy-Weinberg proportions, and another based on the number of alleles and sample size (Heq), assuming MDE. At MDE, both estimates should be similar in the majority of loci analyzed (i.e. He = Heq). If a population experiences a bottleneck, rare alleles will be rapidly lost and therefore Heq will decrease faster than He (i.e. He > Heq). This apparent excess of heterozygosity in a significant number of loci is an indicator of a bottleneck, whereas the converse (i.e. He <Heq) may indicate a population expansion. Estimates of expected heterozygosity under MDE were calculated under the Stepwise Mutation Model (SMM) and Two Phase Models (TPM) with 10%–30% indels larger than the repeat unit. Calculations were done using the software BOTTLENECK 1.2.02. [53]. The long-term effective population size (Ne) was estimated using NEESTIMATOR 1.3 [54] based on the heterozygote excess and linkage disequilibrium models.
Supporting Information
Allele distributions across populations for each of five loci. Alleles are denoted by length (bp), and populations are color coded.
(TIF)
Differentially distributed alleles across populations between two clusters. Top, ANS1; Middle, ANS5; Bottom, ANS6. Differential alleles are color coded, and populations were arranged based on their cluster assignment.
(TIF)
Acknowledgments
A number of people provided field assistance, mosquitoes and information used in the study. We are especially grateful to Zhou Hong-Ning and Gu Yun-An (YUN), Huang Guang-Quan and Chen Guo-Ying (HUB), Shi Yao-Hua (GZH), Li Peng (HEN), Huang Li-Qun (GUD), Zhang Ji-Bo (LIA), Chen Xi-xin (SHD), Huang Ya-Ming (GXI), Lei Xin-Tian (SIC), Xu Bao-Hai (FUJ), Wang Zhi-Guang (HAN), Gao Jia-Fang (JSU).
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This work was supported by the National Natural Science Foundation of China-Yunnan Joint Fund (U0932604) to Yajun Ma and Jiannong Xu, and National Basic Research Program of China (973 Program 2007CB513100) to Yajun Ma. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Harrison BA, Scanlon JE. The subgenus Anopheles in Thailand (Diptera: Culicidae). Contr Amer Ent Inst. 1975;12:1–307. [Google Scholar]
- 2.Tanaka K, Mizusawa K, Saugstad ES. A revision of the adult and larval mosquitoes of Japan (including the Ryukyu Archipelago and the Ogasawara Islands) and Korea (Diptera: Culicidae). Contr Amer Ent Inst. 1979;16:1–987. [Google Scholar]
- 3.Rueda LM, Iwakami M, O'guinn M, Mogi M, Prendergast BF, et al. Habitats and distribution of Anopheles sinensis and associated Anopheles hyrcanus group in Japan. J Am Mosq Control Assoc. 2005;21:458–463. doi: 10.2987/8756-971X(2006)21[458:HADOAS]2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 4.Zhou SS, Wang Y, Fang W, Tang LH. Malaria situation in the People's Republic of China in 2008. Chin J Parasitol Parasit Dis. 2009;27:455–457. [PubMed] [Google Scholar]
- 5.Christophides GK. Transgenic mosquitoes and malaria transmission. Cell Microbiol. 2005;7:325–333. doi: 10.1111/j.1462-5822.2005.00495.x. [DOI] [PubMed] [Google Scholar]
- 6.Lehmann T, Licht M, Elissa N, Maega BTA, Chimumbwa JM, et al. Population structure of Anopheles gambiae in Africa. J Hered. 2003;94:133–147. doi: 10.1093/jhered/esg024. [DOI] [PubMed] [Google Scholar]
- 7.Michel AP, Guelbeogo WM, Grushko O, Schemerhorn BJ, Kern M, et al. Molecular differentiation between chromosomally defined incipient species of Anopheles funestus. Insect Mol Biol. 2005;14:375–387. doi: 10.1111/j.1365-2583.2005.00568.x. [DOI] [PubMed] [Google Scholar]
- 8.Donnelly MJ, Simard F, Lehmann T. Evolutionary studies of malaria vectors. Trends Parasitol. 2002;18:75–80. doi: 10.1016/s1471-4922(01)02198-5. [DOI] [PubMed] [Google Scholar]
- 9.Sun YC, Wang W. The research progress of variation among Anopheles sinensis strains in China. Chin Bull Entomol. 1993;30:56–59. [Google Scholar]
- 10.Ma YJ, Wang JS. Numerical taxonomic study of 5 species and 4 strains of Anopheles hyrcanus group (Diptera: Culicidae). J Guiyang Med Coll. 1990;15:45–48. [Google Scholar]
- 11.Baimai V, Rattanarithikul R, Kijchalao U. Metaphase karyotypes of Anopheles of Thailand and Southeast Asia: I. The Hyrcanus group. J Am Mosq Control Assoc. 1993;9:59–67. [PubMed] [Google Scholar]
- 12.Jung JW, Jung YJ, Min GS, Kim W. Analysis of the population genetic structure of the malaria vector Anopheles sinensis in South Korea based on mitochondrial sequences. Am J Trop Med Hyg. 2007;77:310–315. [PubMed] [Google Scholar]
- 13.Ma YJ, Qu FY, Xu JN, Zheng ZM. Study on molecular genetic polymorphism of Anopheles sinensis populations in China. Acta Entomol Sin. 2001;44:33–39. [Google Scholar]
- 14.Min GS, Choochote W, Jitpakdi A, Kim SJ, Kim W, et al. Intraspecific hybridization of Anopheles sinensis (Diptera: Culicidae) strains from Thailand and Korea. Mol Cell. 2002;14:198–204. [PubMed] [Google Scholar]
- 15.Xu SB, Qu YJ. Studies on chromosomes of thirteen species of anopheline mosquitoes in China. J Med Coll PLA. 1991;6:286–291. [Google Scholar]
- 16.Somboon P, Suwonkerd W, Lines JD. Susceptibility of Thai zoophilic anophelines and suspected malaria vectors to local strains of human malaria parasites. Southeast Asian J Trop Med Publ Health. 1994;25:766–770. [PubMed] [Google Scholar]
- 17.Rongsriyam Y, Jitpakdi A, Choochote W, Somboon P, Tookyang B, et al. Comparative susceptibility of two forms of Anopheles sinensis Wiedemann 1828 (Diptera: Culicidae) to infection with Plasmodium falciparum, P. vivax, P. yoelii and the determination of misleading factor for sporozoite identification. Southeast Asian J Trop Med Publ Health. 1998;29:159–167. [PubMed] [Google Scholar]
- 18.Chow CY. Bionomics of malaria vectors in the Western Pacific region. Southeast Asian J Trop Med Publ Health. 1970;1:40–57. [Google Scholar]
- 19.Lee WJ, Klein TA, Kim HC, Choi YM, Yoon SH, et al. Anopheles kleini, Anopheles pullus, and Anopheles sinensis: potential vectors of Plasmodium vivax in the Republic of Korea. J Med Entomol. 2007;44:1086–1090. doi: 10.1603/0022-2585(2007)44[1086:akapaa]2.0.co;2. [DOI] [PubMed] [Google Scholar]
- 20.Ree HI, Hwang UW, Lee IY, Kim TE. Daily survival and human blood index of Anopheles sinensis, the vector species of malaria in Korea. J Am Mosq Control Assoc. 2001;17:67–72. [PubMed] [Google Scholar]
- 21.Coleman RE, Kiattibut C, Sattabongkot J, Ryan J, Burkett DA, et al. Evaluation of anopheline mosquitoes (Diptera: Culicidae) from the republic of Korea for Plasmodium vivax circumsporozoite protein. J Med Entomol. 2002;39:244–247. doi: 10.1603/0022-2585-39.1.244. [DOI] [PubMed] [Google Scholar]
- 22.Lu BL. Fauna Sinica, Academia Sinica. Science Press, Beijing, China; 1997. Fauna Sinica. Insecta, vol. 9. Diptera: Culicidae II, pp. 12-38. In Commun. [Google Scholar]
- 23.Qian HL, Tang LH, Cheng YL, Yang BJ. Preliminary estimation of malaria transmission potential in areas where Anopheles sinensis is the only vector. Chin J Parasitol Parasit Dis. 1994;12:265–267. [PubMed] [Google Scholar]
- 24.Mirabello L, Vineis JH, Yanoviak SP, Scarpassa VM, Póvoa MM, et al. Microsatellite data suggest significant population structure and differentiation within the malaria vector Anopheles darlingi in Central and South America. BMC Ecology. 2008;8:3. doi: 10.1186/1472-6785-8-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gutiérrez LA, Gómez GF, González JJ, Castro MI, Luckhart S, et al. Microgeographic genetic variation of the malaria vector Anopheles darlingi Root (Diptera: Culicidae) from Córdoba and Antioquia, Colombia. Am J Trop Med Hyg. 2010;83:38–47. doi: 10.4269/ajtmh.2010.09-0381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Scarpassa VM, Conn JE. Population genetic structure of the major malaria vector Anopheles darlingi (Diptera: Culicidae) from the Brazilian Amazon, using microsatellite markers. Mem Inst Oswaldo Cruz. 2007;102:319–327. doi: 10.1590/s0074-02762007005000045. [DOI] [PubMed] [Google Scholar]
- 27.Antonio-Nkondjio C, Ndo C, Kengne P, Mukwaya L, Awono-Ambene P, et al. Population structure of the malaria vector Anopheles moucheti in the equatorial forest region of Africa. Malaria J. 2008;7:120. doi: 10.1186/1475-2875-7-120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Moreno M, Salgueiro P, Vicente JL, Cano J, Berzosa P, et al. Genetic population structure of Anopheles gambiae in Equatorial Guinea. Malaria J. 2007;6:137. doi: 10.1186/1475-2875-6-137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ndo C, Antonio-Nkondjio C, Cohuet A, Ayala D, Kengne P, et al. Population genetics structure of the malaria vector Anopheles nili in Sub-Saharan Africa. Malaria J. 2010;9:161. doi: 10.1186/1475-2875-9-161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ma YJ, Fan Y. Isolation and characterization of polymorphic microsatellite markers from Asian malaria mosquito Anopheles sinensis (Diptera: Culicidae). Mol Ecol Res. 2008;8:1059–1061. doi: 10.1111/j.1755-0998.2008.02154.x. [DOI] [PubMed] [Google Scholar]
- 31.Jung J, Lee E, Kim W. Isolation and characterization of polymorphic microsatellite markers of Anopheles sinensis, a malaria vector mosquito in the East Asia region. Mol Ecology Notes. 2006;6:1272–1274. [Google Scholar]
- 32.Ma YJ, Qu FY, Cao YC, Yang BJ. On molecular identification and taxonomic status of Anopheles lesteri and Anopheles anthropophagus in China (Diptera: Culicidae). Chin J Parasitol Parasit Dis. 2000;18:325–328. [PubMed] [Google Scholar]
- 33.Molina-Cruz A, de Merida AM, Mills K, Mills K, Rodríguez F, et al. Gene flow among Anopheles albimanus populations in Central America, South America, and the Caribbean assessed by microsatellites and mitochondrial DNA. Am J Trop Med Hyg. 2004;71:350–359. [PubMed] [Google Scholar]
- 34.Lehmann T, Besansky NJ, Hawley WA, Fahey TG, Kamau L, et al. Microgeographic structure of Anopheles gambiae in western Kenya based on mtDNA and microsatellite loci. Mol Ecol. 1997;6:243–253. doi: 10.1046/j.1365-294x.1997.00177.x. [DOI] [PubMed] [Google Scholar]
- 35.Michel AP, Grushko O, Guelbeogo WM, Lobo NF, Sagnon N, et al. Divergence with gene flow in Anopheles funestus from the Sudan savanna of Burkina Faso, West Africa. Genetics. 2006;173:1389–1395. doi: 10.1534/genetics.106.059667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Michel AP, Ingrasci MJ, Schemerhorn BJ, Kern MG, Legoff G, et al. Rangewide population genetic structure of the African malaria vector Anopheles funestus. Mol Ecol. 2005;14:4235–4248. doi: 10.1111/j.1365-294X.2005.02754.x. [DOI] [PubMed] [Google Scholar]
- 37.Carnahan J, Zheng L, Taylor CE, Toure YT, Norris DE, et al. Genetic differentiation of Anopheles gambiae s.s. populations in Mali, West Africa, using microsatellite loci. J Hered. 2002;93:249–253. doi: 10.1093/jhered/93.4.249. [DOI] [PubMed] [Google Scholar]
- 38.Gutierrez LA, Naranjo NJ, Cienfuegos AV, Muskus CE, Luckhart S, et al. Population structure analyses and demographic history of the malaria vector Anopheles albimanus from the Caribbean and the Pacific regions of Colombia. Malar J. 2009;8:259. doi: 10.1186/1475-2875-8-259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Collins FH, Mendez MA, Rasmussen MO, Mehaffey PC, Besansky NJ, et al. A ribosomal RNA gene probe differentiates member species of the Anopheles gambiae complex. Am J Trop Med Hyg. 1987;37:37–41. doi: 10.4269/ajtmh.1987.37.37. [DOI] [PubMed] [Google Scholar]
- 40.Nei M. New York: Colombia University Press; 1987. Molecular evolutionary genetics. [Google Scholar]
- 41.Goudet J. FSTAT version 2.9.3.2. A computer software to calculate F-statistics. J Hered. 1995;86:485–486. [Google Scholar]
- 42.Brookfield JF. A simple new method for estimating null allele frequency from heterozygote deficiency. Mol Ecol. 1996;5:453–455. doi: 10.1111/j.1365-294x.1996.tb00336.x. [DOI] [PubMed] [Google Scholar]
- 43.Van Oosterhout C, Hutchinson WF, Wills DPM, Shipley P. Micro-Checker: software for identifying and correcting genotyping errors in microsatellite data. Mol Ecol Notes. 2004;4:535–538. [Google Scholar]
- 44.Raymond M, Rousset F. GENEPOP version 1.2: population genetics software for exact tests and ecumenicism. J Hered. 1995;86:248–249. [Google Scholar]
- 45.Schneider S, Roeddli D, Excoffier L. Genetics and Biometry Laboratory. University of Geneva, Switzerland; 2000. ARLEQUIN, Version 2.000: a software for population genetics data analysis. . [Google Scholar]
- 46.Slatkin M. A measure of population subdivision based on microsatellite allele frequencies. Genetics, 1995;139:457–462. doi: 10.1093/genetics/139.1.457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gaggiotti OE, Lange O, Rassmann K, Gliddon C. A comparison of two indirect methods for estimating average levels of gene flow using microsatellite data. Mol Ecol. 1999;8:1513–1520. doi: 10.1046/j.1365-294x.1999.00730.x. [DOI] [PubMed] [Google Scholar]
- 48.Mantel N. The detection of disease clustering and a generalized regression approach. Cancer Res. 1967;27:209–220. [PubMed] [Google Scholar]
- 49.Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Evanno G, Regnaut S, Goudet J. Detecting the number of clusters of individuals using the software STRUCTURE: a simulation study. Mol Ecol. 2005;14:2611–2620. doi: 10.1111/j.1365-294X.2005.02553.x. [DOI] [PubMed] [Google Scholar]
- 51.Lehmann T, Hawley WA, Grebert H, Fahey TG, Kamau L, et al. The rift valley complex as a barrier to gene flow for Anopheles gambiae in Kenya. J Hered. 1999;90:613–621. doi: 10.1093/jhered/90.6.613. [DOI] [PubMed] [Google Scholar]
- 52.Donnelly MJ, Licht MC, Lehmann T. Evidence for a recent population expansion in the malaria vectors Anopheles arabiensis and Anopheles gambiae. Mol Biol Evol. 2001;18:1353–1364. doi: 10.1093/oxfordjournals.molbev.a003919. [DOI] [PubMed] [Google Scholar]
- 53.Cornuet JM, Luikart G. Description and power analysis of two tests for detecting recent population bottlenecks from allele frequency data. Genetics. 1996;144:2001–2014. doi: 10.1093/genetics/144.4.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Peel D, Ovenden JR, Peel SL. Queensland Government, Department of Primary Industries and Fisheries; 2004. NeEstimator: software for estimating effective population size, Version 1.3. . [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Allele distributions across populations for each of five loci. Alleles are denoted by length (bp), and populations are color coded.
(TIF)
Differentially distributed alleles across populations between two clusters. Top, ANS1; Middle, ANS5; Bottom, ANS6. Differential alleles are color coded, and populations were arranged based on their cluster assignment.
(TIF)