Surveying implicit solvent models for estimating small molecule absolute hydration free energies

Abstract

Implicit solvent models are powerful tools in accounting for the aqueous environment at a fraction of the computational expense of explicit solvent representations. Here, we compare the ability of common implicit solvent models (TC, OBC, OBC2, GBMV, GBMV2, GBSW, GBSW/MS, GBSW/MS2 and FACTS) to reproduce experimental absolute hydration free energies for a series of 499 small neutral molecules that are modeled using AMBER/GAFF parameters and AM1-BCC charges. Given optimized surface tension coefficients for scaling the surface area term in the nonpolar contribution, most implicit solvent models demonstrate reasonable agreement with extensive explicit solvent simulations (average difference 1.0-1.7 kcal/mol and R²=0.81-0.91) and with experimental hydration free energies (average unsigned errors=1.1-1.4 kcal/mol and R²=0.66-0.81). Chemical classes of compounds are identified that need further optimization of their ligand force field parameters and others that require improvement in the physical parameters of the implicit solvent models themselves. More sophisticated nonpolar models are also likely necessary to more effectively represent the underlying physics of solvation and take the quality of hydration free energies estimated from implicit solvent models to the next level.

I. INTRODUCTION

The accurate calculation of absolute hydration free energies for small molecules is an important step towards reliably estimating protein-ligand binding affinities.¹ Appropriate representation of these hydration free energies can provide a realistic basis for modeling the thermodynamic processes of ligand desolvation and subsequent “resolvation” by the protein binding pocket. The quality of these hydration free energies depends both on thorough sampling methods and on high-quality force field parameters that describe the inter- and intra-molecular interactions throughout the simulations. Alchemical free energy simulations have been shown to provide well-converged results for vacuum and explicit solvent simulations within ~0.2 kcal/mol.^2-4 However, these explicit solvent simulations are generally computationally expensive to perform given the many degrees of freedom in the system that need to be explored. Furthermore, to obtain sufficient overlap in the simulated ensembles, several intermediates along the alchemical transformation pathways usually need to be sampled.⁵

Implicit solvent models have been developed as a strategy for representing the aqueous environment of a solute but at a fraction of the cost of explicitly modeling individual water molecules.^6,7 In many implicit solvent models for macromolecules, the solvent is treated as a uniform high dielectric environment while the solute is represented as a low dielectric region with a spatial charge distribution. The Poisson equation provides an exact description of the electrostatic component of this solute-solvent system without explicitly representing the degrees of freedom associated with individual water molecules. The numerical solution of the finite-difference Poisson or Poisson-Boltzman (PB) equation is more computationally efficient than performing explicit solvent simulations, but is still prohibitively expensive for many macromolecular applications.

Generalized Born (GB) models have been developed as a pairwise approximation to the solution of the Poisson equation for continuum electrostatic solvation.^8-20 These GB models depend on efficient strategies to determine the effective Born radii which quantify the degree of “buriedness” of individual charges within the macromolecule. The Born radii provide a correction to Coulomb's law used to calculate the electrostatic energy associated between each pair of charges. GB models differ from one another primarily in how the Born radii are estimated and how the solute volume is defined. Beyond modeling the electrostatics of hydration, the nonpolar contribution to the solvation free energy for macromolecules is required for accurate calculations.^21,22 In many current implicit solvent models for biomolecules, this contribution is estimated from a solvent-accessible surface area (SASA) term that is scaled by an effective surface tension parameter.^14,23 However, other more sophisticated models for the nonpolar component of hydration free energies have also been proposed and implemented.^13,14,23-25

There are two fundamental two classes of parameters in GB models.²⁶ The first class contains “numerical parameters”, that is, parameters that are specific to a given GB model and are optimized to reproduce results from corresponding high-resolution PB calculations. These parameters include solvation free energies of small model compounds and proteins and the effective Born radii. The second class includes “physical parameters”, that is parameters that have well-defined physical meanings, such as the definition of the dielectric boundary, the intrinsic atomic radii for defining the boundary location, and the effective surface tension parameters associated with the nonpolar contribution to hydration free energies. These parameters can be optimized to reproduce high-quality experimental properties. In some GB models, however, parameters are optimized concurrently and so are not neatly separable into these two categories. Additional factors that influence the quality of simulated hydration free energies are the force field parameters for the solute, especially the partial charges assigned to each atom center, as well as limitations in a given sampling protocol. Given the speed of modern computers and efficiency of the GB implementations, sampling limitations can generally be minimal for calculating small molecule hydration free energies.

Several large-scale studies have been published that have focused on estimating absolute hydration free energies for small molecules using a variety of force fields, charge assignment methods and representations of the solvent environment. Rizzo et al. calculated hydration free energies for more than 500 neutral and charged compounds using both a PB and a GB model (TC model in AMBER) with a SASA nonpolar contribution to investigate the quality of different charge models for the ligand parameters.²⁷ For the 460 neutral compounds, the correlation between the PB and GB results for the single-conformer representations of the molecules were excellent regardless of charge method (R²=0.94) and the AM1-BCC charge assignment strategy provided the best agreement with experimental hydration free energies with overall average unsigned errors (AUE) of 1.36 and 1.38 kcal/mol for the PB and GB models respectively. Mobley et al. expanded Rizzo et al.'s database of neutral compounds to include 504 small molecules and explored the value of explicitly treating entropic effects and modeling conformational changes in implicit solvent simulations.²⁸ In their analysis of small molecule hydration free energies estimated using single conformers, multiple conformers or full trajectories, Mobley et al. demonstrated that conformational entropy changes in the solute can be up to 2.3 kcal/mol upon hydration.²⁸ Thus, while they are more time intensive, full trajectories are required for more accurate hydration free energy estimates. In their study, using the Generalized AMBER force field (GAFF)²⁹ with AM1-BCC partial charges^30,31 the implicit solvent simulations yielded estimated absolute hydration free energies with RMS errors of 2.0-2.4 kcal/mol and R² of 0.69-0.77 compared with experiment depending on which AMBER-implemented implicit solvent model was used (PB, TC, OBC2 or GBn). In a subsequent study, using the TIP3P water model in explicit solvent simulations for the same database of compounds, Mobley et al. found improved agreement between the calculated and experimental hydration free energies with RMS errors of 1.2 kcal/mol and an R² of 0.89.²

The quality of the ligand parameters themselves has a significant impact on the reliability of the estimated hydration free energies. A large database of 239 diverse neutral compounds was recently investigated using different force field parameters combined with implicit and explicit solvent simulation strategies for calculating hydration free energies.^3,4 All but 18 of the compounds in this database are also contained in the database that was studied by Mobley et al.^2,28 Shivakumar et al. originally calculated hydration free energy estimates for these 239 compounds using GAFF and CHARMm-MSI ligand parameters combined with charge assignments from ChelpG, RESP or AM1-BCC protocols. Overall, the AM1-BCC charges provided the best correlation between explicit TIP3P solvent simulations calculated hydration free energies and experimental values with the GAFF/AM1-BCC (R²=0.87) yielding higher quality results than the CHARMm-MSI/AM1-BCC parameters (R²=0.76).⁴ In a more recent study, Shivakumar et al. computed hydration free energies from explicit solvent simulations using the OPLS-AA force field and charge parameterization scheme and achieved even better agreement with experiment (R²=0.94).³

In the current study, we focus on the quality of the absolute hydration free energies that are obtained for a large database of 499 compounds using different implicit solvent models for a given set of force field parameters and extensive simulation trajectories. The objective is to identify areas in which the current generation of implicit solvent models implemented in CHARMM and AMBER needs refinement of their parameters in their quest for higher quality hydration free energy estimates. In their original papers, each implicit solvent model has demonstrated reasonable agreement between the electrostatic GB and PB calculations for model compounds. Thus, in this work we are focused primarily on the physical parameters, though we recognize that in some GB models, the physical and numerical parameters are less readily separable from one another. First, we provide a brief overview of the primary differences among the solvent models used in this study. Second, we present the quality of the calculated hydration free energies with respect to reproducing experimental values as well as results from explicit solvent simulations and discuss the similarities among the models. Third, we discuss the results in the context of the chemical classes of compounds that present challenges to the different implicit solvent models. Finally, we explore the nature of the contributions of the nonpolar estimator to the quality of the hydration free energy estimates.

II. THEORY

Overview of implicit solvent models

The specifics of each implicit solvent model are already fully documented in the original papers. Here, we simply highlight the fundamental differences among the implicit solvent models that are investigated in this study; Table 1 provides an overview of these differences. All models that were studied decompose the total hydration free energy into an electrostatic component and a nonpolar component. Each model employs variations of the Generalized Born model to approximate the electrostatic contribution to the solvation free energy. The GB formalism originally proposed by Still and coworkers is described by the equation⁹:

$$\Delta G_{elec}^{GB}=-\frac{1}{2}\left(\frac{1}{{\epsilon }_m}-\frac{1}{{\epsilon }_{solv}}\right)\sum _{i=1}^N\sum _{j=1}^N\frac{q_i{q}_j}{\sqrt{r_{ij}^2+{\alpha }_i{\alpha }_j\exp (r_{ij}^2∕\kappa {\alpha }_i{\alpha }_j)}}$$ (1)

where r_ij is the distance between the charges q_i and q_j, ε_m and ε_solv are the dielectric constants assigned to the solute molecule and solvent respectively, N is the number of solute atoms, α_i is the effective Born radius for atom i and κ has a value of 2 in the work of Still et al.⁹ and typically is set to 4 or 8. The effective Born radius of each solute atom reflects the degree of its burial within the molecule and becomes the key parameter for the calculation of the electrostatic contribution to the solvation free energy. The effective Born radius for atom i can be calculated from the atomic electrostatic self-solvation energy in the Born equation (Eq 1):

$${\alpha }_i=-\frac{1}{2}\left(\frac{1}{{\epsilon }_m}-\frac{1}{{\epsilon }_{solv}}\right)\frac{q_i^2}{G_{elec,i}^{GB}}$$ (2)

The primary advantage of GB models lies in their ability to estimate the Born radii by alternative, computationally-efficient means. Here, we focus primarily on volume-based GB models where the Coulomb Field Approximation (CFA), which approximates the electric displacement around an atom by the Coulomb field, is used to estimate the magnitude of the Born radius:

$$\frac{1}{{\alpha }_i}=\frac{1}{R_i}-\frac{1}{4\pi }{\int }_{solute}\frac{1}{r^4}dV$$ (3)

where R_i is the intrinsic radius of atom i (the Born radius in the absence of all other atoms) and is often set equal to the van der Waals radius and where the second term is the Coulomb field integral which is computed over the volume of the solute excluding the sphere of radius R_i around atom i. Different flavors of GB models employ alternative approaches to calculating and scaling this integral and some include higher order correction terms to account for limitations in the CFA that arise from off-center charges and non-spherical volumes of many systems.

Table 1.

Summary of the differences among the implicit solvent models investigated in this study. (MS=molecular surface)

	TC	OBC	OBC2	GBMV	GBMV2	GBSW	GBSW/MS	GBSW/MS2	FACTS
ΔGelec; αi estimate	3-param	5-param	5-param	2-param; grid	5-param; analytic	2-param	2-param	3-param	5-param
PB boundary	---	---	---	MS	MS	vdW	MS	MS	vdW
Intrinsic radii	Amber6	mbondi2	mbondi2	vdW	vdW	vdW	vdW	vdW	vdW; polarH = 1.0 A
ΔGnp; SASA	LCPO37	LCPO37	LCPO37	SASA-111	SASA-111	SASA10	SASA10	SASA10	5-params34

The Amber6²⁰ set is based van der Waals radii estimated by Bondi⁴⁵ with optimized radii for hydrogen and phosphorus atoms. The modified Bondi set 2 (mbondi2) represents the Bondi van der Waals radii with the radius of hydrogen atoms bound to nitrogen increased from 1.2 to 1.3 Å.

The implicit solvent models explored in this study all approximate nonpolar contributions to the total hydration free energy using a solvent-accessible surface area term. In traditional MM-PSBA and MM-GBSA methods, the total molecular solvent-accessible surface area, SASA, is used and the nonpolar contribution is described by:

$$\Delta G_{np}=\gamma SASA+\beta$$ (4)

where γ and β are the surface tension parameter and off-set values respectively. For a series of linear alkanes, fitting molecular surface area terms to experimental hydration free energies yielded values of γ=0.00542 kcal/(mol·Å²) and β=0.92 kcal/mol.³²

In this study, we also consider an empirical strategy that was recently developed by Caflisch and coworkers.^33,34 In this strategy, atomic Born radii and SASAs are calculated from combinations of a measure of the volume occupied by the solute around this atom, A_i, and a measure of the symmetry of distribution of atoms around this atom, B_i. For specific van der Waals radii, five parameters were optimized to reproduce PB atomic solvation energy values and four parameters were optimized to estimate atomic SASA.

Implicit solvent models implemented in AMBER ³⁵

All the methods that are implemented in AMBER are based on the pairwise descreening formalism for estimating Born radii that was outlined by Hawkins et al.¹⁶ In the early GB model of Hawkins, Cramer and Truhlar (HCT) (with parameters described by Tsui and Case,²⁰TC, igb=1)¹⁶ the molecular volume in the Coulomb field integral is estimated based on the van der Waals sphere of each solute atom and is parameterized for use with the AMBER force field. However, this approximation to the molecular volume creates regions of interstitial high dielectrics that would be too small to accommodate a solvent molecule. Onufriev, Bashford and Case demonstrated how the use of a packing correction factor, λ:

$$\frac{1}{{\alpha }_i}=\frac{1}{R_i}-\frac{\lambda }{4\pi }{\int }_{solute}\frac{1}{r^4}dV$$ (5)

could reduce the influence of these spurious high dielectric regions in the HCT model. An empirical value of λ=1.4 was shown to provide good agreement between charge-charge interaction energies calculated with PB and GB.¹⁹ The Onufriev, Bashford and Case models (OBC; igb=2; OBC2, igb=5)³⁶, however, use an alternative approach to correct the deficiencies of the GB^HCT model for compounds which have significant interior regions. In these OBC models, the effective Born radii are rescaled by empirical parameters that are proportional to the degree of the atom's burial, as quantified by the volume integral in Eq. 3, such that:

$$\frac{1}{{\alpha }_i}=\frac{1}{R_i-s}-\frac{1}{R_i}\tanh (\delta \Psi -\beta {\Psi }^2+\chi {\Psi }^3)$$ (6)

where s=0.09 Å and ψ represents:

$$\Psi =\frac{R_i-s}{4\pi }{\int }_{solute}\frac{1}{r^4}dV$$ (7)

where R_i is the van der Waals radius of atom i; and δ, β, and χ are dimensionless parameters that were optimized to reproduce PB radii. This well-behaved rescaling function has a “smooth” upper bound on R_i as a function of volume integral to ensure numerical stability. The OBC and OBC2 models differ by the values of {δ,β,χ} used in Eq. 6 (OBC: δ=0.8, β=0 and χ=2.90912; OBC2: δ=1.0, β=0.8 and χ=4.851). In the development of the OBC and OBC2 implicit solvent models, parameters were optimized to ensure agreement between the GB and corresponding PB calculations as well as with experimental hydration free energies. Solvent-accessible surface areas were computed by the Linear Combinations of Pairwise Overlap (LCPO) algorithm.³⁷

Implicit solvent models implemented in CHARMM³⁸

Several Generalized Born Molecular Volume (GBMV)^11,12 models are implemented in CHARMM. The first, GBMV, is a two-parameter grid-based method that uses nearly the same molecular volume that is used in conventional Poisson calculations and includes an empirical correction term, ΔG¹_elec, to the Coulomb field approximation, ΔG⁰elec, based on a measure for the deviation from the ideal spherical shape such that:

$$\Delta G_{elec,i}=\Delta G_{elec,i}^0+\Delta G_{elec,i}^1$$ (8)

where the effective Born radii are estimated from:

$${\alpha }_i=\frac{S}{\left(1-\frac{1}{\sqrt{2}}\right)A_4+A_7}+D$$ (9)

In this formalism, A₄ is related to the Coulomb Field term in Eq. 3 and A₇ to the correction term, such that:

$$A_4=\left(\frac{1}{R_i}-\frac{1}{4\pi }{\int }_{solute}\frac{1}{r^4}dV\right)$$ (10)

and

$$A_7={\left(\frac{1}{4R_i^4}-\frac{1}{4\pi }{\int }_{solute}\frac{1}{r^7}dV\right)}^{1∕4}$$ (11)

The second GBMV model, GBMV2, is a five-parameter analytical method in which the molecular volume is constructed from a superposition of atomic functions. The fundamental advantage of this analytical approach over the grid representation is that forces are readily expressed. In GBMV2

$${\alpha }_i=\frac{S}{C_0{A}_4+C_1{A}_7}+D$$ (12)

Generalized Born with a smooth SWitching function model (GBSW)¹⁰ alleviates the numerical instability of solvent force calculations arising from discontinuities in the dielectric boundary by using a simple polynomial switching function to smooth the dielectric boundary. In the original GBSW formalism, a van der Waals surface representation replaces the more expensive molecular surface representation in GBMV. In GBSW, the two parameters C₀ and C₁ in Eq. 12 (with S=1 and D=0) are obtained for various smoothing lengths, 2w, to reproduce the exact self-solvation free energies from Poisson theory using a van der Waals definition of the dielectric boundary. With the smooth switching function, the Coulomb term is described by:

$$A_4=\left(\frac{1}{R_i}-\frac{1}{4\pi }{\int }_{solute}\frac{V(r;\left\{r_{\alpha }\right\})}{{\mid r-r_i\mid }^4}dV\right)$$ (13)

and the correction term is described by:

$$A_7={\left(\frac{1}{4R_i^4}-\frac{1}{4\pi }{\int }_{solute}\frac{V(r;\left\{r_{\alpha }\right\})}{{\mid r-r_i\mid }^7}dV\right)}^{1∕4}$$ (14)

where V(r,{r_α}) is the solute interior volume and is defined by:

$$V(r;\left\{r_{\alpha }\right\})=1-\prod _{\alpha }\mathrm{H}\left(\mid r-r_{\alpha }\mid \right)$$ (15)

and where the atomic volume exclusion function, H_i(r), is given by:

$$\mathrm{H}\left(r\right)=\left\{\underset{1,}{\overset{0,}{\frac{1}{2}}}+\frac{3}{4w}(r-R_i^{PB})-\frac{1}{4w^3}{(r-R_i^{PB})}^3,\begin{array}{c}\hfill r\le R_i^{PB}-w\hfill \\ \hfill R_i^{PB}-w<r<R_i^{PB}+w\hfill \\ \hfill r\ge R_i^{PB}+w\hfill \end{array}\right\}$$ (16)

where {R^PB} are the set of atomic radii that are used to define the dielectric boundary in the PB calculations. Two additional parameterizations of the GBSW model were investigated. In the GBSW/MS model, the adjustable parameters were optimized to reproduce Poisson self-solvation free energies using the sharp, molecular surface description of the dielectric boundary.³⁹ In this case, for w=0.2 Å, C₀=1.204 and C₁=0.187 in Eq. 12. To reflect the importance of reproducing small Born radii accurately since they contribute most significantly to the electrostatic solvation free energies, GBSW/MS2²⁶ was recently parameterized using the equation:

$$\frac{1}{{\alpha }_i}={C^{\prime }}_0{A}_4+{C^{\prime }}_1{A}_7+D^{\prime }$$ (17)

where optimal values of C’₀=1.437, C’₁=0.1631 and D’=-0.0505 were obtained.

The Fast Analytical Continuum Treatment of Solvation model (FACTS)³⁴ is significantly different from the above GB models in that it does not assume the Coulomb Field approximation and does not require the dielectric boundary between the solvent and solute to be defined. Instead FACTS is based on the analytical evaluation of the volume, A_i, and spatial symmetry, B_i, of the solvent that is displaced from around solute atom i. These two measures are combined in empirically parameterized equations to approximate the self-electrostatic energies:

$$\Delta G_{elec,i}^{FACTS}=a_0+\frac{a_1}{1+e^{-a_2(A_i+b_1{B}_i+b_2{A}_i{B}_i-a_3)}}$$ (18)

where a_o and a₁ are determined by using the limiting cases of a fully buried and fully exposed atom respectively. The other parameters: b₁, b₂, a₂, a₃ and R^sphere (which defines the solute volume considered in calculating A_i and B_i) are optimized for each van der Waals radius. The self-electrostatic energies then provide the effective Born radii via Eq. 2. Similarly, the solvent-accessible surface area is approximated by:

$$SAS{A}_i^{FACTS}={\mathcal{C}}_0+\frac{{\mathcal{C}}_1}{1+e^{-c_2(A_i+d_1{B}_i+d_2{A}_i{B}_i-c_3)}}$$ (19)

and its corresponding parameters are optimized to reproduce exact SASA values. Since the FACTS model only requires the vectors between neighboring atom centers it is significantly faster than the corresponding families of GBMV and GBSW calculations and has been documented to be only four times slower than vacuum calculations.³⁴

III. METHODS

Small molecule database

A large database of 499 small neutral organic compounds has been studied. The original database was made available from Mobley et al.² which in turn was compiled from molecules from Rizzo et al.²⁷, Guthrie⁴⁰ and their earlier studies.^41,42 Five duplicate compounds were identified in the original database of 504 compounds and were removed. This database contains a wide variety of chemical environments that are commonly encountered in drug design applications, including saturated and unsaturated hydrocarbons, aromatic and heterocyclic rings, halides and polar functional groups. Checkmol⁴³ was used to classify the functional groups that are represented in each molecule. Table 2 lists the frequency of each class of functional groups that is represented in this database. The full list of ligands that were assigned to each functional group classification is included in Table S1 of the Supplementary Material.

Table 2.

Functional groups designated by Checkmol⁴³ and their frequency of representation in the database of 499 compounds. (ca=carboxylic acid)

Group	No.	Group	No.
acetal	2	ether_alkyl	25
acid	6	ether_aryl	10
alcohol	38	fluoro	10
aldehyde	19	halogen	22
alkane	27	heterocyclic	48
alkene	35	hypervalents	4
alkyne	6	iodo	11
amine	44	ketone	25
aromatic	169	nitro	17
bromo	21	nitrogen	2
ca_amide	10	orthoester	8
ca_ester	47	other	8
ca_ortho	10	phenol	33
carbonitrile	11	sulfur	4
chloro_alkyl	31	thioether	6
chloro_aryl	20	thiol	5
cyclohydrocarbon	9

Small molecule parameterization

AMBER GAFF²⁹/AM1-BCC^30,31 parameters and partial charges for all compounds in the database were obtained directly from the supplementary materials provided by Mobley et al.² which used the Merck-Frosst implementation of the AM1-BCC charge assignments and augmented van der Waals well-depth parameters for triple bonded carbon atoms. The AMBER prmtop files were converted to the corresponding CHARMM topology and parameter files using the conversion tool AMBER2CHARMM which will be incorporated into the MMTSB toolset⁴⁴ (http://mmtsb.org); prmtop charges were scaled by 332.0522173^-1/2 to account for the difference in the charge conversion factors used in AMBER and CHARMM.³⁵ Validation of the consistency between the vacuum energies that are calculated from both AMBER and CHARMM is provided in Appendix A1. In keeping with the intrinsic radii that are suggested in the Amber manual, Amber6 radii were used for the TC analyses whereas modified Bondi van der Waals radii⁴⁵ (mbondi2) were used for the OBC and OBC2 analyses. Appropriate radii were incorporated into the prmtop files using a variation of the AMBER2CHARMM tool.

Molecular dynamics simulations and analysis

Simulation trajectories were generated for each molecule in both vacuum and the GBMV2 implicit solvent environment. Infinite cutoffs were used; covalent bonds involving hydrogen atoms were restrained using the SHAKE⁴⁶ algorithm and the time step was 1.5 fs. The temperature was maintained near 298 K by coupling all heavy atoms to a Langevin heat bath using a frictional coefficient of 10 ps^-1. Simulation trajectories were 10.5 ns in length. Snapshots were saved every 5 ps throughout the last 10 ns for subsequent free energy analysis. Simulation trajectories were generated and energy evaluations associated with the GBMV, GBSW and GBSW/MS and FACTS implicit solvent models were obtained using the CHARMM molecular dynamics package c36a4.^38,47 Energies associated with the GBSW/MS2 implicit solvent model was obtained using a modification of CHARMM provided by Chen.²⁶ Energies calculated with the TC, OBC and OBC2 implicit solvent models were obtained for each of the snapshots using the MMTSB utility⁴⁴enerAMBER.pl. Simulations were analyzed by the Bennett Acceptance Ratio method (BAR)⁴⁸ using a modified version of pyMBAR.⁴⁹ An analysis of the sensitivity of the results to the specific Hamiltonian used to generate the trajectory is provided in Appendix A2. All simulations and calculations were performed on dual 2.66 GHz Intel Quad Core Xeon CPUs.

Standard parameters in the MMTSB utility enerAMBER.pl were employed but with infinite non-bonded cutoffs for the TC, OBC and OBC2 models. The solvent-accessible surface area for the nonpolar contribution to the hydration free energy was calculated using the LCPO model.³⁷ The GBMV model used a dodecahedron angular integration grid, geometric cross-term in the Still equation and κ=8 in Eq. 1; the multiplicative factor, S, and shift, D, of α_i in Eq. 12 were 0.9026 and -0.007998 respectively. The GBMV2 model used a Lebedev angular integration grid with grid size of 38, geometric cross-term in the Still equation and κ=8 in Eq. 1; the multiplicative factor, S, and shift, D, of α_i in Eq. 12 were 0.9085 and -0.102 respectively. For the GBSW and GBSW/MS calculations, the half smoothing lengths, w, were 0.3 and 0.2 Å respectively. The grid spacing in the lookup table was 1.5 Å and the optimized default values for the coefficients for the Coulomb Field approximation and correction terms were used (i.e. C_o and C₁ in Eq. 12). The GBMV and GBSW intrinsic radii were assigned from the van der Waals radii. Default FACTS parameters were employed with infinite nonbonded cutoffs. FACTS parameters were used that had been optimized for a solute dielectric constant of 1. van der Waals radii which had not be investigated in the original FACTS study had FACTS parameters estimated by interpolation or extrapolation from the optimized FACTS parameters using the “tavw” option in CHARMM. To be consistent with the FACTS parameterization strategy, polar hydrogens were assigned van der Waals radii of 1.0 Å.

The nonpolar surface tension coefficient, γ, was systematically varied between 0.0 and 0.07 kcal/(mol·Å²) for each implicit solvent model. The optimal surface tension coefficient was identified for each implicit solvent model to be the value of γ that minimized the average unsigned error for a test set of compounds. The test set was comprised of every tenth molecule in the full dataset sorted by experimental hydration free energies. In addition, the free energies were evaluated for γ=0.00542 kcal/(mol·Å²) with an offset value of β=0.92 kcal/mol.

IV. RESULTS & DISCUSSION

Overall quality of absolute hydration free energy estimates across implicit solvent models

Using optimized values of the nonpolar surface tension parameters, each of the nine different implicit solvent models performs reasonably well in reproducing experimental hydration free energies for the database of 499 compounds. The measures of model quality are summarized in Table 3. Not including GBSW/MS2, the average unsigned errors (AUE) for the implicit solvent models range from 1.1-1.4 kcal/mol; the root mean square (RMS) error varies between 1.5-2.1 kcal/mol and the correlation coefficients lie between R²=0.66 and 0.81. About half of the compounds in the database (44-59%) have hydration free energies that are correctly predicted within 1 kcal/mol of their experimental values. At least three quarters of the compounds (75-83%) have hydration free energies that are correctly predicted within 2 kcal/mol and about 90% of the compounds (87-97%) have hydration free energies that are correctly predicted within 3 kcal/mol. Among the models explored in this study, the GBMV, GBMV2 and GBSW models demonstrate the best overall agreement with experiment. The measures of model quality are systematically poorer for the GBSW/MS2 models in which the average unsigned and signed errors are 1.9 and -1.0 kcal/mol respectively, the RMS error is 2.5 kcal/mol and the R²=0.684.

Table 3.

Overall measures of model quality (in kcal/mol) for absolute hydration free energy predictions for trajectories analyzed using different implicit solvent models and various values for the nonpolar parameters. Trajectories were generated using CHARMM and the GBMV2 implicit solvent model with no nonpolar contribution. “Opt γ” reflects the values of γ (β=0 kcal/mol) which yielded the lowest AUE in the test set of compounds. TIP3P values were calculated from Supplemental Information in Mobley et al.²

Implicit solvent model:	TC	OBC	OBC2	GBMV	GBMV2	GBSW	GBSW/MS	GBSW/MS2	FACTS	TIP3P
Optγ kcal/(mol·A2)	0.01	0.01	0.0075	0.005	0.005	0.01	0.03	0.04	0.005	--
<|Error|>	1.32	1.40	1.42	1.15	1.14	1.20	1.42	1.86	1.25	1.03
<Error>	-0.24	-0.68	-0.83	-0.60	-0.50	-0.58	-0.56	-0.98	0.23	0.67
RMS Error	1.88	2.08	2.05	1.61	1.60	1.52	1.87	2.50	1.80	1.26
R2	0.751	0.723	0.710	0.809	0.784	0.788	0.714	0.684	0.663	0.888
% |Error|<3 kcal/mol	91	89	87	93	94	97	91	83	91	99
% |Error|<2 kcal/mol	76	77	76	85	84	80	75	62	83	92
% |Error|<1 kcal/mol	55	53	52	59	58	51	44	37	53	51
Comparison with	TIP3P
<|Diff|>	1.33	1.53	1.67	1.40	1.29	1.41	1.54	2.05	1.04
<Diff>	-0.91	-1.35	-1.50	-1.27	-1.17	-1.25	-1.23	-1.65	-0.44
R2	0.822	0.856	0.839	0.908	0.911	0.905	0.834	0.794	0.812

All the implicit solvent models also showed reasonable agreement with the hydration free energies reported for TIP3P explicit solvent simulations for the same compounds by Mobley et al.² Again, not including the GBSW/MS2 model, the average unsigned and signed differences are less than 1.7 and 1.5 kcal/mol respectively. While the models show comparable magnitudes of the signed and unsigned differences, the GBMV, GBMV2 and GBSW models show slightly better correlation with the hydration free energies estimated compared with explicit solvent simulations (R²=0.91) whereas the rest of the models have R² < 0.86. Hydration free energies estimated from the GBSW/MS2 model show less agreement with explicit solvent calculations with unsigned and signed differences of 2.1 and -1.7 kcal/mol respectively and R²=0.79. For this size of dataset, R² differences of ~0.03 are statistically significant at the 95% confidence interval level as evaluated by the Fisher transformation.

These overall results are comparable to what has been reported by Rizzo et al.²⁷ and Mobley et al.²⁸ for implicit solvent simulations for GAFF/AM1-BCC parameterization of these compounds. Hydration free energies computed for some individual compounds are significantly different than those reported in Mobley et al.²⁸; however, these differences are primarily due to the AM1-BCC partial charge assignments. In the implicit solvent study, the Antechamber⁵⁰ pre-processor was used to assign the charges whereas in the later explicit solvent study (from which the parameter files were taken for our analysis) the Merck-Frosst implementation was used. Finally, given the trends for the GB models that were reported in Mobley et al.,²⁸ it is anticipated that the recent GB model, GBn,¹⁸ would have comparable or slightly degraded performance relative to the TC and OBC2 models.

Similarities among solvent models

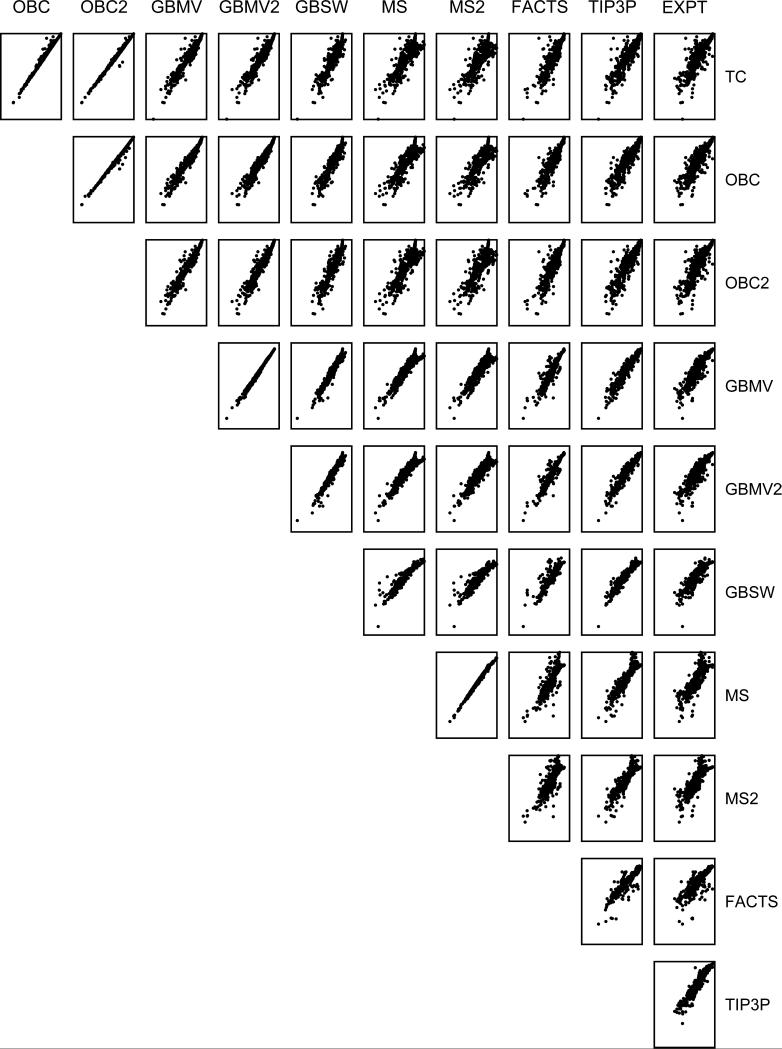
Hydration free energy estimates for individual molecules in the database are highly correlated for different subsets of implicit solvent models. Figure 1 shows the correlations between each pair of implicit solvent models and their correlation with experimental values as well as results from explicit solvent simulations reported by Mobley et al.² The strongest correlations are observed between the OBC and OBC2 models with R²=0.996, the GBSW/MS1 and GBSW/MS2 models with R²=0.995 and between the GBMV and GBMV2 models with R²=0.991. The unsigned difference between the GBMV models averaged over all 499 compounds was 0.25 kcal/mol and the differences were localized primarily in the hydration free energy estimates for the acids and alcohols. The unsigned difference between the OBC and OBC2 models was 0.30 kcal/mol and individual differences were dominated by compounds containing hypervalent sulfur atoms, phosphate groups and alkyl chains. The magnitude of the differences between the GBSW/MS and GBSW/MS2 models were significantly larger with average unsigned and RMS differences of 0.66 and 0.90 kcal/mol respectively; with these models, the differences were dominated by hydration free energy estimates for alcohols, acids, esters, and amines. These correlations are not surprising since the models share basic assumptions in their strategies for efficiently calculating the Born radii. For example, OBC and OBC2 use the same set of intrinsic radii (mbondi2) and use the same functional forms (Eq. 6 and 7) to calculate the Born radii, albeit with slightly different parameters {δ,β,χ}; the GBMV2 model is an analytical representation of the grid-based GBMV model with the same definitions of the dielectric boundary and same set of intrinsic radii (van der Waals radii) as each other. The differences in the individual hydration free energies observed the highly correlated GBSW/MS and GBSW/MS2 models presumably arises from the differences in the functional forms of Eq. 12 and 17 that were used to obtain the numerical parameters in the respective models.

Figure 1.

Correlation between calculated absolute hydration free energies for the 499 compounds in the database for all pairs of implicit solvent models.

Targeting chemical classes for further parameter optimization across all solvent models

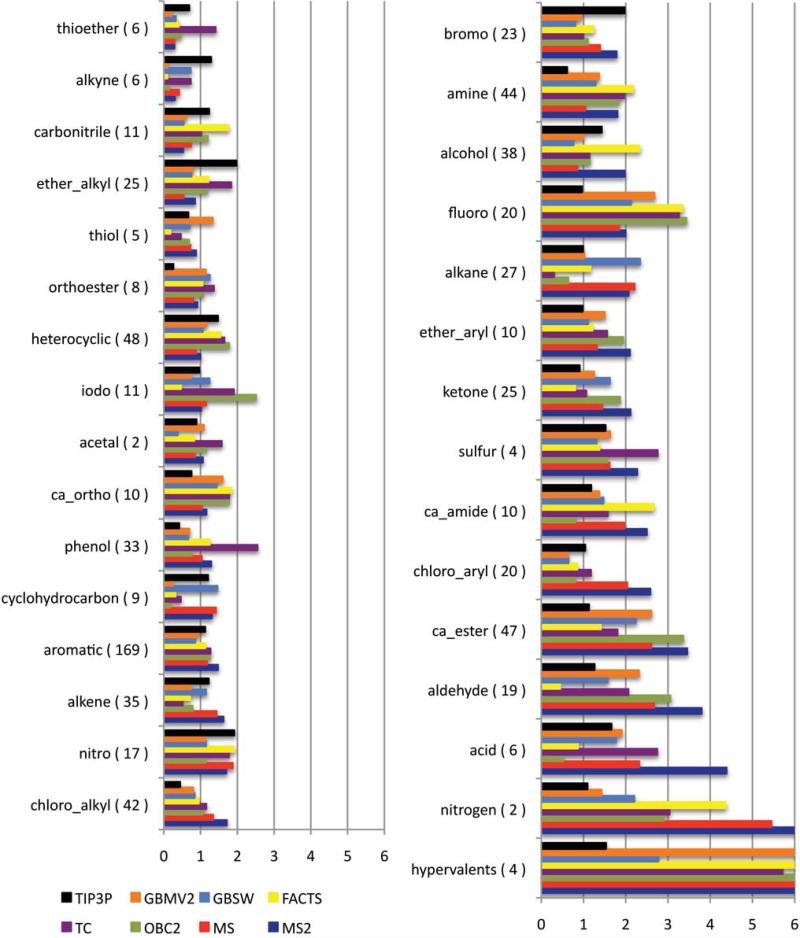
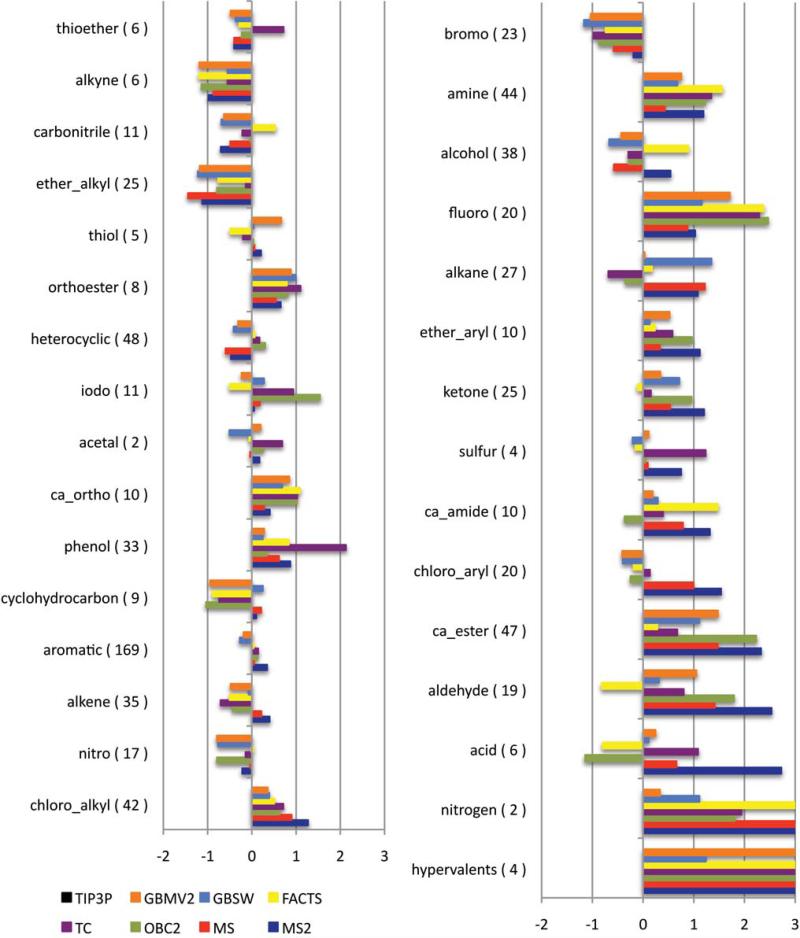
The reliability of hydration free energies calculated for individual compounds is strongly dependent on the functional groups that are represented in the molecule. The quality is related to the ligand parameters, especially the atomic partial charge assignments, as well as the numerical and physical parameters associated with the implicit solvent model. Here, we are primarily interested in identifying those classes of compounds that are not modeled reliably and in trying to decipher the underlying cause of the poor quality estimates. The AUEs for different chemical classes of compounds for the implicit solvent models are depicted in Figures 2 and 3 and the list of compounds that were assigned to each class are included in Supplemental Material Table S1. Given the small differences in hydration free energies estimated using either the GBMV or GBMV2 model and either the OBC or OBC2 model, GBMV and OBC models were omitted from Figures 2 and 3 for clarity.

Figure 2.

Average unsigned errors for subsets of the database classified by functional groups present for select implicit solvent models. Chemical classes are sorted by increasing error in the GBSW/MS2 model. TIP3P values were taken from Mobley et al. Supplementary Information.²

Figure 3.

Differences between hydration free energies estimated from implicit solvent models and explicit solvent simulations. Chemical classes are sorted by increasing differences in the OBC2 model. TIP3P values were taken from Mobley et al. Supplementary Information.

Only the chemical class of compounds that contain hypervalent sulfur atoms has AUEs > 2 kcal/mol, regardless of which implicit solvent model is used. The uniformly poor results in which the AUEs range from 2.8 to 8.4 kcal/mol and average errors range from -9.1 to -2.8 kcal/mol suggest a problem with the ligand force field parameters used to model the hypervalent sulfurs. While Mobley et al.² report improved hydration free energies for the four molecules that are assigned to this chemical group based on explicit solvent simulations (AUE=2.0 kcal/mol)), in another study for a series of drug-like molecules with the AM1-BCC force field modeled in explicit solvent, the average errors for compounds that contained hypervalent sulfurs were reported to be -8.1 kcal/mol.⁵¹ Therefore, it is likely that the errors for the hypervalent sulfur compounds are predominantly due to limitations in force field parameters and, as Mobley et al. suggest, specifically in the GAFF approximation that all sulfur atoms have the same Lennard-Jones parameters.⁵¹ This approximation may be further exacerbated in implicit solvent simulations in which the same intrinsic radii are applied to all sulfur atoms regardless of their chemical environment.

Four additional classes of compounds, the aldehydes, carboxylic acid esters, nitrogens and fluorine-containing compounds, each have AUE > 2 kcal/mol for at least 4 implicit solvent models. In each case, the explicit solvent simulations are reported to have AUEs just over 1 kcal/mol. Therefore, these functional groups appear to be good candidates for re-parameterization of the “physical parameters” associated with how they are treated within the implicit solvent models. One of the primary physical parameters is the set of intrinsic radii that are used to define the dielectric boundary for computing the Born radii, the degree of burial, of each atom. The hydration free energies for these compounds are systematically overestimated relative to experiment suggesting that the current intrinsic radii are too small and, thus, have charges that are closer to the surface. These atoms are essentially more exposed than they should be and consequently have excessively large contributions of the electrostatic component to the free energy.

For four classes of compounds the hydration free energies estimated from implicit solvent simulations are of better quality than the corresponding reported explicit solvent simulations. In two cases, the discrepancy is associated with a change in parameters in the implicit solvent simulations. Improved results from implicit solvent simulations for the alkynes and, to a lesser extent, the carbonitriles arises from the use of the improved van der Waals parameters suggested by Mobley et al. for triple-bonded carbon atoms where the well-depth parameter, ε, was augmented from 0.086 to 0.21 kcal/mol. In fact, for TIP3P simulations with the augmented well-depth parameters, the AUEs improved from 1.9 to 0.5 kcal/mol for the alkynes² and so are in good agreement with the current implicit solvent calculations. The reported explicit solvent simulation results used the original well-depth parameters. For the thioethers and bromide-containing compounds, the discrepancy between results from implicit and explicit solvent simulations suggests that there may be a fortuitous cancellation of error with the implicit solvent calculations for these groups, or alternatively a mismatch between the interaction energy terms between the TIP3P water model and the small molecules. Therefore, these latter two functional groups need further investigation, which is beyond the scope of this paper.

Targeting chemical classes for further optimization in specific implicit solvent models

Within a given class of compounds, most of the implicit solvent models exhibit a level of quality that is comparable to at least one other solvent model. For example, for all classes of compounds except the nitrogen and thiol compounds, the quality of the hydration free energies that are estimated using the GBMV2 formalism is within 0.2 kcal/mol of that estimated from at least one other implicit solvent model. By contrast, hydration free energies estimated using TC, FACTS and GBSW/MS2 models show more variability than the other solvent models. TC models have higher quality results for the alkanes (with an AUE that is 0.3 kcal/mol lower than the next best implicit solvent model result), but significantly poorer results for the sulfurs, phenols, ether alkyls, acetals and thioethers (with AUEs that are 0.4-1.3 kcal/mol higher than the next poorer implicit solvent model result). One of the limitations of the TC model compared with the OBC and OBC2 models is the presence of spurious high dielectric regions within a molecule associated with interstitial spaces between atom spheres. These spaces, which would be physically inaccessible to solvent, lead to inappropriately small Born radii and, thus, to systematically larger electrostatic contributions to the hydration free energy. While, in general, this would be a less serious issue for small molecules with proportionally less burial than for large macromolecular systems, it may be contributing to the poorer quality observed across these classes of compounds.

The FACTS model also shows more extreme behavior among the implicit solvent models in that, for several classes of compounds, FACTS has substantially better or poorer quality than any other model. Specifically, the aldehydes, carboxylic acid esters, ketones, thiols and iodine-containing compounds are all modeled with FACTS with AUEs that are 0.3-1.1 kcal/mol lower than the next best implicit solvent model whereas the AUE associated with the FACTS model for the carbonitriles are 0.6 kcal/mol poorer than any other implicit solvent model. FACTS is one of the most recently developed implicit solvent models in CHARMM and has only been parameterized for protein atoms in the param19 and param22 topology files. Currently, the optimized parameters for intrinsic radii for which parameters do not exist are extrapolated from those that do exist. Therefore, specifically parameterizations based on Eq. 18 and 19 for this database of small molecules or a subset of these compounds, which would reflect greater chemical diversity than is observed in the param22 topology files, would likely further increase the quality of the hydration free energy estimates. Given that FACTS is also one of the fastest methods currently available for estimating solvation free energies, we believe this would be a very promising avenue to pursue.

Finally, the GBSW/MS2 model exhibits significantly poorer results than the other implicit solvent models for the hypervalent sulfurs, acids, aldehydes, nitrogens, chloroalkyls and chloroaryls as well as the bromine-containing compounds with AUEs 0.4-4.3 kcal/mol higher than the next poorer implicit solvent model. The recent parameterization of the GBSW/MS2 model was specifically targeting small Born radii, that is atoms that are on the surface of the molecule, since they will contribute more substantially to the electrostatic energy than their buried counterparts. Since there is relatively little “burial” of atoms to consider in this database of small molecules, this study is likely not effectively probing the strength of this implicit solvent model. Furthermore, efforts for optimizing the physical parameters for the GBMSW/MS2 models were focused on reproducing the strengths of pairwise and three-body interactions among polar and nonpolar side-chain analogues and compounds in explicit solvent simulations and did not include the chemical diversity that is observed in this database of compounds. Therefore, more specific parameterization targeting this database or a subset of this database would likely extend the transferability of this implicit solvent model to a larger chemical palette and likely improve the quality across more chemical classes.

Effect of nonpolar contributions to quality of overall hydration free energies

As has been demonstrated in other work, inclusion of a nonpolar contribution is crucial for obtaining accurate estimates of absolute hydration free energies using implicit solvent models.^22,52 With no nonpolar contribution to the total hydration free energy, all models in this study have average signed errors (ΔG^calc–ΔG^expt) between -3.7 and -1.1 kcal/mol; this systematic error represents a tendency for molecules to be overstabilized in the implicit solvent environment relative to experiment. Furthermore, a comparison of the electrostatic contributions to the total hydration free energies modeled with implicit solvent models in this study and explicit water simulations reported by Mobley et al.² reveals the tendencies for molecules to be overstabilized in each implicit solvent model except FACTS relative to the TIP3P results. The comparison is summarized in Table 4 and indicates that the GB component of the GBMV, GBMV2, GBSW, GBSW/MS and FACTS models have the best agreement with the TIP3P electrostatic contributions with average and unsigned average differences of 0.5-1.1 kcal/mol and R² values greater than 0.825.

Table 4.

Overall comparison between the electrostatic contribution of the implicit solvent models and the electrostatic contributions from the TIP3P simulations reported in the Supplemental Information in Mobley et al.² <Diff> = < ΔG_elec(implicit solvent model) – ΔG_elec(TIP3P) >

Implicit solvent model:	TC	OBC	OBC2	GBMV	GBMV2	GBSW	GBSW/MS	GBSW/MS2	FACTS
<|Diff|>	1.66	2.16	1.75	1.09	0.98	0.53	1.44	2.51	0.71
<Diff>	-1.52	-1.97	-1.45	-0.99	-0.89	-0.05	-1.49	-2.50	0.14
RMS Diff	2.25	2.84	2.35	1.47	1.32	0.79	1.86	3.18	1.16
R2	0.837	0.806	0.790	0.925	0.928	0.925	0.915	0.898	0.825
% |Diff|<3 kcal/mol	85	77	83	94	98	100	91	67	95
% |Diff|<2 kcal/mol	71	58	69	83	88	97	776	50	93
% |Diff|<1 kcal/mol	40	27	38	59	62	85	42	22	79

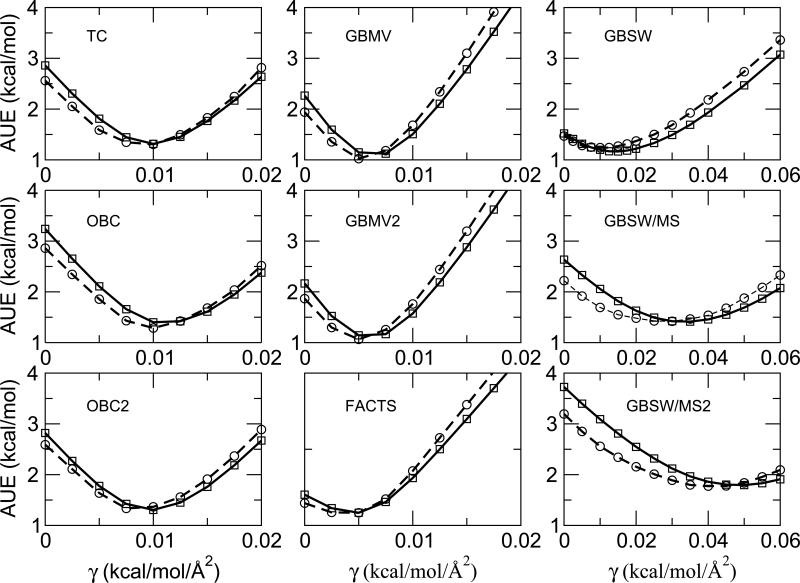
In this work, we have used a simplified model, a solvent-accessible surface area (SASA) term scaled by a surface tension parameter, γ, to estimate the nonpolar contribution to the hydration free energy. A linear scan of the surface tension parameter for each implicit solvent model identified the “optimal” value for γ, that is, the value that minimized the AUE for a test set of compounds. Figure 4 illustrates the overall quality of the hydration free energy estimates as a function of nonpolar surface tension coefficient and demonstrates that similar optimal values are obtained when using either the test set of compounds (Fig 2; dashed line, circles) or the full dataset (Fig 2; solid line, squares).

Figure 4.

Sensitivity of estimated hydration free energies on the surface tension coefficient for each of the implicit solvent models for the test set (dashed line; circles) and full database (solid line; squares). The test set was comprised of every 10^th compound in the database sorted by experimental hydration free energy.

In all models, accounting for a nonpolar contribution with this simplified model significantly improves the average signed errors with respect to experimental hydration free energies, minimizes the differences with respect to explicit solvent simulations and increases the percentage of compounds that are correctly predicted. For all models, except for FACTS, the average errors decreased to between -1.0 to -0.2 kcal/mol, but still demonstrate the systematic overstabilization of compounds in solvent relative to experiment. Table 5 summarizes the results for only the electrostatic contribution and for two other common sets of nonpolar parameters: γ=0.00542 kcal/(mol·Å²) with β=0.92 kcal/mol; and γ=0.005 kcal/(mol·Å²) with β=0 kcal/mol.

Table 5.

Overall measures of model quality (in kcal/mol) for absolute hydration free energy predictions for trajectories analyzed using different implicit solvent models and common values for the nonpolar parameters.

Implicit solvent model:	TC	OBC	OBC2	GBMV	GBMV2	GBSW	GBSW/MS	GBSW/MS2	FACTS	TIP3P
γ=0.005 kcal/(molA2); β=0.92 kcal/mol
<|Error|>	1.33	1.45	1.31	1.19	1.26	1.06	1.58	2.54	1.68	1.03
<Error>	-0.48	-0.91	-0.44	0.45	0.55	0.03	-1.33	-2.43	1.26	0.67
RMS Error	1.93	2.18	1.93	1.56	1.62	1.38	2.09	3.23	2.18	1.26
R2	0.750	0.719	0.708	0.809	0.784	0.796	0.786	0.777	0.663	0.888
% |Error|<3 kcal/mol	90	88	90	94	93	96	89	67	85	99
% |Error|<2 kcal/mol	75	74	76	83	82	88	73	49	65	92
% |Error|<1 kcal/mol	53	54	54	52	48	57	39	22	38	51
Comparison with TIP3P
<|Diff|>	1.44	1.71	1.36	0.78	0.71	0.99	2.09	3.10	1.14
<Diff>	-1.15	-1.59	-1.11	-0.22	-0.12	-0.64	-2.00	-3.10	0.58
R2	0.832	0.863	0.842	0.906	0.910	0.912	0.909	0.892	0.809
γ=0.005 kcal/(molA2); β=0 kcal/mol
<|Error|>	1.81	2.11	1.77	1.15	1.14	1.32	2.33	3.40	1.25	1.03
<Error>	-1.50	-1.94	-1.47	-0.60	-0.50	-0.92	-2.28	-3.38	0.23	0.67
RMS Error	2.40	2.78	2.38	1.61	1.60	1.66	2.79	4.00	1.80	1.26
R2	0.750	0.718	0.708	0.809	0.784	0.797	0.786	0.777	0.663	0.888
% |Error|<3 kcal/mol	81	76	81	93	94	95	75	51	91	99
% |Error|<2 kcal/mol	67	63	69	85	84	77	45	25	83	92
% |Error|<1 kcal/mol	33	27	38	59	58	45	15	8	53	51
Comparison with TIP3P
<|Diff|>	2.27	2.66	2.24	1.40	1.29	1.68	2.95	4.05	1.04
<Diff>	-2.17	-2.61	-2.14	-1.27	-1.17	-1.59	-2.95	-4.05	-0.44
R2	0.833	0.863	0.843	0.908	0.911	0.913	0.910	0.892	0.812
γ=0 kcal/(molA2); β=0 kcal/mol
<|Error|>	2.86	3.24	2.82	2.26	2.17	1.52	2.64	3.73	1.60	1.03
<Error>	-2.77	-3.21	-2.73	-2.21	-2.10	-1.27	-2.62	-3.72	-1.08	0.67
RMS Error	3.37	3.80	3.34	2.67	2.61	1.87	3.08	4.31	2.12	1.26
R2	0.740	0.706	0.697	0.807	0.778	0.800	0.790	0.781	0.650	0.888
% |Error|<3 kcal/mol	63	58	67	76	79	93	67	44	92	99
% |Error|<2 kcal/mol	34	23	34	46	51	73	36	18	69	92
% |Error|<1 kcal/mol	10	6	10	16	22	36	12	5	38	51
Comparison with TIP3P
<|Diff|>	3.48	3.90	3.46	2.89	2.78	1.99	3.29	4.39	1.88
<Diff>	-3.44	-3.88	-3.40	-2.88	-2.78	-1.94	-3.29	-4.39	-1.75
R2	0.835	0.862	0.843	0.923	0.922	0.914	0.912	0.895	0.825

The “optimal” value of γ for each model differed between the models. GBMV, GBMV2 and FACTS models had relatively small optimal γ values of 0.005 kcal/(mol·Å²); TC, OBC, OBC2 and GBSW models had slightly larger values between 0.0075 and 0.01 kcal/(mol·Å²) while GBSW/MS and GBSW/MS2 had relatively large γ values of 0.03 and 0.04 kcal/(mol·Å²) respectively. The optimal value depends on two factors: the magnitude of the SASA term calculated for the given implicit solvent model as well as the magnitude of the AUE calculated from the electrostatic contribution alone. The first factor has a physical meaning while the second can be viewed as a “fudge factor” that compensates for inadequacies in the electrostatic contribution of the solvent models themselves. The average SASA term across all molecules in the database was smallest for the GBSW, GBSW/MS and GBSW/MS2 models (<SASA> ≈ 68 Ų), systematically larger for the AMBER-based models (<SASA> ≈ 253 Ų) and FACTS (<SASA> ≈ 262 Ų) and largest for the GBMV, GBMV2 models (<SASA> ≈ 321 Ų). From these trends, it is apparent that the relatively small values of γ for GBMV, GBMV2, TC, OBC and OBC2 are due to their comparably large SASA calculations. By contrast, the small values of γ for the GBSW and FACTS models are due to their relatively small AUEs for the electrostatic contribution alone. The larger values for γ for the GBSW/MS and GBSW/MS2 models are related to both the smaller SASA terms combined with larger errors when only the electrostatic contribution is considered.

Limitations of this simplified model based linear scaling of the SASA have been demonstrated previously. Mobley et al.'s study found that while the repulsive and attractive components of the nonpolar contribution obtained from TIP3P simulations were correlated with solute surface area or volume the total nonpolar contribution which is a small difference between the two large components showed no correlation with the solute surface area or volume.² Further improvements in the agreement between the calculated and experimental hydration free energies for small molecules could likely be achieved by adopting atom-specific surface tension parameters as proposed by Eisenberg and McLachlan²⁵ and Scheraga and coworkers²³ such that:

$$\Delta G_{np}=\sum _{i=1}^N{\gamma }_{i}SAS{A}_i$$ (20)

where the atomic solvent-accessible surface areas, SASA_i, are scaled by atom-specific surface tension parameters, γ_i. In their study, Rizzo et al.²⁷ demonstrate that PB/SA and GB/SA calculations with atomtype-specific optimized surface tension parameters generally showed improved agreement with experimental hydration free energies over implicit solvent calculations with the optimal linear alkane parameters of γ=0.00542 kcal/(mol·Å²) and β=0.92 kcal/mol. Interestingly, the attractive and repulsive components individually correlate strongly with surface area. However, it is also likely that fundamentally more sophisticated nonpolar models will be required to effectively represent the underlying physics of solvation and significantly improve the quality of hydration free energies estimates.^6,22,53 Levy and coworkers have shown promising results by further decomposing the nonpolar contribution to the total free energy into a component accounting for the cost of cavity formation within the solvent and a component reflecting the solute-solvent van der Waals dispersion interactions.^13,24 This strategy likely contributes to the low reported average unsigned errors of 0.6 kcal/mol reported by Gallicchio et al.^13,24 and Jorgensen et al.¹⁷ for hydration free energies for series of neutral molecules modeled with the OPLS-AA force field. Levy and coworkers have also recently implemented an additional component to the total energy that models first-solvation shell effects around a solute that would account, for example, for solute-solvent hydrogen bonding that is not accurately modeled within a continuum approximation.¹⁴ Fennel et al. have proposed an alternative strategy in which explicit solvent simulations are used to precompute the properties of water molecules around a series of nonpolar solute spheres that exhibit diverse radii and attractive dispersion interactions and information from the precalculated table are assembled to approximate the hydration of an arbitrary solute molecule.⁵⁴ This Semi-Explicit Assembly model seems to provide a better description of attractive interactions and alleviates problems of nonadditivity that is inherent in traditional SASA-based approaches. Finally, due to the challenge of representing charge distributions in small molecules in media with significantly different dielectric properties—for example, free in aqueous solution and buried within a hydrophobic binding pocket—polarizable or fluctuating charge models⁵⁵ may also be required to significantly advance the quality of hydration free energy estimates across diverse chemical space.

V. CONCLUSION

We have presented a comparison of absolute hydration free energies that have been calculated for an extensive database of small neutral molecules using a variety of implicit solvent models. Given GAFF parameters and AM1-BCC partial charge assignments for the solutes and using a simplified SASA model for the nonpolar contribution in the implicit solvent models, most of the common AMBER and CHARMM-implemented implicit solvent models agree reasonably well with extensive explicit solvent simulations (average difference 1.0-1.7 kcal/mol and R²=0.812-0.911) and with experimental hydration free energies (AUE=1.1-1.4 kcal/mol and R²=0.663-0.809). Uniformly poor performance of compounds containing hypervalent sulfurs suggests a need for further optimization of the corresponding sulfur parameters in the GAFF force field. Other chemical classes, specifically, aldehydes, carboxylic acid esters, thioethers, fluorine and bromine-containing compounds, showed poor quality across many of the implicit solvent models, yet had favorable hydration free energy estimates using explicit solvent simulations. Thus, these latter functional groups are proposed as targets for more refined optimization of their associated physical parameters in the implicit solvent models, most likely the intrinsic radii that are used to calculate the effective Born radii. Inclusion of the nonpolar estimator significantly improves the quality of the results, but more sophisticated nonpolar models will also be necessary to effectively represent the underlying physics of solvation and take the quality of hydration free energies estimated from implicit solvent models up to the next level. Given their computational efficiency, implicit solvent models offer a significant practical advantage over explicit solvent models in simulating macromolecular systems. Therefore, further studies that focus on protein-ligand binding affinities will be critical to evaluating the quality of the implicit solvent models in the context of all-atom macromolecular force fields and to ensuring an appropriate balance between the effective desolvation cost for a small molecule and the cost associated with desolvating the binding pocket of the macromolecule that the small molecule targets in vitro.

APPENDIX

A1: Validation of conversion from AMBER to CHARMM formats

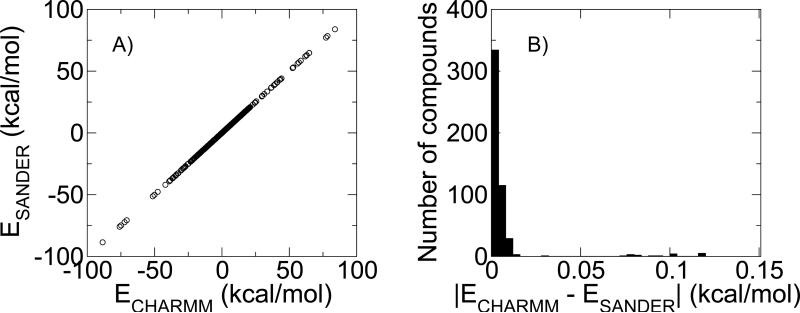
Using snapshots of conformations of each compound in the database we demonstrate the excellent agreement between the total energies calculated in vacuum in SANDER using the MMTSB utilities and those calculated in CHARMM. Figure 5 shows the correlation between the total energies computed in SANDER and CHARMM as well as the distribution of energy differences. The largest energy differences are less than 0.12 kcal/mol and arise from compounds containing CN triple bonds, where the energy difference is localized to the bond angle component involving the triple bond. This energy contribution will be present in each snapshot of the vacuum and solvent calculations and so will cancel out when the energies are subtracted from one another in the BAR analysis; therefore, we have not adjusted the implementation of either program.

Figure 5.

Comparison between SANDER-calculated energies using the MMTSB utility enerAMBER.pl and energies calculated using CHARMM for the 499 small molecules in vacuum. (a) Correlation between SANDER and CHARMM energies (R²=1.00). (b) Distribution of total differences between CHARMM- and SANDER-calculated energies.

A2: Sensitivity of results to trajectory Hamiltonian

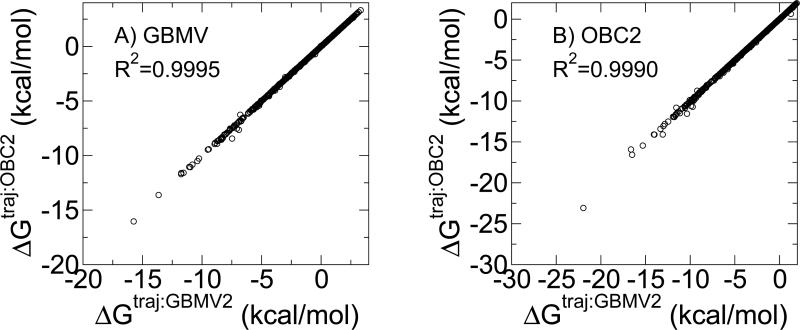
To assess the sensitivity of the hydration free energy estimates for the different implicit solvent models to the GBMV-based Hamiltonian that was used to generate the trajectories, we generated new trajectories using the OBC2 implicit solvent model and re-evaluated the corresponding OBC2 and GBMV2 hydration free energies. In this case, mbondi intrinsic radii were used in conjunction with the OBC2 model. Figure 6 demonstrates the excellent agreement between the calculated hydration free energies regardless of what Hamiltonian was used to generate the trajectory. CHARMM/GBMV2-generated and SANDER/OBC2-generated trajectories give absolute hydration free energies within 0.1 kcal/mol of one another for all but 23 compounds when evaluated with GBMV2. The average unsigned difference is 0.02 kcal/mol and R²=0.9995. Similarly, CHARMM/GBMV2-generated and SANDER/OBC2-generated trajectories give absolute hydration free energies within 0.1 kcal/mol of one another for all but 41 compounds when evaluated with OBC2. The average unsigned difference is 0.04 kcal/mol and R²=0.9990. In both cases, the largest deviations were for propanoic acid with a difference of 0.97 and 1.2 kcal/mol for the GBMV2 and OBC2 hydration free energy estimates respectively. The most common functional groups exhibiting sensitivity to the Hamiltonian used to generate the trajectory were alcohols and acids. Given this substantial agreement between the results based on trajectories generated from different implicit solvent models, we used the GBMV2-generated trajectories for all subsequent analyses.

Figure 6.

Correlation between absolute hydration free energies evaluated by (a) GBMV2 or (b) OBC2 from trajectories generated from CHARMM/GBMV2 and SANDER/OBC2 implicit solvent models.