Powerful tests for detecting a gene effect in the presence of possible gene-gene interactions using garrote kernel machines

Summary

We propose in this paper a powerful testing procedure for detecting a gene effect on a continuous outcome in the presence of possible gene-gene interactions (epistasis) in a gene set, e.g. a genetic pathway or network. Traditional tests for this purpose require a large number of degrees of freedom by testing the main effect and all the corresponding interactions under a parametric assumption, and hence suffer from low power. In this paper, we propose a powerful kernel machine based test. Specifically, our test is based on a garrote kernel method and is constructed as a score test. Here, the term garrote refers to an extra nonnegative parameter which is multiplied to the covariate of interest so that our score test can be formulated in terms of this nonnegative parameter. A key feature of the proposed test is that it is flexible and developed for both parametric and nonparametric models within a unified framework, and is more powerful than the standard test by accounting for the correlation among genes and hence often uses a much smaller degrees of freedom. We investigate the theoretical properties of the proposed test. We evaluate its finite sample performance using simulation studies, and apply the method to the Michigan prostate cancer gene expression data.

1. Introduction

In this paper, we consider the problem of testing for the effect of a gene on a continuous response in the presence of possible gene-gene interactions in a gene set, such as a genetic pathway. There is growing evidence that gene-gene interaction or epistasis ubiquitously contributes to complex traits, partly because of the sophisticated regulatory mechanisms encoded in the human genome. Epistasis is a phenomenon whereby the effects of a given gene on a biological trait are masked or enhanced by one or more genes (Bateson, 1909). It plays an important role in the mechanisms of complex diseases (Moore, 2005). Research has shown that it is important to account for gene-gene interactions in the search for susceptibility genes for complex diseases, and ignoring epistasis could explain difficulties in replicating significant findings (De Miglio et al., 2004; Aston et al., 2005). Developing powerful statistical methods for studying the effect of a gene by accounting for possible gene-gene interactions in a gene set is of significant interest in genetic association studies.

The data example that motivated the current research is the Michigan prostate cancer study data (Dhanasekaran et al., 2001). Recently there have been significant breakthroughs in the effort of finding candidate genes related to prostate cancer. Prostate Specific Antigen (PSA) is commonly used as a biomarker for prostate cancer screening. The early results of Dhanasekaran et al. (2001) indicate that certain functional genetic pathways seemed dysregulated in prostate cancer relative to non-cancerous tissues. There is a considerable literature to study the genetic pathway effects on PSA after adjusting for effects of clinical and demographic covariates (Dhanasekaran et al., 2001), and statistical methods have been developed to test for pathway effects (Liu, Lin and Ghosh, 2007; Liu, Ghosh and Lin, 2008). However, little work has been done on identifying the genes associated with PSA accounting for gene-gene interactions in a pathway.

Our goal in this paper is to develop a testing procedure for the effects of individual genes on a continuous outcome while accounting for possible epistasis and other clinical covariates in a regression model. An usual and popular approach to test for individual gene effects in such a context is to fit a simple linear model with main and interaction terms, e.g., two-way interactions, and conduct an ANOVA based multi-degrees-of-freedom F-test (see for example, Howard et al, 2002; Li et al, 1997, among others). However, this approach has two main disadvantages. First, testing for the effect of a particular gene in the presence of possible gene-gene interactions requires testing for the corresponding interaction effects of the gene under consideration with other genes, resulting in a test using high degrees of freedom and a considerable loss of power, as we will see later. This phenomenon is more pronounced when genes are correlated among each other. In fact, for small sample sizes, such a test for all interaction terms may not be even computationally possible. Second, this also requires a strong parametric assumption, resulting in a power loss if the parametric model is misspecified. In fact, the true form of gene-gene interactions is typically unknown. Modeling the interaction terms using a standard two-way cross-product model may be overly simplistic and the resulting model could be misspecified.

In this paper, we address both issues by considering a general regression problem, where we model the joint effect of genes in a gene set, e.g., pathway or network, using a flexible parametric/nonparametric function. We then propose to test whether the function depends on an individual gene of interest. Specifically, we propose to use the powerful kernel machine framework to develop the test. The kernel machine framework, originally developed in the field of machine learning as a powerful learning technique for multi-dimensional data (Vapnik, 1998; Schølkopf and Smola, 2002), has become popular in genetic studies for dealing with a large number of genes. Popular examples of kernel machine methods include Support Vector Machine (SVM) (Vapnik, 1998), Relevance Vector Machine (RVM) (Tipping, 2000), a probabilistic model whose functional form is equivalent to SVM and Bayesian Gaussian process (Rasmussen and Williams, 2006). Kernel machine methods start with a kernel function which implicitly determines the smoothness property of the unknown function and hence greatly simplify specification of parametric and nonparametric models, especially for multi-dimensional covariates. Liu, Lin and Ghosh (2007) and Liu, Ghosh and Lin (2008) developed kernel machine regression theory for least squares and logistic regression and demonstrated their connections with mixed models, and developed a testing procedure for the whole pathway effect. In contrast, we address in this paper the problem of testing for the effect of an individual gene of interest on a continuous outcome accounting for plausible gene-gene interactions, instead of testing the effect of the entire pathway/network.

To test for the gene effect in the presence of possible gene-gene interactions in a gene set, we introduce the concept of ‘garrote kernel’ where we attach an extra garrote parameter (Breiman, 1995) to the gene of interest in the kernel function and reparametrize our testing problem in terms of the new garrote parameter. The key advantage of this approach is that it allows us to reduce the dimensionality of the testing problem to a scalar parameter. We develop a score based testing procedure for the garrote parameter based on the mixed model framework and investigate theoretical properties. Such a score test effectively reduces the degrees of freedom by accounting for the correlation among genes, resulting in a more powerful test compared to the traditional F-test for all the interaction terms. It also allows for complex interactions.

The rest of the paper is organized as follows. Section 2 describes the joint semiparametric kernel machine regression framework for a gene set. Section 3 proposes the garrote kernel machine (GKM) score test for individual gene effects in the presence of possible gene-gene interactions and studies its theoretical properties. Section 4 discusses a multiple testing procedure in the GKM framework. Section 5 evaluates the performance of our test using simulation studies. Section 6 applies the proposed test to the Michigan prostate cancer gene expression data, followed by discussions in Section 7.

2. Semiparametric Model of Gene Effects in a Gene Set

Suppose we observe data from n subjects. For each subject i = 1,…, n, let Z_i = (Z_i1,…, Z_iM)^T be covariates associated with M genes within a gene set, e.g., a genetic pathway/network, Y_i be a continuous response and X_i be a set of clinical covariates. It is important to note that X and Z can contain both continuous and binary variables. We assume the following model to relate the response to the clinical covariates and the genetic covariates:

$$Y_i={\mathit{X}}_i^{\text{T}}\mathit{\beta }+h(Z_{i1},\dots ,Z_{iM})+{\epsilon }_i,$$ (1)

where β is a set of unknown regression coefficients for the clinical covariate effects, h(·) is an unknown function for the gene effects in a gene set, and ε_i’s are independent random errors having Normal(0, σ²) distribution.

Typically, one assumes a parametric form for h(·) to model the gene effects in a gene set. For example, $h({\mathit{Z}}_i)={\mathit{Z}}_i^{\text{T}}\mathit{\eta }$ corresponds to a model with only main genetic effects, whereas $h({\mathit{Z}}_i)={\sum }_{k=1}^M{Z}_{ik}{\eta }_k+{\sum }_{j<k}{Z}_{ij}{Z}_{ik}{\gamma }_{jk}$ allows for the first order gene-gene interactions. However, these classical specifications make strong parametric assumptions and are often subject to considerable power loss for testing for individual gene effects in the presence of gene-gene interactions as we will show later.

In this paper, we allow h(·) to be specified parametrically and nonparametrically in a unified kernel machine framework, which is more convenient and powerful to work with for multi-dimensional data. Specifically, rather than specifying the function h(·) using the basis functions as above, we specify h(·) using a positive definite kernel function K(·, ·). Mercer’s theorem (Cristianini and Shawe-Taylor, 2000) guarantees that under some regularity conditions, the kernel function K(·, ·) implicitly specifies a unique function space, say , spanned by a particular set of orthogonal basis functions φ_j(z), j = 1 …, J. Here orthogonality is defined with respect to the L₂ norm. Hence, the function space has the property that any function h(·) ∈ can be represented in two ways: using a set of basis functions as $h(\mathit{z})={\sum }_{j=1}^J{\phi }_j(\mathit{z}){\eta }_j$ known as the primal or basis representation; or equivalently using the kernel function as $h(\mathit{z})={\sum }_{k=1}^{L}K({\mathit{z}}_k^{\ast },\mathit{z};\rho ){\alpha }_k$ for some integer L, some constants α₁,…, α_L and some { ${\mathit{z}}_1^{\ast },\dots ,{\mathit{z}}_L^{\ast }$}. The later representation is called the dual representation.

Two most commonly used kernels are the d^th polynomial kernel and the Gaussian kernel. The d^th polynomial kernel $K({\mathit{z}}_1,{\mathit{z}}_2)={(\rho +{\mathit{z}}_1^{\text{T}}{\mathit{z}}_2)}^d$ corresponds to the models with dth-order polynomials including the cross product terms. For example, the first order polynomial kernel (d = 1) corresponds to the model with only main effects $h({\mathit{Z}}_i)={\mathit{Z}}_i^T\mathit{\eta }$, and the second order polynomial kernel (d = 2) corresponds to the model with linear and quadratic main effects and two-way interactions $h({\mathit{Z}}_i)={\sum }_{k=1}^M{Z}_{ik}{\eta }_{1k}+{\sum }_{j<k}{Z}_{ij}{Z}_{ik}{\gamma }_{jk}+{\sum }_{k=1}^M{Z}_{ik}^2{\eta }_{2k}$. The Gaussian kernel is $K({\mathit{z}}_1,{\mathit{z}}_2)=exp\{-{\sum }_{j=1}^M{(z_{1j}-z_{2j})}^2/\rho \}$, where ρ is a tuning parameter. The Gaussian kernel generates the function space spanned by the radial basis functions (Buhmann, 2003) and includes many nonlinear functions. Both dth polynomial kernel (d > 1) and Gaussian kernels allow for gene-gene interactions.

A few additional kernels are useful for modeling gene-gene interactions. For example, we can define the product linear kernel $K({\mathit{z}}_1,{\mathit{z}}_2)={\prod }_{k=1}^M(1+z_{1k}{z}_{2k})$, which corresponds to the model h(z) = β₀ + Σ_k β_1kz_k + Σ_j<k β_2jkz_jz_k + … + β_M z₁ … z_M, which includes all the multiplicative interactions up to the order M. If one wishes to include only two-way interactions in the model along with the main effects, i.e., the primal representation is h(z) = β₀ + Σ_k β_1kz_k + Σ_j<k β_2jkz_jz_k, then the corresponding kernel can be specified as $K({\mathit{z}}_1,{\mathit{z}}_2)=1+{\sum }_{k=1}^M{z}_{1k}{z}_{2k}+{\sum }_{j<k}{z}_{1j}{z}_{2j}{z}_{1k}{z}_{2k}$. We call this kernel the two-way interaction kernel. Examples of other choices of kernel functions include the sigmoid and neural network kernels, and the B-spline kernel (Scholkopf and Smola, 2002).

In theory, given any basis functions φ(z) = {φ₁(z),…, φ_J (z)} in the primal representation, one can construct the corresponding kernel $K({\mathit{z}}_1,{\mathit{z}}_2)={\sum }_{j=1}^J{\phi }_j({\mathit{z}}_1){\phi }_j({\mathit{z}}_2)$ to facilitate the dual representation, and vice versa. For high-dimensional data, it is more convenient to work with the dual representation for h(·) using the kernel function K(·, ·), as will be done in this paper. The estimation and testing procedure will be described below.

3. Testing for a Gene Effect in the Presence of Gene-gene Interactions

In this section, we develop under model (1) a score based test for an individual gene effect accounting for gene-gene interactions in a gene set. Without loss of generality, consider testing for the effect of Z₁. Then our hypothesis is

$$H_0:h(z_1,z_2,\dots ,z_M)=h(z_2,\dots ,z_M),$$

that is, the function h(·) does not depend on z₁. Note that the above formulation is quite general and covers a broad range of models, including the common parametric models for gene-gene interactions. For example, under the main effects only model $h({\mathit{Z}}_i)={\sum }_{j=1}^M{Z}_{ij}{\eta }_j$, H₀ corresponds to the problem of testing for η₁ = 0. Under the classical two-way interaction model

$$h({\mathit{Z}}_i)=\sum _{k=1}^M{Z}_{ik}{\eta }_k+\sum _{j<k}{Z}_{ij}{Z}_{ik}{\gamma }_{jk},$$ (2)

H₀ corresponds to testing for η₁ = γ₁₂ = … = γ_1M = 0, which requires M degrees of freedom and is subject to considerable loss of power.

The central idea of our approach is to use the dual representation of model (1) and introduce a garrote parameter in the kernel function to develop a more powerful test by reducing the degrees of freedom and borrowing information across genes within a gene set. To get the idea across, consider the traditional two-way interaction model (2), which can be specified using the two-way interaction kernel $K({\mathit{z}}_1,{\mathit{z}}_2)=1+{\sum }_{k=1}^M{z}_{1k}{z}_{2k}+{\sum }_{j=1}^{M-1}{\sum }_{k=j+1}^M{z}_{1j}{z}_{2j}{z}_{1k}{z}_{2k}$, and can be rewritten as $K({\mathit{z}}_1,{\mathit{z}}_2)=(1+z_{11}{z}_{21})(1+{\sum }_{k=2}^M{z}_{1k}{z}_{2k})+{\sum }_{j=2}^{M-1}{\sum }_{k=j+1}^{M-1}{z}_{1j}{z}_{2j}{z}_{1k}{z}_{2k}$. To test for the effect of Z₁, we introduce a garrote parameter δ to the terms involving Z₁, and define the garrote two-way interaction kernel as $K_{\text{g}}({\mathit{z}}_1,{\mathit{z}}_2;\delta )=(1+\delta z_{11}{z}_{21})(1+{\sum }_{k=2}^M{z}_{1k}{z}_{2k})+{\sum }_{j=2}^{M-1}{\sum }_{k=j+1}^M{z}_{1j}{z}_{2j}{z}_{1k}{z}_{2k}$. One can easily see that setting the null hypothesis H₀: δ = 0, we have $K({\mathit{z}}_1,{\mathit{z}}_2;\delta =0)=1+{\sum }_{k=2}^M{z}_{1k}{z}_{2k}+{\sum }_{j=2}^{M-1}{\sum }_{k=j+1}^M{z}_{1j}{z}_{2j}{z}_{1k}{z}_{2k}$, which corresponds the two-way interaction model with only Z₂,…, Z_M. This formulation allows us to test for the effect of Z₁ using a single parameter instead of M parameters under the two-way interaction model, suggesting that we could have considerable power gain.

More generally, to test for a gene effect in presence of gene-gene interactions, it is relatively easy to construct a garrote version of any particular kernel that model interactions. For example, the garrote polynomial kernel is given by $K_{\text{g}}({\mathit{z}}_1,{\mathit{z}}_2;\delta ,\rho )={(\rho +\delta z_{11}{z}_{21}+{\sum }_{j=2}^M{z}_{1j}{z}_{2j})}^d$, and the garrote Gaussian kernel function is $K_{\text{g}}({\mathit{z}}_1,{\mathit{z}}_2;\delta ,\rho )=exp\{-\delta {(z_{11}-z_{21})}^2/\rho -{\sum }_{j=2}^M{(z_{1j}-z_{2j})}^2/\rho \}$. One can easily see that under H₀: δ = 0, h(·) corresponds to the model without Z₁ under the dth polynomial kernel and the Gaussian kernel respectively.

In general, given a kernel, the garrote kernel can be obtained by simply multiplying the garrote δ^1/2 to the first component of the covariate vector and constructing the usual kernel using this modified covariates. In this formulation we now test for

$$H_0:\delta =0.$$

This formulation has two main advantages, as we will observe later. First, the testing problem is reduced to a one dimensional problem from a possibly high or infinite dimensional (in the case h(·) is modeled nonparametrically) problem. Second, in contrast to the usual F-test that uses M degrees of freedom to test the effect of Z₁, our method uses a simple scaled chi-squared distribution $m{\chi }_d^2$ with much smaller degrees of freedom that are estimated from the data by accounting for correlation among genes, as we will discuss in Section 3.2. As shown in the simulation studies, d is much smaller than M and hence our test gains more power than the F-test.

3.1 Derivation of the score test statistic

As discussed before, we assume the function h(·) belongs to a functional space 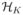with a kernel K(·, ·). Under the full model, β and h(·) are estimated by maximizing the penalized likelihood function, apart from a constant

$$J(\beta ,h)=-\frac{1}{2}\sum _{i=1}^n{\{Y_i-{\mathit{X}}_i^{\text{T}}\mathit{\beta }-h({\mathit{Z}}_i)\}}^2-{\lambda }_{\ast }^{-1}{\left|\right|h\left|\right|}_{{\mathcal{H}}_K}^2/2,$$ (3)

where λ_* is a tuning parameter which controls the trade off between goodness of fit and complexity of the model, and 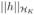denotes the functional norm in the functional space 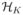. In particular, if we consider the primal representation $h(\mathit{z})={\sum }_{j=1}^J{\phi }_j(\mathit{z}){\eta }_j$, where φ_j, j = 1,…, J are orthonormal basis functions, then ${\left|\right|h\left|\right|}_{{\mathcal{H}}_K}^2$ is written as ${\sum }_{j=1}^J{\eta }_j^2$. However, we will use the dual representation of h(·). Liu et al (2007) discussed the estimation procedure using this penalized loglikelihood function via linear mixed models in detail. Specifically, using the representer theorem (Kimeldorf and Wahba, 1970), the solution of (3) can be written as $h(·)={\sum }_{i=1}^n{\alpha }_{i}K(·,{\mathit{Z}}_i)$, where α = (α₁,…, α_n)^T is an unknown parameter vector. Instead of using the original kernels, we propose to use the garrote kernels K_g(·, ·) to express h(·). As noted in Liu et al (2007), maximization of (3) is equivalent to maximizing

$$J(\mathit{\beta },h)=-{\{\mathit{Y}-{\mathit{X}}^{\text{T}}\mathit{\beta }-{\mathit{K}}_{\text{g}}(\delta ,\rho )\mathit{\alpha }\}}^{\text{T}}\{\mathit{Y}-{\mathit{X}}^{\text{T}}\mathit{\beta }-{\mathit{K}}_{\text{g}}(\delta ,\rho )\mathit{\alpha }\}/2-{\lambda }_{\ast }^{-1}{\mathit{\alpha }}^{\text{T}}{\mathit{K}}_{\text{g}}(\delta ,\rho )\mathit{\alpha }/2,$$ (4)

where Y = (Y₁,…, Y_n)^T, X = (X₁,…, X_n) and K_g(δ, ρ) is an n×n matrix with the (i, j)^th element given by K_g,ij(δ, ρ) = K_g(Z_i, Z_j; δ, ρ). We reiterate that K(·, ·) and K_g(·, ·) denote the kernel and the corresponding garrote kernel functions, and K(·) and K_g(·, ·) denote n×n matrices resulting from applying the kernel functions to the covariates Z.

It is important to note that the criterion function J(β, h) can be viewed as a penalized log-likelihood function of a linear mixed model (Harville, 1977; Laird and Ware, 1982). Specifically, Liu et al (2007) show that one can consider an equivalent linear mixed model regression problem

$$Y_i={\mathit{X}}_i^{\text{T}}\mathit{\beta }+h_i+{\epsilon }_i,$$ (5)

with h = (h₁,…, h_n)^T is a vector of random effects following a Normal{0, λK_g(δ, ρ)} distribution where λ = λ_*σ². In this setup, the parameters λ and ρ can be considered as variance components. Using this formulation, the parameters can be estimated using the standard mixed model theory, see Liu et al (2007) for details.

The main focus of this paper is to test for the main effect of a gene in the presence of gene-gene interactions using the garrote kernel framework, that is, testing for H₀: δ = 0. Specifically, we propose a variance component test for H₀: δ = 0 by using the mixed model formulation (5) and derive a score statistic. Specifically, the marginal covariance matrix of Y under (5) is given by V (θ) = σ²I + λK_g(δ, ρ), where θ = (δ, ρ, λ, σ²). The log-likelihood for θ and β is then given by

$$L_{\text{ML}}=-log\mid \mathit{V}(\mathit{\theta })\mid /2-{(\mathit{Y}-{\mathit{X}}^{\text{T}}\mathit{\beta })}^{\text{T}}{\mathit{V}}^{-1}(\mathit{\theta })(\mathit{Y}-{\mathit{X}}^{\text{T}}\mathit{\beta })/2.$$

One can estimate the variance components λ and ρ by maximizing L_ML. However, a major disadvantage of the maximum likelihood approach is that it does not take into account the loss of degrees of freedom due to estimation of the fixed effects β, and the resulting estimators for the variance components are usually biased (Harville, 1977). We therefore propose to use the restricted maximum likelihood (REML)

$$L_{\text{REML}}=-log\mid \mathit{V}(\mathit{\theta })\mid /2-log\mid {\mathit{X}\mathit{V}}^{-1}(\mathit{\theta }){\mathit{X}}^{\text{T}}\mid /2-{(\mathit{Y}-{\mathit{X}}^{\text{T}}\mathit{\beta })}^{\text{T}}{\mathit{V}}^{-1}(\mathit{\theta })(\mathit{Y}-{\mathit{X}}^{\text{T}}\mathit{\beta })/2.$$

Under H₀: δ = 0, we set θ₀ = (0, ρ, λ, σ²) and

$${\mathit{P}}_0({\mathit{\theta }}_0)={\mathit{V}}^{-1}({\mathit{\theta }}_0)-{\mathit{V}}^{-1}({\mathit{\theta }}_0){\mathit{X}}^{\text{T}}{\{{\mathit{X}\mathit{V}}^{-1}({\mathit{\theta }}_0){\mathit{X}}^{\text{T}}\}}^{-1}{\mathit{X}\mathit{V}}^{-1}({\mathit{\theta }}_0).$$

The REML based score function of δ evaluated at H₀ is

$$S_{\delta ,n}={(\mathit{Y}-{\mathit{X}}^{\text{T}}\mathit{\beta })}^{\text{T}}\mathit{V}{({\mathit{\theta }}_0)}^{-1}\{\lambda {\mathit{K}}_{\text{g},\delta }(0,\rho )\}\mathit{V}{({\mathit{\theta }}_0)}^{-1}(\mathit{Y}-{\mathit{X}}^T\mathit{\beta })/2-\text{tr}\{\lambda {\mathit{K}}_{\text{g},\delta }(0,\rho ){\mathit{P}}_0\}/2,$$

where K_g,δ(δ, ρ) denotes the derivative of K_g(δ, ρ) with respect to δ. To test for H₀: δ = 0, we propose to use the score-based test statistic

$$T_n={(\mathit{Y}-{\mathit{X}}^{\text{T}}\widehat{\mathit{\beta }})}^{\text{T}}\mathit{V}{({\widehat{\mathit{\theta }}}_0)}^{-1}\{\widehat{\lambda }{\mathit{K}}_{\text{g},\delta }(0,\widehat{\rho })\}\mathit{V}{({\widehat{\mathit{\theta }}}_0)}^{-1}(\mathit{Y}-{\mathit{X}}^T\widehat{\mathit{\beta }})/2,$$ (6)

where θ̂₀ = (0, ρ̂, λ̂, σ̂²) and β̂ are estimators of θ₀ and β constructed under the null hypothesis H₀: δ = 0.

It is important to note that a major advantage of our testing procedure is that one only needs to estimate the parameters under the null model. Recall that the full model is given in (1). Under H₀: δ = 0, the reduced model is

$$Y_i={\mathit{X}}_i^{\text{T}}\mathit{\beta }+h(Z_{2i},\dots ,Z_{Mi})+{\epsilon }_i.$$

Define Z_i0 = (Z_2i,…, Z_Mi)^T. The model components for this reduced model can be estimated following the procedure of Liu et al (2007, Section 4) by fitting the linear mixed model formulation

$$Y_i={\mathit{X}}_i^{\text{T}}\mathit{\beta }+h_i+{\epsilon }_i,$$ (7)

where h_i ~ N {0, λK₀(ρ)} and K₀ is the kernel matrix constructed under H₀ using the genes Z₂, ···, Z_M. We can estimate β and h(·) using the best linear unbiased predictors (BLUPs), and estimate the variance components using REML under the null working linear mixed model (7). The numerical properties of BLUPs and REML estimates are well known in the mixed model literature, see for example Harville (1977). We refer to Liu et al (2007) for more details about fitting the null model.

3.2 The Null distribution of the test statistic

To test for H₀: δ = 0, we need to derive the distribution of the score-based test statistics T_n under H₀. To start, we first note that the information matrix of θ based on the REML function is given by

$$\mathit{I}=\left[\begin{array}{cc}{I}_{\delta \delta }& {\mathit{I}}_{\delta {\mathit{\theta }}_0}^{\text{T}}\\ {\mathit{I}}_{\delta {\mathit{\theta }}_0}& {\mathit{I}}_{{\mathit{\theta }}_0{\mathit{\theta }}_0}\end{array}\right],$$

where

$${\mathit{I}}_{{\theta }_j{\theta }_k}=\text{tr}\{{\mathit{P}}_0(\mathit{\theta })\frac{\partial \mathit{V}(\mathit{\theta })}{\partial {\theta }_j}{\mathit{P}}_0(\mathit{\theta })\frac{\partial \mathit{V}(\mathit{\theta })}{\partial {\theta }_k}\}/2.$$

Hence the efficient information of δ accounting for the fact that λ̂, σ̂², ρ̂ are estimated is given by

$${\widehat{I}}_{\delta \delta }=I_{\delta \delta }-{\mathit{I}}_{\delta {\mathit{\theta }}_0}^{\text{T}}{\mathit{I}}_{{\mathit{\theta }}_0{\mathit{\theta }}_0}^{-1}{\mathit{I}}_{\delta {\mathit{\theta }}_0},$$

where all the quantities are evaluated at θ̂₀ computed under H₀. Note that we have used the fact that β and θ are orthogonal in linear mixed models and there is no loss of information for δ when estimating β.

Note that our proposed test statistic T_n is a quadratic form in Y and follows a mixture of chi-squared distribution under H₀: δ = 0. We use the Satterthwaite approximation to approximate its distribution by a scaled chi-squared distribution $m{\chi }_d^2$. The parameters m and d are calculated equating the mean and variance of T_n to those of $m{\chi }_d^2$. Specifically, we solve md = λ̂ tr{P₀(θ̂₀)K_g,δ(0, ρ̂)}/2 and 2m²d = Î_δδ, which in turn gives us the solution

$$\begin{array}{l}\widehat{m}={\widehat{I}}_{\delta \delta }/[\widehat{\lambda }\text{tr}\{{\mathit{V}}^{-1}({\widehat{\mathit{\theta }}}_0){\mathit{K}}_{\text{g},\delta }(0,\widehat{\rho })\}];\\ \widehat{d}={[\widehat{\lambda }\text{tr}({\mathit{V}}^{-1}({\widehat{\mathit{\theta }}}_0){\mathit{K}}_{\text{g},\delta }(0,\widehat{\rho }))]}^2/(2{\widehat{I}}_{\delta \delta }).\end{array}$$

Now the p-value of the test can be obtained using the tail probabilities of the $\widehat{m}{\chi }_{\widehat{d}}^2$ distribution. Note that the degrees of freedom d is estimated from the data and accounts for the correlation among genes. We will demonstrate in the simulation study section that d is often much smaller than M and hence the garrote kernel machine test often has considerably higher power than the M-df F-test.

Note that m̂ and d̂ depend on K_g,δ(·, ·), the derivative of the garrote kernel with respect to the garrote parameter δ. For many frequently used kernels, this matrix can be easily computed. For example, in the case of polynomial kernel, the (i, j)-th element of the derivative matrix is ${\mathit{K}}_{\text{g},\delta ,ij}(\delta =0,\rho )={dZ}_{i1}{Z}_{j1}{(\rho +{\sum }_{k=2}^M{Z}_{ik}{Z}_{jk})}^{d-1}$; for Gaussian kernel, ${\mathit{K}}_{\text{g},\delta ,ij}(\delta =0,\rho )=\{-{(Z_{i1}-Z_{j1})}^2/\rho \}exp\{-{\sum }_{k=2}^M{(Z_{ik}-Z_{jk})}^2/\rho \}$, and for product linear kernel, ${\mathit{K}}_{\text{g},\delta ,ij}(\delta =0)=Z_{i1}{Z}_{j1}{\prod }_{k=2}^M(1+Z_{ik}{Z}_{jk})$.

3.3 Principal Component Analysis (PCA) Based Testing Procedure

Recall that the proposed test statistic T_n given in (6) is a quadratic form and hence follows a weighted mixture of χ²-distribution under H₀. Specifically, let ζ₁,…, ζ_n be the eigenvalues of K_g,δ(0, ρ̂) with corresponding eigenvectors U = [u₁,…, u_n]. Then we can write

$$T_n=\widehat{\lambda }{\mathit{\psi }}^{\text{T}}\mathit{D}\mathit{\psi },$$ (8)

where ψ = U^TV (θ̂₀)⁻¹(Y − X^Tβ̂) and D = diag(ζ₁,…, ζ_n). The Satterthwaite approximation of the distribution of T_n derived in Section 3.2 inherently assumes that the eigenvalues ζ₁,…, ζ_n ≥ 0, that is, the derivative matrix K_g,δ(0, ρ̂) is positive semi-definite. If this condition is violated then T_n can potentially take negative values and the chi-squared approximation becomes invalid.

Note that this problem depends on the choice of the kernel function K(·, ·). For many usual kernel functions, this problem does not arise at all. For example, in the case of the linear kernel, polynomial kernel, product linear kernel and the two-way interaction kernel, one can easily show that the matrix K_g,δ(0, ρ̂) is in fact positive semi-definite and hence the chi-squared approximation in Section 3.2 is valid and the testing procedure remains valid.

One notable exception is the case where one uses the Gaussian kernel $K_{\text{g}}({\mathit{z}}_1,{\mathit{z}}_2;\delta ,\rho )=exp\{-\delta {(z_{11}-z_{21})}^2/\rho -{\sum }_{j=2}^M{(z_{1j}-z_{2j})}^2/\rho \}$. In this case, we have

$${\mathit{K}}_{\text{g},\delta }={\mathit{M}}_1\odot {\mathit{M}}_2,$$

where M₁ and M₂ are matrices such that M_1,ij = −(Z_i1−Z_j1)²/ρ and ${\mathit{M}}_{2,ij}=exp\{-{\sum }_{k=2}^M{(z_{ik}-z_{jk})}^2/\rho \}$, and ⊙ denotes the element-wise product or Schur product of two matrices. In this case, the matrix K_g,δ can be an indefinite matrix and hence the chi-squared approximation in Section 3.2 may not be valid.

To address this problem, we propose a principal component based solution. Specifically, utilizing the form of the test statistic in (8), we propose the following modified test statistic

$$T_n^{\ast }=\widehat{\lambda }{\mathit{\psi }}^{\text{T}}{\mathit{D}}^{\ast }\mathit{\psi },$$

where D^* = diag(|ζ₁|,…, |ζ_n|) is constructed using the absolute values of the eigenvalues. In other words, the $T_n^{\ast }$ can be written as

$$T_n^{\ast }={(\mathit{Y}-{\mathit{X}}^{\text{T}}\widehat{\mathit{\beta }})}^{\text{T}}\mathit{V}{({\widehat{\mathit{\theta }}}_0)}^{-1}\{\widehat{\lambda }{\mathit{K}}_{\text{g},\delta }^{\ast }(0,\widehat{\rho })\}\mathit{V}{({\widehat{\mathit{\theta }}}_0)}^{-1}(\mathit{Y}-{\mathit{X}}^{\text{T}}\widehat{\mathit{\beta }})/2,$$ (9)

where ${\mathit{K}}_{\text{g},\delta }^{\ast }(0,\widehat{\rho })=\mathit{U}{\mathit{D}}^{\ast }{\mathit{U}}^{\text{T}}$ is a reconstruction of K_g,δ(0, ρ̂) using absolute eigenvalues. Note that when K_g,δ(0, ρ̂) is non-negative definite, $T_n=T_n^{\ast }$.

Another option is to consider

$$T_n^{\ast \ast }={(\mathit{Y}-{\mathit{X}}^{\text{T}}\widehat{\mathit{\beta }})}^{\text{T}}\mathit{V}{({\widehat{\mathit{\theta }}}_0)}^{-1}\{\widehat{\lambda }{\mathit{K}}_{\text{g},\delta }^{\ast \ast }(0,\widehat{\rho })\}\mathit{V}{({\widehat{\mathit{\theta }}}_0)}^{-1}(\mathit{Y}-{\mathit{X}}^{\text{T}}\widehat{\mathit{\beta }})/2,$$ (10)

where ${\mathit{K}}_{\text{g},\delta }^{\ast \ast }(0,\widehat{\rho })=\mathit{U}{\mathit{D}}^{\ast \ast }{\mathit{U}}^{\text{T}}$ is a reconstruction of K_g,δ(0, ρ̂) using D^** = diag[ζ₁1(ζ₁ > 0),…, ζ_n1(ζ_n > 0)], where one replaces the negative eigenvalues with zero.

It is important to note that $T_n^{\ast }$ and $T_n^{\ast \ast }$ are valid test statistics, and ${\mathit{K}}_{\text{g},\delta }^{\ast }(0,\widehat{\rho })$ and ${\mathit{K}}_{\text{g},\delta }^{\ast \ast }(0,\widehat{\rho })$, by construction, are positive semi-definite matrices. Hence we can now apply the Satterthwaite approximation on $T_n^{\ast }$ or $T_n^{\ast \ast }$ to obtain the null distribution as a scaled chi-squared distribution as demonstrated in Section 3.2, where one uses ${\mathit{K}}_{\text{g},\delta }^{\ast }(0,\widehat{\rho })$ or ${\mathit{K}}_{\text{g},\delta }^{\ast \ast }(0,\widehat{\rho })$ instead of K_g,δ(0, ρ̂) in all the expressions.

It is worth mentioning that in our simulation study, the proportion of time T_n assumed negative values for the Gaussian kernel case is negligible (0.5–5%) and hence did not pose any real problem. However, the PCA based reconstruction approach is practically very useful when one applies our method to a real data set simply because a negative test statistic in that case will result in p-value being 1.0 whereas the modified test will produce a valid and sensible p-value.

Remark 1

It is worth noting that one can derive the exact distribution of an indefinite quadratic form in multivariate normal variables as in (6), see for example Johnson and Kotz (1970), Section 7. However, the exact distribution and hence the p-value are numerically very difficult to compute and require to perform contour integration on a complex plane. Thus we prefer the PCA based approach for its easy accessibility. If one wants to keep the original indefinite quadratic form, critical values can be determined using simulations.

4. Multiple Comparison Procedure

The score test proposed in Section 3 is developed to test for a single gene at a time. However, when testing for genes in a gene set, the p-values from individual tests can be misleading and may result in false discoveries. Specifically, when comparing M genes in a pathway/network, we are interested in simultaneously testing M null hypotheses each corresponding to one gene. Let the individual p-values be given by p₁,…, p_M. A typical approach is that instead of using the individual p-values, one modifies them to obtain modified p-values adjusted for multiple testing. The simplest example is the Bonferroni correction where the adjusted p-values are given by $p_k^{\mathit{Bon}}=p_{k}M$, k = 1,…, M. However, this approach is overly conservative and does not account for the correlation among the genes, and often leads to a very small number of discoveries. An alternative approach is based on false discovery rates (Benjamini and Hochberg, 1995). However, FDR requires the hypotheses are independent or block-independent. This assumption is not appropriate in many cases, specially if one is interested in testing for genes in a particular pathway where there are gene-gene interactions present.

We instead propose a permutation-based procedure for multiple comparisons that can be used with our proposed score test. We present the procedure for the case where there are no clinical covariates X, and indicate afterward how the clinical covariates can be handled.

Recall that our model is

$$Y_i=h(Z_{i1},\dots ,Z_{iM})+{\epsilon }_i,$$ (11)

where we test each of the M genes one by one using our testing procedure. Let the individual p-values be p₁,…, p_M. The multiple comparison procedure is as follows:

1. Fit the full model (11) and obtain the residual vector ε̂.

2. For any given m ∈ {1,…, M},

   1. Fit the null model Y_i = h(Z_i1,…, Z_i,m−1, Z_i,m+1,…, Z_iM) + ε_i, and estimate the effect under H₀, that is ĥ_−m(·) = ĥ(Z_i1,…, Z_i,m−1, Z_i,m+1,…, Z_iM)

   2. Permute the residual vector ε̂ randomly to obtain ε̂^* and compute Y^* = ĥ_−m(·) + ε̂^*

   3. Perform our proposed score test using Y^* as observations and Z as the covariates and obtain the p-value $p_m^{\ast }$.

   4. Repeat the steps (b) and (c) for a large number, say b = 1,…, B, of times and obtain p-values for the m^th gene $p_{m1}^{\ast },\dots ,p_{mB}^{\ast }$.

3. Repeat step 2 for each m = 1,…, M.

4. Derive the distribution of $p^{\ast }=min(p_1^{\ast },\dots ,p_M^{\ast })$ and compute the adjusted p-value of the m^th gene as the tail probability of this distribution, that is, the p-value of the m^th gene is

   $$p_m^{\text{Adj}}=B^{-1}\sum _{b=1}^{B}I[p_m>min\{p_{1b}^{\ast },\dots ,p_{Mb}^{\ast }\}].$$

5. The m^th hypothesis is rejected al level α if $p_m^{\text{Adj}}<\alpha$.

Note that in presence of extra variables X, one just needs to include X as a linear predictor while fitting the full and null models. The estimation procedure will then be same as described in Section 3.1. The rest of the procedure and computation of the p-values remain the same as above.

5. Simulation Study

We performed a simulation study to evaluate the finite-sample performance of our garrote kernel machine (GKM) test and compare its performance with the usual F-test. The data sets were simulated from the true model

$$Y_i={\mathit{X}}_i^{\text{T}}\mathit{\eta }+h(Z_{i1},\dots ,Z_{iM})+{\epsilon }_i,$$

where X_i = (X_i1, X_i2)^T were generated from a standard bivariate normal distribution and the true value of η = (0.2, 0.2)^T. The random errors ε_i’s were generated from a standard normal distribution. We generated Z₁,…, Z_M from a normal distribution with the compound symmetry correlation structure with marginal variance 1.0 and correlation r. We considered different values of r = 0, 0.2 and 0.5, and four different settings for sample sizes and number of genes: (n, M) = (50, 5), (n, M) = (100, 8), (n, M) = (200, 10) and (n, M) = (200, 20). For each of these settings, we considered four different functions h(·) as follows. First define

$$g(Z_{i1},\dots ,Z_{iM})=1+\sum _{k=1}^M{Z}_{ik}{\beta }_k+\sum _{k=2}^m{Z}_{i1}{Z}_{ik}{\gamma }_k,$$

where m ≤ M. Here M is the number of genes in a pathway/gene set and m is the number of genes that are interacting with Z₁. We test for the effect of Z₁. For example, m = M implies that Z₁ is interacting with all other variables in the model, and m = 2 refers to the case where Z₁ interacts only with Z₂. The four different functions of h(·) are

1. h₁(Z_i1,…, Z_iM) = g(Z_i1,…, Z_iM) with m = 2,

2. h₂(Z_i1,…, Z_iM) = g(Z_i1,…, Z_iM) with m = M,

3. h₃(Z_i1,…, Z_iM) = sign{g(·)}|g(·)|^1/2 with m = 2,

4. h₄(Z_i1,…, Z_iM) = sign{g(·)}|g(·)|^1/2 with m = M.

Note that case (1) and (2) are linear interaction functions and (3) and (4) are nonlinear.

For each of these cases, we applied our testing procedure to test for the effect of Z₁. For type I error and power calculations, we set the true values of β₂ = … = β_M = 0.7 and β₁ = c/10, γ₂ = … = γ_m = c/20, where we varied c = 0, 2, 4, 6, 8. Here c = 0 corresponds to the null hypothesis of no effect of Z₁ and was used to study for the size of the test.

We generated 2,000 data sets for each case to compute sizes and powers of our test at a nominal level of 0.05. To test for the effect of Z₁, we used the GKM test with the Gaussian kernel $K({\mathit{z}}_1,{\mathit{z}}_2)=exp\{-{\sum }_{j=1}^M{(z_{1j}-z_{2j})}^2/\rho \}$ and the two-way interaction kernel $K({\mathit{z}}_1,{\mathit{z}}_2)=1+{\sum }_{k=1}^M{z}_{1k}{z}_{2k}+{\sum }_{j<k}{z}_{1j}{z}_{2j}{z}_{1k}{z}_{2k}$. For the Gaussian kernel, we computed the p-values based on both the scaled chi-squared approximation using the test statistic in (6) as in Section 3.2 and also the PCA based modified test statistics (9) and (10) as described in Section 3.3. Note that for the two-way interaction kernel, the PCA based method and the scaled chi-squared approximation are identical, because K_g,δ(·) is positive definite. Hence we only report results for one test. We also compared the power of our GKM test to that of the usual ANOVA based F-test where one fits a linear model with all main and two-way interaction effects. For linear cases (h₁(·) and h₂(·)), we also present the results for the classical score test assuming the true direction under the alternative (β₁, γ₂,…, γ_m) = c(0.10, 0.05,…, 0.05) is known, that is, one only tests for c = 0 against c ≠ 0. This of course is not possible in real data situations but in our simulation study this test serves as an ideal benchmark. We do not include the results of the classical score tests for the nonlinear models (h₃(·) and h₄(·)) because in our simulations we found that the parametric estimation of these nonlinear models, even under H₀, are unstable and practically infeasible, especially for large p. In fact, this is one of the reasons for adopting a kernel machine based test for nonlinear models.

The results are given in Tables 1 – 4. These results show that all the tests have the size close to the nominal value α = 0.05. The M-df F-test loses power in all the cases, specially when there is correlation among the covariates (r = 0.2) or (r = 0.5). For the two-way interaction models h₁ and h₂, when r = 0, the F-test has a similar performance to that of the two-way interaction kernel but both are outperformed by the Gaussian kernel. When r = 0.2, the two-way interaction kernel-based test improves the power over the F-test considerably, while both are outperformed by the Gaussian-kernel based test. Note that when r = 0, although the covariates (Z₁, ···, Z_m) are independent, however, the interaction terms Z₁Z₂, ···, Z₁Z_m are correlated. The GKM test is able to take such correlation into account when testing for the effect of Z₁ and hence is more powerful. For the nonlinear cases h₃ and h₄, the Gaussian kernel-based test performs much better than both the F-test and the two-way interaction kernel test, as expected.

Table 1.

Results of the simulation study described in Section 5. Displayed are the empirical size (c = 0) and power (c = 2,…, 8) of the proposed garrote kernel machine (GKM) test using the two-way interaction kernel (K_Int), the Gaussian kernel (K_Gauss), the PCA based test statistics $T_n^{\ast }$ and $T_n^{\ast \ast }$ (K_Gauss,PCA1 and K_Gauss,PCA2) using the Gaussian kernel as in Section 3.3, and the usual F-test for different settings with n = 50 and M = 5. Also presented, for the linear cases (h₁(·) and h₂(·)), are the results for the ideal classical score tests assuming the direction of the alternative is known. The nominal level was set be α = 0.05.

	Test	r = 0.0					r = 0.2					r = 0.5
		c = 0	c = 2	c = 4	c = 6	c = 8	c = 0	c = 2	c = 4	c = 6	c = 8	c = 0	c = 2	c = 4	c = 6	c = 8
h1(·)	F-test	0.049	0.142	0.409	0.723	0.940	0.042	0.109	0.356	0.703	0.931	0.047	0.095	0.223	0.494	0.765
	KInt	0.049	0.141	0.435	0.757	0.933	0.042	0.164	0.446	0.771	0.955	0.049	0.127	0.294	0.572	0.819
	KGauss	0.048	0.233	0.685	0.926	0.991	0.050	0.274	0.678	0.941	0.990	0.051	0.236	0.541	0.847	0.977
	KGauss,PCA1	0.049	0.228	0.665	0.915	0.993	0.055	0.267	0.661	0.927	0.990	0.050	0.197	0.502	0.794	0.948
	KGauss,PCA2	0.049	0.238	0.675	0.917	0.992	0.058	0.277	0.671	0.924	0.991	0.055	0.207	0.552	0.804	0.958
	Score test	0.054	0.279	0.726	0.940	0.993	0.054	0.255	0.685	0.925	0.994	0.051	0.221	0.594	0.864	0.970
h2(·)	F-test	0.049	0.143	0.417	0.793	0.945	0.042	0.134	0.446	0.794	0.963	0.047	0.107	0.332	0.661	0.881
	KInt	0.049	0.154	0.474	0.807	0.921	0.042	0.208	0.582	0.857	0.967	0.049	0.189	0.509	0.777	0.925
	KGauss	0.048	0.248	0.665	0.933	0.982	0.050	0.263	0.682	0.917	0.987	0.051	0.230	0.548	0.808	0.938
	KGauss,PCA1	0.049	0.242	0.658	0.920	0.988	0.055	0.278	0.658	0.909	0.982	0.050	0.227	0.580	0.828	0.945
	KGauss,PCA2	0.049	0.248	0.665	0.927	0.982	0.058	0.267	0.681	0.926	0.981	0.055	0.237	0.582	0.824	0.932
	Score test	0.054	0.354	0.881	0.972	0.991	0.054	0.453	0.889	0.983	0.997	0.051	0.637	0.954	0.996	1.000
h3(·)	F-test	0.058	0.083	0.178	0.356	0.544	0.049	0.081	0.137	0.249	0.404	0.056	0.059	0.077	0.149	0.217
	KInt	0.044	0.081	0.213	0.377	0.562	0.046	0.077	0.187	0.330	0.487	0.046	0.067	0.113	0.192	0.290
	KGauss	0.047	0.112	0.351	0.615	0.821	0.051	0.131	0.319	0.581	0.793	0.050	0.117	0.258	0.423	0.599
	KGauss,PCA1	0.052	0.128	0.341	0.583	0.801	0.052	0.132	0.325	0.545	0.749	0.050	0.107	0.232	0.380	0.539
	KGauss,PCA2	0.052	0.130	0.344	0.593	0.820	0.052	0.130	0.328	0.555	0.759	0.050	0.116	0.242	0.401	0.559
h4(·)	F-test	0.058	0.076	0.134	0.293	0.483	0.049	0.071	0.116	0.225	0.389	0.056	0.067	0.083	0.107	0.194
	KInt	0.044	0.066	0.145	0.314	0.527	0.046	0.082	0.152	0.301	0.493	0.046	0.074	0.100	0.155	0.279
	KGauss	0.047	0.100	0.268	0.571	0.804	0.051	0.122	0.274	0.540	0.734	0.050	0.108	0.225	0.357	0.510
	KGauss,PCA1	0.052	0.112	0.254	0.541	0.795	0.052	0.122	0.273	0.498	0.702	0.050	0.101	0.205	0.322	0.498
	KGauss,PCA2	0.052	0.111	0.264	0.551	0.799	0.052	0.121	0.264	0.501	0.713	0.050	0.102	0.209	0.337	0.508

Table 4.

Results of the simulation study described in Section 5. Displayed are the empirical size (c = 0) and power (c = 2,…, 8) of the proposed garrote kernel machine (GKM) test using the two-way interaction kernel (K_Int), the Gaussian kernel (K_Gauss), and the PCA based test statistics $T_n^{\ast }$ and $T_n^{\ast \ast }$ (K_Gauss,PCA1 and K_Gauss,PCA2) using the Gaussian kernel as in Section 3.3 for different settings with n = 200 and M = 20. Also presented, for the linear cases (h₁(·) and h₂(·)), are the results for the ideal classical score tests assuming the direction of the alternative is known. The nominal level was set be α = 0.05. Note that in this case, F-test is not computable.

	Test	r = 0.0					r = 0.2					r = 0.5
		c = 0	c = 2	c = 4	c = 6	c = 8	c = 0	c = 2	c = 4	c = 6	c = 8	c = 0	c = 2	c = 4	c = 6	c = 8
h1(·)	KInt	0.047	0.068	0.147	0.253	0.436	0.039	0.060	0.123	0.217	0.361	0.049	0.060	0.103	0.193	0.310
	KGauss	0.055	0.578	0.988	1.000	1.000	0.055	0.456	0.948	0.999	1.000	0.051	0.348	0.821	0.988	0.999
	KGauss,PCA1	0.055	0.558	0.982	1.000	1.000	0.053	0.425	0.925	1.000	1.000	0.051	0.286	0.779	0.983	0.998
	KGauss,PCA2	0.055	0.578	0.987	1.000	1.000	0.052	0.448	0.937	1.000	1.000	0.049	0.314	0.811	0.985	0.999
	Score test	0.055	0.768	1.000	1.000	1.000	0.053	0.712	0.996	1.000	1.000	0.052	0.607	0.978	1.000	1.000
h2(·)	KInt	0.047	0.120	0.376	0.670	0.847	0.039	0.812	1.000	1.000	1.000	0.049	1.000	1.000	1.000	1.000
	KGauss	0.055	0.582	0.967	0.999	1.000	0.055	0.942	1.000	1.000	1.000	0.051	0.998	1.000	1.000	1.000
	KGauss,PCA1	0.055	0.578	0.963	0.999	1.000	0.053	0.969	1.000	1.000	1.000	0.051	0.999	1.000	1.000	1.000
	KGauss,PCA2	0.055	0.578	0.967	1.000	1.000	0.052	0.967	1.000	1.000	1.000	0.049	0.999	1.000	1.000	1.000
	Score test	0.055	0.827	0.992	0.999	1.000	0.053	0.996	1.000	1.000	1.000	0.052	1.000	1.000	1.000	1.000
h3(·)	KInt	0.038	0.051	0.07	0.090	0.133	0.050	0.045	0.045	0.047	0.051	0.047	0.045	0.057	0.067	0.087
	KGauss	0.055	0.192	0.594	0.896	0.987	0.054	0.193	0.435	0.695	0.912	0.055	0.127	0.272	0.443	0.623
	KGauss,PCA1	0.055	0.188	0.581	0.889	0.986	0.054	0.169	0.379	0.644	0.857	0.055	0.099	0.198	0.372	0.540
	KGauss,PCA2	0.055	0.194	0.604	0.901	0.987	0.054	0.184	0.414	0.672	0.894	0.055	0.106	0.239	0.407	0.600
h4(·)	KInt	0.038	0.044	0.173	0.217	0.312	0.05	0.077	0.104	0.153	0.242	0.047	0.060	0.106	0.138	0.153
	KGauss	0.055	0.112	0.375	0.784	0.946	0.054	0.153	0.438	0.880	0.994	0.055	0.152	0.529	0.955	1.000
	KGauss,PCA1	0.055	0.110	0.383	0.782	0.946	0.054	0.105	0.396	0.708	0.905	0.055	0.109	0.323	0.697	0.889
	KGauss,PCA2	0.055	0.110	0.391	0.798	0.952	0.054	0.150	0.390	0.811	0.906	0.055	0.114	0.311	0.694	0.919

For the Gaussian kernel, we also compared the power of the GKM test with the PCA based tests. It is evident that in all the cases considered, the GKM test and the two PCA based tests perform very similarly. This is simply because the proportion of times the test statistic using the Gaussian kernel takes a negative value is very small in all the cases, ranging between 0.5% to 5% and hence their impact on the power of the test is negligible. However, we recommend the PCA based test for practical purposes when one applies the test to a real data set simply because the original GKM test based on the Satterthwaite approximation may result in a negative test statistic giving a p-value 1.0. In contrast, the PCA based test will provide a valid test and produce a valid and sensible p-value.

Comparing the results from the GKM tests with the ideal score test by hypothetically assuming the true direction of the alternative were known, we see that the GKM test performs closely to the ideal score test for h₁, especially for (n, p) = (50, 5), (100, 8) and (200, 10) with low to moderate correlation (r = 0, 0.2). However, in other cases, the GKM test loses some power compared to the best power possible. This result is expected because the ideal score test assumes that the direction of the alternative is known in advance. This is not feasible in practice. It is also interesting to note that given a known direction of the alternative $({\beta }_1,{\gamma }_2,\dots ,{\gamma }_m)=c({\beta }_1^{\ast },{\gamma }_2^{\ast },\dots ,{\gamma }_m^{\ast })$, and the knowledge of the true form of h(·), one can rewrite $h(z_1,z_2,\dots ,z_m)=h(z_1^{\ast },z_2,\dots ,z_m)$, where $z_1^{\ast }=z_1{\beta }_1^{\ast }+{\sum }_{k=2}^m{z}_1{z}_k{\gamma }_m^{\ast }$. In case of linear functions such as h₁(·) and h₂(·), testing for Z₁ then amounts to using a linear kernel with the covariates $Z_1^{\ast }$, Z₂,…, Z_m and testing for $Z_1^{\ast }$. However for nonlinear cases, one still needs to use Gaussian kernel to capture the nonlinearity of the function. Nevertheless, these tests are still hypothetical as neither the true direction of the alternative or the actual functional form of h(·) are known in practice.

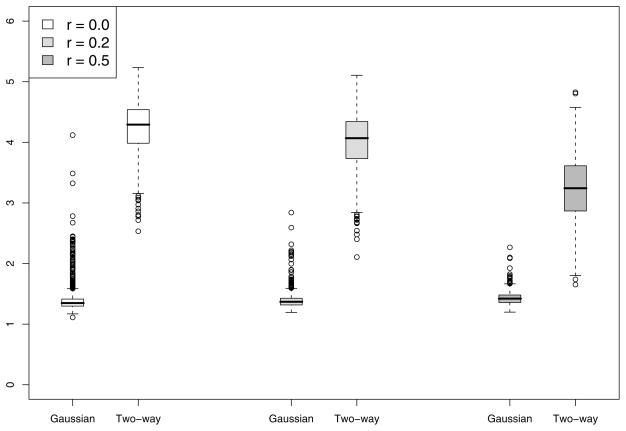
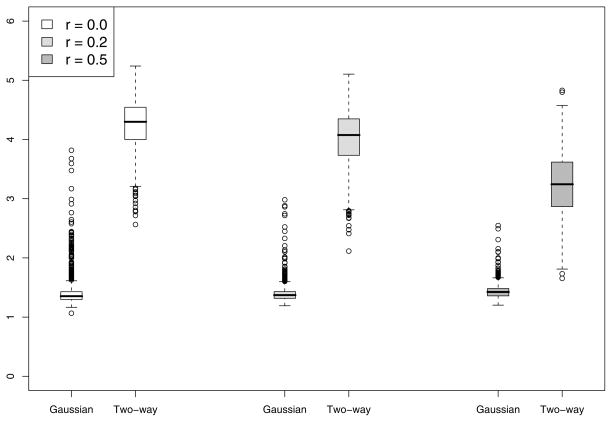
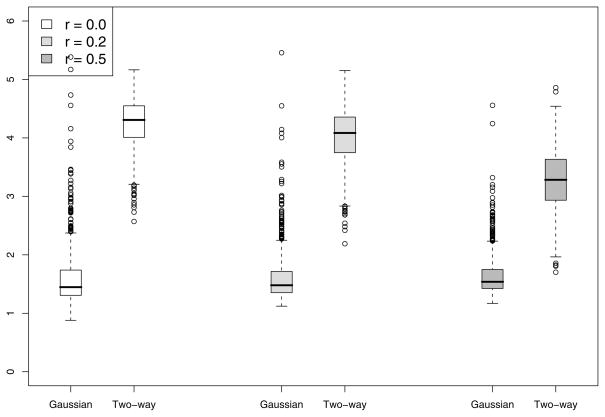
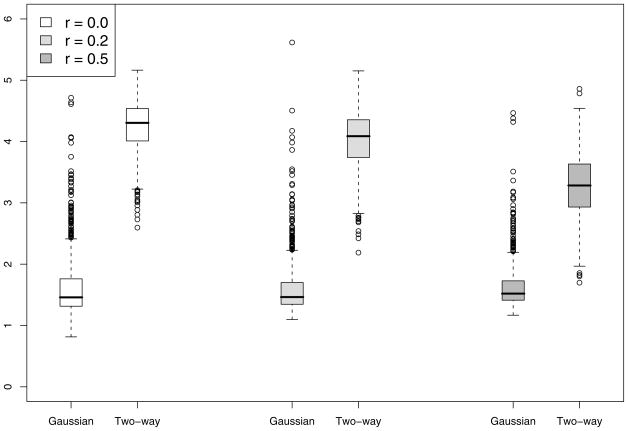
To gain insight about the improvement in power for the Gaussian kernel and two-way interaction kernel over F-test, we summarize the degrees of freedom used for tests based on both kernels. The boxplots of degrees of freedom used in the chi-squared approximation for the case n = 50 and M = 5 with c = 6 in displayed in Figure 1. Note that while the F-test uses 5 degrees of freedom, the Gaussian-kernel based test uses an average 1.5 DF while the two-way interaction kernel test uses an average 4 DF, implying considerable power gain. The Gaussian kernel uses much less degrees of freedom than the two-way interaction kernel and hence performs better than the interaction kernel. As the correlation r among Z₁,…, Z_M increases, the degrees of freedom used by the two-way interaction kernel decreases and hence gaining more power over the F-test. This is also supported by the results in Table 1.

Figure 1.

Results of the simulation study described in Section 5. Presented are the boxplots for the estimated degrees of freedom of our proposed GKM test for the cases h₁(·) (top-left), h₂(·) (top-right), h₃(·) (bottom-left) and h₄(·) (bottom-right) for n = 50 and p = 5 and c = 6. In each boxplot, the three pairs of boxes are for different values of correlation r among the covariates. In each pair, the degrees of freedom are plotted using the Gaussian (left box) and two-way interaction kernels (right box).

6. The Prostate Cancer Pathway Data Example

We applied our proposed GKM testing procedure to analyze the prostate cancer genetic pathway data from the Michigan prostate cancer study (Dhanasekaran, et al, 2001). The data set contained 59 patients who were clinically diagnosed with local or advanced prostate cancer. An objective of the study is to evaluate whether a gene of interest in a genetic pathway has an overall effect on pre-surgery prostate specific antigen (PSA) after adjusting for covariates and accounting for interactions with other genes in the pathway. For each patient, cDNA microarray gene expressions were collected. Liu et al (2007) considered this data set and the cell growth pathway which contains 5 genes. They tested for the joint effect of the whole pathway and found the effect to be statistically significant. We are interested in testing for the effects of the individual genes accounting for gene-gene interactions on PSA level. We took a log transformation of PSA to make the normality assumption more plausible. We included two covariates: age and Gleason score, a well established histological grading system for prostate cancer, in our model,

$$Y_i=X_{i1}{\beta }_1+X_{i2}{\beta }_2+h(Z_{i1},\dots ,Z_{i5})+{\epsilon }_i,$$

where Y denotes the log-PSA level, X₁ and X₂ denote age and Gleason score, and Z_i1,…, Z_i5 denote the gene expression levels of the 5 genes in the cell growth pathway. The symbols and description of the five genes in the pathway are provided in Table 5.

Table 5.

Results of the data example described in Section 6. Displayed are the F-test based p-values of individual gene effects using the linear model with only main effects (3rd column) and using the linear model with main and all the two-way interaction effects (4th column).

Name	Description	Main effects	F-test
MYBL2	v-myb myeloblastosis viral oncogene homolog	0.059	0.111
FGF2	fibroblast growth factor 2	0.077	0.335
FGF7	fibroblast growth factor 7 (keratinocyte growth factor)	0.006	0.063
IGFBP1	insulin-like growth factor binding protein 1	0.889	0.381
IGFBP2	insulin-like growth factor binding protein 2, 36kDa	0.353	0.298

We started by fitting a main effects only linear model, that is, setting h(Z_i1,…, Z_i5) = η₀ + Z_i1η₁ + … + Z_i5η₅, and tested for each gene separately. For comparison purposes, we fit a model including all the main effects and two-way interactions, that is, we set $h(Z_{i1},\dots ,Z_{i5})={\eta }_0+{\sum }_{k=1}^5{Z}_{ik}{\eta }_k+{\sum }_{k=1}^5{\sum }_{j>k}{\eta }_{jk}{Z}_{ij}{Z}_{ik}$. In this setting, we performed the usual F-test for each gene. The individual p-values are reported in Table 5, columns 3 and 4, respectively. Note that the main-effect-only naive test suggests that the gene FGF7 has a significant effect on PSA levels. However, when we incorporated all the two-way interaction, this effect disappears using the 5-df F-test.

We next applied our score testing procedure to test for individual gene effect accounting for gene-gene interactions (epistasis). We used the Gaussian kernel and the two-way interaction kernel to model the function h(·). For the Gaussian kernel, we implemented both the original GKM scaled chi-squared approximation (Section 3.2) and the PCA based modified test based on $T_n^{\ast }$ (Section 3.3). Note that these two tests are identical when the two-way linear kernel is used and hence we only report one p-value for the garrote two-way interaction kernel test. The results are presented in Table 6. The Gaussian kernel based test found the gene FGF7 was significant. However, the two-way linear kernel did not capture this result. This seems to imply that the interaction structure between the genes may not be simply multiplicative and the nonparametric modeling of the covariates is in fact needed. Further as shown in the simulation study, the Gaussian-kernel based test has more power.

Table 6.

Results of the prostate cancer data example described in Section 6 for testing for the individual gene effects in the presence of possible gene-gene interactions (epistasis) in the cell growth pathway. Displayed are the p-values of the proposed garrote kernel machine test using the Gaussian kernel: (p_Gauss denotes the original GKM test and p_Gauss,PCA denotes the PCA based modified test) and the two-way interaction kernel (p_Two-way). Also reported in columns 5–7 are the adjusted p-values for multiple comparison using our permutation method proposed in Section 4.

Name	pGauss	pGauss,PCA	pTwo-way	$p_{\text{Gauss}}^{\ast }$	$p_{\text{Gauss},\text{PCA}}^{\ast }$	$p_{\text{Two}-\text{way}}^{\ast }$
MYBL2	0.287	0.335	0.066	0.832	0.861	0.235
FGF2	0.428	0.593	0.122	0.953	0.988	0.416
FGF7	0.004	0.003	0.062	0.020	0.017	0.227
IGFBP1	0.654	0.729	0.488	0.999	0.998	0.943
IGFBP2	0.339	0.590	0.428	0.883	0.987	0.902

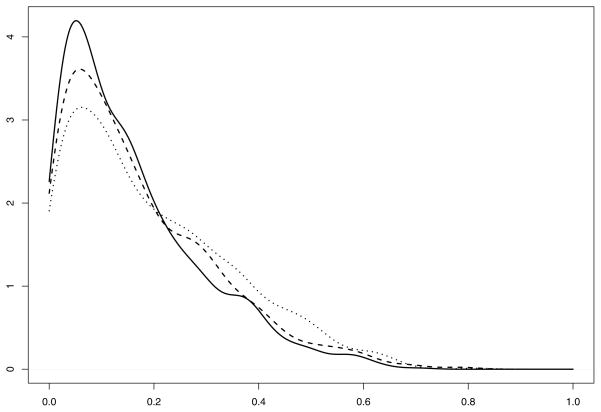
However, individual p-values may be misleading and we need to take into account the multiple testing issue. We employed the multiple comparison procedure described in Section 4 to obtain adjusted p-values. We used B = 10000 permutations to generate the p-value distribution. The distribution of p^* as described in Section 4, step 4 is displayed in Figure 2. The adjusted p-values are displayed in columns 5–7 of Table 6. It is evident that FGF7 is still found to be significant by the Gaussian kernel based tests.

Figure 2.

Results from data analysis. Displayed is the distribution of p-values for the multiple comparison procedure: solid line represents the Gaussian kernel test, dashed line represents PCA based Gaussian kernel test and dotted line represents the two-way interaction kernel.

7. Discussion

We have proposed in this paper a kernel machine framework to test for individual gene effects on a continuous outcome in the presence of possible gene-gene interactions in a gene set/pathway using the garrote kernel (GKM) test. We have developed a garrote kernel based score test by introducing a garrote parameter in the kernel function. This framework does not require us to explicitly test for all interaction terms and allows for modeling the gene effects both parametrically and nonparametrically. We have proposed to calculate the p-value of the GKM test using an easy-to-compute scaled chi-square test, where the degrees of freedom of the test are estimated from the data and account for correlation among the covariates. Our approach reduces the dimensionality of the testing problem to testing for one parameter and provides a significant power gain over the usual F-test by using a considerably smaller DF than the M DFs used by the F-test, especially when the Gaussian kernel is used, as shown in our simulation studies.

To correct for multiple comparisons of testing for individual gene effects in a gene set/pathway in the presence of possible gene-gene interactions, we have proposed a permutation test, which properly accounts for the correlation among the hypotheses, i.e. the same data are used for testing for different hypotheses. It would be useful to develop in the future an analytic test that can effectively accounts for the correlation among the tests. Some discussions about this issue using FDRs can be found in Schwartzman and Lin (2010).

Our permutation method can be easily extended to the case where a gene belongs to multiple pathways. Specifically, if a gene belongs to multiple pathways, to test for its significance, we analyze one pathway at a time by accounting for possible gene-gene interactions under model (1) and calculate the p-value for the gene. We then apply the same permutation procedure in Section 4 to calculate the p-value across multiple pathways, where the minimum of the p-values in step 4 is calculated across all the pathways.

We have mainly focused in this paper on continuous outcomes and a Gaussian regression model. The fundamental idea of introducing a garrote parameter in the kernel framework to conduct powerful tests can still be applied to more general models such as logistic regression or exponential class models. We are currently pursuing the testing problem in this generalized linear model setting. The results will be reported elsewhere.

Table 2.

Results of the simulation study described in Section 5. Displayed are the empirical size (c = 0) and power (c = 2,…, 8) of the proposed garrote kernel machine (GKM) test using the two-way interaction kernel (K_Int), the Gaussian kernel (K_Gauss), the PCA based test statistics $T_n^{\ast }$ and $T_n^{\ast \ast }$ (K_Gauss,PCA1 and K_Gauss,PCA2) using the Gaussian kernel as in Section 3.3, and the usual F-test for different settings with n = 100 and M = 8. Also presented, for the linear cases (h₁(·) and h₂(·)), are the results for the ideal classical score tests assuming the direction of the alternative is known. The nominal level was set be α = 0.05.

	Test	r = 0.0					r = 0.2					r = 0.5
		c = 0	c = 2	c = 4	c = 6	c = 8	c = 0	c = 2	c = 4	c = 6	c = 8	c = 0	c = 2	c = 4	c = 6	c = 8
h1(·)	F-test	0.057	0.160	0.606	0.934	0.996	0.054	0.173	0.546	0.911	0.995	0.053	0.116	0.372	0.739	0.940
	KInt	0.053	0.198	0.658	0.952	0.993	0.052	0.233	0.691	0.954	0.997	0.055	0.149	0.429	0.773	0.948
	KGauss	0.050	0.402	0.943	1.000	1.000	0.051	0.443	0.938	0.998	1.000	0.051	0.332	0.803	0.983	0.999
	KGauss,PCA1	0.051	0.396	0.912	0.998	1.000	0.058	0.385	0.895	0.994	1.000	0.051	0.315	0.796	0.954	0.998
	KGauss,PCA2	0.051	0.406	0.922	0.998	1.000	0.054	0.405	0.904	0.996	1.000	0.051	0.321	0.799	0.961	0.991
	Score test	0.050	0.441	0.947	1.000	1.000	0.054	0.454	0.943	0.996	1.000	0.048	0.335	0.862	0.988	0.998
h2(·)	F-test	0.057	0.197	0.713	0.981	0.999	0.054	0.259	0.808	0.993	1.000	0.053	0.228	0.736	0.970	1.000
	KInt	0.053	0.223	0.758	0.967	0.998	0.052	0.431	0.916	0.998	1.000	0.055	0.453	0.93	0.998	1.000
	KGauss	0.050	0.398	0.921	0.995	0.999	0.051	0.456	0.918	0.995	0.998	0.051	0.469	0.816	0.983	0.998
	KGauss,PCA1	0.051	0.389	0.910	0.992	1.000	0.058	0.420	0.901	0.992	0.999	0.051	0.426	0.857	0.991	0.999
	KGauss,PCA2	0.051	0.407	0.912	0.997	1.000	0.054	0.445	0.914	0.991	1.000	0.051	0.421	0.849	0.983	0.992
	Score test	0.050	0.556	0.961	0.998	1.000	0.054	0.805	0.995	0.999	1.000	0.048	0.991	1.000	1.000	1.000
h3(·)	F-test	0.051	0.095	0.214	0.462	0.701	0.057	0.069	0.138	0.248	0.443	0.051	0.053	0.085	0.123	0.203
	KInt	0.045	0.099	0.234	0.513	0.758	0.046	0.103	0.213	0.380	0.612	0.043	0.069	0.093	0.167	0.280
	KGauss	0.052	0.174	0.535	0.848	0.968	0.050	0.196	0.474	0.748	0.931	0.051	0.155	0.332	0.559	0.740
	KGauss,PCA1	0.053	0.173	0.548	0.820	0.966	0.051	0.197	0.443	0.706	0.914	0.052	0.135	0.295	0.567	0.720
	KGauss,PCA2	0.053	0.171	0.534	0.833	0.971	0.051	0.189	0.451	0.712	0.921	0.052	0.143	0.292	0.541	0.731
h4(·)	F-test	0.051	0.068	0.162	0.360	0.662	0.057	0.069	0.115	0.244	0.414	0.051	0.060	0.09	0.132	0.219
	KInt	0.045	0.067	0.180	0.428	0.700	0.046	0.097	0.196	0.407	0.639	0.043	0.084	0.119	0.260	0.409
	KGauss	0.052	0.143	0.454	0.798	0.963	0.050	0.162	0.389	0.654	0.870	0.051	0.134	0.259	0.464	0.638
	KGauss,PCA1	0.053	0.143	0.402	0.744	0.947	0.051	0.142	0.344	0.603	0.828	0.052	0.116	0.234	0.415	0.602
	KGauss,PCA2	0.053	0.142	0.442	0.787	0.952	0.051	0.136	0.371	0.623	0.837	0.052	0.121	0.255	0.485	0.646

Table 3.

Results of the simulation study described in Section 5. Displayed are the empirical size (c = 0) and power (c = 2,…, 8) of the proposed garrote kernel machine (GKM) test using the two-way interaction kernel (K_Int), the Gaussian kernel (K_Gauss), the PCA based test statistics $T_n^{\ast }$ and $T_n^{\ast \ast }$ (K_Gauss,PCA1 and K_Gauss,PCA2) using the Gaussian kernel as in Section 3.3, and the usual F-test for different settings with n = 200 and M = 10. Also presented, for the linear cases (h₁(·) and h₂(·)), are the results for the ideal classical score tests assuming the direction of the alternative is known. The nominal level was set be α = 0.05.

	Test	r = 0.0					r = 0.2					r = 0.5
		c = 0	c = 2	c = 4	c = 6	c = 8	c = 0	c = 2	c = 4	c = 6	c = 8	c = 0	c = 2	c = 4	c = 6	c = 8
h1(·)	F-test	0.050	0.325	0.940	1.000	1.000	0.052	0.302	0.900	0.998	1.000	0.058	0.183	0.694	0.966	1.000
	KInt	0.054	0.371	0.953	1.000	1.000	0.052	0.355	0.935	0.999	1.000	0.052	0.170	0.646	0.961	0.999
	KGauss	0.052	0.706	1.000	1.000	1.000	0.051	0.668	0.998	1.000	1.000	0.051	0.487	0.948	1.000	1.000
	KGauss,PCA1	0.049	0.716	0.996	1.000	1.000	0.049	0.644	0.996	1.000	1.000	0.048	0.453	0.953	0.999	1.000
	KGauss,PCA2	0.049	0.721	0.999	1.000	1.000	0.049	0.654	0.995	1.000	1.000	0.048	0.477	0.963	1.000	1.000
	Score test	0.051	0.799	1.000	1.000	1.000	0.055	0.756	0.998	1.000	1.000	0.049	0.644	0.990	1.000	1.000
h2(·)	F-test	0.050	0.476	0.990	1.000	1.000	0.052	0.587	0.998	1.000	1.000	0.058	0.589	0.997	1.000	1.000
	KInt	0.054	0.494	0.986	1.000	1.000	0.052	0.829	1.000	1.000	1.000	0.052	0.893	1.000	1.000	1.000
	KGauss	0.052	0.715	1.000	1.000	1.000	0.051	0.701	0.999	1.000	1.000	0.051	0.611	0.988	1.000	1.000
	KGauss,PCA1	0.049	0.730	0.997	1.000	1.000	0.049	0.744	0.997	1.000	1.000	0.048	0.719	0.998	1.000	1.000
	KGauss,PCA2	0.049	0.737	0.996	1.000	1.000	0.049	0.774	0.999	1.000	1.000	0.048	0.709	0.999	1.000	1.000
	Score test	0.051	0.884	0.999	1.000	1.000	0.055	0.992	1.000	1.000	1.000	0.049	1.000	1.000	1.000	1.000
h3(·)	F-test	0.043	0.112	0.414	0.817	0.956	0.044	0.070	0.176	0.419	0.713	0.054	0.065	0.102	0.196	0.305
	KInt	0.044	0.117	0.435	0.837	0.964	0.045	0.094	0.274	0.572	0.841	0.044	0.064	0.099	0.216	0.326
	KGauss	0.049	0.274	0.828	0.989	1.000	0.051	0.253	0.690	0.922	0.987	0.052	0.168	0.443	0.715	0.894
	KGauss,PCA1	0.046	0.293	0.803	0.981	0.999	0.051	0.234	0.641	0.912	0.986	0.051	0.153	0.439	0.712	0.866
	KGauss,PCA2	0.046	0.295	0.819	0.983	0.999	0.051	0.244	0.652	0.914	0.984	0.051	0.171	0.459	0.721	0.881
h4(·)	F-test	0.043	0.091	0.301	0.678	0.944	0.044	0.065	0.168	0.421	0.725	0.054	0.063	0.120	0.207	0.380
	KInt	0.044	0.090	0.328	0.696	0.957	0.045	0.098	0.336	0.661	0.895	0.044	0.089	0.214	0.435	0.676
	KGauss	0.049	0.190	0.700	0.963	0.996	0.051	0.201	0.560	0.857	0.970	0.052	0.133	0.349	0.634	0.835
	KGauss,PCA1	0.046	0.226	0.691	0.964	0.996	0.051	0.177	0.524	0.848	0.972	0.051	0.128	0.331	0.619	0.844
	KGauss,PCA2	0.042	0.215	0.690	0.963	0.996	0.053	0.174	0.534	0.853	0.977	0.051	0.124	0.342	0.606	0.889