A Computational Model for Predicting Experimental RNA and DNA Nearest-Neighbor Free Energy Rankings

Abstract

Hydrogen-bonding, intra-strand base-stacking, and inter-strand base-stacking energies were calculated for RNA and DNA dimers at the MP2(full)/6-311G** level of theory. Standard A-form RNA and B-form DNA geometries from average fiber diffraction data were employed for all base monomer and dimer geometries, and all dimer binding energies were obtained via single-point calculations. The effects of water solvation were considered using the PCM model. The resulting dimer binding energies were used to calculate the 10 unique RNA and 10 unique DNA computational nearest-neighbor energies, and the ranking of these computational nearest neighbor energies are in excellent agreement with the ranking of the experimental nearest neighbor free energies. These results dispel the notion that average fiber diffraction geometries are insufficient for calculating RNA and DNA stacking energies.

Introduction

The three-dimensional structure, conformational flexibility, and overall stability of RNA and DNA are dictated primarily by hydrogen bonding¹ and base-stacking interactions;² however, base-phosphate group interactions³ and base-ribose sugar interactions (in RNA)^3a also play a role. While the nature of hydrogen bonding has been widely studied and well documented,¹ the most important factor in RNA/DNA stabilization is base-stacking interactions, yet significant work remains before they are fully understood.⁴ The literature contains lively debate on the appropriate input geometries to use when computationally predicting relative base-stacking energies for either RNA or DNA. Perhaps the biggest current debate centers on the appropriateness of using RNA or DNA geometries derived from average fiber diffraction data to investigate RNA or DNA base-stacking interactions. The use of average fiber diffraction data to investigate nucleic acid base-stacking has a long history,⁵ and a recent study used B-DNA geometries obtained from average fiber diffraction data to probe the contribution of electrostatics, induction, exchange, and dispersion to the overall base-stacking binding energies via symmetry-adapted perturbation theory.^2b This work has received significant criticism on the basis that geometry averaging can result in repulsive interactions that are not found in nature, and it has been suggested that other methods for geometry selection are superior, such as employing MD simulations.^2a,4 The given reason for the supposed inferiority of RNA or DNA base-stacking geometries obtained from average fiber diffraction data is that they may contain non-natural, repulsive intermolecular contacts and that they give different relative base-stacking energies than other geometry selection methods.⁴ Of course, a much more satisfactory way to evaluate computational approaches is via comparison to experiment. The widely used RNA/DNA nearest-neighbor (NN) free energies⁶ offer the experimental data to evaluate approaches to calculating relative base-stacking energies. Quite surprisingly, however, the authors are unaware of any studies that have justified the use of certain RNA or DNA input geometries by benchmarking the resulting base-stacking energies to the relative NN free energies. In fact, it has been suggested that such a comparison is not even possible and that there is no correlation between calculated base-stacking energies and the experimental NN free energies.^2a This is a sentiment we disagree with for reasons outlined below. Here, we report calculated A-form RNA and B-form DNA base-stacking and hydrogen-bonding energies that employed input geometries obtained from average fiber diffraction data. The resulting base-stacking and hydrogen-bonding energies were used to generate NN energy rankings that are in excellent agreement with the experimental free energy rankings. Furthermore, the agreement with experiment is better than it is for computational approaches that employ MD simulations to obtain base-stacking input geometries.

Computational Approach

Although there are only 10 unique RNA and 10 unique DNA NN combinations, there are 16 possible intra-strand and 20 possible inter-strand base-stacking dimers for each biopolymer, along with the two possible H-bonding dimers. Scheme 1 graphically illustrates these three types of dimers, and the binding energies are shown in Tables 1 and 2. The geometries of the RNA and DNA base monomers and the 38 base dimers in Tables 1 and 2 were obtained from the InsightII (Accelrys, San Diego, CA) RNA/DNA visualization program, which employs average fiber diffraction data to generate the monomer and dimer structures. In each case, the sugar-phosphate backbone was omitted, and the N–C_sugar bond was substituted with either an N–H or N-CH₃ bond, yielding what is termed here RNA-H/DNA-H and RNA-Me/DNA-Me monomers and dimers, respectively. The position(s) of the N–H hydrogen atom and the N–CH₃ methyl group atoms were optimized for each monomer and dimer at the MP2(full)/6-311G** level of theory while the rest of the RNA/DNA base atoms were constrained to their InsightII position. The dimer total energies (E_Tot,Dim) were corrected for basis set superposition error (BSSE) via the counter-poise method,⁷ and the binding energy (E_bind) for each dimer was determined by subtracting the relevant MP2(full)/6-311G** monomer total energies (E_Tot,Mono) from the BSSE-corrected MP2(full)/6-311G** E_Tot,Dim values, as illustrated in Equation 1 where B_m and B_n are any RNA/DNA base. Note that the general B_m•B_n dimers in Equation 1 represent either H-bonding dimers, intra-strand base-stacking dimers, or inter-strand base-stacking dimers. Binding energies were determined both for RNA-H/DNA-H dimers (E_bind,H) and RNA-Me/DNA-Me dimers (E_bind,Me), using the general formula shown in Equation 1, and the values are given in Tables 1 and 2. The MP2(full)/6-311G** level of theory was employed because it has been shown to yield reliable stacking energies for arene-arene interactions.⁸ Finally, all of the E_bind,H and E_bind,Me energies were re-calculated taking into consideration water solvation via the polarized continuum model (PCM),⁹ which has been shown to perform well in modeling solvation effects,¹⁰ and these results are given in parentheses in Tables 1 and 2. The PCM calculations employed the default solute radii scheme and solvent dielectric constant at 310.15 K.⁹ It should be noted that PCM was parameterized for solvation free energies and formally should only be employed to correct for the effects of solvation on gas-phase free energies.¹¹ Of course, obtaining the thermodynamic data required to calculate free energies requires geometry optimization; however, one hallmark of the approach presented here is employing geometries from average diffraction

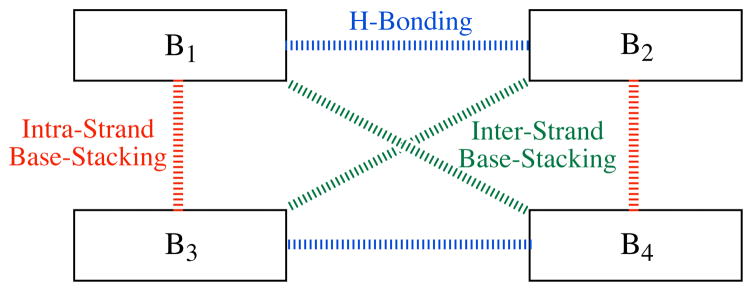
Scheme 1.

H-Bonding, Intra-Strand Stacking, and Inter-Strand Stacking Dimers for a General Four Nucleotide System Containing Monomers B₁ – B₄, where B₁ and B₃ are in one strand and B₂ and B₄ are in the other strand.

Table 1.

MP2(full)/6-311G** Calculated A-Form RNA Hydrogen Bonding, Intra-Strand Base-Stacking, and Inter-Strand Base-Stacking Energies (kcal/mol).^a

Hydrogen-Bonding Energies (kcal/mol)
Bases	Ebind,H	Ebind,Me	Bases	Ebind,H	Ebind,Me
A–U	−9.78	−11.46	C–G	−25.97	−25.86
	(−11.36)	(−12.29)		(−19.35)	(−20.61)
Intra-Strand Base-Stacking Energies (kcal/mol)
Bases	Ebind,H	Ebind,Me	Bases	Ebind,H	Ebind,Me
5’A	−0.14	−3.69	5’G	−5.88	−6.35
3’A	(−5.23)	(−8.87)	3’A	(−8.79)	(−9.59)
5’A	−1.95	−2.56	5’G	−8.80	−9.24
3’C	(−7.81)	(−8.49)	3’C	(−9.19)	(−10.09)
5’A	−5.48	−4.71	5’G	−0.12	−0.56
3’G	(−9.93)	(−8.02)	3’G	(−7.71)	(−8.52)
5’A	−2.06	−3.81	5’G	−0.36	−2.03
3’U	(−6.70)	(−7.56)	3’U	(−7.32)	(−8.36)
5’C	−1.83	−2.38	5’U	+0.38	−3.49
3’A	(−4.46)	(−5.11)	3’A	(−1.83)	(−4.65)
5’C	−0.46	−1.07	5’U	+1.51	−3.23
3’C	(−5.66)	(−6.24)	3’C	(−2.06)	(−5.96)
5’C	−3.17	−3.70	5’U	+0.04	−1.90
3’G	(−3.69)	(−4.39)	3’G	(−3.13)	(−4.69)
5’C	−2.85	−4.52	5’U	+2.20	−0.65
3’U	(−4.61)	(−5.49)	3’U	(−3.08)	(−4.14)
Inter-Strand Base-Stacking Energies (kcal/mol)
Bases	Ebind,H	Ebind,Me	Bases	Ebind,H	Ebind,Me
5’A_3’	−0.24	−0.27	5’_A3’	+1.14	+1.08
3’_A5’	(−1.12)	(−1.02)	3’A_5’	(−3.50)	(−3.55)
5’A_3’	+0.42	+0.42	5’_A3’	0.00	−0.14
3’_C5’	(−0.38)	(−0.24)	3’C_5’	(−3.18)	(−3.22)
5’A_3’	−2.44	−2.39	5’_A3’	−2.95	−3.06
3’_G5’	(−1.19)	(−4.45)	3’G_5’	(−4.33)	(−4.45)
5’A_3’	+1.06	−0.54	5’_A3’	−1.01	−2.70
3’_U5’	(+0.55)	(−0.26)	3’U_5’	(−2.11)	(−3.03)
5’C_3’	+1.14	+0.94	5’_C3’	+7.80	+0.93
3’_C5’	(−0.11)	(−0.11)	3’C_5’	(+4.29)	(−0.10)
5’C_3’	−2.29	−3.00	5’_C3’	−3.37	−3.53
3’_G5’	(+0.04)	(−0.44)	3’G_5’	(−3.26)	(−3.45)
5’C_3’	+1.09	−0.57	5’_C3’	−0.49	−2.27
3’_U5’	(+0.72)	(−0.13)	3’U_5’	(−0.46)	(−1.37)
5’G_3’	+2.79	+15.28	5’_G3’	−0.48	−0.64
3’_G5’	(−1.06)	(−4.45)	3’G_5’	(−3.95)	(−4.22)
5’G_3’	+2.05	+0.52	5’_G3’	+2.68	+1.12
3’_U5’	(+0.68)	(−0.19)	3’U_5’	(−1.37)	(−2.35)
5’U_3’	+3.11	+0.75	5’_U3’	+3.56	+0.74
3’_U5’	(−2.43)	(+0.67)	3’U_5’	(+0.91)	(−0.18)

^aNon-solvated E_bind,H and E_bind,Me values on top and not in parentheses. Solvated E_bind,H and E_bind,Me values on bottom and in parentheses. Solvation accounted for via the PCM method.

Table 2.

MP2(full)/6-311G** Calculated B-Form DNA Hydrogen Bonding, Intra-Strand Base-Stacking, and Inter-Strand Base-Stacking Energies (kcal/mol).^a

Hydrogen-Bonding Energies (kcal/mol)
Bases	Ebind,H	Ebind,Me	Bases	Ebind,H	Ebind,Me
A–T	−13.53	−13.92	C–G	−27.31	−27.40
	(−14.54)	(−15.05)		(−20.35)	(−20.40)
Intra-Strand Base-Stacking Energies (kcal/mol)
Bases	Ebind,H	Ebind,Me	Bases	Ebind,H	Ebind,Me
5’A	−1.60	−4.81	5’G	−6.66	−5.33
3’A	(−7.31)	(−11.52)	3’A	(−10.75)	(−12.19)
5’A	−3.03	−0.41	5’G	−8.04	−8.34
3’C	(−8.46)	(−8.73)	3’C	(−9.01)	(−10.17)
5’A	−5.48	−6.63	5’G	−1.05	−2.39
3’G	(−9.85)	(−11.35)	3’G	(−10.27)	(−11.86)
5’A	−3.81	−3.38	5’G	−2.64	−3.87
3’T	(−9.00)	(−10.51)	3’T	(−9.17)	(−10.40)
5’C	−1.82	−3.35	5’T	−2.62	−4.66
3’A	(−5.80)	(−7.40)	3’A	(−5.55)	(−7.47)
5’C	+0.30	−0.68	5’T	−2.43	−3.39
3’C	(−5.86)	(−6.98)	3’C	(−6.37)	(−7.39)
5’C	−4.24	−5.29	5’T	−3.16	−3.47
3’G	(−5.75)	(−6.94)	3’G	(−6.03)	(−9.38)
5’C	−3.61	−5.00	5’T	−6.26	−2.94
3’T	(−6.91)	(−8.45)	3’T	(−11.10)	(−12.41)
Inter-Strand Base-Stacking Energies (kcal/mol)
Bases	Ebind,H	Ebind,Me	Bases	Ebind,H	Ebind,Me
5’A_3’	+3.72	−0.42	5’_A3’	−1.49	−1.51
3’_A5’	(−2.31)	(−2.37)	3’A_5’	(−4.28)	(−4.39)
5’A_3’	+3.99	+0.27	5’_A3’	+0.79	+0.72
3’_C5’	(+2.27)	(−1.07)	3’C_5’	(−1.83)	(−1.94)
5’A_3’	−2.99	−3.22	5’_A3’	−3.40	−3.39
3’_G5’	(−2.70)	(−2.81)	3’G_5’	(−5.15)	(−5.08)
5’A_3’	−2.29	−2.13	5’_A3’	−0.12	−2.87
3’_T5’	(−2.80)	(−2.45)	3’T_5’	(−1.17)	(−3.33)
5’C_3’	+1.31	+1.15	5’_C3’	+3.05	+2.80
3’_C5’	(−0.37)	(−0.43)	3’C_5’	(−0.16)	(−0.20)
5’C_3’	−4.07	−4.24	5’_C3’	−2.80	−3.06
3’_G5’	(−1.00)	(−1.13)	3’G_5’	(−2.45)	(−2.65)
5’C_3’	−2.19	−2.12	5’_C3’	−1.89	−1.94
3’_T5’	(−2.16)	(−1.93)	3’T_5’	(−2.26)	(−2.11)
5’G_3’	−3.01	+1.36	5’_G3’	−3.01	−3.65
3’_G5’	(−5.79)	(−3.18)	3’G_5’	(−5.79)	(−6.13)
5’G_3’	−3.01	−1.66	5’_G3’	−1.61	−1.80
3’_T5’	(−2.56)	(−2.27)	3’T_5’	(−3.99)	(−3.81)
5’T_3’	−1.34	−1.42	5’_T3’	−1.14	−1.30
3’_T5’	(−2.03)	(−2.01)	3’T_5’	(−2.12)	(−2.11)

^aNon-solvated E_bind,H and E_bind,Me values on top and not in parentheses. Solvated E_bind,H and E_bind,Me values on bottom and in parentheses. Solvation accounted for via the PCM method.

$${\text{E}}_{\text{bind}}({\text{B}}_{\text{m}}•{\text{B}}_{\text{n}})={\text{E}}_{\text{Tot},\text{Dim}}({\text{B}}_{\text{m}}•{\text{B}}_{\text{n}})-({\text{E}}_{\text{Tot},\text{Mono}}({\text{B}}_{\text{m}})+{\text{E}}_{\text{Tot},\text{Mono}}({\text{B}}_{\text{n}}))$$ Equation 1

data. As it is ill advised to calculate free energies using geometries from average diffraction data, which are not gas-phase optimized, we have refrained from doing so. Still, PCM calculations were performed since this was the best available option to account for solvation. All calculations were performed using the Gaussian09 suite of programs.¹²

Results and Discussion

Dimer Binding Energies and Solvation

The hydrogen-bonding, intra-strand base-stacking, and inter-strand base-stacking energies in Tables 1 and 2 show that solvation, at least when accounted for via the PCM model, usually makes the dimer binding energies, E_bind,H and E_bind,Me, more stable with respect to the non-solvated values. Specifically, 33 of the 38 RNA dimer E_bind,H values, 32 of the 38 RNA dimer E_bind,Me values, 32 of the 38 DNA dimer E_bind,H values, and 33 of the 38 DNA dimer E_bind,Me values are more stable when solvation is considered (Tables 1 and 2). All of the RNA and DNA intra-strand base-stacking dimers, those where the bases are directly on top of one another ( $\begin{array}{l}{5}^{\prime }{\text{B}}_1\hfill \\ 3^{\prime }{\text{B}}_3\hfill \end{array}\text{and}\begin{array}{l}{5}^{\prime }{\text{B}}_2\hfill \\ 3^{\prime }{\text{B}}_4\hfill \end{array}$ in Scheme 1), are more stable when solvated by water. The five or six instances for each case (E_bind,H and E_bind,Me, both gas-phase/vacuum and solvated) where the non-solvated gas-phase/vacuum E_bind values are more stable than the PCM water solvated E_bind values are either G–C H-bonding dimers (B₁–B₂ and B₃–B₄ in Scheme 1) or inter-strand base-stacking dimers ( $\begin{array}{l}{\text{B}}_1\_\_\hfill \\ \_\_{\text{B}}_4\hfill \end{array}\text{and}\begin{array}{l}\_\_{\text{B}}_2\hfill \\ {\text{B}}_3\_\_\hfill \end{array}$ in Scheme 1). Solvation leading to more stable dimer binding energies is certainly not always the case. For instance, recent work on amino acid pair interaction energies showed that the introduction of ether or water solvent decreased the binding energy by about half.¹³ In fact, the calculated amino acid binding energies decreased in going from gas-phase/vacuum to ether to water, showing that the greater the solvent polarity the less the binding. In contrast, computational work on the π-π stacking interactions between DNA bases and members of the indenoisoquinoline class of topoisomerase I inhibitors showed that water solvation stabilized the complexes.¹⁴ Thus, gas-phase/vacuum base-stacking interactions where the monomers are directly on top of each other appear to be stabilized when solvated by water. In contrast, interactions where the monomers are not directly on top of one another, such as the H-bonding dimers and the inter-strand base-stacking dimers, appear less likely to be stabilized by water since these are the only instances where a decrease in dimer stability is observed when going from gas-phase/vacuum to water. It is worth noting here that although we employ the term ‘stacking’ for the inter-strand stacking dimers, the monomers are not in the same strand and, while there is more overlap than suggested by the general block diagram view in Scheme 1, the overlap between the monomers is quite small compared to the intra-strand dimers.

The differences in how much water stabilizes, or destabilizes, the dimers compared to gas-phase/vacuum can be explained, to a large degree, by the differential effect of water solvation on the dimer dipole moments. For the purposes of the following discussion, the difference in dipole moment in going from gas-phase/vacuum to water, for the monomers or dimers, will be referred to as ΔD_sol. The average ΔD_sol values for the RNA-H and RNA-Me monomers, ΔD_sol,H and ΔD_sol,Me, are 27.5% and 29.2% respectively, whereas the average ΔD_sol,H and ΔD_sol,Me values for the RNA-H and RNA-Me intra-strand dimers are 129.4% and 135.9% (all calculated RNA and DNA monomer and dimer dipole moments are in the Supporting Information). The fact that the intra-strand base stacking dimers increase in polarity to a much greater extent than do the monomers when going from gas-phase/vacuum to water explains why the intra-strand base stacking dimers are greatly stabilized in water. By comparison, the average ΔD_sol,H and ΔD_sol,Me values for the RNA-H and RNA-Me inter-strand dimers are 50.7% and 83.7%. This shows that the inter-strand dimers increase in polarity to a slightly greater degree than do the monomers when going from gas-phase/vacuum to water, and it is thus not surprising that some of these dimers are destabilized by water solvation while most of them are stabilized. The change in dipole moment upon water solvation for the RNA-H and RNA-Me H-bonding dimers is exactly as expected based on the E_bind values from Table 1. The RNA-H and RNA-Me A–U H-bonding dimer E_bind,H and E_bind,Me values are more stabilized in water compared to gas-phase/vacuum, and the dipole moment of these dimers increases by 42.7% and 47.7%, respectively. Conversely, the RNA-H and RNA-Me G–C H-bonding dimer E_bind,H and E_bind,Me values are destabilized in water, and the dipole moments decrease by 8.9% and 11.0%, respectively. While the average ΔD_sol values work very well in explaining the overall trend in how water solvation affects the E_bind values in Table 1, one should be cautioned against viewing this as a comprehensive approach for explaining how solvation affects trends in binding energies. For instance, three of the RNA-H and RNA-Me intra-strand dimers either decrease in polarity upon water solvation or increase in polarity to a smaller extent than the constituent monomers, yet water solvation stabilizes the E_bind,H values. The same trend occurs for four of the RNA-H inter-strand dimers and five of the RNA-Me inter-strand dimers. Still, almost all of the RNA-H and RNA-Me dimers that are destabilized upon water solvation become less polar in going from gas-phase/vacuum to water. Furthermore, the E_bind values for 30 of the 38 RNA-H dimers and 28 of the 38 RNA-Me dimers can be rationalized via the ΔD_sol values.

Determining Nearest-Neighbor (NN) Energy Rankings

The best way to benchmark the H-bonding and base-stacking energies in Tables 1 and 2 is through comparison with experiment, and the most appropriate experimental data are the well-documented NN thermodynamic parameters.⁶ As noted in the introduction, it has been suggested that this is not a viable approach for evaluating experimental base-stacking calculations;^2a,4 however, we disagree with this sentiment for the reasons outlined here. The approach we propose to evaluate the H-bonding and base-stacking energies in Tables 1 and 2 is to computationally determine NN energies (E_NN) and compare the rankings to the ΔG_NN,exp rankings, as shown in Table 3. The E_NN values are calculated as the sum of the intra-strand base-stacking energies, inter-strand base-stacking energies, and one-half the H-bonding energies. The H-bonding energies were halved due to the manner in which the experimental NN free energies were determined.⁶ Scheme 2 shows an example of how E_NN is calculated for the $\begin{array}{l}{5}^{\prime }\text{C}-\text{G}{3}^{\prime }\hfill \\ 3^{\prime }\text{U}-\text{A}{5}^{\prime }\hfill \end{array}$ NN four nucleotide system. Although this calculation does not include a contribution from entropy, the rankings of the E_NN values are compared to the ΔG_NN,exp rankings. The ΔH_NN,exp rankings were not used due to the large errors associated with enthalpy values derived from optical melting experiments.⁶ In addition to ignoring entropy, the method described here has another limitation. The ΔG_NN,exp values were determined via optical melting experiments,⁶ which from a molecular standpoint involve heating a double-stranded base-paired segment of RNA or DNA in buffered aqueous solution until the segment unwinds and becomes single-stranded.⁶ It is important to recognize that the experimental values are ΔG values, or the difference between the double-stranded state and the single-stranded state. The computational values that we determine, however, calculate the stabilizing energetics involved within the double-stranded state and do not account for the single stranded state. Therefore, there is a significant difference in the magnitude of the computational and experimental numbers. In comparing the relative rankings of the computational and experimental numbers, we are assuming that forces present in the single-stranded state (i.e. decreased base stacking) are relatively independent of sequence.

Table 3.

Relative Rank Comparison between RNA and DNA Experimental Nearest-Neighbor (NN) Free Energies and Computational E_NN Values.^a

RNA Nearest-Neighbor Energies (kcal/mol)
NN	ΔGNN,expb (Rank)	ENN,Calc-Hc (Rank)	ENN,Calc-H,Sold (Rank)	ENN,Calc-Mee (Rank)	ENN,Calc-Me,Solf (Rank)	Ref. 2a Rank
5’AU3’	−0.93	−7.68	−21.24	−19.04	−28.60	2
3’AU5’	(1)	(2)	(2)	(3)	(2.5)g
5’AU3’	−1.10	−10.59	−24.98	−18.61	−28.60	3
3’UA5’	(2)	(3)	(3)	(2)	(2.5)g
5’UA3’	−1.33	−4.78	−20.96	−11.46	−24.47	8
3’AU5’	(3)	(1)	(1)	(1)	(1)
5’CG3’	−2.08	−23.10	−31.64	−26.36	−32.56	4
3’UA5’	(4)	(6)	(7)	(4)	(5)
5’CG3’	−2.11	−21.52	−26.56	−26.57	−30.84	5
3’AU5’	(5)	(5)	(4)	(5)	(4)
5’AU3’	−2.24	−23.12	−32.13	−27.91	−39.12	6
3’CG5’	(6)	(7)	(8)	(7)	(8)
5’GC3’	−2.35	−20.19	−28.70	−27.85	−35.40	7
3’AU5’	(7)	(4)	(5)	(6)	(7)
5’CG3’	−2.36	−31.65	−30.80	−32.96	−33.72	9
3’GC5’	(8)	(8)	(6)	(9)	(6)
5’GC3’	−3.26	−32.21	−35.94	−34.02	−39.26	1
3’GC5’	(9)	(9)	(10)	(10)	(9)
5’GC3’	−3.42	−32.97	−34.50	−28.12	−45.34	10
3’CG5’	(10)	(10)	(9)	(8)	(10)
MADh	–	1.0	1.6	1.0	1.0	1.6
rsi	–	0.88	0.82	0.90	0.90	0.44
DNA Nearest-Neighbor Energies (kcal/mol)
NN	ΔGNN,expb (Rank)	ENN,Calc-Hc (Rank)	ENN,Calc-H,Sold (Rank)	ENN,Calc-Mee (Rank)	ENN,Calc-Me,Solf (Rank)	Ref. 2a Rank
5’TA3’	−0.60	−21.60	−31.96	−26.16	−36.39	7
3’AT5’	(1)	(2)	(1)	(2)	(1)
5’AT3’	−0.73	−18.58	−36.98	−22.40	−40.55	6
3’TA5’	(2)	(1)	(5)	(1)	(2)
5’AT3’	−1.02	−23.80	−36.92	−26.67	−44.76	5
3’AT5’	(3)	(3)	(4)	(3)	(10)
5’AT3’	−1.16	−27.13	−35.93	−33.82	−42.39	2
3’GC5’	(4)	(4)	(2)	(7)	(7)
5’CG3’	−1.38	−30.99	−36.59	−32.99	−41.53	3
3’AT5’	(5)	(6)	(3)	(6)	(5)
5’AT3’	−1.43	−30.97	−40.03	−30.10	−41.77	8
3’CG5’	(6)	(5)	(9)	(4)	(6)
5’GC3’	−1.46	−31.72	−38.95	−30.32	−41.51	4
3’AT5’	(7)	(7)	(7)	(5)	(4)
5’CG3’	−1.77	−34.92	−39.93	−37.77	−43.03	1
3’CG5’	(8)	(8)	(8)	(8)	(8)
5’CG3’	−2.09	−37.49	−38.01	−40.48	−40.84	9
3’GC5’	(9)	(9)	(6)	(10)	(3)
5’GC3’	−2.28	−43.35	−44.30	−39.92	−44.11	10
3’CG5’	(10)	(10)	(10)	(9)	(9)
MADh	–	0.4	1.4	1.2	2.0	2.8
rsi	–	0.98	0.78	0.87	0.37	0.24

^aThe rank for each approach is in parentheses under the E_NN values, with the least energetically favorable nearest-neighbor combination ranked 1 and the most favorable ranked 10.

^bΔG_NN,exp are the experimental nearest-neighbor energies from reference 6.

^cE_NN,Calc-H is the calculated nearest-neighbor energies where the sugar was replaced by an H atom and solvation is not considered.

^dE_{NN,Calc-H,Sol} is the calculated nearest-neighbor energies where the sugar was replaced by an H atom and solvation is considered via the PCM method.

^eE_NN,Calc-Me is the calculated nearest-neighbor energies where the sugar was replaced by a methyl group and solvation is not considered.

^fE_{NN,Calc-Me,Sol} is the calculated nearest-neighbor energies where the sugar was replaced by a methyl group and solvation is considered via the PCM method.

^gThe RNA E_{NN,Calc-Me,Sol} values are the exact same for the nearest-neighbor four nucleotide systems that would be ranked second and third, and thus they were each given a rank of 2.5.

^hMean absolute difference (MAD) is determined by taking the mean of the absolute difference between the NN four nucleotide system ranking of the calculated value and the ranking of the corresponding experimental value.

ⁱThe Spearman rank correlation coefficient (r_s) was determined as shown in Reference 15.

Scheme 2.

Approach Used to Calculate Computational Nearest-Neighbor Energies (E_NN)

Using the approach outlined in Scheme 2, computational NN energies (E_NN) were calculated for the 10 unique RNA and 10 unique DNA NN four nucleotide systems using the E_bind,H and E_bind,Me values in Tables 1 and 2, and the results are presented in Table 3. The E_bind,H and E_bind,Me values in Tables 1 and 2 allow for four different approaches to the calculation of E_NN values. The E_bind,H and E_bind,Me values without consideration of solvation can be employed, and the nearest-neighbor energies that result from these values are termed E_NN,Calc-H and E_NN,Calc-Me, respectively, in Table 3. In addition, the E_bind,H and E_bind,Me values that account for solvation via the PCM method can be used, and the resulting nearest-neighbor energies in Tables 3 are termed E_{NN,Calc-H,Sol} and E_{NN,Calc-Me,Sol}. Of note in Table 3, the RNA and DNA E_NN,Calc-H, E_{NN,Calc-H,Sol}, E_NN,Calc-Me, and E_{NN,Calc-Me,Sol} values are all much larger in magnitude than the corresponding experimental values (ΔG_NN,exp). The discrepancy between the magnitude of the calculated and experimental values in Table 3 is likely due to the reasons outlined above: the E_NN do not account for entropy, nor do they account for the enthalpic/energetic stability of the single-stranded RNA or DNA segments. Other minor issues may be that the ΔG_NN,exp values also contain information on the reorganization of the sugar-phosphate backbone and on the differential solvation of the double- and single-stranded RNA or DNA segments, while the E_NN values would clearly not account for these factors. Of course, the suggestion here is that these factors would affect the magnitude of the E_NN values in Table 3 and not the relative rank. Thus, despite its limitations, the comparison of the relative E_NN values with the relative ΔG_NN,exp values provides a reasonable approach to evaluating the H-bonding and base-stacking energies in Tables 1 and 2.

The numbers in parentheses in Table 3 are the relative rankings of the NN four nucleotide systems using the four different approaches. The least stable NN four nucleotide system is given a ranking of 1 and the most stable is given a ranking of 10. The E_NN,Calc-H, E_{NN,Calc-H,Sol}, E_NN,Calc-Me, and E_{NN,Calc-Me,Sol} columns end with mean absolute deviation (MAD) and Spearman rank correlation coefficient (r_s)¹⁵ values for the computational approach. The MAD values were determined by taking the mean of the absolute difference between the NN four nucleotide system ranking of the calculated value and the ranking of the corresponding experimental value, ΔG_NN,exp. For RNA, the E_NN,Calc-H, E_NN,Calc-Me, and E_{NN,Calc-Me,Sol} numbers each have a MAD of 1.0, while the E_{NN,Calc-H,Sol} values have a MAD of 1.6. For DNA, the E_NN,Calc-H, E_{NN,Calc-H,Sol}, E_NN,Calc-Me, and E_{NN,Calc-Me,Sol} values give MADs of 0.4, 1.4, 1.2, and 2.0, respectively. Most of these MAD values are quite good, and the agreement between the DNA E_NN,Calc-H and ΔG_NN,exp values is excellent (MAD of 0.4). The calculated gas-phase/vacuum E_NN values are either better than, or equal to, the PCM calculated water solvated E_NN values; the MAD values for the RNA E_NN,Calc-Me and E_{NN,Calc-Me,Sol} are both 1.0, and in all other cases, the MADs are better for the gas-phase/vacuum E_NN values than for the water solvated E_NN values (Table 3). This may seem somewhat surprising since the ΔG_NN,exp values were obtained in water; however, recall that there are numerous differences in how the E_NN and ΔG_NN,exp values are determined. Thus, there is no reason to expect calculated water solvated E_NN values would be any better or worse than the calculated gas-phase/vacuum E_NN values.

A statistical approach to test for how well two rankings correlate with each other is the r_s value. The Spearman rank correlation test was applied to the association between the experimental and calculated rankings with a null hypothesis of no association between the rankings. For rankings with 10 data points, an r_s value greater than 0.794 shows the null hypothesis can be rejected at the 99.5% confidence level,¹⁵ and thus there is a correlation between the two rankings. Thus, for all four calculated RNA E_NN values, we can say that the calculated rankings are very strongly correlated with the experimental ΔG_NN,exp ranking. For the calculated DNA E_NN values, only the E_NN,Calc-H and E_NN,Calc-Me rankings have r_s values above 0.794, and thus have strong correlations with the experimental ΔG_NN,exp ranking. For the E_{NN,Calc-H,Sol} ranking, the r_s value is just below the cutoff for association with the ΔG_NN,exp ranking at the 99.5% confidence level, and instead meets the 0.745 standard of the 99% confidence level.¹⁵ The DNA E_{NN,Calc-Me,Sol} ranking has an r_s value of 0.37, and the null hypothesis holds at all confidence levels; there is no correlation with the experimental ranking. Given the strong correlation between all of the RNA E_NN rankings and the experimental ΔG_NN,exp ranking, and between two of the DNA E_NN rankings and the ΔG_NN,exp ranking, it is fair to say the approach presented in Scheme 2 has high predictive value in determining relative RNA and DNA ΔG_NN,exp rankings.

There are two important results in Table 3. First, the MAD and r_s values in Table 3 validate the assumptions that went into using relative E_NN values, calculated using the equation in Scheme 2, as a means for predicting relative ΔG_NN,exp values. Second, and perhaps most important, the very good agreement between the E_NN and ΔG_NN,exp rankings validates the use of average diffraction data to generate RNA and DNA geometries for calculating H-bonding and base-stacking energies. Of note, this is not the first computational study to rank the 10 unique RNA and 10 unique DNA nearest-neighbor four nucleotide systems. Sponer and coworkers also calculated and ranked the NN four nucleotide system energies using RNA and DNA geometries obtained from MD simulations, and the results are shown in the last column of Table 3.^2a Sponer and coworkers did not determine MAD and r_s values for their calculated rankings, and thus we did so and included them in Table 3. The RNA MAD value of 1.6 for the Sponer and coworkers ranking is not that bad, it is the same as for the poorest RNA E_NN value reported in this study, the E_{NN,Calc-H,Sol} value; however, the r_s value of 0.44 is significantly worse than any of the RNA r_s values reported for the E_NN rankings calculated via the approach outlined in Scheme 2, and it suggests there is no correlation between the Sponer and coworkers ranking and the experimental ΔG_NN,exp ranking. The DNA MAD value of 2.8 and the r_s value of 0.24 for the Sponer and coworkers ranking are both very weak, and they too suggest no correlation with the experimental ΔG_NN,exp ranking. Sponer and coworkers “conclude that there is no quantitative correlation between the QM gas phase stacking data, irrespective of the accuracy of the calculations, and the nucleic acids stability.”^2a Although this is certainly true using the approach Sponer and coworkers employed, the results of the present study show this statement is not general; there most definitely is a quantitative correlation between the quantum mechanical (QM) gas-phase stacking data and nucleic acid stability, in the form of the comparison between the relative calculated E_NN values and the relative experimental ΔG_NN,exp values. It is worth mentioning that the format used here to name NN four nucleotide systems is different than the format employed in the papers reporting the experimental values (ΔG_NN,exp),⁶ but it is the same as the format used by Sponer and coworkers.^2a Therefore, the four nucleotide system denoted $\begin{array}{l}{5}^{\prime }\text{A}-\text{U}{3}^{\prime }\hfill \\ 3^{\prime }\text{A}-\text{U}{5}^{\prime }\hfill \end{array}$ here is termed $\begin{array}{l}{5}^{\prime }\text{A}-\text{A}{3}^{\prime }\hfill \\ 3^{\prime }\text{U}-\text{U}{5}^{\prime }\hfill \end{array}$ in the experimental work.⁶ It was determined that being consistent with the work of Sponer and coworkers^2a was more important due to the comparisons made with the study.

Table 3 reveals that the key to attaining a good correlation between calculated relative E_NN values and relative ΔG_NN,exp values is to at least predict that the four nucleotide systems with four H-bonds are least stable, the four nucleotide systems with five H-bonds are of intermediate stability, and the four nucleotide systems with six H-bonds are most stable. That is, four nucleotide systems with only A and U(T) bases need to be ranked 1 – 3, four nucleotide systems with one of each base need to be ranked 4 – 7, and four nucleotide systems with only C and G bases need to be ranked 8 – 10. For the work presented here, of the five instances in Table 3 where the MAD values are 1.2 and below, four of them meet this standard. Only for the RNA E_{NN,Calc-Me,Sol} values, where the MAD value is 1.0, does this not hold; the $\begin{array}{l}{5}^{\prime }\text{A}-\text{U}{3}^{\prime }\hfill \\ 3^{\prime }\text{C}-\text{G}{5}^{\prime }\hfill \end{array}$ four nucleotide system is ranked 8 and the $\begin{array}{l}{5}^{\prime }\text{C}-\text{G}{3}^{\prime }\hfill \\ 3^{\prime }\text{G}-\text{C}{5}^{\prime }\hfill \end{array}$ four nucleotide system is ranked 6. Experimentally, these two four nucleotide systems are ranked 6 and 8, respectively, and since the calculated and experimental rankings are still quite close, it does not negatively affect the MAD value. Not surprisingly, the r_s values for the five computational E_NN rankings with MAD values ≤ 1.2 show the strongest correlation with the respective ΔG_NN,exp rankings. The two cases from the work presented here with four nucleotide system ranking MAD values of 1.6 and 2.0 (Table 3), along with the Sponer and coworkers calculated RNA four nucleotide system ranking (MAD value of 1.6, Table 3),^2a all have two instances where the four nucleotide system rankings do not meet the standard based on number of H-bonds. In the case of the RNA E_{NN,Calc-H,Sol} ranking, with MAD value of 1.6, the r_s value of 0.82 still shows a very strong correlation with the ΔG_NN,exp rankings. However, the DNA E_{NN,Calc-Me,Sol} ranking, with MAD of 2.0, and the Sponer and coworkers RNA ranking, with MAD of 1.6, have very weak r_s values of 0.37 and 0.44 respectively, suggesting there is no correlation with the corresponding ΔG_NN,exp rankings. Surprisingly, the DNA E_{NN,Calc-H,Sol} values have a MAD value of 1.4, yet six of the four nucleotide systems do not meet the standard based on number of H-bonds. Not surprisingly, the slightly weaker r_s value of 0.78 captures the deterioration in correlation with the corresponding ΔG_NN,exp ranking. A quick look at the E_{NN,Calc-H,Sol} column in Table 3 show that it is quite fortuitous that the MAD and r_s values remain decent; the four nucleotide systems that are in the wrong group based on number of H-bonds are still quite close to the experimental ΔG_NN,exp four nucleotide system ranking. As would be expected, the Sponer and coworkers DNA four nucleotide system ranking,^2a with a MAD value of 2.8 and an r_s value of 0.24, has seven of the ten calculated four nucleotide systems ranked in the wrong group according to number of H-bonds (Table 3).

Briefly, it is important to note the differences between the approach presented here and the approach employed by Sponer and coworkers.^2a Of course, Sponer and coworkers employed MD simulations for the selection of RNA/DNA base geometries. Although the geometries do not differ dramatically from the ones employed in this study, relatively minor changes in geometry can significantly impact base-stacking binding energies.¹⁶ In addition, Sponer and coworkers determined four nucleotide system binding energies as the sum of the intra-strand and inter-strand binding energies, along with a many body correction term, which is slightly different than the approach outlined in Scheme 2.

Conclusions

The work presented here outlines an approach for determining relative RNA and DNA nearest neighbor stability via the calculation of nucleic acid base H-bonding dimer energies, intra-strand base-stacking binding energies, and inter-strand base-stacking binding energies. Combining these terms via the equation shown in Scheme 2 for the 10 unique RNA and 10 unique DNA four nucleotide systems (Table 3) and ranking the resulting E_NN values gives very good agreement with the ΔG_NN,exp rankings. For both RNA and DNA, the best agreement with experiment was obtained when the gas-phase/vacuum H-bonding and base-stacking energies were employed to determine the E_NN values. Taking into account solvation via the PCM method always led to more attractive bonding and base-stacking dimers, and more attractive E_NN values, than the corresponding gas-phase vacuum values. This can be explained, to a large degree, by taking into account the change in monomer and dimer dipole moments upon PCM water solvation. One of the most important aspects of this study is that the RNA and DNA base monomer and dimer geometries were taken from average fiber diffraction data via the InsightII RNA/DNA visualization program. Using average fiber diffraction data to calculate RNA and DNA base-stacking energies has been heavily criticized, on quite reasonable grounds, and other approaches to choosing RNA and DNA base monomer and dimer geometries, such as MD simulations, have been touted as being far superior.^2a However, such comparisons ring hollow in the absence of comparison with experiment. The authors are not aware of any studies that use the well documented ΔG_NN,exp four nucleotide system rankings,⁶ or any other experimental values, to justify the calculation of base-stacking energies using a particular approach to obtaining RNA or DNA base monomer and dimer geometries. The findings here show that using RNA and DNA base monomer and dimer geometries obtained from average fiber diffraction data to calculate base-stacking and H-bonding energies and using these energies to determine relative four nucleotide system E_NN rankings gives very good agreement with relative ΔG_NN,exp four nucleotide system rankings. In fact, the agreement with experiment is better than for studies that used RNA and DNA base monomer and dimer geometries obtained from MD simulations, although the MD simulation studies used a different approach to determine relative four nucleotide system stability rankings.^2a This dispels the notion that RNA and DNA base monomer and dimer geometries obtained from average fiber diffraction data are inferior to other methods for geometry selection and suggests, at the very least, that the chosen method for calculating relative four nucleotide system stability, relative E_NN values (Scheme 2) for the work reported here, is as important as the method for selecting the nucleic acid base monomer and dimer geometries. Finally, it should be noted that the calculated E_NN values ignore cooperativity effects between bases. Given the excellent agreement between E_NN and ΔG_NN,exp rankings, this was obviously not a major problem; however, it is possible that properly addressing this issue could lead to improved correlations. Future work will include addressing the assumptions that went into using relative E_NN values to predict relative ΔG_NN,exp values to determine if a better correlation can be obtained and employing this approach to help understand experimental thermodynamic data, such as why replacing an adenine with inosine gives less stable ΔG_NN,exp values.¹⁷