A novel approach for predicting the uptake and toxicity of metallic and metalloid ions

Abstract

Electrostatic nature of plant plasma membrane (PM) plays significant roles in the ion uptake and toxicity. Electrical potential at the PM exterior surface (ψ₀^o) influences ion distribution at the PM exterior surface, and the depolarization of ψ₀^o negativity increases the electrical driving force for cation transport, but decreases the driving force for anion transport across the PMs. Assessing environmental risks of toxic ions has been a difficult task because the ion concentration (activity) in medium is not directly corrected to its potential effects. Medium characteristics like the content of major cations have important influences on the bioavailability and toxicity of ions in natural waters and soils. Models such as the Free Ion Activity Model (FIAM) and the Biotic Ligand Model (BLM), as usually employed, neglect the ψ₀^o and hence often lead to false conclusions about interaction mechanisms between toxic ions and major cations for biology. The neglect of ψ₀^o is not inconsistent with its importance, and possibly reflects the difficulty in the measurement of ψ₀^o. Based on the dual effects of the ψ₀^o, electrostatic models were developed to better predict the uptake and toxicity of metallic and metalloid ions. These results suggest that the electrostatic models provides a more robust mechanistic framework to assess metal(loid) ecotoxicity and predict critical metal(loid) concentrations linked to a biological effect, indicating its potential utility in risk assessment of metal(loid)s in water and terrestrial ecosystems.

GCS Model and Calculation of ψ₀^o

The Gouy-Chapman-Stern (GCS) model combines a classic electrostatic Gouy-Chapman theory and ion binding (Stern model). The Gouy-Chapman theory describes the electric double layer originated from negative charges and dipoles on the hydrophilic outer surface of PMs. The Stern model developed by Kinraide et al.¹ describes the strong interactions for binding of ions to PM sites. Therefore, the GCS model incorporates the intrinsic surface charge density (σ₀) of a membrane, the ion composition of the bathing medium, and ion binding to the membrane.

The Gouy-Chapman portion of the model can be expressed in the Müller (Grahame) equation (derivation presented in Barber²). This equation describes the relationships among the PM exterior surface charge density (σ_PMS), the ion concentrations in bulk-phase medium (BM) ([I^Z]_b), and the electrical potential at the PM surface (ψ₀^o).

$${\sigma }^2=2{\epsilon }_r{\epsilon }_{0}RT{\displaystyle \sum {\left[I^Z\right]}_b\times (\exp [-Z_{i}F{\psi }_0/RT]-1)}$$ Eq. 1

Here, ε_r is the dielectric constant for water; ε₀ is the permittivity of a vacuum; and F, R, T are the Faraday constant, the gas constant and temperature, respectively. σ_PMS is expressed in coulombs per square meter (Cm⁻²). σ_PMS depends on σ_total, the surface charge density in the absence of any bound solute ions. σ_PMS also includes the ions binding to the PM surface.

For the Stern portion of the GCS model, the PM surface was assumed to be composed of two classes of binding sites: one negatively charged (R⁻) and one neutral (P⁰). The model takes this binding into account. The model accommodates 1:1 binding of ions to R⁻ and P⁰. The reactions can be expressed as:

$$R^{}+I^Z\leftrightarrow R{I}^{Z-1}$$ Eq. 2

and

$$P^0+I^Z\leftrightarrow P{I}^Z$$ Eq. 3

Binding constants can be expressed as:

$$\begin{array}{c}{K}_{R,I}=[R{I}^{Z-1]}/([R^{-}]{[I^Z]}_0)\\ K_{P,I}=[P{I}^{Z]}/([P^o]{[I^Z]}_0)\end{array}$$ Eq. 4

where [R⁻], [P⁰], [RI^Z-1] and [PI^Z] indicate membrane surface density (molm⁻²). [I^Z]₀ denotes the concentration of the unbound ion at the PM surface and can be calculated as:

$${[I^Z]}_0={[I^Z]}_b\exp (-Z_{i}F{\text{ψ}}_0/R\text{T})$$ Eq. 5

If the binding constants K_R,I and K_P,I, R_T and P_T and the concentrations of all ions in bulk-phase medium are known, the σ_PMS can be calculated as:

$$\sigma =\{-[R^{-}]+{\displaystyle \sum (Z_i-1)[R{I}^{Z-1}]+{\displaystyle \sum Z_i[P{I}^Z]\}F}}$$ Eq.6

Thus, the electrical potential at the PM surface (ψ₀^o) can be calculated by combining Equations 1 and 6. The up-to-date parameters for the model are presented in Table 3 of Kinraide and Wang³ and were derived and selected from many sources and adjusted by correlation between the computed values of ψ₀^o and the measured Zeta potentials (ζ), which are the electric potential at the hydrodynamic plane of shear at a small distance from the PM exterior surface. A computer program for the GCS model may be obtained from TB Kinraide (USDA) and the authors. When the ionic composition of the bathing medium is known, the values for ψ₀^o can be computed with a simplified method (Equation 11 of Kinrade⁴).

The GCS model, incorporating the parameter values used by us, appears to be quite robust,^1,5–8 but we are least confident the parameter for intrinsic surface charge density (σ₀). We have employed a value of 0.3074 µmol negatively charged sites/m² (σ₀ = −30 mC/m²), but this appears to be somewhat variable with species, tissue and preparation of vesicles and protoplasts.³ The uncertainties mean that the values for ψ₀^o, and the ion activities at the PM exterior surface computed from ψ₀^o with the Nernst equation, may be only proportional to the actual values. The feature of proportionality is very robust,³ and uncertainties regarding the model fail to reduce seriously the great superiority of expressing plant-ion interactions (including uptake, toxicity and the alleviation of toxicity) in terms of surface activities rather than bulk-phase activities,^{3–5,7,9–13} and the results are presented in the present article. As for the value of σ₀ used in the GCS model, much evidence preponderantly supports the suitability of σ₀ = −30 mCm⁻² while noting the occurrence of variability among membranes. This variability is small relative to the difference in estimates of σ₀ by many methods.³ A proposed, fully parameterized GCS model appears to be applicable for the calculation of ψ₀^o and be suitable for the interpretation of many plant responses to the ionic environment.

Electrostatic Models

Increases in major cations concentrations or decreases in pH in root bathing media reduced the negativity of ψ₀^o with negligible effects upon the bulk-phase-to-bulk-phase transmembrane potential difference (E_m). This reduction caused decreases in the activities of metallic cations at the PM exterior surface and increases in the activities of anions, such as H₂AsO₄⁻. The reduced surface negativity increased the surface-to-surface transmembrane potential difference (E_m,surf), thus increasing the electrical driving force for cation transport and decreasing the driving force for anion transport across the PM. Ion uptake and toxicity depended on the balance of the dual effects of ψ₀^o (altered ion PM exterior surface activity and surface-to-surface transmembrane electrical gradients). In light of this knowledge, the electrostatic uptake model (Equations 1 to 4 of Wang et al.¹⁵) and the electrostatic toxicity model (Equations 5 to 7 of Wang et al.¹⁵) were developed to model the uptake and toxicity of both metallic and metalloid ions. Regression analysis of measured uptake and toxicity of ions with the electrostatic models demonstrated the dual effects of ψ₀^o. For example, Parker et al. investigated Cu²⁺ rhizotoxicity to wheat roots (Triticum aestivum L. cv. Yecora Rojo) in response to CuCl₂ (0 ∼ 1.6 µM), variable CaCl₂ (0 ∼ 5.0 mM), MgCl₂ (0 ∼ 4.9 mM) and pH (4.5 ∼ 6.5) in a factorial array. It is clear from the authors' figures that increasing Ca²⁺ or Mg²⁺ concentrations or reducing pH alleviated Cu²⁺ stress (the study considered theoretical aspects of FIAM). In our reanalysis with the electrostatic toxicity model, it is evident from Figure 1 that RRL correlated more strongly with the calculated RRL based on the electrostatic toxicity model (R² = 0.921) than with Cu²⁺ surface activity (R² = 0.878) or bulk-phase activity (R² = 0.745). Similarly, almost all the measured RRLs were within 95% confidence limits of the predicted one based on the electrostatic toxicity model (Fig.-1D), indicating that alleviation of Cu²⁺ by cations and pH was attributed to the dual effects of ψ₀^o.

Figure 1.

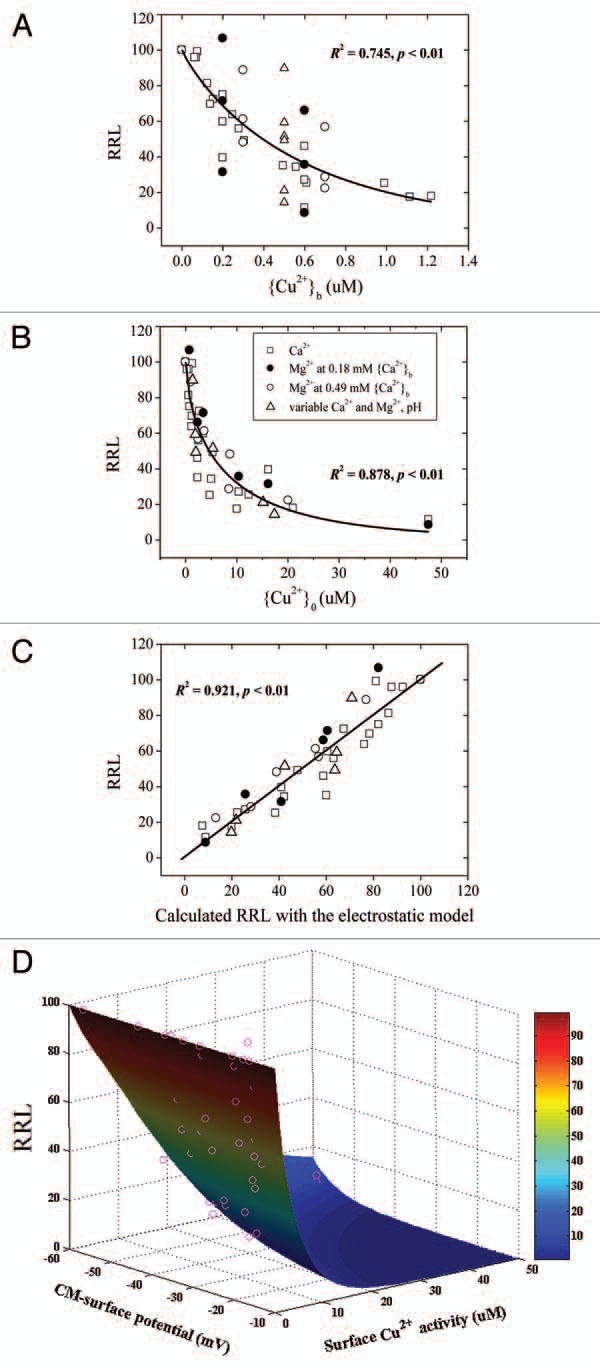
Relative root elongation (RRL) of wheat (cv. Yecora Rojo) seedlings exposed to toxic levels of Cu²⁺ affected by Ca²⁺, Mg²⁺ and pH. Data were taken from Parker et al. The RRL is plotted as functions of (A) Cu²⁺ activities in the bulk medium, (B) Cu²⁺ ion activities at the CMS_e, (C) calculated Cu²⁺ toxicity based on the electrostatic toxicity model or (D) the ψ₀^o (x-axis) and Cu²⁺ surface activity (y-axis).

Prediction of Ion Uptake and Toxicity with the FIAM, SIAM and Electrostatic Models

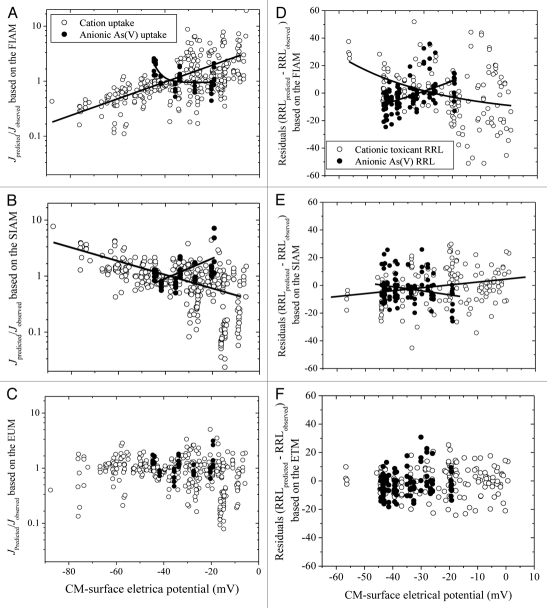
The ion uptake and toxicity predicted by the FIAM, Surface Ion Activity Model (SIAM) and the Electrostatic Uptake Models (EUM) or Electrostatic Toxicity Model (ETM) are compared in Figure 2. For cationic uptake or toxicity, the ratio (predicted J_uptake/observed J_uptake) based on the FIAM increases from 0.1 to 10 (Fig. 2A) and the residuals (RRL_predicted − RRL_observed) become more negative (Fig.-2D) with decreasing negativity of ψ₀^o. That is, the FIAM underestimates the bioavailability and toxicity of metallic ions at a higher negativity of ψ₀^o (possibly corresponding to a situation with lower ion strength or higher pH, which is exactly what was found for the toxicity of copper to aquatic organisms) and overestimates at least one. For the SIAM, the ratio declines and gradually deviates from 1 (Fig. 2B) and the residuals become more positive (Fig. 2E) with decreasing the negativity of ψ₀^o, indicating that SIAM underestimates uptake and toxicity of metallic ions. The SIAM neglects the gradually enhanced uptake and toxicity as ψ₀^o becomes less negative. For anion uptake, such as H₂AsO₄⁻, the situation is reversed. For the EUM or ETM, the ratio and residuals are not significantly different from 1 and 0 (p > 0.05), respectively (Fig. 2 and bottom).

Figure 2.

Predicted J_uptake/observed J_uptake (left column) and residual values (RRL_predicted − RRL_observed) (right column) are plotted against the PM-surface electrical potential (ψ₀^o). The predicted uptake or RRL was based on the free ion activity model (FIAM, top), the surface ion activity model (SIAM, middle) or the electrostatic uptake model (EUM) and electrostatic toxicity model (ETM) (bottom). Curves are plotted where p < 0.05.

General Evaluation of the Electrostatic Approach to Ion Uptake and Toxicity

The BLM is an attempt to generalize the concepts of toxicity and alleviation on the basis of toxic metal ion binding to cell-surface ligands as a key step leading to toxicity. The alleviation of toxicity by major cations is caused by the competition of these ions with toxic ions for binding to the same ligands. These assumptions may not be true in the present study. For example, {Ca²⁺}₀° increased initially and reached a peak value with the increase of {Ca²⁺}_b from 0.25 to 1.0 mM in the bulk medium, and then slightly declined with further increases in {Ca²⁺}_b (Fig. 3A). In contrast, the CMS_e activities of other cations, especially Mg²⁺ and H⁺, declined markedly (Fig. 3B) despite their constant concentrations in the BM. Interestingly, the sum of the PM exterior surface activities of Ca²⁺ and Mg²⁺ was also decreased with increasing {Ca²⁺}_b (Fig. 3B). It is indicated that the competition effect from surface Ca²⁺, if existent, only took place at low {Ca²⁺}_b concentrations (e.g., lower than 1.0 mM; Fig. 3A) and that the overall competition effects from Ca²⁺, Mg²⁺ and H⁺ may be weakened with adding of Ca²⁺ in the BM. However, the surface activity of cationic toxicants at the PM exterior surface declined at all times, caused by a reduction in the negativity of ψ₀^o that accompanied an increase in CaCl₂. Therefore, ψ₀^o effects could give the false appearance of competition in cases where competition is weak or does not occur at all.

Figure 3.

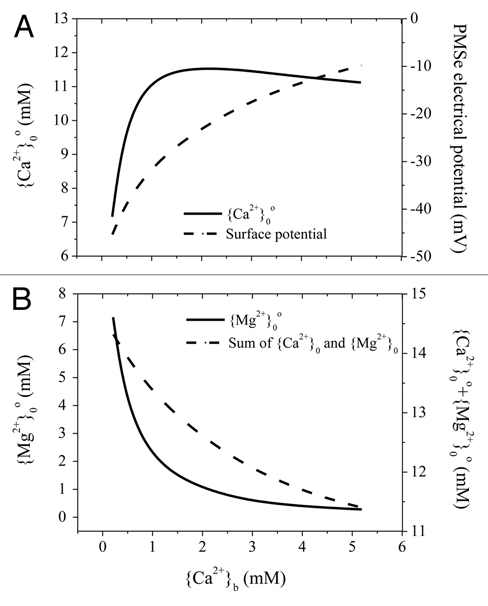
Electrical potentials (ψ₀^o) and activities of Ca²⁺ and Mg²⁺ at the PM exterior surface in response to Ca²⁺ addition to the bulk-phase medium (BM). The subscript b refers to variables in the BM. The subscript 0 refers to variables at the out CM-surface. The values of ψ₀^o were calculated for each datum point with the GCS model, and then surface activities of Ca²⁺ and Mg²⁺ were computed with the Nernst equation. The BM contained 0.25 mM MgCl₂ and variable CaCl₂ at pH 6.0.

The BLM also fails to interpret the enhancement of uptake and toxicity of anions by the treatments that reduce the toxicity of toxic cations.^5,10 These latter phenomena, therefore, require a special interpretation, but we have now shown that electrostatic mechanisms provide a unified interpretation of both phenomena—the cation alleviation of cation uptake and toxicity and the enhancement of anion uptake and toxicity. The alleviation of cation toxicity by ameliorative cations may entail site-specific competitions, but that effect may be not existent or minor.^4,5 In nearly all cases, the dual effects of ψ₀^o (electrostatic enhancement or depletion of cationic or anionic toxicants; increases or decreases in the electrical driving force for cationic of anionic toxicant transport across the PM) is sufficient to explain most ion-toxicant interactions. Most previous studies did not take an electrostatic approach, but their results are better explained by the dual effects.^4,5

Addendum to: Wang P, Kinraide TB, Zhou DM, Kopittke PM, Peijnenburg WJGM. Plasma membrane surface potential: dual effects upon ion uptake and toxicity. Plant Physiol. 2011;155:808–820. doi: 10.1104/pp.110.165985.