Neuronal Responses to Texture-Defined Form in Macaque Visual Area V2

Abstract

Human and macaque observers can detect and discriminate visual forms defined by differences in texture. The neurophysiological correlates of visual texture perception are not well understood and have not been studied extensively at the single-neuron level in the primate brain. We used a novel family of texture patterns to measure the selectivity of neurons in extrastriate cortical area V2 of the macaque (Macaca nemestrina, Macaca fascicularis) for the orientation of texture-defined form, and to distinguish responses to luminance- and texture-defined form. Most V2 cells were selective for the orientation of luminance-defined form; they signaled the orientation of the component gratings that made up the texture patterns but not the overall pattern orientation. In some cells, these luminance responses were modulated by the direction or orientation of the texture envelope, suggesting an interaction of luminance and texture signals. We found little evidence for a “cue-invariant” representation in monkey V2. Few cells showed selectivity for the orientation of texture-defined form; they signaled the orientation of the texture patterns and not that of the component gratings. Small datasets recorded in monkey V1 and cat area 18 showed qualitatively similar patterns of results. Consistent with human functional imaging studies, our findings suggest that signals related to texture-defined form in primate cortex are most salient in areas downstream of V2. V2 may still provide the foundation for texture perception, through the interaction of luminance- and texture-based signals.

Introduction

Information about visual form is signaled by different cues. Forms signaled by differences in luminance are termed “first order.” Forms signaled by differences in texture, such as changes in orientation or contrast, are termed “second order” if they exclude overall luminance changes. Little is known about the neurophysiological correlates of texture perception in the primate brain, particularly at the level of individual neurons. Human fMRI studies have implicated high-level areas in the ventral visual pathway, reporting differential activation to displays containing texture boundaries in areas V4, TEO, and LOC (Grill-Spector et al., 1998; Kastner et al., 2000). Orientation-selective responses to texture-defined form are modest in early visual areas, increasing gradually along the pathway, and strongest in ventral occipital cortex (Larsson et al., 2006). Macaque monkeys with cortical lesions in V2 and V4 show significant behavioral impairments on texture discrimination tasks, suggesting that these areas play an important role in texture processing (Merigan et al., 1993; De Weerd et al., 1996; Merigan, 2000). And neurons in V2 have been shown to be selectively sensitive to a number of visual features more complex than those found in simple stimuli of a single orientation (Hegdé and Van Essen, 2000, 2003, 2007; Ito and Komatsu, 2004; Anzai et al., 2007; Willmore et al., 2010), some of which have aspects in common with texture stimuli commonly used in the study of second-order vision (for review, see Landy and Graham, 2004).

Human psychophysical performance on texture discrimination tasks can be captured by a three-stage processing mechanism, referred to as the “filter–rectify–filter” (FRF) model (for review, see Landy and Graham, 2004). Here, a visual pattern is analyzed by a bank of linear filters sensitive to luminance contrast, and the output is then rectified and pooled by a second stage consisting of a larger linear filter of lower spatial frequency. The resulting second-order channel is sensitive to modulations of orientation or contrast across its spatial extent and can be used to signal the orientation of texture boundaries by comparing image content in neighboring subregions. We wondered whether the stages of the FRF model mapped onto early visual cortical areas V1 and V2. V1 neurons signal the orientation of first-order luminance edges (Hubel and Wiesel, 1959, 1962; De Valois et al., 1982). These neurons operate as if their responses depend on local linear filters (Movshon et al., 1978a,b), summing luminance signals linearly across their spatial extent. V1 receptive fields presumably cannot signal the orientation of texture-defined form in second-order stimuli because average luminance is held constant across those images. V2 neurons receive convergent input from many V1 neurons and have receptive fields approximately twice as large as in V1. Their “wiring diagram” is reminiscent of the one proposed in the FRF framework, with linear subunits (V1 neurons) selective for luminance-defined form converging onto larger operators (V2 neurons). We therefore wondered whether neurons selective for the orientation of texture-defined form might be found in monkey V2. In cat area 18—the V2 homolog—some neurons signaled second-order form, preferring similar orientations of luminance- and contrast-defined form (Zhou and Baker, 1994; Leventhal et al., 1998; Mareschal and Baker, 1998a,b; Song and Baker, 2007). To ask whether “cue-invariant” responses existed in the primate, we used a stimulus design that allowed us to distinguish responses to luminance- and texture-defined form.

Most V2 cells signaled the orientation of luminance-defined form. A subset had luminance-driven responses that were modulated by second-order stimulus features. Only a handful of cells signaled texture-defined form. Data recorded from neurons in monkey V1 were qualitatively similar; we did not find evidence for a cue-invariant representation at either stage of cortical processing.

Materials and Methods

Surgical preparation

We made recordings in 11 macaque monkeys (Macaca nemestrina and Macaca fascicularis; 9 males and 2 females). Nine animals contributed V2 data; two contributed V1 data. Animals were prepared for recording as described previously (Cavanaugh et al., 2002a). Experiments typically lasted 5–6 d, during which anesthesia and paralysis were maintained with continuous intravenous infusion of sufentanil citrate (initially 6 μg · kg⁻¹ · h⁻¹, adjusted thereafter to maintain a suitable level of anesthesia for each animal) and vecuronium bromide (Norcuron; 0.1 mg · kg⁻¹ · h⁻¹) in isotonic dextrose-Normosol solution. Vital signs were monitored (EEG, heart rate, lung pressure, end-tidal pCO₂, temperature, urine flow, and osmolarity) and maintained within appropriate physiological limits. Pupils were dilated with topical atropine, and the eyes were protected with oxygen-permeable contact lenses. Supplementary lenses chosen via direct ophthalmoscopy were used to make the retinas conjugate with the experimental display. All animal care and experimental procedures were done in accordance with protocols approved by the New York University Animal Welfare Committee and conformed to the NIH Guide for the Care and Use of Laboratory Animals.

Unit recording

We made extracellular recordings with quartz–platinum–tungsten microelectrodes (Thomas Recording) advanced mechanically through a craniotomy and durotomy centered 2–4 mm posterior to the lunate sulcus and 10–16 mm lateral to the midline. Electrode penetrations were confined to a parasaggital plane and directed downward at an angle of 0 or 20° from vertical. We identified area V2 by (1) marking transitions between gray and white matter as we traversed surface cortex, followed by a stretch of white matter before reaching V2 on the posterior bank of the lunate sulcus; (2) tracking changes in visual topography along the recording track: receptive fields in surface V1 were located close to the vertical meridian; V2 receptive fields were at 2–5° of visual eccentricity; (3) marking cortical depth along the recording track: at our typical sites, V2 was found 2500–3500 μm from brain surface. Signals from the microelectrodes were amplified, bandpass-filtered (300 Hz to 10 kHz), and fed into a dual window time-amplitude discriminator (Bak Electronics) for spike detection. Spike times were saved with a temporal resolution of 0.1 ms.

Visual stimulation

We presented stimuli on a gamma-corrected CRT monitor (Eizo T966; mean luminance, 33 cd/m²) at a resolution of 1280 × 960 pixels and a refresh rate of 120 Hz. Stimuli were generated using Expo software on an Apple Macintosh computer (http://corevision.cns.nyu.edu).

For each cell, we mapped the receptive field of each eye on a tangent screen. After determining ocular dominance, we presented stimuli monocularly to the cell's dominant eye, occluding the other. We first determined selectivity for orientation and direction, spatial frequency, drift rate, and size using high contrast sinusoidal gratings. We then measured neuronal responses to texture stimuli, which we describe below.

We constructed texture patterns by the spatial modulation of two orthogonal static gratings (carriers) (see Fig. 1B,C) oriented ±45° to a drifting grating (modulator) (see Fig. 1A,D). Each carrier was multiplied by a low spatial frequency modulator (one by M; the other by its inverse −M). The resulting contrast-modulated patterns (see Fig. 1E,F) were then summed to produce a texture pattern, which we term a “herringbone” because of its resemblance to the fabric of that name (see Fig. 1G). Similar patterns have been used in psychophysical and imaging studies of texture perception (Landy and Oruç, 2002; Larsson et al., 2006), although our stimuli differed from these in several details. First, our modulator was drifting (typically at 1–3 Hz), not static. Second, our carriers were high spatial frequency luminance gratings, not spatially filtered noise. Third, we varied texture orientation while keeping a fixed orientation relationship of ±45° between the modulator and carriers. This angle difference allowed us to interpret neuronal responses to different stimulus elements. We presented 16 modulator directions (0–360° in steps of 22.5°). In 5 of the 11 monkey recording experiments, we took the square root of the modulators (M and −M) before multiplying with the carriers, to maintain constant contrast energy across the final stimulus image (Landy and Oruç, 2002). This yielded quantitatively similar neuronal responses but produced stimuli with slightly more complex spectra than the simpler method we used for later experiments.

Figure 1.

Stimulus composition. Texture patterns (herringbones) were composed by periodic modulation of two orthogonal static luminance gratings (carriers) by two drifting gratings (modulators). A fixed orientation difference of ±45° separated modulator and carrier patterns, and was used to distinguish neuronal responses to each. A, D, Low spatial frequency drifting gratings used to modulate the carrier patterns (modulators M and its inverse −M). B, C, High spatial frequency static gratings used as carrier patterns. To produce the texture pattern, each carrier was multiplied by a modulator (carrier 1 with modulator M; carrier 2 with modulator −M). E, F, The resulting contrast-modulated carrier patterns. G, The final herringbone texture pattern was generated by combining the patterns in E and F additively; the modulator orientation (here vertical) defined the orientation of the texture-defined form.

Consider the local spatiotemporal structure of the herringbone pattern. At any fixed point in the image, the static carrier gratings exchange sinusoidally in time. Texture-defined form in these stimuli depends on the spatial structure of the modulator. To control for responses to local carrier exchange, we presented stimuli in which the two carriers were temporally exchanged at the same frequency as the local exchange produced by the moving envelope, but without spatial modulation (in other words, the modulator spatial frequency was set to 0). The local spatiotemporal structure of these “carrier-exchange” controls was identical to that of the herringbone patterns, so that they only differed in global spatial structure.

We optimized stimuli separately for each cell, based on its selectivity to luminance gratings. The texture patch was approximately twice the diameter of the classical receptive field, unless the neuron was strongly surround-suppressed, in which case it was made smaller to reduce suppression. The carrier and modulator spatial frequencies in our stimuli were both within the resolution limit of the neuron (see Fig. 6 and accompanying text). The carrier frequency was chosen to be slightly higher than the optimal spatial frequency; the modulator frequency was typically one-third the carrier frequency (i.e., ∼1.6 octaves below). Stimuli were presented for 2 s, in randomly interleaved blocks that included trials in which the screen was blank at the mean luminance to measure baseline activity.

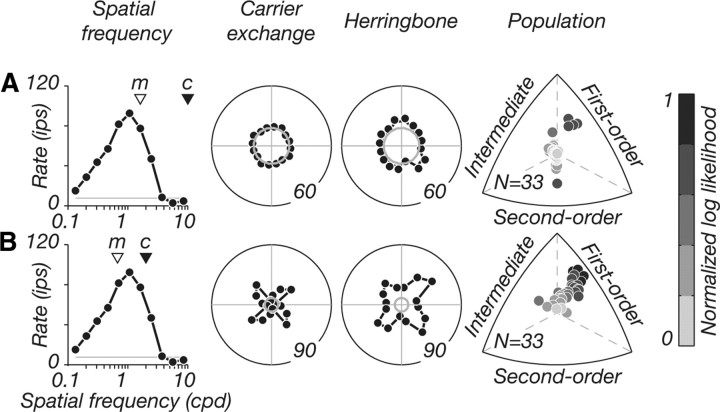
Figure 6.

Responses to carrier spatial frequencies beyond and within the resolution limit. Shown are data from an example V2 neuron. We show the tuning of the neuron for grating spatial frequency (column 1; triangles marked “m” and “c” indicate the modulator and carrier spatial frequencies used), tuning for carrier-exchange controls (column 2), and the herringbone patterns (column 3). A, Patterns composed of carrier spatial frequencies beyond the resolution limit failed to elicit visual responses in this V2 neuron (gray circles in polar plots show baseline firing; numbers on outer circles indicate response magnitude). B, Patterns composed of carrier spatial frequencies within the resolution limit produced orientation-tuned responses to both stimuli. This response pattern was true for most neurons recorded in V2. For a subset of neurons (N = 33), we measured herringbone tuning under both parameter conditions and examined distributions of relative log likelihoods (column 4). With carriers beyond the resolution limit, most neurons responded weakly and were not statistically classified (points near origin in top row, column 4); other neurons were selective for luminance-defined form. With carriers within the resolution limit, responses were well tuned, and most neurons were strongly classified as selective for luminance-defined form.

Analysis

Quantitative measures of grating responses

Direction selectivity index.

We quantified selectivity for grating direction with a vector-based measure of tuning strength, as detailed previously (Smith et al., 2002). We computed the summed response vector and normalized its magnitude by the summed magnitude of all response vectors. Index values range from 0 to 1, where 1 indicates responses only to a single motion direction, and 0 indicates equal responses to all directions. Direction selectivity index (DSI) is related to the “circular variance” measure of orientation bandwidth (CV) (Ringach et al., 1997) computed over the range 0–180°; DSI is 1 − CV, computed over the range 0–360°.

Surround suppression index.

We quantified the degree to which neuronal responses were suppressed by stimuli larger than the classical receptive field, as detailed previously (Cavanaugh et al., 2002a). We computed an index that expressed suppression as a fraction of the peak response. Surround suppression index (SSI) values range from 0 to 1, where 0 indicates no suppression, and 1 indicates complete suppression.

Generating nondirectional grating responses

From the measured responses to drifting gratings (which may be directional for direction-selective neurons) (see Fig. 8, column 1), we generated nondirectional tuning curves (see Fig. 8, column 2). This was done by folding responses to the range 0–180° and averaging, and then replicating the resulting average tuning curve twice to cover 0–360°. These nondirectional tuning curves served as the basis for all our response predictions (see Fig. 2).

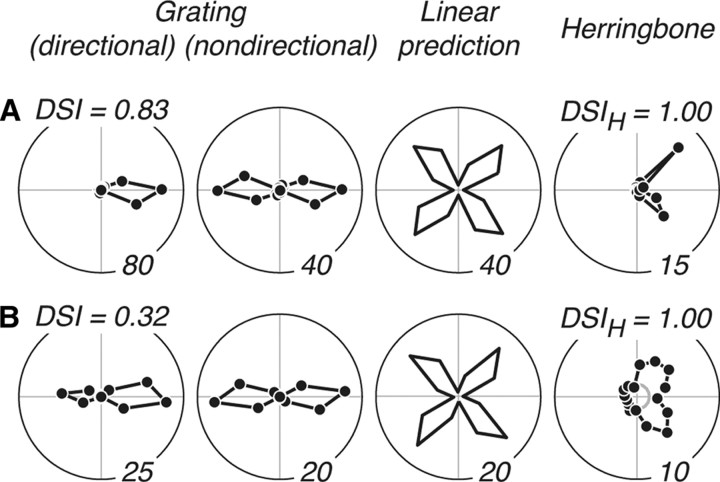
Figure 8.

Direction selectivity for gratings and herringbones. A, B, Data for two example V2 neurons with directional herringbone responses, where only two adjacent tuning lobes were evident. For each, we show the tuning for grating direction (column 1) from which we generated the nondirectional grating tuning curve (column 2) that formed the basis of our linear response prediction (column 3). We also show the measured tuning for herringbone direction (column 4). A, Responses of a neuron that was strongly direction selective for gratings, with a high direction selectivity index (DSI = 0.83). It was also strongly direction selective for herringbones, with a high herringbone direction selectivity index (DSI_H = 1) (see text). B, Responses of a neuron that was weakly direction selective to gratings (DSI = 0.32) but was nevertheless strongly direction selective to herringbones (DSI_H = 1).

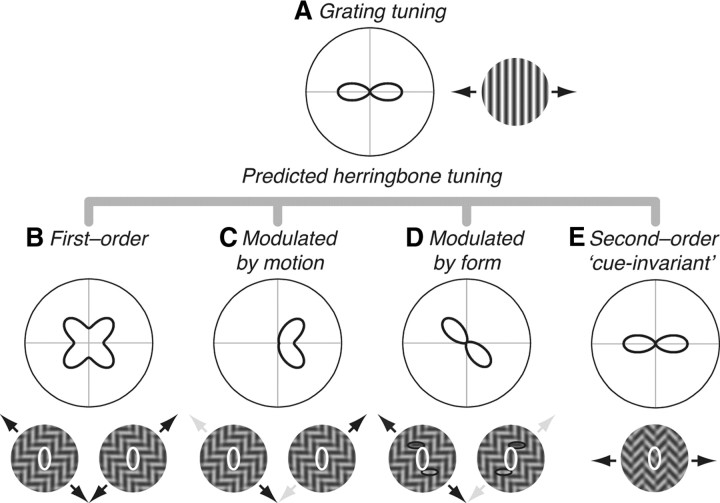
Figure 2.

Response predictions. Tuning of a hypothetical V2 neuron to gratings and herringbones, plotted on polar coordinates; modulator direction is represented along the circumference and response magnitude along the radius. A, Tuning for grating orientation. In this example, the neuron prefers vertical gratings moving right or left (black arrows on the preferred stimulus icon, right). B–D, Possible herringbone response patterns, shown as a function of modulator direction. B, First-order prediction. A neuron selective for luminance-defined form would prefer herringbone patterns containing carriers that match its optimal grating (vertical, shown in white ellipses on the preferred stimulus icons, below). This occurs twice for each carrier, ±45° away from the modulator, resulting in a four-lobed tuning curve. C, Modulated by motion prediction. A neuron selective for both the orientation of luminance-defined form and the direction of second-order motion would prefer herringbone patterns containing vertical carriers (same white ellipses as in B) but only—for example—when the modulator moves rightward. Preferred modulator directions are indicated by black arrows (up/right and down/right); nonpreferred modulator directions are indicated by light gray arrows (up/left and down/left). Predicted herringbone tuning is aligned with the four-lobed linear prediction, but only two adjacent lobes are evident. D, Modulated by form prediction. A neuron selective for the orientation of luminance-defined form and the spatial structure of the second-order envelope would prefer herringbone patterns containing vertical carriers (same white ellipses as in B, C), but only when the flanking horizontal elements (black ellipses) form a particular spatial configuration: for example, a “z” shape configuration (stimulus icon with black arrows) and not when they form an “s” shape configuration (icon with gray arrows). E, The second-order cue-invariant prediction. A neuron selective for the orientation of texture-defined form would prefer herringbone patterns containing a vertical modulator that matches its optimal grating, thus responding similarly to luminance- and texture-defined form.

Statistical comparisons of response predictions

For each neuron, we generated a family of predicted herringbone tuning curves (see Fig. 2 and accompanying text), based on the measured tuning for grating direction. To find the prediction that best accounted for the measured tuning, we evaluated the probability of the data given each prediction by computing the log likelihood as follows:

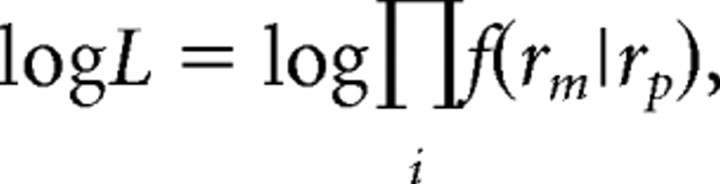where r_m is the measured response, r_p is the predicted response, and i is an index of herringbone modulator direction (0–360°). Assuming Poisson spiking statistics, the equation can be rewritten as the sum of logs as follows:

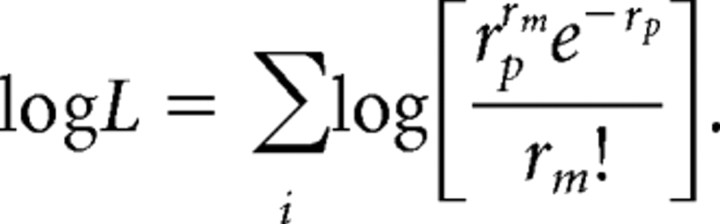We fit each prediction to the data using an iterative procedure that maximized log likelihood. Because the measurements of response to moving carrier gratings were made separately, it was useful to allow for two independent scalars (k₁ and k₂) to modify the baseline response (b) and the predicted response before scaling (r_p′). Thus, in the above equation, the predicted response r_p at direction i was in fact the following:

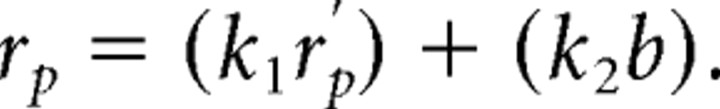The resulting log likelihoods were normalized to upper and lower bounds, determined separately for each neuron [using the method of Stocker and Simoncelli (2006)]. The upper bound was evaluated by fitting the measured herringbone response to itself and the lower bound by fitting the average response of the neuron across all modulator directions to the herringbone response. Thus, the likelihoods were transformed to a scale that ranged from 0 to 1, from the least to the most likely.

Triplot representation

We used a triplot representation, similar to that used by Cavanaugh et al. (2002a), to compare the relative likelihoods of different predictions across the population (see Figs. 4–7). We first reduced the dimensionality of the comparisons; the selectivity of each neuron was defined by three values: the normalized log likelihood of the first-order prediction, of the better of the two second-order predictions (cue-invariant and cue-orthogonal), and of the better of the two intermediate predictions (modulated by motion and modulated by form). These three normalized values can be thought of as defining a unit vector in three dimensions, or equivalently a position on the surface of a sphere. Because all values are positive, the points all lie in one orthant, and the representations in Figures 4–7 show a view of the projection of this orthant onto the plane of the page. Imagine, if you will, the surface of the globe. The north pole is the top vertex, the equator at the Greenwich meridian is the bottom right vertex, and the equator at 90° west longitude is the bottom left vertex. The distance of each point from each edge of the triangle (or equivalently its proximity to the opposite vertex) is therefore proportional to the normalized log likelihood that the labeled prediction accounted for the data. Each triangular segment within the plot corresponds to the zone in which that prediction provides the best fit. Finally, to visually represent the “goodness of fit” (the information lost by normalizing the vectors), the points are color-coded using the log likelihood of the best fitting prediction, with darker colors representing higher likelihoods.

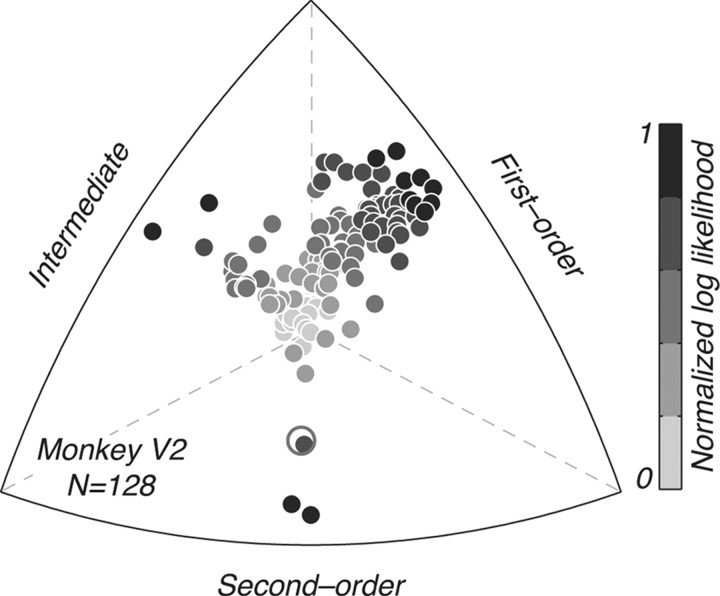
Figure 4.

Distribution of selectivity for luminance- and texture-defined form in V2. Each point represents a single neuron (N = 128); its position relative to each edge of the triplot represents how well each family of response predictions (first-order, second-order, and an “intermediate” family of modulated responses: modulated by motion or form) can account for the observed herringbone tuning (for more detail, see Materials and Methods). The points are color-coded by the log likelihood of the best prediction (compare Fig. 3, column 5); darker shades represent higher likelihoods. Most neurons were best described by the first-order prediction, some cells fell into the intermediate category, whereas only a handful of cells were best described by the second-order prediction. The second-order neuron marked as an open circle is the only cue-invariant neuron we recorded in V2 (Fig. 3D).

Figure 5.

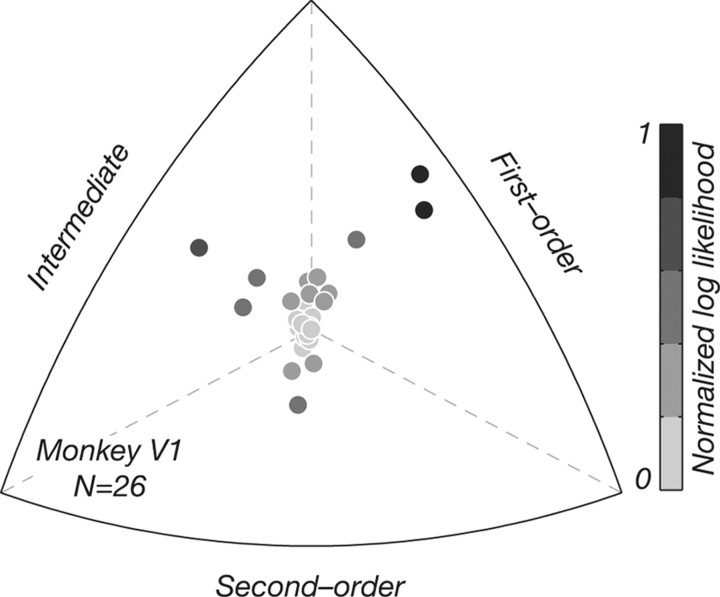
Distribution of selectivity for luminance- and texture-defined form in monkey V1. Control V1 data (N = 26) are represented in the same way as in Figure 4. Most V1 neurons were selective for luminance-defined not texture-defined form. The distribution was qualitatively similar to that recorded in V2 (Fig. 4).

Figure 7.

Responses to full and half herringbone patterns. Shown are data for three example V2 neurons (shown in Fig. 3) to full herringbone patterns (as in Fig. 1G) and the two half herringbone patterns (contrast-modulated gratings, as in Fig. 1E,F). For each neuron, we show the measured grating tuning (column 1), the linear response prediction (column 2), tuning for carrier-exchange controls (column 3), and the full herringbone patterns (column 4, see stimulus icon). We also show tuning for each half pattern (half 1 and half 2, columns 5 and 6; see stimulus icons above). A, Responses of a first-order neuron. Tuning for full herringbone patterns was four-lobed; tuning for each half pattern was two-lobed and aligned with the linear prediction, reflecting the response to each carrier pattern present. B, Responses of a modulated by motion neuron. Full herringbone tuning was directional, with only two of the four tuning lobes evident; tuning for each half pattern was also directional, with only one lobe present, reflecting the response to each carrier. C, Responses of a second-order cue-orthogonal neuron. Full herringbone tuning did not match the four-lobed linear prediction; tuning for each half pattern was also identical in shape, indicating that it was cue-orthogonal for both stimulus types. D, Distribution of relative log likelihoods for V2 neurons tested with full herringbone patterns (N = 25). E, Comparison distribution for the same V2 neurons when tested with half herringbone patterns. We computed likelihoods from the responses to each half separately and plotted the average normalized likelihood for both halves. The distribution was qualitatively similar, with most neurons classified as first order, and a few as “second-order cue-orthogonal.”

Results

We measured the orientation-selective responses of neurons in monkey area V2 to texture-defined form using texture patterns that allowed us to distinguish responses to luminance and texture cues. Patterns were constructed by the spatial modulation of two orthogonal stationary gratings (Fig. 1) (see Materials and Methods); we term these stimuli “herringbones” because they resemble herringbone fabric. We varied the orientation of texture modulation, while keeping the orientation of the stationary luminance carrier elements at ±45° from that orientation. Here, we report results from 128 V2 neurons recorded in nine macaque monkeys. For comparison, we also include results from a smaller set of neurons recorded in monkey V1 (N = 26).

Response predictions

We first measured the tuning of each neuron for grating direction and used these responses to generate predicted tuning curves for the orientation of texture modulation in herringbone patterns. Figure 2 shows the response predictions, plotted on polar coordinates, for a hypothetical V2 neuron that preferred vertical gratings drifting to the right and left (Fig. 2A) (also see the preferred stimulus icon adjacent). We first considered two possible response categories: first order and second order. If a neuron were selective for luminance-defined form (Fig. 2B), it would respond best to herringbone patterns containing carrier orientations that match its preferred grating. As a function of the direction of texture modulation (from 0 to 360°), the preferred vertical carriers (indicated by white ellipses on the preferred stimulus icons below) would appear once in each tuning quadrant—twice for each carrier—yielding a four-lobed response. We therefore computed the first-order linear response prediction by rotating the grating tuning curve both ±45° and summing these responses; this is analytically similar to computing the “component” prediction for direction selectivity to plaid patterns (Movshon et al., 1985; Smith et al., 2005). If a neuron were selective for texture-defined form (Fig. 2E), it would respond best to herringbone patterns containing modulator orientations that match its preferred grating—vertical texture modulation drifting right or left (see preferred stimulus icon below). Such a neuron is cue-invariant because it shows identical tuning curves for gratings and herringbones. We computed the second-order response prediction by replicating the grating tuning curve; this is analytically similar to computing the prediction for pattern direction selectivity (Movshon et al., 1985; Smith et al., 2005).

We realized that our results revealed an intermediate family of response patterns in which a neuron is primarily selective for luminance-defined form, but its responses are influenced by features of the drifting second-order texture envelope. Responses to luminance-defined form could be modulated by the direction of motion of the texture envelope (Fig. 2C); such responses would be strongest to herringbones containing vertical carrier elements, but only when combined with particular directions of second-order motion. For example, the neuron here responds only to herringbones that drift up/right, or down/right (black arrows on stimulus icons), but not to identical stimuli that drift up/left or down/left (gray arrows). As a result, responses are weaker at nonpreferred directions, and two adjacent tuning lobes are reduced. We refer to this class of directional herringbone responses as “modulated by motion.” Note that this response type cannot be attributed to directional responses to the component gratings because the carriers were always stationary. Responses to luminance-defined form could also be modulated by the orientation of the texture envelope (Fig. 2D); such responses are strongest to herringbones containing vertical carrier elements, but only when combined with particular orientations of second-order form. This response pattern arises because of the spatial arrangement of luminance elements within the receptive field of a neuron. For example, the neuron here may respond best to herringbone patterns containing vertical carrier elements (white ellipse) flanked by horizontal carrier elements (black ellipses), which together create a letter “z” configuration (icon with black arrows), and will not respond to patterns containing identical vertical and horizontal elements that create an “s” configuration (icon with gray arrows). As a result of this selectivity for the particular spatial configuration (context) of luminance carrier elements in the receptive field, responses are weaker at nonpreferred envelope orientations, and two opposite tuning lobes are reduced. We refer to this class of contextual herringbone responses as “modulated by form.” Thus, overall, we considered three classes of neuronal selectivity: selectivity for luminance-defined form (first-order), selectivity for texture-defined form (second-order), and selectivity for luminance-defined form that is modulated by second-order features (modulated by motion and modulated by form).

Orientation-selective responses to texture-defined form

Figure 3 shows the responses of five example neurons recorded in V2. For each neuron, we show the nondirectional grating tuning curve (column 1) generated from the measured responses to drifting gratings (see Materials and Methods), and the linear response prediction (column 2). We also show the measured tuning to carrier-exchange controls (column 3) (see Materials and Methods), in which the two static carrier patterns were temporally exchanged without any spatially structured texture modulation. In column 4, we show the measured tuning to the herringbone patterns. To facilitate comparison, we rotated the grating tuning curve of each neuron to a preferred orientation of 0° and applied the same rotation angle to predicted and measured herringbone tuning curves. Figure 3A shows the responses of a neuron selective for luminance-defined form (first order). Its tuning to the carrier-exchange controls and herringbones matched the shape of the linear prediction; it preferred herringbones containing carriers that matched its optimal grating orientation. Figure 3B shows the responses of a neuron that was modulated by motion (compare Fig. 2C). Like the neuron in Figure 3A, its tuning to carrier-exchange controls and herringbones was aligned with the four-lobed linear prediction. It preferred herringbones containing carriers that matched its optimal grating orientation, but its responses were influenced by the second-order motion (modulator direction), resulting in a directional tuning curve, where only two adjacent lobes were evident. Figure 3C shows the responses of a neuron that was modulated by form (compare Fig. 2D). Like the neurons in Figure 3, A and B, its tuning to carrier-exchange controls and herringbones was aligned with the four-lobed linear prediction. It preferred herringbones containing carriers that matched its optimal grating orientation, but its responses were influenced by the second-order form (modulator orientation), resulting in a “contextual” tuning curve, where only two opposite lobes were evident. Figure 3D shows the responses of a cue-invariant (second-order) neuron (compare Fig. 2E). Its grating and herringbone tuning curves were similar in shape and different from the linear prediction. The neuron responded best to herringbones containing modulator orientations that matched its preferred orientation for gratings, thus showing invariant selectivity for the orientation of luminance- and texture-defined form. The response pattern in Figure 3D was seen only once in our experiments, but we occasionally encountered an unexpected but reliable variant response pattern, an example of which is shown in Figure 3E. This neuron responded best to texture patterns containing modulator orientations that were orthogonal to its optimal grating. Like the cue-invariant neuron in Figure 3D, its herringbone tuning was not aligned with the linear prediction, suggesting that it also showed selectivity for the orientation of texture-defined form. However, unlike the previous example, this neuron was cue-orthogonal rather than cue-invariant. We therefore recognize another category of possible second-order responses, which we call “cue-orthogonal.” Interestingly, although this response type has not been previously reported in physiological studies, some psychophysical models of second-order vision have considered the possibility that texture-selective second stage filters in the FRF model may prefer orientations orthogonal to the luminance-selective first stage filters (Graham and Wolfson, 2001, 2004).

Figure 3.

Responses of example V2 neurons to texture patterns. Shown are data from five neurons recorded in monkey V2. For each, we plot the measured grating tuning (column 1), the first-order linear response prediction (column 2) (compare Fig. 2B), tuning for carrier-exchange controls (column 3), and herringbone tuning (column 4). The tuning curves for each neuron were aligned such that its preferred grating orientation was rotated to 0°. A, Responses of a first-order neuron. Herringbone tuning was four-lobed and matched the shape of the linear prediction and carrier-exchange controls. B, Responses of a neuron that was modulated by motion. Herringbone tuning was directional, and only two adjacent tuning lobes were evident. C, Responses of a neuron that was modulated by form. Herringbone tuning had a contextual signature, and only two opposite lobes were evident. D, Responses of a second-order cue-invariant neuron; herringbone and grating tuning curves were similar in shape. E, Responses of a second-order cue-orthogonal neuron; herringbone and grating tuning curves were orthogonal. Baseline firing rates are represented by gray circles; response magnitudes are indicated by numbers on the outer circles of the polar plots. Column 5 shows the log likelihood (probability) of each of the possible response predictions accounting for the measured herringbone tuning. Log likelihoods were normalized separately for each cell, and transformed to a scale of 0 to 1, from the least to the most likely (see Materials and Methods). Labels for the response predictions (abscissa) are abbreviated as follows: first-order (1°), modulated by motion (1° motion), modulated by form (1° form), second-order cue-invariant (2° cue-invariant), and second-order cue-orthogonal (2° cue-orthogonal).

To classify each neuron statistically, we generated predictions for the five possible response patterns to herringbone stimuli (the four shown in Fig. 2 and the cue-orthogonal prediction). We then compared the experimentally measured herringbone tuning curves to each of the predictions in a probabilistic framework (see Materials and Methods). For each neuron, we computed the probability (log likelihood) that each prediction accounted for the observed shape of the tuning curve. These log likelihoods are shown to the right of the tuning curves (Fig. 3, column 5), normalized, and transformed to a scale from 0 to 1, from the least to the most likely. The probabilistic analysis easily classified the example neurons. The first-order prediction had the highest likelihood of accounting for the responses shown in Figure 3A. The modulated by motion prediction was best for the responses in Figure 3B; the modulated by form prediction was best for the responses in Figure 3C. The second-order cue-invariant prediction was best for the responses in Figure 3D; the second-order cue-orthogonal was best for the responses in Figure 3E.

Population data

To characterize our V2 population (N = 128), we asked, for each neuron, which of the five response predictions best accounted for the observed data. To reduce the dimensionality of these comparisons, we collapsed across the two classes of second-order responses (cue-invariant and cue-orthogonal) and the two classes of modulated responses (modulated by motion and modulated by form)—which we now refer to as “intermediate”—taking the better of each family. The selectivity of each neuron was therefore captured by three values: the likelihood of the first-order prediction, of the better of the two second-order predictions, and of the better of the two intermediate predictions. Figure 4 shows the distribution of relative log likelihoods across the population. Each point represents a single neuron; its position relative to each edge depicts how well a given prediction explains the data (for more on the triplot representation, see Materials and Methods), and its intensity represents the normalized log likelihood for the best fitting model (from 0 to 1, darkest points represent highest likelihood). Most neurons (77 of 128; 60%) were best described by the first-order prediction, suggesting that they were only selective for the orientation of luminance-defined form. A smaller subset of neurons (42 of 128; 33%) was best described by the intermediate family of modulated predictions, showing directional or contextual influences of the drifting texture envelope. Only a few cells (9 of 128; 7%) were well fit by the second-order predictions, showing selectivity for the orientation texture-defined form. Interestingly, of the few second-order neurons we encountered, most were cue-orthogonal; only one neuron was cue-invariant (shown as an open circle in Fig. 4 and separately in Fig. 3D).

Note that all of the example neurons whose data are shown in Figure 3 were more responsive to the herringbone stimuli than to carrier-exchange controls, suggesting that there might be an overall preference for the texture patterns regardless of the particulars of neuronal selectivity. A possible mechanism for this would be variations in the strength of surround suppressive mechanisms in the two stimulus cases. The carrier-exchange control, which is composed of two orthogonal carriers interleaved in time, would evoke maximal surround suppression because the surround would “see” the optimal stimulus orientation when the receptive field was most strongly driven (Cavanaugh et al., 2002b).The spatially modulated herringbone pattern would cause weaker suppression because at least part of the surround would receive stimulation at a nonoptimal orientation. We captured this effect by computing the ratio of peak responses to herringbone patterns and carrier-exchange controls. The distribution of peak response ratios in V2 had a geometric mean of 2.1 and a SE of 1.1, indicating that most neurons did indeed respond more vigorously to herringbone patterns than to spatially unmodulated controls. When we examined these distributions separately for neurons statistically classified as first order, intermediate, and second order, we observed an interesting trend. The mean and SE for the distribution of first-order neurons was 1.8 and 1.1, respectively; for the distribution of intermediate neurons, 2.6 and 1.2; for the distribution of second-order neurons, 3.1 and 1.2. Thus, it seems that V2 neurons that showed selectivity for second-order stimulus features had relatively stronger responses to herringbone patterns than to carrier-exchange controls. These neurons had a preference for spatially modulated textures over unmodulated ones, regardless of the details of their specific response pattern.

Comparison with V1

We measured the selectivity of 26 V1 neurons using the same texture patterns. Figure 5 shows the distribution of relative log likelihoods in V1, in the same format used previously in Figure 4. The V1 data were qualitatively similar to those from V2, and no differences were discernible between cells in the two cortical areas based on this small dataset. V1 neurons with the highest likelihoods were mostly selective for luminance- and not texture-defined form, and interestingly many of them were modulated by motion, showing directional herringbone responses, as we saw in V2.

We computed the ratio of peak responses to herringbone patterns and carrier-exchange controls for the V1 cells, as we did for V2. The distribution of peak response ratios in V1 had a geometric mean of 2.0 and a SE of 1.2, indicating that most neurons responded more vigorously to herringbone patterns than to spatially unmodulated controls. The mean and SE for the distribution of first-order neurons was 1.3 and 1.2, respectively; for the distribution of intermediate neurons, 2.6 and 1.3; for the distribution of second-order neurons, 2.0 and 1.3. Thus, as seen in V2, V1 neurons that showed selectivity for second-order stimulus features had relatively stronger responses to herringbone patterns than carrier-exchange controls.

Effect of stimulus parameters

To establish whether our failure to find many true second-order neurons in macaque V2 was due to the choice of stimulus parameters, we experimented with variations in stimulus composition. Our current experimental paradigm differed from the studies previously published in cat area 18 (Zhou and Baker, 1994; Mareschal and Baker, 1998a,b; Song and Baker, 2007) in two important ways: (1) we presented carrier spatial frequencies that were within the resolution limit of the neuron, and (2) our herringbone stimuli were additive combinations of two contrast-modulated gratings, whereas previous studies were based on a single contrast-modulated grating (one-half of our herringbone pattern). We wanted to be certain that these experimental differences did not account for the absence of second-order cue-invariant responses in our data. We therefore attempted to isolate orientation-selective responses to second-order form by choosing modulator and carrier spatial frequencies according to the protocol adopted by previous studies, by setting the modulator to the optimal frequency and the carrier at a high frequency beyond the resolution limit of the cell (hereafter “superresolution carriers”). Figure 6A shows the responses of an example V2 neuron under these conditions. We first measured the spatial frequency tuning of the neuron using drifting sinusoidal gratings (column 1) and used these data to choose the carrier and modulator spatial frequencies (triangles labeled “m” and “c” mark the modulator and carrier frequencies). Adjacent, we show the tuning of the neuron for the carrier-exchange controls (column 2) and the herringbone stimuli (column 3). With “superresolution” carriers (top row), we failed to elicit reliable visual responses (Fig. 6A, polar plots; gray circles indicate baseline firing). This was typical of most V2 neurons. In our earliest recordings, we followed this paradigm exclusively based on published literature and failed to find orientation-selective responses. We therefore modified our parameter choice, setting both the modulator and carrier frequencies within the resolution limit of the neuron. Carrier frequencies were chosen to be slightly higher than the peak; modulator frequencies were typically three times (1.6 octaves) below the carrier frequency (Fig. 6B, column 1). With these new parameter conditions (bottom row), we measured reliable orientation-tuned responses in the example V2 neuron shown, as well as other V2 neurons (Fig. 3).

For 33 neurons in V2, we measured herringbone tuning under both parameter conditions (i.e., with carrier frequencies beyond and within the resolution limit). We used the same probabilistic framework to compute distributions of relative likelihoods for the first-order, second-order, and intermediate predictions. Figure 6A (column 4) shows the distribution of relative log likelihoods for neurons recorded with carrier frequencies beyond the resolution limit; Figure 6B (column 4) shows the comparison distribution for the same neurons recorded with carrier frequencies within the resolution limit. Most V2 neurons were not visually driven in the high carrier frequency case and could not be reliably classified (points near origin)—some neurons were strongly classified as first order, and only one neuron was second order (data not shown) (a neuron whose tuning was classified statistically as second order despite appearing to have very variable responses). However, when carrier frequencies were within the resolution limit, most neurons were well driven and many neurons were strongly classified as first order or intermediate. It is worth noting that the only cue-invariant neuron we recorded (Fig. 3D) was measured with carrier frequencies that were close to the resolution limit of the neuron, although within its passband. We conclude that our protocol for selecting carrier and modulator spatial frequencies used favorable conditions for eliciting reliable visual responses from neurons in monkey V2 and that these choices did not account for our failure to find cue-invariant responses.

Previous studies in cat (Zhou and Baker, 1994) used contrast-modulated gratings (as in Fig. 1E,F), representing one-half of our herringbone stimuli. We therefore wanted to know whether measuring orientation-selective responses for “full” and “half” herringbone patterns had an effect on the classification of neurons into first-order and second-order categories. Figure 7 shows the responses of three example neurons recorded in monkey V2 to both full and half herringbone patterns (data from these neurons were included previously in Fig. 3). For each, we show the measured grating tuning (column 1), the linear response prediction (column 2), tuning for the carrier-exchange controls (column 3), and for the full herringbone patterns (column 4). Adjacent, we show the tuning for each of the half stimuli separately (half 1 and half 2 in columns 5 and 6); data for each half were measured in separate runs. Figure 7A shows the responses of an example first-order neuron (same as in Fig. 3A); its tuning for the carrier-exchange controls and full herringbones was four-lobed, indicating selectivity for luminance-defined form. Tuning for either of the half patterns was also aligned with the four-lobed linear prediction, but only two lobes were evident in each, because in the case of half herringbones only one carrier was present. The tuning of the neuron for both full and half herringbone patterns indicated selectivity for luminance-defined form, and it was classified as first-order in both stimulus cases. Furthermore, the full herringbone tuning reflected the combination of responses to each half. Figure 7B shows the responses of an example modulated by motion neuron (same as in Fig. 3B). This neuron was jointly selective for the orientation of luminance-defined form and the direction of second-order motion. Tuning for full herringbone patterns was aligned with the four-lobed linear prediction, but only two adjacent lobes were evident. Similarly, tuning for each half was also aligned with the linear prediction, but only one lobe was evident because only a single carrier was present in the stimulus. The tuning of the neuron for both full and half herringbone patterns was directional, representing particular directions of second-order motion, and as for the neuron in Figure 7A, full herringbone tuning reflected the combination of directional responses to two half patterns. Figure 7C shows data from an example second-order cue-orthogonal neuron (same as in Fig. 3E). Tuning for the full herringbone pattern was two-lobed but was not aligned with the linear prediction, indicating selectivity for texture-defined form. This neuron preferred herringbone patterns that contained modulator orientations that were orthogonal to its preferred grating. Interestingly, tuning for each half pattern was also two-lobed and identical in shape with the full herringbone tuning; it was classified as second-order cue-orthogonal under both cases.

For 25 neurons in monkey V2, we measured tuning to both full and half herringbone patterns, allowing us to compare distributions of the relative likelihoods of each prediction under both conditions. Figure 7D shows the distribution of responses for full herringbone patterns; Figure 7E shows the comparison distribution for the same neurons for half herringbone patterns. To classify the responses to half herringbone patterns, we modified the predictions in Figure 2 to reflect the presence of a single carrier grating, before running the fitting procedure (e.g., the linear prediction is two-lobed not four-lobed). We also computed the normalized log likelihood separately for each half and used the average log likelihood across both halves to classify each neuron in Figure 7E. The distribution of relative likelihoods was similar for both full and half herringbone patterns, and neurons were classified in all three response categories. From this, we conclude that the results obtained with full and half herringbone patterns are similar. One important virtue of the full herringbone patterns is that they are relatively immune to nonlinearities that could create first-order patterns from distorted or nonlinearly transduced displays.

Relationship between selectivities for texture- and luminance-defined form

We wondered whether the intermediate family of responses (modulated by motion and modulated by form), in which neuronal selectivity for luminance-defined form was shaped by second-order stimulus features, could be predicted by some aspects of the response to simple gratings. We first asked whether directional herringbone responses (modulated by motion) were related to directional responses to gratings. Figure 8 shows example data from two V2 neurons that had directional herringbone tuning. In the first column, we show tuning for grating direction and indicate DSIs (see Materials and Methods) above each plot. The neuron whose responses are shown in Figure 8A was strongly selective for grating direction (DSI = 0.83), showing complete response suppression at null motion directions; the neuron whose responses are shown in Figure 8B was less direction selective (DSI = 0.32). From these grating responses, we generated nondirectional tuning curves (column 2) (see Materials and Methods), which served as the basis for our linear response predictions (column 3). For both neurons, the measured herringbone tuning curves (column 4) were strongly directional, with only two adjacent peaks evident. To measure the influence of second-order motion on neuronal responses to the luminance carriers, we computed a directional index that evaluated the relative strength of adjacent tuning quadrants. We determined the response strength in each of the four polar tuning quadrants (from 0 to 360°) by folding the measured tuning curve to a single quadrant, computing the average curve in this range, then fitting the resultant curve to the measured herringbone responses in each quadrant. The iterative fitting procedure minimized the root mean squared error and allowed only for scalar transformations of response magnitude. The returned scalar values captured the strength of response in each tuning quadrant, and were used to compute a “herringbone direction selectivity index” (DSI_H) as follows:

where a–d represent the strength of response in each tuning quadrant. We computed this index for all combinations of adjacent quadrants (a and b; b and c; c and d; d and a), and took the largest resulting DSI_H. This index is bound between 0 and 1, where 1 represents the strongest direction selectivity. We indicate the value of DSI_H above the herringbone tuning curves in Figure 8. Both neurons showed strongly directional herringbone responses (DSI_H = 1).

We examined the correlation between grating and herringbone direction selectivity indices across the population (Fig. 9). There was a small but significant correlation between these indices (r² = 0.0967; p = 0.0004), suggesting that directional responses to the luminance-defined carriers contributed to the measured directional responses to the herringbone texture patterns. The weak correlation magnitude suggests that, for many neurons, selectivity for grating direction did not account for herringbone direction selectivity. To follow up on this, we took all neurons for which the modulated by motion prediction had the highest likelihood of accounting for the data (N = 28) and examined the angular difference between the preferred grating and herringbone direction (data not shown). We found that 14 of 28 (50%) of neurons had preferred grating and herringbone directions that were within 60° of each other; the other one-half had angular differences in the range 90–180°, suggesting that there was little relationship between their grating and herringbone direction selectivities.

Figure 9.

Relationship between grating and herringbone direction selectivity. For all V2 neurons (N = 128), we plot DSI_H against grating DSI. There was a modest but significant correlation (r² = 0.0967; p = 0.0004), suggesting that directional grating responses may account for some of the directional responses to second-order motion in texture patterns. Points are color-coded by the log likelihood of the modulated by motion prediction; the darker shades represent higher likelihoods.

We also asked whether contextual selectivity for “z” versus “s” configurations in herringbone patterns (modulated by form) could be partly explained by modulatory effects of the extraclassical receptive field surround. Specifically, we wanted to know whether signals originating from the suppressive surround could underlie neuronal preferences for specific spatial configurations of carrier orientations within V2 receptive fields as a result of differences in the distribution of contrast and orientation in the center and surround. Such mechanisms, which exist in both striate and extrastriate visual cortical neurons, can confer some neuronal selectivity for the orientation and spatial frequency of contrast-defined form (Tanaka and Ohzawa, 2009). Figure 10 shows data from two example neurons with contextual herringbone tuning curves. In the first column, we show tuning for grating size and indicate surround suppression indices above each plot (SSI) (see Materials and Methods). Both neurons were strongly suppressed by large stimuli (SSI = 1.0), showing a complete extinction of response when the stimulus extended beyond the classical receptive field center. Adjacent, we show tuning for grating orientation (column 2) and the linear response prediction (column 3). For both neurons, the measured herringbone tuning curves (column 4) showed strong contextual selectivity, with only two opposite peaks evident. To measure the influence of second-order form on neuronal responses to the luminance carriers, we computed a contextual index that evaluated the relative strength of opposite tuning quadrants. We computed a “herringbone contextual selectivity index” (CSI_H) as follows:

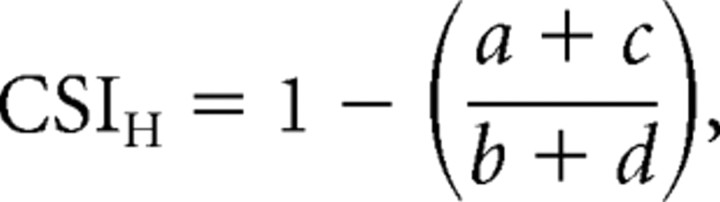where a–d represent the strength of response in each tuning quadrant. We computed this index for both combinations of opposite quadrants (a and c; b and d) and took the largest resulting CSI_H. This index is bound between 0 and 1, where 1 represents the strongest direction selectivity. We indicate the value of CSI_H above the herringbone tuning curves in Figure 10. The neuron whose data are shown in Figure 10A had a strong contextual herringbone response (CSI_H = 0.98), with only two opposite tuning peaks evident. The neuron whose data are shown in Figure 10B had a weak contextual response (CSI_H = 0.14); the response magnitude of two opposite tuning peaks were only moderately attenuated.

Figure 10.

Surround suppression and herringbone contextual selectivity. A, B, Data for two example V2 neurons that showed contextual herringbone responses with two prominent tuning lobes that were opposite. For each, we show tuning for grating size (column 1), for grating orientation (column 2), for herringbone orientation (column 4), and the first-order linear prediction (column 3). A, Responses of a neuron that was strongly suppressed by stimuli that extended beyond the receptive field center, resulting in a high surround suppression index (SSI = 1, above the plot; gray line indicates baseline activity; black line is a descriptive model fit). The neuron showed strong contextual tuning, with a high herringbone contextual selectivity index (CSI_H = 0.98) (see text). B, Responses of a neuron that was also strongly surround suppressed (SSI = 1) but showed only weak contextual herringbone tuning (CSI_H = 0.14).

We examined the correlation between grating surround suppression and herringbone contextual selectivity indices across the population (Fig. 11). We found no significant correlation between these indices (r² = 0.0006; p = 0.7775), suggesting no systematic relationship between the strength of the suppressive surround and selectivity for the spatial arrangement of carrier elements. Approximately one-quarter of our cells were studied with relatively small stimuli to reduce surround suppression; eliminating these from the analysis had no statistically meaningful effect. It is important to note, however, that the surround suppression index only reflects the overall strength of suppressive surround mechanisms. It fails to capture the spatial structure of the extraclassical surround and cannot reveal any spatial inhomogenities, which may account for contextual selectivity. We conclude that the intermediate response patterns cannot be easily attributed to low-level aspects of grating selectivity. We therefore propose that this intermediate family of responses (modulated by motion and form) represents the interaction of first-order and second-order signals and may reflect the gradual emergence of selectivity for texture-defined form as signals pass along the visual pathway.

Figure 11.

Relationship between surround suppression and herringbone contextual selectivity. For all V2 neurons (N = 128), we plot herringbone contextual selectivity index (CSI_H) against grating SSI. There was no significant correlation between these indices (r² = 0.0006; p = 0.7775), suggesting that the overall strength of surround suppression could not easily account for neuronal preferences for particular spatial configurations of carrier elements (“z” vs “s”). Points are color-coded by the log likelihood of the modulated by form prediction; the darker shades represent higher likelihoods.

Discussion

We measured the responses of neurons in macaque area V2 to visual patterns containing texture-defined form. We chose to record in V2 for several reasons. Monkeys with cortical V2 lesions show significant behavioral impairments on texture discrimination tasks (Merigan et al., 1993), suggesting that it plays an important role in texture processing. V2 neurons receive convergent input from many orientation-selective V1 neurons, so that V2 neurons could in principle have the information needed to signal texture cues defined by changes in orientation across an image. Finally, neurons with orientation-selective responses to texture cues have been recorded in cat area 18, the homolog of V2. We found that most V2 neurons (60%) were selective for the orientation of the luminance elements that made up the texture patterns and did not signal the orientation of texture-defined boundaries. For these cells, responses to herringbone patterns were well described by a simple linear prediction based on responses to luminance gratings. Approximately one-third of the neurons we studied gave responses that were also determined by luminance-defined form, but were also modulated by the structure or motion of the texture envelope. Only a few V2 neurons were strongly selective for the orientation of texture-defined form and directly carried second-order information. Of this handful of neurons, only one responded in a cue-invariant way to both gratings and herringbones (Fig. 3D); others displayed an unexpected pattern of cue-orthogonal second-order responses; their preferred grating and herringbone orientations were orthogonal (Fig. 3E). Thus, although cue-invariant responses have been seen in ∼50% of neurons in cat area 18 (Zhou and Baker, 1994; Leventhal et al., 1998; Mareschal and Baker, 1998a,b; Song and Baker, 2007), we found little evidence for such a representation in monkey V2.

In the cat experiments, Baker and his colleagues used superresolution carrier spatial frequencies that were beyond the resolution limit for each cell, allowing them to clearly separate first- from second-order responses. Unfortunately, when we tried to isolate texture-dependent responses in the same way in monkey V2, we were unable to evoke reliable visual responses (Fig. 6). We therefore modified our paradigm, choosing carrier frequencies on the high limb of the spatial frequency tuning curve, and modulator frequencies on the low limb (Fig. 6B). Under these conditions, we could reliably drive V2 neurons. This discrepancy between species might reflect differences in the spatial frequency tuning properties of the two early cortical processing stages. Cat areas 17 and 18 show very different selectivities, with area 18 preferring significantly lower spatial frequencies (Movshon et al., 1978c), whereas monkey areas V1 and V2 respond to more similar frequency ranges (Foster et al., 1985; Levitt et al., 1994). This presumably reflects the fact that the visual activation of monkey V2 is completely dependent on its input from V1 (Schiller and Malpeli, 1977; Girard and Bullier, 1989), whereas area 18 in cat is well driven even when area 17 is silenced (Dreher and Cottee, 1975; Sherk, 1978). Thus, it is possible that Baker and colleagues found carrier frequencies that were beyond the resolution limit of area 18 neurons but still excited their thalamic inputs, allowing them to measure selectivity for second-order envelopes, whereas we could not do the same in the primate. Most input to cat area 18 is from nonlinear Y-cells, which may respond to non-Fourier second-order stimulus components (Demb et al., 2001; Petrusca et al., 2007; Crook et al., 2008; Rosenberg et al., 2010). However, we recorded from a small population of cat area 18 neurons (N = 19) and found qualitatively similar results those in V2 detailed above: neurons did not respond selectively to stimuli with superresolution carriers, a discrepancy with previous results in other laboratories for which we can offer no compelling explanation.

One difference between our procedures and those used in previous studies is that our herringbone stimuli varied in orientation but not in contrast across the display. This has the virtue that they are relatively immune to nonlinearities that could create first-order patterns from distorted or nonlinearly transduced displays, but makes them different from the contrast-modulated patterns commonly used in other laboratories (Zhou and Baker, 1994). We did, however, show for a subset of cells in macaque V2 that a reduced version of our stimulus with contrast modulation (the half herringbone) evoked qualitatively and quantitatively similar responses to the full herringbones (Fig. 7). This suggests but does not prove that differences in stimulus composition do not account for the discrepancy between our results and previously published studies in cat area 18. We are puzzled by our inability to find cue-invariant responses in cat area 18, especially as we took trouble to reproduce the published cat experimental protocols as closely as possible. We can only report, without explanation, that in a limited but otherwise representative set of neurons recorded in cat area 18, we could not demonstrate convincing selectivity for second-order features using our stimuli.

We have not demonstrated pure second-order responses in macaque V2, but our results have implications for the mechanisms of texture perception. In the context of the standard FRF model of texture processing, our data suggest that the first and second stages of filtering do not map directly on to early visual cortical areas V1 and V2, with neurons selective for luminance-defined form in V1 and for texture-defined form in V2. Only a few cells were selective for the orientation of texture-defined form, suggesting that V2 is not the locus for a large set of second-order channels of the kind postulated psychophysically (Landy and Graham, 2004). Moreover, the handful of cue-orthogonal neurons we found in V2 suggest the existence of orthogonally tuned stages; such “inconsistent-orientation mapping” has been considered in previous psychophysical models of texture segregation (Graham and Wolfson, 2001, 2004). The responses of these special cue-orthogonal neurons could mediate the selectivity of some V2 neurons to the orientation of illusory contours defined by orthogonal inducer elements (von der Heydt et al., 1984).

The visual cortex is a house with many rooms, so nothing in its architecture demands that signals be transformed from pure first-order to pure second-order in a single step. A plausible alternative might be a cascade of processing, in which the analysis of texture-defined stimuli is enhanced incrementally, stage by stage. This is compatible with our finding of a substantial minority of neurons whose selectivity, although fundamentally first order, was influenced by the second-order texture-defined signal. These V2 responses might represent one step in the gradual emergence of selectivity for texture-defined form, which may build up as information flows downstream in the extrastriate cortex. Such a cascade is consistent with human functional imaging evidence that shows a graded increase in selectivity for second-order form in higher cortical areas (Larsson et al., 2006).

Another “gradualist” approach to texture analysis could be based almost entirely on modulation of the activity of first-order channels by suppressive mechanisms distributed inhomogeneously in the receptive field surround. Such mechanisms have been shown to exist in early areas of the cat visual cortex (Walker et al., 1999), and they can confer selectivity for the orientation of second-order contours (Tanaka and Ohzawa, 2009). Combined with known variations in the selectivity of different regions of the surround in macaque (Cavanaugh et al., 2002b), such a mechanism might be sufficient to signal not only stimuli defined by contrast modulation but also stimuli like our herringbones that are defined by texture modulation. We asked whether the strength of surround suppression in V2 could predict selectivity for the spatial configuration of luminance elements within herringbone texture patterns, but did not find a strong relationship between the SSI and herringbone contextual selectivity (Fig. 11). But the SSI measure is insensitive to the spatial structure of the suppressive surround and, in particular, to a structural anisotropy that might produce differential responses to two stimulus contexts, such as the letter “z” or “s” configurations in Figure 2D. Another relevant measure is the relative magnitude of responses to the carrier-exchange controls and herringbone stimuli. The degree to which the herringbone stimulus evokes larger responses than the control (in which the carriers are spatially uniform) might measure the degree to which spatial variations in orientation release a cell from surround suppression. Our analysis suggests that neurons selective for second-order features, particularly those that were classified as second-order or intermediate, showed a larger difference in their peak response magnitudes, responding more vigorously to herringbone patterns compared with the carrier-exchange controls. We are presently conducting experiments aimed specifically at examining the spatial structure of the surround and its relationship to neuronal texture selectivity.

Our results complement previous work aimed at understanding mechanisms of intermediate form vision in extrastriate cortex. In our dataset, most V2 neurons had herringbone tuning profiles that matched the linear response prediction derived from the combined responses to the component gratings. This is consistent with reports that the selectivity of V2 neurons for particular angles in “chevron” stimuli can be primarily explained by the combined responses to the component line segments that define those angles (Ito and Komatsu, 2004). These linear (additive) responses are also consistent with grating orientation tuning being spatially uniform across most V2 receptive fields (Anzai et al., 2007). Furthermore, approximately one-third of V2 neurons showed selectivity for second-order stimulus features, a proportion similar to that of V2 neurons that are selective for complex gratings and contours (Hegdé and Van Essen, 2000, 2003, 2007), that have orientation selectivity that is nonuniform over space (Anzai et al., 2007), and that respond preferentially to natural images (Willmore et al., 2010). Finally, we proposed that selectivity for visual features increases in a subtle and gradual manner rather than abruptly (and categorically) across stages of the visual processing hierarchy; this is in agreement with single-unit studies characterizing form selectivity in different cortical areas along the ventral visual pathway (Kobatake and Tanaka, 1994; Pasupathy and Connor, 2001; Brincat and Connor, 2004; Hegdé and Van Essen, 2007; Yamane et al., 2008).

Our findings suggest that, in the primate brain, the analysis of texture-defined form is not complete by the time signals leave V2. We guess that texture-selective responses are mainly found downstream of V2. Area V4 is a plausible candidate site—monkeys with cortical lesions in V4 also show significant impairments on texture discrimination tasks (Merigan, 2000). Future neurophysiological recordings using similar stimuli, which dissociate orientation-selective responses to luminance- and texture-defined form, may help to uncover the transformation of information through successive stages of cortical processing. Physiological and psychophysical studies examining the modulatory effects of second-order cues on the processing of first-order signals may also be important in suggesting alternative frameworks for the computations required by the FRF model. Much of the psychophysical literature on second-order vision concentrates on the idea of a “pure” second-order system operating in parallel with a linear first-order system. But it is useful to consider how much can be accounted for by an “impure” representation mediated by neuronal mechanisms whose responses reflect a complex combination of luminance- and texture-defined signals. Second-order vision may not require second-order channels, just the modulation of first-order channels by second-order information.