Abstract
Relative positions of nematodes, arthropods, and chordates in animal phylogeny remain uncertain. The traditional tree topology joins arthropods with chordates in a coelomate clade, whereas nematodes, which lack a coelome, occupy a basal position. However, the current leading hypothesis, based on phylogenetic trees for 18S ribosomal RNA and several proteins, joins nematodes with arthropods in a clade of molting animals, Ecdysozoa. We performed a phylogenetic analysis of over 500 sets of orthologous proteins, which are represented in plants, animals, and fungi, using maximum likelihood, maximum parsimony, and distance methods. Additionally, to increase the statistical power of topology tests, the same methods were applied to concatenated alignments of subunits of eight conserved macromolecular complexes. The majority of the methods, when applied to most of the orthologous clusters, both concatenated and individual, grouped the fly with humans to the exclusion of the nematode, in support of the coelomate phylogeny. Trees were also constructed using information on insertions and deletions in orthologous proteins, combinations of domains in multidomain proteins, and presence-absence of species in clusters of orthologs. All of these approaches supported the coelomate clade and showed concordance between evolution of protein sequences and higher-level evolutionary events, such as domain fusion or gene loss.
Despite more than a century of extensive phylogenetic studies, major issues in the evolution of the metazoa (animals) remain unresolved (for review, see Hedges 2002). The traditional tree topology based on comparative anatomy includes a clade of animals with a true body cavity (coelomates, such as arthropods and chordates), whereas animals that have a pseudocoelome, such as nematodes, and those without a coelome, such as flatworms, occupy more basal positions in the tree (e.g., Raff 1996). However, a new concept emerged from the phylogenetic analysis of 18S ribosomal RNA, which clustered arthropods and nematodes in a clade of molting animals termed the Ecdysozoa (Fig. 1; Aguinaldo et al. 1997). The ecdysozoan scenario was further supported by independent phylogenetic analysis of 18S RNA (Giribet et al. 2000; Peterson and Eernisse 2001) and by combined analysis of 18S and 28S rRNA sequences (Mallatt and Winchell 2002). The ecdysozoan topology was recovered only when certain species of nematodes, which apparently have evolved slowly, were included in the analyzed sample. On the basis of these observations, the coelomate topology, which emerged both from the classical morphological comparisons and from other molecular phylogenetic studies, has been reinterpreted as a long-branch attraction artifact. Additional support for the ecdysozoan theory has been harnessed from several phylogenetic studies on protein-coding genes, such as Hox (de Rosa et al. 1999) and β-thymosin (Manuel et al. 2000).
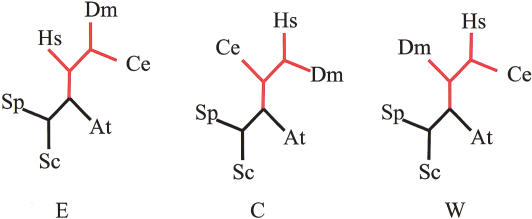
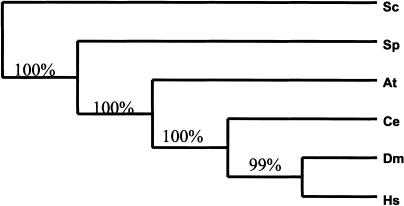
Figure 1.
Three possible topologies of the metazoan phylogenetic tree. At, Arabidopsis thaliana; Sc, Saccharomyces cerevisiae; Sp, Schizosaccharomyces pombe; Ce, Caenorhabditis elegans; Dm, Drosophila melanogaster; Hs, Homo sapiens.
The ecdysozoan topology gained rapid recognition in the “evo-devo” community thanks to its apparent biological plausibility (e.g., Adoutte et al. 2000; Valentine and Collins 2000; Collins and Valentine 2001). However, recent phylogenetic analyses of multiple sets of orthologous proteins seem to turn the tables again by lending stronger support to the coelomate topology. In particular, Mushegian and coworkers (1998) reported phylogenetic analysis of 42 sets of probable orthologs, whereas Blair and coworkers (2002) analyzed ∼100 orthologous nuclear proteins using several phylogenetic methods. Both groups found that the majority of trees supported the coelomate topology. Given the multiple lines of support for each of the alternative tree topologies, the issue is considered unresolved, and the metazoan phylogenetic tree is often cautiously presented as multifurcations (e.g., Hedges 2002).
The principal interest of the coelomate–ecdysozoa conundrum lies in the relationship between phylogeny and biological organization, at both the organismal and molecular levels. The coelomate topology reverberates with the straightforward notions of the hierarchy of morphological and physiological complexity among the considered organisms, which is the main reason why this phylogeny had been accepted since the time of Ernst Haeckel and until the 18S rRNA analysis by Lake and coworkers (Aguinaldo et al. 1997). However, the existence of the ecdysozoan clade is compatible with several aspects of development that are shared by the molting animal phyla.
Large-scale phylogenetic analysis inevitably involves a trade-off between taxon sampling and gene (or, more generally, character) sampling. The relative importance of increasing the number of analyzed taxa and the number of characters for the accuracy of phylogenetic inferences remains an issue of debate (Hillis 1998; Hillis et al. 2003; Rosenberg and Kumar 2003). Taxon sampling had a decisive effect on the outcome of the phylogenetic analysis of rRNAs that led to the ecdysozoan topology (Aguinaldo et al. 1997). However, independent recent simulations and empirical studies suggest that gene sampling, in general, might have a greater effect on phylogenetic tree topology than taxon sampling (Mitchell et al. 2000; Rosenberg and Kumar 2001). We sought to take advantage of the complete eukaryotic genomes and the collection of clusters of orthologous groups of eukaryotic proteins (Tatusov et al. 2003) to greatly increase the size of gene sample available for phylogenetic analysis and reexamine the coelomate versus ecdysozoa problem on the genome scale. Phylogenetic analysis of ∼500 KOGs (eukaryotic orthologous groups) using several phylogenetic methods showed the strongest and most consistent support for the coelomate topology. This result is compatible with the topologies of trees produced using nonsequence-based criteria, such as gene content and multidomain protein composition, indicating a general concordance between tempo and mode in animal evolution.
RESULTS AND DISCUSSION
Phylogenetic Analysis of Concatenated Protein Sequence Alignments
To increase the statistical power of phylogenetic analysis, we constructed concatenated alignments of the subunits of eight macromolecular complexes (hereinafter, the con8 set), under the premise that these proteins are likely to evolve in the same mode and can be legitimately analyzed as a single entity (Table 1). The conserved blocks from each of the concatenated alignments (see Methods) were employed to construct distance matrix trees using the neighbor-joining and least-squares methods as well as parsimony and maximum-likelihood (ML) trees. Both distance-based methods showed a strong preference for the coelomate topology, with bootstrap probabilities >80% (Table 1; data not shown). Both maximum parsimony methods also assigned the coelomate topology to the majority of the analyzed systems, with two exceptions, namely, a weak support for the ecdysozoan topology for the RNA polymerase subunits, and a strong preference for the ecdysozoan topology for the proteasome subunits (Table 2). In contrast, all three ML methods divided the systems between the two competing topologies, with five alignments (chaperonins, clathrins, DNA polymerase subunits, licensing factors, and translation factors) showing preference for the coelomate model (with varying degrees of confidence), and three (proteasome subunits, ribosomal proteins, and RNA polymerase subunits) displaying a strong preference for the ecdysozoan model (Table 2).
Table 1.
Macromolecular Complexes Used for Phylogenetic Analysis of Concatenated Subunit Sequences
| con8 IDa | No. of subunits (KOGs) | Function | No. of sites in blocks |
|---|---|---|---|
| CH | 8 | Chaperonins, TCP-1/cpn60 family | 3970 |
| CL | 5 | Clathrin complex proteins | 2138 |
| DP | 3 | DNA polymerase subunits | 1782 |
| LF | 4 | DNA replication licensing factors | 2284 |
| PR | 12 | 20S proteasome subunits | 2474 |
| RI | 74 | Ribosomal proteins | 11586 |
| RP | 3 | RNA polymerase subunits | 3274 |
| TF | 5 | Translation factors | 2045 |
The members of individual KOGs are listed in the Supplementary Information
Table 2.
Distribution of the Metazoan Tree Topologies for Concatenated Sequences of Macromolecular Complex Subunits With Different Tree Construction Methods
| con8 ID | NJ | MP(F) | MP(S) | ML(AH) | ML(Y) | ML(TP) |
|---|---|---|---|---|---|---|
| CH | C(87%) | C(96%) | C(60%) | C(58%) | C(54%) | C(100%) |
| CL | C(100%) | C(99%) | C(87%) | C(86%) | C(88%) | C(72%) |
| DP | C(82%) | C(87%) | C(71%) | C(51%) | C(50%) | C(64%) |
| LF | C(100%) | C(100%) | C(99%) | C(100%) | C(100%) | C(80%) |
| PR | C(92%) | E(84%) | E(85%) | E(73%) | E(75%) | E(82%) |
| RI | C(100%) | C(77%) | C(75%) | E(65%) | E(72%) | E(90%) |
| RP | C(93%) | C(54%) | E(69%) | E(76%) | E(72%) | E(89%) |
| TF | C(98%) | C(87%) | C(99%) | C(83%) | C(85%) | C(70%) |
For each complex (Table 1) and each method, the preferred tree topology (C, coelomate, E, ecdysozoan) and the bootstrap support or, in the case of ML(TP), Expected Likelihood Weight are given in parentheses. NJ, neighbor-joining (nearly identical results were obtained with the FITCH program; data not shown); MP(F), maximum parsimony (Felsenstein, PHYLIP); MP(S), maximum parsimony (Swofford, PAUP*); ML (AH), Maximum Likelihood (Adachi-Hasegawa; MOLPHY); ML (Y), Maximum Likelihood (Yang; PAML); ML (TP), Maximum Likelihood (Strimmer-von Haeseler; TREE-PUZZLE).
Phylogenetic Analysis of Individual KOGs
Each of the 507 KOGs containing representatives from six eukaryotic species (six507 set) and selected as described in the Methods section were subjected to phylogenetic analysis using the least squares and ML methods, under the gap exclusion and block site selection schemes (see Methods). For each scheme, 35%–44% of the trees failed to recover the monophyly of the metazoa or that of the two yeast species or to cluster paralogs from the same species (when present) into the same lineage. These obvious artifacts were attributed to errors in automatically produced alignments, compositional bias of the sequences, or misidentification of orthologs, and the respective trees were discarded. The remaining 285 to 328 trees (depending on the method) assign one of the three possible topologies to the metazoa, with plants and fungi considered outgroups (Fig. 1). A relatively small minority (12%–14%) of the trees placed the fly in the metazoan root, whereas the rest were divided between the coelomate (53%–67%) and ecdysozoan (21%–35%) topologies (Table 3). The gap exclusion mode (i.e., use of a greater number of relatively variable positions in the phylogenetic analysis) and the least-squares tree reconstruction method favored the coelomate topology. In contrast, the block site selection mode (use of only highly conserved, slow-evolving positions) and the ML method made the split between the two topologies more even (Table 3). Considering only the cases where at least three of the four tree construction schemes agreed on the topology, the distribution shifted even further in favor of the coelomate model, with ∼70% of the robust trees pointing this way (Table 3). Altogether, 202 of the 507 analyzed KOGs (40%) showed complete agreement on the reconstructed topology, which, in itself, is a considerable amount of apparently phylogenetically coherent data; however, this result also points to a notable variability in the outcomes of different analysis schemes.
Table 3.
Distribution of the Metazoan Tree Topologies Obtained With Four Tree Construction Methods for 507 KOGs
| Method | C | E | W | ∼ |
|---|---|---|---|---|
| Gap/ML | 175 (53%) | 114 (35%) | 39 (12%) | 179 (35%) |
| Gap/FI | 216 (67%) | 68 (21%) | 40 (12%) | 183 (36%) |
| Block/ML | 152 (53%) | 95 (33%) | 39 (14%) | 221 (44%) |
| Block/FI | 186 (65%) | 61 (21%) | 38 (13%) | 222 (44%) |
| combined (3 of 4) | 139 (69%) | 48 (24%) | 15 (7%) | 305 (60%) |
| combined (4 of 4) | 91 (72%) | 28 (22%) | 7 (6%) | 381 (75%) |
The number of KOGs is given for each combination of phylogenetic analysis strategy [Gap, gap exclusion mode; Block, block mode; ML, Maximum Likelihood (MOLPHY); FI, Fitch] and topology (C, coelomate; E, ecdysozoan; W, worm-human; ∼, poor tree, monophyly of Metazoa and/or Fungi not recovered). The numbers in parentheses show the percentage of the given topology among the acceptable trees (those with correctly recovered monophyly of the kingdoms) except for the last column (poor trees), in which the percentage of the entire six507 set is indicated.
Branch Length Effects
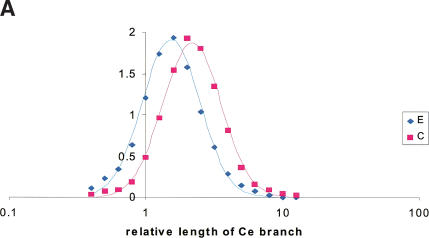
It has been claimed that the coelomate topology is an artifact of the high evolutionary rate in some species of nematodes, particularly Caenorhabditis elegans, which results in long branches that are pushed to a basal position in trees (Aguinaldo et al. 1997). The choice of slow-evolving nematode species seemed to favor the ecdysozoan model. This notion at present cannot be tested systematically because there are too few sequences available from nematodes other than C. elegans. However, we reasoned that, if branch lengths made a major contribution to the metazoan tree topology, a significant correlation between the relative branch lengths and the observed tree topology should be expected. Therefore we examined the 122 coelomate and 73 ecdysozoan trees that were obtained for the six384 set of KOGs with the ML (ProtML) method for tree reconstruction. The ecdysozoan trees tended to have a shorter branch for C. elegans relative to the length of the human branch, compared to the coelomate trees (Table 4), although the distributions of the relative branch lengths showed a large overlap (Fig. 2A); both distributions could be well approximated by the lognormal distribution (data on the goodness of fit not shown).
Table 4.
Relative Branch Lengths for Different Topologies of the Metazoan Tree
| Branch length relative to human | C | E | W | ∼ |
|---|---|---|---|---|
| Worm | 2.13 ± 0.10 | 1.54 ± 0.08 | 2.00 ± 0.19 | 2.03 ± 0.14 |
| (1.97—2.31) | (1.37—1.69) | (1.53—2.19) | (1.78—2.28) | |
| Fly | 1.21 ± 0.04 | 1.06 ± 0.05 | 1.37 ± 0.15 | 1.06 ± 0.05 |
| (1.11—1.27) | (0.98—1.17) | (1.14—1.59) | (1.01—1.20) |
The lengths of the fly and worm branches are given relative to the human branch length, which was assumed equal to 1. Median ± standard deviation and 95% confidence interval (in parentheses) are indicated. The tree topologies are designated as in Table 3.
Figure 2.
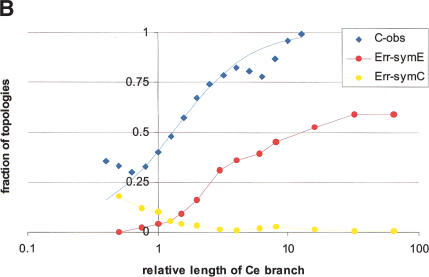
The effect of relative branch lengths of tree topology. (A) Distribution of the relative length of the nematode branch in the six384 set. E, 73 families with the ecdysozoan topology; C, 122 families with the coelomate topology. (B) Relative frequency of topologies reconstructed from real and simulated alignments. C-obs, fraction of trees with the coelomate topology in the six384 set (blue diamonds, calculated from observed distribution density values; blue lines, calculated from the lognormal approximation). Err-simE, fraction of wrong topologies (error rate) for the trees reconstructed from alignments simulated by using model trees with the ecdysozoan topology. Err-simC, fraction of wrong topologies (error rate) for the trees reconstructed from alignments simulated by using model trees with the coelomate topology. Horizontal axis: the length of the nematode branch relative to the human branch.
The fraction of trees with the coelomate topology monotonically increases over the range of the relative lengths of the C. elegans branch (Fig. 2B). Under the hypothesis that the ecdysozoan topology is the correct one and the coelomate topology appears because of long-branch attraction, this corresponds to an increasing rate of erroneous topology assignment with the increase of the relative length of the nematode branch. Whether or not the above hypothesis is realistic, it can be tested by measuring the rate of false topology assignment in model trees with varying relative branch lengths produced from simulated multiple sequence alignments. The alternative hypothesis that the coelomate topology is the correct one can be similarly tested. As shown in Figure 2B, the ML trees reconstructed by using ProtML are remarkably robust to long-branch attraction artifacts. For the alignments simulated with the ecdysozoan tree, even a 64:1 ratio of the nematode to human branch lengths yields an error rate of ∼60%. In the range of branch length ratios where most of the actual data belongs (1:1 to 3:1), ProtML correctly reconstructs 70%–95% of trees for simulated alignments. In contrast, in the trees constructed for the real KOGs, the coelomate trees significantly outnumber the ecdysozoan ones; that is, the “error rate” is ≫50% (Fig. 2B).
Conversely, the fraction of trees with the erroneous ecdysozoan topology reconstructed from alignments simulated with the coelomate model increases with the decrease of the relative length of the nematode branch; however, even when the nematode branch was twice shorter than the human branch, the error rate was only 18% (Fig. 2B). Thus, the results of the tests with simulated alignments and model trees indicate that the presence of both coelomate and ecdysozoan topologies among the trees for the six384 KOG set cannot be attributed solely or even largely to the long (short) branch attraction artifacts.
Trees Built Using the Median Similarity Between Orthologs as a Measure of Evolutionary Distance
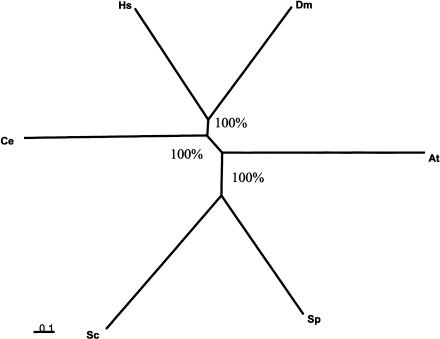
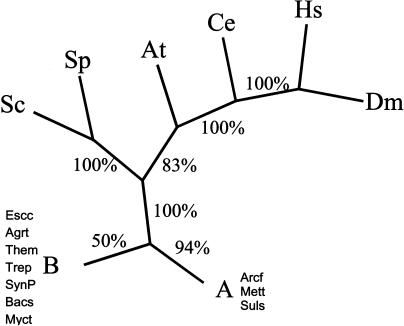
Previous analyses have shown that the distributions of evolutionary distances (or simply percent sequence identity) between pairs of orthologous proteins had the same shape, up to a scaling factor, for a wide range of evolutionary distances (Grishin et al. 2000). Therefore, parameters of such distributions, in particular the median, can be employed to calculate evolutionary distances between species and to construct neighbor-joining or least-squares trees (Wolf et al. 2001, 2002). We were interested in using this approach, in addition to the more standard methods discussed above, in order to take into account the maximum number of detectable orthologs. The metazoan tree constructed using this approach strongly supported the coelomate topology (Fig. 3).
Figure 3.
An unrooted tree constructed using the median similarity between orthologs as a measure of evolutionary distance. The tree was constructed using the least-squares method. The bootstrap values are shown for each internal branch.
Indels as Evolutionary Markers
Insertions and deletions (indels) in proteins are often considered to be suitable characters for inferring evolutionary relationships, under the assumption that independent insertion or deletion in the exact same position of a protein in different lineages (homoplasy) is unlikely (Rokas and Holland 2000; Bapteste and Philippe 2002). We applied the Wagner parsimony analysis, which implements this assumption, to the indels in the six384 set of alignments. The coelomate topology emerged as a clear winner, resulting in significantly fewer homoplasies than any alternative topology (Table 5).
Table 5.
Parsimony Analysis of Indels in Alignments for the six384 Set
| Tree topologya | Total no. of indel events | No. of sites with homoplasiesb | Differencec |
|---|---|---|---|
| C | 1092 | 36 (3.4%) | best |
| E | 1119 | 63 (6.0%) | 27 ± 8.3 |
| W | 1125 | 69 (6.5%) | 33 ± 7.9 |
C, coelomate; E, ecdysozoa; W, clustering of human with nematode
Sites with homoplasies were those for which two or more independent events were indicated by the Wagner parsimony analysis
Difference from the best scenario and its standard deviation as computed by MIX program of PHYLIP package
Trees Based on Gene Content and Domain Co-Occurrence in Multidomain Proteins
Using patterns of gene presence-absence in orthologous sets for tree construction is one of the straightforward genome-tree approaches (Fitz-Gibbon and House 1999; Snel et al. 1999; Wolf et al. 2002). Presence-absence of a gene can be naturally treated as a binary character, and the table of such characters can be subjected to either parsimony or distance phylogenetic analysis. After constructing such a character matrix for the complete set of KOGs, we applied the Dollo parsimony method, which assumes irreversibility of character loss; that is, when a KOG is lost in a lineage, it cannot be regained, which seems to be indisputable in the absence of horizontal gene transfer. Unlike the case of prokaryotic evolution, this assumption seems reasonable for the analysis of the evolution of eukaryotes, where the possibility of horizontal gene transfer can be disregarded. Furthermore, since, in the absence of horizontal gene transfer, each KOG was gained exactly once during eukaryotic evolution and, accordingly, the parsimony algorithm, in this case, minimized only the number of losses, the problem of choosing the appropriate gain and loss weights, which was critical for the analyses of prokaryotic evolution (Snel et al. 2002; Mirkin et al. 2003), did not present itself.
The rooted tree produced using the Dollo method confidently supported the coelomate topology (Fig. 4). Otherwise, however, this tree was at odds with the prevalent taxonomic view (Hedges 2002) in that grouping of animals with plants was observed. This deviation of the gene content tree from the currently accepted phylogeny is probably due to the varying amount of gene loss in different eukaryotic lineages, in particular, massive gene loss in yeasts. As discussed previously in the context of prokaryotic genome analysis, the topology of gene content trees seems to reflect a combination of the phylogenetic signal and other trends in genome evolution that are not necessarily linked to phylogeny, such as parallel gene loss associated with lifestyle similarities (Wolf et al. 2002). The clustering of humans with flies in the gene content tree points to the congruence in gene repertories of these animals. Given the likely effect of parallel gene loss on the topology of this tree, it could not be viewed as independently supporting the coelomate topology. The significance of this tree is different: Given the support for the coelomate phylogeny from the other genome-scale phylogenetic analyses described above, clustering of vertebrates and insects in the gene content tree suggests that, among animal lineages, the patterns of gene loss and emergence at least roughly follow the species divergence.
Figure 4.
Dollo parsimony tree for the presence-absence of species in KOGs. The bootstrap values are indicated for each internal branch.
All eukaryotes have numerous multidomain proteins, which allows one to use the data on domain co-occurrence to construct trees. For this purpose, each pair of co-occurring domains was treated as a binary character, and the Dollo parsimony method was applied to the resulting character table with the same rationale as for the gene presence-absence data; that is, under the assumption that independent origin of the same domain combination is unlikely. The topology of the resulting tree was identical to that of the gene content tree, with an equally strong support for each internal branch (Fig. 5). Thus, evolution of domain fusions seems to follow the pattern of gene emergence and loss. The strong support for the coelomate topology seen in this tree reflects the previously noted higher similarity between the architectures of human and fly multidomain proteins compared to those of the nematode (Koonin et al. 2000; Lander et al. 2001).
Figure 5.
Dollo parsimony tree for domain architectures of multidomain proteins. A selection of prokaryotic species was included to root the tree. B, Bacteria; Escc, Escherichia coli K12; Agrt, Agrobacterium tumefaciens C58; Them, Thermotoga maritima; Trep, Treponema pallidum; SynP, Synechocystis sp. PCC 6803; Bacs, Bacillus subtilis; Myct, Mycobacterium tuberculosis H37Rv; A, Archaea; Arcf, Archaeoglobus fulgidus; Mett, Methanothermobacter thermautotrophicus Delta H; Suls, Sulfolobus solfataricus; the rest of the species abbreviations are as in Figure 1. The bootstrap values are indicated for each internal branch.
DISCUSSION
In this work, we explored metazoan phylogeny by analyzing a large set of orthologous clusters with several widely different approaches for tree construction. Quantitatively at least, there seems to be a clear convergence on the coelomate topology. This topology was supported by both sequence-dependent phylogenetic methods and sequence-independent approaches, such as the analysis of gene content of KOGs and protein domain architectures. This demonstrates the apparent concordance between different types of evolutionary events in animals; that is, gene loss and domain fusions and fissions seem to occur more or less in parallel with the decay of sequence similarity. This is not necessarily the case for the deeper branches in the eukaryotic tree, where the analysis of gene content and domain architectures supported the animal-plant grouping, in contrast to most phylogenetic analyses, including our own reported herein, which suggested the existence of an animal-fungi clade. Similarly, genome-wide phylogenetic studies on the evolution of prokaryotes revealed major differences between trees based on sequence divergence and those constructed on the basis of gene content or gene order data (Wolf et al. 2002).
The phylogenetic approach employed here is one of the “genome-tree” approaches (Wolf et al. 2002) in that we relied on the maximal possible expansion of the number of analyzed orthologous sets rather than taxon sampling. A combination of both strategies probably would provide the optimal solution but, given the practical situation with genome sequencing, this is not feasible in the nearest future. The main objection against the use of a single species from a taxon for phylogenetic analysis is that the results could be prone to artifacts caused by a systematic bias in branch lengths. In particular, if C. elegans evolves faster than Drosophila and/or humans, the coelomate topology could be a branch length-related artifact. However, explicit assessment of the effect of branch length differences on the topology of the recovered trees reported here shows that the topology is remarkably robust and seems to rule out long-branch or short-branch attraction artifacts as the main causes of the observed distribution of topologies.
Thus, the coexistence of the two incompatible topologies among the KOGs emerges as a major outstanding issue. One possible explanation is that the models of amino acid substitutions employed in distance calculations and in maximum likelihood estimates (see Methods) are not necessarily adequate approximations of evolution for all genes. Different biases in substitution probabilities might have differential effects on tree topology. This interpretation of the differences in tree topologies for different orthologous sets assumes that there is a single true topology—conceivably, the one that is observed most frequently, that is, the coelomate topology—and all deviations from it are caused by artifacts of varying nature. However, an alternative hypothesis based on the assumption that different topologies reflect evolutionary realities also could be considered. Specifically, the different topologies could ensue from a duplication of multiple genes (perhaps large parts of the genome) preceding the divergence of the analyzed lineages; in the present case, vertebrates, arthropods, and nematodes. Under this scenario, the most common tree topology still reflects the actual order of lineage divergence, but alternative topologies result from lineage-specific, differential loss of paralogs.
Taken together, the results of the genome-wide phylogenetic analysis described here indicate that the available data support the coelomate topology for animal evolution. To reach a new level of confidence in this solution, representative samples of genome sequences from the relevant taxa and more adequate models of evolution are required.
METHODS
Selection of Sets of Orthologous Proteins (KOGs) for Phylogenetic Analysis
Orthologous sets of eukaryotic proteins (KOGs; (Tatusov et al. 2003; http://www.ncbi.nlm.nih.gov/COG/new/shokog.cgi) were deemed suitable for phylogenetic reconstruction if they met two criteria: (1) representation in six species of eukaryotes, namely, Saccharomyces cerevisiae, Schizosaccharomyces pombe, Arabidopsis thaliana, Caenorhabditis elegans, Drosophila melanogaster, and Homo sapiens, and (2) contained no large paralogous families (at most two paralogs in any of the species). Of the 6162 KOGs, 507 satisfied these criteria and were selected for phylogenetic analysis (“six507” set). Of these, 384 KOGs had no paralogs in metazoa (“six384” set). Sequences were aligned using the T-Coffee program (Notredame et al. 2000) in a completely automatic regime.
Concatenated Alignments of Subunits of Macromolecular Complexes
Eight multisubunit complexes that are conserved in all eukaryotes were selected to construct concatenated alignments (“con8” set). Orthologous sets of individual subunits of each of these complexes were aligned using the T-Coffee program, and first-approximation phylogenetic trees were constructed using the least-squares (Fitch-Margoliash) method as implemented in the FITCH program of the PHYLIP package (Felsenstein 1996). Alignments were examined and manually corrected when necessary. Paralogs, when present, were discarded based on the analysis of alignments (truncated or poorly assembled sequences) and Fitch-Margoliash trees (long branches). Alignments of the individual subunits were then concatenated for further analysis.
Site Selection for Phylogenetic Analysis
Poorly conserved protein regions, especially those rich in insertions and deletions, might be a source of noise, obscuring phylogenetic information contained in alignments. Two methods of site selection, primarily devised to counter the effect of potential misalignment, were used in this study. In the “gap exclusion” mode, all sites containing three or more gap characters were removed. In the “block” mode, alignments were split into blocks completely devoid of indels and flanked by highly conserved columns; only blocks of 20 sites or longer were retained for further analysis.
Sequence-Based Phylogeny
The following methods were used to construct phylogenetic trees from sequence alignments. (1) Neighbor-joining trees (Saitou and Nei 1987) were constructed by using the NEIGHBOR program of the PHYLIP package, with the distance matrix (PAM distance) calculated using the PROTDIST program of PHYLIP (Felsenstein 1996). (2) Least-squares trees (Fitch-Margoliash method; Fitch and Margoliash 1967) were constructed by using the FITCH program of PHYLIP, with same distance matrix as for the neighbor-joining trees. (3) Maximum parsimony trees were constructed using the HSEARCH program of the PAUP* package (Swofford 2000) or the PROTPARS program of PHYLIP. (4) Maximum likelihood (ML) trees were constructed using: (a) the ProtML program (JTT model adjusted for frequencies) of the MolPhy package (Kishino et al. 1990; Adachi and Hasegawa 1992), (b) the CODEML program of the PAML package with the JTT model adjusted for frequencies and γ-distribution parameter α estimated from the data set (other models produced virtually identical results when tested; Yang 1997; data not shown), and (c) the TREE-PUZZLE program with automatic selection of the substitution model and γ-distribution parameter α estimated from the data set (Schmidt et al. 2002). For neighbor-joining, least-squares, and maximum parsimony trees, the robustness of the reconstructed phylogenies was assessed by using bootstrap analysis (100 replications). For ML trees, the Kishino-Hasegawa (Kishino et al. 1990), Shimodaira-Hasegawa (Shimodaira and Hasegawa 2001), and expected likelihood weight (Strimmer and Rambaut 2002) tests included in ProtML, PAML, and TREE-PUZZLE, respectively, were used.
Analysis of the Effect of Relative Branch Lengths on Tree Topology
All pairwise distances between metazoan genes were extracted from PAM distance matrices, which were constructed for the con8 and six384 sets. These distances were transformed into branch lengths in a star-like unrooted tree (bA = (dAB + dAC - dBC)/2, where bA is the length of the branch leading to A and dAB, dAC, and dBC are the distances between A and B, A and C, and B and C, respectively) and normalized by the length of the branch leading to a human sequence. Standard deviations and confidence intervals for the median branch lengths in the six384 sets were obtained from 1000 bootstrap samples of the data.
Four KOGs that stably produced the ecdysozoan topology (KOG1159, KOG1337, KOG1687, and KOG2041) and four KOGs with reliable coelomate topology (KOG0323, KOG1107, KOG2235, and KOG3061) were selected to generate “model” trees required for alignment simulation; each of these KOGs had an estimated evolutionary rate close to the median across the KOGs. Branch lengths from the corresponding ML trees were averaged to produce the ecdysozoan and coelomate model trees. On the basis of each model tree, a series of trees with varying ratios of the nematode to human branch lengths was created. In each of these trees, three branch lengths, nematode, human, and ecdysozoan (or coelomate in the simulations of coelomate topology reconstruction) were changed in such a way that: (1) The sum of branch lengths in the nematode-Drosophila-human star tree remained constant; (2) the relative position of the metazoan root on the human or the nematode branch remained the same; and (3) the ratio of the nematode to human branch lengths in the nematode-Drosophila-human star tree was set to the desired value.
Simulation of multiple sequence alignments corresponding to the evolution of a sequence family according to a given tree was performed using the Pseq-Gen tool (Grassly et al. 1997). Sequence length was set to 200 (a typical protein length) evolutionary model to JTT, amino acid frequencies to those observed in the six507 alignments, and the shape parameter of the γ-distribution of intraprotein variation of evolutionary rates to 1.0 (typical of the values obtained for the conserved block of concatenated alignments using the PAML package, which were considered to be reasonable analogs of the gapless simulated alignments produced by Pseq-Gen). For each tree with a given nematode to human branch length ratio, 1000 alignments were simulated and the relative likelihood of the ecdysozoan and coelomate tree topologies was evaluated for each simulated alignment by using the ProtML program of the MolPhy package (Kishino et al. 1990; Adachi and Hasegawa 1992). The topology with the higher likelihood value in the Kishino-Hasegawa test was considered the winner regardless of the statistical significance of the difference.
Construction of Phylogenetic Trees by Using Distributions of Pairwise Distances Between Orthologs
This analysis was performed essentially as described by Wolf et al. (2001). The sequences of all proteins encoded in the analyzed genomes were compared to each other using the gapped BLASTP program (Altschul et al. 1997). Reciprocal, genome-specific best hits with the expectation (E) value cut-off of 0.001 were collected. The distributions of identity percentage among the reciprocal best hits (probable orthologs) were derived for each pair of species. The medians of the identity percentage distributions were used for estimating evolutionary distances with the geometric distance correction calculated by using the formula d = 1/u - 1, where d is the evolutionary distance, q is percent identity, and u = (q - 0.05)/0.95 (the trees constructed using this approach have been shown to be robust with respect to several methods for evolutionary distance calculation; Wolf et al. 2001). Trees were constructed from the distance matrices obtained with the above distance estimates using the least-squares method as implemented in the FITCH program of PHYLIP. Bootstrap values were estimated by resampling the set of orthologs identified for each pair of genomes 100 times and reconstructing trees from the distributions of the distances from these resampled sets.
Using Indels as Phylogenetic Markers
Reliably identified indels were used for phylogeny reconstruction as binary characters. Adjacent columns of alignment with the same pattern of gap characters were treated as a single indel state (“0” coding for gap and “1” for a nongap character). Indels surrounded by columns without gaps and flanked by highly conserved sites within a 16-amino acid window were regarded as reliable. In addition, another filtering criterion was applied to the indels extracted from the alignments of the six384 set. As a variable number of plant and fungal proteins might be present in these alignments, only those positions that had identical indel states for all nonmetazoan orthologs (ensuring the unambiguous identification of the ancestral state) and nonidentical indel states for all metazoan orthologs (otherwise, a site would not carry any phylogenetic information for metazoa) were considered, with all of the nonmetazoan orthologs collapsed into one “ancestral” node. Indels extracted from the con8 alignments and from the six384 alignments were concatenated into binary character tables consisting of 508 and 1056 sites, respectively. Alternative metazoan topologies were compared using the Wagner parsimony method as implemented in the MIX program of PHYLIP.
Trees Based on Presence-Absence of Species in KOGs
The patterns of presence-absence of seven eukaryotic species in the KOGs were treated as a binary character table (with “0” corresponding to the absence and “1” to the presence of the given species) and used to construct a Dollo parsimony tree with the DOLLOP program of PHYLIP.
Analysis of Domain Architectures of Multidomain Proteins
Occurrences of the members of a nonredundant set of 2548 domains from the CDD collection were identified in six eukaryotic genomes and in 10 completely sequenced prokaryotic genomes (three archaea and seven bacteria) using the RPS-BLASTprogram (Marchler-Bauer et al. 2003). Pairs of different domains cooccurring in multidomain proteins were collected from the entire data set, and their presence or absence in each genome was recorded. The domain co-occurrence table was analyzed as binary character data by using the Dollo parsimony method (the DOLLOP program of PHYLIP).
Availability of Data and Results
All multiple sequence alignments and phylogenetic trees constructed and used in this work are available at ftp://ftp.ncbi.nih.gov/pub/koonin/EUK_PHYLOGENY/.
Acknowledgments
We thank John Spouge and Eva Czabarka for help in estimating the confidence intervals for the relative branch length medians, Anna Panchenko and Siqian He for help with the use of the CDD library, and Alexei Kondrashov and Kira Makarova for useful discussions.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1347404.
References
- Adachi, J. and Hasegawa, M. 1992. MOLPHY: Programs for Molecular Phylogenetics. Institute of Statistical Mathematics, Tokyo.
- Adoutte, A., Balavoine, G., Lartillot, N., Lespinet, O., Prud'homme, B., and de Rosa, R. 2000. The new animal phylogeny: Reliability and implications. Proc. Natl. Acad. Sci. 97: 4453-4456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aguinaldo, A.M., Turbeville, J.M., Linford, L.S., Rivera, M.C., Garey, J.R., Raff, R.A., and Lake, J.A. 1997. Evidence for a clade of nematodes, arthropods and other moulting animals. Nature 387: 489-493. [DOI] [PubMed] [Google Scholar]
- Altschul, S.F., Madden, T.L., Schaffer, A.A., Zhang, J., Zhang, Z., Miller, W., and Lipman, D.J. 1997. Gapped BLASTand PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 25: 3389-3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bapteste, E. and Philippe, H. 2002. The potential value of indels as phylogenetic markers: Position of trichomonads as a case study. Mol. Biol. Evol. 19: 972-977. [DOI] [PubMed] [Google Scholar]
- Blair, J.E., Ikeo, K., Gojobori, T., and Hedges, S.B. 2002. The evolutionary position of nematodes. BMC Evol. Biol. 2: 7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins, A.G. and Valentine, J.W. 2001. Defining phyla: Evolutionary pathways to metazoan body plans. Evol. Dev. 3: 432-442. [DOI] [PubMed] [Google Scholar]
- de Rosa, R., Grenier, J.K., Andreeva, T., Cook, C.E., Adoutte, A., Akam, M., Carroll, S.B., and Balavoine, G. 1999. Hox genes in brachiopods and priapulids and protostome evolution. Nature 399: 772-776. [DOI] [PubMed] [Google Scholar]
- Felsenstein, J. 1996. Inferring phylogenies from protein sequences by parsimony, distance, and likelihood methods. Methods Enzymol. 266: 418-427. [DOI] [PubMed] [Google Scholar]
- Fitch, W.M. and Margoliash, E. 1967. Construction of phylogenetic trees. Science 155: 279-284. [DOI] [PubMed] [Google Scholar]
- Fitz-Gibbon, S.T. and House, C.H. 1999. Whole genome-based phylogenetic analysis of free-living microorganisms. Nucleic Acids Res. 27: 4218-4222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giribet, G., Distel, D.L., Polz, M., Sterrer, W., and Wheeler, W.C. 2000. Triploblastic relationships with emphasis on the acoelomates and the position of Gnathostomulida, Cycliophora, Plathelminthes, and Chaetognatha: A combined approach of 18S rDNA sequences and morphology. Syst. Biol. 49: 539-562. [DOI] [PubMed] [Google Scholar]
- Grassly, N.C., Adachi, J., and Rambaut, A. 1997. PSeq-Gen: An application for the Monte Carlo simulation of protein sequence evolution along phylogenetic trees. Comput. Appl. Biosci. 13: 559-560. [DOI] [PubMed] [Google Scholar]
- Grishin, N.V., Wolf, Y.I., and Koonin, E.V. 2000. From complete genomes to measures of substitution rate variability within and between proteins. Genome Res 10: 991-1000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedges, S.B. 2002. The origin and evolution of model organisms. Nat. Rev. Genet. 3: 838-849. [DOI] [PubMed] [Google Scholar]
- Hillis, D.M. 1998. Taxonomic sampling, phylogenetic accuracy, and investigator bias. Syst. Biol. 47: 3-8. [DOI] [PubMed] [Google Scholar]
- Hillis, D.M., Pollock, D.D., McGuire, J.A., and Zwickl, D.J. 2003. Is sparse taxon sampling a problem for phylogenetic inference? Syst. Biol. 52: 124-126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kishino, H., Miyata, T., and Hasegawa, M. 1990. Maximum likelihood inference of protein phylogeny and the origin of chloroplasts. J. Mol. Evol. 31: 151-160. [Google Scholar]
- Koonin, E.V., Aravind, L., and Kondrashov, A.S. 2000. The impact of comparative genomics on our understanding of evolution. Cell 101: 573-576. [DOI] [PubMed] [Google Scholar]
- Lander, E.S., Linton, L.M., Birren, B., Nusbaum, C., Zody, M.C., Baldwin, J., Devon, K., Dewar, K., Doyle, M., FitzHugh, W., et al. 2001. Initial sequencing and analysis of the human genome. Nature 409: 860-921. [DOI] [PubMed] [Google Scholar]
- Mallatt, J. and Winchell, C.J. 2002. Testing the new animal phylogeny: First use of combined large-subunit and small-subunit rRNA gene sequences to classify the protostomes. Mol. Biol. Evol. 19: 289-301. [DOI] [PubMed] [Google Scholar]
- Manuel, M., Kruse, M., Muller, W.E., and Le Parco, Y. 2000. The comparison of β-thymosin homologues among metazoa supports an arthropod-nematode clade. J. Mol. Evol. 51: 378-381. [DOI] [PubMed] [Google Scholar]
- Marchler-Bauer, A., Anderson, J.B., DeWeese-Scott, C., Fedorova, N.D., Geer, L.Y., He, S., Hurwitz, D.I., Jackson, J.D., Jacobs, A.R., Lanczycki, C.J., et al. 2003. CDD: A curated Entrez database of conserved domain alignments. Nucleic Acids Res. 31: 383-387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mirkin, B.G., Fenner, T.I., Galperin, M.Y., and Koonin, E.V. 2003. Algorithms for computing parsimonious evolutionary scenarios for genome evolution, the last universal common ancestor and dominance of horizontal gene transfer in the evolution of prokaryotes. BMC Evol. Biol. 3: 2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchell, A., Mitter, C., and Regier, J.C. 2000. More taxa or more characters revisited: Combining data from nuclear protein-encoding genes for phylogenetic analyses of Noctuoidea (Insecta: Lepidoptera). Syst. Biol. 49: 202-224. [PubMed] [Google Scholar]
- Mushegian, A.R., Garey, J.R., Martin, J., and Liu, L.X. 1998. Large-scale taxonomic profiling of eukaryotic model organisms: A comparison of orthologous proteins encoded by the human, fly, nematode, and yeast genomes. Genome Res. 8: 590-598. [DOI] [PubMed] [Google Scholar]
- Notredame, C., Higgins, D.G., and Heringa, J. 2000. T-Coffee: A novel method for fast and accurate multiple sequence alignment. J. Mol. Biol. 302: 205-217. [DOI] [PubMed] [Google Scholar]
- Peterson, K.J. and Eernisse, D.J. 2001. Animal phylogeny and the ancestry of bilaterians: Inferences from morphology and 18S rDNA gene sequences. Evol. Dev. 3: 170-205. [DOI] [PubMed] [Google Scholar]
- Raff, R.A. 1996. The shape of life: Genes, development, and the evolution of animal form. University of Chicago Press, Chicago, IL.
- Rokas, A. and Holland, P.W. 2000. Rare genomic changes as a tool for phylogenetics. Trends Ecol. Evol. 15: 454-459. [DOI] [PubMed] [Google Scholar]
- Rosenberg, M.S. and Kumar, S. 2001. Incomplete taxon sampling is not a problem for phylogenetic inference. Proc. Natl. Acad. Sci. 98: 10751-10756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg, M.S. and Kumar, S. 2003. Taxon sampling, bioinformatics, and phylogenomics. Syst. Biol. 52: 119-124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saitou, N. and Nei, M. 1987. The neighbor-joining method: A new method for reconstructing phylogenetic trees. Mol. Biol. Evol. 4: 406-425. [DOI] [PubMed] [Google Scholar]
- Schmidt, H.A., Strimmer, K., Vingron, M., and von Haeseler, A. 2002. TREE-PUZZLE: Maximum likelihood phylogenetic analysis using quartets and parallel computing. Bioinformatics 18: 502-504. [DOI] [PubMed] [Google Scholar]
- Shimodaira, H. and Hasegawa, M. 2001. CONSEL: For assessing the confidence of phylogenetic tree selection. Bioinformatics 17: 1246-1247. [DOI] [PubMed] [Google Scholar]
- Snel, B., Bork, P., and Huynen, M.A. 1999. Genome phylogeny based on gene content. Nat. Genet. 21: 108-110. [DOI] [PubMed] [Google Scholar]
- Snel, B., Bork, P., and Huynen, M.A. 2002. Genomes in flux: The evolution of archaeal and proteobacterial gene content. Genome Res. 12: 17-25. [DOI] [PubMed] [Google Scholar]
- Strimmer, K. and Rambaut, A. 2002. Inferring confidence sets of possibly misspecified gene trees. Proc. R Soc. Lond. B Biol. Sci. 269: 137-142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swofford, D.L. 2000. PAUP*. Phylogenetic Analysis Using Parsimony (* and Other Methods). Version 4. Sinauer Associates, Sunderland, MA.
- Tatusov, R.L., Fedorova, N.D., Jackson, J.D., Jacobs, A.R., Kiryutin, B., Koonin, E.V., Krylov, D.M., Mazumder, R., Mekhedov, S.L., Nikolskaya, A.N., et al. 2003. The COG database: An updated version includes eukaryotes. BMC Bioinformatics 4: 41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentine, J.W. and Collins, A.G. 2000. The significance of moulting in Ecdysozoan evolution. Evol. Dev. 2: 152-156. [DOI] [PubMed] [Google Scholar]
- Wolf, Y.I., Rogozin, I.B., Grishin, N.V., Tatusov, R.L., and Koonin, E.V. 2001. Genome trees constructed using five different approaches suggest new major bacterial clades. BMC Evol. Biol. 1: 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf, Y.I., Rogozin, I.B., Grishin, N.V., and Koonin, E.V. 2002. Genome trees and the tree of life. Trends Genet. 18: 472-479. [DOI] [PubMed] [Google Scholar]
- Yang, Z. 1997. PAML: A program package for phylogenetic analysis by maximum likelihood. Comput. Appl. Biosci. 13: 555-556. [DOI] [PubMed] [Google Scholar]
WEB SITE REFERENCES
- http://www.ncbi.nlm.nih.gov/COG/new/shokog.cgi; complete set of alignments and trees for this work.
- ftp://ftp.ncbi.nih.gov/pub/koonin/EUK_PHYLOGENY/; clusters of orthologs from eukaryotic genomes (KOGs).