Efficiency of the Polymerase Chain Reaction

Abstract

The polymerase chain reaction (PCR) has found wide application in biochemistry and molecular biology such as gene expression studies, mutation detection, forensic analysis and pathogen detection. Increasingly quantitative real time PCR is used to assess copy numbers from overall yield. In this study the yield is analyzed as a function of several processes: (1) thermal damage of the template and polymerase occurs during the denaturing step, (2) competition exists between primers and templates to either anneal or form dsDNA, (3) polymerase binding to annealed products (primer/ssDNA) to form ternary complexes and (4) extension of ternary complexes. Explicit expressions are provided for the efficiency of each process, therefore reaction conditions can be directly linked to the overall yield. Examples are provided where different processes play the yield-limiting role. The analysis will give researchers a unique understanding of the factors that control the reaction and will aid in the interpretation of experimental results.

1. Introduction

The polymerase chain reaction (PCR) enzymatically extends single stranded DNA molecules over a region flanked by a set of primers. Theoretically, the number of templates should double after each cycle. In practice, the DNA increases by a factor of (1+η) where η is the cycle efficiency. Thus an efficiency of η = 1 would imply a doubling of the DNA concentration. Although the efficiency could change from cycle to cycle, therefore warranting the designation η^j to mark the j^th cycle, it is customary to report an overall efficiency (η) for n cycles. Saiki et al. (1985) related the overall efficiency (η) and yield (X) as follows: X = (1+η)ⁿ and this relation became the standard way to express the overall efficiency¹ of PCR processes (Keohavong and Thilly, 1989, Li et al., 1988). A small variation in this relation has been proposed by Newton and Graham (1997) if the original DNA is genomic DNA with a length greater than the target DNA length². It has been experimentally observed that yields can vary from cycle to cycle with a general decreasing trend with increasing cycle numbers (Kainz, 2000; Schnell and Mendoza, 1997a, 1997b; Stolovitzky and Cecchi, 1996). Additional references are listed in Waterfall et al., (2002). Although the use of an overall efficiency is a convenient norm to quantify experiments, it provides no information on cycle-to-cycle changes in efficiency.

The use of X = (1+η)ⁿ to infer starting concentrations of DNA has seen application in real-time PCR (rt-PCR) and it has been widely adopted for use in an array of applications including gene expression studies, mutation detection, forensic analysis and pathogen detection with the aim at both clinical diagnostics and food safety (Champe et al., 2008, Logan et al., 2009, Pfaffl, 2004). Two main quantification methods are the standard curve method and the ΔΔC_T method. The ΔΔC_T method is a relative quantification method that assumes 100% efficiency, and uses the differences in crossover threshold (C_T) values between experiment and control reactions to calculate an estimated fold-change in a target gene. The fold-change is defined as (see Livak and Schmittgen, 2001):

$$2^{\Delta \Delta {\mathrm{C}}_{\mathrm{T}}}=2^{\Delta {\mathrm{C}}_{\mathrm{T},\text{control}}-\Delta {\mathrm{C}}_{\mathrm{T}},\text{experiment}}$$ (1a)

where:

$$\Delta C_{T,\text{control}}=C_{T,\text{control}}^{\text{target}}-C_{T,\text{control}}^{\text{reference}}$$ (1b)

$$\Delta C_{T,\text{experiment}}=C_{T,\text{experiment}}^{\text{target}}-C_{T,\text{experiment}}^{\text{reference}}$$ (1c)

The standard curve method amplifies serial dilutions of known concentrations of both the target and reference gene, along with samples of unknown concentration. The dilution curves are then used to generate a C_T value-concentration curve. When the unknown samples’ C_T values are determined, they are correlated to a certain concentration by placement on this curve. The determined concentrations of the reference and target genes are then used to calculate fold-changes between experimental and control reactions.

Pfaffl (2001) proposed a method that combines the standard curve method and ΔΔC_T method. Like the standard curve method it uses dilution methods to calculate the efficiency for a specific reaction. This efficiency (η) is then used in the fold-change equation used by the ΔΔC_T method:

$${(1+\eta )}^{\Delta C_{T,\text{control}}-\Delta C_T,\text{experiment}}$$ (1d)

Liu and Saint (2002a) followed a similar approach but used fluorescence levels at different points in one curve to calculate the efficiency, instead of the dilution curves. These calculated efficiencies are assumed to be constant throughout the reaction (not varying from cycle to cycle). However, it has been shown that efficiencies are not constant over all cycles and more advanced models have been developed to include the efficiency variations from cycle to cycle (Liu and Saint, 2002b; Platts et al., 2008). However, these models do not provide expressions for the efficiencies of different processes that form part of the overall PCR process and only report a single efficiency per cycle.

Certain models do account for variations in efficiencies of the different stages (denaturing, annealing and elongation) of every cycle (Gevertz et al., 2005; Rubin and Levy, 1996). Gevertz et al. incorporated annealing and elongation efficiencies into the derivation of a single per-cycle efficiency. The evaluation of the efficiencies required the numerical solution of a set of initial value problems for each cycle. Despite being more rigorous, numerical integration does not lend itself to immediate or convenient implementation by other users. Rubin and Levy considered the annealing step, but their work was focused on calculating the probabilities for mispriming events in analyzing the effects of different factors on the specificity of PCR.

In this paper we consider four different efficiencies that each contribute to the overall efficiency. These efficiencies are associated with the denaturing, annealing, ternary complex formation (i.e. polymerase binding to template/primer) and elongation steps. In all cases analytical expressions are provided for the different efficiencies, making it easy for other users to apply and connect the efficiencies with overall yield and PCR conditions.

2. The Mathematical Model

Each PCR cycle consists of three stages: 1) denaturing of the DNA, 2) annealing of primers to ssDNA and 3) enzymatic elongation of the complementary strand by the DNA polymerase. The start of the cycle is defined as the beginning of the denaturing step. The overall PCR efficiency of cycle j , η^j , is the product of all of 2the individual efficiencies for that cycle, i.e. ${\eta }_d^j$ , ${\eta }_a^j$ , ${\eta }_E^j$ , ${\eta }_e^j$ for denaturing, annealing, polymerase binding and target elongation respectively. The denaturing damage efficiency of the polymerase, ${\eta }_{dE}^j$ , is implicit in ${\eta }_a^j$, ${\eta }_E^j$and ${\eta }_e^j$. See the Nomenclature table for detailed description of notations.

The following assumptions have been made in this analysis.

• Symmetry prevails in sense and anti-sense molecules. Thus there are equal numbers of forward and reverse primers and they anneal to equal numbers of sense and anti-sense ssDNA strands.

• Polymerase damage and DNA damage efficiencies are the same for each PCR cycle.

• The annealing temperature is sufficiently below the primer melting temperature that annealing reactions are irreversible.

• No unwanted side reactions such as primer-dimer formation and mis-priming are considered. Some suggestions are made in the Conclusions section how to include the effects of primer-dimer reactions empirically.

The following sections describe the derivation of expressions for the efficiency for each PCR step. Before continuing, the notation for time must be clarified. Each cycle starts with the denaturing step, but we set t = 0 at the beginning of the annealing stage (the denaturing step does not involve integration). Annealing occurs over the span 0 ≤ t ≤ t_a and the elongation stage is t_a≤t≤t_e. The initial number of DNA templates and primers (i.e. before denaturation in the first cycle) are $\stackrel{‒}{D_{\mathit{init}}}$ and $\stackrel{‒}{P_{\mathit{init}}}$. The amount of ssDNA available before annealing in the j^th cycle is denoted by $\stackrel{‒}{S_0^j}$ ; the amount available after annealing is denoted by $\stackrel{‒}{S^j}\left(t_a\right)=\stackrel{‒}{S_a^j}$ and after elongation, $\stackrel{‒}{S^j}\left(t_e\right)=\stackrel{‒}{S_e^j}$. The same is true for all other variables.

2.1. Efficiency of denaturing

Double-stranded DNA molecules (dsDNA) separate into ssDNA at the denaturing temperature. DNA is much more susceptible to hydrolytic attack, oxidation and depurination in the single stranded form (Cadet et al. 2002, Hsu et al. 2004, Lindahl and Nyberg 1972, 1974, Pienaar et al. 2006). Therefore a loss of template may occur in this step. An efficiency of denaturing η_d≤1 is defined; such that at the end of the denaturing step, the number of undamaged single stranded DNA that is available for annealing is:

$$\stackrel{‒}{S_0^j}={\eta }_d\stackrel{‒}{D_e^{j-1}}.$$ (2a)

Denaturing efficiency is not an indication of the extent of strand separation, but of thermal damage to DNA. The denaturing temperature is assumed to be high enough to ensure that all the template strands separate. Since $\stackrel{‒}{D_e^{j-1}}$ is the number of dsDNA molecules available after the elongation phase at the end of the (j – 1)^th cycle, there is a one-to-one relationship between $\stackrel{‒}{D_e^{j-1}}$ and $\stackrel{‒}{S_0^j}$ .

The polymerase may also incur thermal damage at the denaturing temperature. If the initial amount of polymerase is $\stackrel{‒}{E^i}$, then $\stackrel{‒}{E_0^1}={\eta }_{dE}\stackrel{‒}{E^i}$ is the amount that is still active at the end of the first denaturing stage. These denaturation damage efficiencies, η_d and η_dE, are assumed constant from cycle to cycle, since they depend primarily on temperature and the exposure time (denaturing period). Thus, at the end of the j^th cycle, the polymerase amount is

$$\stackrel{‒}{E_0^j}={\eta }_{dE}\stackrel{‒}{E_0^{j-1}}={\left({\eta }_{dE}\right)}^j\stackrel{‒}{E_i}.$$ (2b)

For example, even a 1% loss per cycle, leads to a 33% reduction in active polymerases after 40 cycles.

2.2. Annealing model

The efficiency of the annealing stage depends on competitive binding: 5′-3′ ssDNA, $\stackrel{‒}{S_0^j}$ , could either bind to complementary 3′-5′ ssDNA strands to form dsDNA or to their primers, $\stackrel{‒}{P_0^j}$ , to form binary complexes. The dsDNA molecules are stable at the annealing temperature and, as mentioned in the list of assumptions, the primer/template products are also considered stable; making an analytical treatise possible. The ratio of templates to primers at the start of the annealing stage in the j^th cycle is defined as:

$${\gamma }^j=\stackrel{‒}{S_0^j}∕\stackrel{‒}{P_0^j}.$$ (3)

The ratio is small during earlier cycles (γ^j << 10⁻² ), but the primers are consumed and the templates increase, therefore γ^j increases with cycle number.

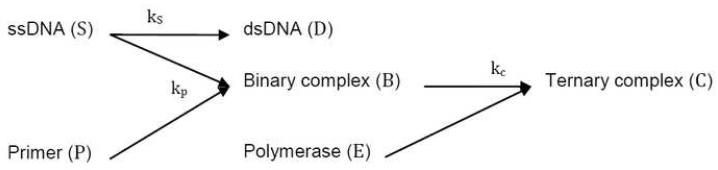
Neglecting non-specific binding or primer-dimer formation, three reactions remain for consideration: (1) two ssDNA molecules $\stackrel{‒}{S^j}$ can bind with rate k_S to form dsDNA $\stackrel{‒}{D^j}$ , (2) a primer can anneal to a ssDNA molecule with rate k_P to form a binary complex, $\stackrel{‒}{B^j}$ , and (3) a polymerase can anneal to a binary molecule with rate k_C to form a ternary complex, $\stackrel{‒}{C^j}$ . Rate constants depend on primer sequences and PCR temperatures, and these constants can be estimated (Mamedov et al., 2008). The annealing reactions are described by the following set of equations (see Figure 1 for a diagram of the reactions and components):

$$\frac{d\stackrel{‒}{S^j}}{dt}=-k_S\stackrel{‒}{S^j}\stackrel{‒}{S^j}-k_P\stackrel{‒}{P^j}\stackrel{‒}{S^j}$$ (4a)

$$\frac{d\stackrel{‒}{P^j}}{dt}=-k_P\stackrel{‒}{P^j}\stackrel{‒}{S^j}$$ (4b)

$$\frac{d\stackrel{‒}{D^j}}{dt}=-k_S\stackrel{‒}{S^j}\stackrel{‒}{S^j}$$ (4c)

$$\frac{d\stackrel{‒}{B^j}}{dt}=k_p\stackrel{‒}{P^j}\stackrel{‒}{S^j}-k_c\stackrel{‒}{B^j}\stackrel{‒}{E^j}$$ (4d)

$$\frac{d\stackrel{‒}{C^j}}{dt}=k_C\stackrel{‒}{B^j}\stackrel{‒}{E^j}$$ (4e)

$$\frac{d\stackrel{‒}{E^j}}{dt}=-k_C\stackrel{‒}{B^j}\stackrel{‒}{E^j}$$ (4f)

Converting to dimensionless form simplifies the analysis. All DNA amounts are scaled by the initial amount of ssDNA at the start of the annealing step of the j^th cycle, $\stackrel{‒}{S_0^j}$ . The dimensionless variables are given by $S^j=\stackrel{‒}{S^j}∕\stackrel{‒}{S_0^j}$, $P^j=\stackrel{‒}{P^j}∕\stackrel{‒}{S_0^j}$, $D^j=\stackrel{‒}{D^j}∕\stackrel{‒}{S_0^j}$ etc. Initial values for each cycle in the dimensionless form are: $S_0^j=\stackrel{‒}{S_0^j}∕\stackrel{‒}{S_0^j}$, $P_0^j=\stackrel{‒}{P_0^j}∕\stackrel{‒}{S_0^j}=1{\gamma }^j$, $E_0^j=\stackrel{‒}{E_0^j}∕\stackrel{‒}{S_0^j}$ and $D_0^j=B_0^j=C_0^j=0$. Time is scaled by the primer/template binding rate constant and the initial DNA quantity, $\tau =t{k}_P\stackrel{‒}{S_0^j}$. (If k_P has units 1/(μM · s) , then $\stackrel{‒}{S_0^j}$ must be expressed in μM .)

Figure 1.

Schematic diagram of annealing phase reactions showing the formation of double-stranded DNA as well as binary- and ternary-complexes.

The dimensionless annealing equations are:

$$\frac{d{S}^j}{d\tau }=-\beta {\left(S^j\right)}^2-P^j{S}^j$$ (5a)

$$\frac{d{P}^j}{d\tau }=-P^j{S}^j$$ (5b)

$$\frac{d{D}^j}{d\tau }=\beta {\left(S^j\right)}^2$$ (5c)

$$\frac{d{B}^j}{d\tau }=P^j{S}^j-\alpha B^j{E}^j$$ (5d)

$$\frac{d{C}^j}{d\tau }=\alpha B^j{E}^j$$ (5e)

$$\frac{d{E}^j}{d\tau }=-\alpha B^j{E}^j$$ (5f)

The parameters α = k_C/k_P and β = k_S/k_P are ratios of the reaction rate constants. The symmetry assumption allows the first term on the right hand side of eq.(5a) to be quadratic in S^j , since it is not necessary to distinguish between forward and reverse template concentrations.

Species balance equations for the primers and enzymes are given by:

$$P_0^j=1∕{\gamma }^j=P^j+B^j+C^j$$ (6a)

$$E_0^j=E^j+C^j$$ (6b)

Analytical approximations can be found for eqns (5a-5e). A full derivation of the approximations may be found in the Appendix. The approximations are given by:

$$S^j\left(\tau \right)\cong \frac{P^j\left(\tau \right)}{\beta -1}\left[{\left(\frac{P^j\left(\tau \right)}{{\delta }^j}\right)}^{\beta }-1\right]$$ (7a)

$$P^j\left(\tau \right)\cong {\left({\gamma }^j\right)}^{-1}{\left[{\left({\gamma }^j{\delta }^j\right)}^{1-\beta }(1-e^{-{\delta }^j\tau })+e^{-{\delta }^j\tau }\right]}^{1∕1-\beta }$$ (7b)

$$B^j\left(\tau \right)\cong 1∕{\gamma }^j-P^j\left(\tau \right)-C^j\left(\tau \right)$$ (7c)

$$C^j\left(\tau \right)\cong E_0^j-E^j\left(\tau \right)$$ (7d)

$$E^j\left(\tau \right)\cong \frac{E_0^j\left(1-{\gamma }^j\left(P^j\right(\tau )+E_0^j)\right)}{(1-{\gamma }^j{P}^j(\tau \left)\right)\exp \left(\frac{\alpha (1-{\gamma }^j(P^j\left(\tau \right)+E_0^j\left)\right)}{{\gamma }^j}\tau \right)-{\gamma }^j{E}_0^j}$$ (7e)

The parameter δ^j is defined as ${\delta }^j=P^j(\tau \to \infty )={\left({\gamma }^j\right)}^{-1}{\left[{\gamma }^j(\beta -1)+1\right]}^{1∕1-\beta }$ . Eqns (7a-7e) hold for β ≠ 1, and the approximation becomes better for larger values of β, which represent more realistic cases.

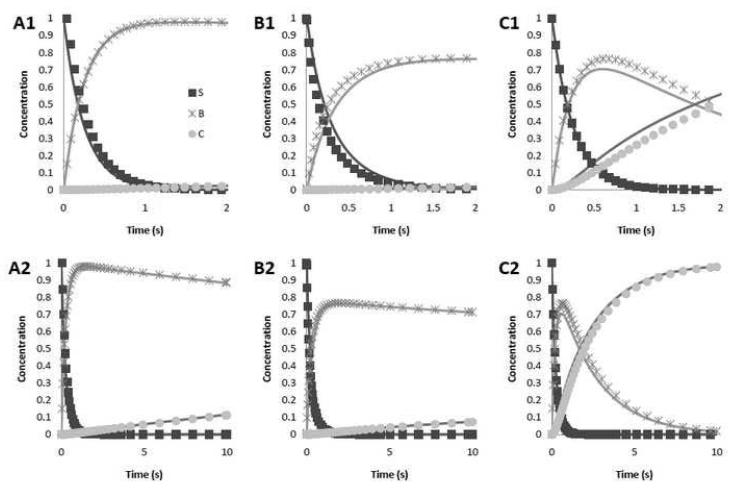
The accuracy of the approximations was estimated by comparing it to numerical solutions of the model above. Numerical solutions were calculated with GNU Octave v. 3.2.3 (Eaton, 2010), using the Dormand-Prince method. It was found that the approximations are extremely accurate, as illustrated in Figure 2. The difference between the approximations and the numerical solutions was calculated for S^j (τ) , B^j (τ) and C^j (τ) . For α <1 and β = 1+10⁻⁶ , it was found that this difference is less than 0.1 for γ = 0.5 and is less than 0.05 for γ < 0.1. The error increases with α and is greatest when β →1. The maximum error was 0.16 when α > 5, β = 1+10⁻⁶ and γ = 0.5 . However, in all cases, the error tends to zero as τ → 0 and τ →τ_a. Thus, for typical PCR conditions, the error is less than 10% during the initial phase of the reaction and negligible towards the end.

Figure 2.

The analytical approximation (solid line) as well as numerical solutions (markers) for different parameter values. The top row shows the first two seconds of the reaction, while the bottom row shows the first ten seconds. (A1&A2): α = 0.03, β = 1 + 10⁻⁶ and γ = 10⁻³. These are the expected values for most PCR experiments. (B1&B2): α = 0.03, β = 1 + 10⁻⁶ and γ = 0.5. The higher value of γ is characteristic of the last and second to last PCR cycles. (C1&C2): α = 1, β = 5 and γ = 10⁻³. This simulation shows that the approximations hold for different values of α and β.

Two conclusions can be reached from the analytical solutions for typical annealing times t_a≤10s:

• $P_a^j\approx {\delta }^j$ and $S_a^j\approx 0$: The primer-DNA annealing reaction approaches completion within t<t_a.

• $C_a^j\approx 0$: Using α <<1, almost no ternary complex is formed during the annealing stage.

2.3. Efficiency of Primer Annealing

The efficiency of primer annealing is defined as:

$${\eta }_a^j=\frac{\mathrm{ssDNA}\text{bound to primers at}{\tau }_{\mathrm{a}}}{\text{total available}\mathrm{ssDNA}}=P_0^j-P^j\left({\tau }_a\right)=B^j\left({\tau }_a\right)+C^j\left({\tau }_a\right).$$ (8)

The right hand side of eq.(8) is obtained by rearranging eq.(6a). The annealing efficiency is the sum of the dimensionless binary and ternary complexes at the end of the annealing period τ = τ_a as a fraction of total available ssDNA. An explicit expression for annealing efficiency is obtained by substituting P^j(τ_a)≈ P^j(τ →∞) = δ^j and $P_0^j=1∕{\gamma }^j$, into eq.(8):

$${\eta }_a^j=\frac{1}{{\gamma }_j}-{\delta }^j$$ (9)

2.4. Efficiency of Polymerase Binding

The efficiency of polymerase binding is defined as:

$${\eta }_E^j=\frac{\text{Total ternary complexes formed at the end of elongation}}{\text{Total binary and ternary complexes formed}}=\frac{C^j\left({\tau }_e\right)}{B^j\left({\tau }_e\right)+C^j\left({\tau }_e\right)},$$ (10)

where τ_e is the dimensionless time at the end of the elongation period. To solve for C^j(τ_e) in eq.(10), we use eqns.(6a,6b) (which are valid for all time), to write eq.(5d) as:

$$\frac{d{B}^j}{d\tau }=-\alpha B^j{E}^j=-\alpha B\left(E_0^j+B^j-{\eta }_a^j\right),\text{for}\tau \ge {\tau }_a.$$ (11)

Note that the term P^jS^j is not present, since S^j (τ) ≈ 0 for τ≥τ_a. Eqns.(11,5e) can be solved analytically for the initial data $B^j\left({\tau }_a\right)=B_a^j$;$C^j\left({\tau }_a\right)=C_a^j={\eta }_a^j-B_a^j$. The parameter α=k_C/k_p is assumed to only change slightly for the elongation conditions, since it depends on the difference in activation energies of the two rate constants in the quotient and the difference between the annealing and elongation temperatures. The analytical solutions to eqns.(11,5e), valid for τ ≥ τ_a, are:

$$B^j\left(\tau \right)=\frac{\left(E_0^j-{\eta }_a^j\right)B_a^j{e}^{-\alpha \left(E_0^j-{\eta }_a^j\right)\left(\tau -{\tau }_a\right)}}{\left(E_0^j-{\eta }_a^j+B_a^j\right)-B_a^j{e}^{-\alpha \left(E_0^j-{\eta }_a^j\right)\left(\tau -{\tau }_a\right)}},$$ (12a)

$$C^j\left(\tau \right)=\frac{\left(E_0^j-{\eta }_a^j+B_a^j\right){\eta }_a^j-B_a^j{E}_0^j{e}^{-\alpha \left(E_0^j-{\eta }_a^j\right)\left(\tau -{\tau }_a\right)}}{\left(E_0^j-{\eta }_a^j+B_a^j\right)-B_a^j{e}^{-\alpha \left(E_0^j-{\eta }_a^j\right)\left(\tau -{\tau }_a\right)}}.$$ (12b)

Results (12a,b) are used in eq.(10) to obtain an explicit form for the efficiency of polymerase binding:

$${\eta }_E^j=\frac{\left(E_0^j-{\eta }_a^j+B_a^j\right)+\left(B_a^j∕{\eta }_a^j\right)E_0^j{e}^{-\alpha \left(E_0^j-{\eta }_a^j\right){\tau }_e}}{\left(E_0^j-{\eta }_a^j+B_a^j\right)-B_a^j{e}^{-\alpha \left(E_0^j-{\eta }_a^j\right){\tau }_e}}.$$ (13)

2.5. Efficiency of Elongation

The number of ternary complexes that extend to full-length copies depends on the elongation time. Not all the ternary complexes form at the same time. Those that form early in the elongation step have a better chance to extend fully, compared to complexes that form later in the elongation stage. The efficiency of elongation is framed within this limitation.

Denote the average extension rate at the elongation temperature as V nucleotides per second. If the length that the primer must extend is l_ext, then the minimum elongation time that is needed to fully extend a ternary complex is Δt_min=l_ext/V. Therefore a cut-off time t_c exists and ternary complexes that form after the cut-off will not extend completely. The dimensionless form is: ${\tau }_c={\tau }_e-\Delta t_{\min }{k}_p{S}_0^j\ge {\tau }_a$.

The efficiency of elongation is defined as the ratio of the ternary complexes that extend fully, divided by all ternary complexes that have formed.

$${\eta }_e^j=\frac{C^j\left({\tau }_c\right)}{C^j\left({\tau }_e\right)}$$ (14)

The solution (12b) is substituted in eq.(14) to arrive at an expression for ${\eta }_e^j$:

$${\eta }_e^j=\left[\frac{\left(E_0^j-C_a^j\right){\eta }_a^j{e}^{\alpha \left(E_0^j-{\eta }_a^j\right)(\tau -{\tau }_a)}-\left({\eta }_a^j-C_a^j\right)E_0^j}{C_a^j-{\eta }_a^j+\left(E_0^j-C_a^j\right)e^{\alpha \left(E_0^j-{\eta }_a^j\right)({\tau }_c-{\tau }_a)}}\right]\left[\frac{C_a^j-{\eta }_a^j+\left(E_0^j-C_a^j\right)e^{\alpha \left(E_0^j-{\eta }_a^j\right)({\tau }_e-{\tau }_a)}}{\left(E_0^j-C_a^j\right){\eta }_a^j{e}^{\alpha \left(E_0^j-{\eta }_a^j\right)({\tau }_e-{\tau }_a)}-\left({\eta }_a^j-C_a^j\right)E_0^j}\right].$$ (15)

Remark

Extension begins as soon as a polymerase has bound to a binary complex. Since the ternary complexes may form any time during the elongation stage, a distribution of product lengths may result. For the sake of simplicity, these incomplete products are not carried over to the next cycle in this model. This will have a negligible effect on the accuracy of the model as the partially elongated ssDNA will act similarly to a primer in the annealing phase of the next cycle.

3. Results and Discussion

Four efficiencies have been defined, given by eqns.(2,9,13 and 15). The overall efficiency for the j^th cycle is the product of the four individual efficiencies;

$${\eta }^j={\eta }_d^i{\eta }_a^j{\eta }_E^j{\eta }_e^j,$$ (16a)

and it takes on the form:

$${\eta }^j={\eta }_d\left[\frac{\left(E_0^j-C_a^j\right){\eta }_a^j{e}^{\alpha \left(E_0^j-{\eta }_a^j\right)({\tau }_c-{\tau }_a)}-\left({\eta }_a^j-C_a^j\right)E_0^j}{C_a^j-{\eta }_a^j+\left(E_0^j-C_a^j\right)e^{\alpha \left(E_0^j-{\eta }_a^j\right)({\tau }_c-{\tau }_a)}}\right].$$ (16b)

The simplicity of eq.(16b) is somewhat misleading. We list the key PCR parameters and where they appear in eq.(16b).

• Starting composition. The starting polymerase and primer concentrations are scaled with respect to $S_0^1$. They appear in eq.(16b), for the 1^st cycle as $E_0^j$ and $P_0^j$ . The templates for the next cycle are obtained from the values at the previous cycle: $S_0^{j+1}=S_0^j+{\eta }^j{S}_0^j$ and the updated template value is used to find the dimensionless polymerase and primer concentrations at the start of the j +1^th cycle. Of course, one must also account for primer consumption each cycle, $P_0^{j+1}=P_0^j-{\eta }^j{S}_0^j$.

• The annealing time is implicitly present in $C_a^j$ (cf. eqns.(7c,d)). The term τ_c depends on the elongation time, elongation speed and template length.

• The kinetic rate constants appear in dimensionless form as β and α. Temperature settings affect the rate constants. For example, increases in the annealing temperature would reduce binary complex formation.

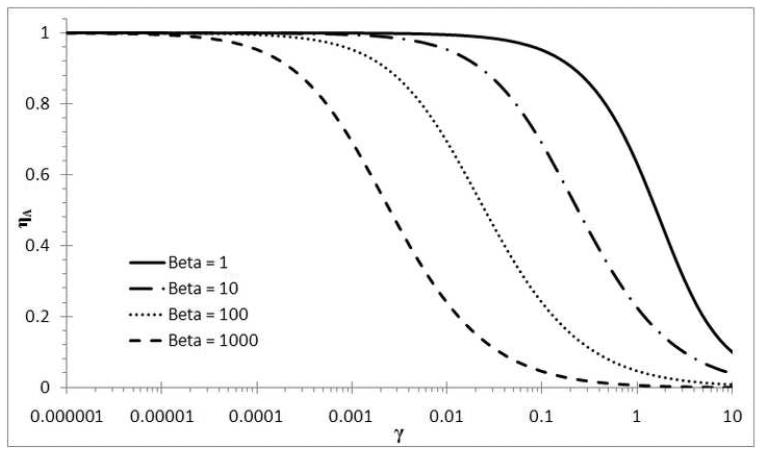
The annealing efficiency, ${\eta }_a^j$, depends only on β and γ^j and it decreases from cycle to cycle due to primer consumption ($P_0^{j+1}<P_0^j$) and template formation ($S_0^{j+1}>S_0^j$). In Figure 3 the efficiency of annealing is plotted as a function of γ^j . For a small γ^j (i.e. case of large excess primers), the annealing efficiency is practically 100%, regardless of the β values. If γ^j >10⁻³, then the efficiency starts to drop. The efficiency is more sensitive to larger values of β , because the reaction to form dsDNA becomes more competitive (cf. eq.(5c)). The limits of ${\eta }_a^j$ are proper; $\underset{{\gamma }^j\to 0}{\lim }\left({\eta }_a^j\right)=1$ and $\underset{{\gamma }^j\to \infty }{\lim }\left({\eta }_a^j\right)=0$.

Figure 3.

The annealing efficiency (η_a) as a function of the template:primer ratio (γ).

The parameter α determines the rate of ternary complex formation. The polymerase binding efficiency, ${\eta }_E^j$, will increase with increasing α . However, it is expected that α is small (Mamedov et al. 2008). The expression for overall efficiency (eq.(16b)) becomes much simpler if no ternary complexes have formed at the end of the annealing stage (i.e. $C_a^j=0$ in eq.(16b)) - this is a good approximation if α <<1.

To illustrate the usefulness of this analysis, we will investigate the roles of the different efficiencies on the overall efficiency for different PCR conditions. Three different polymerase concentrations will be used and for each choice the elongation period will be varied from Δt_e = 5 s to Δt_e = 10 s and Δt_e = 20 s; where Δt_e = t_e−t_a. The parameters that do not change are: D_i = 1×10⁵ copies, β = 5, k_C = 15 (μM s)⁻¹ (Mamedov et al., 2008), η_d = 1, η_dE = 0.99, l_ext=400 nt, P_i = 6×10¹² copies - i.e. 10 picomole, reaction volume is 25 μL (Griep et al., 2006) and the maximum cycle number is 40. We use the simple form of the overall efficiency, i.e. $C_a^j=0$;

$${\eta }^j={\eta }_d\left[{\eta }_a^j-\frac{\left(\stackrel{‒}{E_0^j}-{\eta }_a^j\stackrel{‒}{S_0^j}\right){\eta }_a^j{e}^{-\left\{\stackrel{‒}{E_0^j}-{\eta }_a^j\stackrel{‒}{S_0^j}\right\}{k}_C(t_c-t_a)}}{\stackrel{‒}{E_0^j}-{\eta }_a^j\stackrel{‒}{S_0^j}{e}^{-\left\{\stackrel{‒}{E_0^j}-{\eta }_a^j\stackrel{‒}{S_0^j}\right\}{k}_C(t_c-t_a)}}\right].$$ (17)

Remarks

The variables in eq. (17) are written in dimensional form to allow direct substitution of the values listed above. The value of k_P is not given since k_P cancels out in the product of dimensionless time and α in eq (16b), and only k_C is needed for calculation. In the discussion that follows, we refer to the smallest of η_a, η_E or η_e as the controlling efficiency.

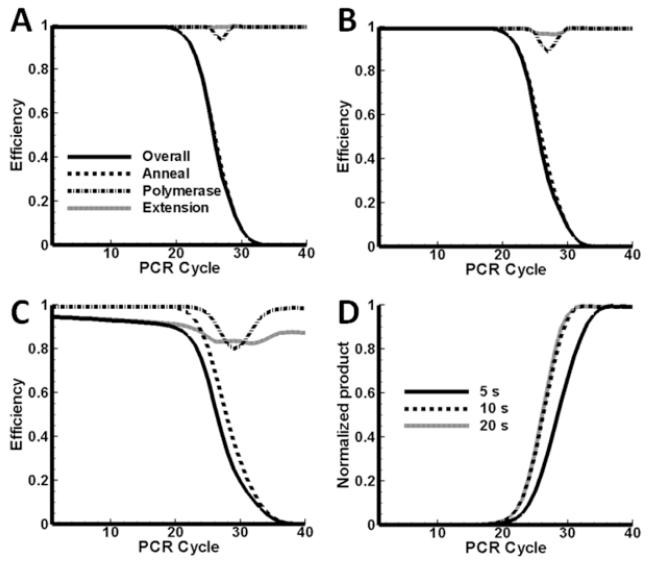
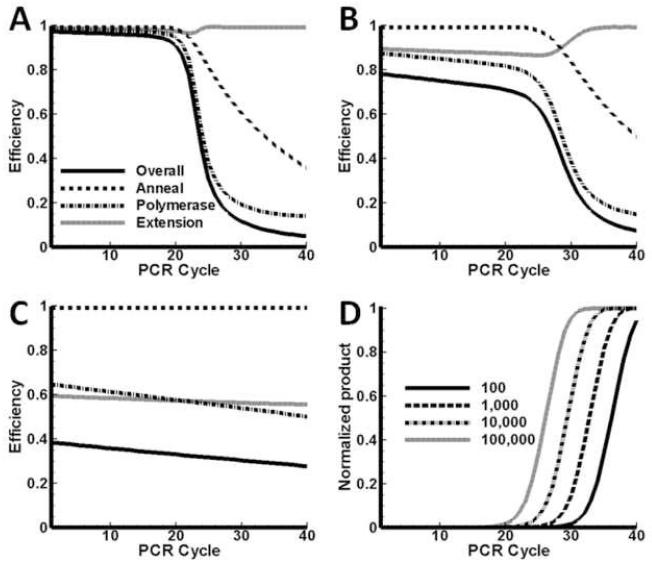
Case 1: $\stackrel{‒}{E_i}=12.6\times {10}^{11}$ copies

Results for case 1 are presented in Figure 4. In Figure 4A the different efficiencies are plotted as a function of cycle number. The elongation time is Δt_e = 20 s. The polymerase is in excess and the system is under the control of the annealing efficiency and it tracks the overall efficiency closely. The overall efficiency drops below 90% after cycle 22. The efficiency is less than 10% after 30 cycles and it is expected that increases in the yield will be exiguous. If the overall yield is calculated using $\stackrel{‒}{D_i}{(\eta +1)}^n=\stackrel{‒}{D_0^n}$, the average value over the first 30 cycles is 81%, but over the 40 cycles it drops to 56%.

Figure 4.

Efficiencies as a function of cycle number. D_i = 10⁵ copies, E_i = 12.6×10¹¹ copies, elongation period is 20 s (A), 10s (B) and 5s (C). (D): Normalized DNA product as a function of cycle number. D_i = 10⁵ copies, E_i = 12.6×10¹¹ copies, at elongation periods 20 s, 10 s and 5 s. The curves had the same maximum before normalization.

It is expected that the elongation efficiency will lower if the elongation time is shorter. In Figure 4B, the efficiencies are shown for the case Δt_e = 10 s (all the other parameters as for Figure 4A). The overall efficiency still tracks the annealing efficiency, however a slight decrease is observed in the polymerase and extension efficiencies. There is a brief period between cycle 26 and cycle 28 where the polymerase efficiency drops below 90%. The extension efficiency also lowers during this period, but only down to 96%. In Figure 4C the results are shown for an even shorter elongation time, Δt_e = 5 s. Here, the system is under extension control through cycle 24 and under annealing control for the remaining cycles. The localized drop in polymerase efficiency is still present, but the trough spans cycles 26 to 33 and it is deeper. There is even a brief period where the polymerase efficiency is less than the extension efficiency. Whereas ${\eta }_a^j$ is a monotonic decreasing function of cycle number, the polymerase and extension efficiencies exhibit local minima.

Normalized predicted PCR product amounts for the 3 elongation times (20, 10 and 5 seconds in Figures 4A-C respectively) are shown in Figure 4D. In all three cases the same number of initial copies is amplified to the same final amount. The effect of shorter extension times is to slow template amplification down; more cycles are required to reach the plateau. The mid-points of the curves shift to higher cycle numbers for shorter elongation times, although the copy number remains the same. In Figure 4D the two longer extension times give mid-points just beyond cycle 26, but for the shortest time Δt_e = 5 s, the mid-point is at cycle position 28.5.

Case 2: $\stackrel{‒}{E_i}=6.3\times {10}^{11}$ copies

Results for case 2 are shown in Figure 5. The initial polymerase concentration is halved with respect to the amount used in case 1. Results for the three extension times (20, 10 and 5 seconds) are shown in Figures 5A-C respectively.

Figure 5.

Efficiencies as functions of cycle number. D_i = 10⁵ copies, E_i = 6.3×10¹¹ copies, elongation period is 20 s (A), 10s (B) and 5s (C). (D) Normalized DNA product as a function of cycle number. D_i = 10⁵ copies, E_i = 6.3×10¹¹ copies, at elongation periods 20 s, 10 s and 5 s.

In Figure 5A the results are shown for Δt_e = 20 s. The reduced polymerase concentration causes a pronounced drop in ${\eta }_E^j$ between cycles 24 and 34 (compare to Figure 4A). During this period the number of binary complexes exceeds the number of polymerase molecules, but after cycle 28 this deficit becomes less and the polymerase efficiency begins to increase again - the explanation is a reduction in the number of binary complexes at later cycles, due to increased formation of dsDNA during the annealing stage. Compared to the results of case 1, the overall efficiency drops off sooner, and 50% overall efficiency is reached at cycle value 24.5. The extension efficiency remains near unity for the whole PCR reaction, with a subtle double minimum observable.

The results for Δt_e = 10 s are shown in Figure 5B. The width of the ${\eta }_E^j$ trough is wider, compared to Figure 5A, but the results are qualitatively similar. Also, the reduction in extension time from 20 s to 10 s enhances the double minima in ${\eta }_e^j$; compare ${\eta }_e^j$in Figure 5A with 5B.

When the extension time is set to Δt_e = 5 s (Figure 5C), the system is under extension control for the first 30 cycles; under polymerase control until cycle 36 and under annealing control for the last four cycles. Here is an example where three different efficiencies controlled the system over the course of 40 cycles. One mechanism overtakes another as being limiting and the results underscore the nonlinear character of the PCR process.

The plots of normalized DNA product vs. cycle number are shown in Figure 5D. The products have been scaled with the same maximum as in Figure 4D. The mid-points for Δt_e = 20 s, Δt_e = 10 s are close, at cycle value 27.8 and 28.5 respectively. These values differ from the results for similar extension times in case 1 earlier, and lie close to the midpoint for Δt_e = 5 s (of case 1). The results show that the midpoints shift if the polymerase concentration changes. The product curve does not reach saturation in the case of Δt_e = 5 s (solid curve, Figure 5D). If more cycles are added, then the curve continues to increase linearly until it finally plateaus when the primers are depleted. Note that all three curves have different slopes in the linear region. The slope decreases as the extension time is shortened, thus lower extension efficiencies lead to a slow-down of the process.

An important conclusion can be drawn at this stage. As long as the system is not under annealing control, the DNA product will not plateau, or in terms of a product vs. cycle number plot, the product will continue to increase at a near constant rate.

Case 3: $\stackrel{‒}{E_i}=2.1\times {10}^{11}$ copies

Results for case 3 are shown in Figure 6. In this case the polymerase concentration is reduced by a factor of 3 with respect to case 2. The results for the three extension times are shown in Figures 6A-C.

Figure 6.

Efficiencies as functions of cycle number. D_i = 10⁵ copies, E_i = 2.1×10¹¹ copies, elongation period is 20 s (A), 10s (B) and 5s (C). (D) Serial dilution study - normalized DNA product as a function of cycle number. D_i = 10², 10³, 10⁴ and 10⁵ (as indicated in the legend), E_i = 12.6×10¹¹ copies, t_E = 20 s.

For Δt_e = 20 s the system remains under polymerase control over all 40 cycles. Both ${\eta }_E^j$ and ${\eta }_a^j$ are monotonically decreasing functions, and ${\eta }_e^j$ exhibits a single minimum.

Results for Δt_e = 10 s are shown in Figure 6B. The extension efficiency is lower in Figure 6B compared to Figure 6A, hence the overall efficiency is lower. However, the system remains under polymerase control. The primers are not depleted at the end of 40 cycles (${\eta }_a^j$ is still relatively high) and amplification will continue beyond this point, albeit very slowly.

Figure 6C presents an example of very poor overall efficiency, where Δt_e = 5 s. For the first 25 cycles the system is controlled by extension, and then by the polymerase concentration. The annealing efficiency remains near unity. The total product formation will be much less than in previous cases.

The final example is a simulation of a serial dilution study. The conditions are the same as for case 1 and the extension time remains constant at Δt_e = 20s. The initial template concentration varies from 10² copies to 10⁵ copies. The results are shown in Figure 6D. The results are as expected for a quantitative PCR experiment. Consecutive midpoints differ by 3.3 cycle values and the slopes are parallel.

4. Conclusions

1. The overall efficiency depends linearly on the denaturing efficiency.

2. If the polymerase is in excess compared to the binary complex and the extension time is long, then the overall efficiency depends linearly on the annealing efficiency, i.e. ${\eta }^j={\eta }_d{\eta }_a^j$. In this case the polymerase binding and elongation are not rate-limiting.

3. If the polymerase is in excess compared to the binary complex but the extension time is short, then the overall efficiency is ${\eta }^j={\eta }_d{\eta }_a^j\left[1-e^{-\left\{\stackrel{‒}{E_0^j}-{\eta }_a\stackrel{‒}{S_0^j}\right\}{k}_C(t_c-t_a)}\right]$.. The system is under control of the extension time and the annealing efficiency.

4. If the binary complex is in excess compared to the polymerase, then ${\eta }^j={\eta }_d\frac{\stackrel{‒}{E_0^j}}{\stackrel{‒}{S_0^j}}$. The system is now under the control of the polymerase concentration.

5. The efficiency changes from cycle to cycle and different mechanisms may control the system over the course of 30 or 40 cycles.

6. The annealing efficiency is a monotonic decreasing function of cycle number, but ${\eta }_E^j$ and ${\eta }_e^j$ are not. A particularly interesting situation arises if the polymerase concentration becomes rate-limiting. Since new templates still form and γ^j continues to increase with each cycle, the annealing efficiency decreases. As a result the binary complexes begin to decrease at some point and the polymerase concentration is no longer deficient – then a notable increase in ${\eta }_E^j$ occurs.

Though some observations from this model (such as the shift in the curves due to shortened elongation time or reduced polymerase) can be intuitive for scientist familiar with PCR, this model uncovers the underlying efficiencies that are affected by these changes. The model also shows that the limiting step in every cycle changes as the reaction progresses. Experimental validation of the theoretical results is outside the scope of this work, but is under way and will be presented in a future publication.

Two other factors may affect the average rate of extension, V. Firstly, the dinucleotide triphosphate (dNTP) concentration may become depleted, in which case the extension rate becomes dependent on the rate of diffusion of dNTPs to the ternary complexes. Secondly, pyrophosphates (PP_i) are produced upon insertion of dNTPS and their concentration builds up in the system. It is possible that a point may be reached where the pyrophosphorolysis reaction could effectively compete with dNTP insertion resulting in slow (if any) net extension. These factors can be accounted for by making V dependent on PP_i and dNTP transport. Secondly, primer-dimer interactions are often problematic and one will have to resort to numerical solutions to account for the effect. The best alternative, if one wishes to use the analytical results presented here, is to assign a loss factor for primers at each cycle, similar to the polymerase and template losses due to thermal damage.

5. Appendix

This section describes the derivation of the annealing model approximations in detail. For simplicity, the superscript j has been dropped, and the following equations all apply to a single cycle.

5.1 Calculating P(τ) and S(τ)

First, the differential equations describing the primer and ssDNA reactions are given by (A1) and (A2):

$$\frac{dP}{d\tau }=-PS$$ (A1)

$$\frac{dS}{d\tau }=-PS-\beta S^2$$ (A2)

Since P(τ) ≠ 0 ∀ τ, we can divide (A2) by (A1) to get (A3):

$$\therefore \frac{dS}{dP}=1+\beta \frac{S}{P}$$ (A3)

This can be solved using an integrating factor to obtain (A4):

$$\begin{array}{cc}\hfill & \therefore \frac{d}{dP}\left(P^{-\beta }S\right)=P^{-\beta }\hfill \\ \hfill & \therefore S=P^{\beta }\left(\frac{P^{1-\beta }}{1-\beta }-\frac{{P_0}^{1-\beta }}{1-\beta }+P_0^{-\beta }{S}_0\right)\hfill \end{array}$$ (A4)

If we define $\delta =\frac{{\left(\gamma \right(\beta -1)+1)}^{\frac{1}{1-\beta }}}{\gamma }$ and use the fact that $P_0=\frac{1}{\gamma }$ and S₀ = 1, then (A4) becomes (A5):

$$\therefore S=P\frac{\left({\left(\frac{P}{\delta }\right)}^{\beta -1}-1\right)}{\beta -1}$$ (A5)

Substituting (A5) into (A1) to obtain (A6):

$$\frac{dP}{d\tau }=-PS=-\left(P\right)P\frac{\left({\left(\frac{P}{\delta }\right)}^{\beta -1}-1\right)}{\beta -1}\approx -aP\frac{\left({\left(\frac{P}{\delta }\right)}^{\beta -1}-1\right)}{\beta -1}$$ (A6)

Here, we approximate P² by aP where a is some constant. We will choose the value of a later. This approximation makes it possible to solve the differential equation to obtain (A7). Using separation of variables and partial fractions:

$${\int }_{P_0}^P\frac{dP}{P\left({\left(\frac{P}{\delta }\right)}^{\beta -1}-1\right)}={\int }_{P_0}^P\frac{{\left(\frac{P}{\delta }\right)}^{\beta -2}dP}{\frac{1}{\delta }\left({\left(\frac{P}{\delta }\right)}^{\beta -1}-1\right)}-{\int }_{P_0}^P\frac{dP}{P}=\left(\frac{1}{\beta -1}\right)\ln \left(\frac{{\left(\frac{P}{\delta }\right)}^{\beta -1}-1}{{\left(\frac{P_0}{\delta }\right)}^{\beta -1}-1}\right)-\ln \left(\frac{P}{P_0}\right)=-\frac{a\tau }{\beta -1}$$

After some manipulation and using P₀ = 1/γ, we obtain (A7):

$$\therefore P\left(\tau \right)={\gamma }^{-1}{\left[{\left(\gamma \delta \right)}^{1-\beta }(1-e^{-a\tau })+e^{-a\tau }\right]}^{\frac{1}{1-\beta }}$$ (A7)

Notice that, P(0) = 1/γ and lim_τ→∞ P = δ. Since P is monotonically decreasing, we have $\frac{1}{\gamma }>P>\delta$. Let us reinvestigate equation (A6). If we let a = P(0) = 1/γ or a = lim_τ→∞ P = δ then:

$$-\left(\frac{P}{\gamma }\right)\frac{\left({\left(\frac{P}{\delta }\right)}^{\beta -1}-1\right)}{\beta -1}<-\left(P^2\right)\frac{\left({\left(\frac{P}{\delta }\right)}^{\beta -1}-1\right)}{\beta -1}<-\left(\delta P\right)\frac{\left({\left(\frac{P}{\delta }\right)}^{\beta -1}-1\right)}{\beta -1}$$

This implies that the approximation with a = 1/γ will decrease at a faster rate than the real situation, and the approximation with a = δ will decrease slower. Hence, letting a = 1/γ provides a lower bound (P_l) on P(τ) and a = δ provides an upper bound (P_u) on P(τ). Since one of the goals is the optimization of the annealing time, using the upper bound on P(τ) will provide a conservative estimate. Hence, we choose a = δ to get (A8):

$$\therefore P\left(\tau \right)={\gamma }^{-1}{\left[{\left(\gamma \delta \right)}^{1-\beta }(1-e^{-\delta \tau })+e^{-\delta \tau }\right]}^{\frac{1}{1-\beta }}$$ (A8)

The value of S can now be calculated using (A5). To determine the accuracy of this approximation, we calculate the ratio of the upper and lower bounds:

$$R(\tau ,\gamma ,\beta )=\frac{P_u\left(\tau \right)}{P_l\left(\tau \right)}={\left[\frac{{\left(\gamma \delta \right)}^{1-\beta }(1-e^{-\delta \tau })+e^{-\delta \tau }}{{\left(\gamma \delta \right)}^{1-\beta }(1-e^{-\tau ∕\gamma })+e^{-\tau ∕\gamma }}\right]}^{\frac{1}{1-\beta }}$$

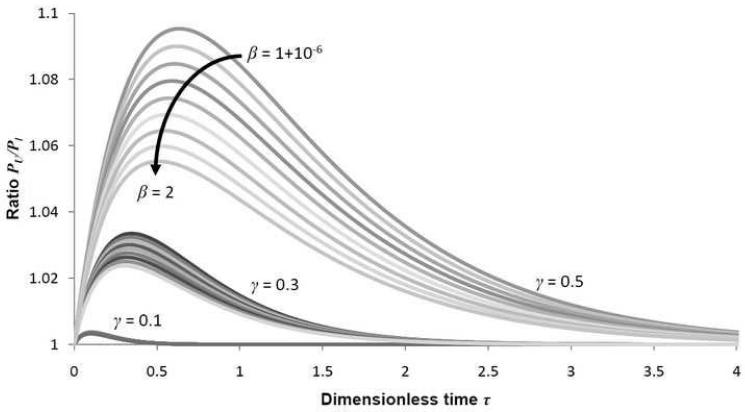
The value of the ratio R(τ, γ, β) is plotted for various values of γ and β on 0 < τ < 4 on Figure A1. The higher the ratio, the greater the difference between the upper and lower bounds and the greater the error in the approximation.

From the figure, it is clear that the ratio attains a maximum somewhere on 0 < τ < 4. The error increases as β → 1 and as γ → 1. The maximum error attained was less than 1.1 with β = 1 + 10⁻⁶ and γ = 0.5. This means that, even in the final cycle where the approximation is expected to be poorest, the error is less than 10%. More importantly, however, the ratio decreases to 1 as τ → ∞, showing that the approximation error tends to 0.

5.2 Calculating B(τ), C(τ) and E(τ)

We have the following kinetic equation for E (A9):

$$\frac{dE}{d\tau }=-\alpha BE$$ (A9)

But the species balances can be rearranged as follows, to obtain (A10):

$$\begin{array}{cc}\hfill & E_0=E+C\to C=E_0-E\hfill \\ \hfill & P_0=P+B+C\to B=P_0-P-C\to B=P_0-P-E_0+E\hfill \\ \hfill & \therefore \frac{dE}{d\tau }=-\alpha E(P_0-P-E_0)\hfill \end{array}$$ (A10)

We can again separate and use partial fractions to obtain (A11):

$$\therefore {\int }_{E_0}^E\left(\frac{1}{E}-\frac{1}{P_0-P-E_0+E}\right)dE=-\alpha {\int }_0^{\tau }(P_0-P-E_0)d\tau$$ (A11)

One cannot integrate P with respect to E as this is a non-homogenous term in the differential equation. Furthermore, the integral ${\int }_0^{\tau }Pd\tau$ is a very complex function. Since the value of P₀ –P remains nearly constant for γ << 1, we assume that P₀ –P ≈ constant. Then (A12):

$$\therefore \ln \left(\frac{E}{E_0}\right)-\ln \left(\frac{E+P_0-P-E_0}{P_0-P}\right)=\ln \left(\frac{E(P_0-P)}{E_0(E+P_0-P-E_0)}\right)=-\alpha (P_0-P-E_0)\tau$$ (A12)

After some rearranging and recalling that P₀ = 1/γ, we find (A13):

$$\therefore E\left(\tau \right)=\frac{E_0\left(1-\gamma \left(P\right(\tau )+E_0)\right)}{\left(1-\gamma P\left(\tau \right)\right)e^{\alpha \left(1-\gamma \left(P\right(\tau )+E_0)\right)\tau ∕\gamma }-\gamma E_0}$$ (A13)

Finally, $B\left(\tau \right)=\frac{1}{\gamma }-P\left(\tau \right)-E_0+E\left(\tau \right)$ and C(τ) = E₀ − E(τ).

Figure A1.

Three separate bands are seen above, corresponding to γ = 0.1, 0.3 and 0.5. In each band, the value of R(τ, γ, β) increases with β, the top curve in each band corresponding to β = 1 + 10⁻⁶. The maximum ratio achieved is less than 1.1, with β = 1 + 10⁻⁶ and γ = 0.5.