Abstract
Social influences on foraging efforts were examined in domestic chicks by investigating the frequency of runs made to feeders and the amount of pecking to gain food. Single or paired chicks foraged in an I-shaped maze equipped with a millet feeder on each end, that distributed one or two grains at variable intervals. Regardless of when the grain(s) were dispensed, chicks ran back and forth between the feeders. Analyses of their movement patterns revealed: (1) running patterns were not directly synchronized with the dispensing of grain(s), (2) running distance was longer in paired chicks than in single chicks, (3) paired chicks partially synchronized their runs between feeders, and (4) social effects were immediate but cumulative after repeated blocks. We further examined the social effects on running by dividing the I-maze into two parallel lanes separated by a transparent wall, so that kleptoparasitic interference of food did not occur. Again, the chicks increased their running speed and were even more synchronized with their partner's movements, indicating that food competition alone was not responsible for increased foraging effort. The number of pecks to get grains was also assessed under conditions where the food tray was gradually replaced, from an easy one to more difficult ones. When tested in the separated I-maze, paired chicks pecked more in the difficult food situation without increase in the number of gained grains. Results suggest that (i) social facilitation leads to increased foraging efforts and (ii) the presence of a conspecific is alone may lead to enhanced foraging efforts in chicks. These findings are discussed in terms of possible ecological background of social facilitation.
Keywords: work, cost, handling, consumption, competition, social foraging, kleptoparasitism
Introduction
Social facilitation, which results in an enhancement of behavioral performance or an increase in work investment when an individual is in the presence of one or more conspecifics, has been widely reported in a variety of animals including humans (Zajonc, 1965 for a review), e.g., ants building a nest (Chen, 1937), cockroaches running in mazes for food (Gates and Allee, 1933), hyenas in drinking behavior (Glickman et al., 1997), and humans engaged in physical work (Triplett, 1898) or mental work (Allport, 1920), leading to recent report on physiological characteristics of the facilitation in cardiovascular responses (Blascovich et al., 1999). While many diverse taxa exhibit socially facilitated behavior, surprisingly little is known about the ecological contexts in which social facilitation occurs.
From an ecological standpoint, social interference by conspecifics is considered an important factor in influencing an individual's foraging strategies. Classical foraging theory typically focuses on the perspective of a single forager (Charnov, 1976); however this neglects the overall interactions that occur in group-living animals. A more recent perspective, coined the “Social Foraging Theory,” suggests that not only individual decision-making, but also conspecific behavior, influences the outcome of an individual's foraging success (Giraldeau and Caraco, 2000). For example, Parasitic Jaegers (Stercorarius parasiticus) will forage in larger groups when engaging in risky behavior such as attacking and steeling fish from Common Terns (Sterna hirundo), even though they could gain more food by foraging in smaller groups or by themselves (Bélisle, 1998). Bélisle (1998) argued that the risk of starving must also be included in foraging theory in addition to such things as net/gross intake rate or efficiency, since group formation is expected to reduce variance of the food-encounter rate.
In behavioral studies using chicks, Tolman and Wilson (1965) reported that paired chicks consumed a larger amount of food than did isolated chicks only when the chicks had been deprived of food. However, their study failed to show conclusive results on the effects of social facilitation on rates of pecking (Tolman, 1967). Tolman and Wilson (1965) also did not control the amount of food chicks could consume, thus it was uncertain whether the increased consumption was a result of the amount of food available rather than mere social facilitation. In our study, we tried to know whether social facilitation could improve individual pay-off [i.e., rate of net gain = (benefit − work cost)/time], or otherwise other currency (e.g., low probability of starvation; Caraco et al., 1980) should be considered.
In the present study, we examined the influence of social facilitation in 1 to 2-week-old domestic chicks (Gallus domesticus). By strictly controlling the amount of food delivered, we examined whether foraging competition (i.e., reduction of gain by interference of other individuals) may socially facilitate an increase in the amount of foraging efforts in chicks. Chicks provide a unique opportunity for studying the neuroscience of decision-making in relation to behavioral ecology and economics (Matsushima et al., 2003, 2008 for reviews), because we can quantitatively control feeding conditions and potential energy budgets in experiments. Furthermore, chicks are precocial animals that begin to forage independently as soon as they hatch, and so individual development can be controlled as well. In our study, we investigated two foraging behaviors, running, and pecking, in order to assess whether foraging efforts would increase under specific social conditions (i.e., social facilitation). Running to, or approaching food, and pecking at, or handling, food have already been shown to have distinct neural substrates involved (ventral striatum/nucleus accumbens and arcopallium, respectively; Matsushima et al., 2008). For example, lesions of the ventral striatum enhanced choices of small/immediate reward against large/distant alternative (Izawa et al., 2003; Aoki et al., 2006a). Similarly, lesions of the arcopallium caused chicks to choose the small/easy reward more frequently than the large/costly alternative (Aoki et al., 2006b). It is therefore possible that social facilitation can occur differently in these two aspects of foraging effort.
Materials and Methods
Subjects
All experiments were conducted under the guidelines and approval of the Committee on Animal Experiments of Hokkaido University. The guidelines are based on the national regulations for animal welfare in Japan (Law for Humane Treatment and Management of Animals; after a partial amendment No. 68, 2005). After the experiments, chicks were sacrificed in carbon dioxide according to the guidelines.
A total of 99 male domestic chicks (G. domesticus, White Leghorn strains) were used. New hatchlings (post-hatch day 1: presumed hatching day) were obtained from a local supplier (Hokuren Central Hatchery, Iwamizawa, Hokkaido, Japan). Chicks were paired and housed in transparent plastic cages (15 cm × 28 cm × 12 cm) under white lighting (12L: 12D; light period starting at 08:00) and thermo-controlled at ca. 30°C. Pairs of chicks in the same cages were trained and tested in the same conditions.
Two types of food were given, grains of millet and chick mash food. The total amount of food per day was kept at a certain level so that (1) the body weight of chicks gradually increased and (2) the chicks actively consumed food during experiments. From post-hatch day 2, chicks were fed mash food. The amounts of mash food were 1 g (post-hatch days 2–5), 1.5 g (days 6 and 7), and 3 g (from day 8). From post-hatch day 3, grains of millet were added. The amounts of grains (per chick per day) were 1 g (day 3), 2 g (day 4), 3 g (day 5), 2.5 g (days 6 and 7), and 2 g (from day 8). Until day 3, all chicks were communally fed. From day 4, chicks were allocated to a communally fed condition or solitarily fed condition depending on experiments: varied among groups in Experiment 1 and solitarily in Experiments 2 and 3. In the groups of solitarily fed chicks, each individual was fed in a cage that was visually separated by a black plastic wall, so that chicks did not see the other chicks eating food; these chicks were communally housed except when the daily diet was given.
Apparatus
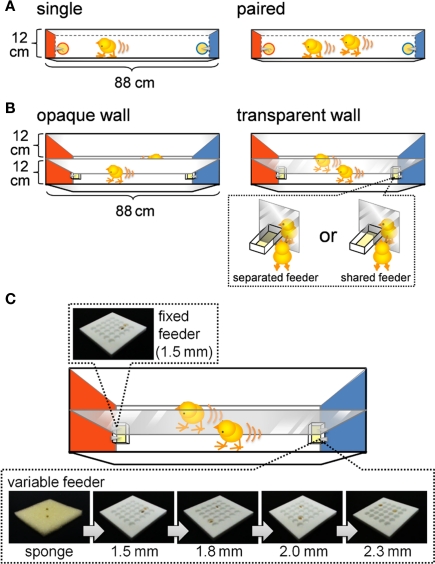
In Experiment 1, an I-shaped maze equipped with one-lane (1-lane maze; 12 cm in width, 88 cm in length and 30 cm in height) was used (Figure 1A). The maze was equipped with a pair of terminal feeders. Walls at the terminals were colored red (left) or blue (right). Each feeder supplied a grain of millet food at variable intervals. Plastic Petri dishes (5.5 cm in diameter to a depth of 1.5 cm) were used as food trays, and the floor of each dish was covered with sponge.
Figure 1.
Experimental apparatus for examining foraging efforts, running distance (A,B), and number of pecks (C). (A) One-lane I-shaped maze equipped with a pair of terminal feeders. Terminal walls of the maze were colored red and blue. The feeders supplied grains of millet according to a variable interval schedule. One grain was supplied at one time in the single-chick condition (left), and two grains were supplied at one time in the paired-chicks condition (right). Note that the paired chicks were competing over food, whereas the single chicks were not. (B) Two-lane I-shaped maze. Chicks and feeders were separated by an opaque (left) or a transparent (right) wall. In the transparent wall condition, the feeders were either separated or shared. Note that the paired chicks in the shared feeder condition were competing for food, whereas chicks in the other condition did not. (C) The 2-lane maze was equipped with a fixed feeder and a variable feeder. The food tray of the fixed feeder was made of a plastic plate with 25 holes (5 × 5), each 1.5 mm deep. The food tray of the variable feeder was either a sponge or plastic plates of variable depth (ranging from 1.5 to 2.3 mm). Supplied grains tumbled into the holes, making it difficult for chicks to obtain the grains. The deeper the holes were, the more difficult it was for chicks to obtain the grains. Trays of the variable feeder were sequentially replaced in an order from the easy sponge to the more difficult plates every ca. 3 min. See text for details.
In Experiment 2, an I-shaped maze equipped with two lanes (2-lane maze; 25 cm in width, 88 cm in length, and 40 cm in height) was used (Figure 1B). These two lanes had the same width as that of the 1-lane maze used in Experiment 1 but were separated by a transparent acryl board in one groups of chicks. In another group, in order to visually separate the two lanes, opaque white cardboard was attached to both sides of the acrylic board so that the chicks could not see each other. On each terminal feeder, two food trays were placed in adjacent positions over the separation board. Rectangle-shaped food trays (3 cm in width, 4 cm in length, and 2 cm in depth) with sponge on the floor were use. In the shared feeder condition, a 4-cm-wide window was opened on each terminal end of the separation board, and the chicks in both lanes shared the food supplied to a food tray (6 cm in width, 4 cm in length, and 2 cm in depth) placed at the center.
In Experiment 3, the same 2-lane maze as that in Experiment 2 was used after a slight modification to the food trays (Figure 1C). Square food trays (width and length of 3.6 cm depth of 1.8 cm) were used with two different types of floor coverage: one with sponge and the other with acrylic plates with 25 holes in the surface (aligned in 5 × 5, 4 mm in diameter). Four different types of acryl plates were used with different depths of the holes: 1.5, 1.8, 2.0, and 2.3 mm. Food trays were manually replaced, and a single replacement took ca. 10 s.
In all experiments, in order to prevent chicks to associate the feeder sound with food reward, sounds of electric motors were replayed at variable intervals from instruments placed around the apparatus; the mean interval was set at 2.5 s, uniformly distributed from 1.5 to 3.5 s. The apparatus was placed in a dark room kept at ca. 25–30°C and illuminated by four 60 W white light bulbs placed above the runway and feeders. Timing of grain delivery and the noise sound were controlled by microrobots (RCX, LEGO Mindstorms). Behavior of the chicks was recorded by a video recorder (DCR-SR65, Sony, Japan) and color CCD cameras (250 k pixels with NTSC output), and the recordings were stored for offline analysis.
Behavioral procedures
In Experiments 1–3, chicks were initially habituated to the experimental maze according to a common procedure for two successive days (pre-1 and pre-2) on post-hatch days 6–15. For habituation, paired chicks (housed in the same cages) were placed on the midway part of the maze in which some food (ca. 100 grains) was given in advance. After the chicks had consumed the food, feeders started to deliver grains by the same procedure as that used in each experiment. Two successive habituation sessions (ca. 20 min in total) were given per day for each of pre-1 and pre-2 except for Experiment 3, in which one long session of habituation (ca. 20 min) was given instead. The experimental data were obtained after the habituation.
Experiment 1: effects of paired foraging on approaching food, an inter-group comparison in the 1-lane maze
Effects of paired foraging in the maze and the cage were examined in regards to subjects’ distance and synchrony during running. Running distance was used to calculate the rate of approaching food at either end of the I-maze, where an increase in distance corresponds to increased running during the experimental condition.
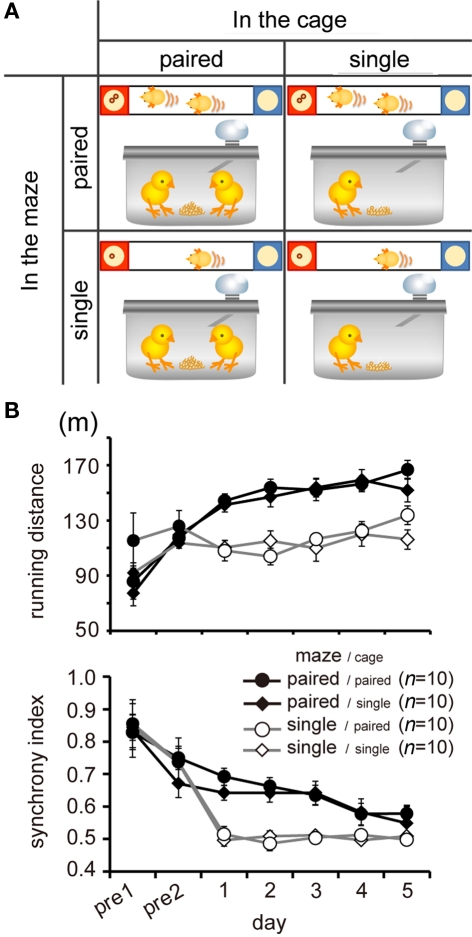
“Paired in the maze” means that chicks foraged in pairs at the test, whereas “paired in the cage” means that the chicks foraged in pairs in the housing cage, in which main diet (mixture of mash food and millet) was supplied (Figure 3A).Chicks were thus divided into four conditions: (1) paired in the maze/paired in the cage, (2) paired in the maze/single in the cage, (3) single in the maze/paired in the cage, (4) single in the maze/single in the cage.
Figure 3.
Paired foraging in the maze, but not in the cage, influenced running (Experiment 1). (A) Chicks were divided into four experimental groups according to 2 × 2 block placement. “In the maze” means chicks were single or paired in the I-shaped maze during the tests, whereas “in the cage” means that chicks foraged in single or paired condition in their home cage. Note that chicks were housed in pairs in all conditions except foraging. (B) Means (±SEM) of running distance (upper) and synchrony index (lower) during feeding time (ca. 8 min) are plotted against the day of the experiment. Open and filled symbols denote paired and single foraging in the maze, whereas circles and rhombi denote paired and single foraging in the cage, respectively, in this and the following figures.
After the habituation (pre-1 and pre-2), experiments were conducted for five consecutive days (days 1–5) and chicks received one test session per day. In each of the sessions, after a short habituation period in the maze (i.e., 1 min after the chick had consumed all of the food available, namely, 20 grains/chick placed in advance in each feeder), each of the two feeders supplied one grain at a time with variable intervals (mean interval of 15 s, uniformly distributed in a range of 10–20 s). In a single session, the programmed food delivery continued 30 times and thus lasted for ca. 8 min. The chicks were then left in the maze for an additional 2 min after they had consumed all of the grains delivered on the food trays, and the test session of the day was terminated.
In the I-shaped maze, the following two parameters were measured: (1) running distance (or how far the chick ran) and (2) synchrony index. Synchrony index was defined as the ratio of time in which both chicks stayed in the same side of the maze, shown as percentage of the total time recorded. The position of each chick's head was automatically and unequivocally given by computer-based video analysis, as either being placed on the red or the blue side of the maze. When both chicks were always in the same end, the synchrony index was 1.0 (in-phase synchrony). When, on the other hand, chicks were in opposite ends, the index was 0.0 (anti-phase synchrony). When both chicks moved in a random and independent fashion, the index would show a chance level of 0.5 (asynchrony).
Experiment 2: effects of paired foraging on approaching food, an inter-group comparison in the 2-lane maze
In order to differentiate food competition from social facilitation by a nearby conspecific, we removed the factor of food competition by separating paired chicks with either a transparent or an opaque partition down the middle of the maze's track, thus creating two separate lanes (Figure 1B). After the habituation (i.e., paired foraging in the maze on pre-1 and pre-2), similar to Experiment 1, test sessions were repeated five times, one session per day (days 1–5). Each of the two feeders supplied one grain at a time with variable intervals (mean interval of 15 s, uniformly distributed in a range of 10–20 s). In a single session, the programmed food delivery continued 30 times and thus lasted for ca. 8 min. The following two parameters were measured: (1) running distance and (2) synchrony index.
Effects of paired foraging on running distance, an intra-individual comparison
The immediate effect of paired foraging was examined in terms of running distance. A group of chicks (post-hatch days 12–14) were re-used after Experiments 1 and 2 (see above); chicks that had been solitary fed in both the maze and the cage were used. Immediately after each chick had been individually placed in the maze, both feeders delivered grain 10 times at variable intervals (mean interval of 15 s, uniformly distributed in a range of 10–20 s, 1 grain per delivery); this term is referred to as the first “single” phase. The companion chick was then introduced into the maze, and the feeders delivered twice as much grain (2 grains per delivery) 10 times; this term is referred to as the second “paired” phase. In the third phase, the companion chick was removed from the maze, and the subject chick received feeding another 10 times. Each phase lasted for ca. 3 min.
Experiment 3: effects of paired foraging on approaching and pecking at food, an inter-group comparison in the 2-lane maze
Effects of visual perception of the other chick on running (i.e., approaching food) and on food pecking (handling food) were examined in the 2-lane maze. The food tray difficulty (estimated on the basis of the number of pecks required for chicks to gain a certain amount of grain) was controlled by systematically changing the types of acryl plates used as the floor of the feeder (Figure 1C). After habituation (i.e., paired foraging in the maze on pre-1 and pre-2), similar to Experiments 1 and 2, test sessions were repeated three times, one session per day (days 1–3); chicks were left untested for 4 days between test days 1 and 2. Each of the two feeders supplied two grains at a time with variable intervals (mean interval of 30 s, uniformly distributed in a range of 20–40 s).
In the tests, the variable feeder initially had a sponge floor. When the variable feeder had delivered six times (12 grains), the sponge was replaced by an acryl plate with 1.5-mm-deep holes. The 1.5-mm plate was subsequently replaced by 1.8, 2.0, and 2.3 mm plates when the variable feeder had delivered 12 grains for each plate. Four CCD cameras were set just above the feeder to record pecking behavior of the chicks were video recorded. The following four parameters were measured: (1) number of pecks, (2) number of gained grains, (3) running distance and (4) velocity. Velocity (cm/s) was measured in the runway except for the areas near the feeders (<10 cm from the walls).
Data analysis
Recording and analyzing approaching behavior
Experiments were videotaped and coded later at rate of 30 frames per second using a Handycam recorder. The Handycam was located directly above the I-maze during testing, providing an aerial view of the subjects and apparatus. Chicks were individually marked by a rectangular piece of fluorescent-colored tape (Yamato Co., Ltd., Japan) affixed to their heads. The position of the fluorescent markers was analyzed by using Move-tr/2D 7.0 software (Library Co., Japan) and the trajectories and running distances were thus calculated.
Statistical analysis of generalized linear mixed model
The following five types of behavioral parameters were analyzed by using R for the platform of statistic calculation: running distance, synchrony index, number of pecks, number of gained grains and velocity. See Appendix for details.
Results
Once habituated, chicks began to actively run between the terminal feeders as soon as they were put in the maze, even without any visual cues. Furthermore, the runs were not in response to the timing of food delivery. Singly tested chicks stopped running within ca. 1 min of the final delivery of food items. We therefore assumed that running distance of the runs represented “approaching effort” and pecks at the feeders represented “handling effort,” rather than reflexive responses to food, and examined food-approaching behaviors in a series of experiments.
Experiment 1: paired foraging increased running distance
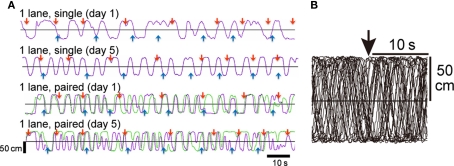
Paired chicks ran more than single chicks did. Figure 2A shows representative running trajectories of single (top and second records) and paired chicks (third and fourth records) at tests. Runs by single chicks were irregular on day 1 (top record), but they were more regular and more active on day 5 (second record). Runs by paired chicks were highly synchronized on day 1 (third record), but they were unsynchronized on day 5 (fourth record). Superimposed trajectories (Figure 2B), however, showed that the runs were not in response to the timing of food delivery.
Figure 2.
Representative running trajectories in the 1-lane condition (Experiment 1). (A) Two minutes records of running trajectories. Purple and green lines represent the trajectory of individuals along the long axis of the maze; upward indicates the direction to the red feeder. Red and blue arrows indicate the time at which a grain(s) was delivered. The top and second records (1-lane, single) were obtained from the same chick on different days (days 1 and 5). The third and fourth records (1-lane, paired) were obtained from a pair of individuals. Comparison of the trajectories on day 1 (top vs. third) and day 5 (second vs. fourth) clearly shows that the paired chicks ran at a higher frequency. (B) Thirty superimposed trajectories aligned at the time of grain delivery from the red feeder (downward arrow at the top). An example obtained from a chick tested in the single condition in the maze. Note that the runs were not in response to the food delivery.
Paired foraging in the maze, but not in the cage, increased running distance and synchrony index. A comparison of running by the four groups of chicks (n = 10 in each groups) is shown in Figure 3B. Based on running distance, AICs were calculated for each of the eight models in which the variables of day (1–5), maze (paired or single), and cage (paired or single) were considered (See Table A1 in Appendix for details). Of these models, the day-maze model yielded the smallest AIC. The day-maze-cage model yielded the same-AIC, but the cage term was not reliable for its coefficient (p = 0.197). Similarly, based on the synchrony index, AIC calculations revealed a facilitating effect of paired foraging in the maze, but not those of paired foraging in the cage (Table A2 in Appendix). We therefore concluded that the presence of other chicks and/or food competition among paired chicks could have caused the increase in approaching effort. It is not clear whether synchronization might be directly (and causally) linked to the increased effort.
Experiment 2: visual perception of the other chick, but not food competition, excessively increased running distance
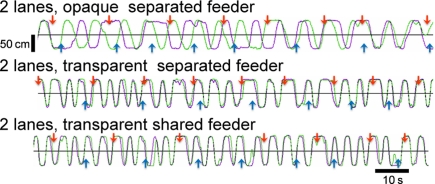
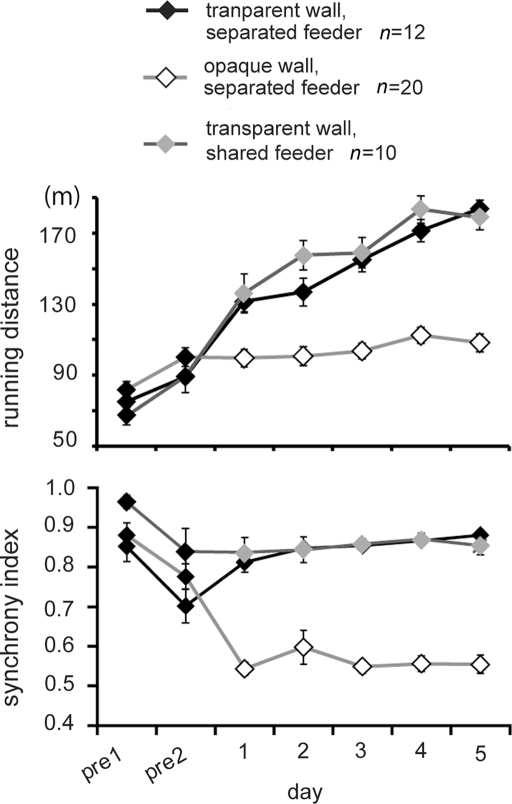
To reveal the cause of the increased running distance, we separated the maze into two lanes by a transparent/opaque wall (see Figure 1B), and we found that visual perception increased both running and synchrony indexes. Figure 4 shows representative trajectories obtained from one pair in each group. When separated by an opaque wall, chicks in the 2-lane maze (therefore with no food competition) ran back and forth between feeders independently (top record in Figure 4). When visually interacting via a transparent wall, chicks ran back and forth in high synchronization (second record). Direct foraging competition at shared feeders (see Figure 1B, bottom) did not result in difference from when the transparent wall separating the feeders was present (compare second and bottom record in Figure 4). It is notable that a high degree of synchrony was maintained until day 5, in contrast to the unsynchronized running seen in Experiment 1 (see Figure 2A, fourth record, and Figure 3B, bottom).
Figure 4.
Representative running trajectories in the 2-lane condition (Experiment 2). When separated by an opaque wall, running trajectories were not synchronized (top). When separated by a transparent wall, runs were more frequent and synchronized regardless of whether the feeder was separated (middle) or shared (bottom). All records were obtained on experimental day 5.
Based on the running distance and synchrony index (Figure 5), AICs were calculated for eight models. As variables, day (1–5), wall (whether the wall was transparent or opaque), and feeder (whether the feeders were separated or shared) were considered (Table A3 in Appendix). For running distance, the day-wall model yielded the smallest AIC (16191). The day-wall-feeder model gave rise to the second-smallest-AIC (16192), but the feeder term was not reliable for its coefficient (p = 0.2921). For synchrony index (Table A4 in Appendix), the day-wall model yielded the smallest AIC, but the day term was not reliable for its coefficient (p = 0.0844); thus, the result is different from the synchrony index in Experiment 1, in which the coefficient of the day was negative. We therefore tentatively conclude that the running distance and synchrony index are not linearly linked. Increased effort is not brought about by changes in synchronized running.
Figure 5.
Social interactions via the transparent wall caused a high degree of synchrony regardless of foraging competition (Experiment 2). Means (±SEM) of running distance (upper) and synchrony index (lower) are plotted against the day of the experiment. Open and filled symbols denote data in the opaque wall and the transparent wall, respectively. Gray symbols denote the data obtained from another group in which the feeders were shared and the wall was transparent.
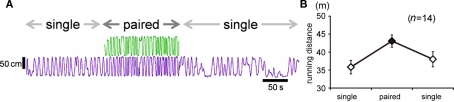
Pairing immediately increased running distance
In both Experiments 1 and 2, difference in running distance between the groups appeared from day 1 of the experiment. In order to determine whether paired foraging could immediately increase the approaching effort, we examined running distances by an intra-individual comparison. As shown in a typical example (Figure 6A), pairing immediately increased running. The average running distance for each condition (mean ± SEM, n = 14) is shown in Figure 6B. The Wilcoxon signed-rank test revealed a significant difference between paired phase and mean of the first and last phases (T = 2, p-value = 0.0003662).
Figure 6.
The run was facilitated as soon as a companion chick was introduced (Experiments 1 and 2). (A) Representative running trajectories of a pair of chicks. Subject chick (purple) received 30 deliveries of food, divided into three phases. In the first phase, the subject was tested in single condition. In the second phase, a companion chick (green) was introduced into the maze. In the third phase, the subject was again tested in single condition. Each phase lasted for ca. 3 min. (B) Means (±SEM) of running distance recorded in the first and third phases of the single condition (open symbols) and in the second phase of the paired condition (filled symbol).
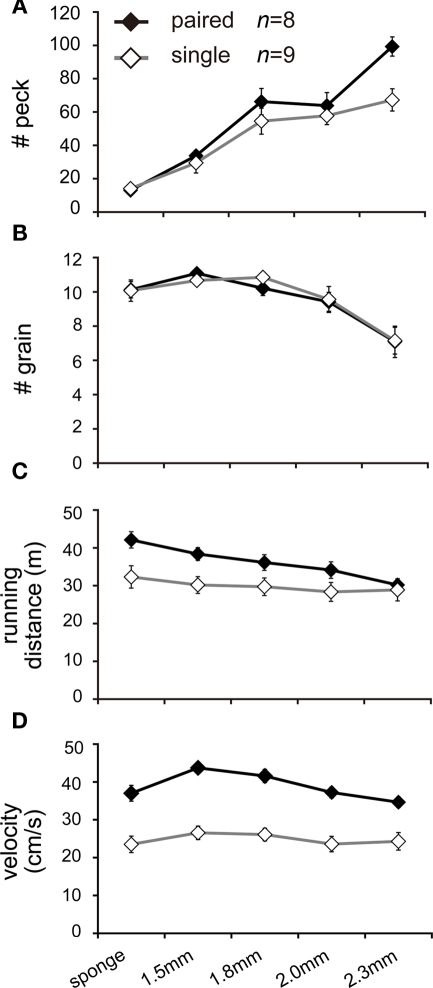
Experiment 3: pairing increased pecks without improved food gain
In order to determine whether paired chicks also increased their handling effort (i.e., efforts to collect food), we examined rates of pecking for food by using a series of trays that modified the difficulty for food collection (Figure 1C). Paired chicks increased the number of pecks, particularly in the difficult food condition (in a range from 1.8 to 2.3 mm; Figure 7A). The number of grains decreased in accordance with increased difficulty of food tray, but the number of grains was not different between the single and paired groups (Figure 7B). Running distance was greater for paired chicks as found in Experiments 1 and 2, but the difference gradually diminished in the difficult food condition (Figure 7C). However, the velocity at which paired chicks ran remained consistently higher than in the single chicks (Figure 7D). The running distance of paired chicks decreased not because they ran slowly but because they stayed at the feeders for a longer time.
Figure 7.
Social interactions of pairing were also found in the number of pecks (handling effort), particularly in the difficult food condition (Experiment 3). Means (±SEM) of two groups of chicks [paired (filled symbols) and single conditions (open symbols)] are plotted against the phases of different food tray difficulty (from the sponge to the plate with deep holes). Each individual chick was repeatedly tested on three successive days, and the values were averaged to yield individual data. Number of pecks (A), total gain of grains (B), running distance (C), and mean velocity (D) are plotted. Note that the chicks spent a shorter time for running but ran at higher velocity in the paired condition, even in the difficult condition.
For all of the data shown in Figures 7A–D, AICs were calculated for five models in which the variables of feeder (food tray difficulty, five steps ranging from sponge to 2.3 mm), maze (paired or single), and their interaction were considered (Tables A5–A8 in Appendix). For the number of pecks, the feeder–maze-interaction model yielded the smallest AIC (Table A5 in Appendix), indicating that the effects of pairing emerged on handling effort only when the food was difficult to obtain. For the number of grains, on the other hand, the maze term was not included in the chosen model (Table A6 in Appendix), indicating that the paired and single chicks had similar gains. For running distance, the feeder–maze-interaction model was chosen (Table A7 in Appendix). The interaction term suggested that the difference between the paired and the single chicks were smaller for the more difficult food trays. For velocity, the maze model was chosen (Table A8 in Appendix).
Discussion
Ecological accounts of the excessive foraging efforts
In this study, we found that visual perception of other individuals, rather than direct foraging competition, increased foraging efforts for approaching food (running distance) as well as for handling food (number of pecks). Increased foraging efforts in this study appear to be a result of social facilitation. Zajonc (1965) argued that social facilitation affects “dominant responses,” meaning that dominant (or well-developed) action patterns are most likely to be socially enhanced. Both running and pecking are well-developed behaviors in actively foraging domestic chicks. It should be noted, however, that chicks never exhibit running or pecking behavior when food is not available (data not shown), indicating that direct inter-individual interactions alone failed to cause social facilitation. It should also be noted that the term “social facilitation” is a psychological label, never specifying its functions in terms of economics/ecology. The idea of social facilitation is therefore not mutually exclusive with the idea of work investment under competition.
Our results suggest that currencies (or value functions) other than the food benefit are critical in social facilitation, in accordance with social foraging theory. According to Koops and Giraldeau (1996), starlings adopt foraging tactics that minimize the probability of energetic shortfall rather than maximize mean intake rate (or the benefit). Chicks may also make use of other individuals’ information at food sites to avoid the risk of starvation, given that chicks have been shown to be risk-averse to food quantities (Kawamori and Matsushima, 2010). However, much remains to be discussed about whether excessive running and pecking was really “inefficient,” since we were not able to calculate the energetic cost of running and pecking in terms of joules/calories. It is still possible that running and pecks are energetically very cheap and that the overt investments found in this study do not cause a negative energetic budget. Precise measurements of physical expenditures for running and pecking actions are needed.
Excessive foraging efforts found in this study might also lead to impulsive choices. Amita et al. (2010) reported that repeated experience of competitive foraging for a few days resulted in a higher level of choice impulsivity, though the chicks were solitarily tested in an inter-temporal choice paradigm. On the other hand, the impulsivity did not change instantaneously when the chicks were tested in competition (Amita and Matsushima, unpublished); the increase in impulsivity was observed even when there was no actual food competition, similar to our results. It remains to be determined whether the visual perception of competitive individuals directly caused the impulsivity or whether the excessive work investments secondarily caused the impulsivity. Further studies are required.
Ecological accounts of synchronized running
The synchronized running observed in this study (Experiments 1 and 2) may be explained by “scramble kleptoparasitism” in behavioral ecology. Kleptoparasitism refers to parasitical exploitation of food that other foragers’ efforts have made available (Giraldeau and Caraco, 2000). Of several variations, scramble kleptoparasitism specifically refers to the simultaneous exploitation of a sharable resource by multiple competitors with little or no aggression. This foraging behavior has also been called “social facilitation” (Curio, 1976). Barnard and Sibly (1981) regarded interactions between kleptoparasitically foraging individuals as “producer/scrounger” relationships, or a pair of alternative strategies.
It is possible that chicks running together acted as producer and scrounger, the one leading acted as a producer and the other following acted as a scrounger. In this study, we found that some individuals behaved predominantly as followers; e.g., in the bottom record of Figure 4, the purple-colored chick tended to follow the green-colored chick. However, the tactics were not always fixed, and chicks often changed their position in reference to the other. Foraging competition did not influence the synchrony of running (Experiment 2, Figure 5, bottom), indicating that chicks did scramble kleptoparasitism due to some innate or developmental factors, rather than to immediate competition over food. In accordance with this, we often observed that a chick was attracted to its pair mate and stayed at the feeder, even though the subject chick had already gained a grain at that feeder (e.g., bottom traces in Figure 4). To reveal the direct cause of synchronization, more elaborate analysis of running synchrony is needed.
The synchronization may also be an adaptive response to predation risk. Hamilton (1971) points out that predation could lead to the evolution of gregarious behavior by considering that predators habitually approach from outside of the herd. Furthermore, gregariousness itself “dilutes” predation risk for any particular individuals (Foster and Treherne, 1981). Highly synchronized runs observed in our study may have resulted from the gregarious instincts in chicks. It is therefore quite interesting to examine if chicks under predation pressure could run in even higher level of synchronization.
Implications for neural mechanisms of social facilitation
In the neuroscience of decision-making, relevant brain regions and neurotransmitters/neuromodulators critical for “effort cost” (such as pressing a lever or climbing a mesh barrier to obtain food pellets) have been intensively explored (Walton et al., 2006; Floresco et al., 2008a). Several brain regions are reported to cause a work cost aversion, meaning a bias away from the costly option (e.g., climbing mesh barrier) to obtain a larger food; i.e., the anterior cingulate cortex (Rudebeck et al., 2006a), the neural pathways between the anterior cingulate cortex and amygdala, and the amygdala itself (Floresco and Ghods-Sharifi, 2007). Systemic administration of dopamine antagonists (Denk et al., 2005; Floresco et al., 2008b) also induced the same effect. Since the anterior cingulate cortex and amygdala are thought to be involved in social behaviors (Rosvold et al., 1954; Rudebeck et al., 2006b), these regions might play a critical role in social influences of behavior by conspecifics. However, no studies have so far integrated the neuroscience of economical decision-making and the behavioral ecology of social foraging. Our next goal is therefore to clarify the neural mechanisms that underlie the social influences on work investments.
Conclusion
When viewed from behavioral economics and ecology, social facilitation can be characterized by increased foraging efforts and synchronization among individuals. The facilitation occurs immediately by visual perception of other individuals, rather than the accompanying food competition. The increased efforts occur not only in the approaching to food resource (running) but also in the handling food (pecking). Other factors than the gain rate should be considered, such as minimizing the starvation risk or adaptation to predation pressure.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This study was supported by grant-in-aid for scientific research to Toshiya Matsushima from the Japanese Society for the Promotion of Sciences (#22570070), as well as that for Innovative Area and from the Japanese Ministry of Education, Culture, Sports, Science, and Technology (The study on the neural dynamics for understanding communication in terms of complex hetero systems; #22120502). We would like to express our gratitude to anonymous referees, who patiently gave us detailed, generous, and critical comments on our initial manuscript.
Appendix
Statistical analysis using generalized linear mixed model
In Experiment 1 and 2, we focused on running distance and total time in which both chicks stayed in the same end of the maze (i.e., numerator of synchrony index) as response variables. In Experiment 3, we focused on number of pecks, number of gained grains, running distance, and velocity as response variables.
We assumed a Poisson distribution for the error structure of the data of running distance, number of pecks, and number of gained grains, considering that they were all non-negative values. Λ(X) (>0) was thus approximated by a Poisson function (log link function) as
| (1) |
On the other hand, we assumed a binomial distribution for the error structure of the data of total time in which both chicks stayed in the same end of the maze, since the time was calculated by the number of video frames and all frames were fallen into either “same end” or “different end” category. Synchrony index = Q(X) (∈ [0, 1]) was thus approximated by a logistic function (logit link function) as
| (2) |
in which a predictor X was linearly given as a weighed sum of explanatory variables.
Experiment 1
| (3) |
Day (variable = 1, 2, 3, 4, or 5) denotes experimental days. Coefficient β1 indicates how the day contributes to running distance or synchrony index. A positive value of estimated β1 thus suggests that the running distance increases as the days elapses.
Maze (categorical variable) denotes foraging condition in the maze (i.e., single or paired). Coefficient β2 indicates how paired foraging in the maze contributes to the response variables. A negative value of estimated β2 suggests that single chicks in the maze ran/synchronized less than paired chicks in the maze.
Cage (categorical variable) denotes foraging condition in the cage when the main diet food was supplied (i.e., single or paired). Coefficient β2 indicates how paired foraging in the cage contributes to the response variables. A negative value of estimated β2 suggests that runs by single chicks in the cage ran/synchronized less than paired chicks in the cage.
Experiment 2
| (4) |
Maze (categorical variable) denotes the type of wall in the maze (i.e., transparent or opaque). Coefficient γ2 indicates how visual perception contributes to the response variables. A negative value of estimated γ2 suggests that chicks mutually invisible ran/synchronized less than chicks mutually visible.
Feeder (categorical variable) denotes whether the feeders were separated or shared. Coefficient γ3 indicates how the actual competition over food intake contributes to the response variables. A negative value of estimated γ3 suggests that the actual competition over food intake decreased running distance/synchrony less than chicks with no competition.
Experiment 3
| (5) |
Maze (categorical variable) denotes foraging condition in the maze (i.e., single or paired).
Feeder (numeric variable; 1, 2, 3, 4, and 5) denotes difficulty of food trays. Coefficient δ2 indicates how increasing difficulty of food trays contributes to the response variables. A positive value of estimated δ2 suggests that the more difficult the food tray was, the larger the response variable was.
Coefficient δ3 indicates how maze and feeder interact.
The intercepts (β0, γ0, and δ0) denote bias at the population level. The random intercept and the random slope (against day and feeder in Experiment 1, 2, and 3, respectively) for each individual (i) was denoted by rii and ris, representing noise that was not experimentally controlled; Gaussian distribution with mean = 0 was assumed.
In Experiment 1, AICs were compared among eight models with different combination of parameters; (i) null model (β0), (ii) day model (β0, β1), (iii) maze model (β1, β2), (iv) cage model (β1, β3), (v) day-maze model (β0, β1, β2), (vi) day-cage model (β0, β1, β3), (vii) maze-cage model (β0, β, β3) and (viii) day-maze-cage model (β0, β1, β2, β3).
Similarly in Experiment 2, AICs were compared among the following eight models; (i) null model (γ0), (ii) day model (γ0, γ1), (iii) maze model (γ0, γ2), (iv) feeder model (γ0, γ3), (v) day–maze model (γ0, γ1, γ2), (vi) day–feeder model (γ0, γ1, γ3), (vii) maze–feeder model (γ0, γ1, γ3), and (viii) day–maze-feeder model (γ0, γ1, γ2, γ3).
In Experiment 3, AICs were compared among the following five models; (i) null model (δ0), (ii) maze model (δ0, δ1), (iii) feeder model (δ1, δ2), (iv) maze–feeder model (δ0, δ1, δ2), and (v) maze–feeder-and-interaction model (δ0, δ1, δ2, δ3).
Most likely values of the intercepts and coefficients (β0, β1, β2, β3, γ0, γ1, γ2, γ3, and δ0, δ1, δ2, δ3) were estimated on the basis of the choice data by using R (version 2.12.0; R Development Core Team, 2010) and the lme4 package (version 0.999375-37; Bates and Sarkar, 2010). AICs were given as a sum of the deviance plus two times the number of parameters. The AICs and the parameter estimates are shown in Tables A1–A8 in Appendix for Experiment 1, 2, and 3, respectively. For interpretations of the statistic computations, see the main text.
Table A1.
The day–maze model yielded the smallest AIC.
| Models | AIC | Estimated coefficients of variables | ||||
|---|---|---|---|---|---|---|
| β0 (Intercept) | β1 (Day) | β2 (Maze) | β3 (Cage) | |||
| 1 | [β0, β1, β2] | 14794 | 9.475460 | 0.033304 | −0.347460 | – |
| 2 | [β0, β1, β2, β3] | 14794 | 9.442871 | 0.033308 | −0.347421 | (0.065203) |
| 3 | [β0, β2] | 14812 | 9.47573 | – | −0.34738 | – |
| 4 | [β0, β2, β3] | 14813 | 9.44303 | – | −0.34736 | (0.06539) |
| 5 | [β0, β1] | 14822 | 9.301773 | 0.033290 | – | – |
| 6 | [β0, β1, β3] | 14823 | 9.269186 | 0.033299 | – | (0.065212) |
| 7 | [β0] | 14841 | 9.30201 | – | – | – |
| 8 | [β0, β3] | 14842 | 9.26935 | – | – | (0.06536) |
AICs for running distance (Experiment 1). AICs and estimated coefficients of variables were calculated for 8 models designed for running distance in Experiment 1. The models are sorted in ascending order of AIC. Coefficients in parentheses represents that the 95% confidence interval (CI) of the estimate included 0. The model [β0, β1, β2] indicates that both day and maze had significant effects, whereas the same-AIC. Model [β0, β1, β2, β3] indicates that cage was not reliable for its coefficient. Most-likely fitting formulas are indicated below:
Single foraging in the maze: X = 9.128 + (0.033304 + ris) × day + rii.
Paired foraging in the maze: X = 9.475460 + (0.033304 + ris) × day + rii.
Table A2.
The day–maze model yielded the smallest AIC.
| Models | AIC | Estimated coefficients of variables | ||||
|---|---|---|---|---|---|---|
| β0 (Intercept) | β1 (Day) | β2 (Maze) | β3 (Cage) | |||
| 1 | [β0, β1, β2] | 4834 | 0.85135 | −0.05698 | −0.83931 | – |
| 2 | [β0, β1, β2, β3] | 4835 | 0.89544 | −0.05698 | −0.83924 | (−0.08825) |
| 3 | [β0, β2] | 4839 | 0.85106 | – | −0.83970 | – |
| 4 | [β0, β2, β3] | 4840 | 0.89519 | – | −0.83963 | (−0.08833) |
| 5 | [β0, β1] | 4862 | 0.43171 | −0.05700 | – | – |
| 6 | [β0, β1, β3] | 4864 | 0.47585 | −0.05698 | – | (−0.08837) |
| 7 | [β0] | 4867 | 0.4311 | – | – | – |
| 8 | [β0, β3] | 4869 | 0.47541 | – | – | (−0.08846) |
AICs for synchrony index (Experiment 1). AICs and estimated coefficients of variables were calculated for 8 models designed for synchrony index (proportion of the number of video flames in which chicks were in the same end of the maze) in Experiment 1. The model [β0, β1, β2] indicates that both day and maze had significant effects, whereas the second-smallest-AIC model [β0, β1, β2, β3] indicates that cage was not reliable for its coefficient.
Single foraging in the maze: X = 0.01204 + (−0.05698 + ris) × day + rii.
Paired foraging in the maze: X = 0.85135 + (−0.05698 + ris) × day + rii.
Table A3.
The day–maze model yielded the smallest AIC.
| Models | AIC | Estimated coefficients of variables | ||||
|---|---|---|---|---|---|---|
| γ0 (Intercept) | γ1 (Day) | γ2 (Maze) | γ3 (Feeder) | |||
| 1 | [γ0, γ1, γ2] | 16191 | 9.320326 | 0.060972 | −0.276690 | – |
| 2 | [γ0, γ1, γ2, γ3] | 16192 | 9.270098 | 0.060971 | −0.226365 | (0.110372) |
| 3 | [γ0, γ1, γ3] | 16196 | 9.128636 | 0.060968 | – | 0.251822 |
| 4 | [γ0, γ1] | 16201 | 9.188624 | 0.060951 | – | – |
| 5 | [γ0, γ2] | 16228 | 9.32036 | – | −0.27610 | – |
| 6 | [γ0, γ2, γ3] | 16229 | 9.27008 | – | −0.22573 | (0.11048) |
| 7 | [γ0, γ3] | 16233 | 9.12902 | – | – | 0.25154 |
| 8 | [γ0] | 16237 | 9.18896 | – | – | – |
AICs for running distance (Experiment 2). AICs and estimated coefficients of variables were calculated for 8 models designed for running distance in Experiment 2. The model [γ0, γ1, γ2] indicates that both day and maze had significant effects, whereas the second-smallest-AIC model [γ0, γ1, γ2, γ3] indicates that feeder was not reliable for its coefficient.
Opaque wall: X = 9.043636 + (0.060972 + ris) × day + rii.
Transparent wall: X = 9.320326 + (0.060972 + ris) × day + rii.
Table A4.
The day–maze model yielded the smallest AIC, but the effect of day was not reliable for its coefficient.
| Models | AIC | Estimated coefficients of variables | ||||
|---|---|---|---|---|---|---|
| γ0 (Intercept) | γ1 (Day) | γ2 (Maze) | γ3 (Feeder) | |||
| 1 | [γ0, γ1, γ2] | 14088 | 1.54956 | (0.04025) | −1.29326 | – |
| 2 | [γ0, γ2] | 14089 | 1.5501 | – | −1.2934 | – |
| 3 | [γ0, γ1, γ2, γ3] | 14089 | 1.42322 | (0.04025) | −1.16667 | (0.27757) |
| 4 | [γ0, γ2, γ3] | 14090 | 1.4236 | – | −1.1667 | (0.2782) |
| 5 | [γ0, γ3] | 14105 | 0.6943 | – | – | 1.0073 |
| 6 | [γ0, γ1, γ3] | 14105 | 0.69392 | (0.04026) | – | 1.00706 |
| 7 | [γ0, γ1] | 14110 | 0.93383 | (0.04022) | – | – |
| 8 | [γ0] | 14111 | 0.9340 | – | – | – |
AICs for synchrony index (Experiment 2). AICs and estimated coefficients of variables were calculated for 8 models designed for synchrony index in Experiment 2. The model [γ0, γ1, γ2] indicates that day had insignificant effects.
Opaque wall: X = 0.2567 + (0.04025 + ris) × day + rii.
Transparent wall: X = 1.5501 + (0.04025 + ris) × day + rii.
Table A5.
The maze–feeder-and-interaction model yielded the smallest AIC.
| Models | AIC | Estimated coefficients of variables | ||||
|---|---|---|---|---|---|---|
| δ0 (Intercept) | δ1 (Maze) | δ2 (Feeder) | δ3 (Maze:feeder) | |||
| 1 | [δ0, δ1, δ2, δ3] | 434.8 | 2.67886 | (0.04795) | 0.39100 | −0.07668 |
| 2 | [δ0, δ2] | 437.7 | 2.69015 | – | 0.35387 | – |
| 3 | [δ0, δ1, δ2] | 439.4 | 2.74001 | (−0.09332) | 0.35381 | – |
| 4 | [δ0] | 490.3 | 2.6991 | – | – | – |
| 5 | [δ0, δ1] | 492.3 | 2.67413 | (0.04772) | – | – |
AICs for the number of pecks (Experiment 3). AICs and estimated coefficients of variables were calculated for 5 models designed for number of pecks in Experiment 3. The model [δ0, δ1, δ2, δ3] indicates that maze per se had no effects in the absence of feeder.
Single: X = 2.72681 + (0.31432 + ris) × feeder + rii.
Paired: X = 2.67886 + (0.39100 + ris) × feeder + rii.
Table A6.
The feeder model yielded the smallest AIC.
| Models | AIC | Estimated coefficients of variables | ||||
|---|---|---|---|---|---|---|
| δ0 (Intercept) | δ1 (Maze) | δ2 (Feeder) | δ3 (Maze:feeder) | |||
| 1 | [δ0, δ2] | 42.02 | 2.48704 | – | −0.07750 | |
| 2 | [δ0, δ1, δ2] | 44.01 | 2.483046 | (0.007534) | −0.077502 | |
| 3 | [δ0, δ1, δ2, δ3] | 45.98 | 2.494080 | (−0.013251) | −0.081384 | (0.007306) |
| 4 | [δ0] | 49.77 | 2.26054 | – | – | |
| 5 | [δ0, δ1] | 51.76 | 2.25654 | (0.00753) | – | |
AICs for the number of gained grains (Experiment 3). AICs and estimated coefficients of variables were calculated for 5 models designed for total gain of grains in Experiment 3. The model [δ0, δ2] indicates that only feeder had significant effects.
X = 2.48704 + (−0.07750 + ris) × feeder + rii.
Table A7.
The maze–feeder-interaction model yielded the smallest AIC.
| Models | AIC | Estimated coefficients of variables | ||||
|---|---|---|---|---|---|---|
| δ0 (Intercept) | δ1 (Maze) | δ2 (Feeder) | δ3 (Maze:feeder) | |||
| 1 | [δ0, δ1, δ2, δ3] | 1640 | 8.41344 | −0.34862 | −0.07784 | 0.04685 |
| 2 | [δ0, δ1, δ2] | 1643 | 8.41253 | −0.34666 | −0.05309 | – |
| 3 | [δ0, δ2] | 1650 | 8.22898 | – | −0.05308 | – |
| 4 | [δ0, δ1] | 1655 | 8.41218 | −0.34806 | – | – |
| 5 | [δ0] | 1662 | 8.22792 | – | – | – |
AICs for running distance (Experiment 3). AICs and estimated coefficients of variables were calculated for five models designed for running distance in Experiment 3. The model [δ0, δ1, δ2, δ3] indicates that maze, feeder and their interaction had significant effects.
Single: X = 8.06482 + (−0.03099 + ris) × feeder + rii.
Paired: X = 8.41344 + (−0.07784 + ris) × feeder + rii.
Table A8.
The maze model yielded the smallest AIC.
| Models | AIC | Estimated coefficients of variables | ||||
|---|---|---|---|---|---|---|
| δ0 (Intercept) | δ1 (Maze) | δ2 (Feeder) | δ3 (Maze:feeder) | |||
| 1 | [δ0, δ1] | 77.45 | 3.65249 | −0.45497 | – | – |
| 2 | [δ0, δ1, δ2] | 77.58 | 3.70838 | −0.45496 | (−0.01875) | – |
| 3 | [δ0, δ1, δ2, δ3] | 78.84 | 3.73782 | −0.52555 | (−0.02872) | (0.02379) |
| 4 | [δ0] | 93.85 | 3.41092 | – | – | – |
| 5 | [δ0, δ2] | 93.98 | 3.46683 | – | (−0.01875) | – |
AICs for velocity (Experiment 3). AICs and estimated coefficients of variables were calculated for 5 models designed for running velocity in Experiment 3. The model [δ0, δ1] indicates that only maze had significant effects.
Single: X = 3.19752 + ris × feeder + rii.
Paired: X = 3.65249 + ris × feeder + rii.
In all tables, models are sorted in the order of AICs. Hyphen means that the model does not include the parameter. Coefficients in parentheses represents that the 95% confidence interval (CI) of the estimate included 0. CI was not considered for the intercepts (β0, γ0, and δ0).
References
- Allport F. H. (1920). The influence of the group upon association and thought. J. Exp. Psychol. 3, 159–182 10.1037/h0067891 [DOI] [Google Scholar]
- Amita H., Kawamori A., Matsushima T. (2010). Social influences of competition on impulsive choices in domestic chicks. Biol. Lett. 6, 183–186 10.1098/rsbl.2009.0748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aoki N., Suzuki R., Izawa E.-I., Csillag A., Matsushima T. (2006a). Localized lesions of ventral striatum, but not arcopallium, enhanced impulsiveness in choices based on anticipated spatial proximity of food rewards in domestic chicks. Behav. Brain. Res. 168, 1–12 10.1016/j.bbr.2005.10.002 [DOI] [PubMed] [Google Scholar]
- Aoki N., Csillag A., Matsushima T. (2006b). Localized lesions of arcopallium intermedium of the lateral forebrain caused a handling-cost aversion in the domestic chick performing a binary choice task. Eur. J. Neurosci. 24, 2314–2326 10.1111/j.1460-9568.2006.05090.x [DOI] [PubMed] [Google Scholar]
- Barnard C. J., Sibly R. M. (1981). Producers and scroungers: a general model and its application to captive flocks of house sparrows. Anim. Behav. 29, 543–550 10.1016/S0003-3472(81)80117-0 [DOI] [Google Scholar]
- Bélisle M. (1998). Foraging group size: models and a test with jaegers kleptoparasitizing terns. Ecology 79, 1922–1938 10.2307/176699 [DOI] [Google Scholar]
- Blascovich J., Mendes W. B., Hunter S. B., Salomon K. (1999). Social “facilitation” as challenge and threat. J. Pers. Soc. Psychol. 77, 68–77 10.1037/0022-3514.77.1.68 [DOI] [PubMed] [Google Scholar]
- Caraco T., Martindale S., Whittam T. S. (1980). An empirical demonstration of risk-sensitive foraging preferences. Anim. Behav. 28, 820–830 10.1016/S0003-3472(80)80142-4 [DOI] [Google Scholar]
- Charnov E. L. (1976). Optimal foraging: attack strategy of a mantid. Am. Nat. 110, 141–151 10.1086/283062 [DOI] [Google Scholar]
- Chen S. C. (1937). Social modification of the activity of ants in nest-building. Physiol. Zoöl. 10, 420–436 [Google Scholar]
- Curio E. (1976). The Ethology of Predation. New York: Springer-Verlag [Google Scholar]
- Denk F., Walton M. E., Jennings K. A., Sharp T., Rushworth M. F., Bannerman D. M. (2005). Differential involvement of serotonin and dopamine systems in cost-benefit decisions about delay or effort. Psychopharmacology (Berl) 179, 587–596 10.1007/s00213-004-2059-4 [DOI] [PubMed] [Google Scholar]
- Floresco S. B., Ghods-Sharifi S. (2007). Amygdala-prefrontal cortical circuitry regulates effort-based decision making. Cereb. Cortex 17, 251–260 10.1093/cercor/bhj143 [DOI] [PubMed] [Google Scholar]
- Floresco S. B., Onge J. R., Ghods-Sharifi S., Winstanley C. A. (2008a). Cortico-limbic-striatal circuits subserving different forms of cost-benefit decision making. Cogn. Affect. Behav. Neurosci. 8, 375–389 10.3758/CABN.8.4.375 [DOI] [PubMed] [Google Scholar]
- Floresco S. B., Tse M. T. L., Ghods-Sharifi S. (2008b). Dopaminergic and glutamatergic regulation of effort- and delay-based decision making. Neuropsychopharmacology 33, 1966–1979 10.1038/sj.npp.1301565 [DOI] [PubMed] [Google Scholar]
- Foster W. A., Treherne J. E. (1981). Evidence for the dilution effect in the selfish herd from fish predation on a marine insect. Nature 293, 466–467 10.1038/293466a0 [DOI] [Google Scholar]
- Gates M. F., Allee W. C. (1933). Conditioned behavior of isolated and grouped cockroaches on a simple maze. J. Comp. Psychol. 15, 331–358 10.1037/h0073695 [DOI] [Google Scholar]
- Giraldeau L.-A., Caraco T. (2000). Social Foraging Theory. Princeton: Princeton University Press [Google Scholar]
- Glickman S. E., Zabel C. J., Yoerg S. I., Weldele M. L., Drea C. M., Frank L. G. (1997). Social facilitation, affiliation, and dominance in the social life of spotted hyenas. Ann. N. Y. Acad. Sci. 807, 175–184 10.1111/j.1749-6632.1997.tb51919.x [DOI] [PubMed] [Google Scholar]
- Hamilton W. D. (1971). Geometry for the selfish herd. J. Theor. Biol. 31, 295–311 10.1016/0022-5193(71)90189-5 [DOI] [PubMed] [Google Scholar]
- Izawa E.-I., Zachar G., Yanagihara S., Matsushima T. (2003). Localized lesion of caudal part of lobusparolfactorius caused impulsive choice in domestic chick: evolutionary conserved function of ventral striatum. J. Neurosci. 23, 1894–1902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawamori A., Matsushima T. (2010). Subjective value of risky foods for individual domestic chicks: a hierarchical Bayesian model. Anim. Cogn. 13, 431–441 10.1007/s10071-009-0293-1 [DOI] [PubMed] [Google Scholar]
- Koops M., Giraldeau L.-A. (1996). Producer-scrounger foraging games in starlings: a test of mean-maximizing and risk-minimizing foraging models. Anim. Behav. 51, 773–783 10.1006/anbe.1996.0082 [DOI] [Google Scholar]
- Matsushima T., Izawa E.-I., Aoki N., Yanagihara S. (2003). The mind through chick eyes: memory, cognition and anticipation. Zool. Sci. 20, 395–408 10.2108/zsj.20.395 [DOI] [PubMed] [Google Scholar]
- Matsushima T., Kawamori A., Bem-Sojka T. (2008). Neuro-economics in chicks: foraging choices based on amount, delay and cost. Brain Res. Bull. 76, 245–252 10.1016/j.brainresbull.2008.02.007 [DOI] [PubMed] [Google Scholar]
- Rosvold H. E., Mirsky A. F., Pribram K. H. (1954). Influence of amygdalectomy on social behavior in monkeys. J. Comp. Physiol. Psychol. 47, 173–178 10.1037/h0058870 [DOI] [PubMed] [Google Scholar]
- Rudebeck P. H., Walton M. E., Smyth A. N., Bannerman D. M., Rushworth M. F. (2006a). Separate neural pathways process different decision costs. Nat. Neurosci. 9, 1161–1168 10.1038/nn1756 [DOI] [PubMed] [Google Scholar]
- Rudebeck P. H., Buckley M. J., Walton M. E., Rushworth M. F. S. (2006b). A role for the macaque anterior cingulate gyrus in social valuation. Science 313, 1310–1312 10.1126/science.1128197 [DOI] [PubMed] [Google Scholar]
- Tolman C. W. (1967). The varieties of social stimulation in the feeding behaviour of domestic chicks. Behaviour 30, 275–286 10.1163/156853968X00351 [DOI] [PubMed] [Google Scholar]
- Tolman C. W., Wilson G. F. (1965). Social feeding in domestic chicks. Anim. Behav. 13, 134–142 10.1016/0003-3472(65)90083-7 [DOI] [PubMed] [Google Scholar]
- Triplett N. (1898). The dynamogenic factors in pacemaking and competition. Am. J. Psychol. 9, 507–533 10.2307/1412188 [DOI] [Google Scholar]
- Walton M. E., Kennerley S. W., Bannerman D. M., Phillips P. E., Rushworth M. F. (2006). Weighing up the benefits of work: behavioral and neural analyses of effort-related decision making. Neural Netw. 19, 1302–1314 10.1016/j.neunet.2006.03.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zajonc R. B. (1965). Social facilitation. Science 149, 269–274 10.1126/science.149.3681.269 [DOI] [PubMed] [Google Scholar]
References
- Bates D. M., Sarkar D. (2010). lme4: Linear Mixed-effects Models Using S4 classes, R Package Version 0.999375-37. Available at: http://cran.r-project.org/web/packages/lme4/index.html
- R Development Core Team (2010). R version 2.12.0.: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing [Google Scholar]