A phenomenological mixture model for biosynthesis and linking of cartilage extracellular matrix in scaffolds seeded with chondrocytes

Abstract

A phenomenological mixture model is presented for interactions between biosynthesis of extracellular matrix (ECM) constituents and ECM linking in a scaffold seeded with chondrocytes. A system of three ordinary differential equations for average apparent densities of unlinked ECM, linked ECM and scaffold is developed along with associated initial conditions for scaffold material properties. Equations for unlinked ECM synthesis and ECM linking include an inhibitory mechanism where associated rates decrease as unlinked ECM concentration in the interstitial fluid increases. Linking rates are proposed to depend on average porosity in the evolving tissue construct. The resulting initial value problem contains nine independent parameters that account for scaffold biomaterial properties and interacting mechanisms in the engineered system. Effects of parameter variations on model variables are analyzed relative to a baseline case with emphasis on the evolution of solid phase apparent density, which is often correlated with the compressive elastic modulus of the tissue construct. The new model provides an additional quantitative framework for assessing and optimizing the design of engineered cell-scaffold systems and guiding strategies for articular cartilage tissue engineering.

1 Introduction

Articular cartilage is a hydrated soft biological tissue lining bone surfaces in diarthrodial joints such as the knee, shoulder and hip. Within these joints, articular cartilage serves as a low-friction, load-bearing material that facilitates joint motion over decades of life (Mow et al. 1992). While primarily comprised of interstitial water (≈ 75–80% by volume), this fluid phase saturates a solid extracellular matrix (ECM) that arises from a cross-linked network of predominantly type-II collagen fibers and proteoglycan macromolecules. Cartilage physiology is regulated by a single population of specialized cells called chondrocytes that are sparsely distributed within the ECM (Stockwell 1979) and maintain a state of homeostasis in healthy tissue. ECM degeneration is primarily associated with osteoarthritis which can lead to complete degradation of cartilage surfaces necessitating total joint replacement.

Chondrocytes can be utilized to regenerate cartilage via tissue engineering approaches in which these cells are seeded in biocompatible and degradable polymer or hydrogel scaffolds. In such systems, biosynthetic activity of the cells in response to their non-native environment results in regeneration and accumulation of ECM constituents concurrent with degradation of the surrounding scaffold material. Mathematical models of tissue regeneration provide quantitative frameworks for characterizing the many diverse factors controlling the dynamic evolution of these biomaterial constructs—see, e.g. Sengers et al. (2007) for a review of modeling approaches in cell-scaffold tissue constructs.

Several cartilage regeneration models are based on systems of partial differential equations (PDEs) and account for coupling between reactive and spatial phenomena. Obradovic et al. (2000) developed a two-dimensional-engineered cartilage model for a rotating bioreactor, with local oxygen and glycosaminoglycan (GAG) concentration as the two primary variables. A reaction-diffusion PDE system was employed with GAG synthesis rate depending on local oxygen concentration. Other spatial models delineate ECM into one soluble and one bound matrix component and include a one-dimensional reaction-diffusion model (Dimicco and Sah 2003), a one-dimensional reaction-diffusion-advection model in the local environment of a spherical chondrocyte (Trewenack et al. 2009), a two-dimensional reaction-diffusion finite element model (Sengers et al. 2004), and a reaction-diffusion model with a moving boundary accounting for cell growth in a diffusive and degrading polymer scaffold (Galban and Locke 1997). Recently, Ateshian et al. (2009) formulated a continuum mixture model for tissue growth accounting for cell division with increased osmolyte content, as well as effects of increasing fixed charge density due to proteoglycan accumulation.

Wilson et al. (2002) adopted a more elementary phenomenological approach in which spatial effects were not explicitly modeled, resulting in an ordinary differential equation (ODE) system for evolution of model variables. A key feature of their model was the incorporation of an inhibitory mechanism that is known to slow down the rate of GAG synthesis as ECM accumulation progresses in a cell-biomaterial system (Buschmann et al. 1992; Handley and Lowther 1977). The resulting two-variable model for accumulating ECM mass and degrading scaffold mass admitted an explicit analytical solution, thus facilitating application to analysis of data from multiple cartilage regeneration studies (Wilson et al. 2002). This model was later extended to include a stochastic component accounting for effects of growth factors (Saha et al. 2004). Other modeling studies have also used ODE systems to model cell growth in polymer scaffolds, e.g. Vunjak-Novakovic et al. (1998).

The goal of this study was to extend the two-variable phenomenological model of Wilson et al. (2002) for cartilage regeneration in chondrocyte-seeded scaffolds to account for additional coupled mechanisms among primary variables in the evolving system. Specifically, cell-synthesized ECM is delineated into contributions from unlinked (soluble) and linked (bound) components. A phenomenological model is developed with three dependent variables that represent average values of apparent densities for three constituents: unlinked ECM, linked ECM and scaffold. A model for linking rates that transform unlinked ECM into linked ECM is proposed to depend on the average porosity in the evolving tissue construct. The use of mixture variables facilitates delineation of experimental outcome measures such as dry mass, wet weight, and volume fractions of the time-varying system constituents. Effects of scaffold properties and interaction mechanisms, represented via parameters in the model, are analyzed in the context of a baseline case calibrated to yield a steady-state solid volume fraction that is representative of healthy, mature articular cartilage.

2 Model development

Previously, Wilson et al. (2002) developed a two-variable phenomenological model for the dynamic composition of engineered cartilage. They modeled evolution of the total ECM dry mass [ECM](t) and the scaffold dry mass [Scaffold](t) using the equations:

$$\frac{\text{d}[\text{ECM}]}{\text{d}t}=k_1({[\text{ECM}]}_{\text{SS}}-[\text{ECM}]),$$ (1)

$$\frac{\text{d}[\text{Scaffold}]}{\text{d}t}=-k_2[\text{Scaffold}].$$ (2)

In Eqs. (1)–(2), the three adjustable parameters are the two rate constants k₁, k₂ and the steady-state ECM mass [ECM]_SS. An attractive feature of this model is that the two differential equations are linear and uncoupled, enabling formulation of explicit solutions for [ECM](t) and [Scaffold](t) via integration.

However, the model does not capture interactions between newly synthesized ECM and the degrading scaffold. In particular, these interactions result in the transformation of free (unbound) ECM constituents, dissolved in the interstitial fluid, into linked ECM that contributes to increasing solid-phase volume in the fluid-saturated mixture. The associated increase in apparent density of the solid phase often correlates to an increase in compressive stiffness, which is a key functional property of the engineered construct. In the following sections, an extended ODE model capturing these features is developed. Mixture variables are used due to their inherent capability to distinguish among the variety of variables that are commonly used to characterize the evolving tissue construct (e.g. dry mass, wet weight, porosity etc.).

2.1 Mixture formulation

The tissue construct is modeled as a fluid–solid mixture with mixture volume denoted by V [cm³]. The mixture is assumed to be saturated so that V = V^w+V^s, where V^w and V^s denote volumes of the fluid and solid phases, respectively. The average porosity of the construct is denoted by ϕ̄^w = V^w/V and the average solid volume fraction is denoted by ϕ̄^s = V^s/V, where

$${\overline{\varphi }}^{\text{w}}+{\overline{\varphi }}^{\text{s}}=1.$$ (3)

The bound solid phase of the mixture is delineated into three sub-phases that are linked ECM (LM), scaffold (Sc) and cells (C), i.e. V^s = V^LM + V^Sc + V^C. Unlinked ECM (UM) is idealized as a dilute solute within the interstitial fluid (V^UM ≈ 0). Consequently, the average solid volume fraction ϕ̄^s in the mixture is expressed as

$${\overline{\varphi }}^s={\overline{\varphi }}^{\text{LM}}+{\overline{\varphi }}^{\text{Sc}}+{\overline{\varphi }}^{\text{C}}.$$ (4)

2.2 Biosynthesis, degradation and linking

Motivated by Eq. (2), the degradation of total scaffold mass m^Sc[g] in the evolving system is modeled via the equation

$$\frac{\text{d}{m}^{\text{Sc}}}{\text{d}t}=-k_{\text{Sc}}{m}^{\text{Sc}},$$ (5)

where k_Sc [(days)⁻¹] is the scaffold degradation rate.

Mass production in the system is idealized to be limited to cell-regulated ECM biosynthesis (i.e. ϕ̄^C constant). ECM constituents are delineated into total unlinked ECM mass m^UM [g] and total linked ECM mass m^LM[g]. The following model for ECM biosynthesis is proposed based on an assumption of product inhibition regulated by cellular detection of unlinked ECM concentration in the interstitial fluid:

$$\frac{\text{d}}{\text{d}t}\left(m^{\text{UM}}+m^{\text{LM}}\right)=V^{\text{C}}{N}^{\ast }{\overline{\varphi }}^{\text{w}}{k}_{\text{UM}}\left({\overline{\rho }}_{\text{UM}}^{\text{w}}-\frac{m^{\text{UM}}}{V^{\text{w}}}\right),$$ (6)

where k_UM [(days mmol/mL)⁻¹] is the unlinked ECM synthesis rate. In Eq. (6), N ^*[mmol/mL] is a saturated nutrient concentration, based on the assumption that diffusive transport of small solutes in the construct is rapid relative to transport mechanisms of synthesized ECM constituents. Production of unlinked ECM is assumed to proceed until an average critical solute concentration ${\overline{\rho }}_{\text{UM}}^{\text{w}}[\text{g}/\text{mL}]$ is reached within the surrounding interstitial fluid.

Accumulation of linked ECM in the system is modeled, in a manner that is consistent with Eq. (6), via the equations

$$\begin{array}{l}\frac{\text{d}{m}^{\text{UM}}}{\text{d}t}=V^{\text{C}}{N}^{\ast }{\overline{\varphi }}^{\text{w}}{k}_{\text{UM}}\left({\overline{\rho }}_{\text{UM}}^{\text{w}}-\frac{m^{\text{UM}}}{V^{\text{w}}}\right)\\ -f({\overline{\varphi }}^{\text{s}})\left({\overline{\rho }}_{\text{UM}}^{\text{w}}-\frac{m^{\text{UM}}}{V^{\text{w}}}\right)m^{\text{UM}},\end{array}$$ (7)

$$\frac{\text{d}{m}^{\text{LM}}}{\text{d}t}=f({\overline{\varphi }}^{\text{s}})\left({\overline{\rho }}_{\text{UM}}^{\text{w}}-\frac{m^{\text{UM}}}{V^{\text{w}}}\right)m^{\text{UM}}.$$ (8)

The new term in these equations models the transformation of unlinked ECM into linked ECM. Specifically, ECM linking is assumed to be regulated by both product inhibition and a continuous set of linking rates f [(days g/mL)⁻¹] that depend on the time-varying average solid volume fraction ϕ̄^s in the construct. Linking rates in the system are modeled using a normal distribution

$$f({\overline{\varphi }}^{\text{s}})=k_{\text{UL}}{e}^{-\frac{{({\overline{\varphi }}^{\text{s}}-{\overline{\varphi }}_{\ast }^{\text{s}})}^2}{2{\sigma }^2}},$$ (9)

where k_UL[(days g/mL)⁻¹] is the maximum linking rate, occurring when ${\overline{\varphi }}^{\text{s}}={\overline{\varphi }}_{\ast }^{\text{s}}$. In Eq. (9), the parameters ${\overline{\varphi }}_{\ast }^{\text{s}}$ and σ delineate regimes in which rates for formation of linked ECM are enhanced or inhibited. At low solid volume fraction ϕ̄^s, linking is assumed to increase with increasing ϕ̄^s due to cell-scaffold biocompatibility (e.g. cell adhesion, promotion of ECM cross-linking, maintenance of cell phenotype). However, as ϕ̄^s increases past ${\overline{\varphi }}_{\ast }^{\text{s}}$, the linking rate is modeled as decreasing with decreasing average porosity (ϕ̄^w = 1 − ϕ̄^s), to capture adverse effects on the spatial distribution of unlinked ECM on the scale of the tissue construct.

2.3 Phenomenological mixture model

The evolving system is idealized as preserving its mixture volume, i.e. V (t) ≈ V (0) ≡ V. In continuum mixture models, the apparent density of phase α is defined over an infinitesimal mixture volume as ρ^α = dm^α/dV (e.g. Ateshian et al. 2009). In our phenomenological model, apparent densities are denoted by ρ̄^α[g/cm³] and interpreted as average values over the sample so that

$${\overline{\rho }}^{\alpha }=\frac{m^{\alpha }}{V}={\overline{\varphi }}^{\alpha }{\rho }_{\text{T}}^{\alpha },\alpha =\text{C},\text{LM},\text{Sc},$$ (10)

where ${\rho }_{\text{T}}^{\alpha }[\text{g}/{\text{cm}}^3]$ is the true density of constituent α and $0\le {\overline{\rho }}^{\alpha }\le {\rho }_{\text{T}}^{\alpha }$. Dividing each of Eqs. (5), (7) and (8) by the mixture volume V, and using Eq. (10) and the relation ϕ̄^w = V^w/V, the following phenomenological mixture model for evolution of (average) apparent densities is obtained:

$$\frac{\text{d}{\overline{\rho }}^{\text{Sc}}}{\text{d}t}=-k_{\text{Sc}}{\overline{\rho }}^{\text{Sc}},$$ (11)

$$\frac{\text{d}{\overline{\rho }}^{\text{UM}}}{\text{d}t}={\overline{\varphi }}^{\text{C}}{N}^{\ast }{\overline{\varphi }}^{\text{w}}{k}_{\text{UM}}\left({\overline{\rho }}_{\text{UM}}^{\text{w}}-\frac{{\overline{\rho }}^{\text{UM}}}{{\overline{\varphi }}^{\text{w}}}\right)-f({\overline{\varphi }}^{\text{s}})\left({\overline{\rho }}_{\text{UM}}^{\text{w}}-\frac{{\overline{\rho }}^{\text{UM}}}{{\overline{\varphi }}^{\text{w}}}\right){\overline{\rho }}^{\text{UM}},$$ (12)

$$\frac{\text{d}{\overline{\rho }}^{\text{LM}}}{\text{d}t}=f({\overline{\varphi }}^{\text{s}})\left({\overline{\rho }}_{\text{UM}}^{\text{w}}-\frac{{\overline{\rho }}^{\text{UM}}}{{\overline{\varphi }}^{\text{w}}}\right){\overline{\rho }}^{\text{UM}}.$$ (13)

In Eqs. (12)–(13), the average solid volume fraction is determined from Eq. (4) and Eq. (10) as

$${\overline{\varphi }}^{\text{s}}=\frac{{\overline{\rho }}^{\text{LM}}}{{\rho }_T^{\text{LM}}}+\frac{{\overline{\rho }}^{\text{Sc}}}{{\rho }_T^{\text{Sc}}}+{\overline{\varphi }}^{\text{C}}.$$ (14)

Assuming that ECM synthesis commences at t = 0, initial conditions are formulated in terms of the scaffold polymer true density and the average initial scaffold porosity ${\overline{\varphi }}_0^{Sc}$ as

$${\overline{\rho }}^{\text{Sc}}(0)={\overline{\varphi }}_0^{\text{Sc}}{\rho }_T^{\text{Sc}},{\overline{\rho }}^{\text{UM}}(0)=0,{\overline{\rho }}^{\text{LM}}(0)=0.$$ (15)

The model consisting of Eqs. (11)–(15) contains nine independent parameters. Parameters associated with the scaffold are its intrinsic biomaterial properties ( ${\overline{\varphi }}_0^{\text{Sc}},{\rho }_{\text{T}}^{\text{Sc}}$) and the scaffold degradation rate (k_Sc). Another important intrinsic biomaterial property of the solid phase is the true density of linked ECM ( ${\rho }_{\text{T}}^{\text{LM}}$). Since ϕ̄^C is assumed constant, the true density of the cells ( ${\rho }_{\text{T}}^{\text{C}}$) is not considered an independent parameter since its value does not affect the solution of the initial value problem. The remaining parameters capture properties of interactions among system constituents and are the peak linking rate (k_UL), the associated critical porosity parameters ( ${\overline{\varphi }}_{\ast }^{\text{s}}$, σ), and the critical unlinked ECM concentration ( ${\overline{\rho }}_{\text{UM}}^{\text{w}}$) that regulates product inhibition. Lastly, the rate controlling unlinked ECM synthesis is an independent parameter and, in the current model, is the product (ϕ̄^Ck_UM N ^*) of average cell volume fraction, saturated nutrient concentration and the unlinked ECM synthesis rate.

2.4 Steady-state analysis

Steady states of the model in Eqs. (11)–(15) in the limit as t → ∞ are now analyzed. First, it can be observed that Eq. (11) implies that ρ̄^Sc (∞) = 0. Equation (13) implies that either ρ̄^UM (∞) = 0 or ${\overline{\rho }}^{\text{UM}}(\infty )={\overline{\rho }}_{\text{UM}}^{\text{w}}{\overline{\varphi }}^{\text{w}}(\infty )$. In the former case, the last term in Eq. (12) is zero, but the first term on the right-hand side is positive unless ϕ̄^w (∞) = 0. Thus, provided that ϕ̄^w(t) > 0 in the system this case leads to a contradiction. The latter case then represents the steady state of the system since, when ${\overline{\rho }}^{\text{UM}}(\infty )={\overline{\rho }}_{\text{UM}}^{\text{w}}{\overline{\varphi }}^{\text{w}}(\infty )$, the right-hand side of Eq. (12) is zero.

Taken together, the model yields a steady state in which the scaffold is eliminated from the system, i.e. ρ̄^Sc (∞) = 0, and unlinked ECM apparent density is constant, i.e. ${\overline{\rho }}^{\text{UM}}(\infty )={\overline{\rho }}_{\text{UM}}^{\text{w}}{\overline{\varphi }}^{\text{w}}(\infty )$. In addition, the steady-state value of the apparent linked ECM density ρ̄^LM (∞) is an unknown in the sense that it is determined by solving the initial value problem.

Thus, the model captures dependence of the average apparent density of linked ECM on several interacting mechanisms in the evolving tissue construct. Furthermore, this apparent density is correlated with measurements of compressive stiffness, e.g. Young’s modulus, that are commonly used to assess functional viability of tissue- engineered cartilage constructs.

3 Results

Simulation of cartilage regeneration using Eqs. (11)–(15) is illustrated based on a set of baseline values of the model parameters. For the baseline case, scaffold parameters were chosen as ${\overline{\varphi }}_0^{\text{Sc}}=0.02,{\rho }_{\text{T}}^{\text{Sc}}=1.1\text{g}/{\text{cm}}^3$, and the degradation rate was fixed at k_Sc = 1/30 (days)⁻¹. The value for the average cell volume fraction was fixed at ϕ̄^C = 0.01, resulting in an initial porosity ${\overline{\varphi }}^{\text{w}}(0)=1-{\overline{\varphi }}_0^{\text{Sc}}-{\overline{\varphi }}^{\text{C}}=0.97$. For the purpose of evaluating the apparent cell density ρ̄^C, the true cell density was fixed as ${\overline{\rho }}_{\text{T}}^{\text{C}}=1.1\text{g}/{\text{cm}}^3$. The saturated nutrient concentration was fixed at N ^* = 0.1 mmol/mL. Based on reported values for the density of collagen dehydrated by organic solvents (Podrazky and Sedmerova 1966), the true density of linked ECM was set at the baseline value ${\rho }_{\text{T}}^{\text{LM}}=1.3\text{g}/{\text{cm}}^3$.

Baseline values of the remaining parameters, which govern interactions within the system, were calibrated to simulate idealized cartilage regeneration in which the average solid volume fraction ϕ̄^s after 180 days was roughly 20%. Specifically, the critical porosity parameters were chosen as ${\overline{\varphi }}_{\ast }^{\text{s}}=0.11$ and σ = 0.04, and the baseline values of the remaining parameters were k_UM = 70 (days mmol/mL)⁻¹, k_UL = k_UM/10 and ${\overline{\rho }}_{\text{UM}}^w=0.07\text{g}/\text{mL}$. For each fixed set of model parameters, solutions of the initial value problem in Eqs. (11)–(15) were evaluated in MATLAB using the routine “ode45”. Accuracy of the ODE numerical solutions was also verified for all cases presented using the alternate MATLAB routine “ode15s”.

3.1 Baseline case

The relation for dependence of ECM linking rates f in Eq. (9) on average solid volume fraction ϕ̄^s is first illustrated (Fig. 1). For scaffolds with very high porosity (ϕ̄^s (0) ≈ 0), rates of ECM linking are initially very slow, reflecting the property that lack of scaffold polymer structure may adversely affect linked ECM formation. As solid phase volume fractions increase up to the critical value ${\overline{\varphi }}_{\ast }^{\text{s}}$, formation of linked ECM in the system is enhanced until the peak linking rate k_UL is achieved. Once the critical value is exceeded, formation of linked ECM is inhibited due to decreasing porosity of the tissue construct that may adversely impact spatial distribution of linked ECM throughout the tissue construct. This linking rate model (Fig. 1) also prevents complete filling of pores with linked ECM since linking rates are effectively zero for solid volume fractions ϕ̄^s that are in excess of values typically associated with mature, healthy cartilage.

Fig. 1.

Linking rates for accumulation of linked ECM in the baseline case, based on Eq. (9) with ${\overline{\varphi }}_{\ast }^{\text{s}}=0.11$, σ = 0.04 and k_UL = 7 (days g/mL)⁻¹

For the baseline case, evolution of the apparent densities and volume fractions of linked ECM, scaffold and the solid phase is shown in Fig. 2. Accumulation rates for the solid-phase volume fraction are observed to be initially slow, but gradually increase until an inflection point is reached, after which time these rates decrease until a steady-state value is attained (Fig. 2b). The interactions affecting this response can be explained by examining the unlinked matrix concentration and ECM linking rate (Fig. 3). In particular, the system exhibits competing mechanisms of increasing and decreasing unlinked ECM concentrations due to accumulation via cellular biosynthesis and removal via linking, respectively. In the early regime (Fig. 3a, < ≈ 30 days), biosynthesis is dominant as ECM linking rates are low (Fig. 3b). In a second regime (≈ 30–55 days), the unlinked ECM concentration decreases (Fig. 3a) as ECM linking rates reach their peak value (Fig. 3b). In the final regime (> ≈ 55 days), the decreasing porosity of the construct causes inhibition of linked ECM accumulation (Fig. 3b), resulting in a monotonically increasing concentration of unlinked ECM to its steady-state value associated with product inhibition (Fig. 3a).

Fig. 2.

Evolution of solid-phase variables for the baseline case: a apparent densities ρ̄^α (α = Sc, LM, s), b volume fractions ϕ̄^α (α = Sc, LM, s)

Fig. 3.

Evolution of: a unlinked ECM concentration, b ECM linking rates, for the baseline case

3.2 Scaffold porosity

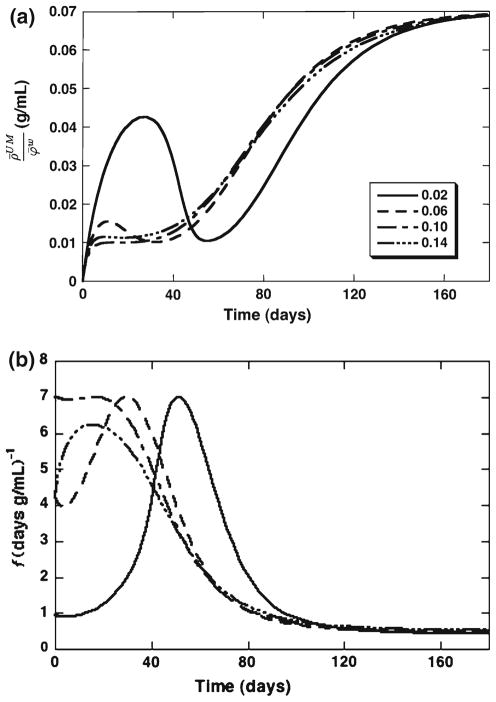
As ECM regeneration proceeds in the tissue construct, the apparent density of the (bound) solid phase ρ̄^s provides an outcome measure that is expected to correlate with construct stiffness. The effects of increasing the initial scaffold solid volume fraction ${\overline{\varphi }}_0^{\text{Sc}}$ on the evolution of this apparent density are illustrated in Fig. 4a. Due to the relatively small scaffold degradation time (≈ 70 days, Fig. 2b), there is higher sensitivity of ρ̄^s to scaffold porosity on the corresponding, earlier, time frame (Fig. 4a). Relationships between ρ̄^s and ${\overline{\varphi }}_0^{\text{Sc}}$ were also simulated at 60, 90 and 120 days and demonstrate nonlinear and non-monotonic trends (Fig. 4b). Examination of the unlinked matrix concentration and ECM linking rate indicates that increasing scaffold density decreases and then eliminates the early regime of slow linking attributed to very low scaffold density (Fig. 5b). Consequently, as ${\overline{\varphi }}_0^{\text{Sc}}$ is increased, the unlinked ECM concentration tends to a monotonic profile that increases toward its limiting value (Fig. 5a). Simulations that varied the true scaffold density ${\overline{\rho }}_T^{\text{Sc}}$ in the range 1.05–1.20 g/cm³ (with ${\overline{\varphi }}_0^{\text{Sc}}=0.02$) were also performed, but exhibited no significant changes in the model variables relative to the baseline case.

Fig. 4.

Effects of the initial scaffold porosity for the cases ${\overline{\varphi }}_0^{\text{Sc}}=0.02,0.06,0.10,0.14$: a solid-phase apparent density ρ̄^s (increasing curves) and scaffold apparent density ρ̄^Sc (decreasing curves), b solid-phase apparent density ρ̄^s versus initial scaffold porosity ${\overline{\varphi }}_0^{\text{Sc}}$ at 60, 90 and 120 days

Fig. 5.

Effects of the initial scaffold porosity for the cases ${\overline{\varphi }}_0^{Sc}=0.02,0.06,0.10,0.14$. Evolution of: a unlinked ECM concentration, b ECM linking rates

3.3 Interaction mechanisms

The model was also used to simulate effects of several interaction mechanisms within the cell-biomaterial system by perturbing the associated model parameters about their baseline values. Variation of the true linked ECM density ${\overline{\rho }}_{\text{T}}^{\text{LM}}$ in the range 1.2–1.4 g/cm³ (Fig. 6) demonstrated a strong, positive, correlation between increasing ${\overline{\rho }}_{\text{T}}^{\text{LM}}$ and the steady- state value of ρ̄^s (Fig. 6a). Porosity of the construct was mildly sensitive to ${\overline{\rho }}_{\text{T}}^{\text{LM}}$ for intermediate times (Fig. 6b) but did not substantially alter the character of the unlinked ECM concentration or the linking rates (Fig. 6c, d). Perturbations of the critical unlinked ECM concentration ${\overline{\rho }}_{\text{UM}}^{\text{w}}$ in the range 0.06–0.08 g/mL resulted in greater sensitivity of the model responses (Fig. 7). The steady-state values of both ρ̄^s and ϕ̄^s were positively correlated to increasing the value of ${\overline{\rho }}_{\text{UM}}^{\text{w}}$ (Fig. 7a, b). With decreasing values of ${\overline{\rho }}_{\text{UM}}^{\text{w}}$, both the initial regime of unlinked ECM synthesis and the subsequent regime with loss of unlinked ECM due to linking were prolonged (Fig. 7c), concurrent with delayed attainment of the peak ECM linking rate (Fig. 7d). The model exhibited high sensitivity to perturbations of the critical porosity parameter ${\overline{\varphi }}_{\ast }^{\text{s}}$ in the range 11.0–11.9% (Fig. 8). Increasing ${\overline{\varphi }}_{\ast }^{\text{s}}$ significantly delayed achievement of the peak ECM linking rate (Fig. 8d), past the time of complete scaffold degradation and until a sufficient amount of linked ECM accumulated in the system. This effect resulted in a concurrent delay in attainment of apparent solid-phase density and solid-phase volume fraction comparable to the baseline case (Fig. 8a, b). At the highest value ${\overline{\varphi }}_{\ast }^{\text{s}}=11.9\%$, ECM linking rates remained very low (Fig. 8d) and far away from the peak value over the duration of the simulation, resulting in poor accumulation of linked ECM (Fig. 8a, b).

Fig. 6.

Effects of perturbations to the true linked ECM density ${\overline{\rho }}_{\text{T}}^{LM}=1.3\text{g}/{\text{cm}}^3$ in the baseline case (solid) on the: a apparent density of the solid phase ρ̄^s, b solid-phase volume fraction ϕ̄^s, c unlinked ECM concentration ρ̄^UM/ϕ̄^w, d ECM linking rate f

Fig. 7.

Effects of perturbations to the critical unlinked ECM concentration ${\overline{\rho }}_{\text{UM}}^{\text{w}}=0.07\text{g}/\text{mL}$ in the baseline case (solid) on the: a apparent density of the solid phase ρ̄^s, b solid-phase volume fraction ϕ̄^s, c unlinked ECM concentration ρ̄^UM/ϕ̄^w, d ECM linking rate f

Fig. 8.

Effects of perturbations to the critical porosity parameter ${\overline{\varphi }}_{\ast }^{\text{s}}=0.11$ in the baseline case (solid) on the: a apparent density of the solid phase ρ̄^s, b solid-phase volume fraction ϕ̄^s, c unlinked ECM concentration ρ̄^UM/ϕ̄^w, d ECM linking rate f

4 Discussion

In this study, a phenomenological mixture model simulating interactions between ECM biosynthesis, scaffold degradation and ECM linking in articular cartilage engineered from scaffolds seeded with chondrocytes was developed. Similar to several previous modeling studies (Dimicco and Sah 2003; Sengers et al. 2004; Trewenack et al. 2009), dependent variables in the model representing the ECM were delineated into contributions from linked (bound) and unlinked (soluble) constituents. In contrast to the aforementioned studies, which accounted for spatial effects in one or two dimensions, the current study employed a one compartment model that was developed using a mixture formulation with average apparent densities of unlinked ECM, linked ECM, and scaffold as the dependent variables. The mixture model accounted for product inhibition of unlinked ECM biosynthesis (Buschmann et al. 1992; Handley and Lowther 1977) via cell-mediated detection of an unlinked ECM concentration in the interstitial fluid phase of the mixture, i.e. in grams of unlinked ECM per milliliter of interstitial fluid. The relative simplicity of this modeling approach, along with its use of mixture variables, can facilitate the quantitative characterization of primary system variables in tissue constructs when detailed spatial data are unavailable or difficult to obtain. In particular, variables within the mixture formulation inherently distinguish between dry mass and wet weight of the scaffold or tissue construct via true and apparent densities in the model, respectively, and the constituent volume fractions that relate them.

The model developed in this study captures competing effects of cell-mediated biosynthesis of unlinked ECM and the, concurrent, decrease in unlinked ECM due to linking via interactions with the evolving solid phase of the mixture. The assumed dependence of ECM linking rates on the solid volume fraction in the mixture [Eq. (9)] results in nonlinear relationships between scaffold design variables and functional outcomes (e.g. Fig. 4). These simulations suggest that scaffold material properties may be tailored to optimize variables such as the solid-phase apparent density (Fig. 4b: 90, 120 days) which is known to correlate with the construct’s elastic Young’s modulus when mixture volume is not significantly altered. Due to the large fluid volume fraction in cartilaginous tissues, it is also noted that small changes in ρ̄^s may be associated with significant variations in the apparent compressive stiffness of the engineered construct.

In a recent experimental study (Erickson et al. 2009), mesenchymal stem cells were seeded in hyaluronic acid hydrogel scaffolds with varying initial density, and the elastic compressive modulus and spatial distribution of cell-synthesized matrix constituents were analyzed over a period of 6 weeks. The equilibrium compressive modulus of the construct was found to decrease significantly as HA macromer density of the scaffold material was increased, and was attributed to poor spatial distribution and linking of cell- synthesized ECM in the tissue construct. The model developed in this study demonstrated that scaffold material properties (e.g. ${\overline{\varphi }}_0^{\text{Sc}}$) can significantly influence solid- phase apparent density of the construct. In addition, cell-scaffold interaction parameters (e.g. ${\overline{\rho }}_T^{\text{LM}},{\overline{\rho }}_{\text{UM}}^{\text{w}},{\overline{\varphi }}_{\ast }^{\text{S}}$) were also shown to strongly influence solid-phase apparent density. The latter category of parameters are likely to vary from one cell-scaffold system to another. Taken together, these findings suggest that a coordinated approach in which mixture modeling is integrated into analysis and design of cartilage regeneration experiments may facilitate detailed characterization and optimization of functional outcomes in engineered constructs.

There are several limitations of the current modeling approach that should be considered in application to experimental data analysis. In development of the current model, the mixture volume V was assumed to remain roughly constant. This assumption is relevant to systems for which the construct is confined or for which the addition of solid-phase volume results in the exudation of a roughly equal volume of interstitial fluid from the mixture. While the model developed in Sect. 2.3 can be applied to experimental systems with changing volume, care should be taken in interpreting the associated findings. For example, cartilaginous tissues exhibiting significant volume changes due to swelling and imbibition of fluid are known to exhibit a tension-compression nonlinearity (Soltz and Ateshian 2000). Under such circumstances, solid-phase apparent density may be inversely correlated with apparent tissue compressive stiffness due to tensile pre-stress effects in the solid phase of the mixture. While several reaction-diffusion models have been applied to experimental data from systems with significant volumetric expansion of the tissue construct (Obradovic et al. 2000; Nikolaev et al. 2009), these models do not enforce balance of momentum in the mixture. It is noted that more general continuum formulations such as those for mixtures with growth (Ateshian et al. 2009) or neutral solute transport in dynamically loaded mixtures (Mauck et al. 2003) provide a foundation for addressing these limitations. The model developed in the current study also neglects the charged nature of unlinked ECM constituents that give rise to a negative fixed charge density in the linked ECM. It also does not account for cell proliferation or for nutrients or growth factors with transport times comparable to those for unlinked ECM constituents. The assumption of uniform nutrient concentration in the model may also be limited to systems with low cell volume fraction or scaffold density when rates of nutrient diffusion and cellular uptake of the same nutrients are comparable. For experimental application of the current model, as well as other models that delineate linked and unlinked ECM components (Dimicco and Sah 2003; Sengers et al. 2004; Trewenack et al. 2009), new experimental techniques may be required to separately measure linked (bound) and unlinked (soluble) fractions of ECM phases in tissue-engineered cartilage constructs. Future model extensions can address the limitations outlined earlier as well as additional factors including delineation of ECM collagen and ECM GAG volume fractions, regulation of biosynthesis and linking via detection of linked ECM constituent densities, effects of crosslinking agents, and spatial effects.

While spatiotemporal (PDE) models are ultimately required for detailed characterization of cartilage regeneration in chondrocyte-seeded scaffolds, phenomenological ODE mixture models can facilitate model formulation, solution and parameter estimation in the context of more limited, or exclusively temporal, experimental data. The model developed in this study contains a diverse set of material parameters that account for several key intrinsic and interactive mechanisms in biomaterial scaffolds seeded with chondrocytes. Application of the model (or extensions) to appropriate experimental data sets provides a quantitative framework for comparing competing scaffold designs and can serve as an additional tool in guiding the development of optimal tissue engineering strategies for articular cartilage regeneration.