The effect of recurrent mutation on the frequency spectrum of a segregating site and the age of an allele

Abstract

The sample frequency spectrum of a segregating site is the probability distribution of a sample of alleles from a genetic locus, conditional on observing the sample to be polymorphic. This distribution is widely used in population genetic inferences, including statistical tests of neutrality in which a skew in the observed frequency spectrum across independent sites is taken as a signature of departure from neutral evolution. Theoretical aspects of the frequency spectrum have been well studied and several interesting results are available, but they are usually under the assumption that a site has undergone at most one mutation event in the history of the sample. Here, we extend previous theoretical results by allowing for at most two mutation events per site, under a general finite alleles model in which the mutation rate is independent of current allelic state but the transition matrix is otherwise completely arbitrary. Our results apply to both nested and nonnested mutations. Only the former has been addressed previously, whereas here we show it is the latter that is more likely to be observed except for very small sample sizes. Further, for any mutation transition matrix, we obtain the joint sample frequency spectrum of the two mutant alleles at a triallelic site, and derive a closed-form formula for the expected age of the younger of the two mutations given their frequencies in the population. Several large-scale resequencing projects for various species are presently under way and the resulting data will include some triallelic polymorphisms. The theoretical results described in this paper should prove useful in population genomic analyses of such data.

1. Introduction

The frequency spectrum for a sample of genetic data taken from a population is a useful statistic, containing more information than single-value summaries like the number of segregating sites, yet remaining more tractable than working with the full data configuration. The sample frequency spectrum for a polymorphic site is defined as the probability distribution of the number of copies of the derived, or mutant, allele in a sample of size n. For a sample with many polymorphic sites, a histogram of the number of sites with i copies of the mutant allele present in the sample, for each i = 1, …, n − 1, can be compared to the sample frequency spectrum. In this manner, one can test the applicability of a given reproductive model by comparing departures of the observed frequency spectrum from its expectation. Most of the widely-used tests of neutrality are either directly or indirectly based on this observation (Achaz, 2009). Under a standard, neutral, coalescent model, and assuming the infinite sites model of mutation, the sample frequency spectrum is known in closed-form:

$$\varphi (i)=\frac{i^{-1}}{{\displaystyle \sum _{j=1}^{n-1}}{j}^{-1}},$$ (1)

where ϕ(i) is the probability that a mutant allele is present in exactly i copies of the sample [Watterson (1975); see Fu (1995), Griffiths and Tavaré (1998) for a coalescent approach]. This appealing result has been generalized to a number of further settings, including variable population size (Griffiths and Tavaré, 1998; Polanski and Kimmel, 2003; Evans et al., 2007), and genic selection (Griffiths, 2003). Bustamante et al. (2001) obtain a number of results related to the frequency spectrum for mutant sites under selection in the Poisson random field model of Sawyer and Hartl (1992).

All of this work assumes the infinite sites model of mutation. In particular, the mutation giving rise to the new allele is assumed to have occurred at most once in the genealogy relating the sample. Since the per-site mutation parameter θ is small (typically 0.001 ≤ θ ≤ 0.01 for humans, where θ = 4Nu, N is the diploid effective population size, and u is the probability of a mutation event per individual per generation), this assumption is usually reasonable. Occasionally, however, one might observe a site that must have undergone more than one mutation: it may be triallelic, or may be incompatible with the gene genealogy inferred from completely linked sites. Moreover, recurrent mutations can affect sites that still appear to conform to the infinite sites assumption. Thus far there have been no clear theoretical grounds for how to deal with nonconforming sites when working with the frequency spectrum. For example, one simple solution is simply to bin both the mutant alleles of a triallelic site and then to treat it as if it were diallelic (e.g. Johnson and Slatkin, 2006), but this is clearly not ideal.

In this work we obtain a more general distribution for the number of copies of mutant alleles at a site, by allowing at most two mutation events in the genealogy relating the sample. We employ a general finite sites model in which a fixed but arbitrary number of alleles, K, may be observed at the site of interest, and mutations between alleles occur according to some transition matrix P. The sample frequency spectrum is then more generally defined to be the joint probability distribution of the number of copies of each of the mutant alleles, conditional on at least one mutant allele. We assume the standard coalescent (Kingman, 1982), and derive our results by arguments using topological constraints induced on the genealogy by the two mutations. This approach is most closely related to the work of Wiuf and Donnelly (1999) and Hobolth and Wiuf (2009), who studied genealogies with one mutation and genealogies with two nested mutations, respectively. Among other results, Wiuf and Donnelly (1999) obtain the density of the age of a single mutant allele given its population frequency, and Hobolth and Wiuf (2009) obtain the joint and marginal sample frequency spectra of two mutant alleles when the mutations are genealogically nested, and the age of the younger of the two nested mutants. In this paper we extend these results to nonnested mutations, which, as we show below, is the more important of the two cases: With increasing sample size, the probability that two mutations are nonnested approaches one, and it is even the most probable outcome for all sample sizes greater than four. With results for both cases in hand, by averaging over whether or not the mutations are nested we obtain the sample frequency spectra of two mutant alleles regardless of their topological placement in the genealogy. Furthermore, Hobolth and Wiuf (2009) treat the two mutants as having occurred at two completely linked but distinct sites, so that the younger and older of the two mutants are always identifiable. In this work we model the two mutations as occurring at the same site, allowing for the more general possibility of parallel mutations or back mutations. Particular choices of P in our model allows one to include the setting of Hobolth and Wiuf (2009) as a special case.

When introducing a model for mutation there are two cases to consider:

1. The allele of the most recent common ancestor (MRCA) of the sample is known, usually by comparison with an outgroup that is related by a suitable evolutionary distance.

2. The type of the MRCA is unknown.

In this work we largely restrict ourselves to the first case. In principle it has more power, since mutant alleles observed i times and n − i times are distinguishable. When we have no prior assumptions regarding which of the alleles is the mutant, one must resort to the folded frequency spectrum, in which the two categories are binned together. In any case, when the type of the MRCA is unknown and the mutation transition matrix takes on a special parent-independent form—that is, P_ij is independent of i, for each pair of alleles i and j—then a closed-form sampling distribution for each site is available, which applies for any number of mutations in the history of the sample. This formula is essentially due to Wright (1949). Use of Wright’s formula for making inferences regarding the site frequency spectrum is considered by Desai and Plotkin (2008). Note that when we assume the allele of the MRCA is known, Wright’s formula does not apply even when mutation is parent-independent. For larger mutation rates, the assumption that a genealogy has undergone at most two mutations and that the allele of the MRCA is known each becomes less justifiable, and without prior information about which allele is mutant one should revert to using a folded site frequency spectrum.

In the special case of parent-independent mutation with the type of the MRCA unknown one can use Wright’s formula as described above. It also applies to a diallelic model (K = 2), which can always be transformed into an equivalent parent-independent one. Aside from these cases, there are no classical results for the sample frequency spectrum under more general transition matrices. In this work we allow P to remain a general transition matrix apart from the restriction that the mutation rate at the locus is independent of its current allelic state. This is equivalent to ensuring P_ii = 0 for each i = 1, …, K, since the effective rate at which an allele mutates to another distinct allele is (θ/2)(1 − P_ii); in more general mutation models, P_ii can vary for different i to allow different rates of transition out of different allelic states. It should be possible to modify our results to relax this assumption, albeit with a noticeable cost in bookkeeping, and so we do not attempt it in this work. An exception can be made when we study triallelic sample configurations later in the paper: genealogies associated with such configurations must have undergone at least two nontrivial mutation events, and we can allow P_ii > 0 without any additional effect. Essentially, having observed a triallelic sample together with the assumption that there were at most two mutation events means we condition on such trivial mutations not having occurred, even if we allow them back into the model. When studying triallelic configurations, we also find that our results simplify substantially with the following additional assumption:

$$P_{\mathit{\text{ab}}}=P_{\mathit{\text{cb}}},\text{ and }{P}_{\mathit{\text{ac}}}=P_{\mathit{\text{bc}}},$$ (2)

where the three observed alleles are a, b, and c, and a is the ancestral allele. The condition (2) is satisfied by, and is weaker than, parent-independent mutation. It requires only that parent-independence holds in relevant entries of P, namely, in the rates of transition to each of the observed mutant alleles from the ancestral allele and from the other observed mutant allele.

Our paper is structured as follows. In Section 2 we introduce the recursion relation for the distribution of the sample configuration, which is well-known and is based on coalescent arguments. We utilize this recursion to obtain results for coalescent trees with one mutation event (Section 3) and two mutation events (Section 4). These results are made tractable in Section 5 by letting the mutation parameter go to zero, from which we can obtain useful expressions when we condition on certain observed patterns (e.g. that the site is triallelic) in Section 6. In Section 7 we also investigate the mean age in the population of a mutant allele at a triallelic site, and in Section 8 we investigate the accuracy of our expressions when the mutation parameter is in fact nonzero. We conclude with some brief discussion in Section 9.

2. Sample recursion

Denote an unordered sample configuration at a particular site by n = (n₁, n₂, …, n_K), where K is the fixed and known number of alleles which could be observed at this site, and denote the sample size by $n={\displaystyle {\sum }_{i=1}^K}{n}_i$. Members of the sample are referred to as gametes, so that n_i denotes the number of gametes in the sample with allele i. We fix the ancestral allele and denote it as a ∈ {1, …, K}. Denote by E_s the event that there are exactly s mutation events in the history of the sample. We will write the probability of observing the configuration n as p(n), and the joint probability of this configuration together with E_s as p(n, E_s). It is implicit in these expressions that we condition on the ancestral allele being a. We can now obtain the sample frequency spectrum from these probabilities. For example, suppose we have two possible alleles, denoted 1 and 2 where 1 is ancestral, so that $P=\left(\begin{array}{cc}0\hfill & 1\hfill \\ 1\hfill & 0\hfill \end{array}\right)$. As θ → 0, we may assume the mutant allele arose as the result of precisely one mutation event, and the distribution (1) is recovered as

$$\varphi (i)=\underset{\theta \to 0}{\text{lim}}p((n-i,i)|E_1)=\underset{\theta \to 0}{\text{lim}}\frac{p((n-i,i),E_1)}{{\displaystyle {\sum }_{j=1}^{n-1}}p((n-j,j),E_1)},$$

i = 1, …, n − 1, since p((n − i, i), E₁) = θi⁻¹ + O(θ²) under this model (see (17) below).

Define a history to be the sequence of configurations n ↦ n′ ↦ … ↦ e_a as we trace the ancestry of the sample back in time. Here, e_i denotes a sample comprised of a single gamete whose allele is i, so e_a denotes the sample comprising only the MRCA. A history can be regarded as an equivalence class in the space of genealogies with mutations that relate the sample. At each step in the sequence, at which the configuration is modified, we do not record which lineages are involved in each event, so there are many possible genealogies associated with any given history.

The probability p(n) satisfies the following recursion relation for n ≥ 2:

$$p(\mathit{n})={\displaystyle \sum _{j=1}^K}\frac{n_j-1}{n-1+\theta }p(\mathit{n}-{\mathit{e}}_j)+\frac{\theta }{n-1+\theta }{\displaystyle \sum _{i=1}^K}{\displaystyle \sum _{j=1}^K}{P}_{\mathit{\text{ij}}}\frac{n_i+1-{\delta }_{\mathit{\text{ij}}}}{n}p(\mathit{n}-{\mathit{e}}_j+{\mathit{e}}_i),$$ (3)

with boundary condition p(e_i) = δ_ia for each i = 1, …, K, where δ_ij is the Kronecker delta. Similarly, the probability p(n, E_s) satisfies, for n ≥ 2,

$$p(\mathit{n},E_s)={\displaystyle \sum _{j=1}^K}\frac{n_j-1}{n-1+\theta }p(\mathit{n}-{\mathit{e}}_j,E_s)+\frac{\theta }{n-1+\theta }{\displaystyle \sum _{i=1}^K}{\displaystyle \sum _{j=1}^K}{P}_{\mathit{\text{ij}}}\frac{n_i+1-{\delta }_{\mathit{\text{ij}}}}{n}p(\mathit{n}-{\mathit{e}}_j+{\mathit{e}}_i,E_{s-1}),$$ (4)

with boundary conditions p(e_i, E_s) = δ_iaδ_s0. Equations (3) and (4) are obtained from similar ones in Griffiths and Tavaré (1994), with slight modifications to the boundary conditions to reflect that we consider the allele of the MRCA to be known. Each path back through the recursions (3) and (4) is associated with a particular history, and we use this observation to obtain our results for the sample frequency spectrum. To illustrate the method, in Section 3 we first consider histories with precisely one mutation event. Henceforth we assume that P_ii = 0 for i = 1, …, K, so that mutation events always result in a change of allele, and subsequent configurations in any history are always distinct. Finally, we also use the following notation: for a nonnegative real number x and a positive integer k,

$${(x)}_k≔x(x+1)\dots (x+k-1)$$

denotes the kth ascending factorial of x.

3. One mutation event

Refer to the intervals back in time while there existed n, n − 1, …, 2 ancestors to the sample as levels. Wiuf and Donnelly (1999) proceed by conditioning on the level at which the unique mutation event occurred, and then considering the distribution of the number of offspring of each lineage from that level. Here, we take a related approach but instead argue directly from (4).

Suppose we observe the sample configuration n = n_ae_a + n_be_b, where b ≠ a is some mutant allele, and we have n_a > 0, n_b > 0, and n_a + n_b = n. Denote the sample configuration immediately before (more recently than) the time of the unique mutation event by l. Conditional on the event E₁, that exactly one mutation event occurred in the history of the sample, l must be of the form l = l_ae_a + e_b for some l_a with 1 ≤ l_a ≤ n_a (Figure 1). We refer to a history that passes through the state l as compatible with l. Thus, a history ℋ₁ that gives rise to n, is compatible with l, and is consistent with E₁, must be a sequence of configurations of the form n ↦ … ↦ l ↦ (l_a + 1)e_a ↦ … ↦ e_a. We make use of the following simple but useful lemma.

Figure 1.

A coalescent tree with one mutation. The allele of each leaf is annotated. Also annotated is the variable l_a (here, l_a = 3), which determines the number of each type at the time of the mutation event.

Lemma 3.1. Conditional on E₁, on the observed sample configuration n = n_ae_a + n_be_b, and on the configuration l = l_ae_a + e_b at the time of the mutation event, the distribution of compatible histories ℋ₁ is uniform. It is given by

$$p({\mathbf{\mathscr{H}}}_1|E_1,\mathit{n},\mathit{l})={\left(\begin{array}{c}\hfill n-l_a-1\hfill \\ \hfill n_b-1\hfill \end{array}\right)}^{-1}.$$

Moreover, the (unconditional) probability of such histories is

$$p({\mathbf{\mathscr{H}}}_1)=p({\mathbf{\mathscr{H}}}_1,E_1,\mathit{n},\mathit{l})=\theta P_{\mathit{\text{ab}}}\frac{(n_a-1)!(n_b-1)!}{{(1+\theta )}_{n-1}}·\frac{l_a}{l_a+\theta }.$$ (5)

A proof of Lemma 3.1, along with our other results, is given in Appendix A. Summing over the $\left(\begin{array}{c}\hfill n-l_a-1\hfill \\ \hfill n_b-1\hfill \end{array}\right)$ histories and over l, we obtain

$$\begin{array}{cc}p(\mathit{n},E_1)\hfill & ={\displaystyle \sum _{l_a=1}^{n_a}}\left(\begin{array}{c}\hfill n-l_a-1\hfill \\ \hfill n_b-1\hfill \end{array}\right)p({\mathbf{\mathscr{H}}}_1,E_1,\mathit{n},\mathit{l})\hfill \\ \hfill & =\{\begin{array}{c}\theta P_{\mathit{\text{ab}}}\frac{(n-1)!}{{(1+\theta )}_{n-1}}{\displaystyle \sum _{l_a=1}^{n_a}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_a-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill l_a\hfill \end{array}\right)}·\frac{1}{l_a+\theta },\hfill \\ \begin{array}{cc}\hfill & \text{if}\mathit{n}=h_a{\mathit{e}}_a+n_b{\mathit{e}}_b,\text{where}b\ne a\text{ and }1\le n_a,n_b\le n,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\hfill \end{array}\hfill \end{array}$$ (6)

We now extend this approach to histories with precisely two mutation events.

4. Two mutation events

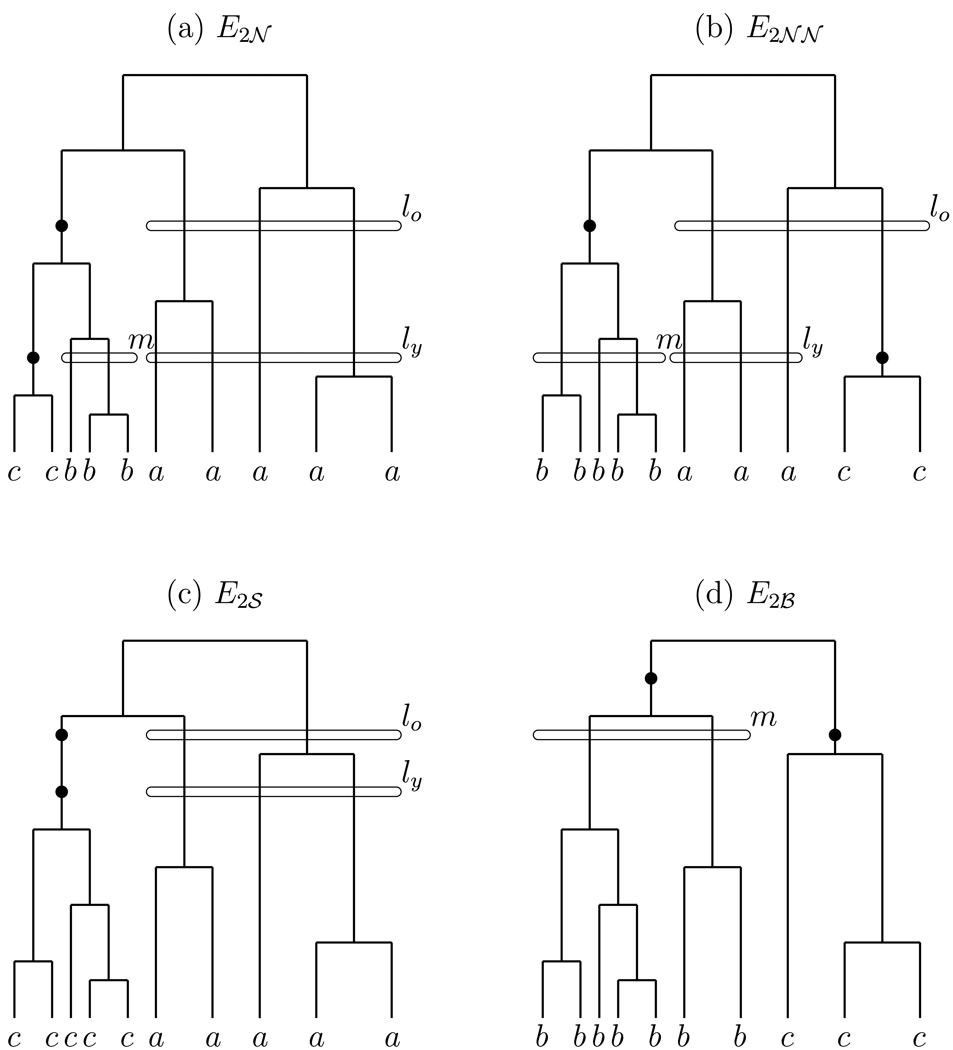
There are four cases to consider (Figure 2). The two mutation events are either nested (denoted E_2𝒩), nonnested (E_2𝒩𝒩), on the same edge (E_2𝒮), or basal (E_2ℬ). We define each of these in further detail below; for now note that nested excludes the case that the mutations occurred on the same edge, and nonnested excludes the case that the mutations reside on the two basal (innermost) edges of the tree. We use superscript notation to further specify the alleles to which the two age-ordered mutation events gave rise, so for example $E_{2𝒩}^{(b,c)}$ (⊆ E_2𝒩) denotes the event that there were precisely two mutation events, the mutations were nested, that the older mutation gave rise to a b allele, and that the younger mutation gave rise to a c allele. Note that in this example we must have a ≠ b and b ≠ c but it may or may not be the case that a = c. The a = c case will be dealt with separately. Similar special cases arise for E_2𝒩𝒩, E_2𝒮, and E_2ℬ. We now consider each of the four events in further detail.

Figure 2.

Coalescent trees with two mutations. (a) Two nested mutations. (b) Two nonnested mutations. (c) Two mutations on the same branch. (d) Two mutations on the basal branches. The allele of each leaf is annotated. Also annotated are variables determining the number of each type at the times of the mutation events; for example, in (a) we have m = 2, l_y = 4, and l_o = 3.

4.1. Two nested mutations

In this case the clade subtended by one mutation is a proper subclade of the other [Figure 2(a)]. The genealogy of two nested mutations was also studied by Hobolth and Wiuf (2009), though using a different model of mutation. Consider the event $E_{2𝒩}^{(b,c)}$, and assume for now that a ≠ c, so our observation is of the form n = n_ae_a + n_be_b + n_ce_c, with n_a, n_b, n_c > 0, and n_a + n_b + n_c = n. The sample configuration immediately before the younger mutation event is of the form l_y = l_ye_a + me_b + e_c, and immediately before the older mutation event it is of the form l_o = l_oe_a + e_b. For the mutations to be nested we must have 1 ≤ m ≤ n_b, and 1 ≤ l_o ≤ l_y ≤ n_a. Denote a history compatible with these requirements by ℋ_2𝒩; this is a sequence of configurations of the form n ↦ … ↦ l_y ↦ (l_y − e_c + e_b) ↦ … ↦ l_o ↦ (l_o − e_b + e_a) ↦ e_a. Using $\left(\begin{array}{c}\hfill n\hfill \\ \hfill n_a,n_b,n_c\hfill \end{array}\right)$ to denote the trinomial coefficient, we have the following lemma:

Lemma 4.1. Conditional on $E_{2𝒩}^{(b,c)}$, on the observed sample configuration n = n_ae_a + n_be_b + n_ce_c, and on the sample configurations l_y = l_ye_a + me_b + e_c and l_o = l_oe_a + e_b immediately before the times of the two nested mutation events, the distribution of compatible histories ℋ_2𝒩 is uniform. It is given by

$$p({\mathbf{\mathscr{H}}}_{2𝒩}|E_{2𝒩}^{(b,c)},\mathit{n},{\mathit{l}}_y,{\mathit{l}}_{\mathit{o}})={\left[\left(\begin{array}{c}\hfill n-l_y-m-1\hfill \\ \hfill n_a-l_y,n_b-m,n_c-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m\hfill \end{array}\right)\right]}^{-1}.$$

Moreover, the (unconditional) probability of such histories is

$$\begin{array}{cc}p({\mathbf{\mathscr{H}}}_{2𝒩})\hfill & =p({\mathbf{\mathscr{H}}}_{2𝒩},E_{2𝒩,}\mathit{n},{\mathit{l}}_y,{\mathit{l}}_o)\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}\frac{(n_a-1)!(n_b-1)!(n_c-1)!}{{(1+\theta )}_{n-1}}\times \frac{{\mathit{\text{ml}}}_o}{(m+l_y+\theta )(l_o+\theta )}·\frac{m+1}{m+l_y+1}.\hfill \end{array}$$ (7)

Proof. See Appendix A.

Summing over compatible histories and over valid combinations of m, l_y, and l_o, we obtain

$$\begin{array}{cc}p(\mathit{n},E_{2𝒩}^{(b,c)})\hfill & ={\displaystyle \sum _{l_y=1}^{n_a}}{\displaystyle \sum _{l_o=1}^{l_y}}{\displaystyle \sum _{m=1}^{n_b}}\left(\begin{array}{c}\hfill n-l_y-m-1\hfill \\ \hfill n_a-l_y,n_b-m,n_c-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m\hfill \end{array}\right)p({\mathbf{\mathscr{H}}}_{2𝒩})\hfill \\ \hfill & =\{\begin{array}{c}{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}\frac{(n-1)!}{{(1+\theta )}_{n-1}}{\displaystyle \sum _{l_y=1}^{n_a}}{\displaystyle \sum _{l_o=1}^{l_y}}{\displaystyle \sum _{m=1}^{n_b}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m+l_y\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y\hfill \\ \hfill m+1\hfill \end{array}\right)}\times \frac{1}{m+l_y+1}·\frac{l_o}{l_o+\theta }·\frac{1}{m+l_y+\theta },\hfill \\ \begin{array}{cc}\hfill & \text{if}\mathit{n}=n_a{\mathit{e}}_a+n_b{\mathit{e}}_b+n_c{\mathit{e}}_c,\text{where}a,b,c\text{are all distinct},\text{and}1\le n_a,n_b,n_c\le n;\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\hfill \end{array}\hfill \end{array}$$ (8)

One can relax the age-ordering on mutations by noting that, for n = n_ae_a + n_be_b + n_ce_c,

$$p(\mathit{n},E_{2𝒩})=p(\mathit{n},E_{2𝒩}^{(b,c)})+p(\mathit{n},E_{2𝒩}^{(c,b)}).$$

Similar relaxations apply to the remaining cases described below.

Finally, we return to the possibility that a = c. We denote this by $E_{2𝒩}^{(b,a)}$, and have a sample of the form n = n_ae_a + n_be_b, with n_a, n_b > 0, and n_a + n_b = n. Now, n_a comprises gametes whose alleles are truly ancestral and gametes whose alleles are atavistic. We can still however apply the previous result [equation (8)], first by treating a and c as if they were distinct, then summing over all possible values for the number of observed a alleles and the number of observed c alleles such that their sum is held fixed, and finally setting c = a in the resulting expression:

$$\begin{array}{cc}p(\mathit{n},E_{2𝒩}^{(b,a)})\hfill & ={\displaystyle \sum _{k=1}^{n_a-1}}p(\mathit{k}{\mathit{e}}_a+n_b{\mathit{e}}_b+(n-n_b-k){\mathit{e}}_c,E_{2𝒩}^{(b,c)}){|}_{c=a}\hfill \\ \hfill & =\{\begin{array}{c}{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ba}}}\frac{(n-1)!}{{(1+\theta )}_{n-1}}{\displaystyle \sum _{l_y=1}^{n_a-1}}{\displaystyle \sum _{l_o=1}^{l_y}}{\displaystyle \sum _{m=1}^{n_b}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m+l_y\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y\hfill \\ \hfill m+1\hfill \end{array}\right)}\times \frac{1}{m+l_y+1}·\frac{l_o}{l_o+\theta }·\frac{1}{m+l_y+\theta },\hfill \\ \begin{array}{cc}\hfill & \text{if}\mathit{n}=n_a{\mathit{e}}_a+n_b{\mathit{e}}_b,\text{where}b\ne a,\text{and}1\le n_a,n_b\le n;\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\hfill \end{array}\hfill \end{array}$$

4.2. Two nonnested mutations

In this case the clades subtended by the two mutations are disjoint [Figure 2(b)]. We also exclude the possibility that the two mutations reside on the basal (innermost) branches of the coalescent tree, which could result in a monomorphic sample. Consider the event $E_{2𝒩𝒩}^{(b,c)}$, where b ≠ c, n = n_ae_a + n_be_b + n_ce_c, with n_a, n_b, n_c > 0, and n_a + n_b + n_c = n. Suppose that, immediately before the younger mutation, the sample configuration is l_y = l_ye_a + me_b + e_c, and immediately before the older mutation it is l_o = l_oe_a + e_b. Consideration of the genealogy [Figure 2(b)] leads to the following restrictions: 1 ≤ m ≤ n_b, 1 ≤ l_y ≤ n_a, and 1 ≤ l_o ≤ l_y + 1. One can argue as in the previous subsection to obtain the following:

Lemma 4.2. Conditional on $E_{2𝒩𝒩}^{(b,c)}$, on the observed sample configuration n = n_ae_a + n_be_b + n_ce_c, and on the sample configurations l_y = l_ye_a + me_b + e_c and l_o = l_oe_a + e_b immediately before the times of the two nonnested mutation events, the distribution of compatible histories ℋ_2𝒩𝒩 is uniform. It is given by

$$p({\mathbf{\mathscr{H}}}_{2𝒩𝒩}|E_{2𝒩𝒩}^{(b,c)},\mathit{n},{\mathit{l}}_y,{\mathit{l}}_o)={\left[\left(\begin{array}{c}\hfill n-m-l_y-1\hfill \\ \hfill n_a-l_y,n_b-m,n_c-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m-1\hfill \end{array}\right)\right]}^{-1}.$$

Moreover, the (unconditional) probability of such histories is

$$\begin{array}{cc}p({\mathbf{\mathscr{H}}}_{2𝒩𝒩})\hfill & =p({\mathbf{\mathscr{H}}}_{2𝒩𝒩},E_{2𝒩𝒩}^{(b,c)},\mathit{n},{\mathit{l}}_y,{\mathit{l}}_o)\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}\frac{(n_a-1)!(n_b-1)!(n_c-1)!}{{(1+\theta )}_{n-1}}\times \frac{l_y{l}_o}{(l_y+m+\theta )(l_o+\theta )}·\frac{l_y+1}{l_y+m+1}.\hfill \end{array}$$ (9)

Using this lemma to sum over compatible histories and over m, l_y, and l_o, after some simplification we obtain

$$\begin{array}{cc}p(\mathit{n},E_{2𝒩𝒩}^{(b,c)})\hfill & ={\displaystyle \sum _{m=1}^{n_b}}{\displaystyle \sum _{l_y=1}^{n_a}}{\displaystyle \sum _{l_o=1}^{l_y+1}}\left(\begin{array}{c}\hfill n-m-l_y-1\hfill \\ \hfill n_a-l_y,n_b-m,n_c-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m-1\hfill \end{array}\right)p({\mathbf{\mathscr{H}}}_{2𝒩𝒩})\hfill \\ \hfill & =\{\begin{array}{c}{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}\frac{(n-1)!}{{(1+\theta )}_{n-1}}{\displaystyle \sum _{m=1}^{n_b}}{\displaystyle \sum _{l_y=1}^{n_a}}{\displaystyle \sum _{l_o=1}^{l_y+1}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m+l_y\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y\hfill \\ \hfill l_y+1\hfill \end{array}\right)}\times \frac{l_o}{l_o+\theta }·\frac{1}{m+l_y+1}·\frac{1}{m+l_y+\theta },\hfill \\ \begin{array}{cc}\hfill & \text{if}\mathit{n}=n_a{\mathit{e}}_a+n_b{\mathit{e}}_b+n_c{\mathit{e}}_c,\text{where}a,b,c\text{are all distinct},\text{and}1\le n_a,n_b,n_c\le n;\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\hfill \end{array}\hfill \end{array}$$ (10)

Also as before, the result (10) can also be used to handle the special case b = c:

$$\begin{array}{cc}p(\mathit{n},E_{2𝒩𝒩}^{(b,b)})\hfill & ={\displaystyle \sum _{k=1}^{n_b-1}}p(n_a{\mathit{e}}_a+\mathit{k}{\mathit{e}}_b+(n-n_a-k){\mathit{e}}_c,E_{2𝒩𝒩}^{(b,c)}){|}_{b=c}\hfill \\ \hfill & =\{\begin{array}{c}{\theta }^2{P}_{\mathit{\text{ab}}}^2\frac{(n-1)!}{{(1+\theta )}_{n-1}}{\displaystyle \sum _{m=1}^{n_b-1}}{\displaystyle \sum _{l_y=1}^{n_a}}{\displaystyle \sum _{l_o=1}^{l_y+1}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m+l_y\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y\hfill \\ \hfill l_y+1\hfill \end{array}\right)}\times \frac{l_o}{l_o+\theta }·\frac{1}{m+l_y+1}·\frac{1}{m+l_y+\theta },\hfill \\ \begin{array}{cc}\hfill & \text{if}\mathit{n}=n_a{\mathit{e}}_a+n_b{\mathit{e}}_b,\text{where}b\ne a,\text{ and }1\le n_a,n_b\le n;\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\hfill \end{array}\hfill \end{array}$$

4.3. Two mutations on the same branch

Here, two mutation events reside on the same edge of the coalescent tree, as illustrated in Figure 2(c). Consider first the subevent $E_{2𝒮}^{(b,c)}$, with a ≠ c, so that n = n_ae_a + n_ce_c, with n_a, n_c > 0, and n_a + n_c = n. Suppose the configuration immediately prior to the younger mutation event is l_y = l_ye_a + e_c, and immediately prior to the older mutation is l_o = l_oe_a + e_b. We argue as before to yield the following:

Lemma 4.3. Conditional on $E_{2𝒮}^{(b,c)}$, on the observed sample configuration n = n_ae_a + n_ce_c, and on the sample configurations l_y = l_ye_a + e_c and l_o = l_oe_a + e_b immediately before the times of the two mutation events, the distribution of compatible histories ℋ_2𝒮 is uniform. It is given by

$$p({\mathbf{\mathscr{H}}}_{2𝒮}|E_{2𝒮}^{(b,c)},\mathit{n},{\mathit{l}}_y,{\mathit{l}}_o)={\left(\begin{array}{c}\hfill n-l_y-1\hfill \\ \hfill n_c-1\hfill \end{array}\right)}^{-1}.$$

Moreover, the (unconditional) probability of such histories is

$$\begin{array}{cc}p({\mathbf{\mathscr{H}}}_{2𝒮})\hfill & =p({\mathbf{\mathscr{H}}}_{2𝒮},E_{2𝒮}^{(b,c)},\mathit{n},{\mathit{l}}_y,{\mathit{l}}_o)\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}\frac{(n_a-1)!(n_c-1)!}{{(1+\theta )}_{n-1}}·\frac{l_o}{l_o+\theta }·\frac{1}{(l_y+1)(l_y+\theta )}.\hfill \end{array}$$ (11)

Hence, summing over compatible histories and then over l_o and l_y, we obtain

$$\begin{array}{cc}p(\mathit{n},E_{2𝒮}^{(b,c)})\hfill & ={\displaystyle \sum _{l_y=1}^{n_a}}{\displaystyle \sum _{l_o=1}^{l_y}}\left(\begin{array}{c}\hfill n-l_y-1\hfill \\ \hfill n_c-1\hfill \end{array}\right)p({\mathbf{\mathscr{H}}}_{2𝒮})\hfill \\ \hfill & =\{\begin{array}{c}{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}\frac{(n-1)!}{{(1+\theta )}_{n-1}}{\displaystyle \sum _{l_y=1}^{n_a}}{\displaystyle \sum _{l_o=1}^{l_y}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill l_y\hfill \end{array}\right)}·\frac{l_o}{l_o+\theta }·\frac{1}{l_y(l_y+1)(l_y+\theta )},\hfill \\ \begin{array}{cc}\hfill & \text{if}\mathit{n}=n_a{\mathit{e}}_a+n_c{\mathit{e}}_c,\text{where}a,b,c\text{are all distinct},\text{and}1\le n_a,n_c\le n;\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\hfill \end{array}\hfill \end{array}$$ (12)

One can relax the restriction on the unobserved allele being b by summing over each possible b. This is achieved simply by replacing P_abP_bc in (12) with (P²)_ac.

When a = c, the sample must be n = ne_a, and repeating earlier arguments we obtain

$$\begin{array}{cc}p(\mathit{n},E_{2𝒮}^{(b,a)})\hfill & ={\displaystyle \sum _{k=1}^{n-1}}p(\mathit{k}{\mathit{e}}_a+(n-k){\mathit{e}}_c,E_{2𝒮}^{(b,c)}){|}_{a=c}\hfill \\ \hfill & =\{\begin{array}{c}{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ba}}}\frac{(n-1)!}{{(1+\theta )}_{n-1}}{\displaystyle \sum _{l_y=1}^{n-1}}{\displaystyle \sum _{l_o=1}^{l_y}}\frac{l_o}{l_o+\theta }·\frac{1}{l_y(l_y+1)(l_y+\theta )},\hfill \\ \begin{array}{cc}\hfill & \text{if}\mathit{n}=\mathit{n}{\mathit{e}}_a,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\hfill \end{array}\hfill \end{array}$$

Again, the stipulation on the unobserved allele being b can be relaxed by replacing P_abP_ba with (P²)_aa.

4.4. Two mutations on the basal branches

Here, the mutations reside on the last two edges in the coalescent tree to exist going back in time, as illustrated in Figure 2(d). Consider first the subevent $E_{2ℬ}^{(b,c)}$, with b ≠ c, so that n = n_be_b + n_ce_c, n_b, n_c > 0, and n_b + n_c = n. Suppose the configuration immediately prior to the younger mutation event is l_y = me_b + e_c. The configuration at the older mutation event must be e_a + e_b. Arguing as in previous subsections yields the following:

Lemma 4.4. Conditional on $E_{2ℬ}^{(b,c)}$, on the sample configuration n = n_be_b + n_ce_c, and on the sample configuration l_y = me_b + e_c immediately before the time of the younger mutation event, the distribution of compatible histories ℋ_2ℬ is uniform. It is given by

$$p({\mathbf{\mathscr{H}}}_{2ℬ}|E_{2ℬ}^{(b,c)},{\mathit{l}}_y)={\left(\begin{array}{c}\hfill n-m-1\hfill \\ \hfill n_c-1\hfill \end{array}\right)}^{-1}.$$

Moreover, the (unconditional) probability of such histories is

$$\begin{array}{cc}p({\mathbf{\mathscr{H}}}_{2ℬ})\hfill & =p({\mathbf{\mathscr{H}}}_{2ℬ},E_{2ℬ}^{(b,c)},\mathit{n},{\mathit{l}}_y)\hfill \\ \hfill & =\frac{{\theta }^2}{1+\theta }{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}\frac{(n_b-1)!(n_c-1)!}{{(1+\theta )}_{n-1}}\frac{1}{(m+1)(m+\theta )}.\hfill \end{array}$$ (13)

Hence, summing over compatible histories and over m, we obtain

$$\begin{array}{cc}p(\mathit{n},E_{2ℬ}^{(b,c)})\hfill & ={\displaystyle \sum _{m=1}^{n_b}}\left(\begin{array}{c}\hfill n-m-1\hfill \\ \hfill n_c-1\hfill \end{array}\right)p({\mathbf{\mathscr{H}}}_{2ℬ})\hfill \\ \hfill & =\{\begin{array}{c}\frac{{\theta }^2}{1+\theta }{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}\frac{(n-1)!}{{(1+\theta )}_{n-1}}{\displaystyle \sum _{m=1}^{n_b}}\frac{\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m\hfill \end{array}\right)}\frac{1}{m(m+1)(m+\theta )},\hfill \\ \begin{array}{cc}\hfill & \text{if}\mathit{n}=n_b{\mathit{e}}_b+n_c{\mathit{e}}_c,\text{where}a,b,c\text{are all distinct},\text{and}1\le n_b,n_c\le n;\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\hfill \end{array}\hfill \end{array}$$ (14)

Finally, when b = c the sample must be of the form n = n_be_b, and the probability of observing such a configuration as a result of two mutation events on the basal branches is given by

$$\begin{array}{cc}p(\mathit{n},E_{2ℬ}^{(b,b)})\hfill & ={\displaystyle \sum _{k=1}^{n-1}}p(\mathit{k}{\mathit{e}}_b+(n-k){\mathit{e}}_c,E_{2ℬ}^{(b,c)}){|}_{b=c}\hfill \\ \hfill & =\{\begin{array}{cc}\frac{{\theta }^2}{1+\theta }{(P_{\mathit{\text{ab}}})}^2\frac{(n-1)!}{{(1+\theta )}_{n-1}}{\displaystyle \sum _{m=1}^{n-1}}\frac{1}{m(m+1)(m+\theta )},\hfill & \text{if}\mathit{n}=\mathit{n}{\mathit{e}}_b,\hfill \\ 0,\hfill & \text{otherwise}.\hfill \end{array}\hfill \end{array}$$

5. The limit θ → 0

To make further progress, we derive expressions in the limit as θ → 0. Results are therefore approximate for nonzero θ, but should still exhibit good accuracy when applied to human single-nucleotide polymorphism data for example, for which θ is small, as noted in the introduction.

Our results will be expressed in terms of harmonic numbers, for which we use the following notation:

$$H_n={\displaystyle \sum _{j=1}^n}\frac{1}{j},\text{ and }{H}_n^{(2)}={\displaystyle \sum _{j=1}^n}\frac{1}{j^2}.$$

Further, let $c_n^{(s)}$ denote the sth order generalized harmonic number (Roman, 1993), defined for s ≥ 0 and n ≥ 1 by

$$c_n^{(s)}=\{\begin{array}{cc}1,\hfill & \text{if}s=0,\hfill \\ {\displaystyle \sum _{j=1}^n}\frac{c_j^{(s-1)}}{j},\hfill & \text{if}s>0.\hfill \end{array}$$

In particular,

$$c_n^{(1)}=H_n,\text{ and }{c}_n^{(2)}={\displaystyle \sum _{j=1}^n}\frac{H_j}{j}=\frac{1}{2}[{(H_n)}^2+H_n^{(2)}].$$ (15)

This last identity is easily verified by induction on n. To simplify notation, we also introduce the function

$$d(n_a,n_b,n_c)=\frac{1}{(n_a+n_b)(n_a+n_b-1)}\left[1+\frac{n}{n_c}-\frac{2n(H_n-H_{n_c-1})}{n_a+n_b+1}\right],$$ (16)

where n = n_a + n_b + n_c.

Theorem 5.1. As θ → 0, the joint probability of observing a particular sample configuration n together with the topological characterization of the genealogy satisfies:

$$\begin{array}{cc}p(\mathit{n},E_1)=\frac{\theta P_{\mathit{\text{ab}}}}{n_b}-{\theta }^2{P}_{\mathit{\text{ab}}}[\frac{H_{n-1}}{n_b}+\frac{1}{n_a}(H_n-H_{n_b-1})]+O({\theta }^3),\hfill & \mathit{\text{if}}\mathit{n}=n_a{\mathit{e}}_a+n_b{\mathit{e}}_b\mathit{\text{ and }}0\mathit{\text{ otherwise}},\hfill \end{array}$$ (17)

$$\begin{array}{cc}p(\mathit{n},E_{2𝒩}^{(b,c)})={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}d(n_a,n_b,n_c)+O({\theta }^3),\hfill & \mathit{\text{if}}\mathit{n}=n_a{\mathit{e}}_a+n_b{\mathit{e}}_b+n_c{\mathit{e}}_c\mathit{\text{ and }}0\mathit{\text{ otherwise}},\hfill \end{array}$$ (18)

$$\begin{array}{cc}p(\mathit{n},E_{2𝒩}^{(b,a)})={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ba}}}\left[\frac{1}{n_b+1}\right[1-\frac{n}{n_b}(H_{n-1}-H_{n_a-1})]+\frac{H_n-1}{n-1}]+O({\theta }^3),\hfill & \mathit{\text{if}}\mathit{n}=n_a{\mathit{e}}_a+n_b{\mathit{e}}_b\mathit{\text{ and }}0\mathit{\text{ otherwise}},\hfill \end{array}$$ (19)

$$\begin{array}{cc}p(\mathit{n},E_{2𝒩𝒩}^{(b,c)})={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}[\frac{1}{n_c(n_b+n_c)}-d(n_a,n_b,n_c)]+O({\theta }^3),\hfill & \mathit{\text{if}}\mathit{n}=n_a{\mathit{e}}_a+n_b{\mathit{e}}_b+n_c{\mathit{e}}_c\mathit{\text{ and }}0\mathit{\text{ otherwise}},\hfill \end{array}$$ (20)

$$\begin{array}{cc}p(\mathit{n},E_{2𝒩𝒩}^{(b,b)})={\theta }^2{P}_{\mathit{\text{ab}}}^2[\frac{H_{n_b-1}}{n_b}-\frac{1}{n_a+1}[1-\frac{n}{n_a}(H_{n-1}-H_{n_b-1})]-\frac{H_n-1}{n-1}]+O({\theta }^3),\hfill & \mathit{\text{if}}\mathit{n}=n_a{\mathit{e}}_a+n_b{\mathit{e}}_b\mathit{\text{ and }}0\mathit{\text{ otherwise}},\hfill \end{array}$$ (21)

$$\begin{array}{cc}p(\mathit{n},E_{2𝒮}^{(b,c)})=\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{n_a}[\frac{n}{n_a+1}(H_n-H_{n_c-1})-1]+O({\theta }^3),\hfill & \mathit{\text{if}}\mathit{n}=n_a{\mathit{e}}_a+n_c{\mathit{e}}_c\mathit{\text{ and }}0\mathit{\text{ otherwise}},\hfill \end{array}$$ (22)

$$\begin{array}{cc}p(\mathit{n},E_{2𝒮}^{(b,a)})={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ba}}}[1-\frac{1}{n}]+O({\theta }^3),\hfill & \mathit{\text{if}}\mathit{n}=n{\mathit{e}}_a\mathit{\text{ and }}0\mathit{\text{ otherwise}},\hfill \end{array}$$ (23)

$$\begin{array}{cc}p(\mathit{n},E_{2ℬ}^{(b,c)})=\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n_b+1}[1-\frac{n_c-1}{n_b}(H_{n-1}-H_{n_c-1})]+O({\theta }^3),\hfill & \mathit{\text{if}}\mathit{n}=n_b{\mathit{e}}_b+n_c{\mathit{e}}_c\mathit{\text{ and }}0\mathit{\text{ otherwise}},\hfill \end{array}$$ (24)

$$\begin{array}{cc}p(\mathit{n},E_{2ℬ}^{(b,b)})={\theta }^2{P}_{\mathit{\text{ab}}}^2[H_{n-1}^{(2)}-1+\frac{1}{n}]+O({\theta }^3),\hfill & \mathit{\text{if}}\mathit{n}=n{\mathit{e}}_b\mathit{\text{ and }}0\mathit{\text{ otherwise}},\hfill \end{array}$$ (25)

where a, b, c are all distinct.

Proof. See Appendix A.

We illustrate the use of Theorem 5.1 with two simple applications. First, it can be used to calculate the sample frequency spectrum of a site that has undergone two mutations. Figure 3 shows the sample frequency spectrum conditional on E₂, for a diallelic model with alleles 1 and 2, a = 1 being ancestral $[\text{so }P=\left(\begin{array}{cc}0\hfill & 1\hfill \\ 1\hfill & 0\hfill \end{array}\right)]$. Suppose we have a large quantity of SNP data, which we incorrectly assume to satisfy the infinite sites model. The occasional second mutation will distort the frequency spectrum. Figure 3 shows that if we had used equation (1) to predict the sample frequency spectrum at a site that had in fact undergone two mutation events, then the main effect would be to slightly underestimate the probability that a mutant is seen in moderate to high frequency, and to grossly overestimate the probability that a mutant is at very low frequency. This does not mean, however, that we should expect the sample frequency spectrum of a site undergoing at most two mutation events to be strongly affected. An upper bound on this effect can be found by considering the distribution of the number of mutation events (Tavaré, 1984):

$$p(E_s)=\frac{n-1}{\theta }{\displaystyle \sum _{j=1}^{n-1}}{(-1)}^{j-1}\left(\begin{array}{c}n-2\hfill \\ j-1\hfill \end{array}\right){\left(\frac{\theta }{j+\theta }\right)}^{s+1}.$$ (26)

Figure 3.

The sample frequency spectrum for a diallelic model with n = 40, conditional on one or two mutation events having occurred (line and stacked bars, respectively), as θ → 0. Monomorphic samples that are a result of two mutations have been included (E_2𝒮 and E_2ℬ); hence, to be directly comparable the plot for one mutation has been scaled down to sum to p(E_2𝒩 | E₂) + p(E_2𝒩𝒩 | E₂).

For example, suppose we compare a histogram of allele frequencies from SNP data with the distribution (1). When θ = 0.01, equation (26) tells us that polymorphic sites resulting from more than one mutation will make up at most 2.3% of the area under the histogram. In other words, we expect the effect of recurrent mutation on the sample frequency spectrum of a randomly chosen polymorphic site to be small. For recurrent mutation to have an appreciable effect, it requires a higher mutation rate (see Table 1).

Table 1.

The probability that the genealogy for a sample of n = 40 gametes contains 0, 1, 2, or more than two mutations, and the probability of more than one mutation conditional on at least one.

θ	p(E0)	p(E1)	p(E2)	p(E≥3)	p(E≥2 | E≥1)
0.001	0.9958	0.0042	0.0000	0.0000	0.0023
0.01	0.9584	0.0406	0.0009	0.0000	0.0229
0.05	0.8100	0.1691	0.0192	0.0017	0.1099
0.1	0.6586	0.2702	0.0601	0.0111	0.2085

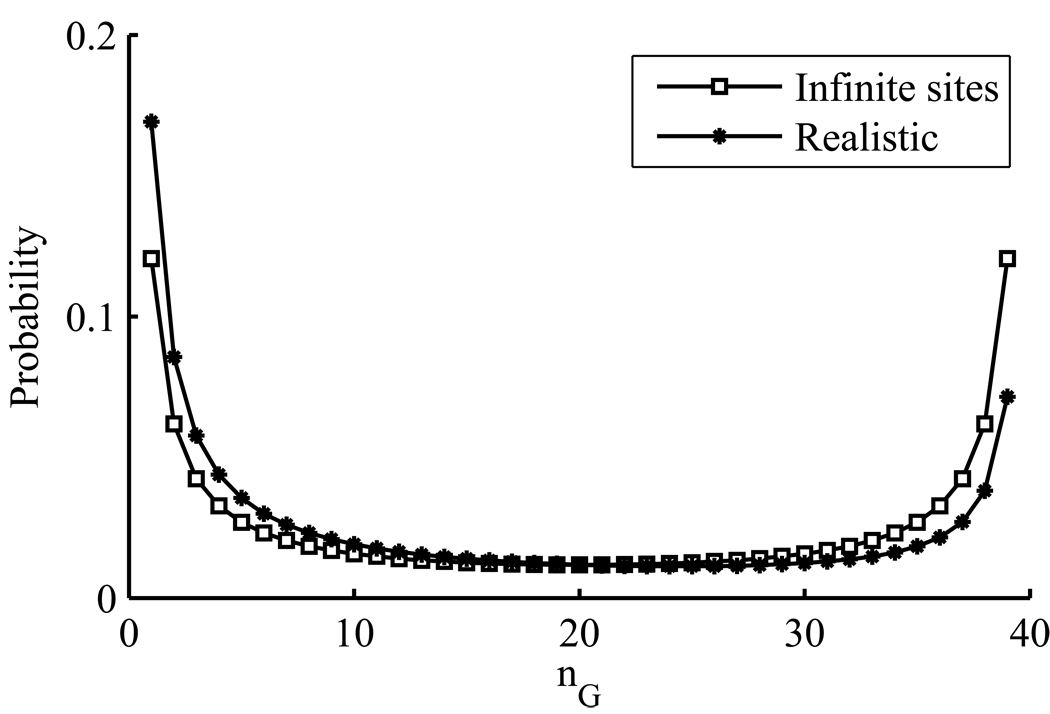
The diallelic model considered above can be seen as a crude approximation of the evolution of a single nucleotide, in which say the transversion rate is zero. A second application of Theorem 5.1 is to investigate more realistic models of sequence evolution, also incorporating uncertainty over the allele of the MRCA. Now let K = 4, representing the nucleotides A, G, C, and T. One way to set a general matrix P is to match its entries to empirical estimation of rates of mutation; for illustration we use those reported in Table 1 of Tamura and Nei (1993) for a human mtDNA sequence dataset (normalizing so that each nucleotide has the same overall mutation rate). Suppose our prior probabilities for the identity of the ancestral nucleotide are (π_A, π_G, π_C, π_T); they may be based on, for example, an outgroup sequence allowing for some probability of error, on the stationary distribution of P, or on empirical base frequencies. Here we use the last option (Tamura and Nei, 1993): (π_A, π_G, π_C, π_T) = (0.321, 0.132, 0.314, 0.233). Equation (17) makes explicit how we should use prior information on the distribution of the MRCA. For example, if we observe an A-G polymorphism, then:

$$\begin{array}{cc}{p}_u(n_{\mathrm{A}}{\mathit{e}}_{\mathrm{A}}+n_{\mathrm{G}}{\mathit{e}}_{\mathrm{G}}|E_1,\{n_{\mathrm{A}},n_{\mathrm{G}}>0\})\hfill & =\frac{{\displaystyle {\sum }_{a\in \{\mathrm{A},\mathrm{G}\}}{\pi }_{a}p(n_a{\mathit{e}}_a+n_{\overline{a}}{\mathit{e}}_{\overline{a}},E_1)}}{p(E_1,\{n_{\mathrm{A}},n_{\mathrm{G}}>0\})}\hfill \\ \hfill & =\frac{{\pi }_{\mathrm{A}}{P}_{\text{AG}}{n}_{\mathrm{G}}^{-1}+{\pi }_{\mathrm{G}}{P}_{\text{GA}}{n}_{\mathrm{A}}^{-1}}{H_{n-1}({\pi }_{\mathrm{A}}{P}_{\mathrm{\text{AG}}}+{\pi }_{\mathrm{G}}{P}_{\text{GA}})}+O(\theta ).\hfill \end{array}$$ (27)

The subscript u is used to denote that the allele of the MRCA is unknown here. We sum a over possible ancestral alleles; the mutant allele is denoted ā. The sample frequency spectrum according to (27), ignoring terms of O(θ), is shown in Figure 4. As is clear from the figure, uncertainty over the MRCA introduces modes at both n_G = 1 and n_G = n − 1, with relative heights determined by π_AP_AG and π_GP_GA. By contrast, a classical approach is equivalent to assuming π_AP_AG = π_GP_GA, leading to a symmetric frequency spectrum; for this reason it is common to report a folded spectrum by binning values for each (n_G, n − n_G) pair, n_G = 1, …, n − 1. Figure 4 demonstrates how additional prior information on the ancestral allele can be incorporated properly, in this example leading to a shift in favour of the mode at n_G = 1 so that the spectrum is no longer symmetric. We also repeated this analysis using equations (19), (21), (22), and (24) to allow for up to two mutations to explain a diallelic site, with the sample frequency spectrum left almost unchanged, as discussed above.

Figure 4.

The sample frequency spectrum of a sample of size n = 40 under realistic assumptions about rates of mutation. The rate matrix P and a distribution over the ancestral allele are based on empirical data described in the main text [see equation (27)]. Also shown is the usual, infinite sites, frequency spectrum when the ancestral allele is unknown (i.e. the folded frequency spectrum, unfolded here for comparison).

We can sum over all possible outcomes for n, b, and c in Theorem 5.1 in order to find the probabilities of the four events illustrated in Figure 2.

Theorem 5.2. The distribution of the number of mutation events, satisfies

$$p(E_s){\displaystyle \sum _{j=0}^{\mathrm{\infty }}}{\theta }^{s+j}{C}_{n-1}^{(s+j)}{(-1)}^j\left(\begin{array}{c}s+j\hfill \\ \hfill j\hfill \end{array}\right).$$ (28)

The series converges for θ < 1. Further, as θ → 0,

$$p(E_{2𝒩}^{(b,c)})=P_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}p(E_{2𝒩})={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}[H_n+\frac{1}{n}-2]+O({\theta }^3),$$ (29)

$$p(E_{2𝒩𝒩}^{(b,c)})=P_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}p(E_{2𝒩𝒩})={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}[\frac{{(H_{n-1})}^2}{2}-\frac{H_{n-1}^{(2)}}{2}-H_n-\frac{1}{n}+2]+O({\theta }^3),$$ (30)

$$p(E_{2𝒮}^{(b,c)})=P_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}p(E_{2𝒮})={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}\left[1-\frac{1}{n}\right]+O({\theta }^3),$$ (31)

$$p(E_{2ℬ}^{(b,c)})=P_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}p(E_{2ℬ})={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}\left[H_{n-1}^{(2)}-1+\frac{1}{n}\right]+O({\theta }^3).$$ (32)

Proof. See Appendix A.

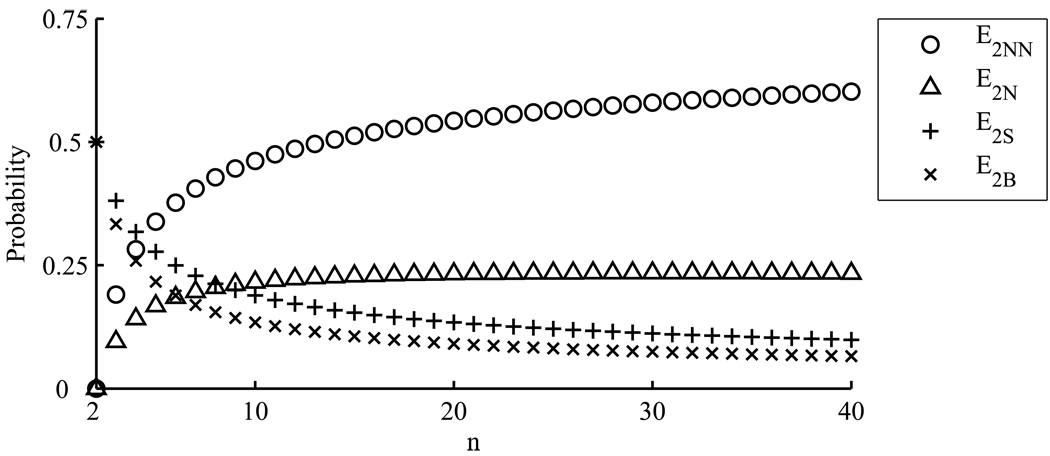
As an application of these results, one can ask: Conditional on precisely two mutation events, what are the probabilities of the four possible outcomes illustrated in Figure 2? Using equations (28) and (29)–(32) and letting θ → 0 yields:

$$\begin{array}{cc}p(E_{2𝒩}|E_2)=\frac{H_n+\frac{1}{n}-2}{c_{n-1}^{(2)}},\hfill & p(E_{2𝒩𝒩}|E_2)=1-\frac{H_{n-1}^{(2)}+H_n+\frac{1}{n}-2}{c_{n-1}^{(2)}},\hfill \\ p(E_{2𝒮}|E_2)=\frac{1-\frac{1}{n}}{c_{n-1}^{(2)}},\hfill & p(E_{2ℬ}|E_2)=\frac{H_{n-1}^{(2)}-1+\frac{1}{n}}{c_{n-1}^{(2)}}.\hfill \end{array}$$

Since $c_{n-1}^{(2)}$ grows like (log n)² with increasing n, we have that p(E_2𝒩 | E₂) declines to zero like 1/log n, p(E_2𝒮 | E₂) and p(E_2ℬ | E₂) decline to zero like 1/(log n)², while p(E_2𝒩𝒩 | E₂) slowly approaches 1 (see Figure 5). Using Theorem 5.1, in a similar manner one could find the relative probabilities of these topologies conditional on the data.

Figure 5.

The probability of each of the four possible topologies conditional on two mutation events as θ → 0. Plots are for two nonnested mutations (E_2𝒩𝒩), two nested mutations (E_2𝒩), two mutations on the same branch (E_2𝒮), and two mutations on the basal branches (E_2ℬ).

6. Observed patterns of polymorphism

We can partition the space of coalescent trees in two ways: either by the topology of the tree, as in Sections 3 and 4, or by the observed pattern of polymorphism. In practice, it is the latter that is important since only these are known. Our next goal is therefore to find expressions for the sample frequency spectrum conditional on observed events. Assuming at most two mutations, the only possible observed outcomes are:

• O₁: No variation, with all alleles ancestral. The sample is of the form n = ne_a.

• O_1𝒮: No variation, but the observed allele differs from that of the MRCA. The sample is of the form n = ne_b, where b ≠ a.

• O₂: A regular diallelic polymorphism, with both the ancestral allele and a mutant allele observed. The sample is of the form n = n_ae_a + n_be_b, where b ≠ a.

• O_2𝒮: A diallelic polymorphism in which the ancestral allele is not observed; instead, we see two mutant alleles. The sample is of the form n = n_be_b + n_ce_c, where a, b, c are all distinct.

• O₃: A triallelic polymorphism, with one observed allele ancestral. The sample is of the form n = n_ae_a + n_be_b + n_ce_c, where a, b, c are all distinct.

Note that we assume that the allele of the MRCA is known without error. However, if one observed O_1𝒮 or O_2𝒮 in practice, then another explanation is that the allele of the MRCA inferred from the outgroup is incorrect, and that a substitution has occurred on the lineage between the MRCA of the sample and the outgroup.

Using the superscript T to denote matrix transpose, we have the following theorem:

Theorem 6.1. As θ → 0, the joint probability of two mutations occurring and the observed pattern of polymorphism is given by:

$$p(O_1,E_2)={\theta }^2{(P^2)}_{\mathit{\text{aa}}}(1-\frac{1}{n})+O({\theta }^3),$$ (33)

$$p(O_{1𝒮},E_2)={\theta }^2{({\mathit{\text{PP}}}^T)}_{\mathit{\text{aa}}}(H_{n-1}^{(2)}-1+\frac{1}{n})+O({\theta }^3),$$ (34)

$$p(O_2,E_2)={\theta }^2\left[{(P^2)}_{\mathit{\text{aa}}}\right(H_n+\frac{1}{n}-2)+(1-{(P^2)}_{\mathit{\text{aa}}})(1-\frac{1}{n})+{({\mathit{\text{PP}}}^T)}_{\mathit{\text{aa}}}(\frac{{(H_{n-1})}^2}{2}-\frac{H_{n-1}^{(2)}}{2}-H_n-\frac{1}{n}+2\left)\right]+O({\theta }^3),$$ (35)

$$p(O_{2𝒮},E_2)={\theta }^2(1-{({\mathit{\text{PP}}}^T)}_{\mathit{\text{aa}}})(H_{n-1}^{(2)}-1+\frac{1}{n})+O({\theta }^3),$$ (36)

$$p(O_3,E_2)={\theta }^2[(1-{(P^2)}_{\mathit{\text{aa}}})(H_n+\frac{1}{n}-2)+(1-{({\mathit{\text{PP}}}^T)}_{\mathit{\text{aa}}})(\frac{{(H_{n-1})}^2}{2}-\frac{H_{n-1}^{(2)}}{2}-H_n-\frac{1}{n}+2\left)\right]+O({\theta }^3).$$ (37)

Proof. See Appendix A.

As above, we may also consider the relative probability of these events conditional on precisely two mutations having occurred. Again, this entails normalizing equations (33)–(37) by dividing by $p(E_2)={\theta }^2{c}_{n-1}^{(2)}+O({\theta }^3)$, and then letting θ → 0. The relative probabilities of these outcomes is illustrated in Figure 6, for a simple 4 × 4 mutation model with each nondiagonal entry in P equal to 1/3.

Figure 6.

The probability of each possible observable outcome given two mutation events, as θ → 0: a triallelic polymorphism (O₃), a regular polymorphism with one allele ancestral and one mutant (O₂), a polymorphism in which both observed alleles are mutant (O_2𝒮), the entire sample is ancestral (O₁), and the entire sample has a mutant allele (O_1𝒮). Here we take a mutation model of four alleles, in which any mutation is to one of the other alleles with probability 1/3.

Further variations on the arguments of Theorem 6.1 are possible. For example, one can proceed in a similar vein by summing over the relevant probabilities in Theorem 5.1, in order to find closed-form expressions for the joint probability of the above events together with a particular sample configuration, n. The resulting expressions are easy to obtain but do not simplify very much, so we do not give them explicitly. There is however one important exception which we now consider in further detail. If we observe a triallelic site then we know that at least two mutations must have taken place, and we would like to know the joint sample frequency spectrum for the number of copies of each of the two mutant alleles.

Theorem 6.2. As θ → 0,

$$p(\mathit{n}|O_3)=\frac{1}{C}[P_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}d(n_a,n_b,n_c)+P_{\mathit{\text{ac}}}{P}_{\mathit{\text{cb}}}d(n_a,n_c,n_b)+P_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}(\frac{1}{n_b{n}_c}-d(n_a,n_b,n_c)-d(n_a,n_c,n_b))],$$ (38)

if n = n_ae_a + n_be_b + n_ce_c, and 0 otherwise, where d(n_a, n_b, n_c) is given by equation (16), and

$$C=[(1-{(P^2)}_{\mathit{\text{aa}}})(H_n+\frac{1}{n}-2)+(1-{({\mathit{\text{PP}}}^T)}_{\mathit{\text{aa}}})(\frac{{(H_{n-1})}^2}{2}-\frac{H_{n-1}^{(2)}}{2}-H_n-\frac{1}{n}+2\left)\right].$$ (39)

Proof. See Appendix A.

We remark that there is no need to condition on E₂ in Theorem 6.2, since O₃ requires at least two mutations, and more than two mutations occurs with probability O(θ³). Furthermore, as we noted in the introduction, Theorem 6.2 is unchanged when we allow P_ii > 0 for any i, since such a “self”-mutation could not lead to O₃ without additional mutations. This is true of all our results for which we condition on O₃, and so for the remainder of this section and for Section 7 we can drop the constraint that the diagonal of P is zero.

Equation (38) simplifies a great deal when the mutation transition matrix takes on a particular form, which we state in the following corollary.

Corollary 6.1. Suppose the mutation transition matrix P satisfies (2). Then, as θ → 0,

$$p(\mathit{n}|O_3)=\frac{P_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{C{n}_b{n}_c},$$ (40)

if n = n_ae_a + n_be_b + n_ce_c, and 0 otherwise, where the normalizing constant C is given by (39).

For the remainder of this section we continue to assume (2) holds. Employing similar arguments, we have that, conditional on observing two particular alleles b and c, the sample frequency spectrum is

$$\underset{\theta \to 0}{\text{lim}}p(\mathit{n}|O_3,\{n_b,n_c>0\})=\frac{{(n_b{n}_c)}^{-1}}{{(H_{n-1})}^2-H_{n-1}^{(2)}},\mathit{n}=n_a{\mathit{e}}_a+n_b{\mathit{e}}_b+n_c{\mathit{e}}_c,$$ (41)

and the marginal spectrum for a particular mutant allele, given that we have observed it, is

$$\underset{\theta \to 0}{\text{lim}}p(n_b|O_3,\{n_b>0\})=\frac{H_{n-n_b-1}{(n_b)}^{-1}}{{(H_{n-1})}^2-H_{n-1}^{(2)}},1\le n_b\le n-2.$$ (42)

One can check that the normalizing constant is correct by summing (42) over n_b, and using the identity

$${\displaystyle \sum _{j=1}^{n-1}}\frac{H_{n-j}}{j}={(H_n)}^2-H_n^{(2)},$$

for n ≥ 2, which is easily verified by induction on n.

Similarly, the marginal spectrum for a particular allele, given that we have observed it and conditional on the number of copies of the other mutant allele, is

$$\underset{\theta \to 0}{\text{lim}}p(n_b|O_3,\{n_b>0\},n_c)=\frac{{(n_b)}^{-1}}{H_{n-n_c-1}},1\le n_b\le n-n_c-1,n_c\ge 1.$$ (43)

Interestingly, the distribution for n_b is proportional to $n_b^{-1}$ regardless of n_c. More generally, Corollary 6.1 tells us: as θ → 0, and given that we observe three particular alleles, one of which is the ancestral allele, the sample frequency spectrum for the two mutant alleles is proportional to the inverse of the product of the number of observed copies of each of the two mutant alleles (scaled by the relative rate P_abP_ac of appearance of these two alleles). This result is a straightforward generalization of the classical result (1), with some mild conditions on P.

There is another way to arrive at Corollary 6.1 when P satisfies (2), and which immediately generalizes to any number of observed alleles, O_l, 2 ≤ l ≤ K. An l-allele version of (2) is to suppose that P_ij = P_j whenever j is an observed mutant allele and i is a different observed mutant allele or the observed ancestral allele. We refer to this condition as parent-independence among observed alleles.

Theorem 6.3. Suppose that we observe l distinct alleles, one of which is the ancestral allele a and the rest are labelled by the set Λ ⊆ {1, …, K}\{a}. Further suppose that P is parent-independent among observed alleles. Then, as θ → 0,

$$p(\mathit{n}|O_l)\mathrm{\propto }{\displaystyle \prod _{j\in \mathrm{\Lambda }}}\frac{P_j}{n_j}.$$

Proof. See Appendix A.

7. The age of a mutant allele

In this section we will be interested in the population limits n_a/n → f_a, n_b/n → f_b, and n_c/n → f_c as n → ∞, and it is implicit throughout that we let θ → 0 and that a, b, c are all distinct. We assume that there have been no more than two mutation events in the history of the population, so f_a + f_b + f_c = 1. Let f = (f_a, f_b, f_c), and A_b, A_c denote the ages at which mutations occurred that gave rise to alleles b and c respectively. Kimura and Ohta (1973) showed that the expected age of a single mutant allele at frequency f in the population is

$$-\frac{2f}{1-f}\text{ln}f.$$

Griffiths and Tavaré (2003) found the expected age of the younger of two nested mutant alleles to be

$$\mathrm{𝔼}[A_c|E_{2𝒩}^{(b,c)},\mathit{f}]=-2f_c\frac{(1+f_c)\text{ ln }{f}_c+2(1-f_c)}{2f_c\text{ ln }{f}_c+(1+f_c)(1-f_c)}.$$ (44)

Here, we extend this result to find the expected age of the younger of two nonnested mutant alleles. From this it is straightforward to obtain the expected age of the younger allele at a triallelic site, regardless of whether the mutations are nested or nonnested—and indeed regardless of whether we know which of the two mutant alleles is younger.

Theorem 7.1. When it is known which of two nonnested mutant alleles is the younger, the expected age of the younger allele is

$$\mathrm{𝔼}[A_c|E_{2𝒩𝒩}^{(b,c)},\mathit{f}]=2f_c\frac{[1+f_c-\frac{{(1-f_c)}^2}{f_b}]\text{ ln }{f}_c+2(1-f_c)+\frac{{(1-f_c)}^3\text{ ln }(f_b+f_c)}{f_b(1-f_b-f_c)}}{\frac{{(1-f_c)}^3}{f_b+f_c}-2f_c\text{ ln }{f}_c-(1+f_c)(1-f_c)}.$$ (45)

Proof. See Appendix A.

Let A denote the age of the younger of two mutant alleles at a triallelic site, when we do not know which of the two is younger. Our goal now is to compute its expectation given the frequencies of the two mutant alleles in the population. This can be achieved by averaging over the possible topologies that could have given rise to a triallelic site:

$$\mathrm{𝔼}[A|O_3,\mathit{f}]=\mathrm{𝔼}[A_c|E_{2𝒩}^{(b,c)},\mathit{f}]p(E_{2𝒩}^{(b,c)}|O_3,\mathit{f})+\mathrm{𝔼}[A_c|E_{2𝒩𝒩}^{(b,c)},\mathit{f}]p(E_{2𝒩𝒩}^{(b,c)}|O_3,\mathit{f})+\mathrm{𝔼}[A_b|E_{2𝒩}^{(c,b)},\mathit{f}]p(E_{2𝒩}^{(c,b)}|O_3,\mathit{f})+\mathrm{𝔼}[A_b|E_{2𝒩𝒩}^{(c,b)},\mathit{f}]p(E_{2𝒩𝒩}^{(c,b)}|O_3,\mathit{f}).$$ (46)

The expectation in each term on the right-hand side is given by equations (44), (45) and their analogues (interchanging the roles of b and c). The probabilities on the right-hand side are also known, since

$$p(E_{2𝒩}^{(b,c)}|O_3,\mathit{f})=\frac{p(\mathit{f},E_{2𝒩}^{(b,c)})}{p(\mathit{f},O_3)},$$

and these terms are found by letting n_b/n → f_b and n_c/n → f_c while n → ∞ in equations (18), (37), and (38). A similar argument applies for the other three terms. We obtain

$$\begin{array}{cc}p(E_{2𝒩}^{(b,c)}|O_3,\mathit{f})\hfill & =\frac{P_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{D{(1-f_c)}^2}(1+\frac{1}{f_c}+\frac{2\text{ ln }{f}_c}{1-f_c}),\hfill \\ p(E_{2𝒩𝒩}^{(b,c)}|O_3,\mathit{f})\hfill & =\frac{P_{\mathit{\text{ab}}}{P}_{\text{ac}}}{D}[\frac{1}{f_b(f_b+f_c)}-\frac{1}{{(1-f_c)}^2}(1+\frac{1}{f_c}+\frac{2\text{ ln }{f}_c}{1-f_c}\left)\right],\hfill \end{array}$$

with similar expressions for $p(E_{2𝒩}^{(c,b)}|O_3,\mathit{f})\text{ and }p(E_{2𝒩𝒩}^{(c,b)}|O_3,\mathit{f})$, where

$$\begin{array}{cc}D\hfill & =p(E_{2𝒩}^{(b,c)}|O_3,\mathit{f})+p(E_{2𝒩}^{(c,b)}|O_3,\mathit{f})+p(E_{2𝒩𝒩}^{(b,c)}|O_3,\mathit{f})+p(E_{2𝒩𝒩}^{(c,b)}|O_3,\mathit{f})\hfill \\ \hfill & =\frac{P_{\mathit{\text{ab}}}(P_{\mathit{\text{bc}}}-P_{\mathit{\text{ac}}})}{{(1-f_c)}^2}(1+\frac{1}{f_c}+\frac{2\text{In}{f}_c}{1-f_c})+\frac{P_{\mathit{\text{ac}}}(P_{\mathit{\text{cb}}}-P_{\mathit{\text{ab}}}}{{(1-f_b)}^2}(1+\frac{1}{f_b}+\frac{2\text{In}{f}_b}{1-f_b})+\frac{p_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{f_b{f}_c}.\hfill \end{array}$$

Substituting these expressions, along with (44) and (45), into (46), we obtain the following:

Theorem 7.2. The expected age of the younger of two mutant alleles at a triallelic site is

$$\mathrm{𝔼}[A|O_3,\mathit{f}]=\frac{2P_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{D(1-f_b-f_c)}(\frac{1}{f_b}+\frac{1}{f_c})\text{ ln }(f_b+f_c)+\frac{2P_{\mathit{\text{ab}}}}{D}[(P_{\mathit{\text{ac}}}-P_{\mathit{\text{bc}}})\frac{1+f_c}{{(1-f_c)}^3}-\frac{P_{\mathit{\text{ac}}}}{f_b(1-f_c)}]\text{ ln }{f}_c+\frac{2P_{\mathit{\text{ac}}}}{D}[(P_{\mathit{\text{ab}}}-P_{\mathit{\text{cb}}})\frac{1+f_b}{{(1-f_b)}^3}-\frac{P_{\mathit{\text{ab}}}}{f_c(1-f_b)}]\text{ ln }{f}_b+\frac{4P_{\mathit{\text{ab}}}(P_{\mathit{\text{ac}}}-P_{\mathit{\text{bc}}})}{D{(1-f_c)}^2}+\frac{4P_{\mathit{\text{ac}}}(P_{\mathit{\text{ab}}}-P_{\mathit{\text{cb}}})}{D{(1-f_b)}^2}.$$

When P additionally satisfies (2) for the observed alleles a, b, and c, this expression simplifies to

$$\mathrm{𝔼}[A|O_3,\mathit{f}]=-\frac{2f_b}{1-f_b}\text{ ln }{f}_b-\frac{2f_c}{1-f_c}\text{ ln }{f}_c+\frac{2(f_b+f_c)}{1-(f_b+f_c)}\text{ ln }(f_b+f_c).$$ (47)

This curious result, for mutation models satisfying (2), tells us that the mean age of the younger of two mutant alleles at a triallelic site is equal to the sum of the mean ages of two independent mutations at frequencies f_b and f_c, minus the mean age of a single mutant at frequency f_b + f_c. Equation (47) is plotted in Figure 8, for various values of f_b and f_c.

Figure 8.

The expected age of the younger of two mutant alleles at a triallelic site [equation (47)]. The mutant alleles are at frequencies f_b (annotated) and f_c (x-axis). The expected age of a single mutant at a diallelic site and at frequency f_c is shown for comparison (dotted line).

Unfortunately, a corresponding expression for the expected age of the older mutation is not analytically tractable, even if we restrict our attention to nested mutations. Hobolth and Wiuf (2009) outline a method of numerical approximation which could also be adapted for nonnested mutations, but we do not pursue this here.

8. Accuracy

It would be interesting to investigate the accuracy of the expressions given in the previous section. For simplicity, we focus on equation (41), and we assume a simple Jukes-Cantor model of mutation in which K = 4, and the daughter allele of each mutation is equally likely, so that off-diagonal entries of P are all 1/3. We wrote a program to solve numerically the system of equations defined by (3), in order to obtain exact results for the sample frequency spectrum for nonzero θ. By solving this system for all sample configurations of a given size, we could calculate exact numerical values of p(n | {n_b, n_c > 0}) for each n. We measured the accuracy of equation (41) by its unsigned relative error:

$$\left|\frac{[\underset{\theta \to 0}{\text{lim}}p(\mathit{n}|O_3,\{n_b,n_c>0\})]-p(\mathit{n}|\{n_b,n_c>0\})}{p(\mathit{n}|\{n_b,n_c>0\})}\right|\times 100\%,$$

for each n. Errors in (41) are a consequence of that fact that in reality θ is nonzero and that there may have been more than two mutation events giving rise to the triallelic sample.

For a given sample size and mutation rate, we summarize the discrepancy between the estimated and actual sample frequency spectrum by the largest relative error across all configurations. Results are summarized in Table 2.

Table 2.

Maximum unsigned relative error (%) across configurations, of equation (41) (top) and equation (48) (bottom), for various samples sizes, n, and mutation rates, θ.

Triallelic
	θ
n	0.001	0.01	0.05	0.1	0.5	1.0
10	0.07	0.72	3.52	6.89	30.21	57.02
20	0.13	1.25	6.15	12.04	53.74	112.16
30	0.17	1.61	7.66	14.89	64.78	143.49
40	0.25	2.45	10.57	17.97	70.05	162.82
50	0.35	3.30	13.81	22.81	72.20	175.36
60	0.44	4.16	16.87	27.17	72.52	187.79
Quadrallelic
	θ
n	0.001	0.01	0.05	0.1	0.5	1.0
10	0.11	1.10	5.24	9.92	35.93	82.38
20	0.25	2.45	11.16	20.05	67.95	181.83
30	0.39	3.75	16.30	28.01	90.50	266.17
40	0.52	5.01	20.86	34.51	108.49	342.24
50	0.66	6.22	24.92	39.90	123.70	412.73
60	0.79	7.40	28.58	44.47	136.98	479.09

As is clear from the table, accuracy diminishes with increasing θ and also diminishes modestly with increasing n. For application to human SNPs, in which generally 0.001 ≤ θ ≤ 0.01, equation (41) provides an excellent approximation to the sample frequency spectrum. For comparison, Table 2 also shows the maximum relative error incurred when we use the analogous result from Theorem 6.3 for a quadrallelic polymorphism under parent-independence among observed alleles:

$$\underset{\theta \to 0}{\text{lim}}p(\mathit{n}|O_4,\{n_b,n_c,n_d>0\})\propto \frac{1}{n_b{n}_c{n}_d},$$ (48)

where n = n_ae_a + n_be_b + n_ce_c + n_de_d, and a, b, c, d, are all distinct. It should be noted that the relative error is dependent on the sample configuration. Figure 7 shows the relative error incurred by using (48) for a representative slice of quadrallelic sample configurations, and, as is evident, the size of the unsigned relative error approaches its maximum across configurations near the boundary n_a = 1. When n = 20 and θ = 0.01 the maximum unsigned relative error of 2.45% is attained at (n_a, n_b, n_c, n_d) = (1, 6, 6, 7). For samples containing more than one copy of the ancestral allele, the size of the relative error can be substantially less than its maximum, as Figure 7 confirms. We obtained qualitatively similar patterns for other slices, not shown.

Figure 7.

The (signed) relative error from assuming the sample frequency spectrum of a quadrallelic site is proportional to (n_bn_cn_d)⁻¹ [equation (48)]. Here, the sample size is n = 20 and the mutation parameter is θ = 0.01. Shown are relative errors for a representative slice through the simplex of configurations, defined by fixing n_d = 2. Positive relative errors are shown in dark grey, negative relative errors in light grey.

Errors in the sample frequency spectrum will also cause errors in its application, such as in the estimation of mutation rates and in tests of neutrality. We explore this issue by examining the use of the frequency spectrum to estimate θ. Here we assume a diallelic model (K = 2) in which each mutation toggles an allele between its ancestral and mutant state, as we did for Figure 3. Suppose we have L sites, and record the counts of the number of sites with zero, one, …, n mutant alleles. There are several ways to combine these counts to define an estimator of θ (Achaz, 2009); we focus on S_n, the number of sites observed to be segregating, and ξ₁, the number of sites observed to be singleton mutants [having configuration n = (n − 1, 1)]. Assuming at most one mutation event per site, moment estimates using these statistics follow from Watterson (1975) and Fu (1995):

$$𝔼(S_n)=L\theta H_{n-1},$$ (49)

$$𝔼({\xi }_1)=L\theta ,$$ (50)

where θ is the population-scaled mutation rate per site. These moments can be corrected to allow for up to two mutation events per site. We have

$$𝔼(S_n)=L{\displaystyle \sum _{i=1}^{n-1}}p((n-i,i)),$$ (51)

$$\begin{array}{c}=L[1-p(E_0)-p(E_{2𝒮})-p(E_{2ℬ})]+O({\theta }^3),\hfill \\ =L[\theta H_{n-1}-\frac{{\theta }^2}{2}[{(H_{n-1})}^2+3H_{n-1}^{(2)}]]+O({\theta }^3),\hfill \end{array}$$ (52)

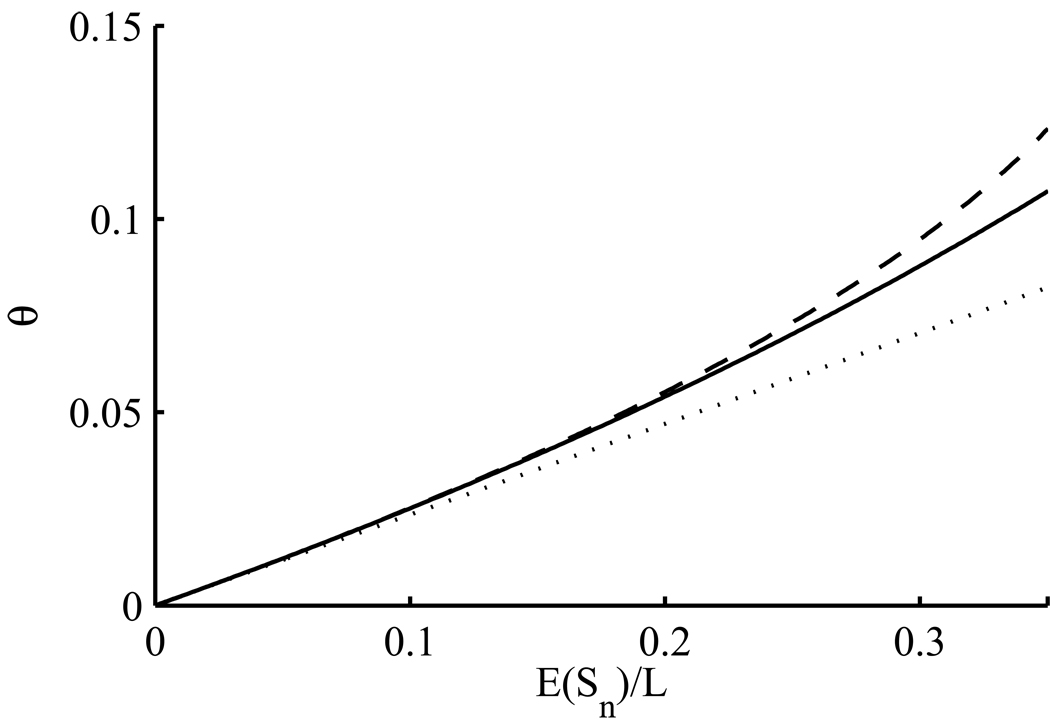
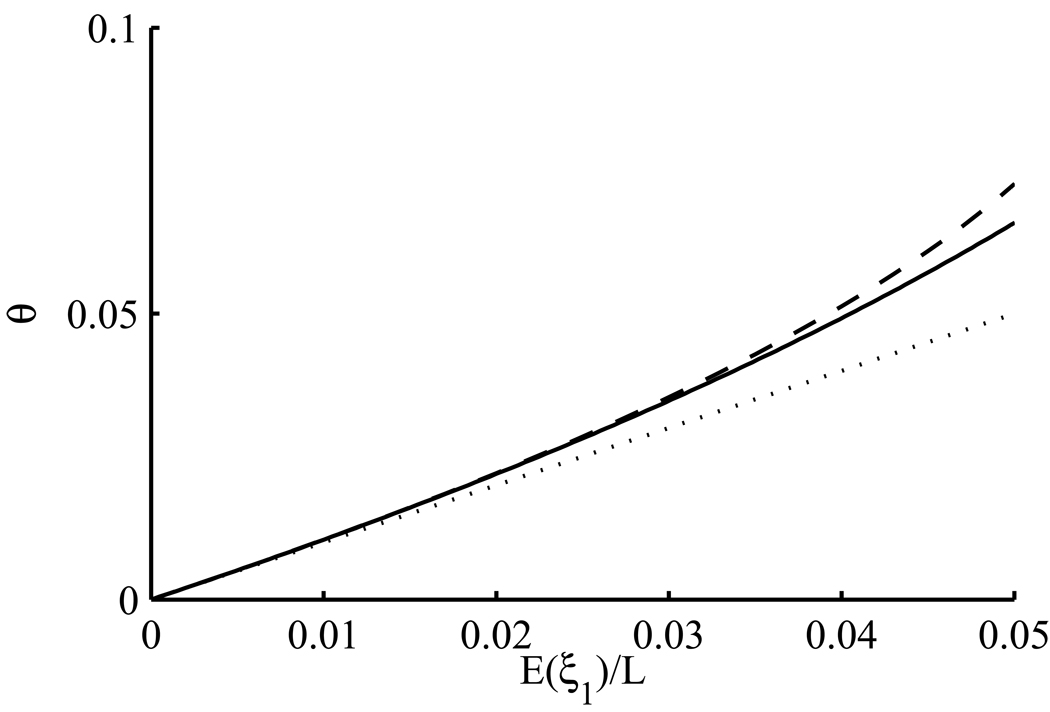
using (28), (31) and (32). If in (52) we drop terms of O(θ³), then we obtain a quadratic equation which can be solved to yield θ in terms of 𝔼(S_n)/L. Replacing this expectation with the observed quantity provides a point estimate of θ. A comparison of this method of estimation with the classical estimate from (49) is given in Figure 9. For comparison, we found the true value of 𝔼(S_n)/L as a function of θ, allowing any number of mutation events, by using our program again to solve the system (3) numerically over a grid of θ-values and plugging the results into (51). This numerical estimate of the relationship between θ and 𝔼(S_n)/L is also plotted on Figure 9. Comparison of this curve with (49) and (52) shows that when few sites are segregating, say s_n/L < 0.1, it is reasonable to assume at most one mutation event per site, whereas for a higher fraction of segregating sites, say s_n/L < 0.25, assuming at most two mutation events per site is still reasonable. When a substantial fraction of sites are segregating, neither assumption is accurate. SNP densities in humans typically have s_n/L < 0.05, so errors from using (49) or (52) will not usually be serious. However, this fraction will only grow in the near future with increasing sample sizes, and regions of the genome of high diversity in cutting-edge datasets already exceed this level (The 1000 Genomes Project Consortium, 2010, Supplementary Figure 3). A similar calculation was performed for 𝔼(ξ₁):

$$𝔼({\xi }_1)=L_p((n-1,1))=L\left[\theta -{\theta }^2\left(H_{n-1}+\frac{3}{2(n-1)}\right)\right]+O({\theta }^3),$$ (53)

with qualitatively very similar results (Figure 10).

Figure 9.

Estimating θ per site by the number s of segregating sites, out of L sites in total. The sample size is n = 40. Estimation of θ assumes at most one mutation event per site [dotted line, (49)], or at most two mutation events per site [dashed line, (52)]. The true relationship between θ and 𝔼(S_n)/L is plotted as a solid line.

Figure 10.

Estimating θ per site by the number ξ₁ of singleton segregating sites, out of L sites in total. The sample size is n = 40. Estimation of θ assumes at most one mutation event per site [dotted line, (50)], or at most two mutation events per site [dashed line, (53)]. The true relationship between θ and 𝔼(ξ₁)/L is plotted as a solid line.

9. Discussion

We have studied the effect of a second mutation on the sample frequency spectrum of a segregating site, under a model of mutation in which the mutation rate is independent of the current allele but the transitions between alleles are otherwise arbitrary. The problem is made tractable by conditioning on whether or not the two mutations are nested in the genealogy, and as a bonus we also obtain the relative probabilities of these topological events. Other key results include the joint sample frequency spectrum of the two mutant alleles at a triallelic site, and the mean age of the younger of the two alleles in the population. These results take on a particularly simple form when we impose mild additional conditions on P, namely (2): Then, the sample frequency spectrum (1) generalizes to ∝ (n_bn_c)⁻¹, and the expected age of the younger mutant is a linear combination of the result for single mutants [equation (47)]. It would be interesting to obtain a more intuitive argument for this formula.

At present, several large-scale projects for various species are under way to resequence the genomes of many individuals (hundreds to thousands) in a population. Hence, it may soon become possible to include triallelic polymorphisms in population genomic studies. Indeed, triallelic sites are becoming interesting objects of study in their own right (Hodgkinson and Eyre-Walker, 2010). We believe that the theoretical results presented in this paper should prove useful in that regard.

Highlights.

• We model the frequency spectrum of a site that has undergone two mutations.

• Our results apply both to genealogically nested and nonnested mutations.

• We find a closed-form expression for the frequency spectrum of a triallelic site.

• We find in closed-form the expected age of the younger mutant at a triallelic site.

Appendix A

Proofs of main results

Proof of Lemma 3.1. We argue by writing down the probability of a compatible history using (4), and observe that it depends only on n and l. It is clear that for any polymorphic sample whose history is explained by precisely one mutation event, only configurations of the form l_ae_a + e_b are possible at the time of this event. So as we trace the history back in time, we must observe n_b − 1 coalescent events of type b alleles and n_a − l_a coalescent events of type a alleles (in some interspersed order), followed by a mutation event taking l_ae_a + e_b ↦ (l_a + 1)e_a, followed by l_a coalescent events of the remaining type a alleles. Think of the history as unwrapping a particular path back through the recursion (4). By multiplying together the coefficients accumulated at each transition, we obtain the probability of this history. Regardless of the order of the interspersed events, this product is

$$\frac{(n_a-1)(n_a-2)\dots (l_a)(n_b-1)!}{(n-1+\theta )(n-2+\theta )\dots (l_a+1+\theta )}\times \frac{\theta P_{\mathit{\text{ab}}}}{l_a+\theta }\frac{l_a+1}{l_a+1}\times \frac{l_a!}{(l_a+\theta )(l_a-1+\theta )\dots (1+\theta )}.$$

Simplifying, we get (5), which indeed depends only on n_a, n_b, and l_a. There are $\left(\begin{array}{c}\hfill n_a-l_a+n_b-1\hfill \\ \hfill n_b-1\hfill \end{array}\right)$ ways to arrange the first n_a − l_a + n_b − 1 events, and thus $\left(\begin{array}{c}\hfill n_a-l_a+n_b-1\hfill \\ \hfill n_b-1\hfill \end{array}\right)=\left(\begin{array}{c}\hfill n-l_a-1\hfill \\ \hfill n_b-1\hfill \end{array}\right)$ such histories.

Proof of Lemma 4.1. We argue in a similar fashion to Lemma 3.1. Any compatible history must exhibit the following order of events:

• an interspersed collection of n_a − l_y coalescence events of type a alleles, n_b − m coalescence events of type b alleles, and n_c − 1 coalescence events of type c alleles,

• a mutation event taking l_y ↦ l_ye_a + (m + 1)e_b,

• an interspersed collection of l_y − l_o coalescence events of type a alleles and m coalescence events of type b alleles,

• a mutation event taking l_o ↦ (l_o + 1)e_a, followed by

• l_o coalescence events of type a alleles.

Regardless of the relative ordering of events within each of these collections, the product of transition probabilities from (4) is

$$\frac{(n_a-1)(n_a-2)\dots (l_y)(n_b-1)(n_b-2)\dots (m)(n_c-1)!}{(n-1+\theta )(n-2+\theta )\dots (m+l_y+1+\theta )}\times \frac{\theta P_{\mathit{\text{bc}}}}{m+l_y+\theta }\frac{m+1}{m+l_y+1}\times \frac{(l_y-1)(l_y-2)\dots (l_o)m!}{(m+l_y+\theta )(m+l_y-1+\theta )\dots (l_o+1+\theta )}\times \frac{\theta P_{\mathit{\text{ab}}}}{l_o+\theta }\frac{l_o+1}{l_o+1}\times \frac{l_o!}{(l_o+\theta )(l_o-1+\theta )\dots (1+\theta )}.$$

Simplifying, we get (7), which is independent of the history except through n, l_y, and l_o. There are $\left(\begin{array}{c}\hfill n-l_y-m-1\hfill \\ \hfill n_a-l_y,n_b-m,n_c-1\hfill \end{array}\right)$ ways to arrange the first collection of coalescence events, and $\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m\hfill \end{array}\right)$ ways to arrange the second collection of coalescence events, so there are $\left(\begin{array}{c}\hfill n-l_y-m-1\hfill \\ \hfill n_a-l_y,n_b-m,n_c-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m\hfill \end{array}\right)$ such histories.

Proof of Lemmas 4.2, 4.3, and 4.4. These are very similar to the proof of Lemma 4.1 and so are omitted.

Proof of Theorem 5.1. The proof for each of the expressions is the same; we expand the denominator and collect the dominant terms in θ. We make use of the following identity:

$${(1+\theta )}_{n-1}=\frac{{(\theta )}_n}{\theta }={\displaystyle \sum _{k=1}^n}s(n,k){\theta }^{k-1},$$

where s(n, k) are the unsigned Stirling numbers of the first kind. Note also that

$$\begin{array}{cc}s(n,1)\hfill & =(n-1)!,\hfill \\ s(n,2)\hfill & =(n-1)!H_{n-1},\hfill \\ s(n,3)\hfill & =\frac{1}{2}(n-1)![{(H_{n-1})}^2-H_{n-1}^{(2)}].\hfill \end{array}$$

We will also make use of standard identities for summing over binomial co-efficients, and one nonstandard one:

$${\displaystyle \sum _{k=1}^n}\frac{1}{k}\left(\begin{array}{c}\hfill n-k\hfill \\ \hfill i-1\hfill \end{array}\right)=\left(\begin{array}{c}\hfill n\hfill \\ \hfill i-1\hfill \end{array}\right)(H_n-H_{i-1}),$$ (A.1)

for 1 ≤ i ≤ n. Equation (A.1) is proven by induction by Fu (1995, equation (33)), and using another method by Griffiths (2003, Appendix B).

Expanding (6):

$$\begin{array}{cc}p(\mathit{n},E_1)\hfill & =\theta P_{\mathit{\text{ab}}}\left[1-\theta \frac{s(n,2)}{s(n,1)}+O({\theta }^2)\right]{\displaystyle \sum _{l_a=1}^{n_a}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_a-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill l_a\hfill \end{array}\right)}·\frac{1}{l_a}\left[1-\frac{\theta }{l_a}+O({\theta }^2)\right],\hfill \\ \hfill & =\frac{\theta -{\theta }^2{H}_{n-1}}{n_a}{P}_{\mathit{\text{ab}}}{\displaystyle \sum _{l_a=1}^{n_a}}\frac{\left(\begin{array}{c}\hfill n_a\hfill \\ \hfill l_a\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill l_a\hfill \end{array}\right)}-\frac{{\theta }^2}{n_a}{P}_{\mathit{\text{ab}}}{\displaystyle \sum _{l_a=1}^{n_a}}\frac{\left(\begin{array}{c}\hfill n_a\hfill \\ \hfill l_a\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill l_a\hfill \end{array}\right)}·\frac{1}{l_a}+O({\theta }^3),\hfill \\ \hfill & =\frac{\theta -{\theta }^2{H}_{n-1}}{n_a}{P}_{\mathit{\text{ab}}}{\displaystyle \sum _{l_a=1}^{n_a}}\frac{\left(\begin{array}{c}\hfill n-1-l_a\hfill \\ \hfill n_b-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_a\hfill \end{array}\right)}-\frac{{\theta }^2}{n_a}{P}_{\mathit{\text{ab}}}{\displaystyle \sum _{l_a=1}^{n_a}}\frac{\left(\begin{array}{c}\hfill n-1-l_a\hfill \\ \hfill n_b-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_a\hfill \end{array}\right)}·\frac{1}{l_a}+O({\theta }^3),\hfill \\ \hfill & \begin{array}{cc}=\frac{\theta -{\theta }^2{H}_{n-1}}{n_b}{P}_{\mathit{\text{ab}}}-\frac{{\theta }^2}{n_a}{P}_{\mathit{\text{ab}}}\frac{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_b-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_a\hfill \end{array}\right)}(H_n-H_{n_b-1})+O({\theta }^3),\hfill & \hfill \text{by}(\mathrm{A}.1),\hfill \end{array}\hfill \end{array}$$

which simplifies to (17), as required. Next, expanding (8):

$$\begin{array}{cc}p(\mathit{n},E_{2𝒩}^{(b,c)})\hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}{\displaystyle \sum _{l_y=1}^{n_a}}{\displaystyle \sum _{l_o=1}^{l_y}}{\displaystyle \sum _{m=1}^{n_b}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m+l_y\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y\hfill \\ \hfill m+1\hfill \end{array}\right)}\frac{1}{(m+l_y)(m+l_y+1)}+O({\theta }^3),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}{\displaystyle \sum _{l_y=1}^{n_a}}{\displaystyle \sum _{m=1}^{n_b}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m+l_y\hfill \end{array}\right)}·\frac{1}{(m+l_y)(m+l_y+1)}+O({\theta }^3),\hfill \\ \hfill & \begin{array}{cc}=\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{n-1}{\displaystyle \sum _{k=3}^{n_a+n_b+1}}{\displaystyle \sum _{l_y=1}^{k-2}}\frac{1}{k}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill k-l_y-2\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}+O({\theta }^3),\hfill & \hfill (k=m+l_y+1)\hfill \end{array},\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{n-1}{\displaystyle \sum _{k=3}^{n_a+n_b+1}}\frac{1}{k}\left(\begin{array}{c}\hfill n_a+n_b-2\hfill \\ \hfill k-3\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}^{-1}+O({\theta }^3),\hfill \end{array}$$ (A.2)

$$\begin{array}{c}=\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{n-1}{\displaystyle \sum _{k=3}^{n_a+n_b+1}}\frac{k-2}{k}\left(\begin{array}{c}\hfill n-k\hfill \\ \hfill n_c-1\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill n_c\hfill \end{array}\right)}^{-1}\frac{1}{n_c}+O({\theta }^3),\hfill \\ =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{n-1}{\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill n_c\hfill \end{array}\right)}^{-1}\frac{1}{n_c}[\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill n_c\hfill \end{array}\right)-2{\displaystyle \sum _{k=1}^n}\frac{1}{k}\left(\begin{array}{c}\hfill n-k\hfill \\ \hfill n_c-1\hfill \end{array}\right)+2\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_c-1\hfill \end{array}\right)+\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill n_c-1\hfill \end{array}\right)]+O({\theta }^3),\hfill \\ =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{n-1}\left[\frac{1}{n_c}-2\left(\begin{array}{c}\hfill n\hfill \\ \hfill n_c-1\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill n_c\hfill \end{array}\right)}^{-1}\frac{1}{n_c}(H_n-H_{n_c-1})+\frac{2(n-1)}{(n_a+n_b)(n_a+n_b-1)}+\frac{1}{n_a+n_b-1}\right]+O({\theta }^3),\hfill \end{array}$$ (A.3)

where the last equality uses (A.1). On rearranging, we recover (18) as required. Note that equation (A.2) is consistent with a result of Hobolth and Wiuf (2009, equation (23). Their expression (24) seems to contain an error; the summation should be over 3, …, n rather than 3, …, n − n_b + 1.) Next, expanding (10):

$$\begin{array}{cc}p(\mathit{n},E_{2𝒩𝒩}^{(b,c)})\hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}{\displaystyle \sum _{m=1}^{n_b}}{\displaystyle \sum _{l_y=1}^{n_a}}{\displaystyle \sum _{l_o=1}^{l_y+1}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y-l_o\hfill \\ \hfill m-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m+l_y\hfill \end{array}\right)\left(\begin{array}{c}\hfill m+l_y\hfill \\ \hfill l_y+1\hfill \end{array}\right)}·\frac{1}{(m+l_y)(m+l_y+1)}+O({\theta }^3),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}{\displaystyle \sum _{m=1}^{n_b}}{\displaystyle \sum _{l_y=1}^{n_a}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m+l_y\hfill \end{array}\right)}·\frac{l_y+1}{m}·\frac{1}{(m+l_y)(m+l_y+1)}+O({\theta }^3),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n-1}{\displaystyle \sum _{k=3}^{n_a+n_b+1}}{\displaystyle \sum _{m=1}^{k-2}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill k-m-2\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}\left(\frac{1}{m}-\frac{1}{k}\right)+O({\theta }^3),\hfill \end{array}$$ (A.4)

$$\begin{array}{c}=\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n-1}{\displaystyle \sum _{k=3}^{n_a+n_b+1}}{\displaystyle \sum _{m=1}^{k-2}}\frac{\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill k-2-m\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}\left[\left(\begin{array}{c}\hfill n_b\hfill \\ \hfill m\hfill \end{array}\right)\frac{1}{n_b}-\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right)\frac{1}{k}\right]+O({\theta }^3),\hfill \\ =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n-1}{\displaystyle \sum _{k=3}^{n_a+n_b+1}}\left[\left(\begin{array}{c}\hfill n_a+n_b-1\hfill \\ \hfill k-2\hfill \end{array}\right)\frac{1}{n_b}-\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill k-2\hfill \end{array}\right)\frac{1}{n_b}-\left(\begin{array}{c}\hfill n_a+n_b-2\hfill \\ \hfill k-3\hfill \end{array}\right)\frac{1}{k}\right]{\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}^{-1}+O({\theta }^3),\hfill \\ =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n-1}{\displaystyle \sum _{k=3}^{n_a+n_b+1}}[\frac{\left(\begin{array}{c}\hfill n-k\hfill \\ \hfill n_c-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill n_a+n_b-1\hfill \end{array}\right)}\frac{1}{n_b}-\frac{\left(\begin{array}{c}\hfill n-k\hfill \\ \hfill n_b+n_c-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill n_a-1\hfill \end{array}\right)}\frac{1}{n_b}-\left(\begin{array}{c}\hfill n_a+n_b-2\hfill \\ \hfill k-3\hfill \end{array}\right)\frac{1}{k}]+O({\theta }^3),\hfill \\ =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n-1}\left[\frac{n-1}{n_c(n_b+n_c)}-{\displaystyle \sum _{k=3}^{n_a+n_b+1}}\left(\begin{array}{c}\hfill n_a+n_b-2\hfill \\ \hfill k-3\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}^{-1}\frac{1}{k}\right]+O({\theta }^3).\hfill \end{array}$$ (A.5)

Finally, apply the same equality relating equations (A.2) and (A.3) to recover (20) as required. Next, expanding (12) and summing over l_o:

$$\begin{array}{cc}p(\mathit{n},E_{2𝒮}^{(b,c)})\hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}{\displaystyle \sum _{l_y=1}^{n_a}}\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill l_y\hfill \end{array}\right)}^{-1}\frac{1}{l_y(l_y+1)}+O({\theta }^3),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{n_a}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_a\hfill \end{array}\right)}^{-1}{\displaystyle \sum _{l_y=2}^{n_a+1}}\frac{1}{l_y}\left(\begin{array}{c}\hfill n-l_y\hfill \\ \hfill n_c-1\hfill \end{array}\right)+O({\theta }^3),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{n_a}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_a\hfill \end{array}\right)}^{-1}\left[\left(\begin{array}{c}\hfill n\hfill \\ \hfill n_c-1\hfill \end{array}\right)(H_n-H_{n_c-1})-1\right]+O({\theta }^3),\hfill \end{array}$$ (A.6)

where the last equality uses (A.1). This simplifies to (22). Finally, expanding (14):

$$\begin{array}{cc}p(\mathit{n},E_{2ℬ}^{(b,c)})\hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}{\displaystyle \sum _{m=1}^{n_b}}\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m\hfill \end{array}\right)}^{-1}\frac{1}{m^2(m+1)}+O({\theta }^3),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n_c}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_b-1\hfill \end{array}\right)}^{-1}{\displaystyle \sum _{m=1}^{n_b}}\left(\begin{array}{c}\hfill n-1-m\hfill \\ \hfill n_c-1\hfill \end{array}\right)\left(\frac{1}{m}-\frac{1}{m+1}\right)+O({\theta }^3),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n_c}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_b-1\hfill \end{array}\right)}^{-1}\left[{\displaystyle \sum _{m=1}^{n_b}}\left(\begin{array}{c}\hfill n-1-m\hfill \\ \hfill n_c-1\hfill \end{array}\right)\frac{1}{m}-{\displaystyle \sum _{m=2}^{n_b+1}}\left(\begin{array}{c}\hfill n-m\hfill \\ \hfill n_c-1\hfill \end{array}\right)\frac{1}{m}\right]+O({\theta }^3),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n_c}{\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_b-1\hfill \end{array}\right)}^{-1}\left[\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_c-1\hfill \end{array}\right)(H_{n-1}-H_{n_c-1})-\left(\begin{array}{c}\hfill n\hfill \\ \hfill n_c-1\hfill \end{array}\right)(H_n-H_{n_c-1})+\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill n_c-1\hfill \end{array}\right)\right]+O({\theta }^3),\hfill \end{array}$$ (A.7)

applying (A.1) to each sum in the penultimate expression. This then simplifies to (24). Expressions for $p(\mathit{n},E_{2𝒩}^{(b,a)}),p(\mathit{n},E_{2𝒩𝒩}^{(b,b)}),p(\mathit{n},E_{2𝒮}^{(b,a)}),\text{ and }p(\mathit{n},E_{2ℬ}^{(b,b)})$ are obtained in a very similar manner and we omit the details.

Proof of Theorem 5.2. By expanding the denominator of (26) for θ < 1 and applying the following identity (Roman, 1993):

$$c_n^{(s)}={\displaystyle \sum _{j=1}^n}\left(\begin{array}{c}\hfill n\hfill \\ \hfill j\hfill \end{array}\right)\frac{{(-1)}^{j-1}}{j^s},$$

we obtain (28). For the remaining results, we sum over all possible observations n consistent with the event of interest:

$$\begin{array}{cc}p(E_{2𝒩}^{(b,c)})\hfill & ={\displaystyle \sum _{n_c=1}^{n-2}}{\displaystyle \sum _{n_b=1}^{n-n_c-1}}p((n-n_b-n_c){\mathit{e}}_a+n_b{\mathit{e}}_b+n_c{\mathit{e}}_c,E_{2𝒩}^{(b,c)}),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{n-1}{\displaystyle \sum _{n_c=1}^{n-2}}{\displaystyle \sum _{n_b=1}^{n-n_c-1}}{\displaystyle \sum _{k=3}^{n-n_c+1}}\frac{1}{k}\left(\begin{array}{c}\hfill n-n_c-2\hfill \\ \hfill k-3\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}^{-1}+O({\theta }^3),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{n-1}{\displaystyle \sum _{n_c=1}^{n-2}}(n-n_c-1){\displaystyle \sum _{k=3}^{n-n_c+1}}\frac{1}{k}\left(\begin{array}{c}\hfill n-n_c-2\hfill \\ \hfill k-3\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}^{-1}+O({\theta }^3),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}}{n-1}{\displaystyle \sum _{k=3}^n}{\displaystyle \sum _{n_c=1}^{n+1-k}}\frac{k-2}{k}\left(\begin{array}{c}\hfill n-n_c-1\hfill \\ \hfill k-2\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}^{-1}+O({\theta }^3),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}{\displaystyle \sum _{k=3}^n}\frac{k-2}{k(k-1)}+O({\theta }^3),\hfill \end{array}$$

which simplifies to (29). The second equality above uses (A.2). Continue in this way for the remaining events. Using (A.4):

$$\begin{array}{cc}p(E_{2𝒩𝒩}^{(b,c)})\hfill & ={\displaystyle \sum _{n_c=1}^{n-2}}{\displaystyle \sum _{n_b=1}^{n-n_c-1}}p((n-n_b-n_c){\mathit{e}}_a+n_b{\mathit{e}}_b+n_c{\mathit{e}}_c,E_{2𝒩𝒩}^{(b,c)}),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n-1}{\displaystyle \sum _{n_c=1}^{n-2}}{\displaystyle \sum _{n_b=1}^{n-n_c-1}}{\displaystyle \sum _{k=3}^{n-n_c+1}}{\displaystyle \sum _{m=1}^{k-2}}\frac{\left(\begin{array}{c}\hfill n-n_b-n_c-1\hfill \\ \hfill k-m-2\hfill \end{array}\right)\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}\left(\frac{1}{m}-\frac{1}{k}\right)+O({\theta }^3),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n-1}{\displaystyle \sum _{n_c=1}^{n-2}}{\displaystyle \sum _{k=3}^{n-n_c+1}}{\displaystyle \sum _{m=1}^{k-2}}\frac{\left(\begin{array}{c}\hfill n-n_c-1\hfill \\ \hfill k-2\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}\left(\frac{1}{m}-\frac{1}{k}\right)+O({\theta }^3),\hfill \\ \hfill & =\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n-1}{\displaystyle \sum _{k=3}^n}{\displaystyle \sum _{m=1}^{k-2}}{\displaystyle \sum _{n_c=1}^{n+1-k}}\frac{\left(\begin{array}{c}\hfill n-n_c-1\hfill \\ \hfill k-2\hfill \end{array}\right)}{\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}\left(\frac{1}{m}-\frac{1}{k}\right)+O({\theta }^3),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}{\displaystyle \sum _{k=3}^n}{\displaystyle \sum _{m=1}^{k-2}}\left(\frac{1}{m}-\frac{1}{k}\right)\frac{1}{k-1}+O({\theta }^3),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}{\displaystyle \sum _{k=3}^n}\left(H_{k-2}-\frac{k-2}{k}\right)\frac{1}{k-1}+O({\theta }^3),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}{\displaystyle \sum _{k=2}^{n-1}}\left[\frac{H_k}{k}-\frac{1}{k^2}+\frac{1}{k}-\frac{2}{k+1}\right]+O({\theta }^3),\hfill \end{array}$$

which simplifies to (30) using (15). Using (A.6):

$$\begin{array}{cc}p(E_{2𝒮}^{(b,c)})\hfill & ={\displaystyle \sum _{n_a=1}^{n-1}}p(n_a{\mathit{e}}_a+(n-n_a){\mathit{e}}_c,E_{2𝒮}^{(b,c)}),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}{\displaystyle \sum _{n_a=1}^{n-1}}{\displaystyle \sum _{l_y=1}^{n_a}}\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill l_y\hfill \end{array}\right)}^{-1}\frac{1}{l_y(l_y+1)}+O({\theta }^3),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}{\displaystyle \sum _{l_y=1}^{n-1}}{\displaystyle \sum _{n_a=l_y}^{n-1}}\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill l_y-1\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill l_y\hfill \end{array}\right)}^{-1}\frac{1}{l_y(l_y+1)}+O({\theta }^3),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{bc}}}{\displaystyle \sum _{l_y=1}^{n-1}}\frac{1}{l_y(l_y+1)}+O({\theta }^3),\hfill \end{array}$$

which gives (31). Using (A.7):

$$\begin{array}{cc}p(E_{2ℬ}^{(b,c)})\hfill & ={\displaystyle \sum _{nb=1}^{n-1}}p(n_b{\mathit{e}}_b+(n-n_b){\mathit{e}}_c,E_{2ℬ}^{(b,c)}),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}{\displaystyle \sum _{n_b=1}^{n-1}}{\displaystyle \sum _{m=1}^{n_b}}\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m\hfill \end{array}\right)}^{-1}\frac{1}{m^2(m+1)}+O({\theta }^3),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}{\displaystyle \sum _{m=1}^{n-1}}{\displaystyle \sum _{n_b=m}^{n-1}}\left(\begin{array}{c}\hfill n_b-1\hfill \\ \hfill m-1\hfill \end{array}\right){\left(\begin{array}{c}\hfill n-1\hfill \\ \hfill m\hfill \end{array}\right)}^{-1}\frac{1}{m^2(m+1)}+O({\theta }^3),\hfill \\ \hfill & ={\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}{\displaystyle \sum _{m=1}^{n-1}}\frac{1}{m^2(m+1)}+O({\theta }^3),\hfill \end{array}$$

which gives (32). To obtain p(E_2𝒩), p(E_2𝒩𝒩), p(E_2𝒮), and p(E_2ℬ) from each of these results we simply sum b and c over 1, …, K.

Proof of Theorem 6.1. The given expressions are obtained immediately from Theorem 5.2 and the following observations:

$$\begin{array}{cc}\hfill O_1\cap E_2& ={\displaystyle \underset{b}{\cup }}{E}_{2𝒮}^{(b,a)},\hfill \\ \hfill O_{1𝒮}\cap E_2& ={\displaystyle \underset{b}{\cup }}{E}_{2ℬ}^{(b,b)},\hfill \\ \hfill O_2\cap E_2& =\left[{\displaystyle \underset{b}{\cup }}{E}_{2𝒩}^{(b,a)}\right]\cup \left[{\displaystyle \underset{b}{\cup }}{E}_{2𝒩𝒩}^{(b,a)}\right]\cup \left[{\displaystyle \underset{b}{\cup }}{\displaystyle \underset{c\ne a}{\cup }}{E}_{2𝒮}^{(b,c)}\right],\hfill \\ \hfill O_{2𝒮}\cap E_2& ={\displaystyle \underset{b}{\cup }}{\displaystyle \underset{c\ne b}{\cup }}{E}_{2ℬ}^{(b,c)},\hfill \\ \hfill O_3\cap E_2& =[{\displaystyle \underset{b}{\cup }}{\displaystyle \underset{c\ne a}{\cup }}{E}_{2𝒩}^{(b,c)}]\cup \left[{\displaystyle \underset{b}{\cup }}{\displaystyle \underset{c\ne b}{\cup }}{E}_{2𝒩𝒩}^{(b,c)}\right].\hfill \end{array}$$

Notice that each of these unions is over disjoint sets, so we can simply sum over the relevant probabilities. For example,

$$p(O_1,E_2)={\displaystyle \sum _{b=1}^K}p(E_{2𝒮}^{(b,a)})={\theta }^2{\displaystyle \sum _{b=1}^K}{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ba}}}\left[1-\frac{1}{n}\right]+O({\theta }^3),$$

which equals (33). The others follow similarly.

Proof of Theorem 6.2. For n = n_ae_a + n_be_b + n_ce_c, the expression (38) for p(n | O₃) follows from

$$p(\mathit{n}|O_3)=\frac{p(\mathit{n},O_3,E_2)}{p(O_3,E_2)}+O(\theta ),$$

where p(O₃, E₂) is given by (37), and p(n, O₃, E₂) is obtained from

$$p(\mathit{n},O_3,E_2)=p(\mathit{n},E_{2𝒩}^{(b,c)})+p(\mathit{n},E_{2𝒩}^{(c,b)})+p(\mathit{n},E_{2𝒩𝒩}^{(b,c)})+p(\mathit{n},E_{2𝒩𝒩}^{(c,b)}),$$

with the right-hand side given by equations (18) and (20).

Proof of Theorem 6.3. We use induction on what is sometimes referred to as the sample complexity, n + l. We show that, for a sample configuration n with l observed alleles including the ancestral allele:

$$p(\mathit{n},O_l)\propto {\theta }^{l-1}{\displaystyle \prod _{k\in \Lambda }}\frac{P_k}{n_k}+O({\theta }^l),$$ (A.8)

the result following by dividing by p(O_l) = O(θ^l−1) and letting θ → 0. We have already seen (A.8) to hold for l = 2 and l = 3, and all n [equations (17) and (40)], and we suppose inductively that it holds for all samples with complexity less than n + l. Let n be a suitable sample with complexity n + l.

Substituting the inductive hypothesis into the first (coalescence) term on the right-hand side of (3) and simplifying, we obtain

$$\frac{{\theta }^{l-1}}{n-1+\theta }\left({\displaystyle \prod _{k\in \Lambda }}\frac{P_k}{n_k}\right)\left[n_a-1+{\displaystyle \sum _{\begin{array}{c}\hfill j:j\ne a,\hfill \\ \hfill n_j\ge 2\hfill \end{array}}}{n}_j\right].$$

For the mutation term on the right of (3), the key here is to observe that contributions of O(θ^l−1) come only from configurations n − e_j + e_i with l − 1 observed alleles and including the ancestral allele; that is, from configurations in which the loss of one gamete with allele j and gain of one gamete with allele i reduces the number of observed mutant alleles in n by one. Thus, we must have had n_j = 1, j ≠ a, n_i ≥ 1, and i ≠ j, with any other possibilities requiring additional mutation events and thus contributing only higher order terms. The mutation term in (3) is therefore proportional to

$$\frac{\theta }{n-1+\theta }{\displaystyle \sum _{\begin{array}{c}\hfill j:j\ne a,\hfill \\ \hfill n_j=1\hfill \end{array}}}{\displaystyle \sum _{\begin{array}{c}\hfill i:i\ne j,\hfill \\ \hfill n_i\ge 1\hfill \end{array}}}{P}_j\left(\frac{n_i+1}{n}\right){\theta }^{l-2}\left({\displaystyle \prod _{k\in \Lambda \backslash \{j\}}}\frac{P_k}{n_k+{\delta }_{\mathit{\text{ik}}}}\right)+O({\theta }^l)=\frac{{\theta }^{l-1}}{n-1+\theta }{\displaystyle \sum _{\begin{array}{c}\hfill j:j\ne a,\hfill \\ \hfill n_j=1\hfill \end{array}}}\left({\displaystyle \prod _{k\in \Lambda }}\frac{P_k}{n_k}\right)+O({\theta }^l).$$

Summing contributions from both coalescence and mutation, (3) tells us

$$p(\mathit{n})\propto \frac{{\theta }^{l-1}}{n-1+\theta }\left({\displaystyle \prod _{k\in \Lambda }}\frac{P_k}{n_k}\right)(n-1)+O({\theta }^l)={\theta }^{l-1}\left({\displaystyle \prod _{k\in \Lambda }}\frac{P_k}{n_k}\right)+O({\theta }^l),$$

as required.

Proof of Theorem 7.1. The argument parallels that of Hobolth and Wiuf (2009), who obtained the corresponding result for two nested mutations. We first condition on the number k of lineages at the time of the younger mutation. Inspection of (A.5) yields

$$p(\mathit{n},k,E_{2𝒩𝒩}^{(b,c)})=\frac{{\theta }^2{P}_{\mathit{\text{ab}}}{P}_{\mathit{\text{ac}}}}{n-1}\left[\left(\begin{array}{c}\hfill n_a+n_b-1\hfill \\ \hfill k-2\hfill \end{array}\right)\frac{1}{n_b}-\left(\begin{array}{c}\hfill n_a-1\hfill \\ \hfill k-2\hfill \end{array}\right)\frac{1}{n_b}-\left(\begin{array}{c}\hfill n_a+n_b-2\hfill \\ \hfill k-3\hfill \end{array}\right)\frac{1}{k}\right]{\left(\begin{array}{c}\hfill n-2\hfill \\ \hfill k-2\hfill \end{array}\right)}^{-1}+O({\theta }^3).$$

Letting θ → 0, n_b/n → f_b and n_c/n → f_c while n → ∞, we find

$$p(k|E_{2𝒩𝒩}^{(b,c)},\mathit{f})=\frac{1}{F}\left[\frac{{(1-f_c)}^{k-2}}{f_b}-\frac{{(1-f_b-f_c)}^{k-2}}{f_b}-\frac{k-2}{k}{(1-f_c)}^{k-3}\right],$$ (A.9)

with normalizing constant

$$\begin{array}{cc}F\hfill & ={\displaystyle \sum _{k=3}^{\infty }}\left[\frac{{(1-f_c)}^{k-2}}{f_b}-\frac{{(1-f_b-f_c)}^{k-2}}{f_b}-\frac{k-2}{k}{(1-f_c)}^{k-3}\right],\hfill \\ \hfill & =\frac{1}{f_c(f_b+f_c)}-\frac{2\text{ ln }{f}_c}{{(1-f_c)}^3}-\frac{1+f_c}{f_c{(1-f_c)}^2}.\hfill \end{array}$$

Under the standard, neutral coalescent model, the mean age of the younger mutation when it occurred during the time that there existed k ancestral lineages is 2/(k − 1) (Hobolth and Wiuf, 2009). Hence

$$𝔼[A_c|E_{2𝒩𝒩}^{(b,c)},\mathit{f}]={\displaystyle \sum _{k=3}^{\infty }}\frac{2}{k-1}p(k|E_{2𝒩𝒩}^{(b,c)},\mathit{f}).$$

Substituting in (A.9), summing over k and simplifying recovers (45).