Inferring cell cycle feedback regulation from gene expression data

Abstract

Feedback control is an important regulatory process in biological systems, which confers robustness against external and internal disturbances. Genes involved in feedback structures are therefore likely to have a major role in regulating cellular processes.

Here we rely on a dynamic Bayesian network approach to identify feedback loops in cell cycle regulation. We analyzed the transcriptional profile of the cell cycle in HeLa cancer cells and identified a feedback loop structure composed of 10 genes. In silico analyses showed that these genes hold important roles in system's dynamics. The results of published experimental assays confirmed the central role of 8 of the identified feedback loop genes in cell cycle regulation. In conclusion, we provide a novel approach to identify critical genes for the dynamics of biological processes. This may lead to the identification of therapeutic targets in diseases that involve perturbations of these dynamics.

1. Introduction

Feedback control is ubiquitous in biomedical systems [1-3]. Biological regulation is achieved by a complex set of networks that include several intertwined feedback loops, sometimes hierarchically related [4]. At the molecular level, with the emergence of high-throughput technologies, it became clear that genes are involved in a large number of feedback regulation processes [5, 6].

Feedback control systems possess a number of very important properties, including robustness to disturbances and the capability of generating state trajectories known as limit cycles, i.e. periodic oscillations, which are commonly present in cell dynamics such as the cell cycle [7]. Thus, there is an increasing interest in analyzing the role and nature of feedback loops, in particular to understand cell fate specification and commitment during development [8, 9] and in cancer [10, 11]. A thorough study of the nature of feedback loops can lead not only to a better understanding of basic molecular mechanisms of cells and tissues, but also to the identification of therapeutic targets and the design of new drug compounds. Genes involved in feedback regulatory structures are indeed likely to have a key role in the regulation of cellular processes.

The understanding of the role and implications of feedback loops on cell dynamics requires techniques able to deal with partial knowledge and non linear behaviours [12-18]. The most interesting approaches proposed in the literature are those that derive networks of causally interconnected genes [19], as they provide two different kinds of information: first, they give a representation of the structure of gene relationships, expressed in terms of networks; second, they usually provide a mathematical model of gene expression dynamics.

In this paper we propose a dynamic Bayesian network approach to the identification of feedback loops and the generation of hypotheses on key regulatory genes in cell cycle expression control. Bayesian networks (BNs) and their dynamic counterpart dynamic Bayesian networks (DBNs) are flexible and easily interpretable models that allow the representation of multivariate probabilistic relationships both at qualitative and quantitative level. Compared to other methodologies for reverse engineering gene networks, such as approaches based on mutual information [20] or differential equations [21], the use of a probabilistic approach offers the advantage of taking into account the uncertainty about gene relationships inferred from experimental data. For this reason BNs and DBNs have been applied in the literature to analyze gene expression data [22]. As the structure of a BN is by definition acyclic, BNs do not allow the direct representation and learning of feedback loop structures. To capture these structures, it is necessary to use DBNs [23-31].

Our novel hypothesis is that the genes involved in feedback loop structures are key regulatory genes of the analyzed biological process. To prove our hypothesis we applied DBNs to the analysis of temporal expression data measured during the cell cycle of a human cancer cell line (HeLa cells) for about 1000 cDNA probes [32] and identified a complex feedback loop structure involving 10 genes. An extensive validation based on literature analysis and comparison with a list of genes experimentally verified to be involved in regulating the cell cycle in cancer cells [33] showed that the proposed approach was able to highlight core cell cycle genes.

2. Material and methods

2.1 Data

Whitfield et al. analyzed gene expression during cell cycle progression in HeLa cells [32]. In order to detect periodic activity in cell cultures it is necessary to synchronize cells, i.e. to force them to stop in a certain cell cycle phase. Subsequently, cells are released from the block and they progress synchronously through cell cycle. Whitfield et al. synchronized cells with three different methods (double thymidine block, thymidine/nocodazole block and mitotic shake-off) and performed five independent experiments, each time using one of these synchronization methods and microarrays containing either 20000 or 40000 features. RNA was isolated from HeLa cells at various time points (1–2 hrs spaced) after release from a synchronous arrest and reverse transcribed into Cy5-labeled cDNA. Reference RNA was prepared from asynchronously growing HeLa cells and reverse transcribed into Cy3-labeled cDNA. Cy5- and Cy3-labeled cDNA were hybridized to cDNA microarrays, manufactured at the Stanford Microarray Facility. The whole database is available on the web [34]. Each probe represented on the microarrays is identified by an IMAGE clone number (a cDNA clone produced by the Integrated Molecular Analysis of Genomes and their Expression Consortium [35]).

To infer the DBN model we used gene expression data of the experiment denoted by Whitfield et al. as “Thy-Thy 3”, in which cell synchronization was achieved through a double-thymidine block, which arrests cells at the start of the cell cycle, i.e. at the G1/S boundary. Gene expression values were measured every hour, from time 0 to 46 hours, with cDNA microarrays containing about 40000 probes. As the estimated cell cycle length in HeLa cells is about 15 hours, the available measurements span three cell cycles [32]. Among the three experiments performed with the 40000 probe arrays this is the one with the highest number of time points. We concentrated our analysis on a subset of about 1000 probes identified by Whitfield et al. as cell cycle regulated (periodically expressed). Our dataset is made up of 1099 variables measured at 47 time points. The measurements we analyzed are log ratios of the expression in synchronized cells (Cy5-labeled) versus the expression in the reference asynchronous population (Cy3-labeled). We annotated the IMAGE clones, retrieving the corresponding Unigene cluster and GeneID, by means of the tool SOURCE [36], developed at Stanford University and available on the web [37]. According to an annotation performed in April 2009, 798 out of 1099 clones have a GeneID identifier. They correspond to 647 different genes: the majority of genes (81.6%) are represented by only 1 clone, 14.8% is represented by 2 clones and the remaining genes (3.6%) are represented by a maximum of 6 clones. We decided to perform analysis at single-probe level, in order to avoid the possible loss of information associated with the choice of a single probe to represent a gene, or alternatively the averaging over the probes mapping to the same gene. Other reasons for preferring a probe-based approach are that the annotation of probes can change when information about a gene's transcripts is refined and the fact that annotation is not available for all probes.

To evaluate our inferred DBN model, we employed expression data of the experiment “Thy-Noc”, in which synchronization was achieved through a thymidine/nocodazole block, which arrests cells during mitosis, i.e. at M phase. In this experiment expression values were measured every 2 hours, from 0 to 36 hours. Compared to the only other available experiment that employed a synchronization method different from double-thymidine, “Thy-Noc” was preferred for the validation as it had a lower number of missing values.

2.2 Dynamic Bayesian network inference

Bayesian networks are probabilistic graphical models formed by two components, a directed acyclic graph (DAG) and a joint probability distribution. Nodes in the DAG represent random variables, while arcs represent probabilistic dependencies. A conditional probability distribution is associated with each node and its parents (the variables with arcs pointing to it) and the overall joint distribution is given by the product of these conditional distributions.

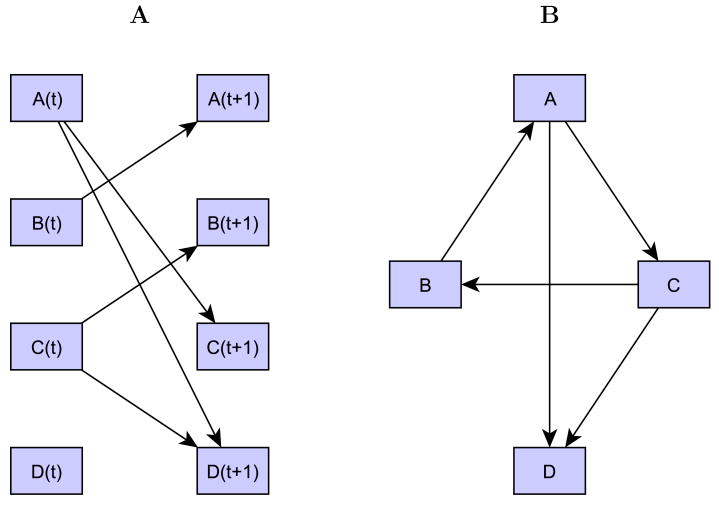
A dynamic Bayesian network is a Bayesian network that models the evolution of random variables (in our case: probe expression values) over time. Under appropriate assumptions, this temporal evolution can be entirely represented by a network of dependencies between variables at time t and time t+1 [38]. Thus, in our case nodes in the DAG represent probe expression values at time t and time t+1 and arcs are always directed from nodes at time t to nodes at t+1 (Figure 1).

Figure 1. A dynamic Bayesian network and its translation into a gene regulatory network.

A) Example of a simple dynamic Bayesian network representing the probabilistic dependencies of four variables (A-B-C-D) between two consecutive time points; B) The network in A) translated into a gene regulatory network. This representation facilitates the identification of the feedback loop involving variables A-C-B.

We assume that variables Y₁… Y_v are continuous and that the conditional distribution of each variable Y_i with respect to its parents is Gaussian, with mean μ_i and variance ${\sigma }_i^2=1/{\tau }_i$ [39]. The parameter τ _i is called precision. The conditional mean μ_i of variable Y_i at time t+1 is assumed to be a linear combination of the values of the p(i) parents at time t:

$${\mu }_{\text{i}}={\beta }_{\text{i}0}+\sum _{\text{j}=1}^{\text{p}(\text{i})}{\beta }_{\text{ij}}{\text{y}}_{\text{ij}}$$ (1)

where y_ij are the parent values and (β_i0, β_i1,…,β_ip(i)) are the regression parameters.

Learning a DBN requires learning both the structure of the DAG and the parameters of the conditional probability distributions. The learning task can be approached by choosing a suitable score and a search strategy. In a fully Bayesian framework the score is the posterior probability p(M∣D) of a network model M with respect to the available data D. By Bayes' theorem, it is possible to write:

$$\text{p}(\text{M}\mid \text{D})\propto \text{p}(\text{D}\mid \text{M})\text{p}(\text{M})$$ (2)

where p(D∣M) is the marginal likelihood, which expresses the likelihood of the model irrespective of the specific parameters' values, and p(M) is the model's prior probability. Assuming all models are a priori equally probable, the posterior is directly proportional to the marginal likelihood, which can thus be employed as score to rank the alternative models.

Using the Gaussian probability model defined above and employing suitable prior distributions for model parameters, the marginal likelihood can be calculated in closed form [39]. Yet, as the number of possible models to be explored is exponential in the number of variables, it is necessary to resort to a heuristic search strategy. We made use of a stepwise search strategy that extends the K2 algorithm by Cooper and Herskovits [40]: the parent set of each variable is initially assumed to be empty; then, the addition of one parent at a time is tried and the model that most increases the marginal likelihood is chosen as the new candidate model. The candidate model is accepted if the ratio between the new and the old marginal likelihood (the so-called Bayes factor) is higher than a specified threshold. In order to avoid the limitations of the greedy search, we added a backward step during forward selection of variables [39]. The algorithm's implementation in Matlab is freely available for academic users upon request from the authors.

2.3 Network Model Evaluation

The evaluation of the network model induced from data consists of two main tasks: assessing its goodness of fit and assessing its predictive accuracy.

The goodness of fit refers to the ability of the model to fit the data from which the model itself was induced. In our case this corresponds to being able to reproduce the analyzed temporal profiles with satisfactory accuracy. In order to test the goodness of fit it is possible to adapt the approach for static BNs proposed by Sebastiani et al., based on blanket residuals [41]. Given the network induced from data, for each case k in the database, the fitted value for every node Y_i given all the other nodes is calculated. By the global Markov property, only the configuration of the Markov blanket of Y_i is used to compute the fitted value: for continuous variables, the fitted value ŷ_ik is taken equal to the expected value of Y_i given its Markov blanket.

In the case of DBNs, the calculation is simplified by the fact that the Markov blanket of a node at time t + 1 is given only by its parents. Therefore we have:

$${\widehat{\text{y}}}_{\text{i}(\text{t}+\text{1})}=\text{E}[{\text{y}}_{\text{i}(\text{t}+\text{1})}\mid {\text{pa}({\text{y}}_{\text{i}})}_{\text{t}}]={\mu }_{\text{it}}={\widehat{\beta }}_{\text{i}0}+\sum _{\text{j}=1}^{\text{p}(\text{i})}{\widehat{\beta }}_{\text{ij}}{\text{y}}_{\text{ijt}}$$ (3)

ŷ_i(t+1) is the fitted value for variable Y_i at time t+1, pa(y_i) are the p(i) parents inferred during network learning, y_ijt are the parent values at time t and (β̂_i0,…,β̂_ip(i)) are the estimates of the regression parameters. Given expression data for T time points, the one-step-ahead prediction is repeated for t = 1,‥, T –1 and the blanket residuals are calculated as:

$${\text{r}}_{\text{i}(\text{t}+\text{1})}={\text{y}}_{\text{i}(\text{t}+\text{1})}-{\widehat{\text{y}}}_{\text{i}(\text{t}+\text{1})}$$ (4)

During the stepwise search for the parent set of a node, it is possible that no single-parent model has a marginal likelihood higher than the one of the model with no parents. Thus, in this case the predicted value of the node will be constant across time and equal to the estimated parameter β̂_i0.

In regression models a commonly used measure for the goodness of fit is the root mean squared error (RMSE). In our case the global RMSE is taken equal to the average of the root mean squared errors relative to each of the v variables (RMSE_i):

$$\text{RMSE}=\frac{1}{\text{v}}\sum _{\text{i}=1}^{\text{v}}{\text{RMSE}}_{\text{i}}$$ (5)

$${\text{RMSE}}_{\text{i}}=\sqrt{\frac{1}{\text{T}-\text{1}}\sum _{\text{t}=1}^{\text{T}-\text{1}}{{(\text{y}}_{\text{i}(\text{t}+1)}-{\widehat{\text{y}}}_{\text{i}(\text{t}+1)})}^2}$$ (6)

As for any model inferred from data, a good fitting doesn't mean that the model performs well when applied to new data. A useful model must be able to generalize well; thus, the evaluation of the network model on an independent test set is very important. This evaluation implies predicting values for variables in the test set relying on the model learned on the training set. In our case, the “predicted values” for each variable are its expected values (Equation (3)) calculated using the parents and the values for the regression parameters inferred on the training set. A summary of the predictive accuracy can be given by the RMSE calculated on the test set.

2.4 Transformation of the DBN into a regulatory network

In order to facilitate the visualization of the topological properties of the inferred network, and in particular feedback loops, the DBN can be transformed into a regulatory network. In this network nodes referring to the same variable at consecutive time points (e.g. A(t) and A(t+1)) are collapsed into a single node and an arc going from variable A to variable B is drawn when in the DBN there is an arc from A(t) to B(t+1) (see Figure 1). Given the fact that in our DBN model variables at time t+1 can depend only on variables at the previous time point, there is a one-to-one correspondence between the DBN and its representation as a regulatory network.

3. Results

3.1 Inferred network model

As described in the section 2.1, the analyzed dataset contains expression values for 1099 variables (probes) measured every hour, from 0 to 46 hours. Each probe of the array is identified by an IMAGE clone. We applied the dynamic Bayesian network algorithm described in section 2.2 to infer the network of dependencies between expression values of the analyzed variables at two consecutive time points. Hyper-parameters for the prior distributions of the precision and the regression coefficients were chosen as previously described [39], while the threshold for the Bayes factor was set equal to 7 so that a new network link is added only if there is substantial evidence in its favor [42].

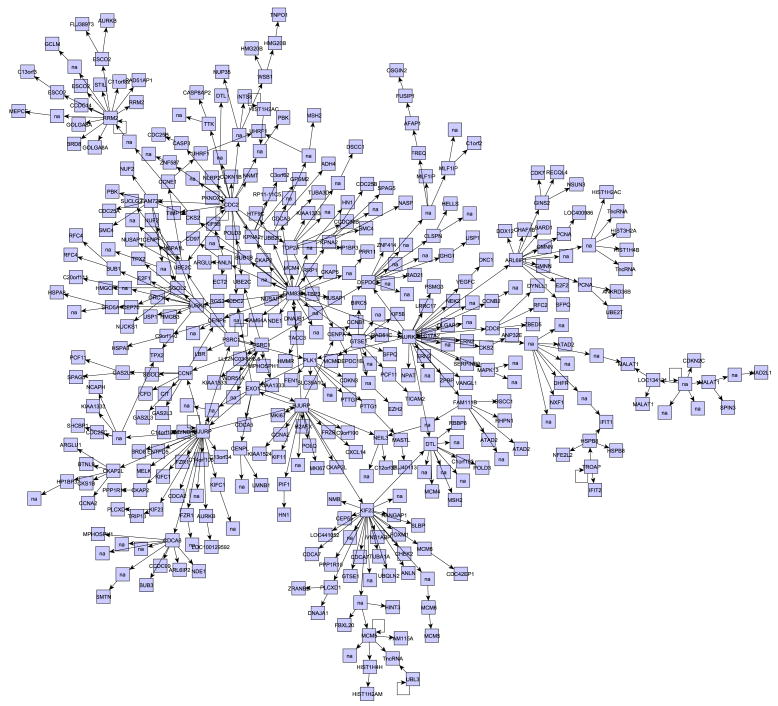
The obtained DBN has been translated into a regulatory network as described in section 2.4. In this network the number of parents for each variable ranges from 0 to 2; more specifically, 638 out of the 1099 analyzed variables had no connections (they have no children and no parents) and 4 had only a self-loop. Among the variables connected with at least one other, a large group of 412 nodes can be found (Figure 2). The relatively large number of nodes with no connections is due to the compromise between the model's ability to fit the data and the model's complexity, which is ensured by setting a threshold for the Bayes factor. Although all analyzed genes are cell-cycle related, the large group of connected nodes reveals a set of genes highly dependent on one another, likely to contain interesting regulatory structures. Thus we focused following analyses on this group.

Figure 2. Gene network inferred analyzing human cell cycle expression data.

Relying on the expression values for 1099 probes measured by Whitfield et al. [32] and on our dynamic Bayesian network inference algorithm, we inferred a gene regulatory network. This network contains a large group of 412 connected probes, shown in the Figure.

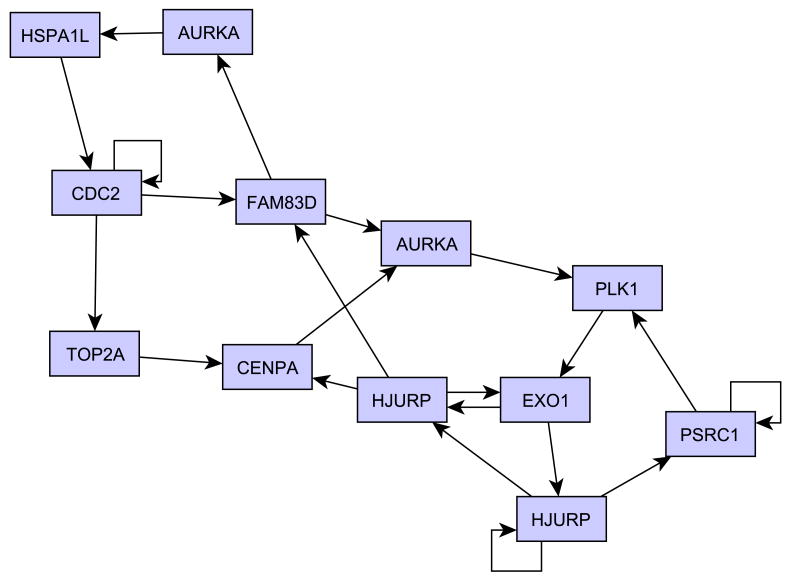
By analyzing the network in Figure 2, we were indeed able to identify a group of 12 probes that are involved in interrelated feedback loops (Figure 3). It is worth noting that the parent variables of the probes in this group are all included in the group itself. The 12 probes map to 10 different genes, some of which are known to be key cell cycle regulators: CDC2, TOP2A, PLK1, AURKA, and CENPA. Table 1 shows the IMAGE clone identifiers relative to the 12 nodes and the corresponding annotation. Please note that in order to ensure that the obtained loop structure does not significantly change when a unique probe is used to represent each gene, we repeated the network inference selecting, for the genes represented by more than one probe, the probe with maximum variance. Results showed that the loop genes and their relationships remained essentially the same.

Figure 3. Inferred feedback loops.

Twelve nodes in the network in Figure 2 are involved in interrelated feedback loops; these probes map to ten different genes. The Figure shows the relationships between the loop nodes.

Table 1. Feedback loop nodes and their annotation.

Each row of the table contains the IMAGE clone ID of a loop probe with the respective Unigene Cluster, Gene Name, Gene symbol, and Gene ID.

CloneID	UGCluster	Gene name	Gene symbol	Gene ID
IMAGE:209066	Hs.250822	Aurora kinase A	AURKA	6790
IMAGE:744047	Hs.592049	Polo-like kinase 1 (Drosophila)	PLK1	5347
IMAGE:447208	Hs.498248	Exonuclease 1	EXO1	9156
IMAGE:2017415	Hs.1594	Centromere protein A	CENPA	1058
IMAGE:703633	Hs.405925	Proline/serine-rich coiled-coil 1	PSRC1	84722
IMAGE:712505	Hs.334562	Cell division cycle 2, G1 to S and G2 to M	CDC2	983
IMAGE:200402	Hs.472716	Family with sequence similarity 83, member D	FAM83D	81610
IMAGE:1540236	Hs.532968	Holliday junction recognition protein	HJURP	55355
IMAGE:66406	Hs.532968	Holliday junction recognition protein	HJURP	55355
IMAGE:50615	Hs.690634	Heat shock 70kDa protein 1-like	HSPA1L	3305
IMAGE:129865	Hs.250822	Aurora kinase A	AURKA	6790
IMAGE:825470	Hs.156346	Topoisomerase (DNA) II alpha 170kDa	TOP2A	7153

3.2 Statistical evaluation of the network model

As assessment of the goodness of fit of the model on the training set, the root mean squared error (RMSE) was calculated and found to be equal to 0.13. The RMSE calculated on relative residuals (normalized, for each probe, with respect to the range of the measured profile) is 0.14. As an example of the fitting accuracy, Figure 4 shows the measured and fitted profiles for four loop probes.

Figure 4. Fitting assessment.

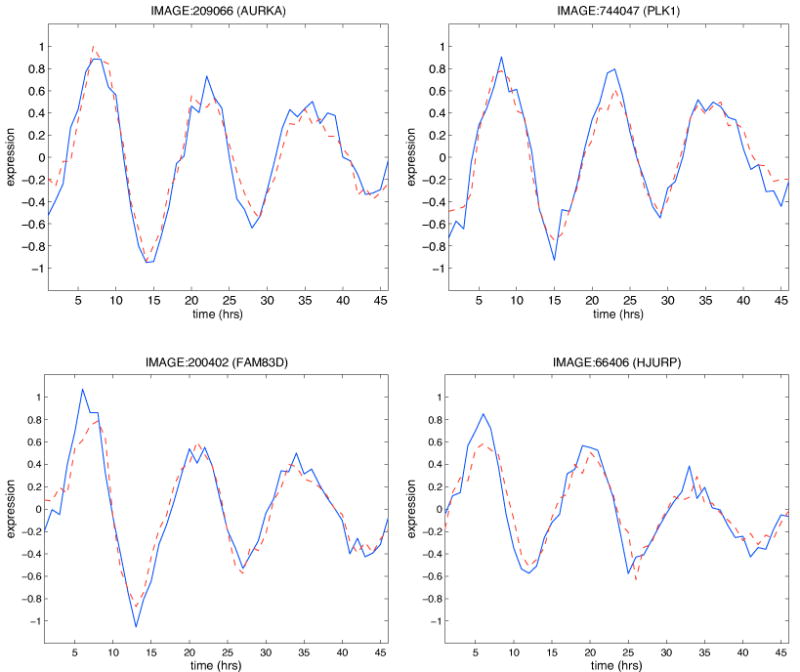
The Figure shows the measured (blue) and fitted (red dashed) profiles for four loop probes. The data are shown starting from the second time point, as the first one is always taken equal to the first measured value.

As pointed out in the section 2.3, a better assessment of model performance is obtained when the model is applied to an independent dataset, different from the one employed to learn the model itself. In the independent test set we employed (see section 2.1), 1095 out of the 1099 analyzed probes were measured and these include all the 412 probes in the connected group. We here recall that, in the test set, the “predicted value” of a probe is equal to its expected value calculated using the parents and the values of the regression parameters inferred on the training set. We found that the RMSE is equal to 0.28 and the relative RMSE equal to 0.23. Figure 5 shows the measured and predicted profiles for the same loop probes as in Figure 4.

Figure 5. Predictive accuracy assessment on an independent test set.

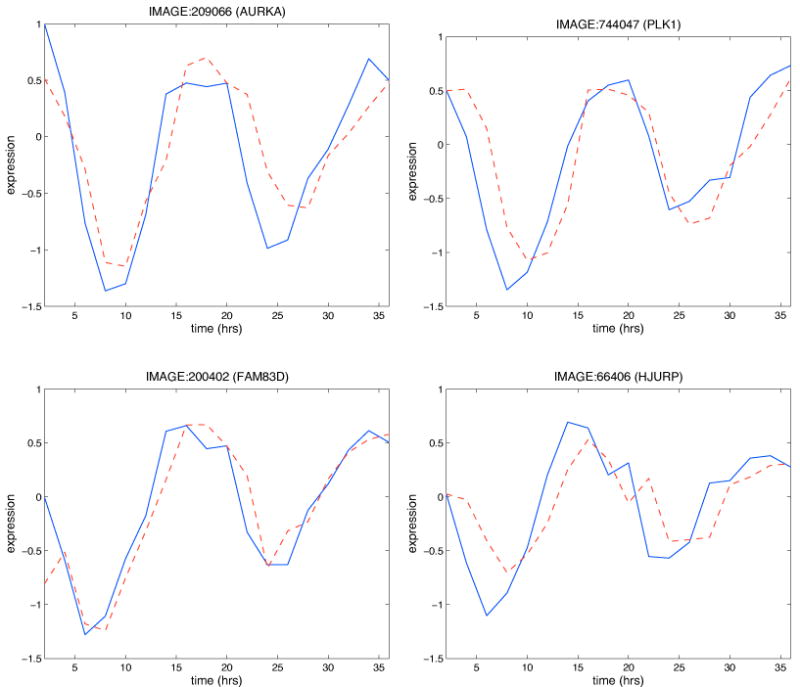
The Figure shows the measured (blue) and predicted (red dashed) profiles for the same loop probes as in Figure 4 but relative to the independent expression dataset employed to evaluate our network model.

3.3 Simulations

Once a DBN model has been learned it can be used to perform in silico analyses of the system. Our goal was to prioritize network nodes on the basis of their influence on the system's dynamics. We devised a 1-input prediction: we considered one node at a time, initialized the system using the measured expression values at time 0 and predicted values at the following time points (up to 46 hours) assuming the values of the considered node are known, while those of all other nodes are not (and therefore for them predicted values instead of measured values are employed for the one-step-ahead prediction). In this way we were able to assign each probe h a score s(h) by calculating the corresponding prediction error (estimated with the RMSE). Using the scores s(h), it is possible to rank the input probes from the one with the lowest error (best predictive ability) to the one with the highest error (worst predictive ability). We performed this 1-input prediction both on the training set and the test set. As possible inputs we considered only the 113 probes out of the group of 412 that have at least one child (which can also be the node itself). When the 1-input prediction was performed on the training set, the 12 loop probes were the first 12 best predictors (Table 2); when the prediction was performed on the test set, 9 of the loop probes were the first 9 best predictors and the other 3 were all within rank 19 (Table 3).

Table 2. Loop probes: results of 1-input prediction on training set.

Observed ranks of the loop probes when the 1-input prediction is performed on the training set.

Rank	Probe	Gene symbol
1	IMAGE:200402	FAM83D
2	IMAGE:712505	CDC2
3	IMAGE:66406	HJURP
4	IMAGE:1540236	HJURP
5	IMAGE:209066	AURKA
6	IMAGE:447208	EXO1
7	IMAGE:744047	PLK1
8	IMAGE:129865	AURKA
9	IMAGE:50615	HSPA1L
10	IMAGE:2017415	CENPA
11	IMAGE:703633	PSRC1
12	IMAGE:825470	TOP2A

Table 3. Loop probes: results of 1-input prediction on independent test set.

Observed ranks of the loop probes when the 1-input prediction is performed on the test set.

Rank	Probe	Gene symbol
1	IMAGE:200402	FAM83D
2	IMAGE:712505	CDC2
3	IMAGE:50615	HSPA1L
4	IMAGE:744047	PLK1
5	IMAGE:1540236	HJURP
6	IMAGE:209066	AURKA
7	IMAGE:703633	PSRC1
8	IMAGE:129865	AURKA
9	IMAGE:447208	EXO1
11	IMAGE:2017415	CENPA
18	IMAGE:825470	TOP2A
19	IMAGE:66406	HJURP

In order to associate a significance measure to this latter ranking, it is possible to empirically estimate the probability of obtaining a “better” ranking. By “ranking” we mean the positions of the 12 loop probes, and we say that a ranking is “better” than the observed one if at least one position is lower and none of the others is higher. As our observed ranking is (1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 18, 19), examples of better rankings are (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 18, 19) or (1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 19). We randomly sampled 12 positions out of the vector z=(1, 2, 3,…,113) for 10⁵ times and estimated the probability of obtaining a better ranking by calculating the proportion of sampled better rankings. The estimated probability was 0. A less restrictive criterion for judging whether a ranking is better consists in considering the average rank of the 12. In this case the probability of obtaining a better ranking can be estimated by the proportion of sampled rankings with lower average rank. Also in this case the empirically estimated probability is 0.

As several research work on network analysis has focused attention on the role of highly connected nodes, the so-called “hubs”, it is interesting to investigate also their predictive ability. By analyzing the distribution of node outdegrees (the number of outgoing connections from a node) in the group of 412 connected nodes, it is possible to find out that the median outdegree is equal to 0 and the 95^th percentile is equal to 6. In particular, the number of nodes with outdegree higher than or equal to 6 is 24: we call these “hub” nodes. By looking at the rank of the hub nodes in the 1-input prediction, it is possible to see that the rank is not inversely proportional to the outdegree and it significantly worsens when considering the test set (Table 4). Moreover, ten of the 12 loop nodes are hub nodes but two are not. This analysis strengthens the hypothesis that feedback loop structures highlight key nodes in the network that are not revealed by simply considering nodes connectivity.

Table 4. Network hubs: results of 1-input prediction.

Network hubs, their outdegree and the observed rank in the 1-input prediction performed on the training and test sets.

Probe	Gene symbol	Outdegree	Rank in 1-input prediction on training set	Rank in 1-input prediction on test set
IMAGE:200402	FAM83D	27	1	1
IMAGE:209066	AURKA	26	5	6
IMAGE:66406	HJURP	25	3	19
IMAGE:788256	KIF23	23	13	13
IMAGE:712505	CDC2	20	2	2
IMAGE:1540236	HJURP	18	4	5
IMAGE:624627	RRM2	14	19	23
IMAGE:51532	ARL6IP1	12	15	113
IMAGE:645565	DEPDC1	10	21	15
IMAGE:129865	AURKA	10	8	8
IMAGE:281898	PSRC1	9	14	10
IMAGE:292936	CDCA8	9	22	16
IMAGE:2019372	GTSE1	9	23	21
IMAGE:126650	DTL	9	26	27
IMAGE:810600	Not available	8	28	104
IMAGE:744047	PLK1	7	7	4
IMAGE:455128	CCNF	7	17	12
IMAGE:1035796	FAM72B	7	18	17
IMAGE:825470	TOP2A	7	12	18
IMAGE:146882	UBE2C	6	20	20
IMAGE:447208	EXO1	6	6	9
IMAGE:703633	PSRC1	6	11	7
IMAGE:1486028	Not available	6	16	14
IMAGE:1564601	FAM111B	6	27	35

Taken together, the 1-input prediction showed that, when the analyzed system is treated as deterministic, the loop probes allow a better reconstruction of the profiles than the other probes.

4. Discussion

4.1 Biological interpretation of results based on a large scale silencing experiment

Recently, Kittler and coworkers performed a genome-wide RNA-interference (RNAi) analysis of HeLa cells in order to identify genes important for cell division [33]. Cells were transfected with endoribonuclease-prepared short interfering RNAs (esiRNAs) to selectively knock down single genes. To determine the function of the deleted genes on cell division the authors measured DNA content 72h after transfection. 17828 genes were targeted and 1351 genes were found to alter cell cycle progression. Using a second non-overlapping set of esiRNAs the authors confirmed the results for 743 genes.

The study of Kittler et al. allows a quantitative evaluation of our method's efficiency in identifying key cell cycle regulators. The 17828 targeted genes include 600 of the 647 genes analyzed in our study. If the 1351 genes affecting the cell cycle are called “positive”, 85 of our 600 investigated genes are positive (14.2%). Out of the 10 loop genes, 9 were tested and 4 were positive (44.4%, Table 5). Thus, the proportion of loop genes with a significant effect on cell cycle progression is much higher than the proportion of total genes with an effect. The statistical significance of the enrichment in the proportion can be assessed by employing the hypergeometric distribution to calculate the probability of at least 4 genes having an effect if 9 genes are randomly chosen out of a group of 600, 85 of which with an effect. This probability is 0.027. Furthermore, if the genes called “positive” are instead considered to be the 743 genes whose phenotype was confirmed using the second set of esiRNAs, 51 of the 600 tested genes have an effect, while all 4 loop genes are still positive. In this case, the p-value is 0.0043. Taken together, the study of Kittler confirmed that our network approach can aid in the identification of key regulators.

Table 5. Biological interpretation of results based on a large scale silencing experiment.

The table lists the silenced loop genes and their observed effect on cell cycle progression as reported in the study by Kittler and colleagues [33].

Gene	Effect reported by Kittler et al.
CDC2	G2 arrest
HSPA1L	None
PLK1	Cell division defect
AURKA	Cell division defect
TOP2A	None
EXO1	None
HJURP	G0/1 arrest
FAM83D	None
PSRC1	None

4.2 Biological interpretation of results based on literature analysis

Even though the study by Kittler et al. provides a great data set to evaluate our study, it might fail in identifying all cell cycle regulators. Therefore, it is important to include available literature into the biological interpretation process.

Out of the 10 genes that we identified as involved in interrelated feedback loops, five encode well-characterized cell cycle regulators. CDC2 (also known as CDK1) is best known for its role in G2/M phase. CDC2 forms with Cyclin B a complex called “mitosis-promoting factor” that regulates the onset of mitosis [43]. The genes PLK1, AURKA, and CENPA encode two kinases (Polo-like kinase 1 and Aurora kinase A) and the centromere protein CENPA. These proteins are key regulators of chromosome segregation [44-48]. siRNA-mediated knockdown of CDC2, PLK1, and AURKA, as well as functional inhibition of CENPA results in delays of cell cycle progression and is often associated with an increase in apoptosis [45, 46, 49, 50]. The importance of these genes for cell cycle progression is underlined by the fact that they have been suggested as potential targets for anti-cancer therapies [51-53]. The gene TOP2A encodes a DNA topoisomerase, an enzyme that is able to modify the topology of DNA. Although TOP2A knockdown did not exhibit a cell cycle phenotype in the study by Kittler et al., it has been demonstrated that this nuclear enzyme is involved in chromosome condensation, chromatid separation, and the relief of torsional stress during transcription and replication of DNA [54].

Recently, it has been discovered that also HJURP, PSRC1 and FAM83D play important roles in cell cycle progression. HJURP was found to be a part of the CENPA centromeric nucleosome associated complex mediating the assembly of CENPA nucleosomes at centromeres [55-57]. Moreover, HJURP plays a key role in the immortality of cancer cells [58]. The gene PSRC1, also known as DDA3, encodes a proline-rich protein. DDA3 is a regulator of spindle dynamics and is essential for mitotic progression [59]. Finally, FAM83D, also known as C20orf129, has been identified as one of the human spindle components [60]. The last two loop genes are poorly characterized. HSPA1L is a heat shock protein. Heat shock proteins help to refold denatured proteins and degrade harmful proteins. The gene EXO1 encodes a protein with exonuclease activity that is involved in processes like DNA repair, recombination, replication, and maintenance of telomere integrity. It is found to be frequently mutated during oncogenesis [61, 62]. Future experiments will reveal whether HSPA1L and EXO1 have a function during cell cycle progression.

In conclusion, our Bayesian network approach proved efficient in the identification of important regulators of the investigated biological system, the cell cycle.

4.3 Sensitivity analysis varying the Bayes factor threshold

The search strategy employed to learn the DBN relies on the Bayes factor (BF) parameter. The higher the value of the chosen threshold for the BF, the more evidence is needed in order to add a new parent. It is agreed in the literature that a BF between 1 and 3 indicates little evidence in favor of a new model versus the currently employed one, while a BF of 3 to 10 already provides substantial evidence in favor of a new model [42]. Thus, a threshold of 7 constitutes a good compromise between the need to add connections conservatively (and thus control the number of spurious connections) and the need to be able to discover novel knowledge. Our choice for the BF threshold is confirmed by a sensitivity analysis on datasets of 100 probes randomly sampled from the entire dataset “Thy-Thy 3” of 40000 probes by Whitfield et al. We indeed expect that the average number of inferred connections in these datasets should be close to zero. We thus sampled 10³ datasets and inferred networks using different thresholds for the BF, namely: (1,3,5,7,10,20,50). Results showed that a threshold of 1 is associated with an average 1.8 connections per node, while thresholds greater than or equal to 3 lead to less than 0.1 connections per node.

In order to assess a posteriori the robustness of the inferred loops, it is possible to consider the BFs relative to the local models of the genes in the loop. In the case in which a gene has only one parent p₁, the BF associated with the gene's local model is: $B{F}_{10}=\frac{M{L}_1}{M{L}_0}$ where ML₁ is the marginal likelihood of the model in which the gene has parent p₁ and ML₀ is the marginal likelihood of the model in which the gene has no parents. BF₁₀ can thus be associated with the link between p₁ and the gene. If instead a gene has two parents p₁ and p₂, two BFs can be considered, namely BF₁₀ and BF₂₁. BF₁₀ is defined as before, while BF₂₁ is given by: $B{F}_{21}=\frac{M{L}_2}{M{L}_1}$. where ML₂ is the marginal likelihood of the model in which the gene has both parents p₁ and p₂. Thus, BF₁₀ can be associated with the link between p₁ and the gene and BF₂₁ can be associated with the link between p₂ and the gene, yet remembering that BF₂₁ represents the increase in the marginal likelihood when p₂ is added to the parent set that already contains p₁. Figure 6 shows the links in the loops annotated with the corresponding BF.

Figure 6. Assessment of the robustness of the inferred feedback loops.

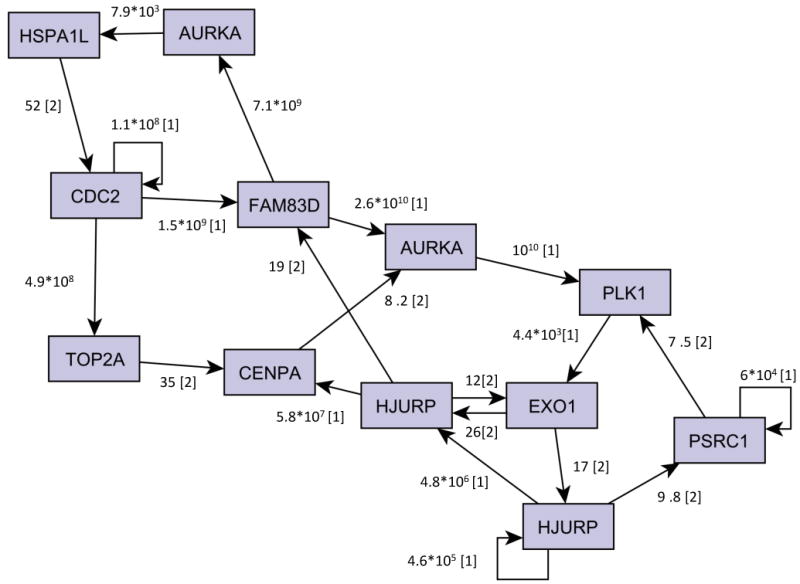
The Figure shows the relationships between the loop nodes annotated with the corresponding BF. In cases in which a gene has two parents, the BF of the first added parent (BF₁₀) is indicated with [1] and that of the second parent (BF₂₁) with [2].

If we set a higher threshold for the BF, some links are going to disappear. Thus, some nodes might not be part of the loops anymore, as there would be no feedback path going through these nodes. In particular, by setting the threshold to 10, three genes, namely TOP2A, CENPA and PSRC1, are no more involved in the loops while the structure involving the other nodes remains unchanged. It is interesting to note that the loop involving CDC2-FAM83D-AURKA-HSPA1L is maintained up to a threshold equal to 50, that is 7 times higher than the one we employed. On the other hand, by lowering the threshold, the complex loop structure involving the 10 genes enlarges and includes more genes.

As our hypothesis is that the feedback loop structure highlights key genes in cell cycle regulation, it is interesting to assess the predictions obtained for different BF thresholds employing Kittler et al. data, as discussed above for threshold=7. Table 6 reports, for BF threshold=(3,5,10,20,50), the number of nodes involved in the feedback loop structure (and the corresponding number of genes, evaluated on the annotated nodes), the number of loop genes tested by Kittler et al. and those with an effect when 743 ‘positive genes’ are considered, with the corresponding p-value. Results show that predictions are significant for all considered thresholds confirming that feedback loop structures are enriched in key cell cycle genes.

Table 6. Loop genes inferred for different Bayes factor thresholds and assessment of their role in cell cycle regulation.

The table reports, for different BF thresholds (BFth), the number of nodes involved in the feedback loop structure (Numloop) and the corresponding number of genes calculated on the annotated probes (Numgeneloop), the number of loop genes tested by Kittler et al. (Numgenetested), the number of loop genes with an effect when the 743 ‘positive genes’ are considered (Neffect743), and the corresponding p-value (pval743). Results for BFth=7 are reported as a reference.

BFth	Numloop	Numgeneloop	Numgenetested	Neffect743	pval743
3	31	23	21	6	0.0057
5	15	12	11	4	0.0098
7	12	10	9	4	0.0043
10	9	7	7	4	0.0014
20	4	4	4	2	0.0381
50	4	4	4	2	0.0381

5. Conclusions

The availability of high-throughput dynamic expression data improves our chances to unravel cellular regulatory mechanisms. DBNs are particularly suited for analyzing these data and infer gene network models. It is important to note that gene networks inferred from expression data alone do not necessarily represent the biological regulation of one gene on another, i.e. a physical/biochemical interaction between gene products. Instead, they are abstract models of the dynamics of gene expression in the analyzed system: an arc from gene A to gene B implies that the expression value of B depends on the expression value of A at the previous time point, i.e. knowledge of A's expression value helps in predicting B's expression value at the following time point. In the case of DBNs, the dependence is probabilistic, which means that the probability of B taking a certain value at time t+1 is conditional on the value of A at time t. At the molecular level, feedback loops identified by DBNs may thus correspond to a variety of regulatory mechanisms. The inferred model represents and summarizes such mechanisms by means of probabilistic relationships between the observed variables. This provides the advantage, at a system level, to identify feedback loops, which appear to be key regulatory elements of the observed dynamics, as they confer systems fundamental properties such as robustness to disturbances and the possibility to exhibit periodic behaviors.

In this paper we have applied a DBN approach to learn feedback control structures from gene expression data measured during the cell cycle in a human cancer cell line [32]. The analysis of the inferred network led us to concentrate our attention on a group of 10 genes involved in various interrelated feedback loops. We refer to these genes as loop genes. We hypothesized that the loop genes have a central role in cell cycle regulation. Simulations of the network dynamics supported our hypothesis and a large-scale silencing assay by Kittler et al. [33] showed that the proportion of loop genes whose silencing causes abnormal cell cycle progression is much higher than the proportion of total analyzed genes with abnormal phenotype. Furthermore, analysis of the current literature showed that 8 loop genes are very important for cell cycle regulation.

Let us note that the approach described in this paper builds on a number of steps for DBN modeling and learning that have been previously published in the literature, although not yet applied to the discovery of feedback loops in cell cycle regulatory networks. Results show that a set of biologically relevant loops can be found by applying a relatively simple model, which is based on linear relationships between genes. Moreover, the model search was performed by resorting to a stepwise modification of the well-known K2 algorithm, which allowed obtaining the solution in a computationally efficient way, so that it was possible to learn gene networks starting from hundreds of probes. Thus, the performed modeling choices constitute a good compromise between the need of obtaining results by processing large number of genes and the goal of keeping the number of false positives (i.e. spurious feedbacks) as low as possible [63].

The cell cycle is particularly suited to apply our method as its understanding is of crucial relevance for cancer research. The obtained results may therefore be important for defining molecular targets of drugs and proposing new therapeutic interventions. Furthermore, the cell cycle is a well studied biological process, for which a large amount of literature for validating results is available. Yet the approach is applicable to other biological systems: it could for example be particularly interesting in the study of developmental/differentiation processes in stem cells to prioritize genes for further biological experiments.