Effects of polymorphism for locally-adapted genes on rates of neutral introgression in structured populations

Abstract

Adaptation to local conditions within demes balanced by migration can maintain polymorphisms for variants that reduce fitness in certain ecological contexts. Here, we address the effects of such polymorphisms on the rate of introgression of neutral marker genes, possibly genetically linked to targets of selection. Barriers to neutral gene flow are expected to increase with linkage to targets of local selection and with differences between demes in the frequencies of locally-adapted alleles. This expectation is borne out under purifying and disruptive selection, regimes that promote monomorphism within demes. In contrast, overdominance within demes induces minimal barriers to neutral introgression even in the face of very large differences between demes in the frequencies of locally adapted alleles. Further, segregation distortion, a phenomenon observed in a number of interspecific hybrids, can in fact promote transmission by migrants to future generations at rates exceeding those of residents.

1 Introduction

Bengtsson (1985) proposed an index of the rate of interspecific gene flow at a neutral locus linked to an incompatibility factor. This framework has been applied to incompatibility selection, under which factors that are selectively neutral in their native species contribute to deleterious effects in interspecific hybrids and their descendants (e.g., Barton and Bengtsson 1986; Navarro and Barton 2003; Fusco and Uyenoyama 2011).

Seminal theoretical work has addressed neutral gene flow across zones of hybridization between species (e.g., Barton 1979; Gavrilets 1997). It has provided a theoretical basis for empirical studies of interspecific introgression (see Barton and Hewitt 1985; Teeter et al. 2008, and references therein). These models typically postulate fixed differences between pure-species populations at both neutral marker loci and targets of selection, implicitly assuming the extinction of foreign alleles on a shorter time scale than their introduction through hybridization. In contrast, Rieseberg and Blackman (2010) have noted that the majority of the candidate loci for speciation genes in plants appear to show intraspecific polymorphism, a marked departure from the rule in animals.

Intraspecific polymorphism may reflect adaptation to local conditions within demes of a structured population. Under certain conditions, local adaptation can proceed to the point of speciation (Rundle and Nosil 2005). Here, we apply the approach of Fusco and Uyenoyama (2011) to explore the implications for neutral introgression of various forms of local adaptation within a two-deme system, irrespective of whether the barriers to gene flow may eventually delineate species.

Numerous workers (e.g., Levene 1953; Moran 1962; Maynard Smith 1966; Karlin and McGregor 1972a) have derived conditions for the maintenance of genetic polymorphism under various forms of geographically-structured selection. One class entails migration acting in opposition to purifying or disruptive selection. In addition to mechanisms of this kind, we address selection regimes capable of maintaining polymorphism within demes even in the absence of migration: overdominance and purifying selection balanced by segregation distortion.

Segregation distortion contributes to the syndrome expressed upon hybridization in a number of exemplar systems for the study of speciation (e.g., Dermitzakis et al. 2000; Tao et al. 2001). Frank (1991) and Hurst and Pomiankowski (1991) suggested that the unmasking upon hybridization of selfish factors that induce meiotic drive of sex chromosomes may account for Haldane’s (1922) rule. Assessments of the role of meiotic drive in postzygotic isolation between species have concentrated on distortions of the sex ratio (Orr and Presgraves 2000; Coyne and Orr 2004, Chap. 8). While perhaps less easily detected than driving sex chromosomes, autosomal segregation distortion also occurs in interspecific hybrids (Fishman and Willis 2005), and moreover within pure-species populations (Fishman and Saunders 2008).

We find that barriers to neutral introgression decline with differences between the local gene pools in the frequencies of alleles subject to purifying or disruptive selection. Less expected is that unless linkage to the target of selection is virtually complete, overdominance favoring different allele frequencies in the two demes imposes minimal barriers to introgression of neutral markers. Segregation distortion balanced by purifying selection also induces weak barriers and can in fact enhance the contribution of migrants to future generations beyond that of residents.

2 General approach

2.1 Local adaptation

Selection in each deme of a two-deme population reflects adaptation to local conditions, with the rate of reproduction determined by genotype at the biallelic A locus:

$$\begin{array}{cccc}\hfill \hfill & \hfill AA\hfill & \hfill Aa\hfill & \hfill aa\hfill \\ \hfill \text{Deme}1\hfill & \hfill {\alpha }_0\hfill & \hfill {\alpha }_1\hfill & \hfill {\alpha }_2\hfill \\ \hfill \text{Deme}2\hfill & \hfill {\beta }_0\hfill & \hfill {\beta }_1\hfill & \hfill {\beta }_2\hfill \end{array}$$ (1)

Following random union of gametes sampled from the local gene pool, selection on the zygotes, and gametogenesis by reproductives, the frequencies of the A allele among gametes produced in the two demes correspond to

$$p_1=f_1\left(x_1\right)=\frac{x_1[x_1{\alpha }_0+2d_1(1-x_1\left){\alpha }_1\right]}{x_1^2{\alpha }_0+2x_1(1-x_1){\alpha }_1+{(1-x_1)}^2{\alpha }_2}$$ (2a)

$$p_2=f_2\left(x_2\right)=\frac{x_2[x_2{\beta }_0+2d_2(1-x_2\left){\beta }_1\right]}{x_2^2{\beta }_0+2x_2(1-x_2){\beta }_1+{(1-x_2)}^2{\beta }_2},$$ (2b)

for x_i the frequency of A in the gamete pool of deme i (i = 1, 2), p_i the frequency of A among gametes produced by reproductives, and d_i the expected proportion of A-bearing gametes among gametes produced by Aa individuals (d₁ = d₂ = 1/2 under Mendelian segregation).

Formation of the gamete pool from which zygotes of the subsequent generation will be derived entails mixing of gametes generated by reproductives in the two demes:

$$x_1^{\ast }=(1-m)p_1+m{p}_2$$ (3a)

$$x_2^{\ast }=m{p}_1+(1-m)p_2,$$ (3b)

in which m represents the proportion of the local gene pool derived from gametes of individuals born in the other deme (backward migration rate). These expressions reflect symmetric gene flow between the demes, but of course asymmetric gene flow can easily be accommodated. At equilibrium, $x_i^{\ast }=x_i$.

It is well-known that f₁(·) and f₂(·) in Equation (2) represent monotone transformations, which in the absence of gene flow (m = 0) implies convergence of allele frequency to the nearest locally stable fixed point (see Karlin and Feldman 1972).

2.2 Genealogical migration rate

In classical neutral models of structured populations (Wright 1969), the backward migration rate (m) represents the fraction of the gene pool of a deme that derives from a different deme in the immediately preceding generation. Apart from genes that influence the propensity of individuals to reproduce in a deme other than their birth deme, all genomic regions are subject to the same backward migration rate (m). The sampling of a gene from the present population entails its descent through ancestors that succeeded in contributing to the present generation, a locus-specific process that may reflect selection targeted either to the gene itself or to associated sites (Karlin 1982).

Central to the distribution of F_ST and other summary statistics of genetic variation in structured populations is the rate of coalescence between lineages sampled from different demes. This rate in turn depends on the waiting time between interdeme transfers in the line of descent of a gene sampled at random from the present population. Modeling the distribution of waiting time as exponential, Fusco and Uyenoyama (2011) termed the parameter of that distribution the “genealogical migration rate”:

$$g=\omega m$$ (4)

for ω the relative reproductive rate. Relative reproductive rate ω (defined in (5)) represents the expected contribution to future generations of a neutral marker gene introduced into the local gene pool on a gamete transmitted by a migrant relative to a gene on a gamete transmitted by a resident. It is conceptually similar to Bengtsson’s (1985) “gene flow factor,” which he defined in terms of “the probability of ultimate inclusion” of a foreign allele into the local gene pool, although he did not address the modification of this allele-based (rather than lineage-based) index for cases involving polymorphism in the foreign and local gene pools. Results from numerical simulations indicated that the distribution of waiting times between migration events along a lineage conforms well to an exponential distribution with parameter g, determined by the method of Fusco and Uyenoyama (2011).

Genealogical migration rate (4) is related to the “neutral effective migration rate” of Kobayashi et al. (2008). While their definition is formulated in terms of the frequency of an allele introduced by migrants, they noted its equivalence under certain conditions to the probability that a lineage sampled at random from the local deme traces back to a different deme in the preceding generation. The allele-based index of Gavrilets (1997) corresponds to the inverse of the frequency of a marker allele in a deme in which it would be absent but for gene flow.

Relative reproductive rate represents the expected number of descendants far in the future of a marker gene on a migrant gamete relative to gene on a resident gamete:

$$\omega =\underset{t\to \infty }{\lim }\frac{v_m{C}^{t}e}{v_r{C}^{t}e},$$ (5)

for C a matrix specifying transmission of the marker on various backgrounds; t the number of generations since the focal transmission events; v_m the distribution of haploid gametic backgrounds of a marker allele introduced on a migrant gamete; v_r the background distribution for a gamete derived from a resident; and e the vector with all elements equal to 1 (Fusco and Uyenoyama 2011). The dimension of v_m and v_r corresponds to the number of gametic backgrounds on which the focal marker allele can occur: b = 2ⁿ, for n the number of biallelic local adaptation loci. Let z denote the number of possible zygotic genotypes; if all local adaptation loci are autosomal, for example, $z=\left(\begin{array}{c}\hfill b+1\hfill \\ \hfill 2\hfill \end{array}\right)$. Transmission matrix C depicts the gamete-to-gamete cycle:

$$\mathit{C}=\mathit{Z}\mathit{S}\mathit{G},$$

for Z (b × z) describing the generation of zygotes from gametes, diagonal matrix S (z × z) the change in zygote numbers due to selection, and G (z × a) the production of gametes by reproducing zygotes.

In the case of a single biallelic locus subject to local adaptation selection, for example, b = 2, with the gametic background of a focal marker gene corresponding to either the A or the a allele. Among gametes of individuals originating in deme i, these backgrounds occur in frequencies p_i and (1 − p_i). In deme 1, for example, the background distributions of marker alleles on gametes generated by a migrant and a resident correspond to

$$v_m=(p_2,1-p_2)v_r=(p_1,1-p_1),$$ (6)

in which the first element corresponds to allele A and the second to allele a, and the transmission matrix to

$$C_1=\left(\begin{array}{cc}\hfill {\alpha }_0{x}_1∕2+d_1(1-r){\alpha }_1(1-x_1)\hfill & \hfill (1-d_1)r{\alpha }_1(1-x_1)\hfill \\ \hfill d_{1}r{\alpha }_1{x}_1\hfill & \hfill (1-d_1)(1-r){\alpha }_1{x}_1+{\alpha }_2(1-x_1)∕2\hfill \end{array}\right),$$ (7)

for r the rate of crossing-over between the marker locus and the target of selection. In cases involving non-Mendelian segregation (d₁ ≠ 1/2), we assume complete linkage between the target of selection and the centromere.

Complete linkage (r = 0) between the marker locus and the target of selection implies a diagonal transmission matrix (7), with nonzero elements proportional to the marginal fitnesses of the alleles under selection. For example, C₁(1, 1) > C₁(2, 2), for C₁(i, j) the element in the i^th row and j^th column of C₁, implies that zygotes produced by fusion of a gamete bearing the A allele with a random gamete from deme 1 have higher expected fitness than those produced from a gamete bearing the a allele. Relative reproductive rate (5) corresponds to the frequency of the allele with higher marginal fitness among gametes transmitted by migrants relative to residents:

$${\omega }_1=\{\begin{array}{cc}{p}_2∕p_1\hfill & \text{if}{C}_1(1,1)>C_1(2,2)\hfill \\ (1-p_2)∕(1-p_1)\hfill & \text{if}{C}_1(1,1)<C_1(2,2)\hfill \\ 1\hfill & \text{if}{C}_1(1,1)=C_1(2,2).\hfill \end{array}\phantom{\}}$$ (8)

3 Results

3.1 Very low backward migration rates

Karlin and McGregor (1972a,b) enumerated the existence and stability conditions for equilibria in structured populations “weakly coupled” by low rates of gene flow (small m). Their main principles include:

• For n₁ and n₂ the numbers of fixed points in the absence of gene flow (m = 0) of the transformations describing evolution in demes 1 and 2, a maximum of n₁n₂ fixed points can exist in a sufficiently weakly coupled system.

• Equilibria in the coupled system that descend from pairs of states that are locally stable in the two demes in the absence of gene flow remain locally stable in the coupled system for sufficiently small m.

We apply these principles to the models explored here, in which the monotonicity of the transformations f₁(·) and f₂(·) in (2) implies the stronger notion of local stability (geometric rate of approach) considered by Karlin and McGregor (1972b).

3.1.1 Stable equilibria

Let $\widehat{\alpha }$ represent a locally stable fixed point (possibly monomorphic) of the transformation (2) in deme 1 in the absence of migration (m = 0):

$$\widehat{\alpha }=f_1\left(\widehat{\alpha }\right)=p_1=x_1.$$

That f₁(·) is a monotone transformation ensures the nonoscillatory, geometric convergence of allele frequency to the nearest locally stable fixed point (e.g., Karlin and Feldman 1972). In particular, $0<f_1^{\prime }\left(\widehat{\alpha }\right)<1$, for the prime indicating the derivative with respect to x₁. Similarly, let $\widehat{\beta }$ represent a locally stable equilibrium in deme 2 in the absence of migration. Karlin and McGregor (1972b) showed that under sufficiently low rates of migration (small m), the joint state

$$x_1=\widehat{\alpha }+{\delta }_1{x}_2=\widehat{\beta }+{\delta }_2$$ (9a)

$$p_1=\widehat{\alpha }+{\delta }_1{f}_1^{\prime }\left(\widehat{\alpha }\right)p_2=\widehat{\beta }+{\delta }_2{f}_2^{\prime }\left(\widehat{\beta }\right)$$ (9b)

represents a locally stable equilibrium in the full system. Taylor series expansions provide expressions for the δ_i:

$${\delta }_1=\frac{-m(\widehat{\alpha }-\widehat{\beta })}{1-f_1^{\prime }\left(\widehat{\alpha }\right)}$$ (10a)

$${\delta }_2=\frac{m(\widehat{\alpha }-\widehat{\beta })}{1-f_2^{\prime }\left(\widehat{\beta }\right)}.$$ (10b)

For example, near the state ($\widehat{\alpha }=1$, $\widehat{\beta }=0$), migration in opposition to local selection increases the frequency of the disfavored allele in deme 1 to

$$1-x_1=-{\delta }_1=\frac{m{\alpha }_0}{{\alpha }_0-2(1-d_1){\alpha }_1},$$

which reduces, for α₀ = 1, α₁ = (1 − s), and d₁ = 1/2, to m/s (compare (2) of Charlesworth et al. 1997).

3.1.2 Relative reproductive rate

We use transmission matrix C₁ (7) to determine the relative reproductive rate (5) for the full system under very low migration rates (m near 0) at stable fixed points (x₁, x₂) descended from $(\widehat{\alpha },\widehat{\beta })$. In this section, we restrict consideration to polymorphisms descended from states of fixation in both demes; Section 3.4 addresses selection regimes that can maintain within-deme polymorphism even in the absence of migration.

$\widehat{\alpha }$ near zero

For $(x_1,x_2)=({\delta }_1+\widehat{\beta }+{\delta }_2)$, C₁ reduces to

$$\left(\begin{array}{cc}\hfill d_1{\alpha }_1(1-r)\hfill & \hfill (1-d_1){\alpha }_{1}r\hfill \\ \hfill 0\hfill & \hfill {\alpha }_2∕2\hfill \end{array}\right)+O\left({\delta }_1\right).$$

Relative reproductive rate (5) corresponds to

$${\omega }_1=\widehat{\beta }\frac{(1-d_1){\alpha }_{1}r}{{\alpha }_2∕2-d_1{\alpha }_1(1-r)}+(1-\widehat{\beta })+O\left({\delta }_1\right).$$ (11)

In the absence of crossing-over between the neutral marker locus and the target of selection (r = 0), this expression confirms (8): ${\omega }_1=(1-p_2)∕(1-p_1)=(1-\widehat{\beta })+O\left({\delta }_1\right)$. More unexpectedly, ω₁ can exceed unity, implying that gametes transmitted by migrants contribute to future generations at higher rates than do residents. Relative reproductive rate exceeds unity for

$${\alpha }_1>\frac{{\alpha }_2}{1-(1-2d_1)(1-2r)}.$$

This condition can be satisfied for sufficiently loose linkage (large r) simultaneously with the local stability condition of the fixation state in the absence of migration (α₂ > 2d₁α₁) provided that

$${\alpha }_1>{\alpha }_2>2d_1{\alpha }_1,$$

which entails 1 > 2d₁. Under Mendelian segregation (d₁ = 1/2), ω₁ < 1.

In the case studied by Bengtsson (1985), migration introduces an allele which would otherwise have been rapidly eliminated by selection because it reduces the fitness of its carriers to σ relative to non-carriers. These assumptions correspond in the present model to d₁ = 1/2, $\widehat{\beta }=1$, α₂ = 1, and α₁ = (1 − s), under which ω₁ (11) reduces to

$$\frac{(1-s)r}{1-(1-s)(1-r)},$$ (12)

in agreement with the findings of Bengtsson (1985) and others.

$\widehat{\alpha }$ near unity

For $(x_1,x_2)=(1+{\delta }_1,\widehat{\beta }+{\delta }_2)$, similar arguments lead to

$${\omega }_1+\widehat{\beta }+(1-\widehat{\beta })\frac{d_1{\alpha }_{1}r}{{\alpha }_0∕2-(1-d_1){\alpha }_1(1-r)}+O\left({\delta }_1\right).$$

This expression confirms ${\omega }_1=p_2∕p_1=\widehat{\beta }+O\left({\delta }_2\right)+O\left({\delta }_1\right)$ in the absence of crossing-over between the neutral marker locus and the target of selection (8), and the Bengtsson (1985) expression (12) for $\widehat{\beta }$ close to zero. Relative reproductive rate exceeds unity for

$${\alpha }_1>\frac{{\alpha }_0}{1-(2d_1-1)(1-2r)}.$$

This condition can be satisfied for sufficiently loose linkage simultaneously with the local stability condition of the fixation state in the absence of migration (α₀ > 2(1 − d₁)α₁), provided that

$${\alpha }_1>{\alpha }_0>2(1-d_1){\alpha }_1,$$

which entails 2d₁ > 1.

3.2 Within-deme polymorphisms maintained by migration

Here, we consider two selection regimes for which all locally stable equilibria are monomorphic in the absence of migration.

3.3 Purifying selection

We consider a model in which selection favors alternative alleles in the two demes (α₀ = β₂ = 1, α₂ = β₀ = τ, and α₁ = β₁ = σ):

$$\begin{array}{cccc}\hfill \hfill & \hfill AA\hfill & \hfill Aa\hfill & \hfill aa\hfill \\ \hfill \text{Deme}1\hfill & \hfill 1\hfill & \hfill \sigma \hfill & \hfill \tau \hfill \\ \hfill \text{Deme}2\hfill & \hfill \tau \hfill & \hfill \sigma \hfill & \hfill 1\hfill \end{array}$$ (13)

with 1 > σ > τ. This model was explored by Levene (1953), under a particular migration scheme (Levene migration), and by Moran (1962, Chapter IX), under the restriction to additivity (2σ = 1 + τ).

In the coupled system (m > 0), allele A increases when rare only if

$$\frac{\sigma [1-m-(1-2m\left)\sigma \right]}{1-(1-m)\sigma }>\tau .$$ (14)

By symmetry, an identical condition holds for the initial increase of allele a.

Free exchange (m = 1/2)

For m = 1/2, (3) indicates that the demes share a common gamete pool, with

$$x_1=x_2=x=(p_1+p_2)∕2.$$

The roots of the fifth-degree polynomial in x obtained from (2) and (3) fall into three categories: fixation states (x = 0, 1); x = 1/2, for which

$$p_1=\frac{1+\sigma }{1+2\sigma +\tau }{p}_2=\frac{\sigma +\tau }{1+2\sigma +\tau };$$

and any valid roots of

$$\sigma -\tau (2-\sigma )+x(1-x){(1+\tau -2\sigma )}^2=0.$$ (15)

We designate x = 1/2 the Type 1 equilibrium and the roots of (15) the Type 2 equilibria.

Type 2 equilibria sum to unity: if $\widehat{x}$ is a root of (15) then $1-\widehat{x}$ is also a root. The pair exist in (0, 1) only if both

$$\tau >\frac{\sigma }{2-\sigma }$$ (16a)

$$\sigma -\tau (2-\sigma )+{(1+\tau -2\sigma )}^2∕4>0.$$ (16b)

These conditions correspond to

$$\min \{\sigma ,3-2\sqrt{2-{\sigma }^2}\}>\tau >\frac{\sigma }{2-\sigma }.$$ (17)

Comparison with (14) indicates that both fixation states (x = 0, 1) are locally stable only under (16a). The Type 1 equilibrium (x = 1/2) is locally stable only under (16b). Consequently, the Type 2 equilibria exist only when all other equilibria (the two fixation states and the Type 1 equilibrium) are locally stable. That only one polymorphic fixed point (Type 1) can be locally stable reflects Principle I of Karlin (1977), which applies to models with Levene migration schemes.

In summary, three kinds of equilibrium structures exist, corresponding to parameter domains delineated by (16):

• Small τ: Reversal of the inequality in (16a) implies instability of both fixation states and the existence of only one polymorphic equilibrium (x = 1/2), which is locally stable.

• Intermediate τ: Under (17), the paired Type 2 equilibria come into existence, one diverging from each of the fixation states. All other equilibria (x = 0, 1/2, 1) are locally stable.

• Large τ: For σ > 1/5, the upper end of the interval in (17) corresponds to the second element in the min bracket. At τ equal to this quantity, the Type 2 equilibria fuse with the Type 1 equilibrium. For τ exceeding this quantity, the Type 1 equilibrium is unstable, with both fixations stable.

Distinct gene pools (0 < m < 1/2)

Appendix A describes the equilibrium states of the coupled system.

Similar to the case with identical gene pools in the two demes (m = 1/2), two types of polymorphic equilibria arise under m ∈ (0, 1/2). At Type 1 equilibria, x₁ + x₂ = p₁ + p₂ = 1, which implies identical mean fitnesses in the two demes (T₁ = T₂, for T_i the denominator of f_i(·) in (2)). Type 2 equilibria occur in pairs: for ${\widehat{x}}_1$ and ${\widehat{x}}_2$ allele frequencies at one Type 2 equilibrium, allele frequencies at the other member of the pair sum to $2-{\widehat{x}}_1-{\widehat{x}}_2$. At most one pair of Type 2 equilibria can exist.

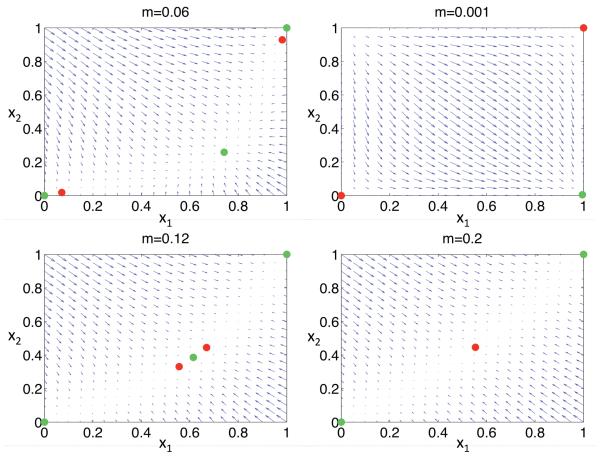
As in the case of complete mixing (m = 1/2), the paired Type 2 equilibria simultaneously depart from fixation states (0, 0) and (1, 1) at the point at which the fixations become unstable (14) and simultaneously fuse with the Type 1 equilibrium at the point at which the Type 1 equilibrium becomes unstable. Figure 1 shows a progression of behaviors as the backward migration rate (m) increases. For low migration rates, all trajectories approach the Type 1 equilibrium, descended from the fixation state (x₁, x₂) = (1, 0). For higher migration rates, the Type 1 equilibrium remains stable as it departs from the (1, 0) corner along the x₁ + x₂ = 1 line. Fixation states (0, 0) and (1, 1) remain unstable as m increases until the paired Type 2 equilbria emerge from them. The unstable Type 2 equilibria demarcate the domain of attraction of the locally stable Type 1 equilibrium from those of the locally stable fixation states. Trajectories appear to show geometric convergence to a manifold connecting all equilibria, with substantially slower movement along the manifold toward stable points. The preceding section shows that under some parameter assignments, the Type 1 equilibrium can remain locally stable even under maximal gene flow (m = 1/2). Under other parameter assignments, the paired Type 2 equilibria fuse with the Type 1 equilibrium as migration rates increase, at which point the single polymorphic equilibrium becomes unstable while the fixation states remain locally stable.

Figure 1.

Local trajectories of allele frequencies under purifying selection (13) with σ = 0.88 and τ = 0.77. Green dots indicate locally stable equilibria and red dots unstable equilbria. Arrows indicate the direction of evolutionary change over a single generation, with the size of the arrow reflecting the magnitude of the change. For a small backward rate of migration m (upper right panel), only the Type 1 equilibrium, descended from the (1,0) fixation state, is locally stable. For somewhat larger m (proceeding counter-clockwise), the Type 1 equilibrium moves into the interior. Trajectories destined for the Type 1 equilibrium appear first to approach to a curve connecting the Type 1 and fixation equilibria and then to move along the curve to the Type 1 equilibrium. The always unstable Type 2 equilibria (red) first emerge from the fixation states, at the point at which the fixations become locally stable (green). As m increases, the unstable Type 2 equilibria approach the Type 1 equilibrium. Upon the fusion of the Type 1 and 2 equilibria, the Type 1 equilibrium becomes unstable.

Relative reproductive rates

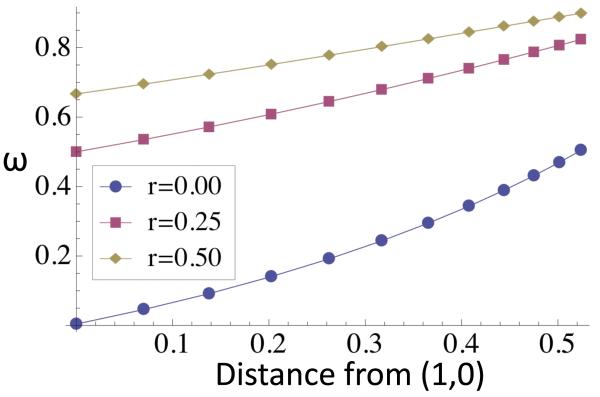
For small m, with the Type 1 equilibrium close to (1, 0), the relative reproductive rate at the neutral marker locus (5) corresponds to (12), in agreement with Bengtsson (1985). Figure 2 illustrates that ω₁, the relative reproductive rate in deme 1, increases with the backward migration rate m and the Euclidean distance of the Type 1 equilibrium from the (1, 0) fixation state. That the succession of points for a given level of linkage (r) increases nearly linearly with distance suggests an approximately linear relationship between ω and (1 − x₁), the frequency of the disfavored allele a in deme 1.

Figure 2.

Relative reproductive rate (5) induced at a neutral marker locus by purifying selection (σ = 0.80, τ = 0.77) at a Type 1 equilibrium under various levels of gene flow. For a given rate of crossing-over between the target of selection and the marker locus (r), the points correspond to an equally-spaced sequence of migration rates from m = 0 to m = 0.11 (beyond which the Type 1 equilibrium fuses with the Type 2 equilibria and becomes unstable). Relative reproductive rate (5) induced at the marker locus (ω) increases with the Euclidean distance of the stable Type 1 equilibrium from the fixation state $(\Vert (x_1,x_2)-(1,0)\Vert =(1-x_1)\sqrt{2}$. For very small backward migration rates (m → 0), the vertical sequence of the leftmost points is very similar to (12), the “gene flow factor” of Bengtsson (1985).

3.3.1 Disruptive selection

Karlin and McGregor (1972a) derived the existence and stability conditions for a selection regime specifying underdominance in both demes:

$$\begin{array}{cccc}\hfill \hfill & \hfill AA\hfill & \hfill Aa\hfill & \hfill aa\hfill \\ \hfill \text{Deme}1\hfill & \hfill 1\hfill & \hfill \sigma \hfill & \hfill 1\hfill \\ \hfill \text{Deme}2\hfill & \hfill 1\hfill & \hfill \sigma \hfill & \hfill 1\hfill \end{array}.$$ (18)

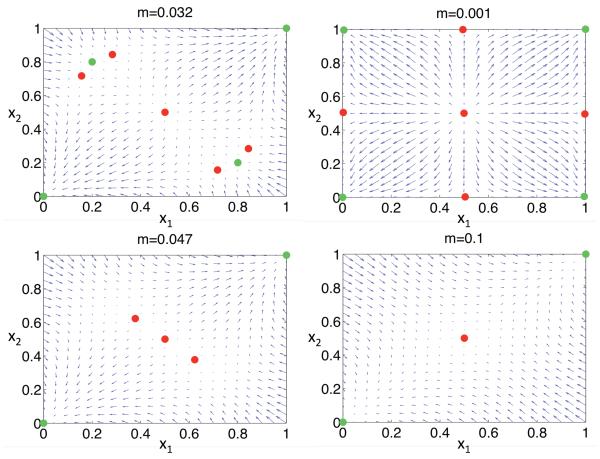
All four fixation states, including (1, 0) and (0, 1), are locally stable in the absence of gene flow (m = 0), which implies two locally stable polymorphisms (designated P⁺ and P⁻ by Karlin and McGregor 1972a) under small migration rates (1 − σ > 4m). Because these equilibria descend from locally stable fixations and satisfy x₁ + x₂ = 1, we call them the Type 1 equilibria. Each Type 1 equilibrium is flanked by a pair of unstable fixed points (designated Q⁺, Q⁻, R⁺ and R⁻), which demarcate the domains of attraction of the Type 1 equilibria while they are locally stable (Fig. 3).

Figure 3.

Local trajectories of allele frequencies in the disruptive selection model of Karlin and McGregor (1972a) under σ = 0.8, with features similar to those of Fig. 1. For a small backward rate of migration m (upper right), the Type 1 equilibria (P⁺ and P⁻), descended from fixation states (1, 0) and (0, 1), are locally stable (green), with the four equilibria (Q⁺, Q⁻, R⁺, and R⁻) close to the unstable polymorphism in one deme and a fixation in the other all unstable (red). As m increases (proceeding counter-clockwise), the Type 1 equilibria remain locally stable as they move into the interior, each flanked by a pair of unstable equilibria demarcating the domains of attraction of the Type 1 equillibria. Upon the fusion of the unstable equilibria with the Type 1 equilibria, all three polymorphic states become unstable, fusing into a single unstable state for larger m.

Relative reproductive rate (5) at the locally stable Type 1 equilibria shows behavior qualitatively similar to that exhibited by our purifying selection model (Fig. 2).

3.4 Within-deme polymorphisms maintained by selection even in the absence of migration

We now address selection regimes that admit stable or unstable polymorphisms within demes even in the absence of migration (m = 0). This class of models includes, for example, overdominance (α₁ > α₀, α₂), underdominance or disruptive selection (α₁ < α₀, α₂), and purifying selection balanced by segregation distortion (e.g., α₀ > α₁ > α₂ with d₁ < 1/2).

3.4.1 Joint polymorphism at the target of selection

Preceding sections have provided conditions ensuring the existence of one or more locally stable polymorphisms under the simple forms of purifying and disruptive selection considered. For the case of overdominance in both demes with

$${\alpha }_1={\beta }_1=1{\alpha }_0={\beta }_2<1{\alpha }_2={\beta }_0<1$$ (19)

and Mendelian segregation (d₁ = d₂ = 1/2), Appendix B shows that a single locally stable polymorphism exists in the coupled system.

As the x_i represent weighted averages of the p_i (3), they lie in the interval bounded by the p_i. At equilibrium ($x_i^{\ast }=x_i$), (3) implies

$$x_1-x_2=(1-2m)(p_1-p_2),$$ (20)

with

$$x_1-p_1=-(x_1-x_2)m∕(1-2m)$$ (21a)

$$x_2-p_2=(x_1-x_2)m∕(1-2m).$$ (21b)

For m ∈ (0, 1/2), any locally stable polymorphism in the coupled system is characterized by either

$$p_1>x_1>x_2>p_2\text{OR}{p}_2>x_2>x_1>p_1,$$ (22)

irrespective of the nature of the selection regime in deme 2.

In the absence of migration, fixed points in deme 1 correspond to the fixation states (0, 1) and

$$\tilde{\alpha }=\frac{2d_1{\alpha }_1-{\alpha }_2}{2{\alpha }_1-{\alpha }_0-{\alpha }_2}.$$ (23)

This value corresponds to a valid stable polymorphism if both

$$f_1^{\prime }\left(0\right)=2d_1{\alpha }_1∕{\alpha }_2>1\text{AND}{f}_1^{\prime }\left(1\right)=2(1-d_1){\alpha }_1∕{\alpha }_0>1,$$ (24)

and to a valid unstable polymorphism if both inequalities are reversed. No polymorphism exists and one fixation state is stable and the other unstable if

$$f_1^{\prime }\left(0\right)>1>f_1^{\prime }\left(1\right)\text{OR}{f}_1^{\prime }\left(0\right)<1<f_1^{\prime }\left(1\right).$$

Under (24), $\tilde{\alpha }\in (0,1)$ is the globally stable fixed point of the monotone function f₁(x₁). Consequently, p₁ > x₁ implies

$$\tilde{\alpha }>x_1.$$

Applying f₁(·) to both sides of this relation implies $\tilde{\alpha }>p_1$. Similarly, x₁ > p₁ implies $x_1>p_1>\tilde{\alpha }$. These arguments show that for $\tilde{\alpha }$ a valid stable polymorphism, (22) can be extended to

$$\tilde{\alpha }>P_1>x_1>x_2>p_2\text{OR}{p}_2>x_2>x_1>p_1>\tilde{\alpha }.$$

3.4.2 Relative reproductive rate at the neutral marker locus

For a locally stable polymorphism (1 > x₁ > 0), transmission matrix (7) corresponds to

$${\mathit{C}}_1=\left(\begin{array}{cc}\hfill T_1{p}_1∕2x_1-d_{1}r{\alpha }_1(1-x_1)\hfill & \hfill (1-d_1)r{\alpha }_1(1-x_1)\hfill \\ \hfill d_{1}r{\alpha }_1{x}_1\hfill & \hfill T_1(1-p_1)∕2(1-x_1)-(1-d_1)r{\alpha }_1{x}_1\hfill \end{array}\right),$$ (25)

for T₁ the denominator of f₁(x₁) in (2).

Absolute linkage

In the absence of crossing-over between the neutral marker locus and the target of selection (r = 0), (8) indicates

$${\omega }_1=\{\begin{array}{cc}{p}_2∕p_1\hfill & \text{for}{p}_1>x_1\hfill \\ (1-p_2)∕(1-p_1)\hfill & \text{for}{p}_1<x_1.\hfill \end{array}\phantom{\}}$$ (26)

In both cases, ω₁ < 1.

Incomplete linkage

For r > 0, C₁ (7) is a positive matrix: it has a positive dominant eigenvalue (λ), associated with an eigenvector with positive elements (Perron-Frobenius theorem, Gantmacher 1959). Examination of the characteristic equation of C₁ indicates that λ lies between T₁p₁/2x₁ and T₁(1 − p₁)/2(1 − x₁). The right eigenvector associated with the dominant eigenvalue corresponds to

$$\mathit{q}={\left(r\right(1-d_1\left){\alpha }_1\right(1-x_1),r{d}_1{\alpha }_1(1-x_1)+\lambda -T_1{p}_1∕2x_1)}^{tr},$$

for tr denoting the transpose, giving

$${\omega }_1=\frac{(p_2,1-p_2)\mathit{q}}{(p_1,1-p_1)\mathit{q}}=\frac{r{\alpha }_1(1-x_1)\left[p_2\right(1-2d_1)+d_1]+(1-p_2)(\lambda -T_1{p}_1∕2x_1)}{r{\alpha }_1(1-x_1)\left[p_1\right(1-2d_1)+d_1]+(1-p_1)(\lambda -T_1{p}_1∕2x_1)}$$ (27)

(see Fusco and Uyenoyama 2011). Comparing ω₁ to unity gives

$$1-{\omega }_1\propto (p_1-p_2)\left[r{\alpha }_1\right(1-x_1\left)\right(1-2d_1)+T_1{p}_1∕2x_1-\lambda ].$$ (28)

This expression indicates that ω₁ can exceed unity, with neutral marker genes on migrant gametes expected to contribute to future generations at higher rates than those on resident gametes. In the case p₁ > x₁ > x₂ > p₂, for which T₁p₁/2x₁ > λ > T₁(1 − p₁)/2(1 − x₁), ω₁ > 1 if

$$T_1{p}_1∕2x_1>\lambda >T_1{p}_1∕2x_1+r{\alpha }_1(1-x_1)(1-2d_1),$$

which requires that d₁ > 1/2. Similarly, if p₂ > x₂ > x₁ > p₁, ω₁ > 1 if

$$T_1{p}_1∕2x_1+r{\alpha }_1(1-x_1)(1-2d_1)>\lambda >T_1{p}_1∕2x_1,$$

which requires that d₁ < 1/2.

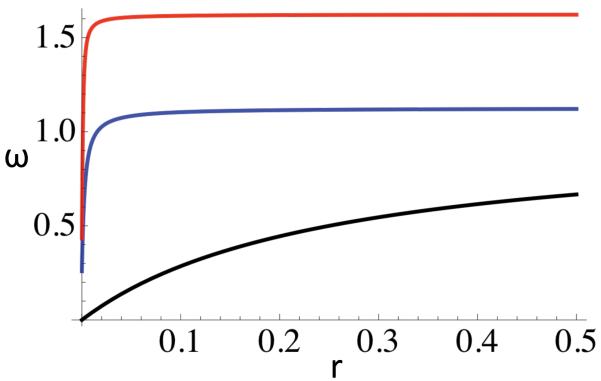
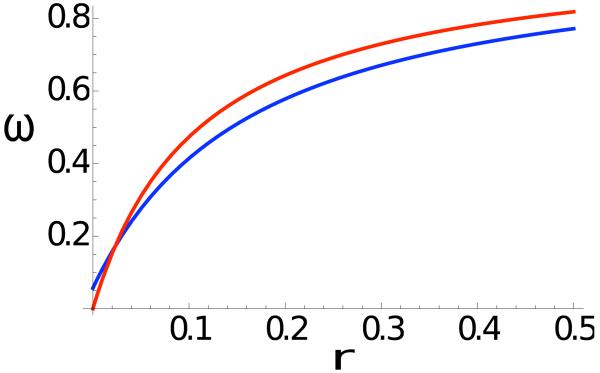
Figure 4 shows examples in which relative reproductive rate ω₁ (27) exceeds unity. For very tight linkage (r → 0), ω₁ converges to the values given by (26). As linkage loosens, ω₁ under either selection regime increases rapidly, showing little dependence on the rate of crossing-over. Relative reproductive rate substantially exceeds the Bengtsson (1985) expectation (12), represented by the black line.

Figure 4.

Relative reproductive rate at a neutral marker locus induced by two selection regimes. In the absence of migration, overdominant selection (α₀ = β₂ = 0.8, α₂ = β₀ = 0.7, α₁ = β₁ = 1) with segregation distortion (d₁ = 0.55, d₂ = 0.45) maintains stable polymorphisms in the two demes separately. The blue line shows relative reproductive rate ω₁ (27) near this joint overdominant polymorphism for m = 0.01. The red line depicts ω₁ under purifying selection (α₀ = β₂ = 1, α₁ = β₁ = 0.8, α₂ = β₀ = 0.2) and segregation distortion (d₁ = 0.2, d₂ = 0.8) for m = 0.001. The black line represents the Bengtsson (1985) expectation (12) with (1 − s) = 0.8.

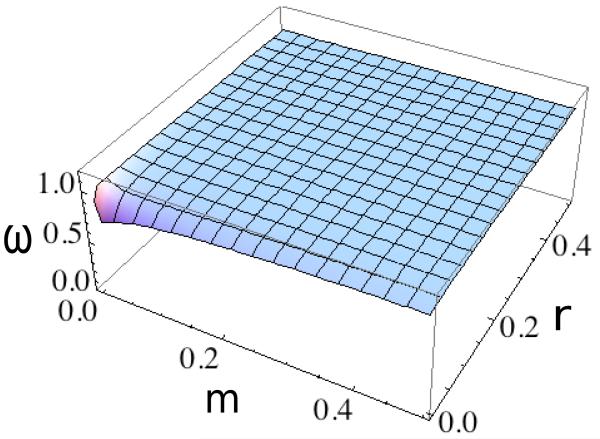
Under Mendelian segregation (d₁ = 1/2), (28) indicates that 1 > ω₁ for either case in (22). Figure 5 shows ω₁ induced by overdominance in both demes (19). Overdominance impedes introgression at a neutral marker locus to only a small extent over nearly the entire range of both the rate of gene flow (m) and the rate of crossing-over (r).

Figure 5.

Relative reproductive rate ω₁ at a neutral marker locus (27) induced by overdominant selection (α₀ = β₂ = 0.8, α₂ = β₀ = 0.7, α₁ = β₁ = 1) in the absence of segregation distortion (d₁ = d₂ = 1/2). With the exception of very tight linkage between the marker locus and the target of selection (r → 0), for which ω₁ converges to the value given by (26), ω₁ remains close to unity.

Very low migration rates

For simplicity, we return to consideration of very low rates of migration (Section 3.1), for which (9) gives expressions for the x_i and the p_i. We consider the joint polymorphism $(x_1,x_2)=(\tilde{\alpha }+{\delta }_1,\widehat{\beta }+{\delta }_2)$, for $\tilde{\alpha }$ given by (23), under the conditions which ensure its local stability (24). Transmission matrix C₁ (25) corresponds to

$$\left(\begin{array}{cc}\hfill T_1{f}_1\left(\tilde{\alpha }\right)∕2\tilde{\alpha }-d_{1}r{\alpha }_1(1-\tilde{\alpha })\hfill & \hfill (1-d_1)r{\alpha }_1(1-\tilde{\alpha })\hfill \\ \hfill d_{1}r{\alpha }_1\tilde{\alpha }\hfill & \hfill T_1(1-f_1(\tilde{\alpha }\left)\right)∕2(1-\tilde{\alpha })-(1-d_1)r{\alpha }_1\tilde{\alpha }\hfill \end{array}\right)+O\left({\delta }_1\right).$$

By definition, $p_1=f_1\left(\tilde{\alpha }\right)=\tilde{\alpha }$, which implies that the dominant eigenvalue of C₁ reduces to T₁/2+O(δ₁). For rates of crossing-over between the target of selection and the neutral marker locus large relative to the rate of gene flow (r > O(m), O(δ₁), O(δ₂)), the right eigenvector corresponding to the dominant eigenvalue equals

$$\mathit{q}={(1-d_1,d_1)}^{tr},$$

to terms larger than O(δ₁), giving relative reproductive rate

$${\omega }_1=\frac{1+(2d_1-1)(1-2\widehat{\beta })}{1+(2d_1-1)(1-2\tilde{\alpha })}+O\left({\delta }_1\right).$$

This expression indicates that for (2d₁−1) large relative to the migration rate, ω₁ is insensitive to the rate of crossing-over (r). In the absence of segregation distortion (d₁ = 1/2),

$${\omega }_1=\frac{r{\alpha }_1(1-x_1)+{\delta }_1({\alpha }_1-{\alpha }_0)(1-\widehat{\beta })}{r{\alpha }_1(1-x_1)+{\delta }_1({\alpha }_1-{\alpha }_0)(1-\tilde{\alpha })}<1.$$

This expression indicates that selection at the local adaptation locus impedes gene flow at the neutral marker locus by a factor on the order of the backward migration rate m, implying a genealogical migration rate (4) indistinguishable from the fully neutral case to the order of the approximation: g = ωm ≈ m.

4 Discussion

Extreme values of F_ST and other indices of population structure have been used to identify candidates for loci that have undergone strong selection favoring locally adapted alleles (e.g. Coop et al. 2009; Holsinger and Weir 2009). Alternatively, local adaptation may also proceed through shifts in standing polymorphism at many loci (Pritchard et al. 2010; Hancock et al. 2010). Such a process would leave signals in neutral variation distinct from those indicative of recent hard sweeps (reviewed by Nielsen et al. 2007). Here, we have addressed the rate of introgression at neutral marker loci in a two-deme population subject to selection promoting local adaptation, accounting explicitly for polymorphism at the target of selection.

4.1 Local adaptation and neutral introgression

We have expanded the discussion of interspecific incompatibility (e.g., Bengtsson 1985; Barton and Bengtsson 1986; Gavrilets 1997; Navarro and Barton 2003; Fusco and Uyenoyama 2011) to include forms of local selection that maintain within-deme polymorphism. We found that the nature of local adaptation selection qualitatively a ects the process of introgression at neutral marker loci. These results may serve as a basis for the interpretation of genome-wide patterns of variation in structured populations of conspecifics as well as between hybridizing species.

In the absence of crossing-over between the neutral marker locus and the target of selection (r = 0), barriers to introgression decline as the relative frequency of the locally advantageous allele in the background of gametes transmitted by migrants increases. Expression (8) indicates that if locally-favored allele A has higher marginal fitness than the alternative allele (C₁₁ > C₂₂), then the relative reproductive rate (5) at the neutral marker locus is proportional to p₂/p₁, the relative frequency of the favored allele (A) among gametes derived from migrants (p₂) compared to residents (p₁).

For general levels of linkage between the marker and the target of selection, one might similarly expect that barriers to introgression increase with the discrepancy between the background distributions of gametes transmitted by migrants and by residents. This expectation is borne out for selection regimes in which the maintenance of polymorphism at the target of selection requires migration opposing purifying or disruptive selection within demes. In contrast, selection regimes capable of maintaining within-deme polymorphism even in the absence of migration engender much lower barriers to neutral introgression. A qualitatively novel finding is that migrants can contribute neutral marker genes to future generations at higher rates than residents (ω > 1).

4.2 Within-deme polymorphism maintained by migration-selection balance

Purifying selection (13) favors different alleles in the two demes and disruptive selection (18) disfavors heterozygotes. In both cases, the stable polymorphisms of the coupled system, (x₁, x₂), for x_i the frequency in deme i, emanate from one of the four combinations of fixation states at the within-deme level. For example, Fig. 1 depicts the departure, as migration rates increase, of the stable polymorphic state (green dot) from the (x₁, x₂) = (1, 0) state; Fig. 3 shows two stable polymorphisms, descended from (1, 0) and (0, 1).

In these cases, for which the stable polymorphic states satisfy x₁ + x₂ = 1 (Type 1 equilibria), the discrepancy between the gametic background distributions of migrants and residents corresponds to ∣p₁ − p₂∣ > ∣x₁ − x₂∣ = ∣2x₁ − 1∣. As the rate of migration (m) increases, this between-deme difference at stable polymorphisms declines. In our purifying selection model (13), for example, the fixation state (1, 0) corresponds to the stable state in the absence of migration (m = 0), and as the migration rate grows, the Euclidean distance of the stable joint polymorphism (x₁, x₂) from this state increases:

$$\Vert (x_1,x_2)-(1,0)\Vert =(1-x_1)\sqrt{2}=x_2\sqrt{2},$$

for (1 − x₁) the frequency of the less favored allele in deme 1. Figure 2 suggests a roughly linear increase of relative reproductive rate ω (5) with this distance. For very low values of the backward migration rate (m → 0), relative reproductive converges to the value (12) given by Bengtsson (1985). Similar results obtain under the disruptive selection model (18).

Charlesworth et al. (1997) studied a model similar to the purifying selection model under the restriction to additive fitnesses. They compared indices of diversity at a neutral marker locus observed in numerical simulations to the theoretical expectation (12), given by Bengtsson (1985). Their simulation results showed excess between-deme diversity under strong purifying selection (their Fig. 5). For the most part, our measure of relative reproductive rate (5), which accounts for the presence of the disfavored gene within the focal deme, gives introgression rates in the opposite direction: equal to or higher than indicated by (12). Even so, Fig. 6 presents an example in which this ordering does not hold, although the effect may not be of sufficient magnitude to account for the discrepancy reported by Charlesworth et al. (1997).

Figure 6.

Relative reproductive rate at a neutral marker locus under purifying selection (13) with σ = 0.9 and τ = 0.01 and backward migration rate m = 0.01. The blue line, corresponding to relative reproductive rate (5), exceeds (12), the “gene flow factor” of Bengtsson (1985), for tight linkage (r small), but imposes a greater barrier to introgression under looser linkage.

4.3 Within-deme polymorphism maintained by selection even in the absence of migration

Qualitatively different barriers to introgression at neutral marker loci arise under selection regimes that permit within-deme polymorphisms at local adaptation loci in the absence of migration. We explored two regimes of this kind: overdominance under Mendelian segregation and segregation distortion balancing selection.

4.3.1 Polymorphism due to overdominance under Mendelian segregation

Overdominance in fitness in each of the two demes can maintain very large between-deme differences in allele frequencies, almost as great as those generated by purifying or disruptive selection. Even so, this form of selection induces very low barriers to introgression at a neutral marker locus unless crossing-over between the marker and the target of selection is virtually complete (Fig. 5). Under complete linkage (26), relative reproductive rate at the neutral marker locus declines as the between-deme difference in allele frequencies increases.

This low barrier to introgression appears to reflect the compensating influence of two consequences of migration. Under Mendelian segregation (d₁ = 1/2), (28) indicates that the departure of relative reproductive rate from unity (no barrier to introgression) is proportional to

$$1-{\omega }_1\propto (p_1-p_2)(T_1{p}_1∕2x_1-\lambda ),$$ (29)

for p₁ and p₂ the frequency of local adaptation allele A in gametes derived from migrants and residents, respectively; x₁ the frequency of A in the local gene pool; T₁ the local mean fitness; and λ the dominant eigenvalue of the matrix (7) describing transmission of the focal marker gene on the possible gametic backgrounds. High backward migration rates (m → 1/2) reduce the between-deme difference in allele frequency ∣p₁ − p₂∣, lowering the barrier to introgression at the neutral marker locus (29). For very low rates of migration (m → 0), p₁ and x₁ lie close to $\tilde{\alpha }$, corresponding to the stable polymorphism expected in the absence of migration. At $\tilde{\alpha }$, the local adaptation alleles have identical marginal fitnesses:

$${\alpha }_0\tilde{\alpha }+2d_1{\alpha }_1(1-\tilde{\alpha })=2(1-d_1){\alpha }_1\tilde{\alpha }+{\alpha }_2(1-\tilde{\alpha })=T_1.$$

At such states, the dominant eigenvalue (λ) equals T₁/2, in which T₁ represents the expected rate of production of descendants bearing either A or a and the 1/2 the probability of transmission of the marker gene, again indicating a very low barrier to introgression at the marker locus. Accordingly, the second quantity in parentheses in (29) converges to zero for small as well as large migration rates. Figure 5 suggests that overdominance poses little barrier to introgression (ω₁ ≈ 1) for intermediate values of m as well, and in fact over nearly the entire permissible range of migration and crossover rates.

Bull et al. (2006) documented large differences among genomic regions in rates of introgression between naturally hybridizing Heliconius butterfly species. They reported recent introgression at the allozyme-encoding mannose-6-phosphate isomerase (Mpi) locus, but not at other nuclear or mitochondrial sites. Beltrán et al. (2002) studied variation in individuals representing 25 species of Heliconius and related genera at the autosomal Mpi locus, at a Z-linked locus, and in mitochondrial regions. Although they could not reject a neutral model of evolution, they hypothesized that balancing selection maintains variation at Mpi, citing a number of characteristics, including sharing of lineages across species, high rates of nonsynonymous substitution, high allelic diversity, and evidence of balancing selection among Mpi allozymes in other organisms. While the nature of the putative balancing selection within the species studied by Bull et al. (2006) may differ from overdominance, the results of our study of overdominance is consistent with their finding of low barriers to neutral introgression near Mpi.

4.3.2 Polymorphism due to balance between selection and segregation distortion

Polymorphisms involving segregation distortion (d₁ ≠ 1/2) also induce low barriers to introgression. Further, marker genes on migrant gametes can have a higher expected contribution to future generations than on resident alleles (ω₁ > 1), as illustrated by Fig. 4.

Segregation distortion draws the equilibrium state of the population away from the allele frequency that would maximize local mean fitness. It is well-known that mean fitness represents an adaptive topology (Lyapunov function) in the absence of segregation distortion, with locally stable states corresponding to local maxima (e.g., Wright 1969). Relative reproductive rate can exceed unity if the local adaptation allele favored by segregation distortion occurs in lower frequency among migrant than resident gametes.

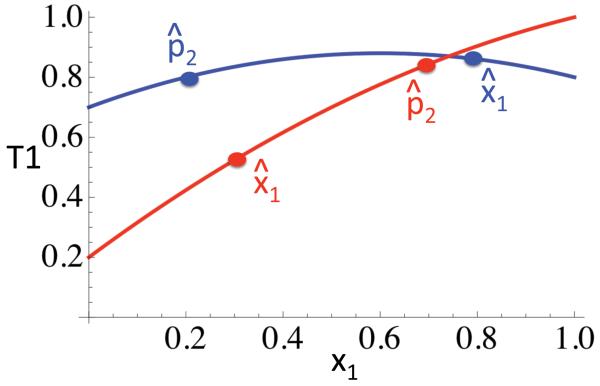
Figure 7 presents adaptive topologies (T₁, the denominator of f_i(x_i) in (2)) for the cases depicted in Fig. 4. Under purifying selection (red line), fixation of the A allele (x₁ = 1) corresponds to the state that confers the highest mean fitness, but segregation distortion in deme 1 reduces its equilibrium frequency to ${\widehat{x}}_1$. In the case depicted, the frequency of A in the background of neutral marker genes introduced on migrant gametes exceeds the frequency in the background of resident gametes: ${\widehat{p}}_2>{\widehat{x}}_1>{\widehat{p}}_1$ (22). Under overdominance (blue line), segregation distortion favoring A moves the local equilibrium frequency ${\widehat{x}}_1$ above the frequency that maximizes T₁, while segregation distortion favoring the alternative allele in the deme 2 causes the frequency of A in the background of migrant gametes ${\widehat{p}}_2$ to fall below ${\widehat{p}}_1$: ${\widehat{p}}_1>{\widehat{x}}_1>{\widehat{p}}_2$ (22). In both examples, migrant gametes bear higher frequencies of the allele disfavored by segregation distortion.

Figure 7.

Adaptive topologies for cases in which relative reproductive rate (5) exceeds unity. Mean fitness T₁ in deme 1 is shown under the same parameter assignments indicated in Fig. 4 for overdominant selection (blue: α₀ = β₂ = 0.8, α₂ = β₀ = 0.7, α₁ = β₁ = 1, d₁ = 0.55, d₂ = 0.45, m = 0.01) and purifying selection (red: α₀ = β₂ = 1, α₁ = β₁ = 0.8, α₂ = β₀ = 0.2, d₁ = 0.2, d₂ = 0.8, m = 0.001). Segregation distortion displaces the equilibrium mean fitness in deme 1 (points labeled ${\widehat{x}}_1$) from the maximum. Gametes transmitted by migrants contain higher frequencies (horizontal position of points labeled ${\widehat{p}}_2$) of alleles disfavored by segregation distortion.

This enhanced introgression of neutral marker genes can be regarded as a form of genetic hitchhiking (Barton 2000). Ingvarsson and Whitlock (2000) noted that the masking in hybrids of recessive deleterious genes that have attained high frequency in the local deme can induce introgression rates in excess of the backward migration rate, but did not explore the origin of the difference between demes in the distribution of deleterious factors nor the effects of introgression on its maintenance. Enhanced introgression due to a balance between selection and segregation distortion involves the introduction of genes already held in the local population in stable polymorphism. Consequently, unlike the case for selective sweeps of previously absent haplotypes, the process is not self-limiting: introgression of migrant gametes merely preserves the stable polymorphism without improving the equilibrium mean fitness.

Interspecific crosses between inbred lines derived from monkeyflower species Mimulus guttatus and M. nasutus revealed an autosomal locus that causes nearly complete segregation distortion in favor of the M. guttatus chromosome in gametes transmitted through seeds (Fishman and Willis 2005). Fishman and Saunders (2008) showed that a natural population of pure-species M. guttatus contained a polymorphism for the driving allele (D) and its nondriving alternatives (D⁻), apparently maintained by strong segregation distortion (58:42 in favor of D) balanced by declines in pollen fertility of DD individuals. To the extent that our simple model approximates this case, our results suggest that the segregation distortion may generate only a weak barrier to interspecific introgression, and may actually enhance gene flow (Fig. 4). In the latter case, if migrant gametes from conspecifics bear higher frequencies of nondriving alleles than resident gametes, the enhanced gene flow would promote cohesion among M. guttatus populations. Alternatively, if gametes derived from M. nasutus individuals are favored, then the enhanced gene flow would promote interspecific introgression. In either case, the in ux of nondriving gametes would likely not destabilize the stable polymorphism at the meiotic drive locus that promotes their entrance, implying the long-term maintenance of a state of elevated introgression rates.

Appendices

Appendix A. Equilibrium states under purifying selection

We characterize the equilibrium states under the purifying selection model (13) for general migration rates in the range 0 < m < 1/2.

From (2) and (3), we obtain an expression for $x_1^{\ast }+x_2^{\ast }$ and set it equal to x₁ + x₂ to obtain a necessary condition for equilibrium:

$$(x_1+x_2-1)\left[T_1{T}_2-\left\{x_1\right(1-x_2)\sigma +[x_1{x}_2+(1-x_1)(1-x_2)]\tau +(1-x_1\left)x_2\sigma \tau \right\}\right]=0.$$ (A.1)

Type 1 equilibria correspond to fixed points satisfying x₁ + x₂ = p₁ + p₂ = 1, which implies identical mean fitnesses across demes (T₁ = T₂). Type 2 equilibria correspond to values under which the second large bracket in (A.1) reduces to zero.

Subtracting the recursions in the x_i to obtain an expression for $x_1^{\ast }-x_2^{\ast }$ produces another necessary condition for equilibrium:

$$T_1{T}_2(x_1-x_2)+(1-2m)\left\{T_1{x}_2\right[\tau x_2+\sigma (1-x_2)]-T_2{x}_1[x_1+\sigma (1-x_1)\left]\right\}=0.$$ (A.2)

Equilibrium states correspond to simultaneous solutions of (A.1) and (A.2).

Type 1 equilibria

At Type 1 equilibria, x₁ + x₂ = p₁ + p₂ = 1, which implies

$$p_1=\frac{x_1-m}{1-2m}{p}_2=\frac{x_2-m}{1-2m}.$$ (A.3)

Further, the Type 1 condition implies T₁ = T₂ in (A.2) and allows elimination of x₂ from (A.2) to produce a polynomial in x₁, any valid roots of which correspond to Type 1 equilibria:

$$x_1^2(2\sigma -1-\tau )+x_1^2[1-m-3\sigma +\tau (2+m\left)\right]+x_1(\sigma -\tau -2m\tau )+m\tau =0.$$ (A.4)

Expressions for p₁ and p₂ (A.3) indicate that under the constraint m < 1/2, any valid roots of (A.4) must have x₁ ∈ (1/2, 1 − m). A single root exists in this range. This Type 1 equilibrium is locally stable only only under parameter values for which a cubic in τ is positive (given in the Mathematica le provided as Supplemental Online Material).

Type 2 equilibria

The remaining equilibria correspond to values that simultaneously satisfy (A.2) and

$$T_1{T}_2-\left\{x_1\right(1-x_2)\sigma +[x_1{x}_2+(1-x_1)(1-x_2)]\tau +(1-x_1\left)x_2\sigma \tau \right\}=0.$$ (A.5)

(from (A.1)). Beyond the fixation states (x₁ = x₂ = 0 and x₁ = x₂ = 1), these conditions reduce to a fourth degree polynomial in x₁, the valid roots of which correspond to the Type 2 equilibria.

A change of variables to D = (x₁ − x₂) and P = S(2 − S) for S = (x₁ + x₂) converts (A.2) and (A.5) into two polynomials of the second degree in P and the fourth degree in D (included in the Mathematica le provided as Supplemental Online Material). This formulation makes evident that as in the free exchange case (m = 1/2, Section 3.3), the Type 2 equilibria occur in pairs: if $\widehat{S}$ is a root, then $2-\widehat{S}$ is also a root. Further, at most one pair of Type 2 equilibria (one root for P) can exist.

Appendix B. Overdominance in both demes

Relations (21) permits reduction of the recursions to a seventh-degree polynomial in x₁ alone. For simplicity, we assume symmetries of the form described by (19), under which the stable polymorphisms expected in the absence of migration in deme 1 ($\tilde{\alpha }$) and deme 2 ($\tilde{\beta }$) satisfy $\tilde{\alpha }+\tilde{\beta }=1$. Without loss of generality, we assume α₀ > α₂, which implies $\tilde{\alpha }>\tilde{\beta }$.

Under these parameter assignments, the equilibrium polynomial in x₁ has factors corresponding to polynomials of the third-degree and fourth-degree. Any valid equilibria appear to correspond to roots of the cubic:

$$x_1^3(2-{\alpha }_0-{\alpha }_2)-x_1^2\left[3\right(1-{\alpha }_2)-({\alpha }_0-{\alpha }_2\left)\right(1-m\left)\right]+(1-{\alpha }_2-2{\alpha }_{2}m)x_1+{\alpha }_{2}m=0.$$

This polynomial has a single root in (0,1), lying between $\tilde{\alpha }$ and $\tilde{\beta }$. This root determines the single valid polymorphism of the full system, which is locally stable.