Abstract
Private microsatellite alleles tend to be found in the tails rather than in the interior of the allele size distribution. To explain this phenomenon, we have investigated the size distribution of private alleles in a coalescent model of two populations, assuming the symmetric stepwise mutation model as the mode of microsatellite mutation. For the case in which four alleles are sampled, two from each population, we condition on the configuration in which three distinct allele sizes are present, one of which is common to both populations, one of which is private to one population, and the third of which is private to the other population. Conditional on this configuration, we calculate the probability that the two private alleles occupy the two tails of the size distribution. This probability, which increases as a function of mutation rate and divergence time between the two populations, is seen to be greater than the value that would be predicted if there was no relationship between privacy and location in the allele size distribution. In accordance with the prediction of the model, we find that in pairs of human populations, the frequency with which private microsatellite alleles occur in the tails of the allele size distribution increases as a function of genetic differentiation between populations.
Keywords: coalescent, microsatellites, private alleles
Introduction
Private alleles are alleles that are found only in a single population among a broader collection of populations. These alleles have proven to be informative for diverse types of population-genetic studies, in such areas as molecular ecology and conservation genetics (e.g. Petit et al., 1998; Parker et al., 1999; Fiumera et al., 2000; Neel & Cummings, 2003; Torres et al., 2003; Kalinowski, 2004) and human evolutionary genetics (e.g. Neel, 1973, 1978; Neel & Thompson, 1978; Calafell et al., 1998; Schroeder et al., 2007; Szpiech et al., 2008).
Some of the first investigations of private alleles trace to studies of private electrophoretic variants in Native American groups from South America (Neel, 1973, 1978; Neel & Thompson, 1978). Using private alleles, Neel and colleagues obtained estimates of per-locus per-generation mutation rates in these populations. Slatkin (1985) and Barton & Slatkin (1986) showed that private alleles can contribute to indicators of gene flow, finding in theoretical models of population structure that the occurrence of private alleles was correlated with the mean number of migrants exchanged per generation between populations, under the assumptions of the infinite alleles mutation model. Private alleles have also been used in empirical studies of human migrations. Calafell et al. (1998) noted that in human populations, the mean number of private alleles decreases with increasing distance from Africa, providing support to models of human migration out of Africa. Schroeder et al. (2007) argued on the basis of a private allele ubiquitous in the Americas that all modern Native American populations are descended from the same founding population.
One recent study, which investigated 678 microsatellite markers in 29 Native American populations from North, Central, and South America (Wang et al., 2007), identified a peculiar property of private alleles. Wang et al. (2007) characterized the distribution of private alleles across four subregions in the Americas, observing that private microsatellite alleles were found in the tails rather than in the interior of the allele size distribution more often than was expected by chance. In other words, private alleles at a locus frequently had very long or very short repeat lengths with respect to the other alleles at the locus.
Here we have taken a modeling approach to examine the reasons underlying the frequent occurrence of private alleles on the edges of the allele size distribution. Using a simple coalescent model, we assess the properties of microsatellite private alleles, thereby helping to explain patterns that exist in the relationship between privacy and allele size across human populations.
Theory
Let {x1x2/x3x4} denote four sampled microsatellite alleles in two populations, where xi indicates the allele size for sampled allele i, and the forward slash separates alleles from different populations. We restrict our attention to cases with four alleles; a scenario with two alleles each in two populations gives the smallest sample size useful for examining the phenomenon of interest, as we will explain below. Because the 4-allele case involves a tractable number of calculations, it is possible in this case to mathematically investigate the position of private alleles in the size distribution.
We map sets of four allele sizes in two populations to one of seven possible configurations of identity and nonidentity, using the letters A, B, C, and D to denote distinct allele sizes. Thus, if two sampled alleles are identical by state (IBS), we indicate this identity by assigning the alleles the same letter. For example, if all four sampled alleles are IBS, we represent the allele configuration by {AA/AA}. If one allele in population 1 is IBS to an allele in population 2 and the other allele in population 1 is IBS to the other allele in population 2 (and no alleles are IBS within populations), then we represent the allele configuration by {AB/AB}. We label the seven possible configurations by Ci for i ∈ {1, …, 7}, and we list them in Table 1.
Table 1.
The seven possible configurations of four alleles in two populations and the counts of shared, private, and total distinct alleles for each configuration.
| Event | Configuration | Number of shared alleles | Number of private alleles | Total number of distinct alleles |
|---|---|---|---|---|
| C1 | {AA/AA} | 1 | 0 | 1 |
| C2 | {AA/AB} | 1 | 1 | 2 |
| C3 | {AA/BB} | 0 | 2 | 2 |
| C4 | {AB/AB} | 2 | 0 | 2 |
| C5 | {AA/BC} | 0 | 3 | 3 |
| C6 | {AB/AC} | 1 | 2 | 3 |
| C7 | {AB/CD} | 0 | 4 | 4 |
We are interested in comparing private and shared alleles on the basis of size. In particular, we wish to examine whether alleles lie on the edges of the size distribution, that is, whether they have the longest or shortest lengths. To have a sensible definition of the “edges” and interior of the allele size distribution, we must have at least three distinct alleles among the four sampled alleles that we consider. Furthermore, because we are concerned with the location of private alleles with respect to shared alleles, we must have at least one shared allele and one private allele. The only one of the seven configurations of four alleles that satisfies both of these requirements—and that therefore enables a computation of the probability that private alleles lie on the edges of the allele size distribution—is C6 (configuration {AB/AC}). This configuration, with sample size four, provides the smallest scenario that contains both private alleles and shared alleles and that contains both edges and an interior of the allele size distribution. We aim to compute the probability that B and C, the two private alleles in configuration {AB/AC}, both lie on the edges of the size distribution, conditional on this configuration being produced.
A naïve argument
If we disregard the genealogical relatedness of the alleles in our two-population four-allele model, what do we expect for the probability that the private alleles lie on the edges? There are six possible orderings of the three allele sizes A, B, and C (A < B < C, A < C < B, etc.), and, if no relationship exists between the size of an allele and its status as shared or private, we expect the six orderings to be equiprobable. Two of the six orderings place the private alleles B and C on the edges of the size distribution. Under this simple argument, we would expect the probability that both private alleles lie on the edges to be 1/3.
This argument gives an initial sense of what might be expected for the probability that the private alleles lie on the edges of the size distribution. However, it disregards the fact that the alleles are related through a common ancestor. We now turn to a genealogical argument that more directly models this relationship.
The probability of microsatellite configurations
To account for the genealogical relatedness of the four alleles in obtaining a prediction of the probability that private alleles lie on the edges of the allele size distribution, we use the coalescent with symmetric stepwise mutation. Initially, we consider the two populations to have instantaneously diverged zero coalescent time units in the past (td = 0). Later, we will consider arbitrary values of the divergence time td.
To calculate the desired probability, we first condition on the {AB/AC} allele configuration (configuration C6), the mutation rate, and the coalescence times of the genealogy. By considering the probability of a net change by d mutational steps along a genealogical branch, we construct the joint probability of an allele configuration and a particular labeled history for the four alleles, where the allele configuration refers to one of the seven scenarios in Table 1 and the labeled history refers to the sequence of coalescences (Figure 1). We then calculate the total probability that the private alleles lie on the edges of the allele size distribution, summing across all labeled histories, and integrating over coalescence times to arrive at the desired probability, conditional only on a mutation rate θ.
Figure 1.
An enumeration of all possible labeled histories relating four sampled alleles. Twelve histories have asymmetric topologies (1–12), and six histories have symmetric topologies (13–18).
Consider the events E1: size(B) < size(A) < size(C), and E2: size(C) < size(A) < size(B). These events are equiprobable, and we aim to calculate the probability
| (1) |
Under the symmetric single stepwise mutation model, a microsatellite allele can mutate by only one step at a time in either a positive or negative direction, and the probability of mutating +1 step is equal to the probability of mutating −1 step, independent of the size of the allele. We work with coalescent time units (units of 2Ne generations, where Ne is the effective size of each population, treated as diploid individuals) and with the population-scaled mutation rate θ = 4Neμ, where μ is the per-locus per-generation mutation rate.
Mutations on a genealogical branch
The probability that a marker evolving according to the symmetric stepwise mutation model with population-scaled mutation rate θ has net change d units along a branch of length t coalescent time units is (Wehrhahn, 1975; Wilson & Balding, 1998)
| (2) |
where
is the modified Bessel function of the first kind (Gradshteyn & Ryzhik, 1980). Because positive and negative mutations are equally likely, we write f as a function of |d| rather than d, which can be positive, negative or zero.
Probability of the set of allele sizes on a genealogical tree
We can use Equation 2 to calculate the probability that changes along a coalescent tree ultimately give rise to a specified set of allele sizes. Considering that each branch evolves independently of the others, we calculate the probabilities of changes along individual branches and then multiply probabilities across branches to get the joint probability of all changes on the tree. There are two unlabeled topologies that we need to consider: an asymmetric topology (Figure 2A) and a symmetric topology (Figure 2B). Each topology is parameterized by a vector of allele sizes, (n2, n3, x1, x2, x3, x4), and a vector of coalescence times, (t2, t3, t4). The x variables represent the sizes of alleles at the leaf nodes, and ni represents the size of the allele at the interior node located at the reduction of the number of distinct lineages to i. The coalescence time ti represents the length of time during which there exist i distinct lineages. Initially, we treat the coalescence times as fixed, and later we will integrate the probabilities against the density of coalescence times to obtain a probability unconditional on t2, t3, and t4. Because we assume that mutation probabilities do not depend on allele size, we can set the allele size of the most recent common ancestor of the four-allele sample (the root node) to 0 without loss of generality. However, following a choice similar to that of Pritchard & Feldman (1996) and Zhang & Rosenberg (2007), we instead choose to set n2 = 0 rather than setting the root node to 0, and we treat the two branches that descend from the root as one branch with length equal to the sum of the lengths of its two constituent branches. This choice makes it possible to consider coalescent trees with five rather than six separate branches, thereby simplifying the computation.
Figure 2.
Example labelings of the two possible unlabeled topologies for gene genealogies with four lineages. (A) The asymmetric topology and (B) the symmetric topology are parameterized by allele sizes at the nodes, (x1, x2, x3, x4, n3, n2), and by coalescence times (t2, t3, t4) indicating the lengths of certain segments of the branches.
Considering the asymmetric caterpillar topology (Figure 2A), we obtain the joint probability of (n2, n3, x1, x2, x3, x4) given (t2, t3, t4) by calculating the probability of changing from n2 to x4 repeats along a branch of length 2t2 + t3 + t4, from n2 to x3 repeats along a branch of length t3 + t4, from n2 to n3 repeats along a branch of length t3, from n3 to x2 repeats along a branch of length t4, and from n3 to x1 repeats along a branch of length t4. Assuming n2 = 0 and multiplying these five probabilities together gives
where Ψ = (τ, θ) is a vector of parameters and τ = (t2, t3, t4) is the vector of coalescence times. Similarly, for the symmetric topology, we calculate the probability of the set of allele sizes in Figure 2B to get
Assigning alleles the roles of A, B, and C
There are 18 labeled histories for the alleles {x1, x2, x3, x4}, which we denote by Ti for i ∈ {1, …, 18} (Figure 1). We can then calculate ℙ[C6|Ti, Ψ] by considering all possible ways to get configuration C6 with labeled history Ti. Because we have defined {x1, x2} to be in population 1 and {x3, x4} to be in population 2, we need to consider four cases for each history, reflecting the four possible assignments of the allele sizes x1, x2, x3, and x4 to the roles of distinct alleles A, B, and C. These four cases are shown in Table 2.
Table 2.
The four allele size relationships possible for the {AB/AC} allele configuration.
| Case | Allele size relationship | Allele roles in {AB/AC} | ||||||
|---|---|---|---|---|---|---|---|---|
| x1 | x2 | x3 | x4 | |||||
| 1 | x1 = x3 | x2 ≠ x4 | x1 ≠ x2 | x1 ≠ x4 | A | B | A | C |
| 2 | x1 = x4 | x2 ≠ x3 | x1 ≠ x2 | x1 ≠ x3 | A | B | C | A |
| 3 | x2 = x3 | x1 ≠ x4 | x2 ≠ x1 | x2 ≠ x4 | B | A | A | C |
| 4 | x2 = x4 | x1 ≠ x3 | x2 ≠ x1 | x2 ≠ x3 | B | A | C | A |
If we represent the size of the shared allele (allele A) by nA and the sizes of the two private alleles (B and C) by nB and nC, respectively, then we can calculate ℙ[C6|Ti, Ψ] by summing the individual probabilities of each of the four cases in Table 2. For example, consider T1:
| (3) |
Here, without loss of generality, we treat the private allele in the first population as the B allele and the private allele in the second population as the C allele. Similar calculations can be performed for the 17 remaining labeled histories (Table 3).
Table 3.
The probability contributions for a given set of values (nA, nB, nC, n3, Ψ) for each of the 18 labeled histories. These probabilities occur in the sums in Equations 6 and 7.
| History number | History | Contribution | |
|---|---|---|---|
| 1 |

|
|
|
| 2 |

|
|
|
| 3 |

|
|
|
| 4 |

|
|
|
| 5 |

|
|
|
| 6 |

|
|
|
| 7 |

|
|
|
| 8 |

|
|
|
| 9 |

|
|
|
| 10 |

|
|
|
| 11 |

|
|
|
| 12 |

|
|
|
| 13 |

|
|
|
| 14 |
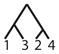
|
|
|
| 15 |

|
|
|
| 16 |
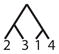
|
|
|
| 17 |
|
|
|
| 18 |

|
|
Summing over labeled histories
In order to calculate ℙ[E1, C6|Ψ], we proceed exactly as in Equation 3, conditioning on each history Ti, but we restrict the bounds of summation on nB and nC to −∞ < nB < nA and nA < nC < ∞, respectively.
We now have
| (4) |
and
| (5) |
Here, ℙ[Ti|Ψ] = 1/18 for all i because each labeled history of four lineages is equally likely under the assumption of the coalescent process that lineages join randomly going back in time. Note that symmetries exist in Vcat and Vsym as a result of exchangeability of certain nodes in the topologies that they consider. For asymmetric topologies,
For symmetric topologies,
Using the list of probability contributions for each labeled history, as given in Table 3, we can exploit these symmetries and collect like terms across labeled histories to write Equation 4 as
| (6) |
and Equation 5 as
| (7) |
Integrating out the coalescence times
Finally, we integrate over the density of coalescence times under the standard coalescent model. Under this model, the time in coalescent time units (units of 2Ne generations) for i lineages to coalesce to i − 1 lineages is exponentially distributed with rate (Wakeley, 2009). Separate coalescence times are independent, and we can write their joint distribution in the four-taxon case as . Using this density, we integrate to get
| (8) |
and
| (9) |
Implementing the computation
To calculate ℙ[E1 ∪ E2|C6, θ] (Equation 1) in practice, we use two approaches, a numerical method and a simulation-based method.
Numerical computation
First, we employ Gaussian quadrature to numerically estimate the numerator (2ℙ[E1, C6|θ], Equation 9) and denominator (ℙ[C6|θ], Equation 8) of ℙ[E1 ∪ E2|C6, θ]. In order to compute the integrals in finite time, we estimate the expression e−tθ/2I|d|(tθ/2) using the GNU Scientific Library (GSL) function gsl sf bessel In scaled(|d|, tθ/2). Additionally, we truncate the bounds of the infinite sums embedded in 2ℙ[E1, C6|θ] and ℙ[C6|θ] to ±10 instead of ±∞. These limits provide bounds on the size that an allele can have at any particular node. We additionally integrate all time parameters from 0 to 10 rather than from 0 to ∞. For small values of θ, these approximations are very accurate, as it is unlikely that an allele will mutate more than a few steps away from its initial number of repeats. However, for large θ, the approximation will become less accurate, as large numbers of mutations are likely to occur. These mutations ultimately cause alleles to shift further from the initial base size and beyond the arbitrary truncation in our approximation, so that the calculation fails to account for a non-trivial portion of probability mass.
Simulation-based computation
In order to calculate ℙ[E1 ∪ E2|C6, θ] accurately for large θ, we obtain the ratio in Equation 1 directly by simulating the coalescent and mutation processes and tabulating the outcomes of interest. The simulation proceeds as follows.
Beginning with k = 4 alleles, arbitrarily define two alleles to be in one population and the other two alleles to be in the other population.
Generate a random time to coalescence from an exponential ( ) distribution.
Randomly choose two alleles to coalesce; set k = k − 1.
If k ≠ 1, go to 2.
For each branch of the genealogy, generate a random number of mutation events, x, from a Poisson distribution with rate θt/2, where t is the branch length.
Assign each mutation a value of +1 or −1 by sampling the number of +1 mutations from a binomial(x,1/2) distribution. Those mutations not chosen to be +1 are assigned a value of −1.
Determine the allele size of each of the four sampled alleles by summing the net value of mutations from the root (allele size 0) down to the leaves.
Classify the collection of four alleles into one of the seven allele configurations (Table 1).
If the alleles are in the C6 configuration, accept the simulation and determine if the sizes of the private alleles (B and C) are on the ends of the distribution (nB < nA < nC or nC < nA < nB). If yes, count a success.
By repeating this algorithm until the number of accepted simulations reaches some pre-specified number (we choose 1, 000, 000), we can estimate the probability that the private alleles lie on the edges of the size distribution by simply dividing the number of successes by the number of accepted simulations.
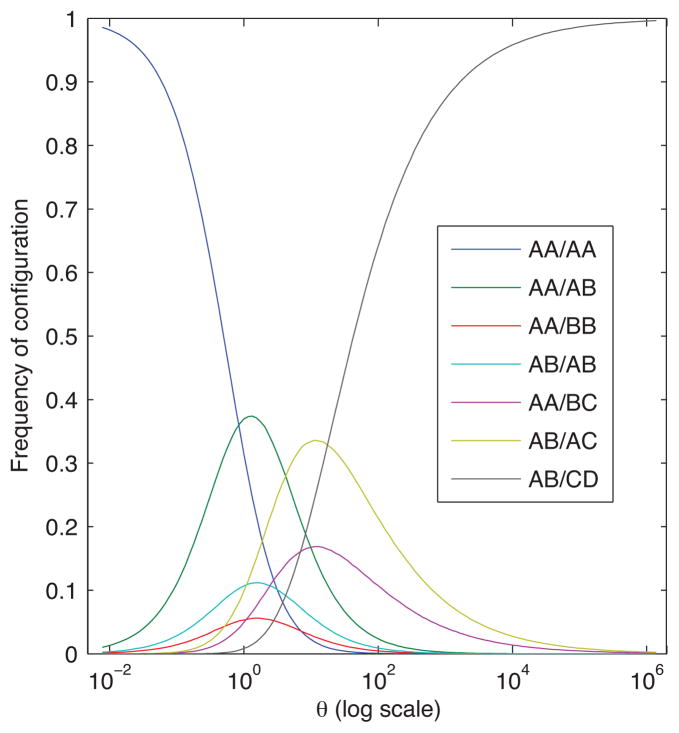
Note that the proportion of simulations that have configuration C6 provides an estimate of ℙ[C6|θ]. Through a separate application of 106 iterations of steps 1 to 8, we estimate the probabilities of all seven configurations as functions of θ. These estimates appear in Figure 3. At small values of θ, we see that most simulations produce configuration C1 ({AA/AA}), a sensible result because mutations are unlikely to happen for small θ. As θ grows larger, more mutations occur, and we see that configurations with two or more distinct alleles begin to rise in frequency. For large values of θ, mutations happen so often that most trees have configuration C7 ({AB/CD}).
Figure 3.
The simulated frequency of occurrence of seven possible allele configurations as a function of scaled mutation rate (θ) on a log scale. 106 trees are simulated per θ step. These simulations utilize four alleles, two in each of two populations. Alleles are related by the coalescent, and they mutate according to the symmetric stepwise mutation model.
Figure 4 shows, as a function of θ, the probability of interest, ℙ[E1 ∪ E2|C6, θ], calculated both by simulation and numerically. Because we must truncate the internal sums for the numerical computation, we plot several numerical calculations at varying truncation values. Most of the numerical computations are quite accurate at small θ: we expect few mutations in this case, and the approximation made by truncating the sums will reasonably cover most of the probability mass. We see that as θ gets large, the numerical results differ from the simulation-based result; at large θ many mutations occur and the numerical approximation is poorer.
Figure 4.
The probability that the private alleles lie on the edges of the size distribution conditional on being an {AB/AC} configuration, as a function of θ (log scale). This probability is plotted from simulations and for a range of truncations for the infinite sums in numerically approximating Equation 1. Simulation results are based on 100, 000 {AB/AC} trees simulated per θ step.
We note that the probability of interest appears to level off well above the naïve calculation of 1/3 as the mutation rate grows large. Furthermore, as θ tends toward zero, we see that the probability remains above 1/3 and appears to tend toward 1/2. We can prove this small-θ limiting result by considering a parsimony-style approximation for our probability near θ = 0.
Small-θ approximation
We can make some simplifications to approximate our calculation of ℙ[E1 ∪ E2|C6, θ] (Equation 1) in the limit as θ becomes small. For small θ, we expect fewer superfluous mutations to occur along a branch with a change of d steps—that is, we expect fewer mutations in one direction to be canceled by mutations in the other direction. Therefore, for very small θ, we can approximate the probability of changing d steps along a branch length t by setting k = 0 in Equation 2 so that no extra mutations occur. Denoting the small-θ approximation to f(|d|, t, θ) by fs(|d|, t, θ), we then obtain
Furthermore, for small θ, we also expect fewer mutations in total to occur on the whole genealogy. The minimum number of mutations needed to provide our pattern of interest, C6, is two (one mutation on each of two branches). Therefore, for sufficiently small θ, we expect to find no more than two mutations on the entire tree. The probability f(|d|; t, θ) in Equation 2 will take one of three forms:
| (10) |
| (11) |
This situation is analogous to a problem in phylogenetics. When rates of change are low, likelihood calculations on trees that consider all possible changes among allelic states converge to calculations of a parsimony score, as only changes of a single unit along a branch have nontrivial likelihood (Felsenstein, 2004). Similarly, our calculation of the probability that the private alleles lie on the edges of the size distribution, considering all possible states for allele sizes, is reduced in the small-θ case to a parsimony-style approximation by replacing f(|d|; t, θ) with fs(|0|; t, θ) and fs(|1|; t, θ). This parsimony approximation further eliminates the sums over n3, nA, nB, and nC, making ℙ[E1 ∪ E2|C6, θ] (Equation 1) tractable to analytically compute.
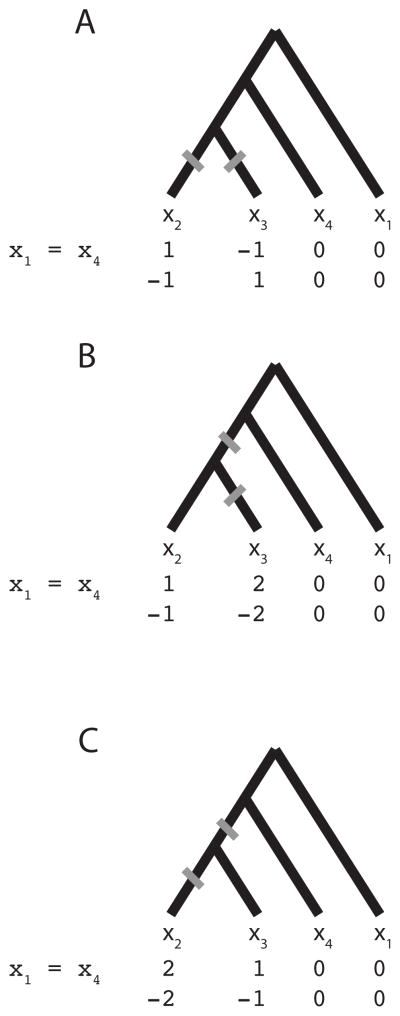
Examining all the ways of placing two mutations on one of the 18 topologies such that the {AB/AC} configuration is produced, each placement will contribute some probability to either the denominator in Equation 1 or to both the denominator and numerator in Equation 1. As an example, consider history 8 from Figure 1. We first examine the four ways of getting configuration C6 by assignment of the roles of A, B, and C to the alleles x1, x2, x3, and x4. We then find all placements of two mutations on the tree that are consistent with this configuration. Each placement will either place the private alleles on both ends of the size distribution, or the shared allele will be on one end. If the private alleles are on both ends, then the term contributes to both the numerator and the denominator. If the shared allele is on an end, then the term contributes to the denominator only. Figure 5 illustrates this approach for the case of x1 = x4.
Figure 5.
A small-θ “parsimony” approximation for calculating the probability that private alleles occur on the edges of the size distribution, for the case of x1 = x4 with history 8. Alleles x1 and x2 are in population 1, and alleles x3 and x4 are in population 2. In (A), the private alleles (±1) lie on the edges of the size distribution (−1 < 0 < 1); however, in (B) and (C) the private alleles (±1, ±2) are not on the two edges of the size distribution (−2 < −1 < 0 or 0 < 1 < 2).
We can substitute fs for f in our definitions of Vcat and Vsym to get the following small-θ versions of the probability of an arbitrary set of allele sizes.
Each possible placement of two mutations on the 18 labeled histories has a probability that falls into one of 12 equivalence classes as a result of symmetries in and . We denote these classes by σi (i ∈ {1, …, 12}), as defined in Table 4.
Table 4.
Definitions for the 12 classes of probability in the small-θ “parsimony” approximation.
| Class | Defined probability | |
|---|---|---|
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
| 10 |
|
|
| 11 |
|
|
| 12 |
|
|
By tabulating in Table 5 the contributions from each class to the numerator and denominator of the probability for each of the 18 labeled histories, we can now compute the numerator, 2ℙ[E1, C6|θ], in Equation 1 as
Table 5.
The small-θ approximation contributions to the numerator (Equation 12) and denominator (Equation 14) of the probability that the private alleles lie on the edges, for each labeled history.
| History number | History | Contribution to numerator | Contribution to denominator | ||
|---|---|---|---|---|---|
| 1 |

|
|
|
||
| 2 |

|
|
|
||
| 3 |

|
|
|
||
| 4 |

|
|
|
||
| 5 |

|
|
|
||
| 6 |

|
|
|
||
| 7 |

|
|
|
||
| 8 |

|
|
|
||
| 9 |

|
|
|
||
| 10 |

|
|
|
||
| 11 |

|
|
|
||
| 12 |

|
|
|
||
| 13 |
|
|
|
||
| 14 |

|
|
|
||
| 15 |

|
|
|
||
| 16 |
|
|
|
||
| 17 |
|
|
|
||
| 18 |
|
|
|
||
| (12) |
which evaluates to
| (13) |
The denominator, ℙ[C6|θ], of Equation 1 is
| (14) |
which evaluates to
| (15) |
Taking the ratio of expressions 13 and 15 and evaluating the limit as θ tends to 0 gives us
| (16) |
This result shows that, for low mutation rates, we expect the private alleles in an {AB/AC} sample of size four to be on the ends of the size distribution approximately 1/2 of the time. This is substantially more often than the value of 1/3 predicted when the relatedness of the alleles was not taken into account.
Arbitrary divergence time
Extending our two-population model, we now consider two populations separated by arbitrary divergence time td (Figure 6). Note that as shown in Figure 6, the definitions of t2, t3, and t4 differ slightly from those used in the calculations for the td = 0 case in Figure 2. We can formulate Equation 1 for arbitrary divergence time td and compute
Figure 6.
The four types of coalescent scenarios with td > 0, with their coalescent time parameterizations. In scenario E11, t3 is defined as the time to coalescence of the two lineages in population 1, and t4 is defined as the time to coalescence of the two lineages in population 2.
| (17) |
Detailed derivations appear in Appendix A. We calculate Equation 17 numerically by Gaussian quadrature and by simulation using methods similar to those used for the td = 0 case (Appendix B).
Figure 7 shows, as a function of θ and td, the probability that the private alleles lie on the edges of the size distribution, as obtained using the simulation in Appendix B. We see that throughout the parameter space, the probability uniformly exceeds the naïve expectation of 1/3. For all values of θ, we observe that increasing the divergence time between the populations increases the probability of finding the private alleles on the edges of the size distribution. Furthermore, we see that for small θ, the probability that private alleles in a sample of size four are found on the edges of the size distribution quickly tends toward 1 as td increases. By applying the small-θ approximation of Equations 10 and 11, we can show that this probability does indeed converge to 1 as td tends to infinity.
Figure 7.
Simulated probability that the private alleles lie on the edges of the size distribution, conditional on production of an {AB/AC} configuration. The plot shows this probability as a function of θ (log scale) and td. 106 {AB/AC} trees are simulated for each choice of θ and td.
Conditioning on each of the four possible scenarios depicted in Figure 6, we follow an approach similar to the td = 0 small-θ derivation to obtain a small-θ approximation for the case of arbitrary divergence time (Appendix C). The resulting limiting expression for this approximation as θ tends to 0 is
| (18) |
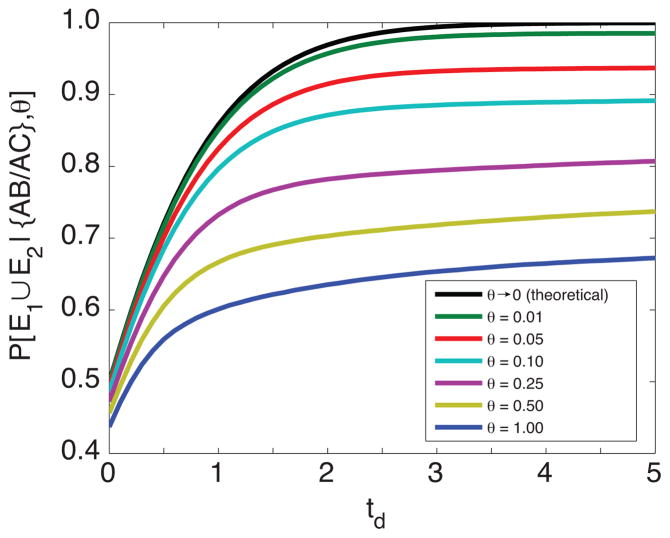
Equation 18 is sensible in that it agrees with the small-θ result of 1/2 at td = 0 (Equation 16), and it approaches the conditional result ℙ[E1 ∪ E2|C6, θsmall, td, E11] = 1 as td increases without bound (Equation C.6). In Figure 8, we plot the function of td in Equation 18 along with simulated results at increasingly small θ. We see that for each θ, the probability that the private alleles lie on the edges of the size distribution increases monotonically as a function of the divergence time, and that the simulated probability approaches the limiting expression as θ approaches 0.
Figure 8.
Simulated small-θ probabilities that the private alleles lie on the edges of the size distribution conditional on production of an {AB/AC} configuration, and the corresponding limiting probability computed analytically for θ → 0 (Equation 18), as functions of td. The simulation approach follows that of Figure 7 and is described in Appendix B.
Properties of the probability that private alleles lie on the edges
In order to investigate the probability that private alleles lie on the edges of the size distribution, we have started with a naïve argument that suggests that this should happen 1/3 of the time in a sample of four alleles, two from each of two populations. However, this naïve argument ignores the relatedness of the four alleles. We have presented a calculation of the desired probability using a coalescent framework for gene relatedness, together with the symmetric stepwise mutation model. When fixing td, we see a monotonic decrease in the probability that the private alleles lie on the edges as θ grows, but for every collection of parameter values evaluated (scaled mutation rate θ and divergence time td between the two populations), the probability remains greater than 1/3.
Furthermore, the probability appears to stay well above 1/3 even for very large θ. For large θ, we might expect so many mutations to occur on the tree that the allele sizes would not be correlated, effectively “erasing” the genealogical relatedness. In this case, we would expect the naïve prediction of 1/3 to hold. However, in order to observe a C6 configuration, two alleles must be identical by state. Thus, when conditioning on configuration C6, the distribution of branch lengths is biased toward shorter branches compared to the unconditional distribution, and even for large θ, the number of mutations tends to be small enough that genealogical relatedness remains important.
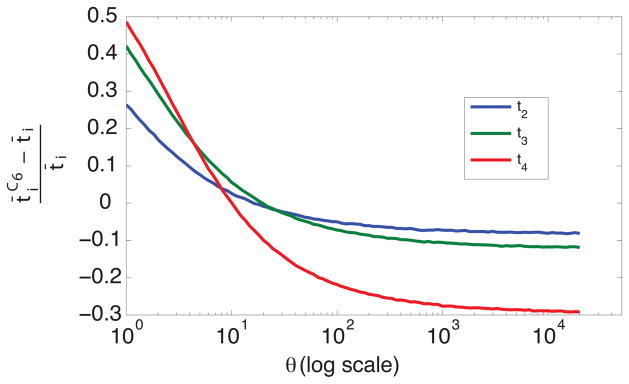
Holding td fixed at 0, Figure 9 plots versus θ, where t̄i is the unconditional expectation of ti under the coalescent and is the conditional expectation given configuration C6, as obtained in 106 simulations that produced this configuration. We see that as θ increases, the relative difference between the conditional mean coalescence times given configuration C6 and the unconditional mean coalescence times becomes increasingly negative. Most notably, t4 becomes particularly short, reflecting the observation that for large θ, scenarios with configuration C6 often have a “cherry” with short external branches of length t4 on which no mutations occur.
Figure 9.
Relative difference between mean coalescence times conditional on obtaining configuration C6 ( ) and unconditional mean coalescence times (t̄i), as a function of θ (log scale). The mean conditional coalescence times were calculated by taking the mean of 106 simulated coalescence times in scenarios that produced configuration C6.
In the small-θ case, we find that for td = 0, the probability that the private alleles lie on the edges in a sample of size four approaches 1/2 as θ tends to zero. By letting the divergence time between the two populations exceed zero (td > 0), we see a monotonic increase in this probability. In fact, in the small-θ limit, the probability that the private alleles lie on the edges in a sample of size four tends to 1 as td tends to infinity.
These results show that the genealogical history of a set of microsatellite alleles is an important factor in determining the prevalence of private alleles in the ends of the allele size distribution, even under circumstances in which we might expect the genealogy to be relatively unimportant. Our calculations also predict that the probability that private alleles lie on the edges of the allele size distribution grows as the divergence time between populations grows.
Application to data
To test the prediction that the probability that private alleles lie on the edges of the allele size distribution grows as the divergence time between populations grows, we analyzed data on microsatellites at 783 loci covering 1048 individuals in 53 worldwide populations from the Human Genome Diversity Panel (Rosenberg et al., 2005). Computations with these microsatellites have established a general increase of genetic differentiation (and hence, divergence time) with increasing geographical distance between a pair of populations (Ramachandran et al., 2005). Thus, although a strict divergence model is only an approximation to the population histories, we can consider the pairwise comparisons of populations that are geographically near each other to represent populations that diverged recently. Similarly, we can consider the pairwise comparisons of populations that are geographically distant from each other to represent populations that diverged relatively farther in the past. Pairwise comparisons of a population with itself can be interpreted as the case in which a population divergence happened at time td = 0 in the past. Based on the theory we have developed, we expect that pairs of geographically separated populations will produce a higher probability that the private alleles will lie on the edges of the size distribution. Similarly, we expect smaller probabilities for pairs of geographically proximate populations and the smallest probabilities for comparisons of populations with themselves. We further expect that measures of genetic differentiation such as FST will correlate with this probability as well, since these measures can be taken as a loose proxy for the divergence time between two populations.
To estimate the empirical frequency that the private alleles in a sample of size four lie on the edges of the size distribution, we perform the following analysis. For each population at each locus, we estimate the allele frequency distribution by counting the total number of observations of each distinct allele size and dividing by the total number of observations in the population. For a pair of populations, we then draw two alleles from the empirical allele frequency distribution in each population. If the set of four alleles has an {AB/AC} configuration, we accept the draw and determine if the private alleles lie on the edges of the size distribution. If so, then the draw is counted as a success. We repeatedly draw sets of four alleles until 100, 000 draws are accepted. Finally, we calculate the empirical frequency that the private alleles lie on the edges of the size distribution for a locus by dividing the number of successes by the number of acceptances, and we calculate the mean of this empirical frequency across loci. By performing this analysis, we get an estimate for the mean frequency that private alleles lie on the edges of the size distribution.
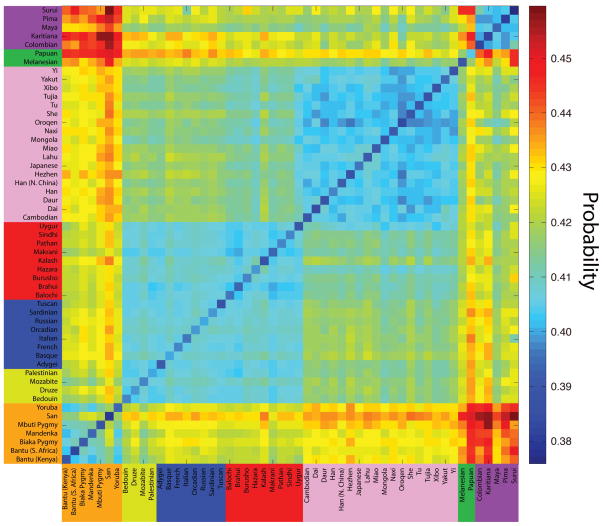
The results of this analysis are plotted in Figure 10, and we find that real populations do indeed follow the expected theoretical trend. The probabilities that private alleles lie on the edges range from 0.3759 to 0.4595. African populations paired with each other have lower probabilities, and a trend towards higher probabilities occurs as African populations are paired with other populations that are more geographically distant. The pairings of African populations with Native American populations (representing the most genetically distant pairs) have the highest probabilities. Furthermore, pairings close to the diagonal in Figure 10 tend to be more closely related than pairings farther away from the diagonal, and for these pairs, we see mostly low probabilities. Finally, the main diagonal represents the analysis of a population paired with itself; this is interpreted as comparing two populations with a divergence time of td = 0. We find that probabilities along the diagonal are the lowest among all pairs considered.
Figure 10.
The empirical probability that private alleles lie on the edges of the size distribution in a sample of size four from a pair of populations. Plotted are pairwise calculations of this frequency for all 53 worldwide populations from the Human Genome Diversity Panel, arranged in major geographic regions. African, Middle Eastern, European, Central/South Asian, East Asian, Oceanian, and American populations are arranged by color in the labels. Blue represents a lower probability, and red represents a higher probability.
Because we also expect the frequency of private alleles on the edges to correlate with measures of genetic differentiation, we calculate pairwise FST between populations using Equation 5.3 from Weir (1996). In Figure 11, FST values are plotted against the frequency with which private alleles occur on the edges of the size distribution, and we find a very tight correlation (r = 0.9333). Thus, our empirical calculations show that our model for explaining the size distribution of private microsatellite alleles is able to predict phenomena observed in real data.
Figure 11.
FST vs. the empirical frequency with which private alleles in a sample of size four lie on the edges of the size distribution. Each point represents a pair among 53 worldwide populations from the Human Genome Diversity Panel, excluding comparisons involving Native American populations and comparisons of populations with themselves. Pearson’s r = 0.9333.
Discussion
We have modeled the phenomenon of private microsatellite alleles lying on the edges of the allele size distribution in order to explain an observation by Wang et al. (2007) that they occupy these locations more often than is expected by chance. Using a simple two-population model with sample size four, we have provided a naïve argument, in which we expect the probability that private microsatellite alleles lie on the edges of the size distribution to be 1/3. Using a coalescent model with symmetric stepwise mutation to explicitly calculate this probability as a function of two parameters (mutation rate θ and divergence time td), we find that this probability appears to always exceed 1/3. Furthermore, the model predicts that the probability that private alleles lie on the edges of the size distribution grows larger as the divergence time between populations increases. We have found that this prediction holds in an analysis of worldwide microsatellite data in humans.
Intuitively, we can understand why ℙ[E1 ∪ E2|C6, θ, td] might be expected to exceed the naïve expectation by considering the process by which private alleles are generated. When an ancestral population splits into two groups, all allele sizes present in the population become shared alleles in the descendant populations, and these shared alleles define the center of the allele size distribution. As allele sizes diffuse away from the center in the separate descendant populations, mutations in either population toward the edges of the size distribution are likely to generate alleles that are novel and therefore private. Conversely, mutations that push alleles toward the center of the size distribution are likely to produce sizes that already exist in both populations, as a result of the shared descent of central allele sizes. Furthermore, to produce shared alleles on an edge of the size distribution, unless the edge allele size is inherited by descent from the ancestral population in both descendant groups, alleles from each population must separately mutate to the same size on the edge. Because more mutations in total are required for producing such a shared allele on the edge compared to the number required in one population to produce a private allele on the edge, we expect private alleles to lie on the edges of the size distribution more often than is predicted under the assumption that there is no relationship between privacy and allele size.
This work augments the coalescent theory of microsatellite markers by providing predictions about the properties of private alleles in a simple model with sample size four. Previous work has examined additional quantities in the case of a four-allele sample. For example, Kimmel & Chakraborty (1996) and Pritchard & Feldman (1996) studied the expectation E[(Xi − Xk)2(Xj − Xℓ)2] for random allele sizes Xi, Xj, Xk, and Xℓ in a stepwise mutation model. Zhang & Rosenberg (2007) studied the genealogies of duplicated microsatellites in a model with four alleles, two each for two paralogous microsatellite loci. Together with these other studies, our work demonstrates that analytical formulas can sometimes be obtained in coalescent-based microsatellite models of non-trivial size.
While our main goal has been to explore the properties of our simple model, the model may potentially enable the inference of θ and td. For each of a collection of loci whose mutational characteristics are assumed to be identical, the probability that private alleles lie on the edges of the size distribution could be estimated from data by repeatedly sampling alleles from the observed allele frequency distributions for pairs of populations. Using this empirical estimate, a likelihood surface could then be constructed to jointly estimate θ and td. This approach might not produce identifiable estimates; however, if θ has already been estimated by another method or if additional summary statistics are combined with a private allele statistic, a potentially viable method for estimating td might be constructed, considering the dramatic effect that this parameter has on the probability that private alleles lie on the edges of the size distribution.
We conclude with a discussion of model limitations. Because of the complexity of the probability calculations, we have restricted our attention to a sample of size four. We have assumed a simple demographic model of two populations, in which population sizes are equal and no migration occurs after the populations diverge. The simple stepwise mutation model assumes symmetry in the direction of mutation and independence of the mutation rate with allele size, and both the demographic model and the mutation model likely reflect conditions that are not strictly met in the human population example that we consider. Indeed, more complex mutation models, allowing for directional bias, multistep mutations, length-dependent mutation rates, or a combination of these factors could potentially be considered (e.g. Calabrese & Durrett, 2003; Whittaker et al., 2003; Watkins, 2007). In general, however, we did not need a more complex model to explain the core observation that private alleles frequently lie on the edges of the size distribution. While the true demographic and mutational phenomena are undoubtedly more complicated than our model captures, we are still able to observe that as predicted, the probability that private microsatellite alleles lie on the edges of the size distribution in a sample of four alleles correlates with the genetic differentiation between pairs of populations.
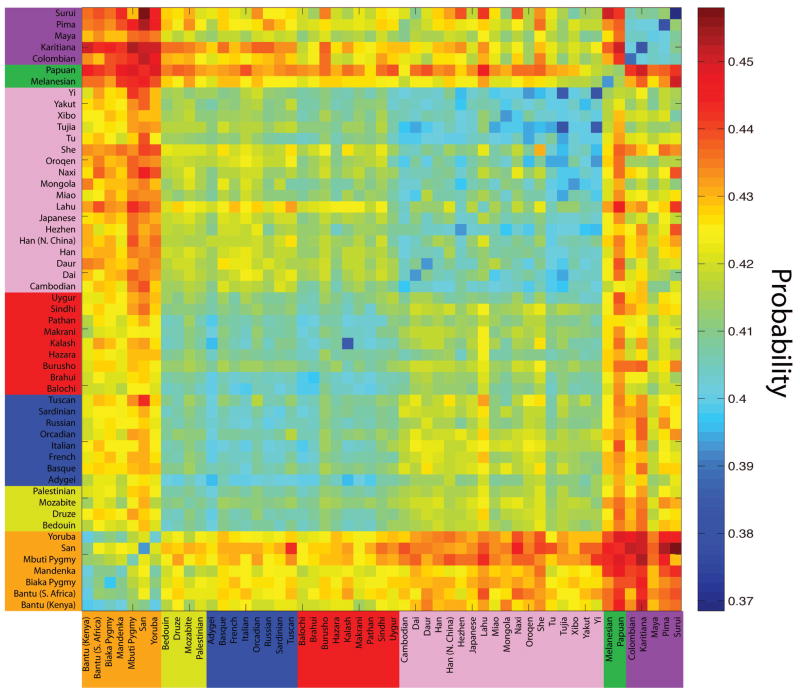
Figure 12.
Figure 1. The empirical probability that private alleles lie on the edges of the size distribution in a sample of size four from a pair of populations. Plotted are pairwise calculations of this frequency for all 53 worldwide populations from the Human Genome Diversity Panel, arranged in major geographic regions. African, Middle Eastern, European, Central/South Asian, East Asian, Oceanian, and American populations are arranged by color in the labels. Blue represents a lower probability, and red represents a higher probability. The plot was obtained using the same approach as in Figure 10, except that individual diploid genotypes rather than random pairs of alleles in populations were drawn in our resampling procedure.
Acknowledgments
Support for this work was provided by NIH grants R01 GM081441 and T32 HG000040, NSF grant DEB-0716904, and a grant from the Burroughs Wellcome Fund.
Appendix A: Derivation for arbitrary divergence time
The expresion that must be calculated in order to obtain the probability that the private alleles lie on the edges of the size distribution for arbitrary td appears in Equation 17. To perform the calculation in Equation 17, we must utilize the probability that two lineages reduce to one lineage during time td as well as the probability that two lineages survive until td. Under the coalescent (Wakeley, 2009), these probabilities are g21(td) = 1 − e−td and g22(td) = e−td, where gij(td) denotes the probability under the coalescent that i lineages reduce to j lineages during time td.
We can partition our probability calculation into four pieces corresponding to the four coalescent scenarios possible by time td (Figure 6). First, in each population, the two lineages could coalesce more recently than td (event E11). Second, the two lineages in population 1 could coalesce more recently than td, and the two lineages in population 2 could survive to td (event E12). Third, the two lineages in population 1 could survive to td, and the two lineages in population 2 could coalesce more recently than td (event E21). Finally, in each population, the two lineages could survive to td (event E22). These four events happen with the following probabilities:
| (A.1) |
| (A.2) |
| (A.3) |
| (A.4) |
We then calculate ℙ[E1 ∪ E2|C6, θ, td] by separately conditioning on E11, E12, E21, and E22 to get
| (A.5) |
in which
| (A.6) |
| (A.7) |
| (A.8) |
and
| (A.9) |
We can determine the values of the conditional probability VEij of the node allele sizes and the conditional coalescence time density ρij by examining which labeled histories are possible for each Eij. For example, for event E11 both pairs of lineages coalesce more recently than time td, and only symmetric histories are possible. Furthermore, x1 will always coalesce with x2 and x3 will always coalesce with x4 in this scenario, leaving only two possible equiprobable histories (histories 13 and 18 in Figure 1). Therefore, we only sum over the Vsym terms that are associated with these histories.
In addition, for each event, compared to the case of td = 0, we must reparameterize the branch lengths of the histories to account for changes due to forced survival of lineages to time td. For event E11, we reparameterize by setting Ψ = (τ, θ) with τ = (t2 + (td −max(t3, t4)), max(t3, t4) − min(t3, t4), min(t3, t4)), as illustrated in Figure 6 and tabulated in Table A.1. By conditioning on one of the four events E11, E12, E21, or E22, the density of coalescence times differs from the corresponding density ρ(t2, t3, t4) defined in the td = 0 case.
For event E11, the distribution of coalescence times is ρ11(t2, t3, t4) = ρ11t2(t2) ρ11t3 ρ(t3) ρ11t4 (t4), where ρ11t2 (t) = e−t and ρ11t3 (t) = ρ11t4 (t) = 1t<tde−t/(1 − e−td). We can then write
| (A.10) |
We proceed with similar arguments for events E12, E21, and E22. The corresponding values for Ψ are tabulated in Table A.1, and the values for VEij and ρij are tabulated in Table A.2.
Table A.1.
The reparameterizations of Ψ for the events Eij.
| Event | Ψ = (τ, θ) |
|---|---|
| E11 | τ= (t2 + td − max(t3, t4), max(t3, t4) − min(t3, t4), min(t3, t4)) |
| E12 | τ= (t2, t3 + td − t4, t4) |
| E21 | τ = (t2, t3 + td − t4, t4) |
| E22 | τ = (t2, t3, t4 + td) |
Table A.2.
The probabilities of node allele sizes and the coalescence time densities conditional on events Eij.
| Event | VEij | ρij(t2, t3, t4, td) = ρijt2 (t2, td) ρijt3 (t3, td) ρijt4 (t4, td) | |||
|---|---|---|---|---|---|
| ρijt2 (t, td) | ρijt3 (t, td) | ρijt4 (t, td) | |||
| E11 |
|
e−t | 1t<tde−t/(1 − e−td) | 1t<tde−t/(1 − e−td) | |
| E12 |
|
e−t | 3e−3t | 1t<tde−t/(1 − e−td) | |
| E21 |
|
e−t | 3e−3t | 1t<tde−t/(1 − e−td) | |
| E22 |
|
e−t | 3e−3t | 6e−6t | |
Appendix B: Implementing the computation for arbitrary divergence time
To implement the calculation of ℙ[E1 ∪ E2|C6, θ, td] (Equation 17) derived in Appendix A, we use Gaussian quadrature and a simulation-based approach. These approaches are analogous to the approaches that we used in the case of td = 0.
Numerical computation
As in the td = 0 case, we use Gaussian quadrature to numerically evaluate ℙ[E1, C6|θ, td, Eij] (Equation A.6) and ℙ[C6|θ, td, Eij] (Equation A.7), once again estimating the expression e−tθ/2I|d|(tθ/2) using the GNU Scientific Library (GSL) function gsl sf bessel In scaled(|d|, tθ/2). We use the same value as in the td = 0 case (±10) to truncate the infinite sums in Equations A.8 and A.9. Additionally, we again integrate all time dimensions in Equations A.6 and A.7 from 0 to 10 rather than from 0 to ∞. As in the case of td = 0, these calculations are very accurate for small values of θ and less accurate for large values of θ (not shown).
Simulation-based computation
As in the td = 0 case, we are able to accurately estimate the quantity ℙ[E1 ∪ E2|C6, θ, td] (Equation 17), directly obtaining the ratio 2ℙ[E1, C6|θ, td]/ℙ[C6|θ, td] by simulating the coalescent and mutation processes and counting the outcomes of interest. The simulation proceeds as follows.
Beginning with k = 4 alleles, arbitrarily define two alleles to be in one population and the other two alleles to be in the other population.
Randomly choose an event E11, E12, E21, or E22 based on their relative probabilities conditional on td (Equations A.1–A.4).
-
If event E11 is chosen:
Generate a random time to coalescence from an exponential ( ) distribution conditional on being less than td.
Coalesce the pair of lineages in population 1; set k = k − 1.
Generate a random time to coalescence from an exponential ( ) distribution conditional on being less than td.
Coalesce the pair of lineages in population 2; set k = k − 1.
-
If event E12 or E21 is chosen:
Generate a random time to coalescence from an exponential ( ) distribution conditional on being less than td.
Coalesce a pair of lineages in population 1 (if event E12) or population 2 (if event E21); set k = k − 1.
Extend all remaining lineages up to td.
Generate a random time to coalescence from an exponential ( ) distribution.
Randomly choose two lineages to coalesce; set k = k − 1.
If k ≠ 1, go to 6.
For each branch of the genealogy, generate a random number of mutation events, x, from a Poisson distribution with rate θt/2, where t is the branch length.
Assign each mutation a value of +1 or −1 by sampling the number of +1 mutations from a binomial(x,1/2) distribution. Those mutations not chosen to be +1 are assigned a value of −1.
Determine the allele size of each of the four sampled alleles by summing the net value of mutations from the root (allele size 0) down to the leaves.
Classify the collection of four alleles into one of the seven allele configurations (Table 1).
If the alleles are in the C6 configuration, accept the simulation and determine if the sizes of the private alleles (B and C) are on the ends of the distribution (nC < nA < nB or nB < nA < nC). If yes, count a success.
As in the td = 0 case, after the number of accepted simulations reaches some pre-specified number (we choose 1, 000, 000), we estimate the probability of the private alleles occurring on the edges of the size distribution by dividing the number of successes by the number of accepted simulations.
Appendix C: Small-θ approximation for arbitrary divergence time
With td > 0, we can consider a small-θ approximation to the probability that the private alleles lie on the edges in a similar way to the corresponding calculation with td = 0. By considering a fixed td, we proceed as before, counting the contributions of each labeled history to the numerator and denominator in Equation 17. The probability distribution of labeled histories depends on td, and the 18 histories are no longer equiprobable when td > 0. Conditional on one of the events {E11, E12, E21, E22}, however, we can determine the possible histories and weight the probability contributions of these histories to the numerator and denominator as before.
Thus, following Equation A.5 for the small-θ case, we wish to calculate
| (C.1) |
Note that although E1 and E2 have the same probability, in this calculation it is convenient to calculate E1 ∪ E2 directly. We do this by tabulating contributions to the numerator and denominator conditional on each event Eij (Table 5), reparameterizing Ψ to augment certain branch lengths by amounts dependent on td (Table A.1).
First, consider event E11. If both pairs of lineages coalesce more recently than the population divergence time, then the only possible histories are 13 and 18, and the conditional contribution to the denominator of Equation C.1 is
| (C.2) |
where tmax = max(t3, t4) and tmin = min(t3, t4). Here, we obtain the coefficients for each σi by referencing histories 13 and 18 in Table 5, and we use the conditional density of coalescence times ρE11 (t2, t3, t4, td) from Table A.2. Equation C.2 also provides the ℙ[E1 ∪ E2, C6|θsmall, td, E11] term in the numerator, because for histories 13 and 18, at small θ, the private alleles always lie on the edges of the size distribution.
Next, consider event Eij (i ≠ j). If the two lineages in one population coalesce more recently than the divergence time, and the two lineages in the other population survive to the divergence time, then the only possible histories are 1, 2, and 18 for E12 or 11, 12, and 13 for E21. Because E12 and E21 differ only in which population contains the coalescence more recent than the population divergence, they have the same probability. The conditional contribution to the denominator for either event is then
| (C.3) |
where the σi coefficients are taken from Table 5 using either set of histories (1, 2, and 18 for E12 or 11, 12, and 13 for E21) and ρEij (t2, t3, t4, td) is taken from Table A.2. Equation C.3 is also equal to the ℙ[E1∪ E2, C6|θsmall, td, Eij] term in the numerator, because for either set of histories, at small θ, the private alleles always lie on the edges of the size distribution.
For event E22, if the two lineages in both populations survive to the divergence time, then all 18 histories are possible. The conditional contribution to the denominator is
| (C.4) |
and the conditional contribution to the numerator is
| (C.5) |
where the σi coefficients are from Table 5 and ρE22 (t2, t3, t4) is from Table A.2.
We can understand how Equation C.1 will behave for large values of td by considering the behavior of ℙ[Eij|td] (Equations A.1–A.4) as td tends toward ∞. Independently of the value of θ, when the divergence time between populations grows very large, we expect each pair of lineages to always coalesce before divergence (event E11). Taking the limits of Equations A.1–A.4, limtd→∞ ℙ[E11|td] = 1 and limtd→∞ ℙ[E12|td] = limtd→∞ ℙ[E21|td] = limtd→∞ ℙ[E22|td] = 0. Thus as td tends to ∞, Equation C.1 reduces to
| (C.6) |
Therefore, for large td, we intuitively expect the small-θ probability that the private alleles lie on the edges of the size distribution to tend to unity.
Note that Equations C.4 and C.5 differ from Equations 14 and 12 only in the definitions of the time parameters and densities of coalescence times. Using the conditional contributions in Equations C.2–C.5 together with ℙ[Eij|td] in Equations A.1–A.4, we can calculate Equation C.1. The resulting expression is unwieldy (not shown), but taking its limit as θ tends to 0, we obtain Equation 18.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Barton NH, Slatkin M. A quasi-equilibrium theory of the distribution of rare alleles in a subdivided population. Heredity. 1986;56:409–415. doi: 10.1038/hdy.1986.63. [DOI] [PubMed] [Google Scholar]
- Calabrese P, Durrett R. Dinucleotide repeats in the drosophila and human genomes have complex, length-dependent mutation processes. Molecular Biology and Evolution. 2003;5:715–725. doi: 10.1093/molbev/msg084. [DOI] [PubMed] [Google Scholar]
- Calafell F, Shuster A, Speed WC, Kidd JC, Kidd KK. Short tandem repeat polyorphism evolution in humans. European Journal of Human Genetics. 1998;6:38–49. doi: 10.1038/sj.ejhg.5200151. [DOI] [PubMed] [Google Scholar]
- Felsenstein J. Inferring Phylogenies. 1 Sinauer Associates, Inc; Sunderland, MA, USA: 2004. [Google Scholar]
- Fiumera AC, Parker PG, Fuerst PA. Effective population size and maintenance of genetic diversity in captive-bred populations of a Lake Victoria cichlid. Conservation Biology. 2000;14:886–892. [Google Scholar]
- Gradshteyn IS, Ryzhik IM. Table of Integrals, Series, and Products. 6 Academic Press; London: 1980. [Google Scholar]
- Kalinowski ST. Counting alleles with rarefaction: private alleles and hierarchical sampling designs. Conservation Genetics. 2004;5:539–543. [Google Scholar]
- Kimmel M, Chakraborty R. Measures of variation at DNA repeat loci under a general stepwise mutation model. Theoretical Population Biology. 1996;50:345–367. doi: 10.1006/tpbi.1996.0035. [DOI] [PubMed] [Google Scholar]
- Neel JV. Private genetic variants and the frequency of mutation among South American Indians. Proceedings of the National Academy of Sciences of the United States of America. 1973;70:3311–3315. doi: 10.1073/pnas.70.12.3311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neel JV. Rare variants, private polymorphisms, and locus heterozygosity in Amerindian populations. American Journal of Human Genetics. 1978;30:465–490. [PMC free article] [PubMed] [Google Scholar]
- Neel JV, Thompson EA. Founder effect and number of private polymorphisms observed in amerindian tribes. Conservation Genetics. 1978;75:1904–1908. doi: 10.1073/pnas.75.4.1904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neel MC, Cummings MP. Effectiveness of conservation targets in capturing genetic diversity. Conservation Biology. 2003;17:219–229. [Google Scholar]
- Parker KM, Sheffer RJ, Hedrick PW. Molecular variation and evolutionarily significant units in the endangered gila topminnow. Conservation Biology. 1999;13:108–116. [Google Scholar]
- Petit R, Mousadik AE, Pons O. Identifying populations for conservation on the basis of genetic markers. Conservation Biology. 1998;12:844–855. [Google Scholar]
- Pritchard JK, Feldman MW. Statistics for microsatellite variation based on coalescence. Theoretical Population Biology. 1996;50:325–344. doi: 10.1006/tpbi.1996.0034. [DOI] [PubMed] [Google Scholar]
- Ramachandran S, Deshpande O, Roseman CC, Rosenberg NA, Feldman MW, Cavalli-Sforza LL. Support from the relationship of genetic and geographic distance in human populations for a serial founder effect originating in Africa. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:15942–15947. doi: 10.1073/pnas.0507611102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg NA, Mahajan S, Ramachandran S, Zhao C, Pritchard JK, Feldman MW. Clines, clusters, and the effect of study design on the inference of human population structure. PLoS Genetics. 2005;1:660–671. doi: 10.1371/journal.pgen.0010070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroeder KB, Schurr TG, Long JC, Rosenberg NA, Crawford MH, Tarskaia LA, Osipova LP, Zhadanov SI, Smith DG. A private allele ubiquitous in the Americas. Biology Letters. 2007;3:218–223. doi: 10.1098/rsbl.2006.0609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slatkin M. Rare alleles as indicators of gene flow. Evolution. 1985;39:53–65. doi: 10.1111/j.1558-5646.1985.tb04079.x. [DOI] [PubMed] [Google Scholar]
- Szpiech ZA, Jakobsson M, Rosenberg NA. ADZE: a rarefaction approach for counting alleles private to combinations of populations. Bioinformatics. 2008;24:2498–2504. doi: 10.1093/bioinformatics/btn478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torres E, Iriondo JM, Pérez C. Genetic structure of an endangered plant, Antirrhinum microphyllum (Scrophulariaceae): allozyme and RAPD analysis. American Journal of Botany. 2003;90:85–92. doi: 10.3732/ajb.90.1.85. [DOI] [PubMed] [Google Scholar]
- Wakeley J. Coalescent Theory: An Introduction. Roberts and Company Publishers; Greenwood Village, CO, USA: 2009. [Google Scholar]
- Wang S, Lewis CM, Jr, Jakobsson M, Ramachandran S, Ray N, amd Bedoya G, Rojas W, Parra MV, Molina JA, Gallo C, Mazzotti G, Poletti G, Hill K, Hurtado AM, Labuda D, Kiltz W, Barrantes R, Bortolini MC, Salzano FM, Petzl-Erler ML, Tsuneto LT, Llop E, Rothhammer F, Excoffier L, Feldman MW, Rosenberg NA, Ruiz-Linares A. Genetic variation and population structure in Native Americans. PLoS Genetics. 2007;3:e185. doi: 10.1371/journal.pgen.0030185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watkins JC. Microsatellite evolution: Markov transition functions for a suite of models. Theoretical Population Biology. 2007;71:147–159. doi: 10.1016/j.tpb.2006.10.001. [DOI] [PubMed] [Google Scholar]
- Wehrhahn CF. The evolution of selectively similar electrophoretically detectable alleles in finite natural populations. Genetics. 1975;80:375–394. doi: 10.1093/genetics/80.2.375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir BS. Genetic Data Analysis II. Sinauer; Sunderland, Massachusetts: 1996. [Google Scholar]
- Whittaker JC, Harbord RM, Boxall N, Mackay I, Dawson G, Sibly RM. Liklihood-based estimation of microsatellite mutation rates. Genetics. 2003;164:781–787. doi: 10.1093/genetics/164.2.781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilson IJ, Balding DJ. Genealogical inference from microsatellite data. Genetics. 1998;150:499–510. doi: 10.1093/genetics/150.1.499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang K, Rosenberg NA. On the genealogy of a duplicated microsatellite. Genetics. 2007;177:2109–2122. doi: 10.1534/genetics.106.063131. [DOI] [PMC free article] [PubMed] [Google Scholar]