Non-cryogenic anatomical imaging in ultra-low field regime: Hand MRI demonstration

Abstract

Ultra-low field (ULF) MRI with a pulsed prepolarization is a promising method with potential for applications where conventional high-, mid-, and low-field medical MRI cannot be used due to cost, weight, or other restrictions. Previously, successful ULF demonstrations of anatomical imaging were made using liquid helium-cooled SQUIDs and conducted inside a magnetically shielded room. The Larmor frequency for these demonstrations was ~ 3 kHz. In order to make ULF MRI more accessible, portable, and inexpensive, we have recently developed a non-cryogenic system. To eliminate the requirement for a magnetically shielded room and improve the detection sensitivity, we increased the frequency to 83.6 kHz. While the background noise at these frequencies is greatly reduced, this is still within the ULF regime and most of its advantages such as simplicity in magnetic field generation hardware, less stringent requirements for uniform fields etc., remaining. In this paper we demonstrate use of this system to image a human hand with up to 1.5 mm resolution. The signal-to-noise ratio was sufficient to reveal anatomical features within a scan time of less than 7 minutes. This prototype can be scaled up for constructing head and full body scanners, and work is in progress toward demonstration of head imaging.

I. Introduction

Magnetic-resonance imaging (MRI) is a powerful diagnostic non-invasive radiation-free method that is widely used in medicine. Because the image quality, such as resolution and signal-to-noise ratio (SNR), improves with the strength of the magnetic field, high-field (> 1 Tesla) MRI systems are most frequently used in medical practice and in research. However, such scanners are quite expensive and some restrictions exist in their applications.

The problem of the high cost of high-field MRI limiting their availability is partially solved with mid- and low-field MRI scanners (low-field is conventionally defined as field below 0.5 T). Currently low-field permanent magnetic based medical whole-body systems are available from several companies: Siemens, GE, Hitachi, and Esaote. They not only provide good quality images at lower cost, but also have additional advantage of an open design to allow or facilitate MRI applications with claustrophobic patients, children requiring parental assistance, and overweight patients. Despite the loss in SNR, there are several other advantages to be obtained at low fields. It has been shown that contrast improves at low fields [1], and this improvement in contrast-to-noise ratio or CNR is very often more important for detecting anomalies such as tumors than high resolution. Susceptibility artifacts are reduced enabling imaging patients with metal implants [2]. The RF power dramatically drops, reducing or eliminating the danger of burns. The acoustic noise level is reduced. Thus there is room for low- and mid-field scanners in medical practice to supplement the high-field scanners and such systems have a significant share of the market [3,4]. One disadvantage of the existing whole-body systems based on permanent magnets is their heavy weight, although for extremities such as arms and legs, much smaller and lighter systems have been developed by Siemens and other companies.

By further lowering the magnetic field to the ultra-low field (ULF) regime, the field generation hardware can be even further simplified and the weight much reduced as demonstrated in the current paper. The energy consumption can be also reduced, which is substantial in the case of large resistive coil systems, also sometimes used instead of permanent-magnet systems at low field. The loss in SNR with reduced magnetic field to achieve these benefits has been shown to be less dramatic than expected from simplistic theories. For example, in Ref. [5] it was shown to be only linear rather than quadratic. The reason for this is that the coil sensitivity is limited by body noise, which slowly increases with frequency. Thus the only gain in SNR with the field is due to polarization. Apart from this, the duty cycle at low field due to shortening of longitudinal relaxation time (T₁) is improved. Furthermore, as we already mentioned, the contrast can be a more important characteristic than SNR. This is one advantage of MRI over X-ray tomography, which gives excellent resolution and SNR, but very low contrast. Since at low field the difference in relaxation time between tissues increases [6], effectively smaller SNR would be required for differentiation of tissues and diagnostics of anomalies. However, even with all these factors taken into account, there is no doubt that SNR and quality are lower at low field, but are they still acceptable, considering trade-off between quality and a lower price of the scanner?

While there is need for more extensive efficacy comparison studies, several reports dedicated to such studies concluded that low-field and high-field scanners have almost equal sensitivity to disease [4,7,8,9,10]. In Ref. [3] it was stated that to produce clinically useful diagnostic images with a 0.1 T scanner the length of the scan needs to be only 3 times longer than at 1 and 1.5 T. In Ref. [8] from multi-center studies of 401 patients the conclusion was drawn that the open low-field scanner evaluated using clinical and surgical gold standards as reference was able to achieve comparable diagnostic accuracy as high-field scanners at lower costs and greater patient comfort. SNR, resolution and scan time limitations due to low field strength were found to be relevant only in a very small number of cases. Even lower field, 0.064 T, have been used for clinical diagnostics [7]. Nevertheless the images obtained in ULF systems (well below 0.1 T) would be completely unacceptable without the use of polarization enhancement with an additional pulsed prepolarization field B_p. Because SNR is directly proportional to the polarization, by increasing the strength of this field it might be possible to achieve as high sensitivity as that of low-field scanners. With pulsed prepolarization, the requirement on the measurement field (B_m) such as uniformity and stability on a relative scale are much lower at ULF than at high field assuming equal requirements on absolute scale. The B_p coil main requirement is the strength and cooling. It is much easier to generate large B_p without restricting it by uniformity requirements, and it is also much easier to make the field uniform on the absolute scale at ULF for acceptable imaging quality. The ability to optimize these two fields is the main advantage of the method.

The idea of using a prepolarization field dates back to 1954 when Packard and Varian first applied a prepolarization field of 100 G to obtain NMR signals in the Earth's field [11]. Since this work, many experiments have been performed using the Earth's field as B_m. However, the sensitivity of Faraday coils at the Earth's field frequency is quite low for medical imaging. Thus later work has used non-Earth B_m, and various schemes of excitation of NMR signal were investigated. Low-field scanners suitable for medical imaging in SNR and resolution have been demonstrated with strong prepolarization field. In particular, [12] built a pulse MRI system by adding 1.2 kG prepolarizing coil to a Toshiba ACCESS 640 Gauss imager. Although such an approach leads to images of improved quality, the cost of the scanner operating at 640 Gauss can be further reduced by lowering the measurement field. Moreover, the enhancement factor in SNR due to B_p is quite moderate, taking into account additional noise arising from the B_p coil implementation. Macovski and Conolly briefly reviewed the previous work on prepolarized MRI emphasizing cost reduction and other advantages, and proposed their own scheme for low-cost MRI [13], although they noted that “the full realization remains speculative.” Most recently, high quality images of extremities using a 0.4 T prepolarization field have been shown to rival high field systems in sensitivity and resolution [14,15]. Various features of the low-field approach such as absence of susceptibility artifacts [15,16] and nitrogen dips were also demonstrated [15,17]. However, the system has never been developed into a large-size imager. Work is still in progress to create clinically adopted scanners based on the pulsed prepolarization idea.

While many prepolarized MRI experiments have been based on pick-up coils owing to their simplicity, to maintain sensitivity while using the Earth-like fields, superconducting quantum interference devices (SQUIDs) with their lower intrinsic noise were also employed [18]. SQUIDs brought several other advantages. They could be configured as highly accurate gradiometers and for non-resonant multi-channel detection. A gradiometer is useful to subtract ambient noise, significant in poorly shielded environments and when a prepolarization coil is added to the system. Multi-channel detection improves SNR and reduces the time of the scan [19]. SQUIDs are also broadband detectors, which is a necessary property at the Earth's field to increase the speed of MRI acquisition. SQUIDs with a cryo-switch can be turned off and on quickly to detect NMR signals that have fast decay times [20]. Since SQUID-based detection provided superior sensitivity at ULF, many novel experiments were conducted with this method. In particular, SQUIDs were used to demonstrate the detection of explosives in an airport [21], where low-frequency operation was required in order to receive NMR signals from inside aluminum cans. There have also been demonstrations of ULF MRI inside a magnetically shielded room using SQUIDs[19], including the first-ever image of the human brain at ULF [22]. An important advantage of SQUID detection is that magnetoencephalography (MEG), a method for high temporal resolution functional brain imaging using SQUID detection, can be combined with the MRI in a single device[22]. This combination of MEG and MRI is traditionally performed only in two separate instruments since the SQUIDs are incompatible with the large magnetic fields of traditional MRI. Combined MEG and MRI in one instrument would reduce the cost of requiring two instruments and remove the additional complexity of data co-registration error [22]. Since the MEG infrastructure already includes the SQUIDs, Dewar, liquid helium supply, and shielded room, an MRI subsystem based on SQUIDs would not appreciably increase the cost. Although the brain MRI at ULF took about an hour and resolution was 3×3×6 mm³, many ways exist to improve the sensitivity and shorten the scan time, including higher prepolarization field (0.4 T prepolarization fields have been demonstrated [14], although for a smaller size imaging) and SQUID operation at higher frequency to reduce noise. It is quite conceivable that this method eventually can result in high-quality fast imaging, but the system would be still very expensive for commercialization owing to the cryogenic operation and the shielded room requirement.

To avoid cryogenics, atomic magnetometers (AMs) were tested in ULF NMR and MRI applications. The first detection with ultra-sensitive AMs of hyperpolarized Xe was demonstrated in [23] and of thermally polarized protons in [24], and the first MRI detection with AM in remote-NMR mode was demonstrated in [25]. Because AMs are as sensitive as SQUIDs (e.g. at 423 kHz an AM sensitivity of 0.24 fT/Hz^1/2 was demonstrated [26] for NQR detection) the requirements for cryogens can be eliminated without sensitivity trade-off. However, to reduce the cost and complexity of the AM and to accommodate sufficient bandwidth for MRI, it is necessary to raise the NMR frequency to about 100 kHz . This leads to the difficult problem that the AM bias field (required to tune the AM) has to be separated from the 3 orders of magnitude larger NMR field. One possible solution of this problem was tested in [27]. A long solenoid, which ideally should have zero field outside and uniform field inside, was introduced into the NMR setup to separate NMR and AM bias fields [23,27]. Unfortunately, the solenoid constructed in [27] was far from ideal and had significant outside field and non-uniform inside field shortening T₂* even of a small NMR sample. Moreover the solenoid was of small diameter (3.5 cm), which restricted imaging of large objects. More advanced equipment or a more complicated coil design might enable the desired field separation. A much simpler solution, however, is to use a flux transformer instead. A flux-transformer (FT) can be used to transfer the NMR signal to the AM which can be positioned away from the NMR coils. Thus the AM and NMR fields can be independently adjusted. The FT-AM detection method was used to demonstrate ULF MRI with a setup that could be scaled for clinical imaging [26]. This setup did not rely on cryogens, with the FT made of a copper wire held at room-temperature. Although convenient for practical implementation, the room-temperature FT has significant Johnson noise. At 3 kHz, the Johnson noise limited the sensitivity of the system to about 10 fT/Hz^1/2, and such sensitivity was not sufficient for medical MRI. However, the noise in the FT can be significantly reduced by increasing the frequency. The work presented here is partially motivated by the need to investigate the performance and noise of such FT at higher frequencies and to develop the other parts of MRI system operating at higher frequencies that would be required. One advantage of the AM in such a configuration is the possibility to run multi-channel acquisition to improve SNR [28] and greatly reduce the required scan time. For example, a 9-channel system can improve SNR and resolution 3 times for a given scan time, or reduce scan time by a factor of 9. It is possible either to use a large atomic cell with multiple output coils of the FTs covering the surface of the cell or small separate atomic cells and coils. From fundamental noise estimates, it should be possible to use 1-mm size chip-scale atomic magnetometers developed by Kitching's group, which have been applied to NMR detection for microfluidic applications [29]. The only problem is that the experimentally demonstrated sensitivity of the chip-scale cells is well below the fundamental sensitivity and is not yet adequate for high-quality MRI, even taking into account the reduced requirement for sensitivity of smaller cells owing to field enhancement of the FT, on the order of the ratio of the diameters of the primary and secondary coils.

As the first step in the development of non-cryogenic ULF scanners, including those based on AMs, we constructed a small-scale prototype for a hand and investigated its performance. A larger-scale system for head imaging is under construction. As the clinical relevance of 0.1 T scanner is more or less established in clinical trials, we will compare the SNR and image resolution obtained with our ULF scanner to that of 0.1 T scanner. We also compare our images with ULF images obtained with liquid helium–cooled SQUIDs in a shielded room to show that ULF MRI techniques developed with SQUIDs can be implemented in non-cryogenic fashion, which will help to realize these techniques in clinical applications.

II. Method

Our ULF MRI system is based on non-cryogenic detection using a pick-up coil. To reach a coil sensitivity needed for anatomical imaging, we employed a proton NMR frequency of 83.6 kHz and a prepolarization field of 1 kG. To achieve sufficient uniformity in B_m, a 4-coil Whiting-Lee configuration [30] was used, which has a much larger volume for a given level of uniformity than a Helmholtz pair. To accommodate an image volume of 10 by 10 cm by 3 cm of the hand, the coil was wound on a 33-cm G-10 cylinder. Imperfections in winding and external gradients were compensated with a set of 3 first-order shim gradients. The shim-gradients were wound on the same cylinder as the main coil. To use an inexpensive and readily available DAQ (100kS/s) and reduce the data load to the computer, we down-converted the signal to low frequency (1-2 kHz) with an analog mixer. To improve phase stability and the effects of external gradients we implemented spin echo pulses. To excite the NMR signal we applied Π/2 pulses. Unlike our previous SQUID-based ULF MRI systems (see for example [22]), the current ULF MRI design does not rely on a magnetically shielded room, and was designed to be compact, light weight, and inexpensive. To understand the issue of magnetic noise at low frequency (60 Hz and harmonics) and ambient field instability, we conducted experiments with our MRI system when it was operated either inside or outside an open-ended mu-metal cylindrical shell. The images in the two cases were of similar quality thus we continued our experiments in an unshielded environment. All results below are reported for the unshielded operation.

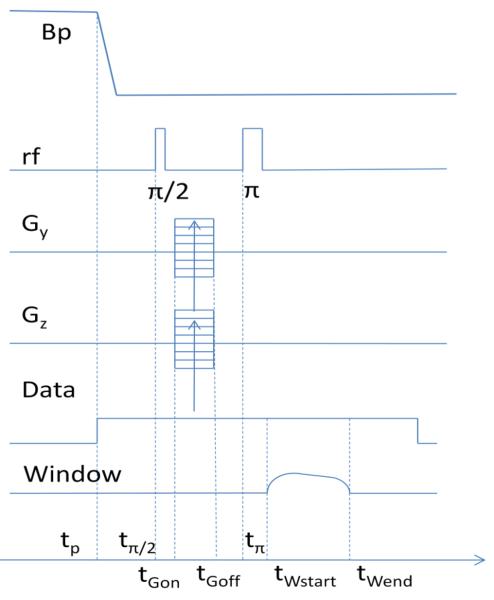
The pulse sequence that we applied for imaging is shown in Fig. 1. The measurement field and the frequency-encoding gradient were kept constant, and are not shown on the graph. At the beginning of each cycle, the prepolarization field B_p, which was collinear with the measurement field B_m, was turned on. At the moment t_p, B_p was turned off, and after some delay necessary for the decay of transients, the Π/2-pulse was applied at t_Π/2. The phase encoding gradients were applied after a small delay of 2 ms and turned off before the Π-pulse. The Π-pulse was applied 25 ms after the Π/2-pulse. The Π/2-pulse had the length of 0.4 ms and Π-pulse 0.8 ms. Data recording began at t_p. The analysis window was applied to data from t_Wstart to t_Wend, adjusted at the analysis stage to remove transients from the Π-pulse and to optimize SNR. The window had smooth profiles at the beginning and the end with adjustable percentage of transition region (10-30%), and superimposed on this was an exponential profile equal to 1 at the beginning with an adjustable final value.

Fig. 1.

Pulse sequence: t_p=340 ms, t_Π/2=t_p+25 ms, t_Π= t_Π/2+25 ms, t_Gon=t_p+27 ms, t_Goff= t_Gon +22 ms t_Wstart= t_p +65 ms, t_W.end= t_Wstart+75 ms. Repetition time is 500 ms.

3D imaging was realized with 1 frequency encoding gradient and 2 phase encoding gradients, Table I. These gradients were combined with the shimming gradients. The transverse gradients were generated by two orthogonal Golay pairs, and the axial gradient (frequency encoding) was generated by a Maxwell pair. The applied gradients and the number of encoding steps for hand and phantom images with 1.5 mm and 2 mm resolutions are given in the table. Total time required for the scan was chosen 6.7 minutes without averaging for both resolutions, and 13.4 minutes for 2-time averaged acquisition.

Table I.

Resolution, applied gradients (G) number of encoding steps (N), and slice thickness; x is the frequency en coding direction, vertical on images, y − is horizontal phase encoding direction, z − is slicing (depth) phase encoding direction. The table also gives the total field of view (FOVy) in the y direction, which is larger than FOV of the presented figures, zoomed on the most interesting features. In the y direction, FOV has no clear boundary and the image gradually fades due to the loss of signal away from the coil resonance and due to the limited geometrical coverage of the coil. Approximately it is 110 mm. The product FOV · Gmax/ 2B_m is less than 1%, so the concomitant gradients are not important.

Resolution (mm2)	Gx (Hz/cm)	Gy max (Hz/cm)	Gz max (Hz/cm)	Slice (mm)	Ny	Nz	FOVH (mm)
2×2	73	± 115	± 42	5.5	65	11	130
1.5×1.5	102	± 160	± 42	5.5	91	9	136

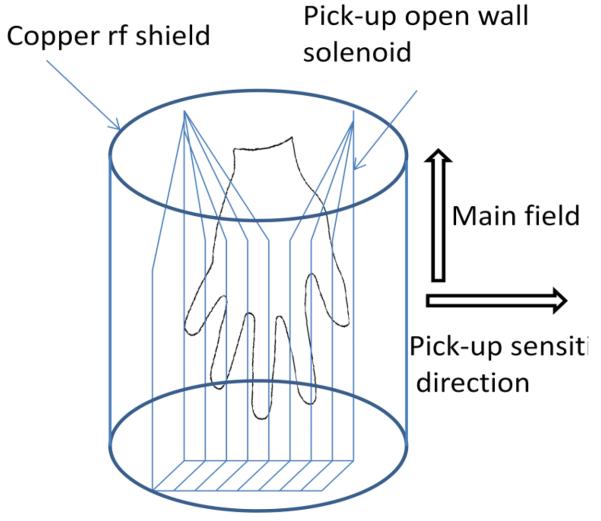
We used a switched prepolarization field of 0.1 T generated by a short air-cooled solenoid. To decrease the noise produced by this solenoid and other external noise we placed a small thin RF shield inside the B_p coil and added filters in the circuit of the B_p power supply (as well as other circuits). The rf shield had minimal effect on the phase encoding gradients, but created some additional thermal noise in the pickup coil. To reduce this additional noise and also to make the sensitivity across the hand more uniform, we made the pick-up coil in the shape of a solenoid that opens at its side as schematically shown in Fig. 2. The opening introduced some non-uniformity in the sensitivity, but this non-uniformity was deemed acceptable, especially for this initial proof-of-principle demonstration. For dedicated imaging of the hand, the solenoid can be extended to image the full hand with minimal distortions.

Fig. 2.

The pick-up coil geometry and its position inside rf shield.

III. Experimental Results

Measurements of SNR

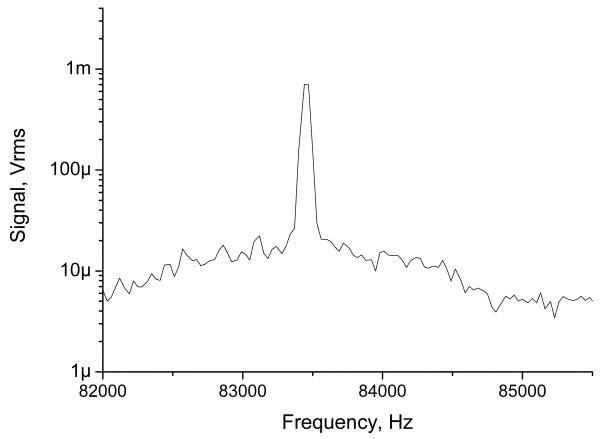
SNR is the primary limiting factor in MRI and is critical for MRI system characterization. It is convenient to use the normalized SNR of the NMR signal for a unit volume of water and bandwidth, ψ. The voxel SNR in MRI can be then calculated from this normalized SNR as $\Psi \rho V\sqrt{N_{\mathit{ex}}\cdot T_S}(1-e^{-t_p∕T_1})\cdot e^{-T_E∕T_2}$, where ρ is the relative proton density of tissue, V = ΔxΔyΔz is the voxel volume defined by the resolution and slice thickness, T_Sis the detection time, and N_exis the number of excitations, t_p is the prepolarization time, T_Eis the echo time [5]. The equation is slightly modified for our application of pulsed prepolarization. We conducted measurements of signal and noise at 83.6 kHz. The NMR signal was obtained from a 2 ml water sample using spin-echo protocol and normalized on the volume and unit bandwidth as described in detail in Fig. 3. We found that ψ was 300 cm⁻³Hz^−1/2. SNR measurements were done with and without a mu-metal cylinder, with results being very similar. To understand if we reached the limit of the intrinsic noise of our coil, we measured the output noise (15 nV/Hz^1/2) and compared it to calculated Johnson noise (12 nV/Hz^1/2 ) from experimental values of the coil parameters at 83.6 kHz: Q=100, L=165 _μH. Also from the coil response (5.2 G/A), prepolarization strength, and sequence timing, we calculated that intrinsic ψ was 383. This is close to the experimental value, which means that we were able to exclude external noise. The SNR of our system operating at 83.6 kHz is comparable to SNR of a 0.12 T scanner, 190 for a torso coil and 944 for a head coil [5], although we are comparing coils of different sizes. For our chosen image acquisition parameters (Table 1), we found that the voxel SNR was 25 for a 2 mm in plane resolution and slice thickness of 5.5 mm with no averaging (6.7 minute scan), or 14 and 20 for 1.5 mm resolution with no averaging (6.7 minute scan) and 2 averages (13.4 minute scan). These image voxel SNRs are close to the criterion SNR>20 for adequate anatomical imaging given in [5]. Further increasing resolution and reducing SNR lead to appearance of noise artifacts on the images. There are several achievable paths forward to further improvement. An additional factor of 4 in SNR can be obtained by increasing prepolarization field from 0.1 T to 0.2 T, the NMR frequency from 84 to 170 kHz, and the coil Q factor from 100 to 200. Alternatively, with these steps the image resolution can be improved to 1×1 mm² to give more detailed hand anatomy. Also longer averaging can be used to further improve the SNR and resolution if necessary for more detailed study.

Fig. 3.

Ten-time RMS-averaged NMR signal from a 2 ml water sample and noise spectrum of noise obtained with prepolarization field 620 G using spectrum analyzer after amplification of 1000 times. The bin size is 32 Hz, window is Hanning. The Pi/2 time is 50 ms from Bp off and echo time 110 ms after Bp off, the starting acquisition time of the spectrum analyzer is 110 ms. Normalized SNR per unit bandwidth, cc, and 1 kG of prepolarization field is 300 1/Hz^1/2/cc/kG where we extrapolated results to infinite prepolarization time and T2.

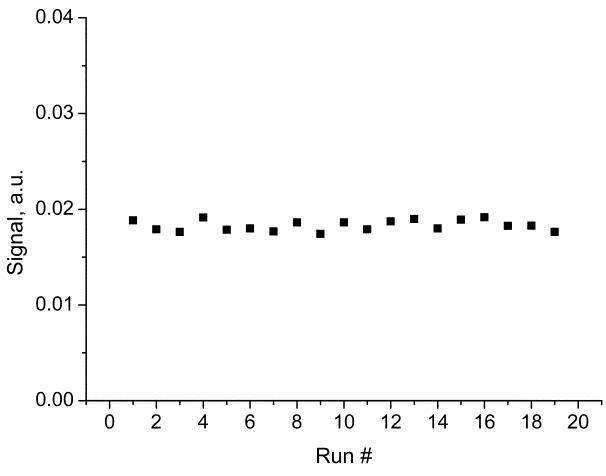
Apart from measurements of SNR of a small sample, we also investigated multiplicative noise that can arise on images from a larger sample. This noise is related to the stability of NMR signal for multiple consecutive scans. In Fig. 4 we plotted NMR signals (FIDs) from our multi-hole phantom described later and analyzed the statistical properties of the signal variation. We found that the variation in the signal was at the level close to the noise when NMR sample was removed, so the multiplicative is not expected to be large on our demonstrated images, considering limited SNR on the order of 20 of our images.

Fig. 4.

Test of the stability of NMR signal for consecutive scans for evaluation of multiplicative noise. The average value is 0.0183 and the standard deviation (noise) is 3%. This value is slightly higher than the noise when the sample was removed, which for in-phase component was 1.8%.

Imaging experiments

We conducted imaging experiments with a phantom and the human hand to evaluate the performance of our unshielded ULF MRI system. An unshielded system will be generally much more convenient in most applications. Shielding may be required in cases where the environmental field is unstable, and gradients are very large. Our lab space was quite limited and the system was located on a steel optical table. Even with electronic equipment positioned in the vicinity of the system, the performance was not significantly impacted if we kept the equipment at least 1 meter away. In other laboratory environments or medical rooms, we believe that the system is expected to perform similarly and would not require much dedicated space.

Phantom experiments

To characterize the performance of our system: brightness uniformity, field of view, resolution, geometrical distortions, and various other possible artifacts, we conducted imaging experiments with a multi-hole phantom. The phantom was made of a Plexiglas plate with 5 mm holes spaced 10 mm between centers in two perpendicular directions. In the frequency encoding direction (vertical in the figure) the phantom had 9 holes, and in the perpendicular horizontal phase encoding direction 7 holes. The phantom was filled with CuSO₄ solution with T₁ and T₂ (both equal to ~140ms) approximating the average T₁ (200 ms) and T₂ (100 ms) of hand tissues. T₂ of the phantom and hand tissues was measured by applying a multiple-echo (CPMG) sequence; T₁ was measured at both prepolarization field strength 0.1 T and measurement field 2 mT by varying the prepolarization time and the excitation delay time, respectively. The imaging parameters for the phantom are described in the method section and were the same as for hand images. A typical phantom image is shown in Fig. 5. Only one slice of the 3D phantom image is shown. This image reveals geometrical distortions and brightness variation. Initially larger brightness variation is reduced by a simple 5-point linearly interpolated adjustment of brightness in the vertical direction.

Fig. 5.

Phantom image with the same parameters as in Fig. 6. Distance between holes 10 mm. Intensity was adjusted in the vertical direction.

The brightness variation across the phantom arises from many factors. First, the rf excitation coil is not 100% uniform, due to the finite volume of the coil and the proximity of the rf shield. Second, the pick-up coil had a bandwidth comparable to the frequency spectrum of the MRI. Its Q factor is about 100 and the response has a Lorentzian profile with FWHM=820 Hz. Third, the pick-up coil shape is not a long ideal solenoid, which would provide high uniformity. It is rather short, has an rf shield surrounding it, and has an opening in the side (Fig. 2). Fourth, the echo Π/2 and Π pulses, which are hard 0.4 and 0.8 ms pulses, have a sinc-like spectral distribution comparable to MRI bandwidth which makes them non-ideal. Fifth, the inner dimension of the prepolization coil, which is a short multi-layer solenoid, is comparable to the length of the object and causes a distribution in the signal strength. Sixth, the transients due to B_p coil switching can lead to additional gradient phase encoding. Experimenting with the phantom, we found that the intensity distribution is sensitive to the position with respect to the prepolarization coil. Despite the multiple origins of brightness variation, we found that most of it can be compensated by simply adjusting the signal levels in the vertical image direction. The resulting corrected image is shown in Fig. 5. The same method was applied to hand images to improve the visibility of the finger tips.

Geometrical distortions are usually related to the non-uniformity of the field. Our NMR measurement field coil was of 33 cm diameter, so it is not surprising that over 9 cm axial length some non-uniformity was revealed. The geometrical distortions are less pronounced on anatomical images of the hand and can be in principle tolerated since relative positions of the anatomical features are most often needed (see the next section). The geometrical distortions can be reduced with better coil design or with software corrections. We have tested a new larger coil set designed for the head MRI (data will be shown in the future publication dedicated this system), and geometrical distortions have almost completely disappeared.

In addition to the analysis of artifacts, the phantom image was used to verify the resolution for the imaging parameters with which the hand image was acquired.

Hand MRI

The main purpose of the current work is the demonstration of anatomical imaging with a non-cryogenic ULF MRI system. For this we performed anatomical imaging of the human hand for proof of principle. Currently we are working on a 2-time scaled up system to image larger objects, for example the human head.

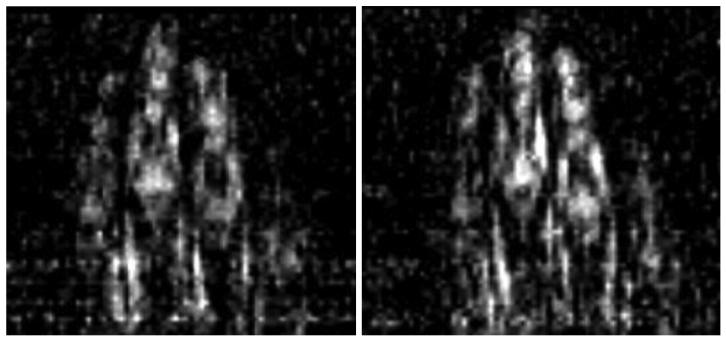
The quality of the anatomical images can be characterized by resolution, SNR, contrast, and the presence/absence of artifacts. In the case of MRI, SNR and resolution are intimately related. There is a minimal SNR level at which the image can be recognized, so the resolution can be increased until SNR reaches this threshold. The resolution defines the voxel size and SNR is proportional to the voxel volume. Because of this, the increase in the resolution for a given slice thickness scales inversely with the square of the pixel size. To understand the resolution limit of the current system, which arises from the SNR threshold and possibly other factors, we performed experiments with the goal to find the best resolution where the noise does not obscure the anatomical features. The result is shown in Fig. 6 where we present the hand image obtained with the resolution 1.5x1.5 mm², as verified with the previously described multi-hole phantom. This image is obtained with adjustment of intensity to correct the signal variation across the image in the vertical direction. This adjustment improves the visibility of the finger tips. No adjustment was done in the horizontal direction since it appears that the decrease in the intensity for the two fingers is caused by uneven slice cut with respect to the fingers' position. We suspect that geometrical distortions also played some role. It is interesting to note that SNR in the initially darker regions (e.g. top part of the image) was no worse than SNR in the brighter regions, so the adjustment did not lead to the appearance. This suggests that the bandwidth of the resonance coil is not as restrictive as can be initially assumed. A physical explanation could be as follows. The coil output for both the signal and noise is equally enhanced by resonance so that the SNR remains approximately constant in a range larger than a few FWHM from the resonance center provided the amplifier's noise is lower than noise of the coil. As we mentioned in the SNR subsection, the coil noise at resonance was about 14 nV/Hz^1/2, while the amplifier sensitivity is 4 nV/Hz^1/2.

Fig. 6.

Hand 1.5-mm resolution image: 91 encoding steps, 9 slice phase encoding steps. Left image: no average (6.7 min scan time); right image: 2 averages (13.4 min scan time); slice thickness: 5.5 mm. Intensity was adjusted to compensate the signal strength variation in vertical direction.

With 1.5 mm resolution, it can be observed that noise starts to appear; so to reduce it we performed imaging with 2 averages. Fig. 6 compares the images without and with averaging. It can be seen that additional averaging improves the quality of the image. On the left image, some dotted lines can be seen due to the coherent noise, although according to our SNR measurement we reached the intrinsic noise level of the coil and expect the image to be predominantly uniform. The coherent noise appears at specific frequencies and can, in principle, be minimized by shifting the NMR frequency to quieter regions of the spectrum and more careful shielding and grounding. The coherent noise does not appear as pronounced in the phantom images, and hence it can be traced to the antenna-effect of the hand. However, even with this noise artifact, the left figure has sufficient SNR to distinguish boundaries of anatomical tissues, and averaging further improves clarity.

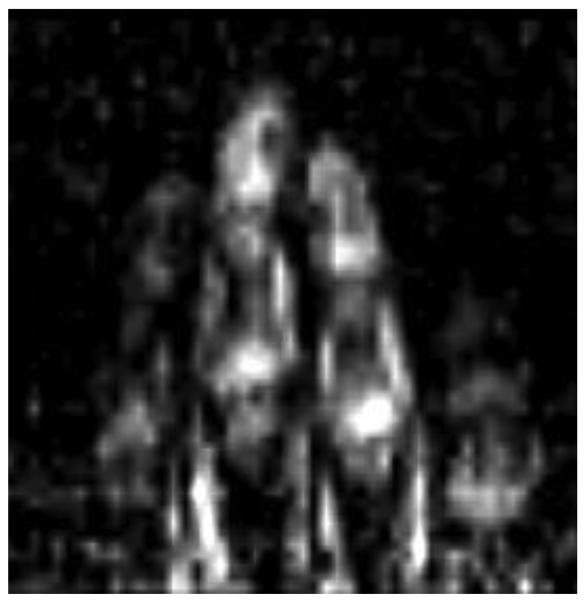
Instead of trying to increase the SNR with longer scan times, we examined the effect of higher SNR on the visibility of anatomical features by increasing the pixel size (Fig. 7). By changing the resolution from 1.5 to 2 mm we improved SNR by a factor of 1.8. With this improvement in SNR, the noise is predominantly removed from the image. This SNR can be obtained for 1.5 mm resolution with about 3 averages or in 20 minutes of acquisition. In terms of image artifacts, the variation in the intensity in the vertical direction can be successfully corrected by adjusting intensity in 5 bands of the image with linear interpolation. We did not correct geometrical distortions. Although they can be clearly seen on the phantom image (Fig. 5), it seems that on the hand image they do not significantly affect the perception of anatomical features. In the future, we would like to address the geometrical distortion issue with computational corrections and with a more carefully designed coil system.

Fig. 7.

Hand 2-mm resolution image: 65 horizontal phase encoding steps, 11 slice encoding steps, scan time 6.7 min. One most informative slice is shown. Intensity was adjusted to compensate the signal strength variation in vertical direction.

IV. Discussion and conclusion

One approach to implement ULF MRI with high sensitivity has been the use of highly sensitive magnetometers such as liquid helium-cooled SQUIDs in a shielded room [18]. The SQUID-based approach has been followed by several research groups, including our SQUID team at Los Alamos. We have made several critical demonstrations such as anatomical imaging of the brain and combined MEG-MRI in a 2-layer mu-metal shielded room [22]. However, the use of SQUIDs and the shielded room limits the applications of ULF MRI scanners due to cost and size. To make ULF MRI attractive for commercialization and wide clinical use, we set the goal to reach high NMR detection sensitivity by using non-cryogenic detectors and to remove the requirement for a shielded room to reduce the size and cost of the system. We have also explored an alternative to SQUIDs – an atomic magnetometer, which also is capable of high sensitivity [26]. Unfortunately the AM is sensitive to ambient fields and gradients and presents the difficult requirement to separate the fields and gradients needed for MRI from the sensitive operation of the magnetometer. A compromise solution was found to decouple these fields with a flux transformer (FT). However, the room-temperature FT introduced significant amounts of noise. To reduce this noise it is necessary to raise the frequency of detection [28]. While the atomic magnetometers with FTs provide benefits for a multi-channel detection, which in turn improves the sensitivity and scan time, if only a single channel is used, the FT and AM can be replaced with a resonant pick-up coil connected to a sensitive amplifier. This type of detection, conventional in MRI, would be most convenient in applications, since AMs can also add complexity and cost to the system. Before we started the work presented in this paper, the question was: would this approach lead to sufficient sensitivity and image quality?

To answer this question, we tested sensitivity and image quality with single-coil detection. To reach sufficient sensitivity for fairly good quality in a reasonable scan time, we increased the NMR frequency from 2-3 kHz to 83.6 kHz. This is still very low frequency by modern NMR and MRI standards (~100 MHz), and many of the advantages of ULF MRI remain, such as low cost, absence of susceptibility artifacts, simple design, compatibility with other equipment, portability, small space requirements, etc. However, in contrast to very low frequencies presented in the SQUID-based applications, at 83.6 kHz a thin copper rf shield can be installed inside the system to suppress and shield external noise. This noise not only decreases with frequency, but is also easier to shield with thin conductive materials to obviate the need for a large shielded room. The system becomes truly portable. The cost of a 100 kHz ULF MRI system is not expected to be high, since it is relatively easy to construct. The cost is expected to be at least an order of magnitude lower than that of any existing low-field scanner.

The images demonstrated in this paper, are not yet ultimately optimized, and work is in progress to improve SNR and resolution. One straightforward approach is to increase the prepolarization field. From the analysis of the thermal heating we found that the system presented here can be used with at least twice larger current, which would increase the field proportionally. This would, however, require a new power supply and forced air cooling of the coil for high duty cycle operation. We are also designing a different NMR measurement field coil to increase the frequency of detection to 200-400 kHz. Such higher frequencies can increase SNR about two times. The sequence itself can be optimized to reduce the loss of the signal due to T₁ and T₂ decays. Further improvement is also possible with a multi-channel detection and atomic magnetometers, as it was demonstrated with a 7-channel SQUID system. Conservative estimates indicated that with 9 detection channels SNR can be improved 3 times. However, for multi-channel detection we will need to use a multi-channel AM, with some increase in complexity. However, an overall improvement of SNR on the order of 10 should be possible, which would result in sub millimeter resolution and very fast scan time.