A rapid protein structure alignment algorithm based on a text modeling technique

Abstract

Structural alignment of proteins is widely used in various fields of structural biology. In order to further improve the quality of alignment, we describe an algorithm for structural alignment based on text modelling techniques. The technique firstly superimposes secondary structure elements of two proteins and then, models the 3D-structure of the protein in a sequence of alphabets. These sequences are utilized by a step-by-step sequence alignment procedure to align two protein structures. A benchmark test was organized on a set of 200 non-homologous proteins to evaluate the program and compare it to state of the art programs, e.g. CE, SAL, TM-align and 3D-BLAST. On average, the results of all-against-all structure comparison by the program have a competitive accuracy with CE and TM-align where the algorithm has a high running speed like 3D-BLAST.

Background

Structural comparison and alignment of proteins is a fundamental step in structural biology. It is essential that proteins with similar structures share common functionality and properties [1]. Accordingly, the tools are widely used to classify all known proteins in the databases or measure similarity of a newly discovered structure to the known classified proteins. Moreover, the tool is utilized to determine evolutionary relationships between proteins that are difficult to detect from protein sequences. Structural alignment algorithms try to find optimal correspondence between two compared structures. The techniques commonly compare geometrical coordinates of the Cα backbone atoms to find the best optimal equivalent pairs of residues. They commonly use heuristic techniques due to the complexity of the problem. Several studies have been done within the past two decades to develop algorithms for pairwise alignment [2, 3, 4] and multiple alignment [5, 6, 7]of protein structure. However, none of the introduced tools are able to guarantee the alignment optimality for any given scoring function. Recently, various studies have been reported to apply sequence alignment techniques in structural comparison and alignment of proteins. TOPSCAN [8] models protein structures in two-level topology strings and then, uses a global dynamic programming algorithm to compare these topology strings and measure the similarity score between two structures. SA-Search [9] is a web-based tool which uses a structural alphabet derived from hidden Markov model. YAKUSA [10] relies on discrete internal angles of protein backbone as a sequence and then, uses a deterministic finite automaton for multiple pattern-matching in order to locate analog fragments through a probabilistic score. 3D-BLAST [11] has the features of BLAST and applies a kappa-alpha (к, α) plot based on a structural alphabet and a new substitution matrix for rapid search of protein structure database. SARST [12] is another method that transforms protein structure into text strings through a Ramachandran map organized by nearest-neighbor clustering and regenerative substitution matrix and then, employs classical sequence similarity search algorithms. Moreover, FragBag [13] represents protein structure as a bag-ofwords of backbone fragments for quickly retrieval of structural neighbours. Finally, Lajolla [14] uses string representation of a macromolecular structure by a structure-to-string translator and a hash table to store n-grams of a certain size for searching. The common effort of the above methods is to encode protein 3D-structure in a one-dimensional linear sequence to adopt a special sequence alignment technique for alignment of two structures. This provides distinct speed advantage where the above methods are able to search large structure databases hundreds of time faster than CE [5] and TM-Align [4]. Additionally, linear encoding schemes provide facilities for multiple structure alignment, fold recognition and genomic annotation studies [12]. However, these methods are faced with a weakness of low accuracy against high accurate search tools like CE and TM-Align. Therefore, considering extensively growing protein structure databases, a linear encoding approach can be used efficiently to develop high performance structure comparison and alignment tools. In this study, we introduce a text modelling based technique for structural alignment of proteins. The method simply transforms secondary and 3Dstructure of proteins into two textual sequences and then, these sequences are used in a step-by-step text alignment procedure. The method is evaluated in a benchmark test and compared with state of the art methods. The results are evidence for high running speed of the method where its accuracy is comparable with the other well-known structure alignment methods.

Methodology

Protein Structure Modeling in Linear Sequences

Generally, proteins are the arrangement of amino acids in a linear sequence which are folded into a complex 3D-structure. Spatial coordinates of amino acids are encoded into a linear sequence called relative residue position sequence based on the relative position of each residue with respect to the position of its previous residue [15]. For each residue i, the position of C_{α i-1} is supposed to be in the origin of 3D-coordinates. Then, relative position of C_{α i} in 3D-coordinates is encoded to a letter. There are 26 different positions in 3D coordinates based on positive and negative directions of x, y and z axes. Therefore, 26 letters of alphabet are used to encode these positions [15]. For example in Figure 1, letter ‘e’ encodes the relative position of C_{α i} located around the positive direction of z-axis which satisfies |x₂-x₁|<t, |y₂-y₁|<t and z₂- z₁>0 conditions. Moreover, letter ‘s’ denotes another area with x₂-x₁>0, y₂-y₁>0 and z₂-z₁>0 conditions. Parameter t was chosen empirically at 0.1 angstrom to identify optimally different locations of a residue in 3D-coordinates. Additionally, proteins in secondary structure are constituted from highly regular substructures of α-helices and β-strands which form the backbone of a protein structure. This level of protein structure mostly is represented in a sequence of secondary structure elements (SSEs) which we call SSEs sequence.

Figure 1.

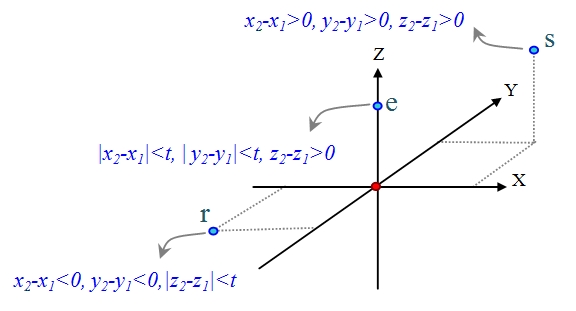
Three sample relative position of residues and their defined labels

Protein Structure Superposition

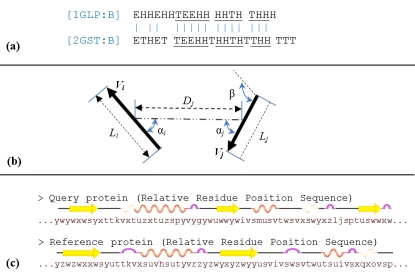
The procedure is started with an initial alignment of SSEs sequences as shown in Figure 2(a). To this end, SSEs sequence of query protein was represented via n-gram model and then, identical words from query and reference proteins were marked as matched. The size of n-gram is decreased in an iterative loop from n (empirically defined at 6) down to m (chosen at 3). The initial map of matched SSEs was revised based on geometrical properties of SSE vectors. As shown in Figure 2(b), these properties are the number of residues (chosen empirically with least 4 common residues), distance and torsion angles with the previous and next matched SSEs (chosen empirically with 2Å and 30° difference respectively at the most) and connectivity of the SSEs. A procedure now revised the list of matched SSEs and confirmed each matched pair if at least three of the above properties are satisfied. Otherwise, the algorithm looked for the next or previous unmatched SSEs to find another substitution. In the sequel, average distance and angle between the matched SSE vectors were computed and a rotation matrix was made and applied to achieve an initial overlap between two structures.

Figure 2.

Structure superposition steps between two proteins. (a) Matching SSEs sequences; (b) Refine matched SSEs based on geometrical properties; (c) Create Relative Residue Position Sequence for query and reference proteins

Structure Alignment Procedure

After initial superposition of two structures, 3D-structure of two proteins was encoded into relative residue position sequence as represented in Figure 2(c). The alignment algorithm used these sequences in the following step-by-step algorithm: (1) inside each pair of matched SSEs, pairs of identical words are located and their corresponding residues are marked as aligned. The alignment is expanded to the ends of the SSEs for pairs of residues, leaving no unaligned pair of residues between the matched ones (Figure 3). (2) For each pair of exclusively identical words from two structures, if connectivity of the aligned residues was not violated and distance of the residues was less than the maximum distance of the previous aligned residues, the corresponding residues were marked as aligned. (3) For words of the reference protein that are identical with more than a word in the query protein, their connectivity with the aligned words in previous steps was considered. Then, residues are marked of the selected matched words as aligned. Note that any number of missing residues between the identical words is ignored (Figure 4). (4) Finally, the remaining unaligned residues, specially, pair of residues located at two adjacent areas in 3D-coordinates are aligned. To this end, the above 26 defined letters are grouped into 8 different sets in Table 1 (see Table 1) based on their adjacency in 3D-coordinates. Therefore, pairs of residues with codes that belonged to a common group are aligned. In steps 2, 3 and 4, pairs of residues are not marked as aligned if they belong to different types of secondary structures.

Figure 3.

Alignment of identical words inside a pair of matched SSEs for 1GLP:B and 2GST:B PDB chains. The first and fourth lines are amino acids sequences and the second and third lines are relative residue position sequences.

Figure 4.

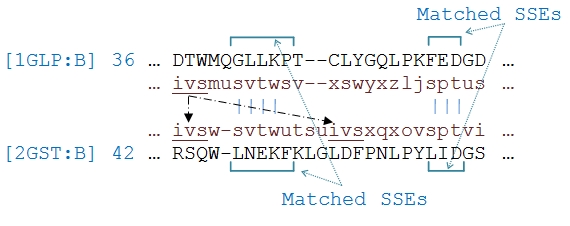
Alignment of the word ‘ivs’ from 1GLP:B PDB chain that is matched with two identical words in 2GST:B PDB chain. Considering connectivity of the aligned words, the word ‘ivs’ at position 42 of 2GST:B is aligned.

Finding Optimal Correspondence

To achieve the optimal spatial correspondence between two structures, we employed a heuristic iterative procedure based on Kabsch's rotation matrix [16]. The procedure started with the largest neighboring fragment of aligned residues and applied Kabsch rotation matrix. To select the starting fragment from a list of fragments with proximate length, the algorithm computed TM-score [17] for each item and chooses the fragment with the highest value (see supplementary material). Optimality of the procedure in selection of the starting fragment was confirmed by an experiment using 954 proteins from PDB database with less than 40% sequence identity. The results represent only 76 (8%) items with different values of TM-score suggesting an alternative choice. According to the convergence of the alignment after 3 or 4 iterations based on the above rotation matrix, the proximity of the results to the optimal alignment seemed to be enough.

Results and Discussion

To study performance of the algorithm and compare it to other well-known structure alignment tools, we used the set of 200 non-homologous protein chains that were collected by Zhang and Skolnick [4] from the PDB with range of 46 to 1058 residues in size and a pairwise sequence identity of less than 30%. We compared the results of our method to outputs from three known geometrical alignment tools, CE [5], SAL [18] and TM-align [4] which are reported by Zhang and Skolnick [4] and 3D-BLAST as a known linear encoding method. Tables 2 & 3 (see Tables 2 & 3) represent a summary of the alignments. The results are averages over all-against-all comparison of the structures. The table represents the accuracy of the alignment by RMSD, length of alignment and the coverage which is defined as fraction of residues aligned within the target protein [4]. As it can be seen from the table, the methods with higher coverage generally produce an output with lower accuracy. For instance, the highest coverage of 47.3% belongs to SAL which gives the lowest accuracy of 7.33 Å for RMSD. Also, the highest accuracy of 4.99 belongs to TM-align. The accuracy of our method ranks second after TM-align where its alignment length is less than TM-align. Moreover, our method outperforms 3D-BLAST in terms of RMSD and length of alignment. Different evaluation scores show different ranking between the methods in Table 2Table 2. Certainly, different requirements are needed for high quality of alignment by achieving a lower RMSD and a higher length of alignment. TM-score is appropriate to measure the quality of alignment that computes a reasonable balance between the accuracy and coverage parameters as defined in equation (1). The results of average TM-score in Table 2 represents that TM-align is the best. Our method is in the third rank where its value is close to SAL. The results in Table 2 are averaged over all pairs of structures in the dataset where they are collected from different protein folds. Another significant comparison is performed considering only the pair having the highest TM-score for each query protein in the dataset. The results in table 3 are averaged for all 200 query proteins and their most similar pair. In this table, our method ranks second in terms of TM-score. The last column in Table 2 shows the average processing time the CPU takes for comparison of each protein pair. The experiments are performed using a 1.26 GHz CPU for all of the methods. 3D-BLAST and our method rank first where their running speeds are about 200, 800 and 3000 times faster than TM-align, CE and SAL methods respectively.

According to the above benchmark test which evaluates and compares two linear encoding schemes and three geometrical algorithms for protein structure alignment, sequence-based methods run hundreds of time faster than the methods that use directly the geometry of protein structure. Indeed, these methods overcome the complexity of the problem by summarizing protein 3Dstructure to 1D-sequence. Moreover, our method adopts a relatively simple procedure to initially superimpose two structures and then, align them in a stepby- step algorithm. Further, the Kabsch rotation matrix is utilized to obtain an optimal correspondence between two structures which converges after 3-4 iterations. Therefore, this method is competitive, in terms of running speed, with 3D-BLAST as a quick alignment tool. Geometrical methods generally gain higher accuracy in structure alignment while compared to linear encoding methods. This is because of missing details of 3D-structure during creation of sequence from protein structure [12]. However, our method has improved accuracy in terms of TM-score which is a balance between RMSD and length of alignment. This improvement in accuracy may be obtained due to the utility of Kabsch rotation matrix to achieve optimal correspondence between two structures.

Conclusion

We have developed a text modelling technique for structural alignment of proteins. The technique firstly superimposes two structures by a procedure for matching secondary structure elements and then, encodes the 3D-structure of each protein in a sequence called relative residue position sequence. The map of matched SSEs and relative residue position sequences are submitted to a step-by-step procedure to align two structures. Moreover, to achieve an optimal correspondence between two structures, an iterative algorithm is employed based on Kabsch rotation matrix. The uniqueness of the introduced method is that it utilizes linear encoding scheme and geometrical techniques concurrently to obtain optimal alignment. Therefore, it gains the advantages of both. According to the results, the method obtains a high running speed and its precision is comparable with other high accurate tools. The current study provides evidence that linear encoding algorithms have the capability to achieve competitive accuracy with conventional structure alignment methods. However, the introduced method in this paper still has the potential to improve and develop more efficiently to solve the structure alignment problem. In future investigations, we will focus on linear encoding of secondary structure geometry to make a pure representation of protein structure in linear sequences.