Resolution of gene regulatory conflicts caused by combinations of antibiotics

SUMMARY

Regulatory conflicts occur when two signals which individually trigger opposite cellular responses are present simultaneously. Here, we investigate regulatory conflicts in the bacterial response to antibiotic combinations. We use an Escherichia coli promoter-GFP library to study the transcriptional response of many promoters to either additive or antagonistic drug pairs at fine two-dimensional resolution of drug concentration. Surprisingly, we find that this dataset can be characterized as a linear sum of only two principal components. Component one, accounting for over 70% of the response, represents the response to growth inhibition by the drugs. Component two describes how regulatory conflicts are resolved. For the additive drug pair, conflicts are resolved by linearly interpolating the single drug responses, while for the antagonistic drug pair, the growth-limiting drug dominates the response. Importantly, for a given drug pair, the same conflict resolution strategy applies to almost all genes. These results provide a recipe for predicting gene expression responses to antibiotic combinations.

INTRODUCTION

Cells respond to signals present in their environment by altering the transcription levels of their genes (Alberts, 2008; Lopez-Maury et al., 2008). Global gene regulatory responses to changes in the cellular environment have been studied for many different organisms and environments. In particular, transcriptional responses to a wide range of specific signaling molecules as well as more general signals such as nutrients, stress conditions, and drugs have been characterized in great detail (Camilli and Bassler, 2006; Davies et al., 2009; Dwyer et al., 2007; Hughes et al., 2000; Kohanski et al., 2010; Kohanski et al., 2007; Kohanski et al., 2008; Kolodkin-Gal et al., 2008; Lee et al., 2010; Mesak et al., 2010; Shaw et al., 2003). In their natural environments, cells are usually exposed to multiple signals simultaneously. Though the responses of specific genes to combinations of signals have been studied (Geva-Zatorsky et al., 2010; Kaplan et al., 2008; Kuhlman et al., 2007; Setty et al., 2003), there has not been a systematic genome-wide investigation into responses to combined signals.

The number of possible combinations of signals a cell can be exposed to is huge even if we consider only a relatively small set of signals: for a set of N different signals, the number of pair-wise combinations scales as N² while the number of possible combinations of m signals scales as N^m. In contrast, the information processing capabilities of the cellular machinery which has to detect and respond to these signals are probably rather limited. Hence, it is implausible that cells have evolved specific responses for each possible combination and each regulated gene – it is more likely that their response to a combination of signals is based on their responses to the individual signals. It is therefore possible that relatively simple, general rules connecting the cellular response to individual signals with the response to a combination of signals may exist. This possibility is highlighted by a recent study which revealed that the temporal response of 15 different protein levels in a human lung cancer cell line to combinations of anticancer drugs is a linear superposition of the individual drug responses (Geva-Zatorsky et al., 2010). However, to reveal general rules, these issues will need to be explored in a range of different model systems, including prokaryotes. Moreover, genome-wide studies of drug combination effects at fine two-dimensional resolution of drug concentration will be needed to achieve this goal. If it is indeed possible to identify rules that describe how the response to a combination of signals or drugs is determined by the responses to each of the individual signals or drugs, this could be extremely helpful in understanding complex cellular responses in situations such as apoptosis where many competing signals are often present (Gaudet et al., 2005; Janes et al., 2005; Janes et al., 2006) and for the rational design of combination therapy.

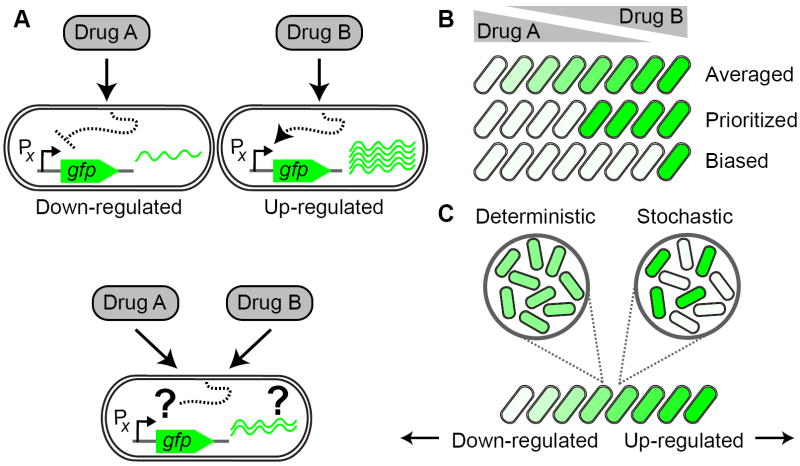
The general question we set out to address is how gene regulatory conflicts are resolved. We define a gene regulatory conflict as a situation in which a gene is regulated in opposite directions by two signals or drugs present in a combination. For example, drug A might lead to the down-regulation of a gene while drug B leads to its up-regulation (Figure 1A). The response to the drug combination will certainly depend on the ratio of the two drug concentrations, but there are many possibilities for how the two responses could be combined. For example, cells might linearly interpolate (‘average’) the conflicting individual drug responses (Figure 1B). Alternatively, they might respond to only one of the drugs, e.g. the drug that is present at the higher effective dose (‘prioritized response’, Figure 1B). The prioritized response may be biased, i.e. genes may respond exclusively to one of the drugs even when it is only present at relatively low dosage (Figure 1B, see also Geva-Zatorsky et al., 2010). Finally, it is not clear whether the entire population of cells will respond uniformly to the drug combination: for example, individual cells could decide stochastically to prioritize their response to either one of the drugs (Figure 1C).

Figure 1. How do bacteria resolve conflicts in gene regulation caused by simultaneous exposure to two different drugs?

(A) Schematic example for a conflict in gene regulation: Promoter X is down-regulated in response to drug A, but up-regulated in response to drug B. How is promoter X regulated when the cell is faced with a combination of both drugs A and B? (B) In the combination of two drugs, cells may linearly superpose the response to the individual drugs (‘averaged response’, top row) or respond only to one of the drugs while ignoring the presence of the other drug (‘prioritized response’, middle row), depending on the concentration ratio of the two drugs. In a prioritized response, both drugs may affect the cell’s response equally (middle row) or one of the drugs may have a stronger impact on the response (‘biased response’, bottom row; the response is biased towards drug A in the example shown). Down-regulation is indicated by white cell-interior, up-regulation by green. (C) At the single cell level, all cells may show the same response to the drug combination (‘deterministic response’, left) or different cells may randomly respond primarily to only one of the drugs in the combination (‘stochastic response’, right).

In bacteria, different antibiotics are known to elicit specific gene regulation programs that often affect a considerable fraction of the genome (Brazas and Hancock, 2005; Davies et al., 2006; Fajardo and Martinez, 2008; Goh et al., 2002; Kohanski et al., 2007; Kohanski et al., 2008; Linares et al., 2006; Shaw et al., 2003; Tsui et al., 2004; Yim et al., 2007). We therefore expect that many genes will be subject to regulatory conflicts in the presence of multiple different antibiotics, making this a promising model system for the investigation of conflict resolution in gene regulation. We used fluorescent reporters in Escherichia coli to measure the transcription of about 100 genes in response to a complete two-dimensional gradient of two different pairs of antibiotics which, at the level of growth inhibition, show additive and antagonistic drug interactions, respectively (Bliss, 1939; Chait et al., 2007; Loewe, 1928, 1953; Yeh and Kishony, 2007). By simultaneously measuring the effect of the drugs on growth rate we separated drug-specific effects on gene expression from nonspecific contributions through growth rate changes. We then applied Principal Component Analysis to identify characteristic ways in which cells respond to drug combinations.

RESULTS

Antibiotic combinations lead to gene regulatory conflicts

To identify conflicts in gene regulation, we first investigated the bacterial gene expression response to three different bacteriostatic antibiotics applied individually: trimethoprim (TMP), spiramycin (SPR), and tetracycline (TET; Table 1). This selection allowed us to compare pairs of drugs with similar modes of action (TET and SPR) and unrelated modes of action (TMP and SPR). We used an automated robotic system and an E. coli library of fluorescent transcriptional reporter strains (Shachrai et al., 2010; Zaslaver et al., 2006; Zaslaver et al., 2009), focusing on a genome-wide sample of 103 promoters which represent key cellular functions including metabolism, stress response, DNA repair, and ribosome synthesis (Table S1). We simultaneously measured changes in gene expression and growth rate across a range of antibiotic concentrations. The robotic system measured optical density and GFP fluorescence at multiple time points during exponential phase. We used antibiotic concentrations that slow but do not completely stop growth since our main interest here is the cellular response in conditions where key cell functions are not too severely impaired. The exponential growth rate was obtained from the increase in OD over time (Figure 2A) and gene expression level changes (γ) were obtained from the effect of the drug on the average GFP signal per OD during exponential phase (γ = [GFP/OD] / [GFP/OD]_{no drug}; Figure 2A and Experimental Procedures). These simultaneous measurements enabled us to compare the expression level of each promoter in the presence of different drugs at the same level of growth inhibition (Figure 2B).

Table 1.

Antibiotics used in this study, abbreviation, MIC of the MG1655 E. coli strain, and main mode of action.

Antibiotic	Abbreviation	MIC (μg/ml)	Mode of action
Trimethoprim	TMP	1.5	Folic acid synthesis
Spiramycin	SPR	120	Protein synthesis, 50S
Tetracycline	TET	1.5	Protein synthesis, 30S

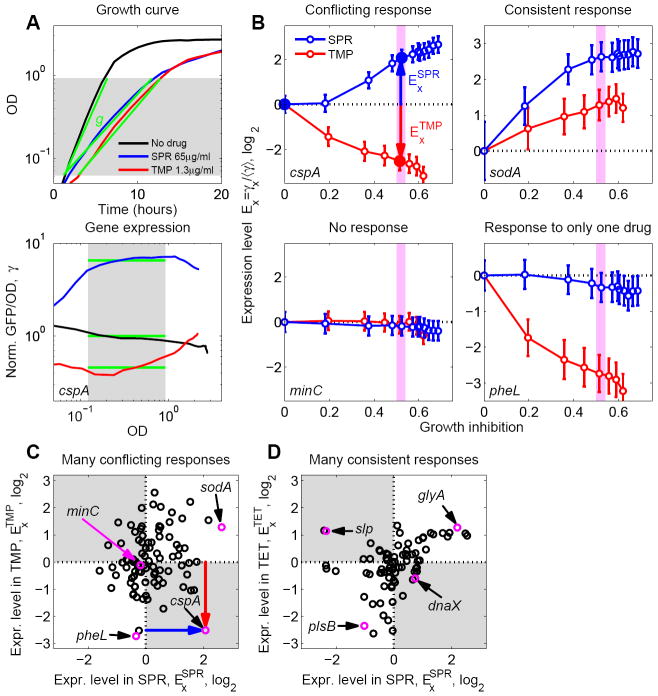
Figure 2. Gene regulation responses to pairs of antibiotics frequently show conflicts.

(A) Example data demonstrating measurement of drug effect on growth rate and transcription reporters. Optical Density (OD) and GFP expression from various promoters (shown, as an example, is the cspA promoter) are measured as a function of time for various drug concentrations. Shown are no drug (black), 65μg/ml SPR (blue), and 1.3μg/ml TMP (red). Top: Growth rates are defined by linear regression (green lines) to the OD curves. Bottom: Expression level γ (green lines) is defined as GFP fluorescence intensity per OD, averaged over an OD range of exponential growth (shaded region) and normalized to no drug control (thus γ = 1 for the no drug control). (B) Normalized expression levels E_x of example promoters cspA, sodA, minC, and pheL as a function of growth inhibition in various concentrations of SPR (blue) and TMP (red). Growth inhibition is the fraction by which the growth rate in the absence of drug is reduced. For each promoter X, E_x is defined as expression level γ_x, normalized to the median expression level ⋨γ⋩ of all promoters in the same drug concentration (Experimental Procedures). The three larger filled points for cspA correspond to the drug concentrations shown in A. The promoter cspA shows a clear regulatory conflict for these two drugs. In contrast, sodA is consistently up-regulated in response to both drugs while pheL is only regulated in response to TMP and minC shows no response to either drug. (C) Scatterplot of $E_x^{\mathit{TMP}}$ versus $E_x^{\mathit{SPR}}$ (changes in expression at inhibition level indicated by light magenta bands in panels B, g=0.45-0.5, cf. red and blue arrows in B) for a genome-wide sample of promoters (Table S1). Promoters with regulatory conflicts (e.g. cspA, magenta), are located in the gray quadrants. Promoters that respond to only one of the drugs (e.g. pheL, magenta), are located near the horizontal and vertical dotted lines. Promoters showing the same qualitative response to both drugs (e.g. sodA, magenta), are located in the white quadrants. Note that many promoters show conflicts for this drug pair. (D) As C but for TET-SPR drug combination. Most promoters lie in the white quadrants, showing that conflicts occur less frequently for this drug pair. However, some promoters show conflicts (e.g. slp and dnaX, magenta). Error-bars in (B) correspond to two standard deviations estimated from replicate measurements done on different days (Experimental Procedures).

When the responses of a given gene to different antibiotics are compared, several qualitatively different cases appear: some promoters show no response to either of the two drugs, e.g. minC which plays a role in cell division (Keseler et al., 2009) responds to neither TMP nor SPR (Figure 2B). Other promoters respond to only one of the drugs, e.g. pheL which plays a role in amino acid biosynthesis (response exclusively to TMP; Figure 2B). Promoters that respond to both drugs can show a consistent response in which the sign of the regulation (up or down) is the same for both drugs. For example, this is the case for soda which plays a role in the oxidative stress response (Figure 2B). However, there are also promoters showing conflicting responses: up-regulated by one drug and down-regulated by the other (e.g., cspA, a major cold shock protein, Figure 2B).

We next asked how frequent conflicting responses to antibiotic pairs are. To this end, we compared the gene regulation responses to antibiotics at a fixed level of growth inhibition (normalized growth rate g=0.5, Figure 2C,D, Table S1). Looking globally at the gene expression response of all promoters in our genome-wide sample, we found that conflicting responses (in which the directions of gene regulation are opposite) occur almost as often as consistent responses (in which the direction of gene regulation is the same) for the TMP-SPR drug pair (compare density of promoters in gray and white quadrants, respectively, in Figure 2C). In contrast, for the TET-SPR pair the majority of promoters shows consistent responses to both antibiotics, with a smaller number of promoters showing conflicts (e.g. slp, dnaX, Figure 2D). TET and SPR are both ribosomal inhibitors, though they act at different locations (Table 1), while TMP acts through inhibition of folic acid synthesis (folA, dihydrofolate reductase, DHFR). These observations are in agreement with the simple expectation that drugs with different modes of action might present more cases of conflicting responses.

Different promoters show a wide range of regulatory responses to antibiotic pairs

As gene expression responses to different antibiotics can differ substantially (Figure 2C), we now face the question of how cells respond when both drugs are present simultaneously. Even for promoters that do not show regulatory conflicts the response to the drug combination is unclear: do promoters which show no response to the individual drugs (e.g. minC, Figure 2B) respond to the combination? Do consistent responses, where a promoter is e.g. up-regulated in response to both drugs alone typically lead to an amplified up-regulation in the combination, as would be the case if a ‘separation of variables’ scenario applied (Kaplan et al., 2008)? To address these questions, we measured the regulatory response of our genome-wide sample of promoters to the simultaneous presence of two antibiotics. To resolve the effects of different drug concentration ratios, we set up two-dimensional drug concentration matrices on 96-well plates and determined growth rates and gene expression levels in these conditions (103 × 96 = 9,888 time curves, Figure 3A, Experimental Procedures). We performed these measurements for the antibiotic pair TMP-SPR which triggers many gene regulatory conflicts (Figure 2C) as well as the antibiotic pair TET-SPR which has fewer conflicts (cf. Figure 2C,D). These two drug pairs show different drug interactions (Bliss, 1939; Loewe, 1928, 1953): while TET and SPR show an additive interaction, i.e. their effect on growth when combined is essentially as if they were the same drug, the TMP-SPR combination shows an antagonistic interaction, i.e. at high concentrations of one drug, adding the other one has little effect on growth (Chait et al., 2007; Yeh et al., 2006).

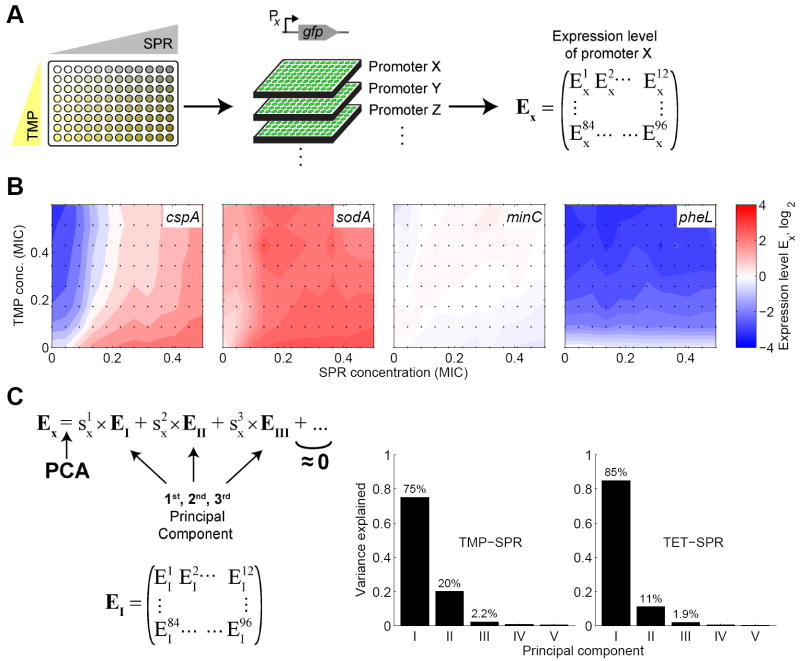
Figure 3. The gene regulation response to combinations of two antibiotics is largely explained by just two principal components.

(A) Schematic of experimental procedure for measuring gene expression responses to combinations of two antibiotics. Two-dimensional drug concentration gradients were set up on 96-well plates (left). One promoter-GFP reporter strain was grown on each plate (middle). For each condition in the two drug space, the expression level E_x is obtained as in Figure 2, yielding the matrix of expression levels E_x of promoter X. (B) Examples for different types of gene expression responses in two-dimensional concentration gradients of TMP and SPR. Expression level E_x is shown in color code: Blue indicates down-regulation, red up-regulation, and white no change in gene expression. The promoter cspA shows a conflicting response, sodA a consistent response, minC no response, and pheL responds only to TMP (cf. Figure 2B,C). In these examples, the expression level in the drug combination lies between the levels in the individual drugs which is the case for most promoters. Responses of other promoters are shown in Figures S1 and S2. Drug concentrations are in units of the Minimal Inhibitory Concentration (MIC, see Table 1). (C) Principal Component Analysis (PCA) is performed on the expression level matrices E_x, yielding the principal components (PCs) E_I, E_II,…. The scores $s_x^1,s_x^2,\dots$ capture how strongly each PC contributes to the total response of promoter X (Experimental Procedures). Bar charts: Variance explained by the first five PCs for drug combination of TMP-SPR (left bar chart) and TET-SPR (right bar chart). Most variability is explained by the 1^st PC, but the 2^nd PC is also important. Almost the entire data set is explained by the first three PCs which thus capture the most typical features of the responses of all promoters.

We observed a wide spectrum of gene expression responses to the TMP-SPR combination (Figures 3B and S1). In general, the level of promoter expression in response to a combination of drugs lies between the expression levels it shows in the individual drugs, whether the drug actions on the promoter are in conflict (e.g. cspA in Figure 3B, hdeA, cysB in Figure S1A), consistent (e.g. sodA in Figure 3B, nhaA, pykF in Figure S1B), or give no response (e.g. minC in Figure 3B, tolC, malZ in Figure S1C). For promoters which respond to only one of the drugs when applied individually, the response to the drug combination is usually similar to the response to this drug alone (e.g. pheL in Figure 3D, serA, bioB in Figure S1D). The TET-SPR drug combination shows broadly similar behavior (Figure S2).

The complete response to antibiotic combinations is explained by just few principal components

Our next goal was to identify general features of the response to these drug pairs. We used Principal Component Analysis (PCA) to analyze the response of our genome-wide sample of promoters to the antibiotic pairs. PCA exposes the main modes of responses by removing redundancy and correlated data (Halabi et al., 2009; Jolliffe, 1986; Pearson, 1901); it represents the response of each promoter as a sum of a few basic ‘principal component’ (PC) modes of response. If promoters respond in similar ways, the complete genome-wide sample of Figure 3 could potentially be represented by only few basic response modes.

We performed PCA on the gene expression response data sets for the TMP-SPR and TET-SPR drug combinations separately. In this analysis, we treated the expression levels $E_x^1,E_x^2,\dots ,E_x^{96}$ at different points in the two-dimensional drug concentration space as variables (Figure 3A,C) and each different promoter X as an observation (Experimental Procedures). For both drug pairs, we find that almost all of the variability in the data (97%) is explained by just three PCs, with the first one capturing more than 70% of the variability, the second less than 25% and the third about 2% (Figure 3C). Each gene expression response E_x to the drug combinations can therefore be presented as a linear superposition of only a few PCs: ${\mathbf{E}}_{\mathbf{x}}=s_x^1\cdot {\mathbf{E}}_{\mathbf{I}}+s_x^2\cdot {\mathbf{E}}_{\mathbf{II}}+s_x^3\cdot {\mathrm{E}}_{\mathbf{III}}+\cdots$ (where the same E_I, E_II, and E_III, are used for all promoters, Figure 3C). This reduction in the number of variables means that the complete response of each promoter to the full two-dimensional drug matrix can be specified by just three numbers or ‘scores’, $s_x^1,s_x^2,s_x^3$ – a great simplification compared to the original representation in which each promoter’s response is described by the full set of expression levels at 96 positions in the two-dimensional drug concentration space $E_x^1,E_x^2,\dots ,E_x^{96}$ (Figure 3A). Overall, this analysis revealed that the gene regulation response to antibiotic pairs has a relatively simple structure in that the responses of different promoters are largely captured by just two or three numbers.

What is the biological meaning of the first PC? Since the drugs affect growth rate which in turn systematically affects gene expression (Brauer et al., 2008; Bremer and Dennis, 1996; Fazio et al., 2008; Gonzalez et al., 2002; Hua et al., 2004; Levy and Barkai, 2009; Scott et al., 2010), we compared the different PCs with the measured growth inhibition in the two-dimensional drug treatment. We found that for both drug pairs considered here, the first PC (Figure 4A) tracks the growth rate contour in the two-dimensional drug concentration space (Figure 4B) remarkably precisely. Plotting the first PC along lines of constant growth rate shows that it is essentially constant along such growth rate isoboles (Figure 4C). This finding implies that the first PC can be approximately written as a function of only the growth rate: E_I = F(g). This observation strongly suggests that the first PC captures the physiologically determined response to growth inhibition. Thus, for the two combinations we have studied, a large part of the gene regulation response to drug combinations is explained by growth inhibition rather than the specific effects of the drugs.

Figure 4. The first principal component of the gene regulation response captures the effects of growth rate changes.

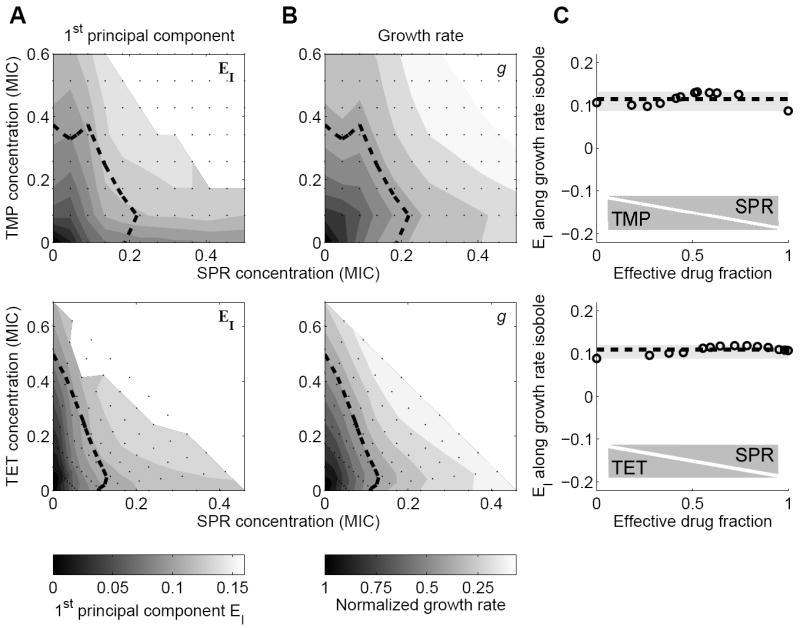
(A) First Principal Component (PC) of gene expression response to two-drug environments TMP-SPR (top) and TET-SPR (bottom). Dashed line: line of constant growth rate (normalized growth rate g=0.5). White region in top right: No data due to low growth rates (Experimental Procedures). (B) Growth rate in two-drug environments TMP-SPR (top) and TET-SPR (bottom). Note similarity to corresponding 1^st PC shown in B. (C) 1^st PC along isobole g=0.5 (dashed line in A, B) as a function of the ‘effective drug fraction’ (see Experimental Procedures for formal definition). This PC is approximately constant along isoboles, showing that the first PC simply captures a generic transcriptional response to growth rate change, which is drug-independent.

To remove growth rate dependent regulation from our analysis, we analyzed expression level changes along fixed growth rate isoboles in the two drug space. To parameterize the position along an isobole in a combination of two drugs A and B, we use a dimensionless measure – the ‘effective drug fraction’ – which measures the relative contributions of the drugs to growth inhibition (Experimental Procedures). This measure equals zero when only drug A is present, one when only drug B is present and one half when both drugs are present at concentrations leading to matched growth inhibition (Figure 4C). Using this growth independent presentation, we next focused on the 2^nd PC as well as the response of individual promoters.

Cells resolve gene regulatory conflicts by prioritizing or averaging

For both drug pairs, the 2^nd PC varies from negative to positive values along a growth rate isobole (Figure 5A,B). Such a sign change in the expression level is the defining characteristic of a regulatory conflict. Consequently, this observation suggests that the 2^nd PC captures the general way in which cells resolve gene regulatory conflicts for a specific drug pair. Thus, it describes how promoters that are down-regulated in one drug, but up-regulated in the other respond to the simultaneous presence of both drugs at different ratios. The 2^nd PC accordingly explains a larger fraction of the gene expression response for the TMP-SPR combination (20%, Figure 3C) which shows many conflicts (Figure 2C), than for the TET-SPR combination (11%, Figure 3C) which shows considerably fewer conflicts (Figure 2D).

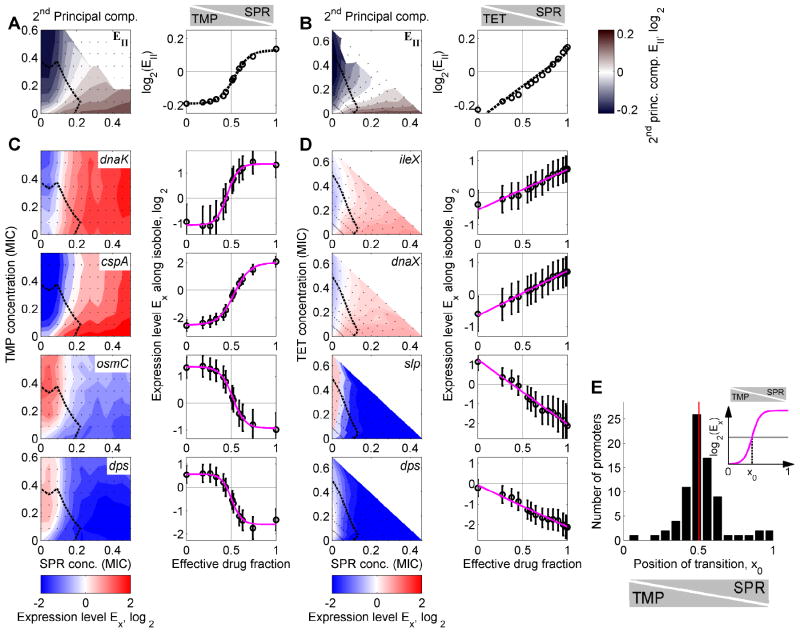
Figure 5. Bacteria resolve gene regulatory conflicts by prioritizing their response to one of the drugs or by averaging the responses to the individual drugs.

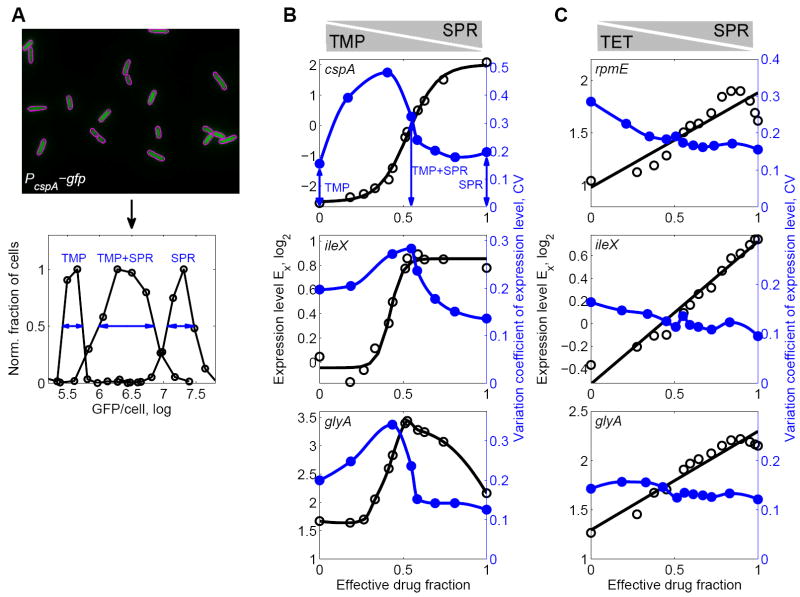
(A) 2^nd PC of the global transcriptional response to TMP-SPR in color code (left panel). Blue indicates down-regulation, red up-regulation, and white no change in gene expression. Dashed black line: Growth rate isobole g=0.5. The 2^nd PC shows a gene regulatory conflict and how it is resolved in the two-dimensional drug concentration space. Right panel: 2^nd PC along growth rate isobole g=0.5. Note the nonlinear shape of the transition; dashed black curve, sigmoidal fit (Experimental Procedures). (B) As A but for TET-SPR. Note the linear shape of the transition in the right panel; dashed black curve, linear fit (Experimental Procedures). (C) Expression levels of genes dnaK, cspA, osmC, and dps in two-dimensional drug concentration space of TMP-SPR. Gene expression levels along the growth rate isobole (dashed black line, normalized growth rate g=0.5) are shown on the right. Magenta lines: sigmoidal fits (Experimental Procedures). Conflicts in gene expression are resolved in a prioritized response, leading to a relatively sharp transition between the conflicting expression levels as TMP is continuously replaced with SPR (cf. Figure 1B). (D) As B, but for different example genes ileX, dnaX, slp, and dps, which show conflicts in the two dimensional drug concentration space of TET-SPR. Magenta lines: linear fits (Experimental Procedures). Conflicts in gene expression are smoothly averaged, leading to a linear transition between the conflicting expression levels (cf. Figure 1B). (E) Inset: Schematic of sigmoidal fits to curves from (A,C) with fit parameter x₀ characterizing the position of the transition between the two different gene expression responses. Histogram of fit results for x₀ for drug combination of TMP-SPR (Experimental Procedures). The distribution of x₀ is narrowly localized around 0.5 showing that the response of most genes is not biased towards either of the drugs (cf. Figure 1C) though a few genes are biased towards TMP (bars near x₀=1). Error-bars correspond to two standard deviations estimated from replicate measurements done on different days (Experimental Procedures).

In the TMP-SPR combination, the second PC shows a relatively sharp transition from a low to a high gene expression level when TMP is increasingly replaced with SPR at fixed growth rate (Figure 5A). This transition is not perfectly step-like but occurs in a relatively narrow region in the two-dimensional drug concentration space, dividing this space into two domains that show qualitatively different responses. These are the characteristic features of a prioritized response (cf. Figure 1B). In particular, the response to the drug combination is similar to the response to the drug that has the stronger effect on growth at each given concentration ratio. In contrast, in the TET-SPR combination, the second PC along a growth rate isobole shows a much smoother transition, well-approximated by a straight line as TET is continuously replaced with SPR (Figure 5B) – the characteristic behavior of an averaged response (cf. Figure 1B). The fact that the second component captures most of the variability in the data indicates that the solution of regulation conflicts for a given drug pair is very similar in all promoters. Indeed, almost all promoters in our genome-wide sample with clear gene regulatory conflicts show the same characteristic resolution of these conflicts: in TMP-SPR, 42 out of 44 promoters with clear regulatory conflict show prioritization, and in TET-SPR all promoters with conflicts show averaging (see Figures 5C,D and S3). Resolution of regulation conflicts is not promoter specific; it is similar across different promoters genome-wide.

Response to antibiotic pairs is rarely biased towards either of the two drugs

We next looked for individual promoters whose prioritized responses are biased towards one of the drugs (cf. Figure 1B). For the TET-SPR pair, there are no such biased responses since gene regulatory conflicts are smoothly averaged for these drugs. For the TMP-SPR pair, however, we made use of the fact that the expression level along a growth rate isobole is well-fit by a sigmoidal function for most promoters. The sigmoidal fit defines a transition point x₀ for each promoter (Figure 5E, inset; Experimental Procedures). We found that the vast majority of promoters transitions near x₀ = 1/2, where each of the drugs’ individual contribution to growth inhibition is equal (Figure 5E). Thus, the relative impact of these drugs on growth inhibition coincides with their relative impact on the gene expression response; the cells primarily respond to the drug that inhibits their growth more severely.

We did find a small number of promoters that show a regulatory response that is biased towards one of the drugs. In particular, a few promoters are almost fully biased towards TMP (bars near x₀ = 1 in Figure 5E), i.e. they show the response to TMP even if SPR is present at concentrations that have a stronger effect on growth. These promoters include hipB which controls a toxin-antitoxin system and the promoters serC, aroH, pheL, and serA (Figure S4) which all play a role in amino acid biosynthesis (Keseler et al., 2009). The only promoter in our data set that is biased towards SPR is that of the antitoxin dinJ. In summary, these observations show that most promoters show an unbiased prioritized response (i.e. they respond to the drug with the greater effect on growth), with the notable exception of some genes in amino acid metabolism which respond almost exclusively to the TMP signal.

A few promoters show combination-specific responses to antibiotic combinations

The fact that most promoters show stereotypical behaviors captured by the first two PCs enabled us to identify promoters which show responses to the two drug environment that deviate from this norm. To this end, we calculated the scores $s_x^1,s_x^2,s_x^3,\dots$ of the different PCs for each promoter (Figure 3C). These scores reflect how strongly each PC contributes to the promoter’s response. Promoters with responses that are not captured by the first two PCs have large scores for the higher PCs, such as the third PC (Figure 6A). The third PC exhibits a clear peak in the TMP-SPR drug combination, i.e. unlike the first two PCs it describes expression levels in the drug combination that do not fall between the expression levels in the individual drugs (Figure 6B). This observation suggests that the third PC captures the drug combination-specific response of promoters whose expression levels in the drug combination lie outside the range bounded by the expression levels in the individual drugs. Indeed, promoters with a large score for the third PC show such drug combination-specific responses (Figures 6C,D and S5A).

Figure 6. A few promoters show a specific response to the drug combination in which the expression level does not lie in between the two responses to the individual drugs.

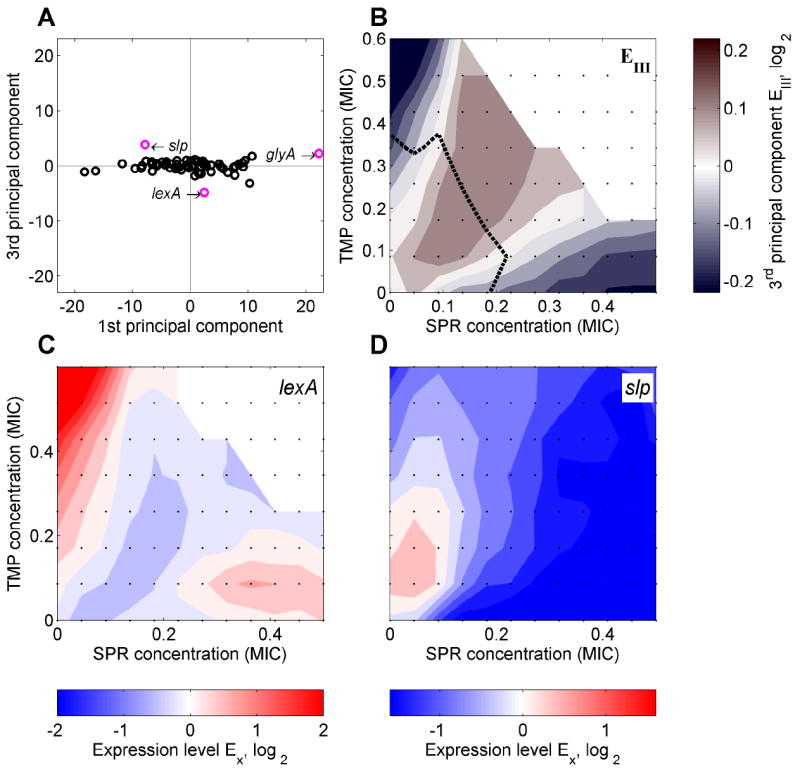
(A) Scatterplot of scores of the 3^rd versus those of the 1^st PC for TMP-SPR drug combination. While the 3^rd PC contributes relatively little to the response of most promoters (cf. Figure 3C), it plays an important role for a few promoters (including lexA, slp, and glyA; highlighted in magenta). (B) 3^rd PC in two-dimensional drug concentration space of TMP-SPR shown in color code. The 3^rd PC has a clear peak in the drug combination. The few promoters which show higher or lower expression levels in response to the drug combination than in response to either of the individual drugs are captured by this component. (C,D) Promoters lexA (C) and slp (D) which have a relatively large 3^rd PC score (A) indeed show lower (C) or higher (D) expression levels in the drug combination. For glyA, see Figure S5A.

An example is the lexA promoter which controls transcription of the master regulator of the DNA damage (‘SOS’) response (Walker, 1996). This promoter is up-regulated in response to TMP (Mesak et al., 2008; Walker, 1996) and slightly up-regulated in response to SPR, but shows no up-regulation or even a slight down-regulation in the drug combination (Figure 6C). This observation could be explained by the idea that adding translation inhibitors like SPR to TMP leads to a reduction in the amount of DNA damage in the cell. Another interesting case is slp, a promoter known to respond to starvation conditions (Keseler et al., 2009): slp is down-regulated in response to SPR and slightly down-regulated at higher concentrations of TMP, but shows up-regulation in a combination of both drugs (Figure 6D). The fact that this promoter is regulated by multiple transcription factors (GadW, GadX, and possibly MarA) suggests that such drug combination-specific responses usually require the integration of more than one regulatory input. Consistent with this view the glyA promoter, which shows a combination-specific response (Figures 6A, S5A), is regulated by two different transcription factors (PurR and MetR; Keseler et al., 2009). This view is further supported by the fact that the only promoter which shows a combination-specific response to the TET-SPR combination (uspA, Figure S5B) is also regulated by two different transcription factors. In summary, we found that only few promoters do not strictly follow the general rule set by the 1^st and 2^nd PCs but instead show drug combination-specific responses. These promoters often have multiple transcriptional regulatory inputs. Identifying such genes and their regulation may be important to advance our understanding of cellular responses to drug combinations.

Increased cell-to-cell variability in gene expression occurs at the transition point of a prioritized response

We have shown that cells can average the responses to individual drugs in a drug combination (Figure 5B,D). However, this averaged response was observed at the population level and could in principle be due to a stochastic response at the single-cell level (Eldar and Elowitz, 2010; Gefen and Balaban, 2009; Gefen et al., 2008; Rotem et al., 2010) in which different subpopulations of cells randomly show the response to either one of the two drugs (cf. Figure 1C). To fully discriminate between different possible response strategies to drug combinations (Figure 1), we need to investigate cell-to-cell variability in gene expression responses. To this end, we measured transcriptional responses to drug combinations in single cells. Specifically, we integrated ten GFP transcriptional reporters (Zaslaver et al., 2006) into the E. coli chromosome to avoid noise caused by plasmid copy number variability (Elowitz et al., 2002; Freed et al., 2008; Experimental Procedures). We selected promoters that show clear regulatory conflicts in either the TMP-SPR or the TET-SPR drug combination (Figure 5C,D), but also a few promoters that show no clear conflicts, or unusual behaviors (Figure 6, Table S1). We then grew these strains in two-dimensional concentration gradients of either TMP-SPR or TET-SPR (Figure 3A), imaged cells at a fixed time point, and quantified single cell GFP fluorescence using automated image analysis (Figure 7A, Experimental Procedures). For each promoter, we sampled at least eight different drug conditions which reflect different drug ratios at fixed growth inhibition.

Figure 7. Prioritized response coincides with increased cell-to-cell gene expression variability in the drug combination.

(A) Top: GFP fluorescence from E. coli cells. In this example, GFP is driven by the cspA promoter. Magenta outlines show segmentation (Experimental Procedures). Bottom: Histogram of GFP intensities per cell in TMP alone (left), SPR alone (right) and the combination of TMP-SPR (middle). While the distributions of gene expression levels are unimodal in all conditions, a much wider distribution is observed when TMP and SPR are present simultaneously (blue arrows). (B) Population average measurements of expression level E_x (black circles) along growth rate isobole g = 0.5 as in Figure 5C, for promoters cspA, ileX, and glyA in TMP-SPR drug combination. Black lines are sigmoidal fits (cf. Figure 5) except for glyA where black line shows cubic spline. Blue circles show variation coefficient of GFP/cell along a similar growth rate isobole. The coefficient of variation (CV) is a measure of the relative cell-to-cell variability in gene expression and defined as the empirical standard deviation of GFP/cell (shown in A) divided by its mean (Experimental Procedures). Blue lines are cubic splines. Gene expression cell-to-cell variability peaks in drug combination near the point where a sharp transition between two different responses occurs. (C) As B but for TET-SPR showing promoters rpmE, ileX, and glyA which have regulatory conflicts in this drug combination. Note that gene expression cell-to-cell variability does not peak in the drug combination.

We found unimodal distributions of expression levels in all conditions. This observation indicates that bimodal stochastic responses to drug combinations (Figure 1C) are rare, even when the drugs elicit conflicting responses. Hence, our analysis of population level measurements (Figures 2-6) does not suffer from this potential complication. Importantly, for promoters which show a prioritized response to the TMP-SPR combination, we found that expression level cell-to-cell variability, measured by the variation coefficient, often has a clear peak in the drug combination (Figure 7B). This peak is located near the point where a sharp transition in gene expression level occurs (Figure 7B). Near such a sharp transition, small fluctuations in the detection of the drugs by bacteria (‘input noise’; Tkacik et al., 2008) may be amplified to yield large fluctuations in gene expression level (‘output noise’). This role of input noise offers a plausible explanation for the observed increase in cell-to-cell gene expression variability at the boundary between the two sharply separated response domains in the two-dimensional drug space. Consistent with this view, cell-to-cell variability did not exhibit peaks for any promoter showing a conflict in the TET-SPR combination where conflicts do not lead to sharp transitions between the different expression level states but are smoothly averaged (Figure 7C). These observations provide further support for our conclusion that gene regulatory conflicts lead to two sharply separated response domains in the TMP-SPR drug combination while they are smoothly averaged in the TET-SPR combination.

DISCUSSION

We found that regulatory conflicts in which a gene is up-regulated in response to drug A and down-regulated in response to drug B (Figure 1) play a key role in the bacterial gene regulation response to combinations of antibiotics. Such conflicts occur for many genes, in particular when the two drugs have different modes of action (Figure 2). Using PCA, we found that over 70% of the gene regulation response to antibiotic combinations can be explained simply as a response to the growth rate change caused by the drugs (Figures 3 and 4). Importantly, the remainder of the response is almost entirely captured by generic ways of gene regulatory conflict resolution in a given drug combination: (a) Cells can linearly superpose (‘average’) the responses to the individual drugs, or (b) they can ‘prioritize’ their response to one of the drugs and essentially ignore the presence of the other drug (Figure 5, cf. Figure 1). Which mode of conflict resolution is used depends on the drug pair, but applies to virtually all genes that show conflicting regulation. Only few genes show responses to drug combinations that are not explained by growth rate effects and conflict resolution alone (Figure 6). Finally, for the prioritized response, we found that the cell-to-cell variability in gene expression peaks when both drugs are present, at the location in two-drug space where the cells switch their response from one drug to the other (Figure 7). Together, these results show that there are relatively simple, general relations between the transcriptional responses to drug combinations and those to the individual drugs.

It is striking that just two PCs largely explain the bacterial response to antibiotic combinations. While these PCs generally have non-trivial shapes that depend on the drug pair, only two numbers (scores) suffice to characterize the complete response of a given promoter once the PCs are known (Figure 3C). The first score $s_x^1$ quantifies how strongly promoter X responds to growth rate changes. The second score $s_x^2$ measures the extent to which the promoter shows the drug pair stereotypical conflict resolution. The fact that these two numbers are enough to capture the response of most promoters implies that the full response matrix to the two-drug environment can be predicted from a relatively small number of measurements: once the first two PCs for a given drug pair are identified (which can be done by measuring the gene expression response to the full two drug environment for a relatively small number of genes), three measurements (e.g. no drug, single dose of drug A, and single dose of drug B) would suffice to determine the first two scores $s_x^1$ and $s_x^2$ for that gene. From these scores, a prediction for the expression levels across the entire two drug space can be readily calculated. Hence, our results provide a way to predict the transcriptional response to a drug combination for most genes from their response to the individual drugs.

A notable observation we made is that the response of the vast majority of genes is not biased towards either of the drugs (cf. Figure 1B): the transition between the two sharply separated response domains of a prioritized responses occurs almost exactly at the point where growth inhibition by both drugs (TMP and SPR) is equally strong (Figure 5E). Interestingly, these two drugs have an antagonistic/buffering effect on growth (Bollenbach et al., 2009; Chait et al., 2007), i.e. adding one drug at low concentration when the other one is present at higher concentration does not lead to a decrease in growth. These observations are consistent with a simple scenario in which the cells’ response is primarily determined by (a) the overall growth inhibition (first PC) and (b) the drug that limits their growth (second PC). If present, the third PC may describe promoters that show specific responses to both drugs, including the drug that does not limit growth. While this picture appears plausible, more work will be needed to elucidate the mechanism that underlies the observed strategies of conflict resolution. Specifically, one could measure the levels of factors that act upstream of promoters (such as guanosine tetraphosphate, ppGpp) in two-drug environments. In addition, one could study the effects on conflict resolution of targeted genetic manipulations which affect such global regulators (e.g. relAspoT deletions).

Moreover, it will be interesting to investigate the questions addressed in this article for a large set of different drugs with a range of different cellular targets (including DNA replication, cell wall synthesis, translation; Walsh, 2003), and different pair-wise drug interactions (additive, synergistic, antagonistic; Bliss, 1939; Loewe, 1928, 1953; Yeh et al., 2006). Further, it is promising to extend our investigation to much higher drug concentrations of both bacteriostatic and bactericidal drugs. This approach would help to identify which types of drug pairs lead to conflict resolution by averaging, which ones to prioritizing, and if there are drug pairs that trigger yet other behaviors. Such a comprehensive data set might allow us to reveal a general relation between the drug interaction or mechanism similarity and the cellular strategy for the resolution of regulatory conflicts in the combination.

The approach presented here, in particular the principal component analysis of gene expression responses to drug combinations, is generally applicable to other organisms, including yeast and human cancer cell lines, different types of drugs, and to combinations of more than two drugs. Extending our approach to yeast would be relatively straightforward since similar tools for fluorescence based transcriptional measurements (Huh et al., 2003) and drugs with similar mode of action are available. In other model systems GFP-reporter libraries covering a considerable part of the genome may have to be constructed first (Cohen et al., 2008). Alternatively, other methods for genome-wide measurements of mRNA or protein levels could be adapted to extend the approach described here to other systems. Independently of methodology, it will be interesting to see to what extent the behaviors identified in this study extend to other systems. It is quite possible that eukaryotes, in which transcriptional regulation is more complex than in prokaryotes, may resolve gene regulatory conflicts in new, unexpected ways. The long-term prospect of predicting the cellular response to a multi-drug treatment from the responses to the individual drugs may lay the foundation for controlling cellular gene expression by targeted combinations of drugs (Geva-Zatorsky et al., 2010). In particular, multi-drug combinations may be designed in ways that exploit gene regulatory conflicts to restore a healthy cell state in human tissues, to circumvent cellular defense strategies, or slow down the evolution of drug resistance in chemotherapy.

EXPERIMENTAL PROCEDURES

Media, strains, and drugs

Experiments were conducted in M9 minimal medium with 0.4% glucose as carbon source and 0.2% amicase. Drug solutions were made from powder stocks, filter-sterilized, stored at -20°C in the dark and added as indicated. All strains used were derived from E. coli K-12 strain MG1655. Promoter-GFP constructs for cspA, rmf, rpmE, dps, glyA, slp, recA, rrsA, wrbA, and ileX (Zaslaver et al., 2006) were integrated into the attTn7 locus of strain MG1655 as described (McKenzie and Craig, 2006). We used primers ggggaccactttgtacaagaaagctgggtccgattctgataacaaactagcaacacc and ggtgaagacgaaagggcctcgtagagcctgcttttttgtacaaacttgtcccc for PCR, and BP Clonase (Invitrogen) to move promoter-GFP constructs into the delivery plasmid pGRG37. This plasmid was slightly modified such that the cloning reactions could be performed with BP Clonase and attB-flanked PCR products. Wild type MG1655 were transformed with this plasmid. Integrations at the attTn7 site were verified by colony PCR using primers gatgacggtttgtcacatgga and cccctatagtgagtcgtattacatgg. Curing of the delivery plasmid in final strains was verified by testing for ampicillin sensitivity.

Growth rate and gene expression assay

Overnight cultures were diluted ~200-fold and grown on an automated robotic system (Caliper) at 30°C with rapid shaking in 96-well microtiter plates (Costar) containing 200μl medium per well. Absorbance at 600nm (A₆₀₀, proportional to optical density OD₆₀₀ via OD₆₀₀ = 3.1 A₆₀₀) and GFP fluorescence were recorded by a plate reader (Victor III, Perkin-Elmer) at intervals of 35-55min for 24h, and background subtracted. Growth rates were calculated using Matlab (The MathWorks) by linear regression of log(OD₆₀₀) (Matlab function ‘regress’) during exponential growth (0.02<A₆₀₀<0.3). The measurement error was evaluated as the 95% confidence interval of the linear regression and was typically well below 10%. The growth rate at each drug concentration was obtained as the median growth rate over the whole set of GFP reporter strains measured in identical drug conditions. MIC was defined as the lowest concentration at which background subtracted A₆₀₀ did not exceed 0.02 after 24h.

GFP background of GFP reporter strains was subtracted as previously described (Zaslaver et al., 2006). We defined the expression level as the mean GFP/A₆₀₀ in the interval 0.04<A₆₀₀<0.3 (Figure 2A). Only promoters with a clearly detectable GFP signal were used for analysis, reducing the total number to 93 promoters (Figure 2C,D). Expression level changes γ relative to the drug-free control were normalized to the median expression level change ⟨γ⟩ of all promoters in the same drug environment. Changes in the median expression level of all promoters reflect non-specific effects such as pH changes or changes of the reporter plasmid copy number. We previously verified that the effect of plasmid copy number on the measured expression level is independent of the GFP promoter (Bollenbach et al., 2009). Error-bars in Figures 2, 5, S3, and S4 were calculated from day-to-day variability of replicate measurements as previously described (Bollenbach et al., 2009). The white regions in the top right of panels that show promoter expression in two-dimensional dug environments (Figures 4, 5, 6, S1, S2, S3, and S5) reflect no data due to low growth rates or drug concentrations not sampled.

Two-dimensional drug concentration matrices were set up on 96-well plates (see black dots in Figure 4A for concentrations used). Expression levels along growth rate isoboles were calculated by linear interpolation using Matlab functions ‘griddata’ (for the TET-SPR data set) and ‘interp2’ (for the TMP-SPR data set). The ‘effective drug fraction’ (Figures 4C, 5, and 7B,C) is defined as I_SPR/(I_TMP + I_SPR) where I_D is the relative growth inhibition at the same concentration of drug D alone: I_D = 1 − g with the normalized growth rate g. Linear fits shown in Figures 5B,D, 7C, and S3B were performed by fitting the function f (x) = mx + b to the data with m and b as fit parameters using Matlab function ‘fit’. Sigmoidal fits were performed by fitting the function g(x) = h tanh((x − x₀) / w)+r to the data, using x₀, w, h, and r as fit parameters in Matlab function ‘fit’. Here, x₀ is the position of the transition (Figure 5E, inset), w is a measure for the width of this transition, h measures the magnitude of gene regulatory conflict, and r reflects the expression level change due to growth rate. Only promoters with R² > 0.8 were used in the analysis of sigmoidal fits (Figure 5E). Lower values of R² typically occurred for promoters with no regulatory conflict, such that a sigmoidal fit to a constant expression level along the growth rate isobole did not yield meaningful results for the fit parameters x₀ and w.

Single cell fluorescence microscopy assay

Cultures of chromosomally integrated promoter-GFP reporter strains were grown to A₆₀₀ ~ 0.14, mounted on agar pads, and imaged (GFP fluorescence and phase contrast). For each reporter strain the exposure time was adjusted to ensure that the highest signal was well below detector saturation. Several hundred cells of each reporter strain were imaged in 8 to 11 different drug conditions and background fluorescence was subtracted. Images were segmented automatically using custom Matlab code (Figure 7A) and manually verified. GFP fluorescence per cell (Figure 7) was defined as the maximum GFP intensity detected in the area of each cell (using the mean or median GFP intensity yielded similar results).

Principal component analysis (PCA)

PCA was performed on the expression level matrices E_x, treating the expression levels at all positions in the two dimensional drug concentration space as variables and the corresponding expression levels of the different promoters at these positions as observations (Figure 3C). PCA was performed independently on the TMP-SPR and TET-SPR data sets using Matlab function ‘princomp’. Only promoters with a clearly detectable GFP signal were used for PCA (Table S1). Only drug concentrations at which data was available for all promoters were used in PCA (at high concentrations of both drugs some reporter strains did not reach sufficiently high OD values).

HIGHLIGHTS.

• Transcriptional response to drug combinations is explained by only two principal factors

• Cells resolve regulatory conflicts in drug combinations by ‘averaging’ or ‘prioritizing’

• Few promoters show combination-specific responses to antibiotic combinations

• Cell-to-cell variability in gene expression can be increased in regulatory conflicts