Computational Intelligence in Early Diabetes Diagnosis: A Review

Abstract

The development of an effective diabetes diagnosis system by taking advantage of computational intelligence is regarded as a primary goal nowadays. Many approaches based on artificial network and machine learning algorithms have been developed and tested against diabetes datasets, which were mostly related to individuals of Pima Indian origin. Yet, despite high accuracies of up to 99% in predicting the correct diabetes diagnosis, none of these approaches have reached clinical application so far. One reason for this failure may be that diabetologists or clinical investigators are sparsely informed about, or trained in the use of, computational diagnosis tools. Therefore, this article aims at sketching out an outline of the wide range of options, recent developments, and potentials in machine learning algorithms as diabetes diagnosis tools. One focus is on supervised and unsupervised methods, which have made significant impacts in the detection and diagnosis of diabetes at primary and advanced stages. Particular attention is paid to algorithms that show promise in improving diabetes diagnosis. A key advance has been the development of a more in-depth understanding and theoretical analysis of critical issues related to algorithmic construction and learning theory. These include trade-offs for maximizing generalization performance, use of physically realistic constraints, and incorporation of prior knowledge and uncertainty. The review presents and explains the most accurate algorithms, and discusses advantages and pitfalls of methodologies. This should provide a good resource for researchers from all backgrounds interested in computational intelligence-based diabetes diagnosis methods, and allows them to extend their knowledge into this kind of research.

Abbreviations: ADAP - adaptive learning routine; ANFIS - artificial neuro-fuzzy inference system; ANN - artificial neural network; ARTMAP - adaptive resonance theory mapping; ARTMAP-IC - adaptive resonance theory mapping instance counting; BPNN - back-propagation neural network; CART - classification and regression trees; CART-DB - classification and regression trees distribution-based; ESOM - evolving self-organizing maps; FIS - fuzzy inference system; GCS - growing cell structure; GDA - generalized discriminant analysis; GNG - growing neural gas; GRG2 - generalized reduced gradient 2; GRNN - general regression neural network; k-NN - k-nearest neighbor; LDA - linear discriminant analysis; LM - Levenberg-Marquardt; LS-SVM - least square support vector machine; LVQ - learning vector quantization; ME - mixture of experts; MEA - multimodal evolutionary algorithm; MFNNCA - modified feed forward neural network constructive algorithm; MKS - multiple knot spline; MLP - multi-layer perceptron; MLPNN - multi-layer perceptron neural network; MLNN - multilayer neural networks; MME - modified mixture of experts; NFIS - neuro-fuzzy inference system; NG - neural gas; NHANES - National Health and Nutrition Examination Survey; PC - principal components; PCA - principal component analysis; PID - Pima Indian diabetes dataset; PNN - probabilistic neural network; RBF - radial basis function; SOM - self-organizing map; SSVM - smooth support vector machines; SVM - support vector machine; UCI - University of California, Irvine

Introduction

Diabetes has been recognized as a continuing health challenge for the twenty-first century, both in developed and developing countries. It is understood that diabetes prevalence is increased because of modern lifestyles, urbanization, and economic development [1]. It is a global problem with devastating human, social, and economic impact, affecting around 300 million people worldwide [2].

Type 2 diabetes is a chronic disease that occurs either when the pancreas does not produce enough insulin, or when the body cannot effectively use the insulin it produces. It is frequently asymptomatic [3]. Although detection is improving, the delay from disease onset to diagnosis may exceed 10 years [4]. To diagnose diabetes, a physician has to analyze many factors. Undoubtedly, the evaluations of data obtained from patients and expert decisions are critical for diagnosis. However, factors such as lack of experience by the experts, or their fatigue, may lead to erroneous diagnosis. Early intervention with lifestyle modifications or pharmacotherapy has been shown to effectively delay or prevent type 2 diabetes and its complications in adults [5].

For prevention of type 2 diabetes, a comprehensive guideline was issued specifying lifestyle changes [6]. Various strategies have also been put forward to reduce diabetes risk [7]. Naturally, prevention is preferable, but current treatment methods are not yet fully adequate to reach this goal. Hence, there is a growing need for early detection of diabetes. To address this need, and to provide more detailed and rapid analysis of medical data, risk assessment tools and their various algorithms have been widely investigated.

For early detection of diabetes, various risk scores have been devised. A detailed survey of these tools with their specificity and sensitivity has been provided by Schwarz et al. in which the authors found the Finnish Diabetes Risk Score as the most convenient tool for early diagnosis of diabetes [8]. However, as this method involves human intervention in deciding criteria and score, it may by be exposed to the human error. Therefore, machine learning and statistical pattern recognition has been the subject of tremendous interest in the biomedical community as these approaches offer promise for improving the sensitivity and/or specificity of detection and diagnosis of disease. At the same time, these approaches reduce the potential for human error in the decision making process [9]. In particular, further development of methods that explicitly incorporate prior knowledge and uncertainty into the decision-making process would be very important for diabetes detection. Extensive studies by many researchers have demonstrated higher performance and accuracy in predicting clinical outcomes of diabetes diagnosis using neural network strategies (Table 1). Advantages and pitfalls of using various algorithms in diabetes prediction are listed in Table 2.

Table 1. Artificial intelligence approaches for early diabetes detection.

Legend: PID: Pima Indian dataset. MFNNCA: modified feed forward neural network constructive algorithm. GRG2: generalized reduced gradient 2. ANFIS: adaptive neuro-fuzzy inference system. GRNN: general regression neural network. MLP: multi-layer perceptron. RBF: radial basis function. ARTMAP-IC: adaptive resonance theory mapping instance counting. MEA: multimodal evolutionary algorithm. ESOM: evolving self-organizing maps. GNG: growing neural gas. GCS: growing cell structure. k-NN: k-nearest-neighbor. CART: classification and regression trees. LVQ: learning vector quantization. LDA: linear discriminant analysis. CART-DB: classification and regression trees distribution-based. SVM: support vector machine. SSVM: smooth support vector machine. MKS-SSVM: multiple knot spline smooth support vector machine. GDA: generalized discriminant analysis. LS-SVM: least square support vector machine. PCA-ANFIS: principal component analysis and adaptive neuro-fuzzy inference system. LDA-ANFIS: linear discriminant analysis and adaptive network based fuzzy inference system. C4.5: sample class 4.5 algorithm. MLPNN: multi-layer perceptron neural network. ME: mixture of experts. MME: modified mixture of experts. See [15-17, 23, 25, 27, 38, 44, 47, 49, 51, 52, 53, 54, 55, 56]

Table 2. Advantages and disadvantages of algorithms commonly used in diabetes prediction.

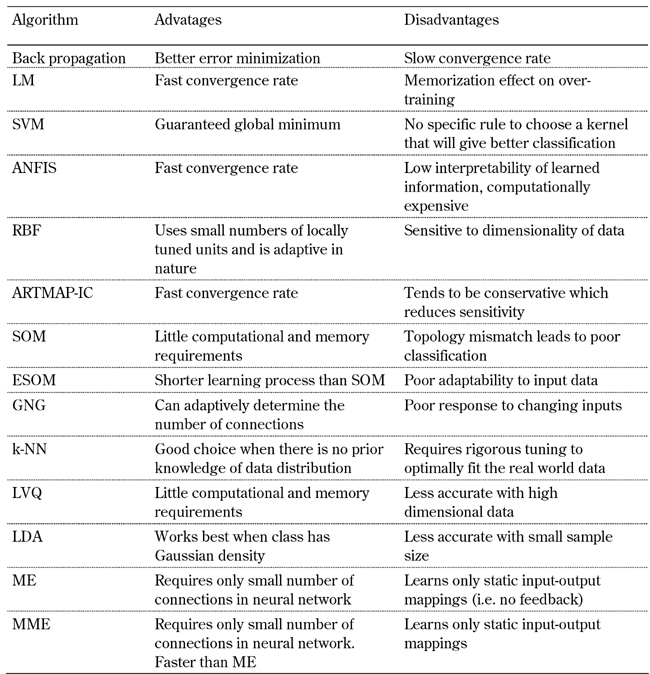
Legend: SVM: support vector machine. ANFIS: adaptive neuro-fuzzy inference system. RBF: radial basis function. ARTMAP-IC: adaptive resonance theory mapping instance counting. SOM: self-organizing maps. ESOM: evolving self-organizing maps. GNG: growing neural gas. k-NN: k-nearest-neighbor. LVQ: learning vector quantization. LDA: linear discriminant analysis. ME: mixture of experts. MME: modified mixture of experts.

Datasets for diabetes diagnosis

Significant work has been reported on Pima Indian diabetes datasets (PID). These studies applied different methods to the given problem, and achieved high classification accuracies using the dataset taken from the University of California, Irvine (UCI) machine learning repository [10]. This database provides a well validated data resource to explore the prediction of diabetes. The eight variables in the dataset include:

- number of times pregnant,

- plasma glucose concentration at 2 hour in an oral glucose tolerance test,

- diastolic blood pressure (mmHg),

- triceps skin fold thickness (mm),

- 2-h serum insulin (IU/ml),

- body mass index (weight in kg/height in m),

- diabetes pedigree function, and

- age (years).

While PID is one of the mostly used datasets for prediction of type 2 diabetes, some researchers prefer to investigate diagnosis using data from hospitals, and to incorporate their own parameters of interest. Kazemnejad et al. used the Tehran Lipid and Glucose Study dataset which consists of variables like age, body mass index, waist-to-hip ratio, gender, history of hyperlipidemia, and history of hypertension [11]. In another study conducted by Dey et al. on data of 530 patients from Sikkim Manipal Institute of Medical Sciences, risk factors such as random blood sugar test results, fasting blood sugar test results, post plasma blood sugar tests, age, sex, and occupation were taken into account [12].

The third National Health and Nutrition Examination Survey (NHANES III, http://www. cdc.gov/diabetes/) dataset resulted from a survey conducted on a US population. The eighteen variables identified as important for diabetes risk prediction include body mass index, height, weight, waist circumference, waist-to-hip ratio, age, sex, race/ethnicity, taking blood pressure medication, taking cholesterol medication, gestational diabetes, high blood pressure, high cholesterol, history of diabetes (any blood relative), history of diabetes (parent or sibling), history of diabetes (parent), history of diabetes (sibling), and exercise [13].

Data analysis through logistic regression

Logistic regression can be applied when the data consist of a binary response and a set of explanatory variables [14]. At first, the maximum likelihood estimates for the parameters of the logistic regression model are estimated using an iteratively reweighted least squares algorithm. Then, it is possible to calculate the predicted probability of an individual having diabetes by using the following logistic function:

Θ = 1⁄(1 + e^{-(β₀ + β₁x₁ + β₂x₂ + ... + β_nx_n)})

Here X is a vector of variables and β is the regression coefficient estimated by using maximum likelihood methods. Shanker applied logistic regression on eight variables in PID and obtained a significant accuracy of 79.17% [15]. Statistically least significant (at 0.05 level) variables were deleted sequentially in the training sample. Logistic regression with the remaining four statistically significant parameters, e.g. number of times pregnant, glucose tolerance test, body mass index, and diabetes pedigree function, resulted in an overall classification accuracy of 80.21%. Heikes et al. have developed a diabetes risk calculator tool based on logistic regression function to identify people at high risk of diabetes [13]. It was built upon NHANES III dataset with a sensitivity of 75%.

Clustering techniques

Most quality prediction models are based on clustering techniques that make use of k-means, mixture-of-Gaussians, self-organizing map (SOM) and neural gas (NG) for diagnosis. According to the k-nearest neighbor (k-NN) algorithm, a new input pattern x is assigned to the class voted by the majority of its k-nearest training patterns [16]. The weight change in k-NN is given by:

ΔW_j = f(x) = γ(X - W_j), if j = i(X), 0 otherwise

where γ is the learning rate and i(x) is the winning node. While the accuracy of k-NN on diabetes detection problem ranges between 71-78% [16, 17], a more sensitive performance with accuracy of 92.38% was achieved with a hybrid model of k-NN and C4.5 algorithms [18, 19].

SOM is a sheet-like artificial neural network (ANN). Cells of this ANN become specifically tuned to input patterns [20]. In order to overcome the topology mismatches that occur with the original SOM algorithm, and to achieve an optimal use of the neurons, the geometry of the lattice has to match with the data manifold. For this purpose, several so-called growing (incremental) SOM algorithms have been developed. The growing neural gas (GNG) algorithms start with two randomly placed, connected neurons [21]. After a fixed number of time steps, the neuron i with the largest accumulated error is determined, and a new neuron inserted between i and one of its neighbors. It does not require predetermination of the neuron quantity or topology of structure to be used. It starts with a minimal neuron structure that is incremented during training until it reaches a maximum number limit for clusters defined by the user.

The growing cell structure (GCS) algorithm assumes a fixed dimensionality for the lattice [22]. It is well suited for generating a dimensionality-reducing mapping from the input space to the lattice space. Deng and Kasabov applied GNG and GCS algorithms to the diabetes diagnosis problem, and reported accuracies of 74.6% and 73.8%, respectively [23]. Both GNG and GCS need to calculate local resources for prototypes, which introduces extra computational effort and reduces their efficiency. Deng and Kasabov proposed the evolving self-organizing maps (ESOM) network structure, which is similar to that of GNG [21]. When applied to diabetes diagnosis, they obtained 78.4% classification accuracy using ESOM.

Support vector machine (SVM)

Support vector machine (SVM) operates by finding a linear hyperplane that separates the positive and negative examples with a maximum interclass distance [24]. We can define z_i as an indicator variable which specifies whether a data vector x_i is in class diabetics or non-diabetics (e.g., z_i = -1 if x_i is in the diabetic class and z_i = 1 if x_i is in the non-diabetic class). The distance of a hyperplane w to a (transformed) data vector y is defined as | f (y)|/w. Together with the fact that the separating hyperplane ensures z_i f(y_i) ≥ 1 for all n data vectors i, we can express the condition on the margin m as:

z_if(y)⁄w ≥ m, where i = 1,...,n

The goal of SVM training is to find the weight vector w that maximizes the margin m. Barakat et al. employed SVM to process the inputs, and extracted the rules using an electic approach [25]. This approach was then used to predict the diagnosis of diabetes using a questionnaire based on demographic, historic, and anthropometric measures. The authors achieved a prediction accuracy of 94%.

A cascade learning system based on generalized discriminant analysis (GDA) and least square support vector machine (LS-SVM) has been proposed for early diagnosis of Pima Indian diabetes disease [26]. The accuracy reported in this study was 78.21% with 10-fold cross-validation. Purnami et al. applied smooth support vector machines (SSVM) to the diabetes detection problem [27]. SSVM, developed by Lee et al., is an extension to SVM in which smoothing function is applied to solve the problem [28]. With SSVM, the investigators achieved a 76.73% accuracy. To improve efficiency, they proposed a new multiple knot spline (MKS) smoothing function for SSVM. Replacing the default-plus function of SSVM by MKS, they enhanced the automated diagnosis performance of SSVM with an accuracy of 93.2%.

Neural networks

Multi-layer neural networks

Multilayer neural networks (MLNN) are composed of one or more hidden layers between input and output (Figure 1) [29]. In the training phase, the training data is fed through the input layer. The data is propagated from the hidden layer to the output layer (Figure 2), which is called forward pass. During this phase, each node in the hidden layer gets input from all the input layer nodes, which are then multiplied by the randomly assigned weights before summing up. Similarly, the output layer node receives inputs from all nodes of the hidden layer, which are then multiplied by the randomly assigned weights and summed up. This forms the output of the output layer.

Figure 1.

Architecture of a single neuron.

Figure 2.

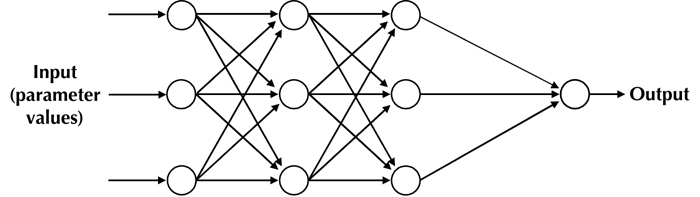
Multi-layer neural network with 3 neuron layers.

The input to each hidden layer is calculated by:

y = ∑w_i ∗ input value

where w_i is the weight for neuron i. The output of the hidden layer is calculated by using an activation function. The activation function acts as a squashing function, such that the output of a neuron in a neural network is between certain values (usually 0 and 1 for sigmoid, or -1 and 1 for hyperbolic tangent). Common activation functions used in diabetes diagnosis are the sigmoid (a) and hyperbolic tangent (b) function:

a) f(x) = 1⁄(1 + e^-x) b) f(x) = (e^x - e^-x)⁄(e^x + e^-x)

with sigmoid range = [0, 1], and hyperbolic range = [1, , 1, ]. Error rates are calculated as follows:

Error = f(x) ∗ [1 - f(x)] ∗ [target value - f(x)]

Back-propagation neural networks

The back-propagation neural network (BPNN) algorithm is widely recognized as a powerful tool for training of the MLNN. In this algorithm, errors are back-propagated to the hidden layers, weights are reassigned, and the process continues until the error rate is a minimum. The new weights are calculated based on the following equation:

Weight (new) = weight + η ∗ error ∗ f(x)

where η is the learning rate. However, since it applies the steepest descent method to update the weights, it suffers from a slow convergence rate, and often yields suboptimal solutions [30, 31]. Jaafar et al. used the back propagation neural network algorithm for diagnosing diabetes [32]. The inputs to the system were glucose tolerance test, diastolic blood pressure, triceps skin fold thickness, serum insulin, body mass index, diabetes pedigree function, number of times pregnant, and age. BPNN was used to predict the glucose level [33], and also to train and test its performance using diabetes patients [12].

Although the BPNN algorithm is widely used, one major drawback is that it requires a complete set of input data. However, most diabetes datasets are often incomplete in the one respect or another. Back propagation algorithm cannot interpret the missing values (if any) which may prevent the identification of factors leading to rare outputs. To overcome this problem, Jayalakshmi and Santhakumaran proposed a new approach to deal with the missing values [34]. They achieved an accuracy of 99.9% by replacing the missing values with its mean, and then normalizing the data with a principal component analysis (PCA) technique [35]. PCA is an extraction method aimed at describing the data variance by constructing a set of new orthogonal features called principal components (PCs). The PCs are a linear combination of the data variables that are mutually orthogonal. Every new PC describes a part of the data variance not explained by components used previously. Due to this fact, a few first PCs are usually enough to represent the data variance well.

It was reported that the Levenberg-Marquardt (LM) algorithm [36] provides generally faster convergence and better estimation results than other training algorithms [37]. However, this method can cause a memorization effect when overtraining occurs. If a neural network starts to memorize the training set, its generalization starts to decrease, and its performance may not be improved for untrained test sets. Kayaer and Yildirim used the LM algorithm on a Pima Indian dataset, and achieved an accuracy of 77.08% [38], which was lower than other algorithms. Temurtas et al. trained the neural network optimally with a probabilistic neural network (PNN) along with a LM algorithm [39, 40]. They achieved an 82.37% accuracy with this approach.

Radial basis function (RBF)

In neural networks, radial basis functions (RBFs) are used as a replacement for the sigmoidal hidden layer transfer function in multi-layer perceptrons (MLP) [41]. The only parameters adjusted in the learning process are the linear mapping from the hidden layer to the output layer. Hence, RBF networks have the advantage of not suffering from local minima.

RBF shows good performance in regression applications where the input space dimension is relatively small. However, in prediction problems like diabetes diagnosis, only 68.23% efficiency has been reported, which is far less than other algorithms. RBF networks have the disadvantage of requiring good coverage of the input space by radial basis functions. Determination of RBF centers is heavily dependent on the distribution of the input data without reference to the prediction task.

General regression neural network (GRNN)

The general regression neural network (GRNN) is related to the radial basis function network and is based on a standard statistical technique called Kernel regression [42]. It approximates any arbitrary function between input and output vectors, and draws the function estimate directly from the training data. It does not require an iterative training procedure, as in MLP. For an input estimator ‘x’, corresponding to diabetes risk factor variables, GRNN produces an output estimator ‘y’ which minimizes the estimation error. GRNN works on following formula:

E[y|x] = ∫yf(x,y)dy/∫f(x,y)dy

where E[y|x] is the expected value of output y, given the input vector x, and f(x, y) the joint probability density function of x and y.

GRNNs produce a real-valued prediction between 0 and 1. A cut-off value decides the criteria to identify positive prediction. The best result achieved by GRNN on PID is 80.21% using 0.5 as cut-off value for the decision [38].

Neuro-fuzzy inference systems (NFIS)

A neuro-fuzzy network is a fuzzy inference system in an artificial neural network [43]. Depending on the fuzzy inference system (FIS) type, there are several layers that simulate the processes involved in a fuzzy inference like fuzzification, inference, aggregation, and defuzzification. Embedding a FIS in the general structure of an artificial neural network (ANN) has the benefit of using ANN training methods to find the parameters of a fuzzy system. Linear discriminant analysis (LDA) is used to separate the two types of feature variables in a given dataset [44]. Dogantekin et al. used LDA along with artificial neuro FIS (ANFIS) for the detection of diabetes [45]. In this method, LDA is used to separate feature variables between healthy and diabetes data. In the second phase, both the healthy and diabetes features obtained in the first phase are given to inputs of the ANFIS classifier. They achieved an 84.61% accuracy with this approach.

Smith et al. used the PID data set to evaluate the perceptron-like adaptive learning routine (ADAP), and achieved a prediction accuracy of 76% [46]. The performance of fuzzy adaptive resonance theory mapping (ARTMAP) on the same database was 66% [47]. ARTMAP is a supervised learning algorithm for input binary vectors. However, the ARTMAP algorithm required fewer rules and was comparatively faster. Carpenter and Markuzon have presented an instance counting algorithm (ARTMAP-IC) and obtained an 81% accuracy against the test set [47].

Expert systems

In real world problems like diabetes detection, a simple classifier is too weak for accurate prediction. The use of expert systems and different artificial intelligence techniques for classification systems in medical diagnosis is increasing gradually. Mixture of experts and modified mixture of experts have been successfully implemented to the problem of diabetes diagnosis prediction.

Mixture of experts

The new supervised learning algorithm called mixture of experts (ME) was proposed by Jacobs et al. [48]. This algorithm divides a learning task into appropriate subtasks, each of which can be solved by simple expert network. The global output of the ME system is derived as a convex combination of the outputs from a set of N experts, in which the overall predictive performance of the system is generally superior to any of the individual experts.

ME architecture is composed of several expert networks and a gating network (Figure 3). The gating network produces a scalar output from a vector input X. The gating network operates on a generalized linear function where the output for ith input variable is given by:

Figure 3.

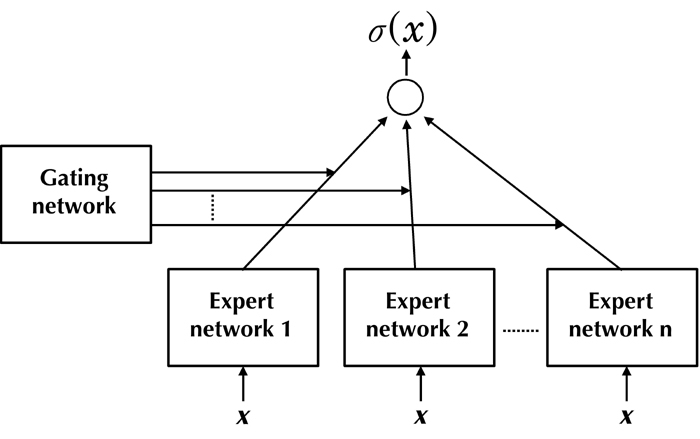
General architecture of mixture of experts.

g(x,v_i) = e^ξ_i⁄∑e^ξ_k

where ξ_i = V_i^T x, and V_i is the weight vector. Each expert network produces an output vector for an input vector based on the following generalized linear equation:

σ_i(x) = f(W_ix)

where W_i is a weight matrix. The final output of ME is the sum of multiplications of the outputs from gating and expert networks:

σ(x) = ∑g(x,v_k)σ_k(x)

Ubeyli presented an approach to test the performance of ME on PID with a classification accuracy of 97.93% [49], which was better than conventional MLNN. Moreover, the computational time required for classification using ME was comparatively small.

Modified mixture of experts (MME)

Ubeyli [49] employed a new, fast, and effective modified mixture of experts (MME) approach proposed by Chen [50] to further improve the classification accuracy of ME.

The MME architecture is composed of an assembly of N expert networks and a gate-bank (Figure 4). For k different features, expert networks are divided into k groups, each comprising of N expert networks. Similarly, the gate-bank is composed of k gating networks. The resultant output of the gate-bank is a convex weighted sum of outputs produced by all the gating networks. Finally, the overall output of MME is obtained by linear combination of outputs of all N expert networks weighted by the output of the gate-bank.

Figure 4.

General architecture of modified mixture of experts.

Ubeyli applied the MME algorithm to the diabetes diagnosis problem and achieved an accuracy of 99.17% [49]. Apart from outperforming all other algorithms, the computational time required for classification was very small.

Conclusions

Despite of the rapid development of theories for computational intelligence, application to diabetes diagnosis remains a challenge. This is due to specific problems of data use. These problems arise when statistical models of data are unknown or time-dependent, or when the parameters of the learning system need to be updated incrementally, while only a partial glimpse of incoming data is available. Based on the promising outcomes of studies applying computational algorithms to the problem of diabetes diagnosis, it is clear that a more sophisticated risk score could be developed. This would significantly decrease healthcare costs via early prediction and diagnosis of type 2 diabetes.

Some algorithms work better on the diabetes diagnosis problem than others. It will be important to compare outcomes further to find the most reliable algorithm for clinical application. Neural network methodology has outperformed classical statistical methods in cases where input variables are interrelated. Because clinical measurements are usually derived from multiple interrelated systems, it is evident that neural networks might be more accurate than classical methods in multivariate analysis of clinical data.

Trained models of diabetes risk factors should be incorporated into easy-to-use software solutions such that medical practitioners, who are not experts in artificial intelligence and computational techniques, may apply them easily. For this purpose, graphical user interface-enabled tools need to be developed by which medical practitioners can simply enter health profiles of their patients and receive an instant diabetes prediction with an acceptable degree of confidence. If the ANN-based prediction approach shows improved medical diagnosis, then it may become more widely accepted as a means to assist patient care in more hospitals and clinics.

Though the PID dataset provides a well validated data for predicting diabetes diagnosis, it is possible that models trained on such a dataset may not perform equally well on profiles of patients from other ethnic group. Therefore, it is recommended that models of choice must be trained on a dataset that closely represents patient profiles of medical practitioners within specific geographic regions.

Disclosures (conflict of interests statement): The authors report no conflict of interests.