The Role and Specificity of the Catalytic and Regulatory Cation-binding Sites of the Na⁺-pumping NADH:Quinone Oxidoreductase from Vibrio cholerae

Abstract

The Na⁺-translocating NADH:quinone oxidoreductase is the entry site for electrons into the respiratory chain and the main sodium pump in Vibrio cholerae and many other pathogenic bacteria. In this work, we have employed steady-state and transient kinetics, together with equilibrium binding measurements to define the number of cation-binding sites and characterize their roles in the enzyme. Our results show that sodium and lithium ions stimulate enzyme activity, and that Na⁺-NQR enables pumping of Li⁺, as well as Na⁺ across the membrane. We also confirm that the enzyme is not able to translocate other monovalent cations, such as potassium or rubidium. Although potassium is not used as a substrate, Na⁺-NQR contains a regulatory site for this ion, which acts as a nonessential activator, increasing the activity and affinity for sodium. Rubidium can bind to the same site as potassium, but instead of being activated, enzyme turnover is inhibited. Activity measurements in the presence of both sodium and lithium indicate that the enzyme contains at least two functional sodium-binding sites. We also show that the binding sites are not exclusively responsible for ion selectivity, and other steps downstream in the mechanism also play a role. Finally, equilibrium-binding measurements with ²²Na⁺ show that, in both its oxidized and reduced states, Na⁺-NQR binds three sodium ions, and that the affinity for sodium is the same for both of these states.

Introduction

The sodium-pumping NADH:quinone oxidoreductase (Na⁺-NQR)² is the entry site for electrons into the respiratory chain of many marine and pathogenic bacteria, including Vibrio cholerae (1–9). Na⁺-NQR catalyzes the electron transfer from NADH to ubiquinone, and uses the energy released by the redox reaction to pump sodium ions, creating an electrochemical gradient (10–13). In different bacteria, the sodium gradient supplies energy for a variety of fundamental processes, including amino acid and sugar transport, ATP synthesis, pH regulation, drug efflux, and toxin extrusion (12). Na⁺-NQR is composed of five subunits with transmembrane spanning segments (NqrB-F) and one hydrophilic subunit (NqrA) (14). The enzyme contains five redox cofactors: two covalently bound FMNs, in the hydrophilic domains of subunits NqrB (FMN_B) and NqrC (FMN_C) (15–19), one FAD and one 2Fe-2S center, in the cytosolic domain of NqrF (20, 21), and one riboflavin in NqrB (22–24). With the exception of riboflavin, all of the cofactor-binding sites have been identified in the sequence. Flavin molecules are flexible electron carriers that can participate in one- or two-electron reactions, although the two-electron reactions are thermodynamically favored and produce relatively more stable products. Interestingly, in Na⁺-NQR, the two FMNs and the riboflavin cofactor undergo only one-electron transitions in the reaction cycle of the enzyme. Furthermore, riboflavin is found as a stable neutral radical (RibH^•) in the air-oxidized form of the enzyme (15).

Our group has previously shown that electrons move through the enzyme along a linear pathway: FAD → 2Fe-2S → FMN_C → FMN_B → Rib (25). We have also determined that the reduction of FMN_C and the reduction of the riboflavin neutral radical are the two steps involved in sodium translocation (39). These results argue against a localized coupling mechanism of the enzyme, in which the reduction of a single cofactor is directly involved in sodium capture and release. Instead, we have proposed that Na⁺-NQR has a pumping mechanism in which different conformations of the enzyme capture sodium on one side of the membrane and release it on the opposite side.

To fully understand the sodium pumping mechanism of Na⁺-NQR, the structural and functional properties of sodium binding to the enzyme must be defined. In this work, we have analyzed the role and specificity of the cation-binding sites in Na⁺-NQR. Na⁺-NQR is stimulated by sodium and lithium and it is also able to transport both cations. The cation selectivity of the enzyme is not controlled exclusively by the binding site, but by other steps in transport. By analyzing the activity of the enzyme in the presence of sodium and lithium together, it became evident that the enzyme contains at least two functional sodium-binding sites. Also, Na⁺-NQR does not translocate K⁺ or Rb⁺, and turnover is not stimulated by either of these ions alone. However, our studies revealed a regulatory site that is selective for potassium; rubidium can compete for this site but acts as an inhibitor.

Finally, equilibrium binding measurements with ²²Na⁺ show that, in both its oxidized and reduced states, Na⁺-NQR binds three sodium ions, and that this change in redox state does not significantly alter the Na⁺ binding affinities. This clarifies an outstanding issue about the relationship between the redox state of Na⁺-NQR and its affinity for sodium, which has significant consequences for the coupling mechanism of the enzyme.

EXPERIMENTAL PROCEDURES

Protein Purification

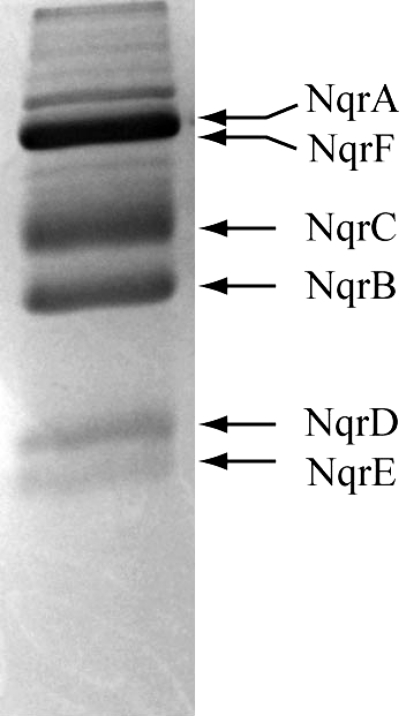
V. cholerae cells containing a recombinant nqr operon, cloned into the pBAD vector, were grown in Luria-Bertani medium, using arabinose to induce expression of the Na⁺-NQR complex (1). Cells were harvested, washed, and passed three times through a microfluidizer cell disrupter and the plasma membranes were obtained by differential centrifugation. Na⁺-NQR was purified by Ni-NTA affinity chromatography in the presence of n-dodecyl-β-d-maltoside, as described previously (1). To further purify Na⁺-NQR, the sample was subjected to cation exchange chromatography using DEAE-Sepharose, with a linear gradient of NaCl (0–500 mm). The enzyme was collected, concentrated, and passed twice through a HiLoad Superdex 200 16/60 PG column, obtaining purity higher than 95%, judged by densitometric analysis (26) (Fig. 1). Na⁺-NQR concentration was measured spectrophotometrically as reported previously (25).

FIGURE 1.

SDS-acrylamide gel of Na⁺-NQR purified using affinity chromatography (Ni-NTA), anion exchange (DEAE-Sepharose), and gel filtration chromatography (HiLoad Superdex 200). The purity of the sample was assessed densitometrically, using ImageJ software (26).

Activity Measurements

NADH dehydrogenase activity was measured spectrophotometrically at 340 nm, using a molar absorptivity of 6.22 mm⁻¹ cm⁻¹ for NADH. CoQ reductase activity was measured at 282 nm, using the difference between the molar absorptivity of CoQ and CoQH₂ in aqueous solution (10.2 mm⁻¹ cm⁻¹). The enzymatic assays were performed in a buffer containing 250 μm K₂-NADH, 50 μm ubiquinone-1 (CoQ-1), 50 mm Tris-HCl, 1 mm EDTA, 5% (v/v) glycerol, 0.05% n-dodecyl-β-d-maltoside, pH 8.0. The activity was measured in the presence of different concentrations of NaCl, LiCl, RbCl, and KCl.

Reconstitution of Na⁺-NQR in Proteoliposomes and Generation of Membrane Potential

Purified Na⁺-NQR was mixed with Escherichia coli phospholipids and n-octyl glucoside (detergent/phospholipid ratio = 1.3) in buffer containing 100 mm KCl, 50 mm HEPES, 1 mm EDTA, pH 7.0. The detergent was removed slowly by adding SM Bio-Beads, following the protocol reported by Verkhoskaya et al. (27). Cation transport was measured indirectly by following membrane potential (ΔΨ) generation in the presence of different monovalent cations. ΔΨ was measured spectrophotometrically by following oxonol VI at 625 − 587 nm. The reaction buffer contained 5 μm oxonol VI, 200 μm NADH, 100 μm CoQ-1, 50 mm HEPES, 1 mm EDTA, pH 7.5, and 150 mm NaCl, KCl, LiCl, or RbCl.

Fast Kinetics Experiments

Fast spectrophotometric measurements were performed in an Applied Photophysics SX.18MV-R stopped-flow instrument, equipped with a PD.1 diode array, as reported before (25). The reduction kinetics was studied in a buffer containing 250 μm K₂-NADH in the absence and presence of saturating concentrations of the different cations. The raw data were averaged and analyzed as reported previously (23, 25). The kinetic phases of the redox reactions were assigned by comparison to our previous data (25).

Equilibrium Sodium Binding Experiments

²²Sodium binding to purified Na⁺-NQR was assayed in a buffer containing 2.5 nCi of ²²Na⁺ (PerkinElmer Life Sciences), 150 mm KCl, 50 mm KH₂PO₄, 1 mm EDTA, 0.05% n-dodecyl-β-d-maltoside, 100 units/ml of catalase, 100 units/ml of superoxide dismutase, 100 μm Na⁺-NQR, and different concentrations of sodium (0.5–20 mm). Reduced samples contained 20 mm K₂-NADH. In the absence of CoQ, oxygen is consumed by Na⁺-NQR and produces superoxide; catalase and superoxide dismutase were included in the samples to facilitate the complete reduction of oxygen to water by eliminating oxygen radicals. In these conditions after 3–5 min the oxygen concentration was in the micromolar range (estimated spectrophotometrically by following myoglobin (28)). The enzyme solution was mixed with 200 μl of Ni-NTA resin and centrifuged for 10–15 s in a spin minicolumn and the flow-through discarded. The enzyme was eluted with 200 μl of 0.1 m HCl and radioactivity was measured in the eluate by scintillation counting using a MicroBeta TriLux Liquid Scintillation and Luminescence Counter (PerkinElmer Life Sciences). The radioactivity of a parallel sample that did not contain the enzyme was subtracted, to compensate for nonspecific binding of sodium to the resin.

RESULTS

Cation Specificity of Na⁺-NQR

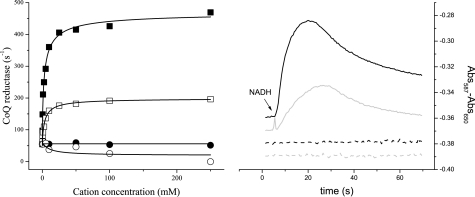
Ubiquinone reductase (CoQ reductase) activity was tested in the presence of different concentrations of sodium, lithium, potassium, and rubidium (Fig. 2A). Na⁺-NQR is stimulated eight to nine times (k_cat = 460 s⁻¹) by sodium with a K_m of 2.5 mm, close to values reported before (42). The enzyme was also stimulated by lithium, with a similar K_m (3.4 mm), but the maximal stimulation was only 3-fold (k_cat = 140 s⁻¹). Potassium and rubidium had little or no effect on the activity, when used individually. Acceleration of the reaction by lithium could be due to replacement of sodium as a substrate, or if lithium uncouples the pumping reaction, allowing the redox reaction to proceed without creating an ion gradient. To test these possibilities, the generation of membrane potential by the enzyme was measured in phospholipid vesicles, to determine whether steady-state turnover, in the presence of Li⁺ would generate a membrane potential. Results in Fig. 2B demonstrate that in these conditions the enzyme generates a significant membrane potential, indicating that Na⁺-NQR is able to transport lithium at a rate consistent with the results of steady-state kinetic measurements (as well as stopped-flow measurements; see below). The ability to use lithium as a substrate is a relatively common feature of sodium transporters and channels (29–34). The fact that lithium can be used as a substrate by Na⁺-NQR, whereas potassium and rubidium cannot, is consistent with differences in the properties of these alkali metals. Lithium has a smaller ionic radius than sodium, whereas potassium and rubidium are much larger (34). Also, binding sites for sodium usually includes six ligands, while lithium can be bound by five, while rubidium and potassium typically require eight ligands (33, 34).

FIGURE 2.

Cation specificity of Na⁺-NQR. Left, steady-state measurements of Na⁺-NQR activity. CoQ reductase was measured at different concentrations of NaCl (■), LiCl (□), KCl (circle), and RbCl (○). Kinetic parameters (K_m and k_cat) were calculated by fitting the curves to the Michaelis-Menten equation. Right, membrane potential generation (ΔΨ) by Na⁺-NQR with 100 mm NaCl (black line), LiCl (gray line), KCl (dashed black line), and RbCl (gray dashed line). Transport of the cations was measured indirectly by following ΔΨ, using oxonol VI.

Traditionally Na⁺-NQR has been regarded as completely selective for sodium and other cations, including lithium, were not believed to be able to serve as substrates. This may be because, most previous measurements were carried out in membranes, where the activity of the entire respiratory chain was studied (35).

Effect of Potassium and Rubidium on the Activity of Na⁺-NQR

Despite the fact that potassium and rubidium cannot serve as substrates for Na⁺-NQR, it has been reported that K⁺ increases the apparent affinity for Na⁺, suggesting that K⁺ and possibly Rb⁺ could be regulators of enzyme activity. To address this question, the saturation kinetics by sodium were measured using different concentrations of potassium, rubidium, and in the presence of both ions. The data were fit using a model in which the enzyme can form complexes with sodium, potassium, and rubidium, and ternary complexes with sodium and potassium, and sodium and rubidium, although the only productive complexes are enzyme-sodium and enzyme-sodium-potassium. The data were analyzed using Equation 1,

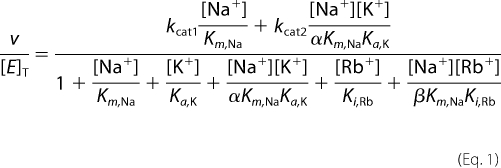v is the initial activity of the enzyme, [E]_T is the total enzyme concentration, k_cat1 and k_cat2 are the catalytic constants of the enzyme-sodium and enzyme-sodium-potassium complexes, respectively; K_m,Na, K_a,K, and K_i,Rb are affinity constants for sodium, potassium, and rubidium, respectively. The parameter α describes the factor by which the dissociation constant of potassium changes when the sodium-binding site is occupied, or equivalently the factor by which the dissociation constant for sodium changes when the potassium-binding site is occupied. The parameter β is analogous to α, but describes the interactions between the rubidium- and sodium-binding sites.

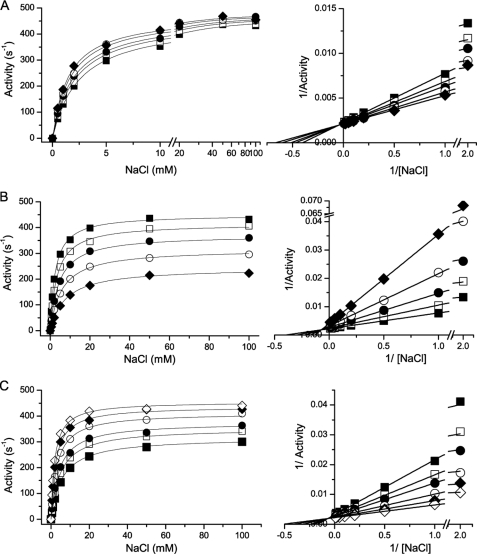
The effect of potassium on the sodium saturation kinetics of Na⁺-NQR is shown in Fig. 3A. Potassium behaves as a nonessential activator of the enzyme, with a K_a,K = 50 mm. Saturating amounts of potassium result in a small, but reproducible increase of the maximal activity (k_cat2/k_cat1 = 1.1) and increase the apparent affinity by a factor of 2 (αK_m,_Na = 1.2 mm). Indeed, Lineweaver-Burk plot shows lines intersecting in the second quadrant, characteristic of systems in which both the k_cat and K_m/k_cat ratio are altered. On the other hand, rubidium behaves as a mixed inhibitor with an affinity constant (K_i,_Rb) of 45 mm, causing a decrease in both the apparent k_cat value and the apparent affinity of the enzyme for sodium (βK_m,_Na = 14 mm) (Fig. 3B). The double-reciprocal plots show an intersecting pattern, which illustrates the effect on the k_cat and K_m/k_cat parameters.

FIGURE 3.

Effect of potassium and rubidium on the saturation kinetics for sodium in Na⁺-NQR. The activity of the enzyme was measured at different concentrations of potassium and rubidium, or a mixture of both. Left-hand panels show the direct plots and right-hand panels show the Lineweaver-Burk plots. A, effect of potassium on the saturation kinetics for sodium. KCl: 0 (■), 10 (□), 20 (●), 50 (○), and 100 mm (◆). B, effect of rubidium on the saturation kinetics for sodium. RbCl, 0 (■), 20 (□), 50 (●), 100 (○), and 200 mm (◆). C, effect of potassium on the rubidium-induced inhibition of Na⁺-NQR. In these experiments the saturation kinetics of sodium were measured with a fixed concentration of RbCl (100 mm) and different concentrations of potassium; KCl, 0 (■), 10 (□), 20 (●), 50 (○), 100 (◆), and 200 mm (△).

To understand the interaction of potassium and rubidium with the enzyme, the saturation kinetics of sodium were analyzed using a mixture of the two ions. The data were fit to a model in which potassium and rubidium can each be bound to the free form of the enzyme and to the enzyme-sodium complex, but their binding is mutually exclusive. Thus, potassium and rubidium compete for the same site and the inhibition by rubidium can be overcome by adding potassium. Fig. 3C shows the de-inhibition caused by the addition of potassium to the enzyme in the presence of 100 mm RbCl, supporting the model.

Competition of Sodium and Lithium for the Cation-binding Sites

The sodium dependence and saturation kinetics of the steady-state reaction (CoQ-reductase) were studied in the presence of different concentrations of lithium. Several models were tested to understand the interaction between these two ions. The best fitting was obtained using a model with two sodium/lithium-binding sites, in which the two ions compete for both sites. In this model, the enzyme can form complexes with individual ions (enzyme-sodium and enzyme-lithium), with two ions of the same type (enzyme-sodium-sodium or enzyme-lithium-lithium), and with both ions (enzyme-sodium-lithium), where all the ternary complexes are productive (enzyme-sodium-sodium, enzyme-sodium-lithium and enzyme-lithium-lithium). Equation 2 was used to fit the data,

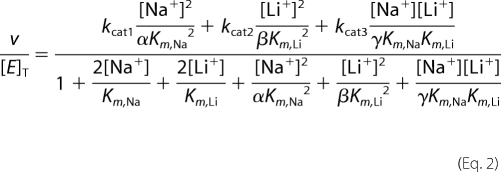k_cat1, k_cat2, and k_cat3 are the catalytic constants of the enzyme-sodium-sodium, enzyme-lithium-lithium, and enzyme-sodium-lithium complexes, respectively. K_m,_Na and K_m,_Li are affinity constants for sodium and lithium, respectively. The parameters α, β, and γ describe the factor by which the dissociation constant of one site changes when the other site is occupied, for the case of Na⁺/Na⁺, Li⁺/Li⁺, and Na⁺/Li⁺, respectively.

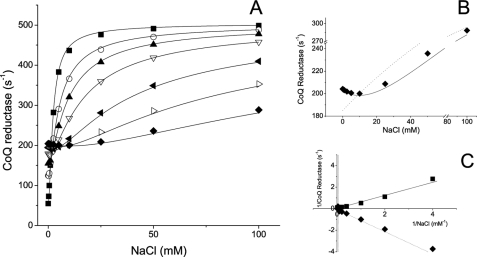
Fig. 4A shows the competition of sodium and lithium for the binding sites on Na⁺-NQR. The initial activity (without sodium) increases with increasing concentrations of lithium, reflecting the ability of the enzyme to use lithium as a substrate. The activity further increases as the sodium concentration is increased (except for a few points at which substrate inhibition occurs, see below). This increase in activity is the result of a shift in enzyme population, from the enzyme-lithium-lithium form, to the enzyme-sodium-sodium form, which is three times more active. Other models were able to explain this general behavior, for example, a single site competition scheme. However, only models with at least two ion-binding sites (or more) were able to explain the substrate inhibition produced by small amounts of sodium at high initial lithium concentrations. Fig. 4B shows both a single-site and two-site model fittings. The substrate inhibition is more evident in the double-reciprocal plots (Fig. 4C). The enzyme without lithium shows typical linear behavior, with all the experimental points in the first quadrant (the initial activities without sodium have been subtracted, to linearize the data). The double-reciprocal plot of the activity in the presence to 100 mm lithium falls in the fourth quadrant; due to the subtraction of the initial activity, the first points have negative values. According to our model, the substrate inhibition is produced by the formation of ternary complexes; under saturating lithium concentrations the additions of small amounts of sodium produce a shift in the equilibrium to forms that are not fully saturated and that as a population have a lower activity. The model also predicts that the two sites show positive cooperativity for sodium and lithium; the binding of the first ion increases the affinity of the second by a factor of four (αK_m,_Na = 0.6 mm, βK_m,_Li = 0.9 mm, γK_m,_Na = 0.65 mm, and γK_m,_NaLi = 0.9 mm), which indicates that once the enzyme has bound either lithium or sodium, the binding of the other cation is favored. Interestingly, the ternary complex with lithium and sodium is also active, with an activity close to the activity of the enzyme lithium-lithium form (k_cat2 = 160 s⁻¹ and k_cat3 = 190 s⁻¹).

FIGURE 4.

Competition of sodium and lithium for cation-binding sites in Na⁺-NQR. A, the saturation kinetics of sodium was measured using different concentrations of lithium: 0 (■), 2.5 (□), 5 (●), 10 mm (○), 25 (▴), 50 (△), and 100 mm (▾). B, Na⁺-NQR activity measured at different concentrations of sodium in the presence of 100 mm LiCl. Solid line represents a two-site model fitting and dashed line represents a single-side model fitting. C, double-reciprocal plots of data obtained in the absence of LiCl (■) or in the presence of 100 mm LiCl (♦). The initial point (NaCl = 0) was subtracted to linearize the data. The black line represents a fit to a simple Michaelis-Menten kinetics, the dashed line represents a fit to the double cation-binding site model (Equation 1).

²²Na⁺ Binding Assays

The steady-state kinetic measurements in the presence of sodium and lithium show that Na⁺-NQR has more than one functional sodium-binding site. However, these measurements were unable to identify the exact number of sites involved or the actual dissociation constants (rather than apparent or kinetic constants). To determine both the number of cation-binding sites and their affinity, equilibrium ²²Na binding experiments were performed in the oxidized and fully reduced forms of the enzyme. Previously, Bogachev et al. (38) studied the interactions of sodium with Vibrio harveyi Na⁺-NQR, using ²³Na NMR spectroscopy (36). They found that the line width of the ²³Na NMR signal was significantly larger in the presence of the reduced, than the oxidized, enzyme and calculated sodium affinity constants of 30 μm and 24 mm, respectively. The same authors subsequently questioned the validity of these equilibrium constants (37), because it is uncertain whether equilibrium conditions are achieved on the time scale of the NMR measurement (38).

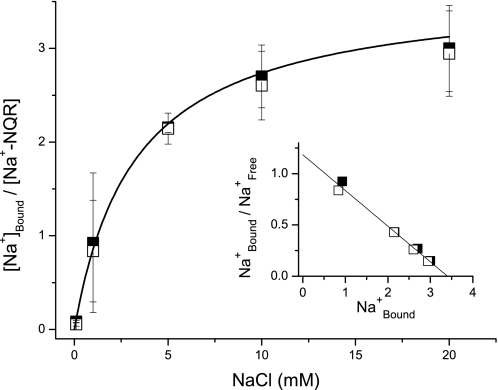
To obtain sodium binding data under true equilibrium conditions, we used a ²²Na⁺ radioactive assay in which an affinity resin was used to trap the enzyme with ²²Na⁺ bound. With this method we determined both the number of sodium-binding sites and their affinities in the oxidized and fully reduced forms of the enzyme. Fig. 5 shows that Na⁺-NQR has three independent sodium-binding sites and that there is no cooperativity among these sites. The three sites have similar affinity for Na⁺ (K_D = 2–3 mm). Due to the number of sites it is difficult to establish the individual affinities conclusively. It should be noted that the presence of these three equilibrium Na⁺-binding sites is not inconsistent with finding of at least two catalytically active sites in the kinetic studies described above, because the equilibrium measurements account for all the binding sites in the enzyme. To prevent nonspecific binding, the experiments were performed in the presence of a high ionic strength (150 mm KCl and 50 mm KH₂PO₄). Thus, the binding sites observed are specific for Na⁺. Furthermore, the observed Na⁺ binding is unlikely to be due to contaminants in the enzyme, because the purity of the Na⁺-NQR preparation is higher than 95% (Fig. 1). In contrast with the conclusions of the earlier ²³Na NMR study (36), our results clearly show that the affinity of Na⁺-NQR for sodium does not change between the fully oxidized and fully reduced states of the enzyme.

FIGURE 5.

Equilibrium ²²Na binding to 20 mm NADH-reduced (□) and air-oxidized (■) Na⁺-NQR. The enzyme was mixed with ²²Na⁺ in 250 μl of buffer containing 150 mm KCl, 50 mm KH₂PO₄, 1 mm EDTA, 0.05% n-dodecyl-β-d-maltoside, 100 units/ml of catalase, 100 units/ml of superoxide dismutase, supplemented with 200 μl of Ni-NTA. The suspension was applied to a minicolumn and spun in a microcentrifuge. The enzyme was eluted by adding 200 μl of 0.1 m HCl and the radioactivity in the eluate was counted. Inset shows Scatchard plot.

The Effect of Cation on the Transient Kinetics of Reduction of Na⁺-NQR

To understand the specific effect of monovalent cations on the activity of the enzyme, the kinetics of the reduction Na⁺-NQR by NADH were studied in the presence of saturating concentrations of the various ions. We have reported previously (25) that the reduction of the enzyme takes place in four consecutive steps: the reduction of the FAD (FAD → FADH₂), the reduction of the riboflavin neutral radical (RibH^• → RibH₂), the reduction of the FMNs (2FMN → 2FMN^⨪), and the reduction of the anionic FMN_C to the fully reduced form (FMN_C^⨪ → FMN_CH₂) (Table 1). We have also shown that the last two steps are too slow to be part of the catalytic cycle of the enzyme. Despite the fact that riboflavin is the last cofactor in the sequence, it becomes reduced in the second phase, and behaves as the sodium-sensitive step of the reaction (25, 39). However, the redox step that is actually stimulated by sodium is the one-electron reduction of FMN_C, which is also the rate-limiting step of the reaction. The last two steps of the electron transfer (FMN_C → FMN_B → RibH^•) are the fastest reactions in the reduction process, and are downstream of the rate-limiting step (2Fe2s → FMN_C), which produces the apparent sodium sensitivity of the reduction of the riboflavin neutral flavosemiquinone.

TABLE 1.

Rate constants of the reduction of the different cofactors of Na⁺-NQR

Cation	Rate constant
	FAD → FADH2	RibH•→ RibH2	2(FMN → FMN⨪)	FMNC⨪ → FMNCH2
	s−1
No cation	232.3 ± 10.5	17.4 ± 2.6	2.1 ± 0.7	0.1 ± 0.07
Sodium	179 ± 8.6	179 ± 8.6	30.1 ± 3.5	0.56 ± 0.33
Lithium	210.1 ± 9.4	53.1 ± 7.8	5.5 ± 0.8	0.25 ± 0.12
Potassium	220 ± 12.3	24.1 ± 4.3	4.5 ± 0.7	0.3 ± 0.18
Rubidium	200 ± 16.3	22.13 ± 6.5	4.1 ± 1.4	0.5 ± 0.36

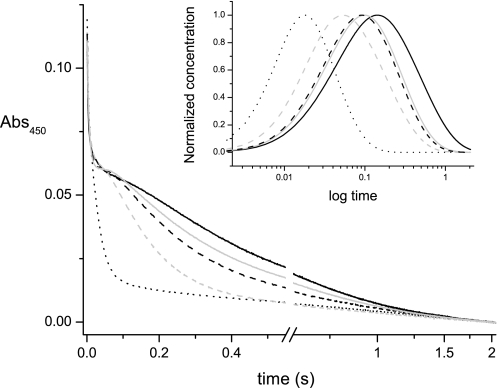
The results of fast kinetic measurements show that lithium is also able to stimulate the reduction of Na⁺-NQR (Fig. 6), specifically by increasing the reduction rate of riboflavin (RibH^• → RibH₂) (Table 1 and Fig. 6, inset). These data indicate that lithium binds to the same site and follows the same transport pathway as sodium. It is interesting that even at saturating concentrations of lithium, the stimulation was not as large as that due to sodium. This suggests that the enzyme has a selectivity filter beyond the sodium-binding site; otherwise, saturation by sodium and lithium should yield the same rate. Rubidium and potassium did not have major effects on the reduction rate of Na⁺-NQR, consistent with the results of the steady-state and transport measurements.

FIGURE 6.

Reduction kinetics of Na⁺-NQR by NADH in the presence of different cations. Time course at 450 nm showing the phases of reduction of the enzyme in the absence of cations (black line), or in the presence of 100 mm NaCl (black dotted line), 100 mm LiCl (gray dashed line), 100 mm KCl (black dashed line), or 100 mm RbCl (solid gray line). Inset shows the time course of the accumulation of the four-electron reduced enzyme (FADH₂-2Fe-2S_red-RibH₂), whose rate of appearance is dependent on sodium or lithium.

DISCUSSION

Cation-binding Sites in Na⁺-NQR

A first essential step to understand the reaction catalyzed by Na⁺-NQR and the mechanism of sodium transport is to establish the role of the substrate-binding sites in the catalytic cycle. In particular, to understand the Na⁺ translocation function of the enzyme, the number of cation-binding sites in the enzyme and their properties must be characterized. Several structural moieties involved in the catalytic mechanism of the enzyme have been identified, by the use of site-directed mutagenesis (20) and confirmed by recent crystallographic studies (40), including the binding sites for NADH, FAD, and the 2Fe-2S center, all located in NqrF. The attachment sites of the two covalently bound FMN molecules have also been characterized. They are located in the hydrophilic domains of subunits NqrB and NqrC. The FMNs are linked through phosphoester bonds to threonine residues in the conserved sequence Ser/Thr-aliphatic-aliphatic-Thr (16). The ubiquinone-binding site is still poorly defined, but Hayashi et al. (41) have suggested that this site is located in NqrB.

In contrast, the sites at which Na⁺ binds to the enzyme are still largely undefined. Specifically, the number of such sites, their locations, and their functional properties are unknown. Our recent work has shown that three residues (NqrB-D397, NqrD-D133, and NqrE-E95) participate in sodium uptake (42). Surprisingly, these residues are found in transmembrane helices of three different subunits (NqrB, NqrD, and NqrE), each of which has 6–9 membrane spanning helices (14). These helices contain many other conserved residues with a partial negative charge, such as serine, threonine, tyrosine, and cysteine, which could be ligands in sodium-binding sites, or that could participate in other structures, such as passageways, vestibules, or other hydrophilic cavities responsible for sodium transport. Therefore, it is plausible that the enzyme could contain more than one cation-binding site. Indeed, the ²³Na NMR measurements by Bogachev et al. (36) suggest that the enzyme has more than one sodium-binding site.

The aim of the present study was to define the number of cation-binding sites in Na⁺-NQR, their selectivity for monovalent cations, and their role in catalysis. Measurements in whole cells, which evaluated the effect of different cations on the turnover of the complete respiratory chain, have suggested that Na⁺-NQR was completely selective for sodium, leading to a general inference that the enzyme functions exclusively as a Na⁺ pump. Our current results using the purified enzyme indicate that Na⁺-NQR translocates sodium preferentially, but that lithium can also be taken up and transported, although less efficiently. By measuring the activity of the enzyme in a mixture of sodium and lithium, it became evident that Na⁺-NQR contains at least two sodium-binding sites, which show positive cooperativity and that participate in the catalytic mechanism. ²²Na binding experiments demonstrate that Na⁺-NQR has three sodium-binding sites. However, due to the number of sites, the individual dissociation constant for sodium cannot be established, although it is possible that the affinity of the different sites is similar (ranging from 2 to 3 mm), because the saturation curves did not show a cooperative behavior; negative cooperativity is expected in cases where two or more sites have large differences in affinity. Although positive cooperativity between the sodium-binding sites was predicted by the steady-state data, this effect was not observed in the binding experiments (Fig. 2A). The interactions between the sites, their specific roles, and their localization could be clarified using previously described acid-residue mutants (42).

The steady-state kinetics results show that the enzyme has a similar affinity for sodium and lithium, but the maximum activity is significantly higher in the presence of sodium. Thus, even when the enzyme is saturated with lithium, it is able to transport sodium more efficiently, indicating that the selectivity filter is not exclusively the cation-binding site of the enzyme. Such a selectivity filter is probably controlling the rate of FMN_C reduction. According to our model, sodium uptake occurs in the three-electron reduced enzyme. Once sodium is bound, the fourth electron can be donated to FMN_C, probably because the binding of sodium triggers a conformational change that bring the 2Fe-2S center and FMN_C into close proximity, which should increase the rate of electron transfer. For lithium, this conformational change can still happen but at a smaller rate. Binding of sodium might lower an activation barrier more than binding of lithium. Considering the difference in ionic radii and preferred number of ligands, the geometry of the site with sodium bound might be different from the geometry with lithium bound. Finally, our data also indicate the presence of a regulatory site, where potassium binding stimulates enzyme activity. This is consistent with potassium producing a more active conformation with a higher affinity for sodium. The potassium-binding site can also accept rubidium, which interestingly, has an inhibitory effect on enzyme activity.

Regulation of Sodium Affinity by the Redox State of the Enzyme

Previous experiments by Bogachev et al. (36) using ²³Na NMR have been interpreted that the fully reduced enzyme has a 1000-fold higher affinity for sodium than the oxidized form. The authors have pointed out that an increase in affinity triggered by the reduction of the enzyme would be an indication that the pumping mechanism depends on thermodynamic (or localized) coupling (43), i.e. the electron transfer to a specific cofactor is directly coupled to sodium capture and release. However, the interactions of sodium with the protein may not satisfy the fast exchange conditions required by the NMR measurement (38).

In this paper, we show that under equilibrium conditions, there are no significant differences in the binding of sodium to the oxidized and reduced forms of the enzyme, which is in agreement with the results of redox titrations (44–46), and argues against direct thermodynamic coupling. However, equilibrium Na⁺ binding data must be used with caution in predicting the properties of the intermediates involved in sodium pumping. The sodium binding measurements have been carried out on equilibrium redox states: oxidized (one electron reduced, as prepared) and fully (eight-electron) reduced enzymes, the latter of which do not form part of the catalytic cycle (25). The forms of the enzyme that are involved in Na⁺ uptake and transport across the membrane are observed in kinetic measurements, and are not equilibrium states. Sodium uptake is associated with a three-electron reduced form, in which FAD and the 2Fe-2S center are reduced. Release of sodium on the opposite side of the membrane, as evidenced by the formation of ΔΨ, is associated with a four-electron reduced state in which FAD, the 2Fe-2S center, and FMN_B are reduced (25). These states are clearly catalytically competent, but their sodium-binding properties are unknown, and cannot be inferred directly from other redox states or forms of the enzyme. In light of the current results, it is possible that the difference in binding properties between the reduced and oxidized forms of the enzyme measured by ²³Na NMR represent changes in sodium accessibility to the binding site rather than changes in affinity. Specifically, the difference in binding kinetics may represent the operation of a gating mechanism that regulates the solvent accessibility of the sodium-binding sites.

Redox titrations of the enzyme have shown that the midpoint potentials of the redox cofactors are independent of bulk sodium concentration and are not significantly affected by pH (45), in contrast to the predicted behavior for a thermodynamic pump. According to the localized coupling hypothesis (47), the capture of Na⁺ in a low dielectric environment (such as the membrane) counterbalances the negative charge of the electron of a specific reduced cofactor (the coupling site); hence the midpoint potential of the coupling cofactor should be dependent on sodium concentration. In contrast with this prediction, our recent results indicate that two redox transitions and four cofactors are required for the translocation of sodium across the membrane (39). Moreover, localized coupling cannot account for the cation selectivity of the enzyme, because under this mechanism any cation that has access to the coupling cofactor should produce the same effect as sodium. Here, we show that although lithium can bind to the enzyme, it does not stimulate activity to the same extent as sodium. Thus, there is mounting evidence that the sodium pump of Na⁺-NQR relies on kinetic coupling, likely mediated by conformational changes.