Dynamical reweighting: Improved estimates of dynamical properties from simulations at multiple temperatures

Abstract

Dynamical averages based on functionals of dynamical trajectories, such as time-correlation functions, play an important role in determining kinetic or transport properties of matter. At temperatures of interest, the expectations of these quantities are often dominated by contributions from rare events, making the precise calculation of these quantities by molecular dynamics simulation difficult. Here, we present a reweighting method for combining simulations from multiple temperatures (or from simulated or parallel tempering simulations) to compute an optimal estimate of the dynamical properties at the temperature of interest without the need to invoke an approximate kinetic model (such as the Arrhenius law). Continuous and differentiable estimates of these expectations at any temperature in the sampled range can also be computed, along with an assessment of the associated statistical uncertainty. For rare events, aggregating data from multiple temperatures can produce an estimate with the desired precision at greatly reduced computational cost compared with simulations conducted at a single temperature. Here, we describe use of the method for the canonical (NVT) ensemble using four common models of dynamics (canonical distribution of Hamiltonian trajectories, Andersen thermostatting, Langevin, and overdamped Langevin or Brownian dynamics), but it can be applied to any thermodynamic ensemble provided the ratio of path probabilities at different temperatures can be computed. To illustrate the method, we compute a time-correlation function for solvated terminally-blocked alanine peptide across a range of temperatures using trajectories harvested using a modified parallel tempering protocol.

INTRODUCTION

Dynamical properties, such as diffusion constants, position and velocity autocorrelation functions, rotational correlation times, frequency-dependent dielectric constants, and reaction or isomerization rates play a critical role in our understanding of various phenomena in chemistry and biology. Besides providing physical insight, calculation of these properties from simulations is often necessary for making comparison with spectroscopic experiments (such as FTIR, 2DIR, NMR, dynamic light scattering, or neutron correlation spectroscopy) or to make predictions about material or structural properties under conditions difficult to access experimentally or of substances yet to be created in physical form.

When these phenomena involve enthalpic barriers or entropic bottlenecks in systems obeying classical statistical mechanics, averages of these properties can be extremely slow to converge in standard molecular dynamics simulations, requiring tediously long simulations to produce estimates with the desired statistical precision. Additionally, the temperature-dependence of these properties is often of interest, requiring either the use of simulations at numerous temperatures, where each simulation must be long enough to ensure the difference in estimates between different temperatures is statistically significant, or the assumption of a kinetic model, such as Arrhenius behavior for rate processes.

In recent years, a number of algorithmic advances have helped ameliorate difficulties for the computation of equilibrium expectations or thermodynamic properties caused by the presence of significant enthalpic and entropic barriers. Chief among these have been simulated^{1, 2, 3} and parallel^{4, 5, 6, 7}tempering, in which the time required to cross enthalpic (entropic) barriers is reduced by allowing the system to access higher (lower) temperatures during the simulation. The use of random temperature-switching proposals and a Metropolis-like criterion for their acceptance embeds the simulations in a Markov chain that ensures, in the long run, the stationary distribution at thermal equilibrium is sampled at each temperature.⁸ The advantages of this procedure are twofold: convergence times for averages at a single temperature can often be reduced by appropriate choice of temperatures to enhance mixing,^{8, 9, 10, 11} and data from all temperatures can be combined to produce superior estimates of equilibrium expectations over a range of temperatures using histogram reweighting^{12, 13, 14, 15} or histogram-free^{16, 17} statistical analysis methods.

While helpful in the calculation of equilibrium expectations of mechanical observables that are functions only of the atomic coordinates and momenta, the data produced by simulated and parallel tempering simulations are generally not directly useful for the computation of dynamical quantities. This is due to the fact that replica trajectories include unphysical changes in temperature, and permuting the data to separate trajectories by temperature results in discontinuous trajectories for each temperature, with a complicated correlation structure entangling the temperatures.^{15, 18} The short trajectory segments generated between exchanges, however, are valid dynamical trajectories that can be used to estimate dynamical properties, as in Ref. 19.

Here, we show how trajectories from multiple temperatures (including those harvested from tempering simulations) can be reweighted to produce optimal estimates of dynamical quantities at the temperature(s) of interest, and how these estimates might be superior to those from single-temperature simulation if the crossing of enthalpic barriers or entropic bottlenecks is accelerated at some of the replica temperatures. Application of this reweighting scheme to simulated and parallel tempering simulations requires little, if any, modification of the simulation protocol. We require only that the time between exchanges is long enough to compute dynamical expectations of interest, the model of dynamics used to propagate the replica samplers in between exchanges is of a form amenable to reweighting, and the temperature spacing is close enough to permit estimation of appropriate normalization constants. We illustrate this approach by estimating a slowly-convergent property—the normalized fluctuation autocorrelation function for a conformational state of terminally-blocked solvated alanine peptide that is only sparsely populated at 300 K—and show that dynamical reweighting provides significant advantages over standard estimates from single temperatures alone.

THEORY

We now lay out the main theoretical tools necessary for estimating dynamical expectations by making use of simulations at multiple temperatures. In Sec. 2A, we provide a precise definition of the dynamical expectations we can estimate through reweighting schemes. Next, in Sec. 2B, we review the generalized path estimator for making optimal use of trajectories sampled from multiple ensembles. As this estimator requires we compute path action differences at different temperatures for every trajectory sampled, Sec. 2C presents simplified, convenient forms of these quantities for several common models of dynamics within the canonical ensemble. Finally, Sec. 2D describes a modified parallel tempering protocol that can be used to easily sample trajectories from multiple temperatures in a way that they can easily be used with this estimation-by-reweighting procedure.

Dynamical expectations

The equilibrium thermodynamic expectation of some static (non-kinetic) property A for a system obeying classical statistical mechanics can be written as

$$\begin{array}{c}\hfill 〈A〉\equiv \int dxp\left(x\right)A\left(x\right),\end{array}$$ (1)

where x denotes the instantaneous configuration of the system (such as the coordinates and momenta of all particles), A(x) is often referred to as a phase function or mechanical observable, and p(x) is the equilibrium probability density, given by

$$\begin{array}{c}\hfill p\left(x\right)=Z^{-1}q\left(x\right);Z\equiv \int dxq\left(x\right),\end{array}$$ (2)

where Z is a normalizing constant or partition function, and q(x) > 0 is an unnormalized probability density. (Here, we will choose q(x) to contain terms that depend explicitly on x; x-independent multiplicative terms will generally be absorbed into Z throughout.) In the canonical ensemble, for example, the system is in contact with a heat bath and held at fixed volume, and we have q(x) = e^−βH(x), where H(x) is the Hamiltonian and β = (k_BT)⁻¹ is the inverse temperature.

We can write an analogous expression for equilibrium dynamical expectations of a kinetic property A as

$$\begin{array}{ccc}\hfill 〈\mathcal{A}〉& =& \int dXp\left[X\right]\mathcal{A}\left[X\right],\hfill \end{array}$$ (3)

where A[X] now denotes a functional of a trajectory X ≡ x(t), p[X] is the probability density of trajectories, and the integral is taken over the space of all such trajectories with respect to an appropriate measure dX. Analogous to the case of phase space probability densities, p[X] can also be written in terms of an unnormalized density q[X] > 0,

$$\begin{array}{c}\hfill p\left[X\right]=Z^{-1}q\left[X\right];Z\equiv \int dXq\left[X\right].\end{array}$$ (4)

As we will see in Sec. 2C, the precise definition of p[X] will depend on the dynamical model under consideration.

While the expectation of any trajectory functional can, at least formally, be computed this way, the most common dynamical quantities of interest are time-correlation functions of the form

$$\begin{array}{ccc}\hfill C_{AB}\left(t\right)& \equiv & 〈A\left(0\right)B\left(t\right)〉,\hfill \end{array}$$ (5)

for some pair of phase functions A and B. This corresponds to the choice

$$\begin{array}{ccc}\hfill \mathcal{A}\left[X\right]& \equiv & A\left(x\right(0\left)\right)B\left(x\right(t\left)\right).\hfill \end{array}$$ (6)

For practical purposes, we will henceforth presume that the functional A[X] is temporally local, in that it can be expressed in a way that operates on a finite time interval that can be bounded by some fixed duration τ. We can then restrict ourselves to considering trajectory objects X ≡ x(t) of fixed length τ, so that x(t) is defined only on the interval t ∈ [0, τ]. In the case of time-correlation functions C_AB(t) above, for example, t ⩽ τ.

Expectations with respect to some altered trajectory probability density p_*[X] can also be computed within this equilibrium expectation framework by simply incorporating the weighting factor p_*[X]/p[X] into the trajectory functional A. For example, to compute time-correlation functions such as Eq. 6 with respect to nonequilibrium initial conditions, A[X] could be redefined to include a factor of ρ[X]/p[X] to account for non-equilibrium (or even non-canonical) initial phase space density ρ[X].²⁰

Dynamical reweighting

The groundwork for reweighting trajectories sampled from multiple thermodynamic states in order to produce an optimal estimate of some dynamical expectation was laid in work by Minh and Chodera.²¹ Though presented in the context of nonequilibrium experiments (in which the consequences of the Crooks fluctuation theorem^{22, 23} were explored), the estimator is sufficiently general that it applies to equilibrium trajectories sampled from different equilibrium thermodynamic states within the same thermodynamic ensemble, producing an asymptotically optimal estimate of properties within the thermodynamic state of interest. The generalized path ensemble estimator²¹ is in turn based on the statistical inference framework of extended bridge sampling,^{24, 25, 26} which provides a solid statistical foundation for earlier estimation and reweighting schemes found in statistical physics and chemistry.^{12, 13, 14, 16, 27}

Here, we briefly review the general estimator formalism and examine its application to common schemes used to model dynamics at constant temperature. While we restrict our consideration to the canonical (NVT) ensemble, extension to other thermodynamic ensembles (such as the isobaric and semigrand-canonical ensembles) and other schemes for generating trajectories within the canonical and other thermodynamic ensembles is operationally straightforward.

Suppose we have K path ensembles at different thermodynamic conditions, indexed by i ∈ {1, …, K}, characterized by trajectory probability densities

$$\begin{array}{c}\hfill p_i\left[X\right]=Z_i^{-1}{q}_i\left[X\right];Z_i\equiv \int dX{q}_i\left[X\right],\end{array}$$ (7)

where q_i[X] > 0 is an unnormalized density and Z_i an unknown normalization constant, from which we have collected N_i trajectories of duration τ. We denote these trajectories X_n, where the trajectory index n runs from 1 to $N\equiv {\sum }_{k=1}^K{N}_k$, with the trajectories from different path ensembles indexed in arbitrary order. The association of a trajectory with the path ensemble from which it was sampled will not be relevant in the estimating equations.

The optimal estimator for a dynamical expectation,

$$\begin{array}{c}\hfill {〈\mathcal{A}〉}_i=\int dX{p}_i\left[X\right]\mathcal{A}\left[X\right],\end{array}$$ (8)

was shown by Minh and Chodera²¹ to be given by

$$\begin{array}{ccc}\hfill {\widehat{\mathcal{A}}}_i& =& \sum _{n=1}^N{w}_{ni}\mathcal{A}\left[X_n\right],\hfill \end{array}$$ (9)

where the N × K weight matrix W ≡ (w_ni) containing the appropriate trajectory weights for all trajectories n in all path ensembles i is given by

$$\begin{array}{ccc}\hfill w_{ni}& =& {\widehat{Z}}_i^{-1}{\left[\sum _{k=1}^K{N}_k{\widehat{Z}}_k^{-1}{q}_k\left[X_n\right]∕q_i\left[X_n\right]\right]}^{-1}.\hfill \end{array}$$ (10)

Here, w_ni denotes the weight contribution from trajectory n in the aggregated pool of N trajectories for estimating expectations for state i. The presence of the leading normalizing factor ${\widehat{Z}}_i^{-1}$ ensures that the weights are normalized such that ${\sum }_{n=1}^N{w}_{ni}=1$ for any state i. The unnormalized path densities q_k[X_n]/q_i[X_n] represent the ratio of how likely a particular trajectory X_n is to appear in path ensemble k over path ensemble i, up to some ratio of normalizing constants Z_i/Z_k that is trajectory-independent. Importantly, the estimator expression in Eqs. 9, 10 holds even if no trajectories are sampled from some of the path ensembles, such that N_i = 0 for these unsampled ensembles, but there are still samples from other path ensembles such that N > 0.

The normalizing constants $\left\{{\widehat{Z}}_i\right\}$, determined only up to an arbitrary multiplicative constant, are determined by solving the coupled set of K nonlinear equations for i = 1, …, K, under the constraint that ${\sum }_{n=1}^N{w}_{ni}=1$:

$$\begin{array}{ccc}\hfill {\widehat{Z}}_i& =& \sum _{n=1}^N{\left[\sum _{k=1}^K{N}_k{\widehat{Z}}_k^{-1}{q}_k\left[X_n\right]∕q_i\left[X_n\right]\right]}^{-1}.\hfill \end{array}$$ (11)

This can be done efficiently through a number of methods.^{17, 21} For example, the simplest such approach is to iterate a form of Eq. 11 to self-consistency. Suppose we choose an initial guess ${\widehat{Z}}_i^{\left(0\right)}=0$, i = 1, …, K. We can employ an iterative update procedure

$$\begin{array}{ccc}\hfill {\widehat{Z}}_i^{(n+1)}& =& \sum _{n=1}^N{\left[\sum _{k=1}^K{N}_k{\left[{\widehat{Z}}_k^{\left(n\right)}\right]}^{-1}{q}_k\left[X_n\right]∕q_i\left[X_n\right]\right]}^{-1}\hfill \end{array}$$ (12)

to generate a new set of estimates $\left\{{\widehat{Z}}_i^{(n+1)}\right\}$ from a previous set of estimates $\left\{{\widehat{Z}}_i^{\left(n\right)}\right\}$. Each iteration of the update procedure requires only that we be able to compute the ratio q_k[X_n]/q_i[X_n] for all trajectories in the pool of N trajectories; these ratios can be precomputed and stored. This iterative procedure is continued until these estimates converge to within some specified tolerance.^{17, 21} For numerical stability, it is convenient to work with $\ln Z_i^{\left(n\right)}$ instead of $Z_i^{\left(n\right)}$ directly.¹⁷

In the canonical ensemble, the probability distributions are parameterized by a temperature T, or equivalently, the inverse temperature β ≡ (k_BT)⁻¹. The expectation of observable A at some arbitrary inverse temperature β, 〈A〉_β, estimated from simulations at fixed inverse temperatures β₁, …, β_K, can then be estimated as

$$\begin{array}{ccc}\hfill \widehat{\mathcal{A}}\left(\beta \right)& =& \sum _{n=1}^N{w}_n\left(\beta \right)\mathcal{A}\left[X_n\right],\hfill \end{array}$$ (13)

where the temperature-dependent trajectory weights w_n(β) are

$$\begin{array}{ccc}\hfill w_n\left(\beta \right)& =& \widehat{Z}{\left(\beta \right)}^{-1}{\left[\sum _{k=1}^K{N}_k{\widehat{Z}}_k^{-1}q\left[X_n\right|{\beta }_k]∕q\left[X_n\right|\beta ]\right]}^{-1},\hfill \end{array}$$ (14)

with normalization constants Z_k ≡ Z(β_k), and

$$\begin{array}{ccc}\hfill \widehat{Z}\left(\beta \right)& =& \sum _{n=1}^N{\left[\sum _{k=1}^K{N}_k{\widehat{Z}}_k^{-1}q\left[X_n\right|{\beta }_k]∕q\left[X_n\right|\beta ]\right]}^{-1}.\hfill \end{array}$$ (15)

Once the normalizing constants $\left\{{\widehat{Z}}_k\right\}$ have been determined by solving the coupled nonlinear equations in Eq. 11, no further nonlinear equation solution iterations are necessary to estimate $\widehat{\mathcal{A}}\left(\beta \right)$ at other temperatures of interest.

Perhaps surprisingly, Eqs. 10, 14 do not contain any information linking a trajectory X_n with the path ensemble p_j[X] from which it was sampled; this fact is a direct, if unobvious, consequence of the extended bridge sampling formalism.^{25, 26}

The unnormalized trajectory probability density q[X|β] will depend on the model of dynamics within the canonical ensemble used in the simulations; we give expressions for several popular models in Sec. 2C. In all the cases treated here, however, q[X|β] is a continuous and differentiable function of β, meaning that A(β) will also be continuous and differentiable. The utility of this estimate will depend on a number of contributing circumstances; the estimate is only expected to be reliable within the range of temperatures sampled, but estimates can, in principle, be obtained for any temperature.

The statistical uncertainty in $\widehat{\mathcal{A}}\left(\beta \right)$ can be computed in a straightforward manner from an estimate of the asymptotic variance of $\widehat{\mathcal{A}}\left(\beta \right)$.^{17, 21} Briefly, the estimating equations are linearized about the optimal estimator and the variance in the estimating equations is propagated into the corresponding variance in the estimator (see, for example, the Appendix in Ref. 26). Operationally, the N × K weight matrix W is augmented by two additional columns, indexed (for convenience) by a and A, consisting of

$$\begin{array}{c}\hfill w_{na}=w_n\left(\beta \right);w_{nA}=\frac{\mathcal{A}\left[X_n\right]}{\widehat{\mathcal{A}}\left(\beta \right)}{w}_{na},\end{array}$$ (16)

where β is the temperature of interest.

The variance in $\widehat{A}\left(\beta \right)$ can be computed from the asymptotic covariance matrix Θ, which is estimated by

$$\begin{array}{ccc}\hfill \widehat{\mathit{\Theta }}& \equiv & {\mathbf{W}}^T·{[{\mathbf{I}}_N-\mathbf{W}\mathbf{N}{\mathbf{W}}^{\mathrm{T}}]}^{+}·\mathbf{W},\hfill \end{array}$$ (17)

where I_N is the N × N identity matrix, N = diag(N₁, N₂, …, N_K, 0, 0), and A⁺ denotes the pseudoinverse of a matrix A. For cases where the columns of W are linearly independent (which will be the case when β ≠ β_i for all i ∈ {1, …, K} and β_i ≠ β_j for i ≠ j), a simpler expression that requires pseudoinversion of only O(K)×O(K) can be used:

$$\begin{array}{ccc}\hfill \widehat{\mathit{\Theta }}& =& {[{\left({\mathbf{W}}^{\mathrm{T}}\mathbf{W}\right)}^{+}-\mathbf{N}]}^{+}.\hfill \end{array}$$ (18)

Efficient computation of $\widehat{\mathit{\Theta }}$ by other means is discussed in the Appendix of Ref. 17.

The uncertainty in $\widehat{\mathcal{A}}\left(\beta \right)$ is then estimated as

$$\begin{array}{ccc}\hfill \mathrm{var}\widehat{\mathcal{A}}\left(\beta \right)& \equiv & ⟨{(\widehat{\mathcal{A}}\left(\beta \right)-⟨\widehat{\mathcal{A}}\left(\beta \right)⟩)}^2⟩\hfill \\ & \approx & {\left[\widehat{\mathcal{A}}\left(\beta \right)\right]}^2[{\widehat{\Theta }}_{aa}-2{\widehat{\Theta }}_{aA}+{\widehat{\Theta }}_{AA}].\hfill \end{array}$$ (19)

Near $\widehat{A}\left(\beta \right)\equiv 0$, the uncertainty estimation in Eq. 13 may run into numerical issues; in this case, it is recommended that the relative uncertainty $\mathrm{var}\widehat{A}\left(\beta \right)∕{\left[\widehat{A}\left(\beta \right)\right]}^2$ be computed instead.

Similarly, the covariance between two estimates $\widehat{\mathcal{A}}\left(\beta \right)$ and $\widehat{\mathcal{B}}\left({\beta }^{\prime }\right)$ at respective temperatures β and β′ (which may be the same or different) can be computed by augmenting W with additional columns,^{17, 21}

$$\begin{array}{c}\hfill w_{nb}=w_n\left({\beta }^{\prime }\right);w_{nB}=\frac{\mathcal{B}\left[X_n\right]}{\widehat{\mathcal{B}}\left({\beta }^{\prime }\right)}{w}_{nb},\end{array}$$ (20)

yielding

$$\begin{array}{ccc}& & \mathrm{cov}(\widehat{\mathcal{A}}\left(\beta \right),\widehat{\mathcal{B}}\left({\beta }^{\prime }\right))\hfill \\ & \equiv & ⟨(\widehat{\mathcal{A}}\left(\beta \right)-⟨\widehat{\mathcal{A}}\left(\beta \right)⟩)(\widehat{\mathcal{B}}\left({\beta }^{\prime }\right)-⟨\widehat{\mathcal{B}}\left({\beta }^{\prime }\right)⟩)⟩\hfill \\ & \approx & \widehat{\mathcal{A}}\left(\beta \right)\widehat{\mathcal{B}}\left({\beta }^{\prime }\right)[{\widehat{\Theta }}_{ab}-{\widehat{\Theta }}_{aB}-{\widehat{\Theta }}_{Ab}+{\widehat{\Theta }}_{AB}].\hfill \end{array}$$ (21)

This can be extended to more than two expectations if the covariance of many such pairs is desired simultaneously.^{17, 21}

For purposes of numerical stability, it is convenient to work with the logarithms of quantities like q[X|β_i]/q[X|β_j] and ${\widehat{Z}}_i∕{\widehat{Z}}_j$. We therefore define a trajectory action functional S[X|β] as

$$\begin{array}{ccc}\hfill S\left[X\right|\beta ]& \equiv & -\ln q\left[X\right|\beta ].\hfill \end{array}$$ (22)

Note that this definition differs from standard definitions (e.g., Ref. 28) in that only terms that depend on both trajectory X and temperature β are included in q[X|β] and S[X|β]—any remaining multiplicative terms in the path probability density p[X|β] are subsumed by the normalization constant Z(β) to simplify the subsequent development. Inclusion of explicit multiplicative terms that depend on β but not X could reduce the variance of dynamical reweighting estimates, but this is not done here for simplicity.

For all of the models of dynamics considered in Sec. 2C, the trajectory- and temperature-dependent action S[X|β] is linear in the inverse temperature β, having the form

$$\begin{array}{ccc}\hfill S\left[X\right|\beta ]& =& \beta \mathcal{H}\left[X\right],\hfill \end{array}$$ (23)

where the quantity H[X] plays the role of a generalized path Hamiltonian that operates on trajectory space, analogous to the role of the standard Hamiltonian H(x) that operates on microstates in phase space. We note that the path Hamiltonian can be trivially computed from the action S[X|β] or unnormalized path density q[X|β] as

$$\begin{array}{ccc}\hfill \mathcal{H}\left[X\right]& =& {\beta }^{-1}S\left[X\right|\beta ]=-{\beta }^{-1}\ln q\left[X\right|\beta ].\hfill \end{array}$$ (24)

We also define the dimensionless path free energy f_i of path ensemble i as

$$\begin{array}{ccc}\hfill f_i& \equiv & -\ln Z_i.\hfill \end{array}$$ (25)

The logarithms of the trajectory weights w_n(β) can then be written in terms of the path Hamiltonians H[X] and dimensionless free energies f_i as

$$\begin{array}{ccc}\hfill \ln w_n\left(\beta \right)& =& \widehat{f}\left(\beta \right)-\ln \sum _{k=1}^K{N}_k{e}^{{\widehat{f}}_k-({\beta }_k-\beta )\mathcal{H}\left[X_n\right]},\hfill \end{array}$$ (26)

where the temperature-dependent dimensionless free energy $\widehat{f}\left(\beta \right)$ is given by

$$\begin{array}{ccc}\hfill \widehat{f}\left(\beta \right)& =& -\ln \sum _{n=1}^N{\left[\sum _{k=1}^K{N}_k{e}^{{\widehat{f}}_k-({\beta }_k-\beta )\mathcal{H}\left[X_n\right]}\right]}^{-1},\hfill \end{array}$$ (27)

and the ${\widehat{f}}_k\equiv \widehat{f}\left({\beta }_k\right)$. Practical notes about working with the estimation equations in a numerically stable and efficient manner are given in.^{17, 21} Due to the analogous nature of estimating static equilibrium expectations using the Bennett acceptance ratio (MBAR) method,¹⁷PYMBAR, the PYTHON package for performing MBAR analysis (available at http:∕/simtk.org∕home∕pymbar), can be used for the computation of dimensionless path free energies ${\widehat{f}}_i$, expectations $\widehat{A}$, and covariances $\mathrm{cov}(\widehat{A},\widehat{B})$ by using path actions S[X] in place of the reduced potential energy u(x). This scheme was used for the calculations presented here.

Models of dynamics in the canonical ensemble

While the path ensemble estimator (described for temperature-dependent dynamics in Sec. 2B, and more generally in Ref. 21) can be applied to dynamics in any thermodynamic ensemble in which the unnormalized trajectory probability density ratios q_i[X]/q_j[X] are finite and nonzero over the same domain, we restrict our consideration to the canonical (NVT) ensemble in classical statistical mechanics. As the concept of a thermodynamic ensemble is a purely equilibrium construct, it specifies only the relative probability p(x|β) with which a configuration or phase space point x is observed at equilibrium. To write a probability density over equilibrium trajectories at inverse temperature β, p[X|β], we must further specify a particular scheme for modeling dynamics within this ensemble. The choice of model used to simulate dynamics within this ensemble is not unique—many schemes can be employed that will generate the same equilibrium density in phase space p(x|β), but will have different trajectory probability densities p[X|β]. This choice must therefore be guided by both a desire to mimic the relevant physics for the system of interest (such as whether the system must be allowed to exchange energy with an external heat reservoir during the course of dynamical evolution), balanced with computational convenience (e.g., the use of a stochastic thermostat in place of explicitly simulating a large external reservoir).

We consider four common models for simulating dynamics within the NVT ensemble for which the ratio of unnormalized trajectory probability densities q[X|β_i]/q[X|β_j] can be computed: (i) Hamiltonian dynamics with canonically-distributed initial conditions, (ii) an Andersen thermostat,²⁹ (iii) Langevin dynamics, and (iv) overdamped Langevin (sometimes called Brownian) dynamics. Notably, the deterministic nature of the Nosé-Hoover thermostat^{30, 31} and the way that the inverse temperature β appears in its equations of motion means a trajectory X ≡ x(t) generated at inverse temperature β_i will have identically zero probability p[X|β_j] at inverse temperature β_j ≠ β_i, preventing its use in the reweighting scheme described here. The same is true of the Berendsen weak-coupling algorithm,³² though any usage of this form of thermal control is highly discouraged because of its failure to generate a canonical ensemble^{33, 34, 35} or be ergodic.³⁴

Canonical distribution of Hamiltonian trajectories

Consider a collection of trajectories of length τ in which initial phase space points x₀ ≡ x(0) are sampled from the canonical density p(x₀|β), and whose dynamical evolution is governed by Hamiltonian mechanics. Physically, this corresponds to the statistics of a situation where the system is initially in contact with a thermal reservoir at inverse temperature β, but the evolution time τ is short enough that effectively no heat is exchanged with the reservoir during this time. Practically, an ensemble of these trajectories can be generated in a number of ways: For example, the initial configurations x₀ could be generated from the desired canonical ensemble p(x₀|β)∝e^−βH(x₀) by a form of Metropolis-Hastings Monte Carlo³⁶ or hybrid Monte Carlo.³⁷

The trajectory probability density p[X|β] is given by

$$\begin{array}{ccc}\hfill p\left[X\right|\beta ]& =& Z{\left(\beta \right)}^{-1}{e}^{-\beta H\left(x_0\right)},\hfill \end{array}$$ (28)

where H(x) denotes the Hamiltonian for the system and x₀ ≡ x(0) is the initial phase space point. While the normalization constant can be written as

$$\begin{array}{ccc}\hfill Z\left(\beta \right)& =& \int dx{e}^{-\beta H\left(x\right)},\hfill \end{array}$$ (29)

we do not need to compute it for use in dynamical reweighting.

The path Hamiltonian H[X] can then be identified (via Eq. 24) as being identical to the Hamiltonian

$$\begin{array}{ccc}\hfill \mathcal{H}\left[X\right]& =& H\left(x_0\right).\hfill \end{array}$$ (30)

We note that, while the Hamiltonian is invariant along the trajectory for true Hamiltonian dynamics, numerical integrators will not exactly preserve this property.

Andersen thermostat

The Andersen thermostat^{29, 38} allows the system to exchange heat with an external thermal reservoir through stochastic collisions with virtual bath particles. These “collisions” simply cause the real particle's velocity to be reassigned from a Maxwell-Boltzmann distribution corresponding to the thermostat temperature, ensuring that the canonical ensemble is sampled.²⁹

Two schemes are commonly used. In the first scheme, the system undergoes so-called massive collisions, in which all momenta are reassigned from the Maxwell-Boltzmann distribution at fixed intervals; evolution between collisions occurs by normal Hamiltonian dynamics. This collision interval can have a large effect on the kinetic properties of the system, so this scheme is usually used only for studying static thermodynamic properties.

In the second scheme, each particle has a fixed probability per unit time ν of having its momenta reassigned. This corresponds to a scenario in which each particle undergoes independent stochastic collisions with fictitious bath particles, with the system evolving according to Hamiltonian dynamics between collisions. Andersen suggested a physically-motivated collision frequency ν could be selected based on the thermal conductivity κ of the sample²⁹

$$\begin{array}{ccc}\hfill \nu & =& \frac{2a\kappa }{3k_B{\rho }^{1∕3}{N_p}^{2∕3}},\hfill \end{array}$$ (31)

where a is a dimensionless constant that depends on the shape of the system, ρ is the density, and N_p is the number of particles. Note that, as the system size increases with N_p, the collision frequency ν decreases as $N_p^{-2∕3}$, such that the dynamics will approach that of a Hamiltonian system for large systems. Further elaborations of this thermostatting scheme attempt to model physically realistic dynamics of large solutes, such as solvated biological macromolecules, by coupling the thermostat only to solvent degrees of freedom (see, e.g., Ref. 39). Systems with constraints will require the velocity components along the constraints to be removed prior to integration by an algorithm such as RATTLE.⁴⁰

For either thermostatting scheme, the probability of sampling a trajectory X ≡ x(t) at inverse temperature β is therefore determined by the probability of selecting the initial configuration x₀ ≡ x(0) from equilibrium and the probability of generating the resulting sequence of random collisions. Up to irrelevant temperature-independent multiplicative constants that simply determine the probability that a given sequence of N_c particle collisions occurred, this probability is

$$\begin{array}{ccc}\hfill p\left[X\right|\beta ]& \propto & e^{-\beta H\left(x_0\right)}\prod _{n=1}^{N_c}{\pi }_v\left({\mathbf{v}}_n\right|m_n,\beta ),\hfill \end{array}$$ (32)

where the index n in the product runs over all particle collisions that occurred during integration (either at regular intervals or stochastically determined), indexed in arbitrary order. v_n is the velocity of the particle after the nth massive collision, m_n its mass, and π_v(v|m, β) is the Maxwell-Boltzmann distribution for the velocity vector of a particle of mass m at inverse temperature β:

$$\begin{array}{ccc}\hfill {\pi }_v\left(\mathbf{v}\right|\beta ,m)& \propto & e^{-\beta m{v}^2∕2}.\hfill \end{array}$$ (33)

The path Hamiltonian H[X] can therefore be identified as the Hamiltonian for the initial phase space point x₀ plus the new kinetic energies of all particles that have undergone collisions during the course of integration:

$$\begin{array}{ccc}\hfill \mathcal{H}\left[X\right]& =& H\left(x_0\right)+\frac{1}{2}\sum _{n=1}^{N_c}{m}_n{v}_n^2,\hfill \end{array}$$ (34)

where again, v_n is the new velocity of the particle that had undergone collision indexed by n, and m_n is its mass.

Langevin dynamics

In Langevin dynamics, stochastic forces are used to mimic the influence of degrees of freedom that are not explicitly represented by particles in the system, such as solvent molecules whose influence is incorporated into the potential by mean-field interactions. The memoryless Langevin equations of motion for phase space point x ≡ (r, v), consisting of Cartesian atomic positions r and velocities v, are

$$\begin{array}{ccc}\hfill {\dot{r}}_i\left(t\right)& =& v_i\left(t\right),\hfill \\ \hfill m_i{\dot{v}}_i\left(t\right)& =& F_i\left(\mathbf{v}\left(t\right)\right)-{\gamma }_i{v}_i\left(t\right)+R_i\left(t\right),\hfill \end{array}$$ (35)

where m_i is the mass associated with degree of freedom i, F_i(q) ≡ −∂H/∂q_i is the systematic force component, and γ_i is an effective collision frequency or friction coefficient for that degree of freedom, with units of inverse time (e.g. 91 ps⁻¹ for water-like viscosity). γ_i is related to the temperature-dependent diffusion constant D_i(β) by

$$\begin{array}{ccc}\hfill D_i\left(\beta \right)& =& {\left(\beta {\gamma }_i{m}_i\right)}^{-1}.\hfill \end{array}$$ (36)

The stochastic force R_i(t) has zero mean and satisfies the fluctuation-dissipation theorem,

$$\begin{array}{ccc}\hfill ⟨R_i\left(t\right)R_j\left(t^{\prime }\right)⟩& =& 2{\beta }^{-1}{m}_i{\gamma }_i{\delta }_{ij}\delta (t-t^{\prime }).\hfill \end{array}$$ (37)

The Langevin Leapfrog integrator⁴¹ is an accurate and stable algorithm for integrating the Langevin equations of motion. Updating of positions r_t and velocities v_t by a discrete timestep Δt is handled by the following scheme:

$$\begin{array}{ccc}& v_{i,t+\frac{1}{2}}& =a_i{v}_{i,t}+b_i\Delta t{m}_i^{-1}{F}_i\left(X_t\right)+c_i{m}_i^{-1∕2}{\xi }_{it},\hfill \\ & r_{i,t+1}& =r_{i,t}+\Delta t{v}_{i,t+\frac{1}{2}},\hfill \\ & v_{i,t+1}& =a_i{v}_{i,t+\frac{1}{2}}+b_i\Delta t{m}_i^{-1}{F}_i\left(X_{t+1}\right)+c_i{m}_i^{-1∕2}{\xi }_{i(t+1)},\hfill \end{array}$$ (38)

where we have defined the dimensionless constants a_i, b_i, and c_i associated with each degree of freedom i as

$$\begin{array}{ccc}\hfill a_i& \equiv & e^{-{\gamma }_i\Delta t∕2},\hfill \\ \hfill b_i& \equiv & (1-e^{-{\gamma }_i\Delta t∕2})∕\left({\gamma }_i\Delta t\right),\hfill \\ \hfill c_i& \equiv & {(1-e^{-{\gamma }_i\Delta t})}^{1∕2}.\hfill \end{array}$$

As the collision rate γ_i → 0, we have a_i → 1, b_i → 1/2, and c_i → 0, resulting in the standard leapfrog integrator scheme.

ξ_it is a unit-bearing random normal variate with zero mean and variance β⁻¹ = k_BT, simply denoted

$$\begin{array}{ccc}\hfill {\xi }_{it}& \sim & \mathcal{N}(0,{\beta }^{-1}).\hfill \end{array}$$ (39)

Note that ξ_it has units of the square-root of energy.

Propagation for N_t steps of Langevin leapfrog integration from initial configuration x₀ ≡ (r₀, v₀) for a system with N_d degrees of freedom requires generating the sequence of random variates ξ_it. Ignoring multiplicative factors not involving both trajectory X and temperature β, the unnormalized equilibrium probability of sampling a trajectory X which originates at x₀ and has noise history ξ_it at inverse temperature β is given by

$$\begin{array}{ccc}\hfill q\left[X\right|\beta ]& =& e^{-H\left(x_0\right)}\prod _{t=0}^{N_t}\prod _{i=1}^{N_d}\phi ({\xi }_{it};0,{\beta }^{-1}),\hfill \end{array}$$ (40)

where ϕ(x; μ, σ²) is the normal probability density,

$$\begin{array}{ccc}\hfill \phi (y;\mu ,{\sigma }^2)& \propto & \exp \left[-\frac{1}{2{\sigma }^2}{(y-\mu )}^2\right].\hfill \end{array}$$ (41)

The path Hamiltonian can therefore be computed from the initial phase space point x₀ and unit-bearing noise history ξ_it, as

$$\begin{array}{ccc}\hfill \mathcal{H}\left[X\right]& =& H\left(x_0\right)+\frac{1}{2}\sum _{t=0}^{N_t}\sum _{i=1}^{N_d}{\xi }_{ti}^2,\hfill \end{array}$$ (42)

which can easily be accumulated during integration.

Note that, if γ_i = 0 for a degree of freedom i, the corresponding noise term ${\xi }_{ti}^2$ does not contribute to the integration in Eq. 38 and can be omitted from the path Hamiltonian above.

Overdamped Langevin (Brownian) dynamics

At high friction, momentum relaxation becomes fast compared to particle motion, such that inertial motion may be neglected. A common integrator for this overdamped regime, in which only coordinates q are explicitly integrated, is given by Ermak and Yeh^{42, 43}

$$\begin{array}{ccc}\hfill r_{t+1,i}& =& r_{ti}+\frac{\Delta t}{{\gamma }_i{m}_i}{F}_i\left(x_t\right)+\sqrt{2}{\left(\frac{\Delta t}{{\gamma }_i{m}_i}\right)}^{1∕2}{\xi }_{ti},\hfill \end{array}$$ (43)

where the stochastic component ξ_ti is again a unit-bearing normal random variate with zero mean and variance β⁻¹ = k_BT,

$$\begin{array}{c}\hfill {\xi }_{ti}\sim \mathcal{N}(0,{\beta }^{-1}),\end{array}$$ (44)

with units of the square-root of energy, and γ_i is a collision rate of friction constant for degree of freedom i, with units of inverse time, where the temperature-dependent diffusion constant D_i is again related by Eq. 36.

Ignoring irrelevant multiplicative factors that do not depend on both trajectory X and temperature β, the unnormalized probability functional for a realization of N_t steps of this process is then

$$\begin{array}{ccc}\hfill q\left[X\right|\beta ]& =& e^{-\beta U\left(x_0\right)}\prod _{t=1}^{N_t}\prod _{i=1}^{N_d}\phi ({\xi }_{ti};0,{\beta }^{-1}),\hfill \end{array}$$ (45)

where U(x) = U(r) denotes the potential energy and ϕ(y; μ, σ²) again denotes the normal probability density. This allows us to identify the path Hamiltonian as

$$\begin{array}{ccc}\hfill \mathcal{H}\left[X\right]& =& U\left(x_0\right)+\frac{1}{2}\sum _{t=1}^{N_t}\sum _{i=1}^{N_d}{\xi }_{ti}^2.\hfill \end{array}$$ (46)

Modified parallel tempering protocol

An especially convenient way to harvest trajectories from multiple temperatures is through the use of parallel tempering.^{4, 5, 6, 7} As illustrated by Buchete and Hummer,⁴⁴ the trajectory segments generated in between exchange attempts are valid dynamical trajectories sampled from the corresponding replica temperatures. Simulated tempering can likewise be employed, though we will not discuss this here.

Below, we enumerate several considerations that must be taken into account for the use of a parallel tempering protocol to collect trajectories for use in dynamical reweighting.

First, the dynamics in between exchange attempts must use a scheme amenable to reweighting, such as one of the models of dynamics within the canonical ensemble described in Sec. 2C. While this means some popular choices, such as Nosé-Hoover dynamics^{30, 31} and the Berendsen weak-coupling algorithm⁴⁵ cannot be used, considerable flexibility remains in which dynamical schemes are permitted, including Hamiltonian, Andersen, Langevin, and overdamped Langevin (Brownian) dynamics, as discussed in Sec. 2C.

Second, the time between exchange attempts should be at least as long as τ, the time over which the computed dynamical observable A[X] is temporally local. For example, if a correlation function C_AB(t) ≡ 〈A(0)B(t)〉 is desired for t ∈ [0, τ], the time between exchanges should be at least τ. This may, in some circumstances, impact the efficiency of parallel tempering in producing uncorrelated samples. For functions A that require a large τ, much of the benefit of the exchanges in parallel tempering may be lost if few exchange attempts occur during the simulation. Often, the best choice is to make this time exactly τ, since the enhanced mixing properties of parallel tempering simulations diminish as the time between exchanges grows (for fixed total simulation time).⁴⁶

Thirdly, it is necessary that there is sufficient overlap in the distribution of path Hamiltonians sampled from neighboring temperatures for dynamical reweighting to be effective. While the standard replica-exchange acceptance criteria⁷ will lead to the correct distribution of trajectories at each temperature, the fraction of accepted exchange attempts reports on the quality of overlap of potential energies, rather than the overlap of path Hamiltonians; as a result, poor reweighting performance may be obtained despite a high exchange acceptance fraction. A simple way to ensure both good overlap in path Hamiltonian between neighboring temperatures and correct sampling of the equilibrium distribution is to use a modified exchange criterion based on the trajectory action:

$$\begin{array}{ccc}\hfill P_{\mathrm{exch}}({\beta }_i,{\beta }_j)& =& \min \left\{1,\frac{p\left[X_i\right|{\beta }_j]p\left[X_j\right|{\beta }_i]}{p\left[X_i\right|{\beta }_i]p\left[X_j\right|{\beta }_j]}\right\}\hfill \\ & =& \min \left\{1,e^{-({\beta }_j-{\beta }_i)(\mathcal{H}\left[X_i\right]-\mathcal{H}\left[X_j\right])}\right\},\hfill \end{array}$$ (47)

where, again, H[X]=β⁻¹S[X|β]=−β⁻¹lnq[X|β] denotes the path Hamiltonian for trajectory X defined in Eq. 24. The resulting procedure can be considered a form of parallel tempering transition path sampling,⁴⁷ with the difference that new trajectories are generated from old ones in the more conventional fashion of integrating equations of motion from the final configuration x_T of the previous trajectory, rather than some form of transition path sampling.^{28, 48} Note that, even for the case of a canonical distribution of Hamiltonian trajectories, the modified acceptance criteria of Eq. 47 differs from the standard acceptance criteria,⁷ as the total Hamiltonian in the modified criteria replaces the potential energy in the standard criteria.

Attempting to swap temperatures β_i and β_j for an arbitrarily chosen pair of replicas (i, j) will ensure that the trajectories are correctly distributed from equilibrium at their new (or old) temperatures after the exchange attempt guarantees each replica visiting temperature β_i samples from p[X|β_i] in the long run;^{8, 49, 50} as a result, their individual timeslices x_t will also be distributed from the corresponding equilibrium distribution p(x|β_i). If there is poor overlap between the trajectory action distributions, then the exchange attempts between these temperatures will rarely succeed; on the other hand, if the overlap is good, then the exchange rate will be accepted with significant probability. Because the cost of a single exchange attempt is insignificant compared to the computational cost of propagating all K replicas by another time τ, it is recommended that many swaps between pairs (i, j) chosen with uniform probability be attempted in order to ensure the replicas are well-mixed. Monitoring of attempted and accepted exchanges early in the simulation can help diagnose whether there is sufficient coupling between all temperatures for successful reweighting.

While it is not strictly necessary to employ this modified acceptance probability, some care must be taken to ensure that a canonical distribution is actually obtained. For example, swapping using an exchange criteria based only on potential energies (as suggested by Sugita et al.⁷) and failing to rescale velocities may lead to an incorrect distribution. On the other hand, rescaling the velocities by (β_old/β_new)^1/2 as recommended,⁷ or subsequently redrawing the initial velocities from a Maxwell-Boltzmann distribution at the new temperature^{6, 51}—a process equivalent to “massive collisions” for the Andersen thermostat, is not problematic. However, extra care must be taken to ensure the temperatures are spaced such that there is sufficient overlap in trajectory action between neighboring temperatures.

Finally, we note that the temporally sequential trajectories produced by each replica will have some degree of correlation in the observable A[X]. If this correlation is significant, the uncertainty estimate produced by Eq. 19 will be an underestimate of the true statistical error, as the samples used in the estimation are assumed to be uncorrelated. A simple way to remove this correlation is to construct the timeseries A_t≡A[X_t] over the sequentially-sampled trajectories X_t from a single replica (without having permuted the replicas to collect trajectory data by temperature) and estimate the statistical inefficiency g_A from the integrated autocorrelation time of the timeseries A_t, t = 0, 1, ….^{17, 52, 53, 54, 55} If an equally-spaced subset of N∕g_A trajectories from the replicas is generated, these samples will be effectively uncorrelated. Alternatively, the time between exchanges τ can be increased to ensure that sequential A_t are decorrelated.

CORRELATION FUNCTIONS OF A SOLVATED TERMINALLY-BLOCKED ALANINE PEPTIDE

To illustrate the application of dynamical reweighting to a condensed-phase system, we consider the estimation of the normalized fluctuation autocorrelation function for a long-lived conformational state of terminally-blocked alanine peptide in water that is sparsely populated at 300 K. Additional simulation details are given in Appendix A. All code, datasets, analysis scripts, and plotting scripts used for this application are made available for download at http:∕/simtk.org∕home∕dynamical-reweighting.

The modified parallel tempering protocol described in Sec. 2D was used to sample many 10 ps trajectories from each of 40 exponentially-spaced temperatures spanning 300–600 K, using the “canonical distribution of Hamiltonian trajectories” model of dynamics described in Sec. 2C1. Replica temperatures were chosen to be exponentially spaced so that T_k = (T_max − T_min)exp [(k − 1)/(K − 1)] + T_min for k = 1, …, K; this is equivalent to geometrically-spaced replicas, which would achieve equal acceptance rates among replicas if the system being simulated was an ideal gas. These temperatures may not be optimal in terms of reducing replica correlation times or equalizing acceptance probabilities for the system studied here. While numerous schemes for intelligently choosing or adapting temperatures exist,^{56, 57, 58, 59, 60} no attempt was made to do so here. The modified protocol makes use of the exchange criteria of Eq. 47, where path Hamiltonians instead of potential energies are used in computing the probability of accepting a proposed temperature swap between replicas; this amounts to simply using the total energies H(x) in the exchange criteria, the sum of potential and kinetic energies, instead of only the potential energies in standard parallel tempering protocols. A total of 6720 iterations were conducted (67 ns∕replica, or 2.7 μs aggregate), where each iteration consisted of a temperature exchange phase, assignment of new velocities from the Maxwell-Boltzmann distribution at the appropriate replica temperature, and generation of a 10 ps trajectory segment.

To ensure thorough mixing of the replica associations with temperatures, 40³ = 64 000 exchange attempts among randomly selected pairs of replicas were attempted each parallel tempering iteration. Because exchanges are attempted among all temperatures, and not just neighboring ones, the probability any two temperatures are exchanged during the simulation is diagnostic of whether there is sufficient overlap among temperatures for successful reweighting; in particular, if no swaps occur between specified subsets of temperature, reweighting will produce highly uncertain estimates. Over the course of the simulation, 31.5% of proposed neighbor swaps were accepted, 4.5% of next-neighbor swaps, and 1.1% of more remote proposed exchanges accepted. The second-largest eigenvalue of the empirical temperature exchange matrix was less than unity—estimated to be 0.99801—indicating that the set of temperatures did not decompose into two or more subsets with extremely poor exchange properties between them; were there two subsets of temperatures with no transitions in between, this eigenvalue would have been unity. This indicates that a sufficient number of replicas were chosen to span the range of temperatures with reasonably good exchange among temperatures.

A statistically uncorrelated subset of trajectories generated from the modified parallel tempering simulation were extracted according to the procedure described in Sec. 2D. The statistical inefficiency g of the timeseries u_n was computed, where u_n is defined as the effective reduced potential for the replica ensemble, defined in terms of the instantaneous joint configuration of all replica conformations X≡{X₁,...,X_K}:

$$\begin{array}{ccc}\hfill u_n& \equiv & u\left({\mathcal{X}}_n\right)=\sum _{k=1}^K{\beta }_k\mathcal{H}\left[X_{kn}\right].\hfill \end{array}$$ (48)

Here, X_kn denotes the trajectory sampled from the replica at temperature β_k at iteration n of the parallel tempering simulation, and H[X] the path Hamiltonian. As the quantity u_n denotes the log-probability of the overall replica-exchange joint probability distribution function P(X₁, …, X_K|β₁, …, β_K), and the statistical inefficiency of the timeseries u_n, n = 1, …, N roughly corresponds to the number of parallel tempering iterations required to generate an independent set of samples. After discarding the first 50 iterations to equilibration, the statistical inefficiency was estimated to be 3.1 iterations.

We define the α_R conformation as ψ ∈ [ − 124, 28) degrees, based on examination of the one-dimensional potential of mean force (PMF) in the ψ torsion at 300 K (Figure 1), which was estimated using the multistate Bennett acceptance ratio (MBAR) (Ref. ¹⁷) and a Gaussian kernel density estimator with a bandwidth of 20 degrees. This state has a low population at 300 K (9.6 ± 0.5% as estimated by MBAR), but a relatively long lifetime compared to other conformational transitions in this peptide model. As an observable, we chose the indicator function for the α_R state:

$$\begin{array}{ccc}\hfill h\left(x\right)& =& \left\{\begin{array}{cc}\hfill 1,& \hfill \psi \left(x\right)\in [-124,28)\mathrm{degrees},\\ \hfill 0,& \hfill \mathrm{else}.\end{array}\right.\hfill \end{array}$$ (49)

We compute the normalized fluctuation correlation function C(τ; β),

$$\begin{array}{ccc}\hfill C(\tau ;\beta )& \equiv & \frac{{〈\delta h\left(0\right)\delta h\left(\tau \right)〉}_{\beta }}{{⟨\delta h^2⟩}_{\beta }},\hfill \end{array}$$ (50)

where we use the shorthand δh(t) ≡ h(x(t)) − 〈h〉_β. We note that, while the correlation function C(τ; β) describes the relaxation dynamics out of the defined region ψ ∈ [ − 124, 28) degrees, this correlation function may contain multiple exponential timescales due to the simplistic definition of the α_R stable state. Estimation of accurate rate estimates would require calculation of a quantity robust to imperfect definition of dividing surface, such as examination of the reactive flux correlation function^{61, 62} or the Markov model described in a companion paper.⁶³

Figure 1.

Terminally-blocked alanine in explicit solvent and potential of mean force of ψ torsion at 300 K. The dark shaded region denotes a 95% confidence interval (two standard errors) in the free energy difference between the plotted ψ torsion and the lowest point on the potential of mean force (near ψ = 150 degrees). The labeled light shaded region denotes the α_R conformation. The PMF and error bars were estimated from the parallel tempering dataset using MBAR as described in the text.

Because C(τ; β) is not easily expressed as a single expectation, we write it as a combination of two elementary path expectations. For a fixed choice of τ, we define the path functionals A and B as

$$\begin{array}{ccc}\hfill \mathcal{A}\left[X\right]& \equiv & h\left(x\right(0\left)\right)h\left(x\right(\tau \left)\right),\hfill \\ \hfill \mathcal{B}\left[X\right]& \equiv & h\left(x\right(0\left)\right).\hfill \end{array}$$ (51)

The correlation function C(τ; β) can then be written as

$$\begin{array}{ccc}\hfill C(\tau ;\beta )& =& \frac{{〈\mathcal{A}〉}_{\beta }-{〈\mathcal{B}〉}_{\beta }^2}{{〈\mathcal{B}〉}_{\beta }-{〈\mathcal{B}〉}_{\beta }^2}.\hfill \end{array}$$ (52)

and hence its estimator, in terms of $\widehat{\mathcal{A}}\left(\beta \right)$ and $\widehat{\mathcal{B}}\left(\beta \right)$, is

$$\begin{array}{ccc}\hfill \widehat{C}(\tau ;\beta )& =& \frac{\widehat{\mathcal{A}}\left(\beta \right)-\widehat{\mathcal{B}}{\left(\beta \right)}^2}{\widehat{\mathcal{B}}\left(\beta \right)-\widehat{\mathcal{B}}{\left(\beta \right)}^2},\hfill \end{array}$$ (53)

where we have used the fact that (B[X]⁾²=B[X] because [h(x)]² = h(x). The statistical uncertainty in $\widehat{C}(\tau ;\beta )$ is determined by simple propagation of error. Suppressing the functional dependence on β, we have

$$\begin{array}{ccc}\hfill {\delta }^2\widehat{C}& =& {\left[\frac{\partial \widehat{C}}{\partial \widehat{\mathcal{A}}}\right]}^2{\delta }^2\widehat{\mathcal{A}}+{\left[\frac{\partial \widehat{C}}{\partial \widehat{\mathcal{B}}}\right]}^2{\delta }^2\widehat{\mathcal{B}}+2\left[\frac{\partial \widehat{C}}{\partial \widehat{\mathcal{A}}}\right]\left[\frac{\partial \widehat{C}}{\partial \widehat{\mathcal{B}}}\right]\delta \widehat{\mathcal{A}}\delta \widehat{\mathcal{B}},\hfill \end{array}$$ (54)

where the partial derivatives are given by

$$\begin{array}{c}\hfill \frac{\partial \widehat{C}}{\partial \widehat{\mathcal{A}}}=\frac{1}{\mathcal{B}(1-\mathcal{B})};\frac{\partial \widehat{C}}{\partial \widehat{\mathcal{B}}}=\frac{\mathcal{A}-1}{{(\mathcal{B}-1)}^2}-\frac{\mathcal{A}}{{\mathcal{B}}^2}.\end{array}$$ (55)

Where the quantities ${\delta }^2\widehat{\mathcal{A}}\equiv \mathrm{var}\widehat{\mathcal{A}}$, ${\delta }^2\widehat{\mathcal{B}}\equiv \mathrm{var}\widehat{\mathcal{B}}$, and $\delta \widehat{\mathcal{A}}\delta \widehat{\mathcal{B}}\equiv \mathrm{cov}(\widehat{\mathcal{A}},\widehat{\mathcal{B}})$ represent the statistical errors (variance or covariance) of the estimators $\widehat{\mathcal{A}}$ and $\widehat{\mathrm{B}}$.

Estimates for C(τ; β) were computed using either the pool of uncorrelated trajectories at each replica temperature, or for a superset of temperatures (including the simulation temperatures) by dynamical reweighting as described in Sec. 2B. For the former case, statistical error estimates were computed using sample (co)variances; for the latter case, statistical errors were computed using covariances obtained using Eqs. 19, 21. Figure 2 compares correlation functions estimated for a few temperatures using single-temperature data and multiple-temperature data using dynamical reweighting.

Figure 2.

Normalized fluctuation autocorrelation functions for indicator function on α_R conformation. In both plots, single-temperature estimates are shown as points with error bars, and the dynamical reweighting estimate is shown as a solid line with shaded error interval. Error bars denote 95% confidence intervals (two standard errors).

To demonstrate how dynamical reweighting produces a smooth estimate throughout the temperature range, even at temperatures not sampled, Figure 3 shows the estimate of C(τ; β) for τ = 10 ps. Clearly, the reweighted estimate produces a smoother, continuous estimate across all temperatures, with a uniformly reduced statistical uncertainty compared to the estimates computed from individual temperatures. While some features in the reweighted estimate are likely spurious, the 95% confidence interval envelope (shaded region) still permits a smooth, well-behaved curve within its boundaries.

Figure 3.

Temperature dependence of the normalized fluctuation autocorrelation function C(τ; β) for τ = 10 ps. Single-temperature estimates are shown as points with error bars denoting a 95% confidence interval; the dynamical reweighting estimate is shown as a solid line with shaded confidence interval.

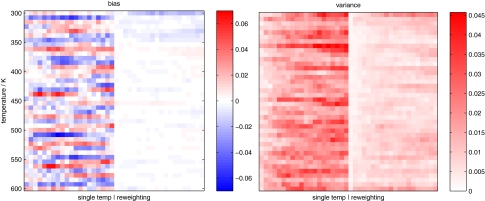
Finally, we compare the bias and variance of single-temperature estimates with the dynamical reweighting estimate in a manner independent of the statistical error estimator. The replica-exchange trajectory was divided into 20 contiguous blocks of equal length, and C(τ; β) estimated independently on each block. Using the dynamical reweighting estimate over the entire dataset as a reference, the bias and variance of the single-temperature and dynamical reweighting estimators were assessed by computing the estimators for each of 20 consecutive subsets of the simulation, and computing the mean deviation or standard deviation of the estimates over the blocks. The bias, which is defined as the expectation over many independent realizations of the experiment of the deviation of the estimate from the true value, was estimated as the sample mean of the block estimates minus the estimate computed using all data; the variance, which represents the expected squared-deviation of the estimator from its expectation over many independent realizations of the experiment, was estimated by the sample variance over the blocks. Figure 4 depicts the estimated bias and variance in $\widehat{C}(\tau ;\beta )$ for all times τ ∈ [0, 10] and all simulation temperatures β_k. The advantage of dynamical reweighting is clear. Bias is minimized by virtue of the fact that contributions to the dynamical property can occur at any temperature and are incorporated with their appropriate weight, rather than relying upon small-number statistics where the events of interest may occur few or no times within the simulation at the temperature of interest. Similarly, inclusion of data from multiple temperatures reduces the overall variance component of the statistical error, resulting in improved estimates at all temperatures.

Figure 4.

Bias and variance of single-temperature estimate versus dynamical reweighting estimates. The estimated bias (left) and variance (right) of the estimated normalized fluctuation correlation function estimated by dividing the simulation into 20 blocks of equal length. The left half of each color block shows the statistic for single-temperature estimates, while the right half shows the statistic for dynamical reweighting estimates employing data from all temperatures. Each horizontal row represents the estimated bias or variance for the correlation function C(τ; β) over τ ∈ [0, 10] ps for one temperature; temperatures are ordered from lowest (top) to highest (bottom).

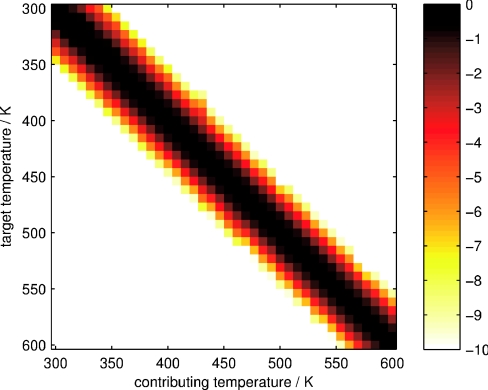
Figure 5 shows the total trajectory weight contributing from each sampled temperature as a function of target temperature β, where the per-trajectory weight w_n(β) from Eq. 14 is summed over all trajectories from the contributing sampled temperature and plotted on a base-10 logarithmic scale, normalized so that the target temperature has a total contributing weight of unity (zero on log scale). After the target temperature, neighboring temperatures contribute the most trajectory weight to averages at the target temperature, with the contribution rapidly falling off for more distant temperatures. Note that this does not mean that distant temperatures are unhelpful, as they may still serve to reduce the effective replica correlation time if correlation times at high temperatures are especially short.⁸

Figure 5.

Logarithmic total weight contributed from all trajectories at each sampled temperature to various temperatures. The base-10 logarithm of the sum of weights w_n(β) from all trajectories sampled from each contributing temperature is shown for each target (reweighted) temperature corresponding to inverse temperature β. The contribution from the target temperature is normalized in this plot to have a total weight of unity (zero logarithm).

Normalizing the total trajectory weight contributed from each temperature to the weight contributed from the target temperature allows us to roughly estimate how much useful data in total we are extracting by making use of reweighting in this system by summing this total relative weight over all temperatures. This quantity, averaged over all target temperatures, is ∼2.4, suggesting that approximately 2.4 times as much data is provided in this system by making use of reweighting instead of just the data collected from the replicas that visit the target temperature. Increasing the quantity of data collected by a factor of 2.4 should decrease the standard error by $\sim \sqrt{2.4}\approx 1.6$, an amount consistent with the difference in confidence interval widths depicted in Figure 2.

DISCUSSION

The dynamical reweighting scheme outlined here provides a convenient way to estimate equilibrium dynamical properties from simulations at multiple temperatures, complementing reweighting schemes for estimating static expectations [such as the related multistate Bennett acceptance ratio, or MBAR, method,¹⁷ or the histogram-based WHAM (Refs. ^{13, 15, 18})]. Dynamical reweighting provides a way to make use of all the data from a parallel or simulated tempering simulation, provided the dynamical model employed is amenable to reweighting by the unnormalized density ratios q[X|β]/q[X|β′] being both finite and nonzero. This condition is fulfilled for the common models of dynamics in the canonical ensemble—canonical distribution over Hamiltonian trajectories; Andersen, Langevin, and overdamped Langevin∕Brownian stochastic dynamics, reviewed in Sec. 2C—but not Nosé-Hoover or Berendsen.

While not all properties will benefit greatly from the use of reweighting, some dynamical expectations—particularly those that involve large contributions from trajectories that are rare at the temperature of interest, but more plentiful at elevated (or reduced) temperatures—will especially benefit in terms of reduced variance. For example, though not shown here, transitions along the ϕ torsion for terminally-blocked alanine involve conformational states with high free energy which may not even be sampled at some temperatures in simulated or parallel tempering simulations of typical length, necessitating the use of reweighting to provide an estimate of rates involving these states (illustrated in detail in a companion paper).⁶³ Even in the case where little or no temperature-dependent enhancement of the phenomena is expected, neighboring temperatures from a simulated or parallel tempering simulation often carry a reasonably large amount of information about the temperature of interest, and their inclusion will further reduce the expected statistical error in the estimated expectation if the data is available anyway.

The variety of models of dynamics within the canonical ensemble presented in Sec. 2C, all of which lead to the same static equilibrium distribution of configurations, naturally leads one to ask which model is most appropriate. In some regimes—such as the low-friction regime of Langevin dynamics and the canonical distribution of Hamiltonian trajectories containing large baths of explicit solvent—these models may give nearly identical expectations, while in other regimes—those where the Andersen collision rate ν or Langevin collision rate γ is large—the expectations for dynamical properties may differ considerably. Which situation is more physically reasonable will undoubtedly depend on both the system under study and the properties of interest, but a detailed investigation of this is beyond the scope of this work.

The efficiency of reweighting—that is, the degree to which temperatures β′ ≠ β contribute to expectations at temperature β—will depend both on the size of the system and, for stochastic dynamics, the trajectory length. To understand this behavior, consider a standard parallel tempering simulation using the conventional exchange criteria based on potential energies⁷. In order for the ensembles at two temperatures to have good potential energy overlap, and hence good exchange acceptance rates, their temperatures should be spaced roughly the half-width of the potential energy distribution, $\delta U\sim {⟨{(U-⟨U⟩)}^2⟩}^{1∕2}=T\sqrt{k_B{C}_{v^{\prime }}}$. The heat capacity for the potential energy, C_v ≡ (∂/∂T)〈U〉_T, tells us that the temperature shift δT corresponding to this energy shift δU is roughly $T\sqrt{k_B∕C_v}$.

Analogously, good path Hamiltonian overlap [and good exchange acceptance rates using the modified acceptance criterion in Eq. 47] can be assured with a temperature spacing of roughly $T\sqrt{k_B∕{\mathcal{C}}_v}$, where C_v is a generalized form of the heat capacity for path Hamiltonians H[X]:

$$\begin{array}{ccc}\hfill {\mathcal{C}}_v& \equiv & \frac{\partial {⟨\mathcal{H}⟩}_T}{\partial T}=k_B{\beta }^2{⟨{(\mathcal{H}-⟨\mathcal{H}⟩)}^2⟩}_{\beta }\hfill \end{array}$$ (56)

For the canonical distribution of Hamiltonian trajectories, this generalized path heat capacity C_v is identical to the heat capacity for the total energy, (∂/∂T)〈H〉_T = C_v + N_dk_B/2, which grows linearly with the number of degrees of freedom N_d.

For Andersen, Langevin, and Brownian dynamics, the generalized path heat capacity C_v differs from the thermodynamic heat capacity C_v. Because the variance of a sum of uncorrelated random variables is simply the sum of the variances, we can compute this difference analytically. For Andersen dynamics, C_v=C_v+N_ck_B∕2, where N_c is the number of collisions that occur during realization of the trajectory, where roughly N_c ∼ N_dN_tν, with ν is the per-step collision probability and N_t is the number of integration timesteps in the trajectory. For Langevin dynamics, C_v=C_v+N_d(N_t+1)k_B∕2, and for Brownian dynamics, C_v=C_v+N_dN_tk_B∕2 (where C_v here denotes the heat capacity for the potential energy contribution only for Brownian dynamics). For constant, nonzero collision rates, the generalized heat capacity is therefore extensive in N_dN_t; as the systems grow larger or the trajectories grow longer, the efficiency of reweighting is therefore expected to diminish.

The form of the path Hamiltonians suggests a further analogy with the equilibrium statistical mechanics governing single configurations. For Hamiltonian dynamics, a path is uniquely identified by its initial phase space point. For the stochastic forms of dynamics (Andersen, Langevin, Brownian), a trajectory given an initial phase space point can be thought of as an ideal polymer consisting of N_t “monomers” that are replicates of the N_p-particle system, one replicate per trajectory timeslice, where the only interactions are “bonds” between corresponding atoms in sequential timeslices. The interaction energies for these “bonds” are harmonic in the noise variables ξ_ti corresponding to the atomic displacement between sequential timeslices.

Surprisingly, the path Hamiltonians and generalized path heat capacities are independent of the choice of collision rate γ_i for Langevin and Brownian dynamics, except when γ_i is identically zero, at which point the particles with zero associated collision rates no longer contribute to the path Hamiltonian or heat capacity since they evolve by deterministic dynamics. This is analogous to the fact that the heat capacity of an ideal polymer is independent of the spring constant and particle masses. Only in the case of Andersen dynamics will the collision rate ν modulate the heat capacity through determining the number of particle collisions observed in a trajectory of fixed length N_t.

It should be noted that there is often additional information available that could be incorporated into the reweighting scheme through the use of control variates.²⁶ For example, for the model of Hamiltonian trajectories with randomized momenta, the normalization constants ${\widehat{Z}}_i$ that are inferred during the procedure actually contain the temperature-dependent momentum partition function, which can be computed analytically. Incorporation of this as a constraint, or other integrals of the dynamics that are known exactly, can further reduce the variance in the estimated properties of interest, though the degree to which this may occur will be problem-dependent.

APPENDIX A: ADDITIONAL SIMULATION DETAILS FOR ALANINE DIPEPTIDE

Using the LEAP program from the AMBERTOOLS 1.2 molecular mechanics package,⁶⁴ a terminally-blocked alanine peptide (sequence ACE-ALA-NME, see Figure 1) was generated in the extended conformation, with peptide force field parameters taken from the AMBERPARM96 parameter set.⁶⁵ The system was subsequently solvated with 749 TIP3P water molecules⁶⁶ in a cubic simulation box with dimensions chosen to ensure all box boundaries were at least 9 Å from any atom of the extended peptide. The system was subjected to energy minimization using L-BFGS⁶⁷, ⁶⁸ to reduce the root-mean-square force to less than 1 kJ/mol/nm, and then equilibrated for 1 ns with a leapfrog Langevin integrator⁴¹ at a control temperature of 300 K, using a 2 fs timestep and collision rate of 5/ps. During equilibration, an isotropic Monte Carlo barostat with a control pressure of 1 atm was applied, with volume moves attempted every 25 timesteps, and the range of volume change proposals automatically adjusted to give an approximate acceptance probability of approximately 50%.⁶⁹ All bonds to hydrogen, and hydrogen-hydrogen distances in waters, were constrained by the CCMA (Ref. ⁷⁰) and SETTLE (Ref. ⁷¹) algorithms, as appropriate. The particle-mesh Ewald (PME) method⁷² was used to treat electrostatics, using a real-space cutoff of 9 Å. PME parameters were automatically selected by an algorithm that attempts to find the most efficient set of parameters for which an error bound is less than a specified error tolerance,⁶⁹ which was set to the default of 5 · 10⁻⁴. Lennard-Jones interactions were truncated at 9 Å without switching, and a homogeneous analytical long-range dispersion correction⁷³ was employed to compensate for dispersion interactions outside the cutoff. The resulting system had a box volume of 23 073.7 ų, and the box volume was fixed in the subsequent parallel tempering simulation.

A custom Python code making use of the GPU-accelerated OPENMM package⁷⁴, ⁷⁵, ⁷⁶ and the PYOPENMM Python wrapper⁷⁷ was used to conduct the simulations. Because OPENMM lacks a velocity Verlet integrator, a hybrid velocity Verlet⁷⁸/leapfrog⁷⁹, ⁸⁰ integration scheme was used for integration of the equations of motion, implemented as follows. At the beginning of the dynamical propagation phase of parallel tempering iteration, on-step velocities were first generated from the Maxwell-Boltzmann distribution at the current replica temperature. Components of the velocity along constrained bonds (all bonds to hydrogen and the hydrogen-hydrogen bonds of TIP3P water) were removed using the RATTLE algorithm⁴⁰ with 10⁻¹⁶ relative tolerance, and a 1 fs “half-kick backwards” applied to the modified velocities using the force evaluated at the current positions. The OPENMM Verlet integrator was then used to evolve the positions by 0.5 ps (250 steps with a 2 fs timestep) on the GPU, and a 1 fs “half-kick forwards” was applied to the velocities to synchronize them with the positions after again applying the RATTLE algorithm. During leapfrog integration, the CCMA and SETTLE algorithms were used to constrain bonds, as appropriate.