A smoothly decoupled particle interface: New methods for coupling explicit and implicit solvent

Abstract

A common theme of studies using molecular simulation is a necessary compromise between computational efficiency and resolution of the forcefield that is used. Significant efforts have been directed at combining multiple levels of granularity within a single simulation in order to maintain the efficiency of coarse-grained models, while using finer resolution in regions where such details are expected to play an important role. A specific example of this paradigm is the development of hybrid solvent models, which explicitly sample the solvent degrees of freedom within a specified domain while utilizing a continuum description elsewhere. Unfortunately, these models are complicated by the presence of structural artifacts at or near the explicit∕implicit boundary. The presence of these artifacts significantly complicates the use of such models, both undermining the accuracy obtained and necessitating the parameterization of effective potentials to counteract the artificial interactions. In this work, we introduce a novel hybrid solvent model that employs a smoothly decoupled particle interface (SDPI), a switching region that gradually transitions from fully interacting particles to a continuum solvent. The resulting SDPI model allows for the use of an implicit solvent model based on a simple theory that needs to only reproduce the behavior of bulk solvent rather than the more complex features of local interactions. In this study, the SDPI model is tested on spherical hybrid domains using a coarse-grained representation of water that includes only Lennard-Jones interactions. The results demonstrate that this model is capable of reproducing solvent configurations absent of boundary artifacts, as if they were taken from full explicit simulations.

INTRODUCTION

The desire to obtain converged sampling within a biomolecular simulation often demands a compromise between computational efficiency and resolution of the applied forcefield. Solutions to quantum mechanics (QM) calculations are only possible for relatively small collections of molecules, and simulations using polarizable forcefields^{1, 2, 3, 4} can be intractable for most systems of interest. Current technology has allowed the use of all-atom molecular mechanics (MM) forcefields with explicit solvent representations to be used on very large systems and long timescales.^{5, 6, 7} However, forcefields with an even coarser representation of molecular components have arisen from the desire to model larger systems than those that are manageable with an all-atom representation.^{8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23} Similarly, implicit solvent models aim to reduce computational demand by replacing the explicitly sampled solvent degrees of freedom with an approximate, continuum description of the bulk solvent potential of mean force (PMF). Implicit solvent models are commonly used at all levels of molecular granularity, from QM (Refs. ^{24, 25, 26, 27}) and polarizable methods^{28, 29, 30} to MM forcefields.^{31, 32, 33, 34} Unsurprisingly, lower resolution forcefields and solvent models often incur penalties on accuracy and require the development of model parameters that may not be transferable under different thermodynamic conditions or chemical environments.^{35, 36}

The development of multiscale methodologies have allowed for a union between the efficiency of coarse-grained models and the accuracy of more detailed techniques within a single simulation. Examples of such methods include QM∕MM models^{27, 37, 38, 39} and MM methods that contain varying levels of all-atom and combined-atom forcefields across the simulation domain.^{40, 41, 42, 43} Similarly, hybrid solvent models have been developed that solvate a region of interest with explicit molecules and use an implicit solvent model elsewhere. Such hybrid models capture the salient features of both techniques: the explicit solvent molecules near a solute interface are capable of sampling relevant local interactions, while the implicit solvent model is used to reproduce the effects of bulk solvent. This hybrid solvation both reduces computational expense and removes the artifacts that may arise from the use of periodic simulations.⁴⁴ A number of such hybrid models have been previously developed,^{23, 24, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63} many of which take advantage of particularly efficient implicit solvent models for the simple geometries of the defined explicit regions.^{45, 46, 54, 55}

Hybrid solvent models are subject to artifacts due to the inability of simple continuum methods to accurately reproduce the bulk solvent PMF near the explicit∕implicit boundary. Similar problems exist in other methods that couple varying levels of atomic detail, and the boundaries for any such model must be handled carefully in order to ensure appropriate chemical behavior in transition regions.^{38, 39, 40, 42} The boundary artifacts present in hybrid solvent models require the use of large enough explicit regions so that the thermodynamic properties of the solute remain hopefully unpolluted. Even with large explicit regions, the presence of unrealistic solvent configurations is troubling, especially under consideration of the significance of long-ranged solvent mediation that occurs in confined systems.^{64, 65, 66}

Significant efforts have been directed at alleviating this problem with effective potentials^{45, 51, 53, 57, 59, 61, 62, 63} that reproduce forces from the bulk region as faithfully as possible. While these methods have demonstrated considerable success, the full removal of boundary artifacts is not expected unless the solvent PMF is accurate within a very small tolerance. Such a task has thus far only been accomplished using methods unsuitable for molecular dynamics simulations, such as integral equation or other calculations that generate the solvent response using a self-consistent approach.^{67, 68, 69, 70, 71, 72} In this work, we introduce a model that attempts to remove artificial boundary interactions using a smoothly decoupled particle interface (SDPI), a switching region over which the explicit particles are slowly annihilated and the implicit representation is “grown” in. This method slowly removes the local structure of the solvent. As a result, the requirement of the implicit solvent model is simplified from a many-body function that estimates the more complex features of specific interactions to a single-body term that reproduces bulk behavior according to an elementary theory. We test this method on uncharged systems using the MARTINI coarse-grained forcefield,^{22, 23} for which water is modeled as a monatomic Lennard-Jones (LJ) fluid, in spherical hybrid models. The result is an explicit region void of boundary artifacts that effectively samples solvent configurations as if they were taken from an infinite bath.

TRADITIONAL HYBRID MODEL

We will refer to hybrid models that instantaneously switch from explicit to implicit solvent as “traditional” hybrid models. In Sec. 3, we introduce the details of the SDPI formalism.

Supersystem partition function

Consider a solute immersed in bulk solvent. The partition function of this system is

$$Z=\frac{1}{{\Lambda }_U^3{\Lambda }^{3N}N!}{\int }_{\Omega }d\left({\mathbf{X}}_U\right)\int d\left({\mathbf{x}}_1\right),...,d\left({\mathbf{x}}_N\right)\exp \left[-\beta U\right],$$ (1)

where U is the total potential energy of the system, β is the inverse thermal energy 1/(k_BT), Λ_U and Λ^N are the thermal de Broglie wavelengths of solute and N solvent molecules, and (X_U, x₁, …, x_N) represent the degrees of freedom of the solute and N (identical) solvent molecules.

If we partition our domain Ω into arbitrary interior and exterior portions (Ω=Ω_i+Ω_o), we can rewrite this integral in terms of the number of molecules confined to the inner portion. Following the notation of previous developments,⁴⁹ we define

$${\delta }_{n{n}^{\prime }\left({\mathbf{X}}_N\right)}=\left\{\begin{array}{cc}\hfill 1,& \hfill \mathrm{if}n=n^{\prime }\left({\mathbf{X}}_N\right)\\ \hfill 0,& \hfill \mathrm{otherwise}\end{array},\right.$$ (2)

where (X_N) = (x₁, …, x_N) and

$$n^{\prime }\left({\mathbf{X}}_N\right)=\sum _{i=1}^{N}C\left({\mathbf{x}}_i\right),$$ (3)

$$C\left({\mathbf{x}}_i\right)=\left\{\begin{array}{cc}\hfill 0,& \hfill \mathrm{if}{\mathbf{x}}_i\in {\Omega }_{\text{o}}\\ \hfill 1,& \hfill \mathrm{if}{\mathbf{x}}_i\in {\Omega }_{\text{i}}\end{array}\right..$$ (4)

The function n′(X_N) thus returns the number of solvent molecules within the inner domain. We can now rewrite the partition function as

$$\begin{array}{ccc}& & Z=\frac{1}{{\Lambda }_U^3{\Lambda }^{3N}}\sum _n\frac{1}{N!}\hfill \\ & & \times \int d\left({\mathbf{X}}_U\right)\int d\left({\mathbf{x}}_1\right)\cdots d\left({\mathbf{x}}_N\right){\delta }_{n{n}^{\prime }\left({\mathbf{X}}_N\right)}\exp \left[-\beta U\right].\hfill \end{array}$$ (5)

Noting that the use of Eq. 2 introduces restricted integral domains in Eq. 5,

$$\begin{array}{ccc}\hfill Z& =& \sum _n\frac{1}{{\Lambda }_U^3{\Lambda }^{3N}}\int d\left({\mathbf{X}}_U\right){\int }_{{\Omega }_{\text{i}}}\frac{1}{n!}d\left({\mathbf{X}}_n\right)\hfill \\ & & \times {\int }_{{\Omega }_{\text{o}}}\frac{1}{\left(N-n\right)!}d\left({\mathbf{Y}}_{N-n}\right)\exp \left[-\beta U\right],\hfill \end{array}$$ (6)

where the vectors X_n and Y_{N − n} correspond to the configurations of molecules located in the inner (Ω_i) and outer (Ω_o) regions, respectively, and the numbered subscripts indicate the number of solvent molecules restricted to these regions.

Subsystem configurational probability

We are in a position to write the joint probability of finding n solvent particles within the inner, or explicit, domain and the configuration of interior coordinates (X_U, X_n) as

$$\begin{array}{ccc}\hfill P\left({\mathbf{X}}_U,{\mathbf{X}}_n,n\right)& =& {\left[Z{\Lambda }_U^3{\Lambda }^{3N}n!\left(N-n\right)!\right]}^{-1}\hfill \\ & & \times {\int }_{{\Omega }_{\text{o}}}d\left({\mathbf{Y}}_{N-n}\right)\exp [-\beta U\left({\mathbf{X}}_U,{\mathbf{X}}_n,{\mathbf{Y}}_{N-n}\right)].\hfill \end{array}$$ (7)

It is useful to decompose the total potential into inner-inner (U_ii(X_U,X_n)), inner-outer (U_io(X_U,X_n,Y_N−n)), and outer-outer (U_oo(Y_N−n)) components and then define the PMF W as⁷³

$$\begin{array}{c}\hfill \exp \left[-\beta W\left({\mathbf{X}}_U,{\mathbf{X}}_n\right)\right]=\frac{{\int }_{{\Omega }_{\text{o}}}d\left({\mathbf{Y}}_{N-n}\right)\exp \left[-\beta U\left({\mathbf{X}}_U,{\mathbf{X}}_n,{\mathbf{Y}}_{N-n}\right)\right]}{{\int }_{\Omega }d\left({\mathbf{Y}}_{N-n}\right)\exp \left[-\beta U\left({\mathbf{Y}}_{N-n}\right)\right]}\end{array}$$ (8a)

$$\begin{array}{ccc}& =& \frac{\exp \left[-\beta U_{\text{ii}}\left({\mathbf{X}}_U,{\mathbf{X}}_n\right)\right]{\int }_{{\Omega }_{\text{o}}}d\left({\mathbf{Y}}_{N-n}\right)\exp \left[-\beta \left(U_{\text{io}}\left({\mathbf{X}}_U,{\mathbf{X}}_n,{\mathbf{Y}}_{N-n}\right)+U_{\text{oo}}\left({\mathbf{Y}}_{N-n}\right)\right)\right]}{{\int }_{\Omega }d\left({\mathbf{Y}}_{N-n}\right)\exp \left[-\beta U\left({\mathbf{Y}}_{N-n}\right)\right]}\hfill \\ & =& \exp \left[-\beta \left(U_{\text{ii}}\left({\mathbf{X}}_U,{\mathbf{X}}_n\right)+\Delta W\left({\mathbf{X}}_U,{\mathbf{X}}_n\right)\right)\right],\hfill \end{array}$$ (8)

where ΔW is the bulk solvent PMF. Inserting this into Eq. 7:

$$\begin{array}{ccc}\hfill P\left({\mathbf{X}}_U,{\mathbf{X}}_n,n\right)& =& \frac{\exp \left[-\beta \left(U_{\text{ii}}\left({\mathbf{X}}_U,{\mathbf{X}}_n\right)+\Delta W\left({\mathbf{X}}_U,{\mathbf{X}}_n\right)\right)\right]}{Z{\Lambda }_U^3{\Lambda }^{3N}n!\left(N-n\right)!}\hfill \\ & & \times {\int }_{\Omega }d\left({\mathbf{Y}}_{N-n}\right)\exp [-\beta U\left({\mathbf{Y}}_{N-n}\right)].\hfill \end{array}$$ (9)

Noting that, in the limit of an infinitely large domain, we can take

$$\begin{array}{ccc}& & \underset{N\to \infty ,\frac{N}{V}\to \rho }{\lim }\frac{1}{{\Lambda }^{3N-3n}\left(N-n\right)!}\hfill \\ & & {\int }_{\Omega }d\left({\mathbf{Y}}_{N-n}\right)\times \exp [-\beta U\left({\mathbf{Y}}_{N-n}\right)]\propto \exp \left[-\beta (N-n)\mu \right],\hfill \end{array}$$ (10)

where V is the volume of the domain, ρ is the bulk density, and μ is the chemical potential of one of the solvent molecules. We now have

$$\begin{array}{ccc}\hfill P\left({\mathbf{X}}_U,{\mathbf{X}}_n,n\right)& & \propto \frac{1}{{\Lambda }_U^3{\Lambda }^{3n}n!}\exp [-\beta (U_{\text{ii}}({\mathbf{X}}_U,{\mathbf{X}}_n)\hfill \\ & & +\Delta W({\mathbf{X}}_U,{\mathbf{X}}_n)+(N-n)\mu \left)\right].\hfill \end{array}$$ (11)

Transition probabilities

Define the ratio of equilibrium probability densities for state a, with n_a solvent molecules, and state b, with n_b solvent molecules, as

$$\begin{array}{ccc}\hfill \frac{P\left({\mathbf{X}}_{U_b},{\mathbf{X}}_{n_b},n_b\right)}{P\left({\mathbf{X}}_{U_a},{\mathbf{X}}_{n_a},n_a\right)}& =& \frac{n_a!{\Lambda }^{3n_a}}{n_b!{\Lambda }^{3n_b}}\exp [-\beta (W({\mathbf{X}}_{U_b},{\mathbf{X}}_{n_b})\hfill \\ & & -W({\mathbf{X}}_{U_a},{\mathbf{X}}_{n_a})-(n_b-n_a)\mu \left)\right].\hfill \end{array}$$ (12)

We now wish to substitute in the excess chemical potential μ′, noting that

$$\mu ={\mu }^0+{\mu }^{\prime }$$ (13)

and

$${\mu }^0=\frac{1}{\beta }\ln \left[\rho {\Lambda }^3\right]$$ (14)

is the chemical potential of a monatomic ideal gas that has the same density and particle mass of our solvent. Making these substitutions,

$$\begin{array}{c}\hfill \frac{P\left({\mathbf{X}}_{U_b},{\mathbf{X}}_{n_b},n_b\right)}{P\left({\mathbf{X}}_{U_a},{\mathbf{X}}_{n_a},n_a\right)}=\frac{n_a!}{n_b!}{\rho }^{n_b-n_a}\exp [-\beta (W({\mathbf{X}}_{U_b},{\mathbf{X}}_{n_b})\\ \hfill -W({\mathbf{X}}_{U_a},{\mathbf{X}}_{n_a})-(n_b-n_a){\mu }^{\prime }\left)\right].\end{array}$$ (15)

Equation 15 represents the relative probabilities for two states with a different solute configuration and a different number of interior solvent molecules within our hybrid simulation.

Insertion∕deletion attempts

We wish to perform grand canonical Monte Carlo (GCMC) insertion and deletion moves over some subdomain Ω_id⊆Ω_i. Since the entire domain Ω_i is not subject to GCMC control, Eq. 15 must be modified for the criteria governing insertion or deletion attempts. If we label the number of molecules in state a within Ω_id as $n_a^{\text{id}}$, the configurational probability distribution requires the additional counting factor $\frac{n_a!}{n_a^{\text{id}}!\left(n_a-n_a^{\text{id}}\right)!}$. For a single insertion or deletion attempt, we note that $n_b-n_b^{\text{id}}=n_a-n_a^{\text{id}}$ and Eq. 15 becomes

$$\begin{array}{ccc}\hfill \frac{P\left({\mathbf{X}}_{U_b},{\mathbf{X}}_{n_b},n_b\right)}{P\left({\mathbf{X}}_{U_a},{\mathbf{X}}_{n_a},n_a\right)}& =& \frac{n_a^{\text{id}}!}{n_b^{\text{id}}!}{\rho }^{n_b-n_a}\exp [-\beta (W({\mathbf{X}}_{U_b},{\mathbf{X}}_{n_b})\hfill \\ & & -W({\mathbf{X}}_{U_a},{\mathbf{X}}_{n_a})-(n_b-n_a){\mu }^{\prime }\left)\right].\hfill \end{array}$$ (16)

Assuming that we do not attempt to insert or delete more than one molecule at a time and that the probabilities of attempting an insertion or deletion are both equal to p_id, the total selection probability for inserting or deleting a particular molecule is

$$\begin{array}{ccc}\hfill S_{\text{ins}}& =& \frac{p_{\text{id}}}{(n^{\text{id}}+1)V_{{\Omega }_{\text{id}}}},\hfill \\ \hfill S_{\text{del}}& =& \frac{p_{\text{id}}}{n^{\text{id}}},\hfill \end{array}$$ (17)

where V_Ωid is the volume of Ω_id. The factor of (n^id+1) in the denominator of the insertion selection is consistent with the presented formulation and corresponds to giving an inserted molecule a random label.

The detailed balance condition imposes that, for a transition between initial i and final f states, the forward and reverse acceptance probabilities (A) must satisfy

$$\begin{array}{ccc}& & P\left({\mathbf{X}}_i\right)S\left({\mathbf{X}}_i\to {\mathbf{X}}_f\right)A\left({\mathbf{X}}_i\to {\mathbf{X}}_f\right)\hfill \\ & & =P\left({\mathbf{X}}_f\right)S({\mathbf{X}}_f\to {\mathbf{X}}_i)A({\mathbf{X}}_f\to {\mathbf{X}}_i).\hfill \end{array}$$ (18)

The Metropolis criterion satisfies this requirement:

$$A({\mathbf{X}}_i\to {\mathbf{X}}_f)=\min \left(1,\frac{S({\mathbf{X}}_f\to {\mathbf{X}}_i)}{S({\mathbf{X}}_i\to {\mathbf{X}}_f)}\frac{P\left({\mathbf{X}}_f\right)}{P\left({\mathbf{X}}_i\right)}\right).$$ (19)

Combining equations 16, 17, 18 into the Metropolis algorithm gives the following acceptance probabilities for insertion and deletion attempts:

$$\begin{array}{ccc}& & A\left[\left({\mathbf{X}}_U,{\mathbf{X}}_n,n\right)\to \left({\mathbf{X}}_U,{\mathbf{X}}_{n+1},n+1\right)\right]\hfill \\ & & =\min \left(1,\frac{⟨n⟩\exp [-\beta (W({\mathbf{X}}_U,{\mathbf{X}}_{n+1})-W({\mathbf{X}}_U,{\mathbf{X}}_n)-{\mu }^{\prime })]}{n+1}\right),\hfill \end{array}$$

$$\begin{array}{ccc}& & A\left[\left({\mathbf{X}}_U,{\mathbf{X}}_n,n\right)\to \left({\mathbf{X}}_U,{\mathbf{X}}_{n-1},n-1\right)\right]\hfill \\ & & =\min \left(1,\frac{n\exp [-\beta (W({\mathbf{X}}_U,{\mathbf{X}}_{n-1})-W({\mathbf{X}}_U,{\mathbf{X}}_n)+{\mu }^{\prime })]}{⟨n⟩}\right),\hfill \end{array}$$ (20)

where ⟨n⟩=ρV_Ωid. We see that these acceptance probabilities reduce to the form familiar to GCMC movesets.^{74, 75, 76, 77, 78, 79}

Implicit solvent model

The computational benefit of a hybrid solvent model arises from using simple, inexpensive, implicit solvent models to reproduce the bulk solvent PMF defined by Eq. 8. For this work, which includes no charged interactions, we model the solvent PMF as a combination of repulsive and attractive components, ΔW(X_U, X_n) = Δw^(rep)(X_U, X_n) + Δw^(att)(X_U, X_n). This separation closely mirrors the Weeks-Chandler-Andersen (WCA) decomposition of the LJ interaction, given by

$$U^{\text{LJ}}\left(r_{ij}\right)=4{\epsilon }_{ij}\left[\frac{{\sigma }_{ij}^{12}}{r_{ij}^{12}}-\frac{{\sigma }_{ij}^6}{r_{ij}^6}\right],$$ (21)

where r_ij is the distance between atoms i and j, ε_ij gives the minimum value of this energy, and 2^1/6σ_ij is the distance at which that minimum occurs. The WCA decomposition⁸⁰ separates this potential, U^LJ(r_ij) = u^(rep)(r_ij) + u^(att)(r_ij), where the components are defined as follows:

$$\begin{array}{ccc}\hfill u^{\left(\mathrm{rep}\right)}\left(r_{ij}\right)({\mathbf{x}}_i,{\mathbf{x}}_j)& =& \left\{\begin{array}{cc}\hfill U^{\left(\mathrm{LJ}\right)}\left(r_{ij}\right)+{\epsilon }_{ij},& \hfill r_{ij}<2^{1∕6}{\sigma }_{ij}\\ \hfill 0,& \hfill r_{ij}\ge 2^{1∕6}{\sigma }_{ij}\end{array},\right.\hfill \end{array}$$ (22)

$$\begin{array}{ccc}\hfill u^{\left(\mathrm{att}\right)}\left(r_{ij}\right)& =& \left\{\begin{array}{cc}\hfill -{\epsilon }_{ij},& \hfill r_{ij}<2^{1∕6}{\sigma }_{ij}\\ \hfill U^{\left(\mathrm{LJ}\right)}\left(r_{ij}\right),& \hfill r_{ij}\ge 2^{1∕6}{\sigma }_{ij}\end{array}\right..\hfill \end{array}$$ (23)

The attractive PMF contribution is modeled as a sum of atomic components, each integrating the attractive component of the WCA potential over the system domain:

$$\Delta w^{\left(\mathrm{att}\right)}({\mathbf{X}}_U,{\mathbf{X}}_n)=\rho \sum _i{\int }_{\Omega }{u}^{\left(\mathrm{att}\right)}\left(∥{\mathbf{x}}_i-\mathbf{y}∥\right)h_i\left({\mathbf{x}}_i,\mathbf{y}\right)d\mathbf{y},$$ (24)

where y ∈ Ω, ρ is the average solvent particle density, h_i(x_i, y) is the reference distribution used to describe the mean normalized solvent density surrounding atom i at position x_i, and the summation is performed over all atoms.

An appropriate approximation for the distribution function would be a set of overlapping Heaviside functions H for the explicit region (which is centered at the origin) and each particle of the system:

$$\begin{array}{ccc}\hfill h_i\left({\mathbf{x}}_i,\mathbf{y}\right)& =& h\left({\mathbf{X}}_u,{\mathbf{X}}_n,\mathbf{y}\right)=H\left(\parallel \mathbf{y}\parallel -R_o-{\sigma }_e\right)\hfill \\ & & \times \prod _{i}H\left(\parallel \mathbf{y}-{\mathbf{x}}_i\parallel -{\sigma }_i\right),\hfill \end{array}$$ (25)

$$H\left(x\right)=\left\{\begin{array}{cc}\hfill 0,& \hfill x<0\\ \hfill 1,& \hfill x\ge 0\end{array}\right.,$$ (26)

where σ_i is the radius applied to particle i and is calculated as ${\sigma }_i=\frac{1}{2}{2}^{1∕6}{\sigma }_{ii}+{\sigma }_s$, with σ_s representing a parameterized probe radius. R_o corresponds to the radius of the spherical explicit region. The parameter σ_e is added to augment this surface definition and adds significant accuracy to this simple approximation of the distribution function. This distribution function excludes bulk solvent density from the inner domain and regions of overlap between explicit particles and the outer domain. Unfortunately, the use of Eq. 25 necessitates an expensive numerical calculation for the evaluation of the presented implicit solvent model. For this reason, such a distribution function is used for analysis of the implicit solvent model but is not implemented for hybrid simulations.

Instead, we will approximate the distribution function for atom i with a simple two body overlap between this atom and the explicit domain:

$$h_i\left({\mathbf{x}}_i,\mathbf{y}\right)=H\left(\parallel \mathbf{y}\parallel -R_o-{\sigma }_e\right)H\left(\parallel \mathbf{y}-{\mathbf{x}}_i\parallel -{\sigma }_i\right).$$ (27)

This representation of the distribution function allows for a decomposition of the overall PMF into atomic components that can be calculated analytically.

The repulsive component of the implicit solvent model is proportional to the volume of the explicitly defined region, Δw^(rep)(X_U, X_n) = pV(X_U, X_n) , where p is a parameterizable constant used to represent the bulk solvent pressure and V is the system volume. Though the choice of using volume over surface-area for this PMF component may seem curious, such volume terms were present in early developments of scaled particle theory.⁸¹ The volume dependence of cavity formation has indeed been demonstrated for sub-nanometer length scales,^{82, 83, 84, 85, 86, 87} expected and shown⁸⁸ to be the relevant length scale for atomic solvation forces. A surface area term is still expected to contribute to the absolute cost of cavity formation for the explicit region, but is omitted from our calculations since there are no large-scale geometry changes within the simulations. The volume of our system is calculated as

$$V\left({\mathbf{X}}_U,{\mathbf{X}}_n\right)={\int }_{\Omega }\left(1-\sum _i{h}_i\left({\mathbf{x}}_i,\mathbf{y}\right)\right)d\mathbf{y}.$$ (28)

This is not equivalent to the volume of the inner domain Ω_i and approximates the effect of explicit particles that overlap with the outer domain.

It is important to note that when used in these hybrid solvent models, the above implicit solvent PMF requires no solute parameterization as long as the solute atoms do not overlap with the boundary, and thus requires a total of three parameters only. This significantly simplifies the parameterization procedure when compared to implicit solvent models that often require new radii or other parameters for each atom present within the simulation.^{31, 32, 34}

Mean force analysis

The implicit solvent model will be compared to explicit solvent results using mean-force analysis on a system of bulk solvent. Following Eq. 8, we can define the mean force for atom i given the static configuration of explicit solvent molecules (X_n) as^{73, 88, 89, 90}

$$\begin{array}{ccc}\hfill F_i\left({\mathbf{X}}_n\right)& =& -\frac{\delta \Delta W\left({\mathbf{X}}_n\right)}{\delta {\mathbf{x}}_i}\hfill \\ & =& \frac{{\int }_{{\Omega }_{\text{o}}}d\left({\mathbf{Y}}_{N-n}\right)\left(-\frac{\delta U_{\text{io}}\left({\mathbf{X}}_n,{\mathbf{Y}}_{N-n}\right)}{\delta {\mathbf{x}}_i}\right)\exp \left[-\beta \left(U_{\text{io}}\left({\mathbf{X}}_n,{\mathbf{Y}}_{N-n}\right)+U_{\text{oo}}\left({\mathbf{Y}}_{N-n}\right)\right)\right]}{{\int }_{{\Omega }_{\text{o}}}d\left({\mathbf{Y}}_{N-n}\right)\exp \left[-\beta \left(U_{\text{io}}\left({\mathbf{X}}_n,{\mathbf{Y}}_{N-n}\right)+U_{\text{oo}}\left({\mathbf{Y}}_{N-n}\right)\right)\right]}\hfill \\ & =& -{〈\frac{\delta U_{\text{io}}\left({\mathbf{X}}_n,{\mathbf{Y}}_{N-n}\right)}{\delta {\mathbf{x}}_i}〉}_{{\mathbf{Y}}_{N-n}},\hfill \end{array}$$ (29)

where 〈⋯〉_YN−n indicates an ensemble average over Y_{N − n}, the configurations of solvent in the outer region. This mean force can be calculated from explicit solvent simulations by averaging the force on atom i from solvent molecules in the exterior domain. This quantity is then compared to the forces obtained with the implicit solvent model using the full distribution function (Eq. 25).

When using the approximate, two-body distribution function given in Eq. 27, we are assuming that the mean forces on atom i are independent of all other explicit particles in the inner domain. Therefore, it is useful to define the analogous force from the full system as

$$F_i\left({\mathbf{x}}_i\right)=-{〈\frac{\delta U_{\text{io}}\left({\mathbf{X}}_n,{\mathbf{Y}}_{N-n}\right)}{\delta {\mathbf{x}}_i}〉}_{{\mathbf{x}}_{j\ne i},{\mathbf{Y}}_{N-n}}={〈F_i\left({\mathbf{X}}_n\right)〉}_{{\mathbf{x}}_{j\ne i}},$$ (30)

where, in addition to all outer solvent molecules, we are now also averaging over all molecules x_{j ≠ i} in the inner region. Note that this corresponds to simplifying the total PMF to a single-body term, a common approximation for simple implicit solvent models.^{51, 53, 62, 63} For this study on spherical systems, these forces must be spherically symmetric. Equation 30 then calculates a radial mean force that is used to produce the optimal parameter set for the implicit solvent model.

THE SMOOTHLY DECOUPLED PARTICLE INTERFACE

Addition of an intermediate domain

Equation 11 presents a target configurational probability density from a hybrid simulation and exactly reproduces any thermodynamic property that is a function of (X_U, X_n), as long as the function ΔW(X_U, X_n) is accurately calculated. In practice, however, developing accurate approximations to ΔW(X_U, X_n) in the form of implicit solvent models is a formidable challenge when attempting to reduce computational expense. For the SDPI model, we will derive an alternate formalism that provides the same theoretical result as Eq. 11 but in practice provides a much more straightforward and accurate approximation to the solvent PMF.

Consider partitioning the total system domain into three regions (Ω=Ω_i+Ω_s+Ω_o). The interior and exterior regions (Ω_i and Ω_o, respectively) are now separated by an intermediate, or switching, region Ω_s and are not in contact. The vectors X_n, ${\mathbf{Y}}_m^{\text{s}}$, ${\mathbf{Y}}_{N-n-m}^{\text{o}}$ correspond to the configurations of the subscripted molecules within the interior, intermediate, and exterior regions, respectively. Following the reasoning outlined above, Eq. 6 can be extended to include this additional subregion:

$$\begin{array}{ccc}\hfill Z& =& \frac{1}{{\Lambda }_U^3{\Lambda }^{3N}}\sum _n\frac{1}{n!}\int d\left({\mathbf{X}}_U\right){\int }_{{\Omega }_{\text{i}}}d\left({\mathbf{X}}_n\right)\sum _m\frac{1}{m!\left(N-n-m\right)!}\hfill \\ & & \times {\int }_{{\Omega }_{\text{s}}}d\left({\mathbf{Y}}_m^{\text{s}}\right){\int }_{{\Omega }_{\text{o}}}d\left({\mathbf{Y}}_{N-n}^{\text{o}}\right)\exp \left[-\beta U\right].\hfill \end{array}$$ (31)

Using the development of Sec. 2B, we can integrate over the coordinates of the outermost region to obtain a joint probability of finding n solvent molecules within the interior region, m molecules within the intermediate region, and the configuration $\left({\mathbf{X}}_U,{\mathbf{X}}_n,{\mathbf{Y}}_m^{\text{s}}\right)$:

$$\begin{array}{ccc}\hfill P\left({\mathbf{X}}_U,{\mathbf{X}}_n,n,{\mathbf{Y}}_m^{\text{s}},m\right)& \propto & \frac{1}{n!m!{\Lambda }_U^3{\Lambda }^{3(n+m)}}\exp [-\beta (U_{\text{ii}}\left({\mathbf{X}}_U,{\mathbf{X}}_n\right)\hfill \\ & & +U_{\text{is}}\left({\mathbf{X}}_U,{\mathbf{X}}_n,{\mathbf{Y}}_m^{\text{s}}\right)+U_{\text{ss}}\left({\mathbf{Y}}_m^{\text{s}}\right)\left)\right]\hfill \\ & & \times \exp [-\beta (\Delta W\left({\mathbf{X}}_U,{\mathbf{X}}_n,{\mathbf{Y}}_m^{\text{s}}\right)\hfill \\ & & +\left(N-n-m\right)\mu \left)\right],\hfill \end{array}$$ (32)

where U_is is the interaction potential between particles in Ω_i and those in Ω_s, etc.

We will now introduce an unphysical potential U^λ for all interactions with the m molecules in the intermediate region. The nature of this potential will be described in more detail below. The configurational probability of this new system is

$$\begin{array}{ccc}\hfill P\left({\mathbf{X}}_U,{\mathbf{X}}_n,n,{\mathbf{Y}}_m^{\text{s}},m\right)& \propto & \frac{1}{n!m!{\Lambda }_U^3{\Lambda }^{3(n+m)}}\exp [-\beta (U_{\text{ii}}({\mathbf{X}}_U,{\mathbf{X}}_n)\hfill \\ & & +U_{\text{is}}^{\lambda }\left({\mathbf{X}}_U,{\mathbf{X}}_n,{\mathbf{Y}}_m^{\text{s}}\right)+U_{\text{ss}}^{\lambda }\left({\mathbf{Y}}_m^{\text{s}}\right)\left)\right]\hfill \\ & & \times \exp [-\beta (\Delta W^{\lambda }\left({\mathbf{X}}_U,{\mathbf{X}}_n,{\mathbf{Y}}_m^{\text{s}}\right)\hfill \\ & & +\left(N-n-m\right)\mu \left)\right].\hfill \end{array}$$ (33)

For nontrivial cases, the introduction of this non-physical potential will alter the configurations of molecules within the intermediate region so that they no longer match the configurations expected from the original supersystem. However, we note that if we can ensure that

$$\begin{array}{ccc}\hfill \frac{1}{{\Lambda }^{3m}}{\int }_{{\Omega }_{\text{s}}}d{\mathbf{Y}}_m^{\text{s}}\exp [& -& \beta (U_{\text{is}}^{\lambda }\left({\mathbf{X}}_U,{\mathbf{X}}_n,{\mathbf{Y}}_m^{\text{s}}\right)+U_{\text{ss}}^{\lambda }\left({\mathbf{Y}}_m^{\text{s}}\right)\hfill \\ & +& \Delta W^{\lambda }\left({\mathbf{X}}_U,{\mathbf{X}}_n,{\mathbf{Y}}_m^{\text{s}}\right)\left)\right]\hfill \\ & =& \exp \left[-\beta \Delta W\left({\mathbf{X}}_U,{\mathbf{X}}_n\right)\right],\hfill \end{array}$$ (34)

where the right side represents the solvent PMF developed in Sec. 2B, then the configurations sampled from the innermost region will have the same equilibrium probability as those sampled from the original supersystem. This equation demonstrates that the overall goal of the SDPI model is to reproduce the bulk solvent PMF using an implicit solvent model in conjunction with sampling over the degrees of freedom located within the switching region.

It is straightforward to extend the results of Sec. 2 to include this intermediate region and potential. Most notably, the acceptance criteria for insertion and deletion attempts (Eq. 20) become

$$\begin{array}{ccc}& & A\left[\left({\mathbf{X}}_U,{\mathbf{X}}_{n_a},n_a,{\mathbf{Y}}_{m_a}^{\text{s}},m_a\right)\to \left({\mathbf{X}}_U,{\mathbf{X}}_{n_b},n_b,{\mathbf{Y}}_{m_b}^{\text{s}},m_b\right)\right]\hfill \\ & & =\min \left(1,\frac{⟨n⟩\exp \left[-\beta \left(W^{\lambda }\left({\mathbf{X}}_U,{\mathbf{X}}_{n_b},{\mathbf{Y}}_{m_b}^{\text{s}}\right)-W^{\lambda }\left({\mathbf{X}}_U,{\mathbf{X}}_{n_a},{\mathbf{Y}}_{m_a}^{\text{s}}\right)-{\mu }^{\prime }\right)\right]}{n_b^{\text{id}}+m_b^{\text{id}}}\right),\hfill \\ & & A\left[\left({\mathbf{X}}_U,{\mathbf{X}}_{n_b},n_b,{\mathbf{Y}}_{m_b}^{\text{s}},m_b\right)\to \left({\mathbf{X}}_U,{\mathbf{X}}_{n_a},n_a,{\mathbf{Y}}_{m_a}^{\text{s}},m_a\right)\right]\hfill \\ & & =\min \left(1,\frac{\left(n_b^{\text{id}}+m_b^{\text{id}}\right)\exp \left[-\beta \left(W^{\lambda }\left({\mathbf{X}}_U,{\mathbf{X}}_{n_a},{\mathbf{Y}}_{m_a}^{\text{s}}\right)-W^{\lambda }\left({\mathbf{X}}_U,{\mathbf{X}}_{n_b},{\mathbf{Y}}_{m_b}^{\text{s}}\right)+{\mu }^{\prime }\right)\right]}{⟨n⟩}\right),\hfill \end{array}$$ (35)

where the id superscript once again notates molecules located within Ω_id⊆(Ω_i∪Ω_s), the subdomain subject to GCMC control. Here, ⟨n⟩=ρV_Ωid and it is assumed that $n_b^{\text{id}}+m_b^{\text{id}}=n_a^{\text{id}}+m_a^{\text{id}}+1$. In the limit of instantaneous switching and an infinitely thin intermediate region Ω_s, these results reduce to those of the traditional hybrid model presented in Sec. 2.

Introduction of a decoupling potential

The purpose of an intermediate region that interacts with an unphysical potential is to smoothly decouple the particles between the explicit and implicit regions. For the spherical systems of this study, we define the decoupling parameter as a simple polynomial:

$$\begin{array}{ccc}\hfill \lambda \left(r\right)& =& \left\{\begin{array}{cc}\hfill 1,& \hfill r\le R_i\\ \hfill {\displaystyle 1+\frac{2{\left(r-R_i\right)}^3}{{\left(R_o-R_i\right)}^3}-\frac{3{\left(r-R_i\right)}^2}{{\left(R_o-R_i\right)}^2},}& \hfill R_i<r<R_o\\ \hfill 0,& \hfill r\ge R_o\end{array}\right.,\hfill \end{array}$$ (36)

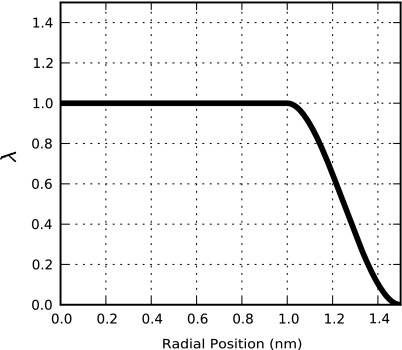
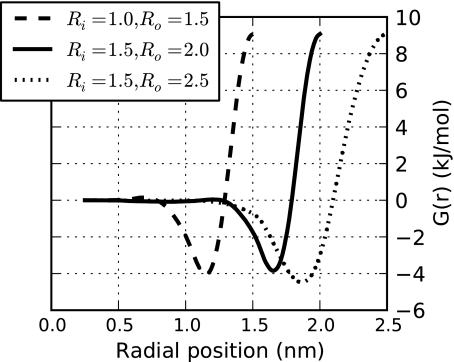
where the intermediate domain Ω_s corresponds to the spherical shell bound by the radii R_i and R_o. This parameter smoothly transitions particles between the fully interacting (λ = 1) and the fully decoupled (λ = 0) states, as demonstrated in Fig. 1. Figure 2 illustrates the spatial arrangement of molecules within the separate regions of both the traditional and SDPI hybrid models.

Figure 1.

Behavior of the coupling parameter for a SDPI model in which R_i = 1.0 nm and R_o = 1.5 nm. Equation 38 utilizes this parameter to determine the extent to which a particle at a given radial position interacts with the rest of the system.

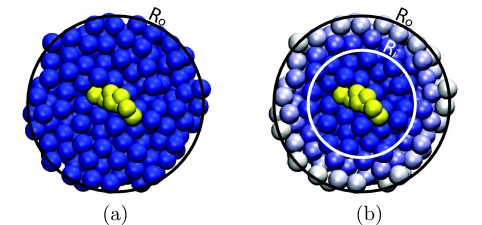
Figure 2.

Composition of spherical hybrid models (R_o = 2.5 nm) centered on a cholesterol molecule (yellow) and containing MARTINI CG water particles. (a) Traditional hybrid model. All solvent molecules within R_o are explicit. Contributions to the PMF from the region outside of R_o are approximated using implicit solvent methods. (b) SDPI model. The innermost region (Ω_i) contains explicit particles and is bound by R_i (1.5 nm for this example). The exterior region (Ω_o, outside of R_o) is accounted for using implicit solvent methods. The intermediate, or switching, region (Ω_s) is bound by R_i and R_o. The particles in this region are colored by the strength of their interactions with the rest of the system. The particles at R_i are fully interacting (blue) and become decoupled (white) as they approach R_o.

A SDPI simulation will contain explicit particles from the innermost and intermediate domains. The total energy of this system is

$$\begin{array}{ccc}\hfill W^{\lambda }\left({\mathbf{X}}_U,{\mathbf{X}}_n,{\mathbf{Y}}_{n_{\text{s}}}^{\text{s}}\right)& =& \sum _i{W}_i\left({\mathbf{x}}_i\right)=\sum _i[\lambda \left(∥{\mathbf{x}}_i∥\right)\Delta w_i\left({\mathbf{x}}_i\right)\hfill \\ & & +\left(1-\lambda \left(∥{\mathbf{x}}_i∥\right)\right)K_i+G\left({\mathbf{x}}_i\right)\hfill \\ & & +\frac{1}{2}\sum _{j\ne i}{U}^{\lambda }\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)],\hfill \end{array}$$ (37)

where, assuming that the center of the spherical domain is placed at the origin, ∥x_i∥ represents the radial position of atom i. The terms G(x_i) and K_i, described in more detail below, are used to counteract the gradient in chemical potential experienced by particles in the switching region. The implicit solvent component of the total potential, ΔW, is our approximation to the bulk solvent PMF and, for this study, is decomposable into atomic components Δw_i. Since the solvent used here interacts only via the LJ potential, we decouple this interaction in a manner directly analogous to that used in free energy studies:⁹¹

$$U^{\lambda }\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)=\lambda \left(∥{\mathbf{x}}_i∥\right)\lambda \left(∥{\mathbf{x}}_j∥\right)U^{LJ}\left(r_{\text{sc}}\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)\right),$$ (38)

where U^LJ is given by Eq. 21 and

$$r_{\text{sc}}\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={(\alpha {\sigma }_{ij}^6{\left(1-\lambda \left(∥{\mathbf{x}}_i∥\right)\lambda \left(∥{\mathbf{x}}_j∥\right)\right)}^p+{∥{\mathbf{x}}_i-{\mathbf{x}}_j∥}^6)}^{\frac{1}{6}}.$$ (39)

The terms α and p modulate the scaling of interactions and are set to 0.5 and 1, respectively.

Thus, a particle within this system interacts both with other explicit particles (via U^λ(x_i, x_j)) and with the bulk region (via Δw_i(x_i)). As can be seen by the above equation, a particle close to the outer boundary R_o is essentially non-interacting. The result of such a decoupling will be a gradient in chemical potential across the switching region that will lead to large differences in the solvent density. In order to ensure Eq. 34, we will attempt to correct for this gradient so that the solvent will maintain the appropriate bulk density everywhere (note that this is not absolutely necessary and that there are other methods that could satisfy Eq. 34). We introduce the constant factor K_i, corresponding to the implicit solvent PMF for atom i isolated from any other explicit regions or particles. This term is approximately equal to the excess chemical potential of our solvent. Scaling this term by (1 − λ(∥x_i∥)) mostly accounts for the drop in chemical potential across the boundary. However, it is still necessary to introduce the factor

$$G\left({\mathbf{x}}_i\right)\approx -\left(1-\lambda \left(∥{\mathbf{x}}_i∥\right)\right)K_i-{\int }_0^{∥{\mathbf{x}}_i∥}dr〈\frac{d{W}_i\left(r\right)}{dr}〉,$$ (40)

equivalent to the difference between the expected and actual excess chemical potential associated with inserting a solvent particle at position x_i, since a simple scaling by (1 − λ(∥x_i∥)) does not appropriately account for any path-dependent effects. The addition of these terms ensures that the solvent maintains bulk density across the domain. Of course, higher-order structural metrics cannot be expected to be recovered within the intermediate region.

We approximate G(x_i) using a set of overlapping Gaussians,^{62, 63}

$$G\left({\mathbf{x}}_i\right)=\sum _{j=0}^{N_j}{g}_j(∥{\mathbf{x}}_i∥-r_j)=\sum _j{a}_j\exp \left[-\frac{{(∥{\mathbf{x}}_i∥-r_j)}^2}{2{\sigma }_{\text{g}}^2}\right],$$ (41)

where the Gaussian centers are equally spaced at r_j=(j+0.5)σ_g and $N_j=(\frac{R_o}{{\sigma }_{\text{g}}}+4)$. The Gaussians centered outside of R_o are added to ensure appropriate behavior of G(x_i) and its derivatives at the boundary. The coupling of Eqs. 38, 40 warrants a self-consistent procedure for the determination of the coefficients a_j, described in more detail in Sec. 4.

For the calculation of Δw_i(x_i), we will use the same implicit solvent model presented in Sec. 2D (Eqs. 28, 24) with an analogous two-body distribution function:

$$h_i^{\left(\mathrm{rep}\right)}\left({\mathbf{x}}_i,\mathbf{y}\right)=\left(1-\lambda \left(\parallel \mathbf{y}\parallel \right)\right)H\left(\parallel \mathbf{y}-{\mathbf{x}}_i\parallel -{\sigma }_i\right),$$ (42)

where λ(∥y∥) is given by Eq. 36.

Therefore, the SDPI hybrid model assumes that single-body potentials can effectively correct the chemical potential gradient and approximate the solvent PMF. This is analogous to the use of a single-body potential term used in the traditional hybrid model, and in Sec. 5 we attempt to demonstrate that such an assumption is much more valid when coupled with the intermediate switching domain present in the SDPI model.

METHODS

Simulation methodology

Simulations were conducted using a monatomic water model from the MARTINI coarse-grained force field^{22, 23} and a modified version of GROMACS 3.3.1.⁹² All simulations were performed using Langevin dynamics integration with a 10 fs time step (a conservative value for this forcefield²²) coupled to a heat bath at 400 K with a friction coefficient of 91 ps⁻¹. Explicit solvent trajectories were maintained at constant pressure (1 atm) using the Berendsen coupling algorithm.⁹³ Explicit solvent and traditional hybrid models used a LJ potential that is switched at 0.9 nm and cut off at 1.2 nm in conjunction with a dispersive tail correction.⁹⁴ Because this work attempts to demonstrate accuracy and not computational efficiency, the SDPI hybrid models employ a full LJ interaction that is not cut off. This allowed for a more straightforward implementation of the implicit solvent methods for this model. More optimized methods are currently being implemented for future analyses.

All thermodynamic properties presented in this study were calculated at a frequency not higher than once every picosecond, or 100 MD steps. Simulation lengths for all analyses were typically between 10 and 100 ns (10⁶ to 10⁷ MD steps), depending on the convergence of results, which were determined using a bootstrapping analysis.

Hybrid model parameters

All results were compiled with both the traditional and SDPI hybrid models at three different sizes (spheres of radii R_o = 2.5, 2.0, and 1.5 nm). The inner radii for these three systems in the SDPI hybrid simulations were R_i = 1.5, 1.5, and 1.0 nm, respectively. The switching region length of 0.5 nm for the two smaller hybrid models corresponds to roughly one solvation layer for this coarse-grained (CG) system.

Traditional hybrid models were simulated using 250 insertion∕deletion GCMC attempts for every 100 steps of MD. Such moves were only attempted over a “buffer region” covering the outer 0.5 nm of the radial domain. SDPI hybrid models, which were subject to much higher acceptance ratios, included 100 insertion∕deletion attempts at an interval of every 100 MD steps over a buffer region covering the outermost 0.3 nm of the radial domain.

Mean force analysis

Bulk explicit solvent mean forces were calculated on a system of pure solvent via Eq. 30 from a full explicit simulation from which radial forces on all particles within a 2.0 nm spherical domain were averaged at 0.01 nm intervals. These forces were then compared to the analogous implicit solvent forces (for a traditional hybrid model) over a range of values for the parameters defined in Sec. 2D. Specifically, σ_s ∈ [0.05, 0.39] nm and σ_e ∈ [0.00, 0.06] nm, tested in intervals of 0.01 nm. The optimal value for pressure (p) for each parameter set was found via least-squares fitting. The overall best-fit parameters were chosen based on the minimum value of mean-squared error,

$${\chi }^2=\frac{1}{N_r}\sum _{i=0}^N{\left(F_i\left({\mathbf{x}}_i\right)-\frac{d\Delta w_i\left({\mathbf{x}}_i\right)}{d{\mathbf{x}}_i}\right)}^2,$$ (43)

where N_r is the number of radial data points (201).

In addition, true mean forces (via Eq. 29) were calculated by choosing an equilibrium configuration from a bulk explicit solvent simulation, freezing all water molecules within a 1.5 nm spherical domain, and averaging forces on these molecules while sampling over all solvent exterior to this region. These were then compared to the implicit solvent forces calculated using the traditional hybrid model with the two-body approximation (Eq. 27) as well as the many-body distribution function (Eq. 25). For the calculations using the many-body distribution function, Δw^(att) was calculated via numerical integration on a three-dimensional grid of 0.0012 nm spacing. The volume derivatives of the system were calculated using the Shrake-Rupley quadrature method⁹⁵ with 996 grid points on the surface of the sphere. Finally, the explicit mean forces were compared to mean forces calculated using the SDPI hybrid model with R_i = 1.5 nm and R_o = 2.5 nm. SDPI mean forces were calculating by freezing all molecules within R_i and averaging forces on these molecules while sampling over all solvent within the switching region.

Parameterization of G(r)

The effective chemical potential term, G(r), was found using an adaptive method implemented in a pure MC simulation for which the insertion∕deletion attempts described above were augmented with translation moves for SDPI models of unrestrained solvent. The simulations used σ_g = 0.0125 nm and began with all Gaussian coefficients a_i set to zero. As the simulation progressed, if the difference between the bulk density (8.28 particles/nm³ for the CG water studied at these thermodynamic conditions) and the calculated density within a radial shell of the hybrid simulation was, within statistical error, higher or lower than a prescribed tolerance, the coefficients were raised or lowered accordingly. This procedure is similar to that used in the development of other effective potentials for hybrid models.^{62, 63} As the radial bulk density profile approached the correct value, the tolerance in error was lowered along with the amount by which the coefficients were altered. All Gaussian coefficients a_i centered at radii r_j<0.5 nm were held at 0. The optimal G(r) curve was chosen once the maximum relative error in density along the radial coordinate was less than 1%. To ensure smooth forces, a double-exponential smoothing method⁹⁶ was then applied to G(r). The resulting potentials demonstrated larger deviations (less than 2% maximum relative error in density) but were more stable for dynamics simulations.

Density profiles and free energy calculations

To determine the extent to which boundary artifacts are present in the hybrid models studied, density profiles were calculated for systems containing no solute and in which all solvent molecules were unrestrained. In the absence of any boundary artifacts, one would expect to find the average density to be equivalent to that of the bulk value ρ everywhere within the spherical domain.

Solvation free energies for water and cholesterol molecules²³ were calculated using the hybrid models and compared to the analogous values obtained from pure explicit solvent simulations. All free energies were calculated using the multistate Bennet acceptance ratio estimator (MBAR).⁹⁷ The soft-core LJ potential⁹¹ was used to decouple the solute from the simulation (analogous to that of Eq. 39). This potential was decoupled according to the parameter λ_MBAR, which for a particular simulation was held fixed at a prescribed value between 1.0 (fully interacting) and 0.0 (fully decoupled) at equally spaced intervals of 0.05. Thus, separate simulations for 21 values of λ_MBAR were performed for each free energy calculation. Intramolecular interactions of cholesterol were not decoupled. For the SDPI simulations, the λ(r) parameter for the molecule being decoupled (given by Eq. 36) was simply scaled by λ_MBAR.

For water free energies calculated using the hybrid models, the water molecule being annihilated was constrained to various positions within the hybrid model to test the uniformity of results across the domain. The cholesterol molecule was restrained to the center of the hybrid regions using a simple harmonic potential applied to the center of mass with a spring constant of 75 kJ/mol/nm².

RESULTS AND DISCUSSION

Mean force analysis and parameterization

Figure 3 compares the explicit solvent radial mean forces (given by Eq. 30) and the best-fit implicit solvent forces. These forces were calculated on solvent molecules within Ω_i by averaging the force contribution from all molecules outside of this region. The parameters for the optimal implicit solvent forces are σ_e = 0.03nm, σ_s = 0.22nm, and p = 86.76 kJ/mol/nm³, giving an average mean-squared error value of χ² = 0.30(kJ/mol/nm)². These parameters are used in all hybrid calculations.

Figure 3.

Comparison of implicit solvent forces to the analogous radial forces obtained from explicit solvent simulations. This optimal fit is associated with an average mean-squared error value of χ² = 0.30(kJ/mol/nm)².

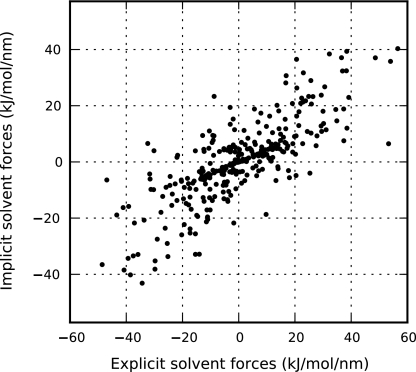
Despite the excellent fit, it is important to note that these are not true mean forces, but the projection of such forces onto a single-body radial term. True explicit mean force components (given by Eq. 29) and the corresponding optimal implicit solvent forces are shown in Fig. 4. These optimal implicit solvent forces give an average mean-squared error of χ² = 105.25(kJ/mol/nm)². Figure 5 compares these same explicit forces to implicit forces obtained using the full geometrical distribution function (Eq. 25) rather than the two-body approximation, resulting in an average mean-squared error of χ² = 120.70(kJ/mol/nm)². These results demonstrate that this implicit solvent model is not capable of reproducing the true mean forces and that even the use of the full geometrical distribution function does not provide any benefit. Nevertheless, the extremely good fit shown in Fig. 3 is noteworthy and demonstrates that any single-body potential capable of reproducing explicit solvent configurations must match the behavior predicted by the simple theory used in this study and outlined in Sec. 2D. Additionally, any model that would hope to improve upon these results would require a more detailed and computationally expensive representation of the solvent density than that which is used here, most likely through heuristic many-body terms⁶¹ or integral equation and other more complex theories.^{70, 71, 72}

Figure 4.

For a static configuration of solvent particles within the interior domain, comparison of implicit solvent forces obtained using the two-body distribution function to the true mean forces obtained from explicit solvent simulations. This optimal fit is associated with an average mean-squared error of χ² = 105.25(kJ/mol/nm)².

Figure 5.

For a static configuration of solvent particles within the interior domain, comparison of implicit solvent forces obtained using the full many-body distribution function to the true mean forces obtained from explicit solvent simulations. This optimal fit is associated with an average mean-squared error of χ² = 120.70(kJ/mol/nm)².

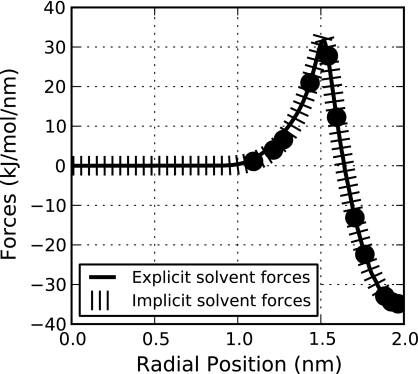
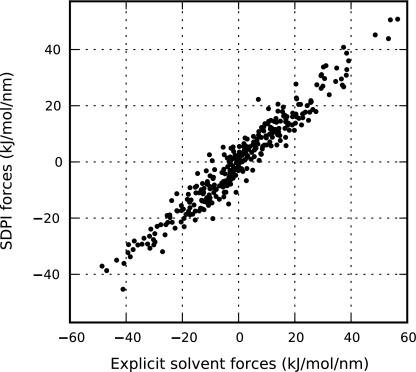
Figure 6 illustrates the ability of the SDPI model to reproduce mean forces within the explicit region. These forces give an average mean-squared error of χ² = 20.24(kJ/mol/nm)², a significantly more accurate result than that obtained with the implicit solvent model used in the traditional hybrid methods.

Figure 6.

For a static configuration of solvent particles within the interior domain, this plot illustrates SDPI mean solvent forces calculated from the implicit solvent model as well as by averaging over configurations of solvent in the switching region. These forces are compared to those obtained from explicit solvent simulations and are associated with an average mean-squared error of χ² = 20.24(kJ/mol/nm)².

Figure 7 displays the converged curves of G(r) for the three hybrid models tested. These curves were parameterized separately, but the level of quantitative similarity suggests that it may be possible to develop a simple transformation of a particular G(r) potential for use in hybrid models of other dimensions. We are currently attempting to develop such a transformation, which would simplify the parameterization of these models significantly.

Figure 7.

The fit potential G(r), given by Eq. 40, for the three hybrid models tested. This term counteracts the variations in chemical potential experienced by decoupled particles and maintains the correct bulk density throughout the switching region.

Density profiles

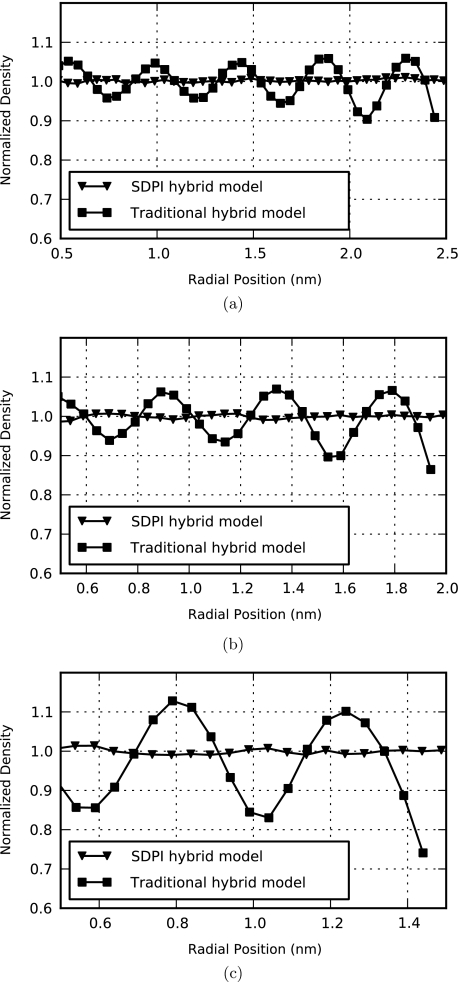
Figure 8 displays the density profiles for solutions of bulk CG water and lists the maximum error in density found for each model. These systems contain only unrestrained solvent, so a value of the bulk density ρ is desired at all positions within the spherical domain. Using the optimal parameter set, very good results are obtained with the traditional hybrid model. Nevertheless, local deviations from bulk density are observed, particularly for the models with smaller explicit regions. SDPI hybrid models demonstrate nearly perfect results at all positions within the explicit domain with a maximum relative error of 1.4% among all models tested, compared to maximum errors in the 10%-26% range for traditional models. Density profiles taken from the traditional hybrid model also exhibit solvent layering, which may be indicative of a higher-order effect resulting from errors in the solvent PMF near the explicit∕implicit boundary.

Figure 8.

Density profiles for the three hybrid model sizes tested, for which the maximum relative error excludes radial positions below 0.5 nm. (a) 2.5 nm hybrid models. The maximum relative error is 9.6% for the traditional model and 1.1% for the SDPI model. (b) 2.0 nm hybrid models. The maximum relative error is 13.5% for the traditional model and 1.2% for the SDPI model. (c) 1.5 nm hybrid models. The maximum relative error is 25.9% for the traditional model and 1.4% for the SDPI model.

Free energies

Table 1 lists the solvation free energies for CG water molecules at various radial positions within the hybrid models. The one-body implicit solvent potential used in this study performs very well in the traditional hybrid model, and the free energy values obtained from these simulations are quite accurate at a variety of positions within the explicit domain. Still, there are regions within these domains that produce free energies of relatively large error. It is interesting to note that the free energies are most erroneous near the center of the explicit region, a result that again suggests that the errors associated with such traditional hybrid models are a higher-order effect in which large density fluctuations throughout the explicit region result from small errors near the boundary. The free energies obtained using SDPI hybrid methods exhibit nearly perfect quantitative results everywhere, with the largest error being 0.25 ± 0.06 kJ∕mol (at the center of the region for which R_i = 1.5, R_o = 2.0 nm).

Table 1.

Comparison of free energy values obtained from traditional and SDPI hybrid models. Free energies of CG water were obtained at variable radial positions within the spherical explicit domain. The values in parentheses represent the absolute error with respect to the value calculated from a full explicit solvent simulation (−21.72 ± .04 kJ∕mol). Values of R_i are only relevant for SDPI models.

Domain radii Ro ∕ Ri (nm)	Radial Position (nm)	Traditional	SDPI
2.5 ∕ 1.5	0.0	−23.03 (−1.31) ± 0.06	−21.66 (0.06) ± 0.06
	0.5	−22.07 (−0.35) ± 0.06	−21.56 (0.16) ± 0.06
	1.0	−22.16 (−0.44) ± 0.06	−21.73 (−0.01) ± 0.06
	1.5	−21.96 (−0.24) ± 0.06	−21.84 (−0.12) ± 0.06
	2.0	−21.66 (0.06) ± 0.06	−21.65 (0.07) ± 0.02
	2.4	−21.66 (0.06) ± 0.06	−21.72 (0.00) ± 0.00
2.0 ∕ 1.5	0.0	−22.00 (−0.28) ± 0.07	−21.47 (0.25) ± 0.06
	0.5	−22.25 (−0.53) ± 0.07	−21.70 (0.02) ± 0.06
	1.0	−21.88 (−0.16) ± 0.07	−21.61 (0.11) ± 0.06
	1.5	−21.50 (0.22) ± 0.10	−21.81 (−0.09) ± 0.05
	1.9	−21.58 (0.14) ± 0.06	−21.72 (0.00) ± 0.00
1.5 ∕ 1.0	0.0	−18.48 (3.24) ± 0.06	−21.88 (−0.16) ± 0.06
	0.5	−21.65 (0.07) ± 0.06	−21.76 (−0.04) ± 0.06
	1.0	−21.43 (0.29) ± 0.06	−21.71 (0.01) ± 0.05
	1.4	−21.46 (0.26) ± 0.05	−21.72 (0.00) ± 0.00

Table 2 lists the solvation free energies for cholesterol obtained from hybrid simulations. The traditional hybrid model performs well but is again subject to significant error. The SDPI hybrid model is consistently more accurate, even when comparing results from the smallest SDPI model (absolute error of 0.22 ± 0.12 kJ∕mol for R_o = 1.5 nm) and the largest traditional model (absolute error of −1.81 ± 0.10 kJ∕mol for R_o = 2.5 nm). The absolute error obtained in the 1.5 nm SDPI model is particularly relevant to note: given that the switching region for these simulations was bound by the radii R_i = 1.0 nm and R_o = 1.5 nm, and that the end-to-end distance of cholesterol is occasionally more than 2.0 nm, these results demonstrate that a high level of accuracy is still obtained from simulations in which the explicit domain is tightly fit around the solute.

Table 2.

Comparison of free energy values for cholesterol obtained from traditional and SDPI hybrid models of varying sized explicit regions. The values in parentheses represent the absolute error with respect to the value calculated from a full explicit solvent simulation (−32.70 ± .06 kJ∕mol). Values of R_i are only relevant for SDPI models.

Domain radii Ro/Ri (nm)	Traditional	SDPI
2.5 ∕ 1.5	−34.51 (−1.81) ± 0.10	−33.10 (−0.40) ± 0.09
2.0 ∕ 1.5	−33.64 (−0.94) ± 0.09	−32.38 (0.32) ± 0.12
1.5 ∕ 1.0	−34.21 (−1.51) ± 0.10	−32.48 (0.22) ± 0.12

For the traditional model, one would expect to obtain the best results for larger systems or near the center of the explicit region. It is interesting to note that this is not the case. We suspect the reason for this to be a higher-order mediation caused by small artifacts near the explicit-implicit boundary, not unlike the role that solvent has been shown to play under confinement.^{64, 65, 66}

CONCLUSIONS

This work demonstrates that the accurate calculation of the bulk solvent PMF for hybrid models with an instantaneous switching at the explicit-implicit boundary is a formidable challenge, and that even well-parameterized models can result in boundary artifacts that lead to less accurate (and somewhat unpredictable) results. We present a new method, termed the SDPI hybrid model, in which explicit particles are slowly decoupled from the system across a switching region, allowing for a smooth removal of local interactions with the bulk solvent. The theoretical development of this model presents the conditions that are necessary to reproduce equilibrium properties from the original supersystem. This work does not present an analogous condition for the reproduction of kinetic properties from any particular thermostat. Given the finite domain and inclusion of Monte Carlo moves, it is expected that certain kinetic properties (such as detailed water dynamics near the explicit∕implicit boundary) will deviate from those calculated using full explicit methods. However, we expect any such artifacts to play a minor role for molecules within the explicit region and for timescales longer than the relaxation of water. Future work on more complex solutes will be used to determine which kinetic quantities can be faithfully reproduced.

The SDPI model presents nearly perfect thermodynamic results with respect to full explicit simulations at all regions within the explicit domain. It is important to note that the addition of this switching region does not add to the computational complexity of traditional hybrid models and actually provides a significant computational advantage by allowing one to simulate a much smaller number of particles while obtaining more accurate results. This advantage may be further highlighted when one considers that simpler implicit solvent models (such as the radial potential of this work) can now be used without penalizing model's accuracy. The model used in this work requires no additional parameters for any solute and three additional parameters for the solvent (σ_e, σ_s, and p, defined in Sec. 2D). This is a substantial benefit over implicit solvent models that require new parameters for each atom type.

The SDPI model necessitates the use of a parameterized potential to counteract the gradient in chemical potential experienced by decoupled particles. Current work is aimed at extending the transferability of SDPI methods by developing a simple method of transforming this potential for use with explicit domains of varying shapes and sizes. Additionally, we are currently adapting these methods for use in more complex solvents that can be used for a wider range of biomolecular applications. While the theoretical development for such applications of the SDPI method will remain unchanged, the incorporation of polar solvents will likely require an orientational dependance of the chemical potential correction term, G(r), and that the electrostatic implicit solvent model appropriately accounts for the change in solvent dielectric across the switching region. This could be accomplished by models utilizing simple geometrical overlaps similar to the nonpolar model used in this work³⁵ or by solutions to Poisson's equation that incorporate a smoothly varying dielectric.^{98, 99} We are particularly excited to see the potential applications of the SDPI model with popular three-point water models.