Limits to Catalysis by Ribonuclease A

Abstract

Bovine pancreatic ribonuclease A (RNase A) catalyzes the cleavage of the P–O^5′ bond in RNA. Although this enzyme has been the object of much landmark work in bioorganic chemistry, the nature of its rate-limiting transition state and its catalytic rate enhancement had been unknown. Here, the value of k_cat/K_m for the cleavage of UpA by wild-type RNase A was found to be inversely related to the concentration of added glycerol. In contrast, the values of k_cat/K_m for the cleavage of UpA by a sluggish mutant of RNase A and the cleavage of the poor substrate UpOC₆H₄-p-NO₂ by wild-type RNase A were found to be independent of glycerol concentration. Yet, UpA cleavage by the wild-type and mutant enzymes was found to have the same dependence on sucrose concentration, indicating that catalysis of UpA cleavage by RNase A is limited by desolvation. The rate of UpA cleavage by RNase A is maximal at pH 6.0, where k_cat = 1.4 × 10³ s⁻¹ and k_cat/K_m = 2.3 × 10⁶ M⁻¹s⁻¹ at 25°C. At pH 6.0 and 25°C, the uncatalyzed rate of [5,6-³H]Up[3,5,8-³H]A cleavage was found to be k_uncat = 5 × 10⁻⁹ s⁻¹ (t_1/2 = 4 years). Thus, RNase A enhances the rate of UpA cleavage by 3 × 10¹¹-fold by binding to the transition state for P–O^5′ bond cleavage with a dissociation constant of <2 × 10⁻¹⁵ M.

INTRODUCTION

Catalysis has its limits. On one extreme, the rate of a “catalyzed” reaction must exceed that of the same reaction in the absence of the catalyst. At the other extreme, the rate of a catalyzed reaction cannot exceed the rate at which the catalyst encounters its substrate or releases its product.

The energetics of enzymatic catalysis are defined by these limits. Enzymes catalyze reactions by binding to the transition states for the chemical interconversion of substrate and product (1–3). The ability of an enzyme to bind to this transition state is given by the ratio of k_cat/K_m for the enzyme-catalyzed reaction and k_uncat for the nonenzymatic reaction (4). This analysis requires, however, that the catalyzed and uncatalyzed reactions have the same rate-limiting transition state. Thus, calculating the transition state binding affinity from the value of k_cat/K_m alone requires that catalysis be limited by the conversion of enzyme-bound substrates to enzyme-bound products. This constraint does not always (or even often) hold (5, 6). If the free energy of the transition state for substrate binding or product release exceeds that for the interconversion of Michaelis complexes, then the decrease in k_cat/K_m reflects only a fraction of the ability of an enzyme to bind to the chemical transition state.

Despite its considerable importance to bioorganic chemistry, information on the uncatalyzed rates of metabolic reactions is now sparse (7). The information coffers are relatively full, however, for the uncatalyzed cleavage of biopolymers. The rate constant for the uncatalyzed cleavage of a peptide bond has been measured at 25°C and near-neutral pH (8). Although too slow to measure directly, the rate constant for the uncatalyzed cleavage of DNA can been inferred from data for the hydrolysis of dimethyl phosphate (7). Here, we measure the rate constant for the cleavage of a P–O^5′ bond in RNA at 25°C and near-neutral pH in the absence of a catalyst. We also elucidate the nature of the rate-limiting transition state in catalysis by bovine pancreatic ribonuclease A (RNase A¹; EC 3.1.27.5), which catalyzes the cleavage of this same P–O^5′ bond in RNA (Fig. 1). Together, these results enable us to reveal the limits to catalysis by RNase A, as well as to compare the energetics of catalysis by RNase A, its mutants, and other ribonucleases.

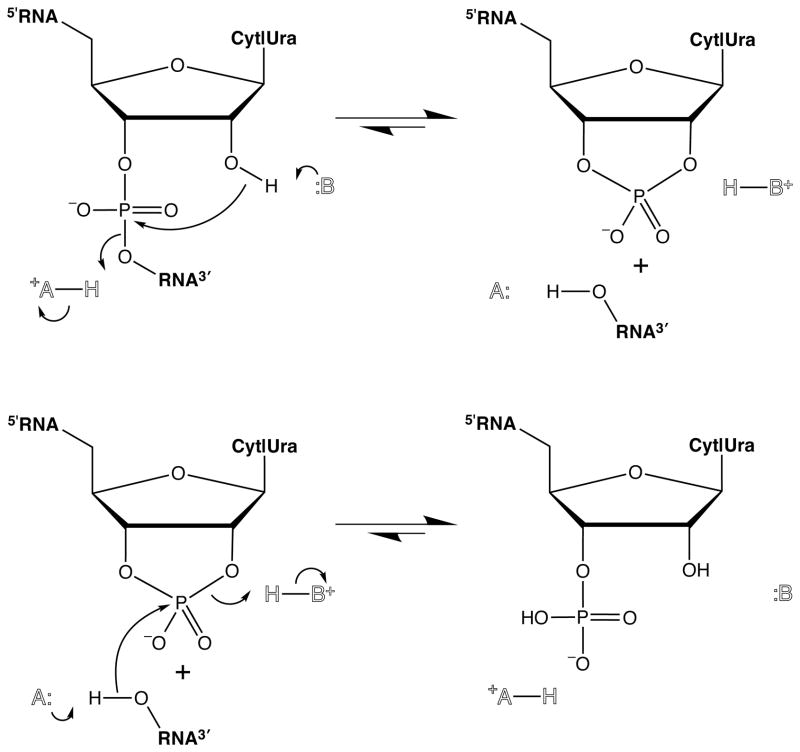
Fig. 1.

Simplest mechanism for the transphosphorylation (top) and hydrolysis (bottom) reactions catalyzed by ribonuclease A that is consistent with existing data (9).

METHODS

General

UpA was synthesized by the methods of Ogilvie et al. (10) and Caruthers and Beaucage (11). UpOC₆H₄-p-NO₂ was synthesized by the method of Williams and co-workers (12). RNase A (type X-A) was from Sigma Chemical (St. Louis, MO). K41A RNase A was prepared as described for other mutants of RNase A (13). [5,6-³H]UTP and [3,5,8-³H]ATP were from Amersham (Arlington Heights, IL).

Ultraviolet absorbance measurements were made on a Cary Model 3 spectrophotometer equipped with a Cary temperature controller (Varian; Sugar Land, TX). ³H content was determined in Biosafe scintillation counting fluid (Research Products International; Mount Prospect, IL) with a TriCarb 1900CA liquid scintillation analyzer (Packard; Meridan, CT).

Cosolvent Dependence of k_cat/K_m

The nature of the rate-limiting transition state in catalysis by RNase A was probed by the addition of cosolvents (6), here, glycerol and sucrose. The enzyme-catalyzed cleavage of UpA and UpOC₆H₄-p-NO₂ was monitored directly at 286 and 330 nm, respectively. Substrate concentrations were determined by uv absorption using ε₂₆₀ = 24,600 M⁻¹cm⁻¹ at pH 7.0 for UpA (14) and ε₄₀₈ = 18,300 M⁻¹cm⁻¹ in 0.4 M NaOH for UpOC₆H₄-p-NO₂. Ribonuclease concentration was determined by using ε_1cm ^0.1% = 0.72 at 277.5 nm (15). Each reaction contained (in 0.8 ml) substrate [UpA, 0.10–0.50 mM; UpOC₆H₄-p-NO₂, 25 μM–0.15 mM] in 50 mM Mes– HCl buffer, pH 6.0, containing NaCl (0.10 M) and glycerol (0, 10, 20, or 30% v/v) or sucrose (0 or 30% v/v).

In the absence of cosolvent, Δε₂₈₆ = −620 M⁻¹cm⁻¹ for the cleavage of UpA and Δε₃₃₀ = 4560 M⁻¹cm⁻¹ for the cleavage of UpOC₆H₄-p-NO₂. New values of Δε₂₈₆ and Δε₃₃₀ for the cleavage reactions were determined for each buffer containing a cosolvent. In each buffer, reaction velocities for at least five concentrations of substrate were determined by monitoring the initial changes in absorbance with time at 25°C. These data were fit to the Michaelis–Menten equation with the program HYPERO (16) to obtain values of k_cat/K_m.

Synthesis of [5,6-³H]Up[3,5,8-³H]A

[5,6-³H]Up[3,5,8-³H]A was synthesized by an enzymatic and chemical route analogous to that described previously for the synthesis of [5,6-³H]UpA (17). Here, both [5,6-³H]UTP (100 μCi) and [3,5,8-³H]ATP (100 μCi) were included in the run-off transcription reaction, along with ATP (12 μM) and UTP (12 μM). Reactions were monitored by TLC on PEI–cellulose plates (Alltech; Waukegan, IL) as described (17).

[5,6-³H]Up[3,5,8-³H]A was purified by HPLC using instrumentation from Waters (Millipore; Bedford, MA). To facilitate its purification, the radiolabeled material was mixed with a small amount of unlabeled UpA. The resulting mixture was injecting onto a Novapak C-8 reversed phase column that had been equilibrated with aqueous ammonium acetate (0.10 M). The loaded column was eluted isocratically with aqueous ammonium acetate (0.10 M) at a flow rate of 0.8 ml/min. Under these conditions, UpA eluted at 2.6 min.

Uncatalyzed Rate of UpA Cleavage

The rate of UpA cleavage in the absence of a catalyst was determined by using HPLC to monitor the time-course of the degradation of [5,6-³H]Up[3,5,8-³H]A. To eliminate contamination from ribonucleases, glassware and plasticware used in this experiment were soaked overnight in aqueous SDS (1% w/v), rinsed with absolute ethanol, and then dried. Likewise, the buffer used in the incubation was treated overnight with DEPC (0.05% v/v), and then autoclaved.

[5,6-³H]Up[3,5,8-³H]A (5 μCi, 15 nmol) was dissolved in DEPC-treated 50 mM Mes– HCl buffer, pH 6.0, containing 0.10 M NaCl, and the resulting solution was incubated at 25°C. At timed intervals, aliquots (50 μl) were removed, and combined with an equimolar mixture of seven unlabeled carriers. These carriers were UpA, the four products that could result from the cleavage of the P–O^5′ and P–O^3′ bonds of UpA (U>p + A and U + 5′-AMP), and the two isomeric products that could result from the hydrolysis of U>p (3′-UMP and 2′-UMP). The resulting mixture was injected onto a C-18 reverse phase column that had been equilibrated with 12 mM potassium phosphate buffer, pH 7.0, containing TBAP (4 mM) as an ion-pairing agent. The loaded column was eluted at 0.8 ml/min with 18.0 ml of equilibration buffer, a linear gradient (1.0 ml + 1.0 ml) from equilibration buffer to methanol–water (1:1 v/v), and 8.0 ml of methanol– water (1:1 v/v). Under these conditions, the retention times were: U, 1 min; U>p, 4 min; A, 7 min; 5′-AMP, 13 min; 3′-UMP, 19 min; 2′-UMP, 21 min; and UpA, 25 min. Fractions of each unlabeled carrier were collected. Solvent was removed from each fraction with a vacuum centrifuge. The resulting residues were dissolved in water, and their ³H content was determined.

RESULTS

Cosolvent-Dependence of k_cat/K_m

The value of k_cat/K_m = 2.3 × 10⁶ M⁻¹s⁻¹ (18) for the cleavage of UpA by wild-type RNase A is typical of that for substrate association (41). In contrast, the value of k_cat/K_m = 200 M⁻¹s⁻¹ (Messmore and Raines, unpublished results) for the cleavage of UpA by K41A RNase A is indicative of a reaction that is limited by a chemical transition state. As shown in Fig. 2, the k_cat/K_m for the cleavage of UpA by wild-type but not K41A RNase A was inversely related to glycerol concentration. The glycerol-dependence of k_cat/K_m for the cleavage of poly(C) by wild-type RNase A is within error of that for the cleavage of UpA (data not shown). If catalysis by the sluggish mutant enzyme is indeed limited by a chemical transitions state, then the glycerol-dependent change in the value of k_cat/K_m for catalysis by the wild-type enzyme indicates that a transitions other than that for the conversion of bound substrate to bound products limits the rate of catalysis for the cleavage of UpA.

Fig. 2.

Plots of the glycerol-dependence (A) and sucrose-dependence (B) of the relative second-order rate constant for the transphosphorylation of UpA by wild-type RNase A (●) and K41A RNase A (○), and for the transphosphorylation of UpOC₆H₄-p-NO₂ by wild-type RNase A (◇). (k_cat/K_m)° refers to the absence of cosolvent. The dashed lines have slopes of 0.

The value of k_cat/K_m = 5.7 × 10⁴ M⁻¹s⁻¹ (19) for the RNase A-catalyzed cleavage of UpOC₆H₄-p-NO₂ is approximately 40-fold lower than that for cleavage of UpA. As shown in Fig. 2A, added glycerol had little effect on the value of k_cat/K_m for the cleavage of UpOC₆H₄-p- NO₂ by wild-type RNase A. Again, the lack of a glycerol-dependence indicates that the rate of this slow reaction is limited by a chemical transition state.

In contrast to the results with glycerol, the sucrose-dependence of k_cat/K_m is identical for catalysis by wild-type and K41A RNase A, as shown in Fig. 2B. Thus, the rate-limiting transition state for catalysis by wild-type RNase A is altered differently by glycerol and sucrose. This finding indicates that catalysis by the wild-type enzyme is not limited by diffusion, since the addition of glycerol or sucrose has a similar effect on solution microviscosity (6). Rather, since glycerol but not sucrose is known to interact strongly with single-stranded nucleic acid [(42) and references therein], the data in Fig. 2A and 2B indicate that the cleavage of UpA by wild-type RNase A is limited by substrate desolvation.

Synthesis of [5,6-³H]Up[3,5,8-³H]A

Purified [5,6-³H]Up[3,5,8-³H]A produced a single spot during TLC on PEI–cellulose plates with a mobile phase of aqueous LiCl (0.5 M). Analysis by HPLC of this material indicated that ≥99.44% of the total ³H in the sample was in [5,6-³H]Up[3,5,8-³H]A.

Uncatalyzed Rate of RNA Cleavage at pH 6.0 and 25°C

After 20 days of incubation at pH 6.0 and 25°C, approximately 1% of the [5,6-³H]Up[3,5,8-³H]A had degraded. Essentially all of the ³H from the cleaved UpA appeared in U>p and A, indicating that these were the products of the uncatalyzed cleavage of UpA. Rate constants for this reaction were obtained by plotting the appearance of ³H in U>p and A and the loss of ³H in UpA, as shown in Fig. 3. The first-order rate constant measured for the appearance of U>p + A was k_uncat = 5 × 10⁻⁹ s⁻¹ (t_1/2 = 4 years). This value is in good agreement with that determined for the disappearance of UpA, which was 6 × 10⁻⁹ s⁻¹.

Fig. 3.

Plot of the time-course for the degradation of tritiated UpA at pH 6.0 and 25°C. Products other than UpA, U>p, and A accounted for <0.1% of the radioactivity at each time point.

The uncatalyzed rate of UpA cleavage was measured at 25°C in 50 mM Mes–HCl buffer, pH 6.0, containing NaCl (0.10 M). These conditions are typical for our assays of catalysis by RNase A (13, 18–20, 21). Experiments were not performed to extrapolate the uncatalyzed rate constant to zero buffer and salt concentration. The effects of 50 mM buffer and 0.10 M salt on the rate constant are, however, likely to be negligible for our present purposes. For example, the effect of morpholine buffer on the rate of UpU cleavage is modest (22). Also, adding metal ions, varying ionic strength, and changing buffer type had no detectable effect on the uncatalyzed rate of peptide bond cleavage (8).

The uncatalyzed rate constant measured here is twofold slower than that measured for UpU at 80°C in 10 mM Hepes buffer, pH 7.0 (23). Although this small difference is surprising given the large difference in temperature, other differences in reaction conditions (such as pH) preclude a detailed comparison of these data.

DISCUSSION

Nature of the Rate-Limiting Transition State

Catalysis of the transphosphorylation of UpA by RNase A is not limited by a chemical interconversion. In this sense, RNase A belongs to the family of enzymes that Albery and Knowles have called “perfect” (24–27).² Any further decrease in the free energy of the transition state for the chemical step will not be manifested in an increase in the rate of transphosphorylation.

This limit to catalysis has consequences for the practicing enzymologist. The effect of mutations to RNase A on the intrinsic rate constant for P–O^5′ bond cleavage cannot be determined simply from a decrease in the value of k_cat/K_m for the cleavage of UpA. Rather, such a decrease merely provides a lower limit on the affinity of the enzyme for the chemical transition state. For example, although K41A RNase A is a 10⁵-fold poorer catalyst than is the wild-type enzyme, changing Lys41 to an alanine residue must result in a >10⁵-fold decrease in the affinity for the chemical transition state.

Uncatalyzed Rate of UpA Cleavage

The products of the uncatalyzed cleavage of UpA are the same as those in the enzyme-catalyzed reaction. The identity of these reaction products is consistent with the uncatalyzed and catalyzed reactions proceeding by the same mechanism. If a reaction does proceed by the same mechanism in the absence and presence of an enzyme, then the ratio of k_cat/K_m for the enzyme-catalyzed reaction to k_uncat for the uncatalyzed reaction provides a measure of the affinity of the enzyme for the rate-limiting transition state during catalysis, as is shown in Scheme 1 (4). RNase A catalyzes the transphosphorylation of UpA with a k_cat/K_m of 2.3 × 10⁶ M⁻¹s⁻¹. Under identical conditions, the uncatalyzed rate of UpA transphosphorylation is 5 × 10⁻⁹ s⁻¹. The dissociation constant for the rate-limiting, diffusive transition state during the transphosphorylation of UpA is therefore K_TX = k_uncat/(k_cat/K_m) = 2 × 10⁻¹⁵ M. Since the rate-limiting transition state is diffusive, this value for K_TX is an upper limit for the dissociation constant of the enzyme bound to the chemical transition state for P–O^5′ bond cleavage.

Scheme 1.

What is the origin of the affinity of RNase A for the chemical transition state? Replacing Lys41 with an alanine residue removes a potential hydrogen bond donor from the active site of RNase A. Recent work in our laboratory indicates that it is the ability of this residue to donate a hydrogen bond that effects catalysis (21). The loss of a hydrogen bond from residue 41 costs the enzyme 10⁵-fold in rate acceleration. Similarly, replacing His12 or His119, the general base and general acid in catalysis (Fig. 1), slows catalysis by 10⁴- to 10-fold (19). Finally, the B2 subsite of RNase A is also significant contributor to catalysis. This subsite, which interacts with the base of the residue that is part of the scissile phosphodiester bond, is composed of Gln69, Asn71, and Glu111 (29). The values of k_cat/K_m for the RNase A-catalyzed transphosphorylation of substrates with different 5′ leaving groups decrease in the order adenosine > guanosine > cytidine > uridine > methanol (30). CpA is transphosphorylated by RNase A with k_cat/K_m = 3 × 10⁶ M⁻¹s⁻¹; CpOMe with k_cat/K_m = 250 M⁻¹s⁻¹ (31). If CpA interacts most strongly with the B2 pocket and CpOMe does not interact at all, then the binding of adenosine to the B2 subsite provides a 10⁴-fold rate acceleration. Thus, four factors (Lys41, His12, His119, and the B2 subsite) individually contribute at least 10⁴-fold in rate enhancement. Since the overall rate enhancement is 3 × 10¹¹, these factors cannot contribute independently to catalysis. Evaluating the synergy between Lys41, His12, His119, and the B2 subsite is the focus of on-going work in our laboratory.

Each of the four interactions listed above is important, but not essential, to catalysis. Although a mutant enzyme that is missing any one of these interactions appears to be a poor catalyst relative to wild-type RNase A, it still retains far more catalytic activity than it has lost. The same may not be true, however, for enzymes that have lost two or more of these interactions. Unfortunately, the catalytic activity of mutants of RNase A that have lost >10⁶-fold in rate enhancement cannot be assessed conveniently by spectrophotometric assays. Hence, our ability to assay ribonuclease activity by monitoring the cleavage of [5,6-³H]Up[3,5,8-³H]A will be a useful tool with which to study minimalist catalysts.

Limits to Catalysis by other Ribonucleases

The ability of RNase A to bind to its rate-limiting transition state can be compared to that of other ribonucleases. Of course, not all ribonucleases are assayed under the conditions under which we obtained our uncatalyzed rate. Nonetheless, different enzymes can be compared if assayed under similar conditions (that is, room temperature, ionic strength near 0.1 M, and pH 5– 7) and if the scissile P–O^5′ bond in the RNA substrate is as reactive as that in UpA. Table 1 shows a comparison of the transition state binding affinities for RNase A, RNase T1, and the hammerhead ribozyme. Each of these catalysts binds to the chemical transition state with a dissociation constant of ≤0.2 pM.

TABLE 1.

Binding of the Transition State for Cleavage of the P–O^5′ Bond of RNA at 25°C

Catalyst	Substrate	Rate-limiting transition state	kcat/Km (M−1s−1)	KTX (M)
Ribonuclease A	UpA	Desolvation (this work)	2.3 × 106 (18)	2 × 10−15
Ribonuclease T1	GpA	Desolvation (33)	1.7 × 106 (34)	3 × 10−15
Hammerhead ribozyme	ACGGUCUCpACGAGC	?	2.8 × 104 (32)	2 × 10−13

^aCalculated by assuming that k_uncat = 5 × 10⁻⁹ s⁻¹, as determined in this work.

^bAt 30°C.

Implications for Biopolymer Stability

Our data allow a comparison to be made of the intrinsic stabilities of DNA, RNA, and protein in dilute aqueous solution. A phosphodiester bond in DNA suffers cleavage with an estimated t_1/2 of only 1 × 10⁵ years (7). In contrast, a phosphodiester bond in RNA is cleaved with t_1/2 of 4 years, and a peptide bond in a protein is cleaved with t_1/2 of 7 years (8). Thus, RNA and protein, the two biopolymers that are most frequently synthesized and degraded during the lifetime of a cell, have a similar and relatively low intrinsic stability.

The free energies for the two steps in the hydrolysis of RNA are shown in Fig. 4. These diagrams are drawn for an RNase A concentration of 0.1 mM, which is that found in the cow pancreas (37). At pH 6.0 and 25°C, the intrinsic kinetic barrier for cleaving a P–O^5′ bond in RNA is almost identical to that for hydrolyzing the P–O^2′ or P–O^3′ bond in a nucleotide 2′,3′-cyclic phosphodiester. These phosphodiester bonds are far less stable than are those in DNA, which suffer cleavage at a 10⁴- to 10⁵-fold lower rate. Apparently, the proximity of the 2′-hydroxyl group to the phosphorous atom in RNA and the strain (38) [or poor solvation (39)] inherent in a nucleotide 2′,3′-cyclic phosphodiester contribute equally to an enhanced rate of decomposition.

Fig. 4.

Free energies for the uncatalyzed (---) and RNase A-catalyzed (—; 0.1 mM) transphosphorylation of UpA (left) and hydrolysis of U>p (right). Free energies of activation were calculated for the reaction at pH 6.0 and 25°C with the equation ΔG^‡ = −RTln[kh/(k_bT)] and the values of k_cat/K_m (18) and k_uncat (this work) for UpA transphosphorylation, k_cat/K_m for U>p hydrolysis (13), and k_uncat (36) for C>p hydrolysis. The free energy of 3′-UMP relative to that of U>p was calculated at pH 6.0 and 25°C with the equation ΔG° = −RTlnK and K = 1.0 × 10³ (35). The uncatalyzed hydrolysis of U>p also produces 2′-UMP (not shown).

Ribonucleases are usually thought be catabolic enzymes (37), yet RNase A [like other ribonucleases (17)] has evolved to be far more efficient at cleaving RNA than at hydrolyzing nucleotide 2′,3′-cyclic phosphodiesters (Fig. 4). Since cleaving RNA renders indecipherable its encoded information, ribonucleases are cytotoxic. The recent illumination of the biological mechanism or ribonuclease cytotoxicity [(40) and references therein], which animals have recruited for a variety of physiological purposes, has revealed the versatility of these venerable enzymes.