Graded Structures for All-ceramic Restorations

Abstract

One failure mode of all-ceramic restorations is radial cracking at the cementation surface, from occlusally induced flexure of the stiffer ceramic layer(s) on the softer dentin underlayer. We hypothesize that such failure may be substantially mitigated by an appropriate grading of elastic modulus through the ceramic thickness. In this study, we fabricated graded structures by infiltrating glass into zirconia plates, with resulting diminished modulus in the outer surfaces. The plates were then bonded to a polymeric base and subjected to flexure by contact loading until fracture. Comparison of infiltrated specimens with non-infiltrated controls showed a significant increase in the fracture loads, by a factor of nearly 2. Finite element analysis revealed the cause of increase in the load-bearing capacity to be diminished tensile stresses within the lower-modulus graded zone, corresponding to an increase in material strength. The results confirmed that suitably graded structures can be highly beneficial in the design of next-generation all-ceramic restorations.

Introduction

Ceramic coatings are commonly used in dental restorations, due, in part, to their aesthetic value and chemical inertness. However, ceramics are brittle and therefore highly susceptible to flexural stresses at the cementation surface from occlusal loading (McLean, 1979; Scherrer and deRijk, 1993; Kelsey et al., 1995; Anusavice and Tsai, 1997; Fradeani and Aquilano, 1997; Kelly, 1997, 1999, 2004; Malament and Socransky, 1999a,b, 2001; Sjogren et al., 1999a,b; McLaren and White, 2000; Deng et al., 2002; Fradeani and Redemagni, 2002; Rudas et al., 2005; Lawn et al., 2007; Rekow and Thompson, 2007; Lee et al., 2008). One way to counter this brittleness is to grade the material composition with a lower modulus at the external surfaces (Huang et al., 2007). Preliminary studies have demonstrated the feasibility of such a process, by infiltrating the surfaces of ceramic plates with an appropriate silicate glass (Zhang and Kim, 2009; Zhang and Ma, 2009). Care needs to be taken to use glasses with similar coefficients of thermal expansion (CTE), to minimize residual stresses in the structure during the fabrication. Such a gradation is predicted to diminish the tensile stress intensity at the outer plate surfaces (Jitcharoen et al., 1998), thereby rendering the structure less susceptible to fracture.

In this study, we sought to provide a quantitative analysis of the effects of a graded modulus on the ensuing load-bearing capacity of an all-ceramic crown-like layer structure. To this end, we used an yttria tetrahedral zirconia polycrystal (Y-TZP), now most widely adopted as a framework material for all-ceramic dental crowns and multi-unit bridges. Such graded structures not only diminish stress concentrations in the surface layers, where fractures tend to initiate, but also provide improved aesthetics/shades relative to monolithic Y-TZP. A silicate glass composition with CTE close to that of zirconia was chosen as an infiltration material (Zhang and Kim, 2009; Zhang and Ma, 2009). We conducted routine nano-indentation testing to determine the modulus gradients, and used a simple flexural testing arrangement to measure failure loads of the infiltrated plate structures.

Materials & Methods

A previously characterized 3 mol% Y-TZP zirconia of strength 1.10 ± 0.13 GPa (mean and standard deviation, n = 10) was chosen as the base dental ceramic material for this work (Zhang and Kim, 2009; Zhang and Ma, 2009). This material was pressureless-sintered from a fine-sized (d ~ 28 nm) yttria-stabilized zirconia powder (5.18 wt% Y₂O₃, TZ-3Y-E grade; Tosoh, Tokyo, Japan) and had thermal and mechanical properties comparable with those of commercially available dental zirconias (Zhang and Kim, 2009). Plates of 12-mm fixed side length were ground and polished from the stock material to 2 thicknesses, d = 0.4 mm and 1 mm (Fig. 1a). A silicate glass with specific components by weight (65.5% SiO₂, 11.7% Al₂O₃, 10.0% K₂O, 7.3% Na₂O, 3.0% CaO) was fabricated with CTE matching that of the zirconia (10.5 x 10⁻⁶ °C⁻¹) (Zhang and Kim, 2009; Zhang and Ma, 2009). The glass was reduced to a frit and applied in slurry form to the top and bottom surfaces of pre-sintered Y-TZP plates (1400°C for 1 hr in air). The coated plates were then infiltrated (1450°C for 2 hrs), producing a glass/zirconia/glass (G/Z/G) layered structure (Fig. 1a). Heating and cooling rates were slow enough (900°C/hr) to prevent cracking of the structures. After cooling, excess glass was polished off each surface. Selected specimens were sectioned through the thickness to facilitate characterization of the infiltrated material.

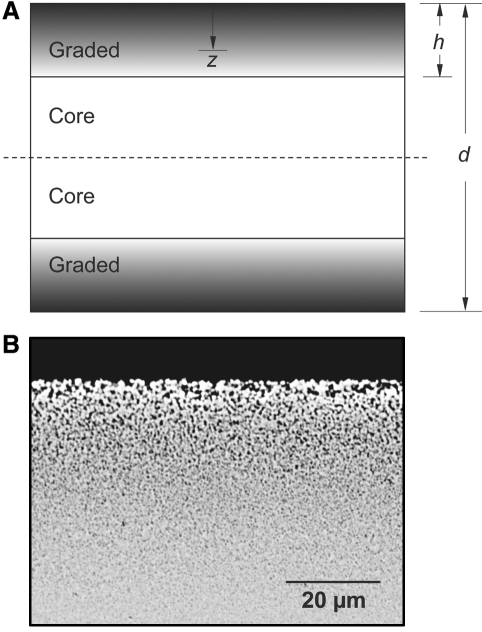
Figure 1.

Morphology of the graded zone. (a) Schematic of graded structure, defining coordinates. d and h are the thicknesses of plate and graded layer, respectively, and z is the distance from the free surface. (b) Section view of graded zone of glass-infiltrated Y-TZP, in back-scattered electron microscopy.

Nano-indentations by means of an instrumented Berkovich diamond pyramid were made across the specimen sections at intervals of 3 µm and at a peak load of 40 mN (3D OmniProbe Tribometer, Hysitron, Minneapolis, MN, USA). Elastic modulus at each point was evaluated from the unloading portions of the indentation load-displacement records according to a routine software protocol (Oliver and Pharr, 1992). Vickers diamond micro-indentations were placed on the top surfaces of non-sectioned G/Z/G and control Y-TZP specimens at a peak load of 50 N to produce impressions with well-defined corner cracks. Fracture toughness of each structure was then evaluated from the measured crack sizes by the well-documented Anstis equation (Anstis et al., 1981).

The load-bearing capacities of the G/Z/G and Y-TZP specimens were determined by a simple contact flexural test (Chai et al., 1999). Six specimens (n = 6) for each thickness (d = 1 mm or 0.4 mm) were fabricated for each material type (G/Z/G and Y-TZP). Individual plates were first bonded to a 12.5-mm-thick polycarbonate block (Hyzod, AlN Plastics, Norfolk, VA, USA) by means of an epoxy resin (Harcos Chemicals, Bellesville, NJ, USA). The top surfaces of the plates were then loaded with a hard tungsten carbide sphere (radius, 3.18 mm) on a screw-driven universal testing machine (Model 5566, Instron Corp., Canton, MA, USA). This essentially point-load configuration produces flexural tension at the surface of the plate in contact with the compliant polycarbonate support, akin to the stress state experienced by dental crowns on dentin (Chai et al., 1999; Deng et al., 2002). The crosshead speed was maintained at a fixed rate of 1 mm/min, which resulted in fracture at the adhesive surface within a minute or two. A video camera mounted below the polycarbonate block was used to record the instant of fracture in the plate specimens, and the corresponding critical loads were documented.

We used a commercial finite element code (Ansys, Canonsburg, PA, USA) to evaluate the stress distributions within the loaded plates (Chai et al., 1999). To accommodate modulus gradients across the specimen sections in the infiltrated ceramics, the graded zone was divided into 10 discrete sublayers. The elastic modulus for each sublayer was taken from the nano-indentation tests, with a stepwise representation of the data. The modulus for the polycarbonate support block was 2.35 GPa, from a previous study (Chai et al., 1999). Poisson’s ratio was taken as 0.22 for the ceramic materials and 0.35 for the polycarbonate. The loading was treated as axisymmetric, effectively reducing the configuration to a two-dimensional problem. The flexural tensile stresses were determined within the specimen sections at the measured fracture loads.

Results

A cross-section of a glass-infiltrated Y-TZP specimen in back-scattered electron microscopy revealed the graded structure (Fig. 1b). The dark areas in this image indicate glass, and the lighter areas indicate zirconia. For the heat treatments used, the thickness of the graded layer was h = 120 ± 10 µm (mean and standard deviation, 6 specimens), independent of the original thickness d of the zirconia. Previous analysis of this structure has shown that the glass content varied from 45-50% at the top surface to 0% at h = 120 µm (Zhang and Kim, 2009; Zhang and Ma, 2009).

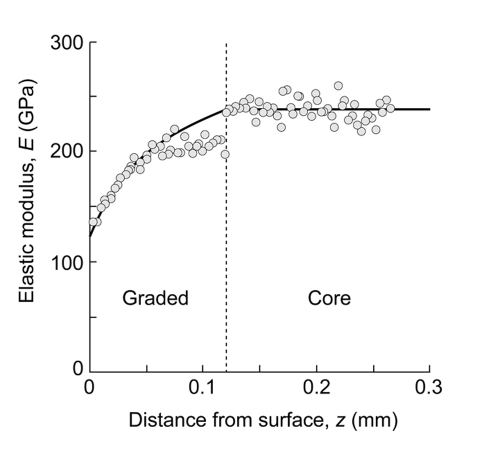
The results of the nano-indentation measurements of Young’s modulus E across the section reveal the gradient in properties (Fig. 2). The datapoints in this figure are experimental measurements. The solid line within the graded layer is a best-fit to the data in accordance with an empirical power-law relation

Figure 2.

Modulus profile across a section of infiltrated G/Z/G, plotted as a function of distance z from outer tensile surface. Note gradation of values within the graded zone, and constant value within bulk. Number of tests n = 90.

$$E=E_s+(E_b-E_s){(z/h)}^m$$ (1)

with z the distance from the outer surface, m = 0.56 the power-law exponent, and E_s = 125 GPa and E_b = 240 GPa the modulus at the outer surface and in the bulk zirconia, respectively. The modulus in the core is constant, within the data scatter.

Micro-indentations with a Vickers pyramid revealed well-defined corner crack patterns in both control Y-TZP and graded G/Z/G specimen surfaces (Fig. 3), at a common load 50 N. The indentation patterns do not differ greatly in the two materials, indicating little change in toughness resulting from the infiltration process. We obtained toughness values T = 3.53 ± 0.20 MPa·m^1/2 for Y-TZP and 3.76 ± 0.30 MPa·m^1/2 for G/Z/G (mean and standard deviation, 6 specimens). Note that the radial dimensions of the crack arms measured from the indent center are about 80 µm, relative to the thickness 120 µm of the graded layer; since the cracks tend to be penny-like in geometry, this dimension can be taken as a measure of the crack depth. Hence, the toughness value for G/Z/G is an average through the graded section.

Figure 3.

Vickers indentation impression at a 50-N load in the outer surface of (a) Y-TZP and (b) graded G/Z/G. Similarity in pattern indicates little change in material fracture properties from infiltration.

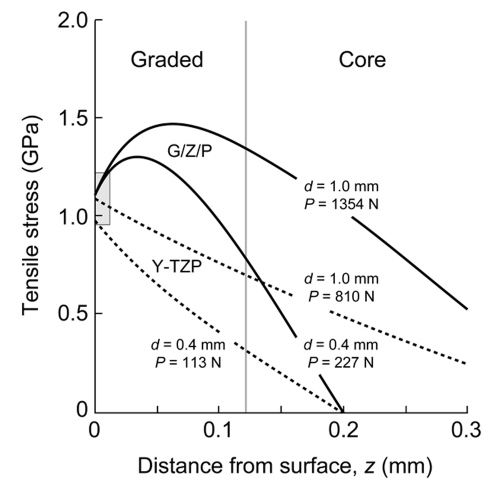
The contact loads P required to break the ceramic plates in sphere-loaded flexure were as follows (mean and standard deviation, n = 6 per specimen type): for G/Z/G, P = 1354 ± 131 N at d = 1.0 mm, P = 227 ± 20 N at d = 0.4 mm; for Y-TZP, P = 810 ± 53 N at d = 1.0 mm, P = 113 ± 10 N at d = 0.4 mm. Hence, the load-bearing capacity of the infiltrated materials was close to twice that of the zirconia controls of the same thickness. Note that the breaking loads were considerably higher for thicker specimens of each given specimen, consistent with an expected P ~ d² dependence from plate theory (Chai et al., 1999). Plots of the FEA-calculated stress vs. distance z from the tensile surface of the flexing plate help to explain these results (Fig. 4). Curves are FEA predictions, calculated at the mean breaking loads for each configuration. The vertical line indicates the boundary between infiltrated and inner core layers, at h = 120 µm. The hatched box on the vertical axis represents the previously measured strength 1.10 ± 0.13 GPa (standard deviation bounds) of the core zirconia. While the distribution of internal stresses varies widely for the four cases shown, all curves tend to the strength value of the base zirconia at the outer surface (z = 0), suggesting that the improvement in load-bearing capacity in the infiltrated structures is indeed due to stress redistribution from the infiltration rather than to an increase in material strength.

Figure 4.

Stress distributions in G/Z/G and Y-TZP plates subject to flexural loading from contact with a hard sphere at the top surface, as a function of distance z from tensile surface. Curves calculated from FEA for each specimen thickness, at breaking loads measured experimentally (mean for n = 6 per specimen type).

Discussion

The results of this study indicate the beneficial influence of graded structures in the design of all-ceramic crowns and bridges, and possibly also abutments and posts, where flexural tensile stresses can be critical. By the infiltration of zirconia with a low-modulus glass, the stresses responsible for failure from surface flaws are substantially diminished. This behavior was apparent in the plotted stress distribution curves appropriate to the measured fracture loads in infiltrated relative to non-infiltrated zirconia plates. Substantially higher loads were required to break the plates after infiltration under otherwise identical conditions, by a factor of close to 2. However, the stresses at the specimen surfaces, where the flaws responsible for failure typically reside, were the same in all cases, within the experimental scatter. Physically, this was attributable to the reduced modulus in the near-surface regions, with much of the stress borne by the stiffer material within the specimen interior (stress transfer). Of special note is the shift in maximum stresses from the outer surface to within the graded layer. Even though those stresses were up to 40% higher, the absence of large internal flaws, coupled with the somewhat diminished effectiveness of any such internal flaws as stress concentrators (Lawn, 1993), rendered the graded material more flaw-tolerant.

Following this last point, it is of interest to estimate the flaw dimensions involved. A characteristic flaw size c_f may be estimated from the well-documented strength relation S(πc_f)^1/2 = T (Lawn, 1993). Using the toughness values T measured above, along with the average surface stress values S at z = 0, yields c_f = 3.7 ± 1.4 µm for G/Z/G compared with c_f = 3.5 ± 1.3 µm for Y-TZP (uncertainty levels estimated assuming nominal 10% error in measurements of both S and T). The similarity in c_f between the 2 material groups suggests that infiltration has relatively little influence on flaw population, again reinforcing the hypothesis that improved performance is due primarily to stress redistribution rather than to microstructural modification.

We acknowledge the empirical nature of the analysis given here. We have represented the modulus gradients by a simple power-law relation as a first approximation. The FEA calculations used to evaluate stress distributions under flexural load usefully account for the stress redistributions within the graded layers, but have only limited predictive capacity. In this approach, the best materials for optimizing failure resistance, and the best heat treatments for affecting the gradients without introducing deleterious residual stresses, must be determined on a case-by-case basis. We have also focused on cracking at the inner cementation surface due to flexural plate-loading, whereas other fracture modes can occur in crown-like structures. In all cases, however, reduction in surface stress concentrations may be expected to diminish susceptibility to premature failure. A more detailed analysis in terms of closed-form equations, incorporating material and geometric variables, with consideration given to different crack modes and with allowance for the influence of modulus gradients under different heat treatments, and with due attention to aesthetic considerations, lies beyond the scope of the present study.

Our work has focused on improved resistance of dental materials to static loading. We are conducting tests to determine fatigue and wear properties on our graded structures, and early results indicate substantial improvement. The results of these studies will be reported at a later date.