Approximating Model Probabilities in Bayesian Information Criterion and Decision-Theoretic Approaches to Model Selection in Phylogenetics

Abstract

A priori selection of models for use in phylogeny estimation from molecular sequence data is increasingly important as the number and complexity of available models increases. The Bayesian information criterion (BIC) and the derivative decision-theoretic (DT) approaches rely on a conservative approximation to estimate the posterior probability of a given model. Here, we extended the DT method by using reversible jump Markov chain Monte Carlo approaches to directly estimate model probabilities for an extended candidate pool of all 406 special cases of the general time reversible + Γ family. We analyzed 250 diverse data sets in order to evaluate the effectiveness of the BIC approximation for model selection under the BIC and DT approaches. Model choice under DT differed between the BIC approximation and direct estimation methods for 45% of the data sets (113/250), and differing model choice resulted in significantly different sets of trees in the posterior distributions for 26% of the data sets (64/250). The model with the lowest BIC score differed from the model with the highest posterior probability in 30% of the data sets (76/250). When the data indicate a clear model preference, the BIC approximation works well enough to result in the same model selection as with directly estimated model probabilities, but a substantial proportion of biological data sets lack this characteristic, which leads to selection of underparametrized models.

Introduction

Likelihood-based phylogenetic approaches have come to dominate systematic biology and are applied to an increasing array of evolutionary questions. Over the past four decades, the set of candidate models has grown from a small handful of named models such as F81 (Felsenstein 1981) and TrN (Tamura and Nei 1993) to a combinatorial explosion of thousands, which has motivated the development of formalized model selection methods. Goodness-of-fit tests (Goldman 1993, Bollback 2002) can recognize models that do not adequately fit data, but model rejection is of limited use when considering many candidate models because many candidate models may remain after rejecting a subset of the candidates (Ripplinger and Sullivan Forthcoming). Furthermore, the issues of identifying optimal model fit and identifying an adequate model for inferring phylogenies are separate issues (Steel 2005, Sullivan and Joyce 2005). Specifically, models selected for inferring phylogenies should be sufficiently complex to capture historical signal in the sequence data; the decision-theoretic (DT) approach of Minin et al. (2003) directly addresses this point. Initial statistical attempts at model selection for phylogeny estimation relied on iterated hierarchical likelihood ratio tests (hLRTs; Huelsenbeck and Bull 1996, Frati et al. 1997, Sullivan et al. 1997), typically using the ModelTest program (Posada and Crandall 1998). However, hLRTs cannot compare nonnested models; the Akaike information criterion (AIC) (Akaike 1974), the Bayesian information criterion (BIC) (Schwarz 1978), and the DT approach solve this problem by avoiding direct model comparisons in any computational step prior to final model ranking.

Both the BIC and DT approaches rely on a conservative approximation to compute model probabilities. Specifically, they use a diffuse prior centered on a maximum likelihood (ML) estimate and two terms of a Taylor-series expansion (Raftery 1995). The nature of the BIC's assumed prior is of particular import in the context of this study because it does not remotely correspond to the priors applied for the Markov chain Monte Carlo (MCMC)-based direct estimates. The BIC's diffuse prior tends to make it conservative with regard to model complexity (Raftery 1999), even compared with the “uninformative” priors often used for Bayesian MCMC analyses.

DT model selection measures relative performance of all pairs of candidate models and minimizes the risk due to poor model choice in the context of all possible choices and outcomes. Conceptually, DT methods do not strive to choose the absolute best-fit model; rather, DT methods minimize the risk of choosing a model that performs poorly relative to all the other candidates. Suppose that there are three models to choose among. Risk can be calculated for each model choice by summing the conditional costs of the possible outcomes. In the matrix below, C_ABP(O_B|A) is the cost of choosing model A when model B was the best choice (C_AB), times the conditional probability that B was the best choice (P(O_B|A)), which is proportional to its posterior probability. This results in a matrix from which risks can be computed for each possible choice.

	Outcome A	Outcome B	Outcome C	Risk
Choice A	CAAP(OA|A)	CABP(OB|A)	CACP(OC|A)	∑i = AC CAiP(Oi|A)
Choice B	CBAP(OA|B)	CBBP(OB|B)	CBCP(OC|B)	∑i = AC CBiP(Oi|B)
Choice C	CCAP(OA|C)	CCBP(OB|C)	CCCP(OC|C)	∑i = AC CCiP(Oi|C)

Choosing the model with the lowest risk is fundamentally different than choosing the optimal model under some optimality criterion because the choice directly takes into account all candidate models.

Berry and Gascuel (1996) and Holder et al. (2008) applied decision theory to provide justification for consensus trees derived from nonparametric bootstrap and Bayesian posterior distributions, respectively. Minin et al. (2003) and Abdo et al. (2004) applied decision theory to model selection based on the risk function

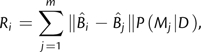(1)

where is the Euclidean distance between branch length vectors estimated under models i and j for a fixed topology, and P(M_j|D) is the probability of model j given the data. Thus, the performance criterion penalizes branch length estimation error. In the aforementioned previous studies, model probabilities were approximated

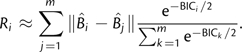(2)

The approximation for P(M_j|D) is based on the BIC (Raftery 1995), where BIC_i = − 2lnL + K_ilnn; lnL is the maximum log-likelihood of a fixed tree topology with branch lengths optimized under model i, K_i is the number of free parameters in model i, and n is the sample size (assumed to be the number of characters for lack of an obvious value). The summations are across m candidate models.

Suchard et al. (2001) first applied reversible jump MCMC to choosing among a small set of substitution models, and Huelsenbeck et al. (2004) demonstrated that MCMC (Metropolis et al. 1953, Hastings 1970) with reversible model jumps (Green 1995) can be used to estimate posterior model probabilities (e.g., the rightmost term in eq. 1) for all 203 special cases of the general time reversible (GTR) model (Yang 1994a). In the most general case, the GTR model allows for unequal nucleotide base frequencies (π_A, π_C, π_G, and π_T) and unequal substitution rates (α, β, γ, δ, ε, and η), which are used to form a stochastic matrix that is of the form:

From\To	A	C	G	T
A	—	πCα	πGβ	πTγ
C	πAα	—	πGδ	πTϵ
G	πAβ	πCδ	—	πTη
T	πAγ	πCϵ	πGη	—

The relative mutation rate parameters can be constrained to form simpler models. For example, setting β = ε and α = γ = δ = η reduces the mutation rate parameters from five free parameters to one and happens to be one of the named models, Hasegawa–Kishino–Yano (HKY; Hasegawa et al. 1985).

In this study, we further extended the set of candidate models from 203 to 406 by developing an MCMC proposal to sample among models with and without Γ-distributed among-site mutation rate variation. We adapted the DT model selection methods of Minin et al. (2003) to evaluate the 406 GTR + Γ models and computed model probabilities using both the approximate method and the MCMC estimation method. We analyzed the 250 diverse TreeBASE (http://www.treebase.org/) data sets selected by Ripplinger and Sullivan (2008) to gain insight into the extent that approximating model probabilities impacts model selection.

Methods

Model Selection

For each of the 250 aligned data sets selected by Ripplinger and Sullivan (2008), we used PAUP* (Swofford 2002) to compute pairwise paralinear (LogDet) distances (Lake 1994, Lockhart et al. 1994), generated a neighbor joining (NJ) tree (Saitou and Nei 1987, Studier and Keppler 1988), optimized branch lengths for each of the 406 GTR + Γ-family models and computed the model-specific maximum log-likelihoods. We used the branch lengths to compute Euclidean distances between models and the log-likelihoods to approximate model probabilities (eq. 2).

Markov Chain Monte Carlo

In order to estimate the model probabilities necessary for equation 1, we extended Crux (Evans 2009) to utilize reversible jump MCMC for sampling among the 406 GTR + Γ-family models. We used the proposal developed by Huelsenbeck et al. (2004) to sample among the 203 GTR-family models. However, rather than using Dirichlet priors and multivariate proposals for mutation rates (and state frequencies), we used normalized independent exponential priors and updated the rates individually, as suggested by Lewis et al. (2005). This approach has the same effect but avoids the need for multivariate proposals. State frequencies were allowed to vary for all experiments.

Γ-distributed among-site mutation rate variation is commonly approximated using discrete rate categories (Yang 1994b), and we used eight categories. Rather than directly using the shape parameter (α) to parametrize the Γ distribution, we used an exponential prior on ω = 1/α, as suggested by Lewis et al. (2005). This has the advantage of allowing α = ∞ (no Γ-distributed among-site rate variation), which is particularly relevant to sampling among models with/without + Γ. We developed MCMC proposals to add/remove + Γ that, while straightforward, are to our knowledge original, so we provide the derivations in the Appendix.

Polytomies

Restricting consideration to fully resolved trees has been shown to negatively impact Bayesian approaches due to the star tree paradox (Suzuki et al. 2002, Cummings et al. 2003, Lewis et al. 2005). The star tree paradox applies to any MCMC analysis that considers only fully resolved trees for data that lack adequate support to resolve one or more polytomies. Minor stochastic variations in the data can cause one resolution of such polytomies to be strongly favored over the others, thus misleading the researcher to conclude that the phantom branches are well supported. To avoid any potential artifacts stemming from the star tree paradox in estimates of model probabilities, we used the polytomy proposals for sampling polytomous trees developed by Lewis et al. (2005), as well as the branch length change proposal, which modifies the length of a single branch using a log-scaled sliding window. We also used a generalization (Evans and Sullivan Forthcoming) of the extending tree bisection and reconnection proposal described by Lakner et al. (2008). This approach allows branch-count–preserving topology transformations to any (nonstar) tree, including polytomous trees and resolved four-taxon trees, which improves mixing for large data sets (Evans and Sullivan Forthcoming).

Priors

We used a flat polytomy prior, which means that each resolution class (trees in each class have the same number of internal branches) is equally likely (Lewis et al. 2005). Trees within each resolution class were assumed to be equally likely. Similarly, we assumed a flat prior for the 203 GTR-family models, and a flat prior for models with versus without Γ-distributed among-site rate variation. For models with Γ-distributed rates, we used an exponential (λ = 1) prior for 1/α. We assigned branch lengths an exponential (λ = 10) prior.

Convergence

We used the online convergence diagnostic to automatically terminate analyses once enough samples were available and the diagnostic indicated convergence (Brooks and Gelman 1998, p. 441). Given multiple independent runs as inputs, erects a (1 − α) credibility interval for each run, computes the proportion of the pooled samples that is covered, and averages the per interval coverages. When the average coverage comes within some ε of (1 − α), we consider the runs to have converged. For each analysis, we executed two independent runs using random fully resolved starting trees for a minimum of 5 million steps each, discarded the first half of each run as burn-in, sampled every 1,000 steps thereafter, and used on the lnL values with α = 0.05 and ε = 0.01.

Because we were mainly interested in the distribution of model frequencies, we also applied a more rigorous post hoc convergence analysis to verify model frequency convergence. We used here as well, also with α = 0.05 and ε = 0.01, but we erected each credibility “interval” by taking the first 95% of the distribution in frequency-ordered sample histograms. That is, for each distribution, we counted the number of times each model was sampled, ranked the models from most to least sampled, then extracted the models that accounted for the top 95% of samples. We used this diagnostic to verify that independent MCMC runs sampled primarily from the same set of models. Note that the number of models in the 95% credibility interval is a useful indication of information content within the sequence alignment; a large number of models indicates low information content.

Metropolis Coupling

All of our MCMC analyses were performed using four Metropolis-coupled chains (Geyer 1991) per independent run. Metropolis coupling is a convenient method for parallel sampling, and it tends to guard against entrapment at local optima during sampling. To decrease program execution times, we distributed each analysis across 8–64 computer processors on a 512-node Beowulf cluster using a combination of the Open Message Passing Interface library (http://www.open-mpi.org/) and multithreading, based in part on the methods developed by Altekar et al. (2004).

Results

Assuming uniform priors across models, if the BIC approximation is sufficient, the model with the best BIC score is expected to be that with the highest posterior probability. This was the case for 70% of the data sets (174/250; table 1). In most cases, where there was a difference between the model with the highest probability and the one with the best BIC score, the BIC-favored model was simpler; for 54 data sets, the BIC model had only one fewer parameters. For 12 data sets, the BIC selected a model with one more parameter than the model with the highest posterior probability.

Table 1.

K_P(M|D) versus K_BIC (pairwise model choice parameter counts) for 250 Data Sets. The BIC Tended to Choose Slightly Simpler Models, as Evidenced by a Disproportionately Large Number of Data Sets below the Diagonal

	KBIC
KP(M|D)	3	4	5	6	7	8	9
3
4	1		1
5		7	27	2
6		3	18	63	6
7			4	18	67	3
8				2	9	17
9				1		1

The BIC approximation versus direct estimation DT methods for computing model probabilities resulted in differing model choice for 45% of the data sets (113/250). The number of parameters chosen by the approximation method (K_approx) averaged 6.32. The number of parameters chosen by the estimation method (K_estim) was somewhat higher at 6.75. Table 2 depicts the pairwise model choice parameter counts. The direct estimation method chose comparatively simpler models for only 13 data sets, whereas the approximate method chose comparatively simpler models for 83 data sets.

Table 2.

K_estim versus K_approx (pairwise model choice parameter counts) for 250 Data Sets. The Estimation Method Tended to Choose Slightly more Parameter-Rich Models, as Evidenced by a Disproportionately Large Number of Data Sets below the Diagonal

	Kapprox
Kestim	3	4	5	6	7	8	9
3
4		1
5			19	1
6	1	2	16	47	5
7		2	10	28	65	7
8		1	3	4	12	21
9				1	3		1

Figure 1 shows pairwise risk plots for six of the data sets analyzed. For all the data plots shown, the model selection methods chose different models, though for data set 47, the methods closely agreed on model risks. The plots shown are a broad sampling of varied patterns; most of the 250 plots look much like those for data sets 47 or 211. Data set 128 exhibits a common pattern, wherein the + Γ models all have much lower risk than any of the models that lack + Γ. For data set 153 (and to a lesser extent data set 28), the approximate method strongly prefers models lacking + Γ, and the estimation method strongly prefers + Γ models. For data set 93, the approximate method computes more scattered risks than does the estimation method.

FIG. 1.

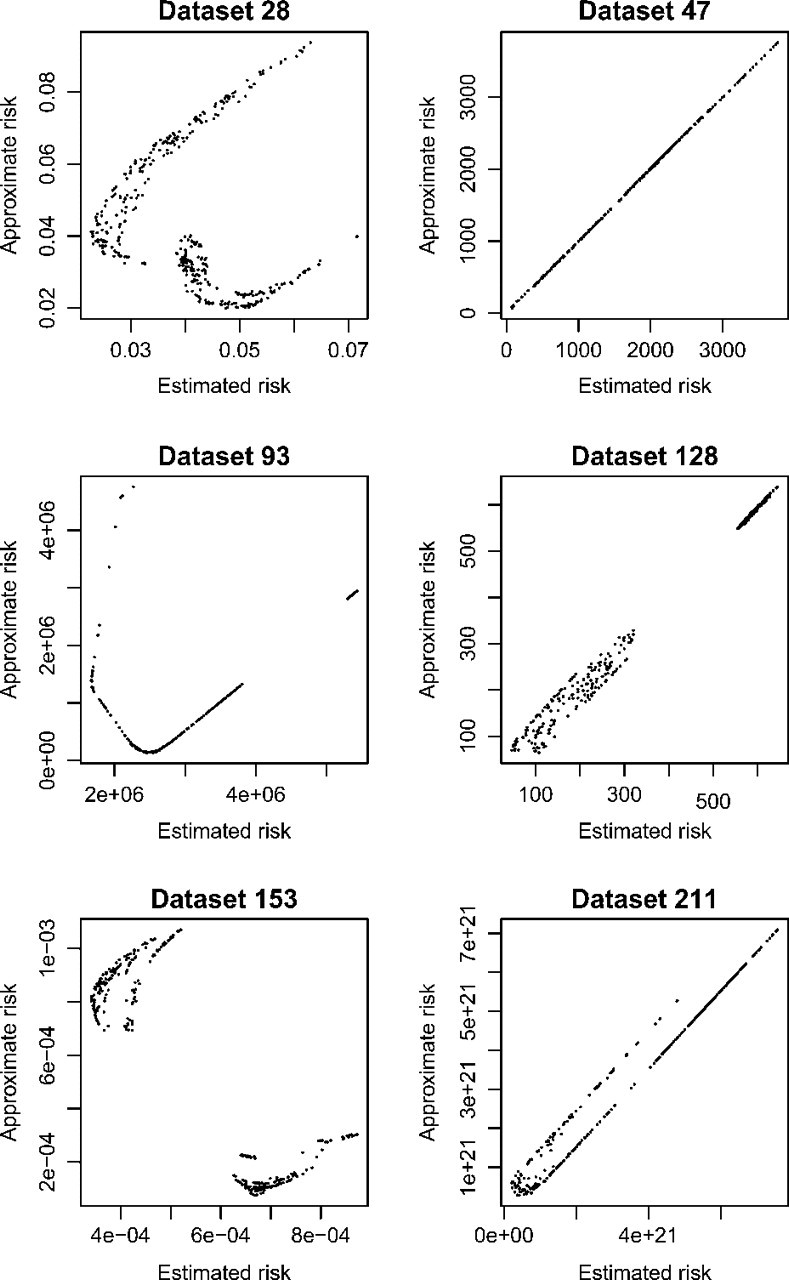
Approximate versus estimated risk plots. Model choice differed for all the data sets shown, though just barely for data set 47. Many of the plots look much like that for data set 47, sometimes with a gap along the diagonal between + Γ and non- + Γ models.

Analysis

We looked for relationships between parameter richness and various other statistics that could elucidate the differences in model choices for the two methods, such as the number of taxa, number of characters, and number of unique site patterns. The only obvious correspondence was with the size of the frequency-ordered 95% credible set of models sampled via MCMC. To compute the credible set for each MCMC analysis, we counted the number of times each model was sampled, ranked the models from most to least sampled, then counted the number of models that accounted for the top 95% of samples. In cases where the model selection methods chose the same model, the 95% credible sets averaged only 10.99 (of 406) versus 22.67 where the model choice differed.

In cases where DT model selection chose different models depending on the use of approximate versus estimated model probabilities, we performed paired MCMC analyses that were configured as described earlier except that the rate classes and + Γ (or not) were fixed according to the two different models chosen. We compared the sample distributions from the paired analyses in the following manner. We first needed to represent the tree distributions in a manner amenable to statistical analysis. Therefore, we followed (Carstens et al. 2004) by computing the Robinson–Foulds distance (RF distance; Robinson and Foulds 1981, Moret et al. 2004) between the NJ tree generated for the BIC approximation method (i.e., a reasonable anchor tree) and every tree in each sample. We then used a two-sided pooled t-test at the α = 0.05 level to test whether the samples could have been drawn from the same underlying tree distribution. This is a weak test for detecting differences in samples because RF distances do not indicate direction within tree space, but when RF distance distributions do differ, it is a clear indication that the tree samples were drawn from distinct distributions. According to this test, at least 57% of the tree distributions (64/113) differed significantly. In the larger context of all 250 data sets, this means that the model selection methods resulted in significantly different tree distributions for at least 26% of the data sets.

This is an important result because it shows that analyses based on the BIC approximation DT method failed to achieve results indistinguishable from those of the more rigorous direct estimation DT method for over a quarter of all the data sets analyzed. For these data sets, Ripplinger and Sullivan (2008) used parametric bootstrap tests to show that ML trees estimated under even more strongly different models (e.g., GTR + I + Γ vs. HKY + Γ) are rarely significantly different. In the tests reported here, we examined distributions of trees rather than point estimates. Although the point estimates (i.e., ML trees) do not differ significantly (Ripplinger and Sullivan 2008), the posterior distributions for different models are not drawn from the same underlying distributions of topologies. The effect that this would have on macroevolutionary inferences that account for phylogenetic uncertainty by sampling from the posterior distribution (e.g., biogeographic reconstructions; Nylander et al. 2008) is beyond the scope of this paper.

Discussion

Our experiments clearly show that approximating model probabilities for DT model selection impacts results, often causing underparametrized models to be chosen. If the underparametrization were simply caused by BIC-based approximation overpenalizing model complexity, it might be feasible to determine a more refined penalization term, but there appears to be no such simple solution.

In this study, we chose among 406 GTR + Γ-family models, whereas DT-ModSel only considers 56 of the 812 GTR + I + Γ-family models. This makes direct comparisons to the original model selection experiments of Ripplinger and Sullivan (2008) of limited use, but we note with interest that for the 250 data sets studied, DT-ModSel chose models with an average of 6.7 parameters, which is higher than the 6.32 our approximation-based implementation averaged. There are two reasons for this: 1) DT-ModSel can choose models with a maximum of ten parameters versus nine for our implementation and 2) our implementation offers the full set of rate class choices, so the most parameter-rich models are rarely chosen.

Direct estimation of model probabilities is a promising avenue for improving model-based phylogeny estimation. Current approximation approaches (BIC and DT) perform rather well on average, especially when there is much information in the data with respect to model preference. They either select the same models as the direct estimates (55% for DT; 70% for BIC) or they select a model that is very close, usually simpler by a single parameter. However, when the different models are used to sample the posterior distribution of topologies, the distributions are sometimes statistically different. We have not assessed the biological significance of the different distributions, but work by Ripplinger and Sullivan (2008) suggests that it may be small.

Nevertheless, because not all data sets exhibit strong preference across models, the uncertainty associated with model choice could be accommodated in phylogeny estimation through model averaging (e.g., Posada and Buckley 2004, Sullivan and Joyce 2005). Reversible jump MCMC is perhaps the best justified approach for doing so (e.g., Huelsenbeck et al. 2004), and this can be accomplished in the simple manner used here or by using mixture models (Pagel and Meade 2004, Evans and Sullivan Forthcoming).

APPENDIX

In this appendix, we describe MCMC proposals that are to our knowledge original. As applied to phylogenetic inference, each sample in a Markov chain is a super parameter τ that includes tree topology, branch lengths, mutation rates, etc. Each proposed state τ^′ is based on τ and is accepted with probability α_m(τ,τ^′) according to the proposal ratio

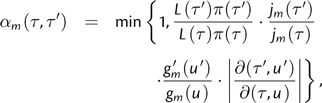(3)

where L(τ)π(τ) is the likelihood of state τ times its prior probability, j_m(τ) is the probability of choosing move m when in state τ, g_m(u) is the density transformation for the vector u of random variables, and 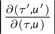is the Jacobian that accounts for change of variables from (τ,u) to (τ^′,u^′) (Green 2003). If the proposed state change is rejected, then the current τ is preserved, which results in sequential chain samples that are identical. In the limit, the Markov chain converges on the stationary distribution.

Γ-distributed Rate Model Jumps

Sampling among models both with and without Γ-distributed mutation rates requires a pair of dimension-changing proposals, one proposal for adding + Γ to the model and the other proposal for removing + Γ from the model. In the following derivations, we assume that the probability of proposing a + Γ model jump remains constant, regardless of whether + Γ is being added or removed. If this assumption were relaxed, j_m(τ) and j_m(τ^′) would not cancel. In practice, maintaining such balance between such paired proposals simplifies implementation and has no obvious disadvantages.

Recall that ω = 1/α is exponentially distributed, where α is the Γ shape parameter. Therefore, the prior density for ω is π(ω) = θ_ωe ^{− θ_ωω}, where the expected value of ω is E(ω) = 1/θ_ω. We assign a prior probability π _{+ Γ} to models that incorporate Γ-distributed rates, which leads to W = (1 − π _{+ Γ})/π _{+ Γ}. 0 < W < 1 favors + Γ models, W = 1 indicates a flat prior, and W > 1 discriminates against + Γ models.

Add + Γ

Proposing the addition of + Γ to a model requires generation of the inverse shape parameter, ω^′ = x/θ_ω. The density transformation is g_m(x) = e ^{− x}, where x = − ln(1 − u) is an auxiliary variable that is used to draw x∼Exp(1) random numbers, and u∼Unif[0,1) is easily computer generated. The prior density for ω^′ is

(4)

So, the prior ratio is

(5)

The Jacobian that accounts for change of variables from x to ω^′ is

(6)

The resulting proposal ratio (ignoring the likelihood ratio) is

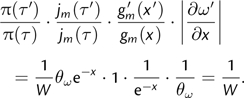(7)

Remove + Γ

Proposing the removal of + Γ from a model simply involves computing the proposal ratio such that it is consistent with the + Γ addition proposal. Therefore, x^′ = θ_ωω, and the density transformation on x^′ is g_m^′(x^′) = e ^{− θ_ωω}. The prior ratio is

(8)

The Jacobian that accounts for change of variables from ω to x^′ is

(9)

The resulting proposal ratio (ignoring the likelihood ratio) is

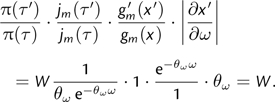(10)