Abstract
The conventional kilovoltage (kV) x-ray-based dual-energy CT (DECT) imaging using two different x-ray energy spectra is sensitive to image noise and beam hardening effects. The purpose of this study was to evaluate the theoretical advantage of the DECT method for determining proton stopping power ratios (SPRs) using a combination of kV and megavoltage (MV) x-ray energies. We investigated three representative x-ray energy pairs: 100-kVp and 140-kVp comprised the kV-kV pair, 100-kVp and 1-MV comprised the kV-MV pair, and two 1-MV x-ray beams – one with and one without external filtration comprised the MV-MV pair. The SPRs of 34 human tissues were determined using the DECT method with these three x-ray energy pairs. Small perturbations were introduced into the CT numbers and x-ray spectra used for the DECT calculation to simulate the effects of random noise and beam hardening. An error propagation analysis was performed on the DECT calculation algorithm to investigate the propagation of CT number uncertainty to final SPR estimation and to suggest the best x-ray energy combination. We found that the DECT method using each of the three beam pairs achieved similar accuracy in determining the SPRs of human tissues in ideal conditions. However, when CT number uncertainties and artifacts such as imaging noise and beam hardening effects were considered, the kV-MV DECT improved the accuracy of SPR estimation substantially over the kV-kV or MV-MV DECT methods. Furthermore, our error propagation analysis showed that the combination of 100-kVp and 1-MV beams was close to the optimal selection when using the DECT method to determine SPRs. Overall, the kV-MV combination makes the DECT method more robust in resolving the effective atomic numbers for biological tissues than the traditional kV-kV DECT method.
Keywords: proton stopping power ratios, dual-energy computed tomography, MV computed tomography, proton therapy, treatment planning
1. Introduction
Charged particle radiotherapy is sensitive to range uncertainties because the exact position of the distal falloff of a charged particle beam depends on the accurate estimation of the radiological path length, which, in turn, depends on the stopping power ratios (SPRs) along the beam’s path in the patient. Typically, CT imaging is used in treatment planning of charged particle radiotherapy and for calculating radiation doses in patients. If the SPRs in patients for a charged particle beam (we assume proton therapy in this work, but the results will also apply to other charged particle beams) are not known accurately, range uncertainty will occur. To account for the range uncertainty, a large treatment margin is typically used in proton treatment planning (Moyers et al., 2001). However, a large treatment margin prevents us from realizing the full benefit of proton therapy, i.e., sparing critical organs immediately distal to the target while still delivering a high radiation dose to the target. Other sources of range uncertainty include setup error and internal organ motion, but one of the major sources of range uncertainty is the estimation of proton SPRs in patients.
In current practice, the SPRs are determined from the CT number through a CT number-to-SPR calibration curve, which needs to be specifically determined for each CT scanner. The popular method of determining the calibration curve is the stoichiometric calibration method developed by Schneider et al (1996). The range uncertainty owing to the uncertainty in SPRs derived from a single CT number and a single calibration curve was estimated to be 3.5% (Moyers et al., 2009).
In a previous study, we proposed using a dual-energy CT (DECT) method to estimate the proton SPRs of human tissues (Yang et al., 2010). In the DECT method, proton SPRs are derived from electron density ratios (EDRs) and effective atomic numbers (EANs). The advantage of the DECT method over the conventional calibration method is that the SPR estimation using the DECT method is based on both the electron density information and the elemental compositions. As a result, the SPR determined using the DECT method was shown to be less sensitive to tissue composition variation than was that determined by the conventional method.
However, the DECT method tends to be sensitive to CT number variations due to image noise and other uncertainties in the imaging and image reconstruction processes. The purpose of this study was to investigate whether the DECT method using a kilovoltage (kV)-megavoltage (MV) x-ray beam pair can improve the accuracy of proton SPR estimation compared to the traditional kV-kV DECT method. The first part of this study was to compare the DECT using different combinations of x-ray beams in the presence of different uncertainties such as tissue composition variations, random noise, and beam hardening effects. The second part was to investigate the propagation of uncertainty in SPR estimation using the DECT method and suggest the best x-ray beam energy combination for use in SPR estimation.
2. Materials and methods
2.1. DECT method to derive proton SPRs of human tissues
In the DECT method, each patient has two CT scans using x-ray beams with different energy spectra. For each CT voxel, the EDR and EAN are calculated from the two CT numbers. The mean ionization energy (Im) is determined from the EAN based on an empirical relationship discovered by Yang et al (2010) between the Im and EAN of human tissues. With both the EDR and Im known, the SPR of a material can be calculated using the Bethe-Bloch equation, which can be approximated by
| (1) |
where me is the electron mass, cβ is the velocity of the proton beam, are the proton SPR and EDR, respectively, of the material relative to water and Iw is the mean ionization energy of water. The procedure of calculating the EDR and EAN from two CT numbers was described in more detail in our previous publication (Yang et al., 2010) but is briefly reviewed here.
The CT number (Hounsfield Unit or HU) is usually defined as , where 〈μx〉 and 〈μw〉 are the linear attenuation coefficients of the material being scanned and the water averaged over the x-ray beam spectrum, respectively. In this study, the following definition was used for convenience:
| (2) |
In this way, the relative change in the CT number is equal to the relative change in the linear attenuation coefficient. The linear attenuation coefficient 〈μx〉 for a material can be computed by
| (3) |
where ρx is the density of the material, wj is the weighting function for energy Ej in the polyenergetic beam, and ωi, Zi, Ai and (μ/ρ)i(Ej) are the mass weight, atomic number, atomic mass and mass attenuation coefficient at energy Ej of the ith element of the material. In this study, the values of (μ/ρ)i(Ej) used in equation (3) to calculate 〈μx〉 were from the photon cross sections database (XCOM) supplied by the National Institute of Standards and Technology (NIST) (Berger et al., 2005). The CT number of a material calculated based on its elemental compositions and the x-ray spectrum using equations (2) and (3) was referred to as the true CT number.
For a monoenergetic photon beam with maximum energy below 1.02 MeV, the linear attenuation coefficient (μ) of a single element can be calculated by μ = ρe[Z4F(E,Z) + G(E,Z)], where ρe, Z, and E are the electron density, atomic number, and x-ray beam energy, respectively. The terms ρeZ4F(E,Z) and ρeG(E,Z) describe the photoelectric attenuation and the combining term of Compton scatter and coherent scatter attenuation, respectively. For a polyenergetic beam with maximum energy below 1.02 MeV, the linear attenuation coefficient of a composite material can be calculated by
| (4) |
where wi is the weighting function of the energy spectrum of the polyenergetic beam and Zx is the EAN of the composite material. Combine equations (2) and (4) and yield . The equation above can be rewritten to
| (5) |
where .
There are two unknowns— and Zx —in equation (5), which is solvable when two CT numbers are provided. Since SumF(Zx) and SumG(Zx) do not depend on Zx strongly, can be calculated iteratively by solving
| (6) |
where . Two x-ray beams with different energy spectra are used in the DECT method; one x-ray beam has relatively low energy and is referred to as the low-energy x-ray beam (denoted by subscript L) while the other one is referred to as the high-energy x-ray beam (subscript H). With the value of Zx known, can be determined by
| (7) |
In this study, the EDR and EAN (Zx) calculated from two CT numbers using equations (6) and (7) were referred to as the estimated EDR and EAN, respectively. The mean excitation energy (Im) determined from the estimated EAN based on the empirical relationship was referred as the estimated mean excitation energy. The SPR calculated based on the estimated EDR and mean excitation energy using the Bloch equation (equation (1)) was referred as the estimated SPR. On the contrary, the EDR, EAN and mean excitation energy calculated directly from material composition information using the following equations were referred as the true EDR, EAN and mean excitation energy, respectively:
| (8) |
| (9) |
and
| (10) |
where ωi, Zi, Ai and Ii are the mass weight, atomic number, atomic mass and mean excitation energy of the ith element of the material, and ρx is the density of the material (Seltzer and Berger, 1982). The SPR calculated from the true EDR and mean excitation energy using the Bloch equation (equation (1)) was referred as the true SPR.
2.2. Selection of x-ray pairs for DECT
In this study, three pairs of x-ray beams were selected for DECT. The first pair was a 100-kVp beam coupled with a 140-kVp beam, referred as the kV-kV pair. The second pair was a 100-kVp beam coupled with a 1-MV beam, referred as the kV-MV pair. The third pair was two 1-MV beams with different external filtration, referred as the MV-MV pair. The 100-kVp and 140-kVp beam pair was chosen because it is currently available in the clinic. The 100-kVp and 1-MV beam pair was chosen because it has a larger difference in energy spectra than the kV-kV pair. We wanted to investigate whether a larger spectra difference could improve the accuracy of DECT calculation. The x-ray source with the highest peak energy available to us was a compact linac from Varian Medical Systems (Palo Alto, CA); it had a peak energy of up to 1 MeV. We chose two 1-MV beams with different external filtrations because high-energy x-ray spectrum tends to be sensitive to external filtration and because it was convenient to use external filters instead of two separate x-ray tubes.
Similar to our previous DECT study (Yang et al., 2010), CT numbers used for the DECT calculation in this study were not acquired through measurement but through calculations based on beam spectra and material elemental compositions according to the standard CT number definition (equations (2) and (3)). The advantages of using a calculation technique rather than a measurement technique were explained in our previous study. With the calculation technique, we estimated proton SPR accuracies for ‘nonstandard’ human tissues. The term ‘standard’ refers to human tissues with densities and elemental compositions equal to the average values, while ‘nonstandard’ human tissues are those with densities and elemental compositions slightly different than the average values. In addition, the calculation technique enabled us to estimate proton SPR accuracies when the beam hardening effect was considered. All beam spectra were generated using Monte Carlo simulations based on x-ray tube specifications. For Monte Carlo simulations, we used BEAMnrc and EGSnrc from the National Research Council of Canada (Rogers et al., 2005; Kawrakow et al., 2009). The x-ray tube in the GE RT16 CT scanner (GE Healthcare, Wauwatosa, Wisconsin) was simulated to generate the 100-kVp and 140-kVp beams. The compact linac made by Varian was simulated to generate the 1-MV beams with different filtrations (Clayton et al., 2009).
In our previous study (Yang et al., 2010), we found there was a linear relationship between EAN and Im, which could depend on the energy pair selected for the DECT system. We have determined the optimal exponent E in the original publication (equation (11)) to be 3.25, 3.26 and 3.29 for the kV-kV, kV-MV and MV-MV pairs, respectively. This demonstrates that the relationship is insensitive to the energy pair selection. For convenience and simplicity, we decided to use just a single value − 3.3 throughout this study.
2.3. Human tissue variation and partial volume mixing
The DECT method is based on the empirical relationship existing between the EANs and ln Im of standard human tissues. As shown in our previous study, variations in elemental composition can cause additional uncertainty to the SPR estimation using the DECT method (Yang et al., 2010). Therefore, we wanted to compare SPRs estimated using all three x-ray beam pairs when such a variation was considered.
For the present study, we chose the same 34 types of human tissues we used in our previous study. The recommended values of the densities and elemental compositions of the human tissues were taken from the International Commission on Radiation Units and Measurements (ICRU) Publication 44 (ICRU, 1989) and White et al (1987) and were listed in detail in our previous paper (Yang et al., 2010). The standard human tissues were used as templates to generate the nonstandard human tissues by introducing variations to key quantities, such as density and the percentages of key elements. The human tissues were divided into two groups—soft tissues and bone tissues. The division was based on the percentage of calcium (Ca) in the tissue as soft tissue contains an insignificant amount of Ca and bone tissue contains a significant amount of Ca. For soft tissues, we found the key element was hydrogen (H), while it was Ca for bone tissues. The density of a nonstandard human tissue was determined from a Gaussian distribution ~ N(μ, σ), where μ and σ are the mean and standard deviation, respectively. The value of μ was set to be equal to the density of the corresponding standard human tissue template, and the value of σ was set to be equal to a certain percentage of μ. Similarly, the percentage of the key element of a nonstandard human tissue was determined from a Gaussian distribution with μ and σ equal to the original percentage and a certain percentage, respectively. In this way, individual variations were introduced to the standard human tissues. The values of the standard deviation for the density, H, and Ca percentages were determined to be 4%, 1%, and 2%, respectively, based on our previous study (Yang et al., 2010). We generated 1000 nonstandard human tissues for each tissue type.
Another source of variation to consider was the partial volume averaging effect. In a current treatment planning CT image, the dimensions of one CT voxel in the axial plane are normally 1 mm × 1 mm and the slice thickness is normally 2 mm to 5 mm. When one CT voxel contains more than one tissue type, the tissue compositions inside that voxel can be very different from those of the standard human tissues, especially when mixing bone tissues with soft tissues. Therefore, it was important to compare the accuracy of all three energy pairs when the partial volume averaging effect was considered. As in our previous study, we only considered cases in which two different tissues were mixed in equal volumes for simplicity. The ‘cell nucleus’, one of the 34 standard tissues, was not included in this partial volume study because it will not cause partial volume effect. In this way, we generated 33 * 32 / 2 = 528 mixing tissues.
2.4. Random noise and beam hardening effect
Various artifacts in CT imaging—such as random noise, beam hardening effect, metal artifact, etc.—will cause the CT number to deviate from its true value. The DECT calculation is known to be sensitive to CT number variation because the EDR and EAN are derived based on the difference between the two CT numbers, which is usually small (Williamson et al., 2006). Therefore, we wanted to compare the accuracy of all three x-ray beam pairs when CT artifacts were considered.
The random noise in a CT image is believed to follow the Gaussian distribution (Chvetsov and Paige, 2010), which was assumed in this study. We added random noise by replacing the original CT number with a random number from a Gaussian distribution with μ equal to the original CT number. The noise level in the CT number was controlled by the ratio of standard deviation over mean of the Gaussian distribution: . In this way, we drew 1000 CT numbers for each tissue type from the Gaussian distribution with various values of . The SPRs derived from the CT numbers with random noise were then compared to the true SPRs.
Polyenergetic x-ray beams are used in current CT scanners. It will become ‘harder’ along the beam path because lower energy photons are removed preferentially as they penetrate through a patient, which is normally referred as the beam hardening effect. Because of that, the x-ray spectrum varies with patient size, the position inside the patient, etc. The DECT calculation algorithm requires knowing the x-ray spectra of the CT scanner to model linear attenuation coefficients. Therefore, we could only use the estimated average spectra for our DECT calculation. The spectrum at the middle point of a typical patient was regarded as the average spectrum by us. The typical patient diameter was estimated to be 32 cm. So the average x-ray spectrum was determined by passing the x-ray beam coming out from the x-ray source through a 16 cm water slab. In the rest of this study, CT numbers were calculated based on this type of average spectra unless specifically mentioned otherwise, assuming that the average spectra modeled the CT scanner perfectly. In reality, we knew that the x-ray spectra vary due to the beam hardening effect which causes the measured CT number to vary. To evaluate how the x-ray spectra variation could affect the accuracy of DECT calculation for different x-ray beam pairs, we generated various x-ray spectra of non-standard ‘hardness’ by passing the original x-ray beam through a water slab with various thicknesses ranging from 0 cm to 32 cm. CT numbers of standard human tissues were calculated based on those spectra. The proton SPRs estimated based on these CT numbers using the DECT method were compared to the corresponding true proton SPRs. The difference between the varied spectra and the average spectra were quantified by the difference between the thickness of water slabs used to generate the spectra of non-standard ‘hardness’ and the average spectra of standard ‘hardness’.
2.5. Error propagation
The Bethe-Bloch equation (equation (1)) can be rewritten as
| (11) |
where A = ln[2mec2β2/(1 − β2)] −β2 and B = ln[2mec2β2/Iw(1 − β2)] −β2. The values of constants A and B were calculated to be 12.8 and 8.45, respectively, assuming the proton energy to be 175 MeV and the mean excitation energy of water (Iw) to be 75 eV. Based on the empirical relationship between the ln Im and EANs of human tissues, the Im of a human tissue can be determined from its EAN (Zx) by
| (12) |
The values of the constants C and D were found to be 0.121 and 3.40 for soft tissues and 0.103 and 3.31 for bone tissues. After plugging equation (12) into equation (11) and performing differential derivative of equation (11), we obtained
| (13) |
The factor was calculated for each human body tissue based on its true EAN (Zx) calculated using equation (8). The calculated values of were found near constant within each tissue group, which ranges from 1.40% to 1.45% for soft tissues and from 1.22% to 1.28% for bone tissues. Therefore, equation (13) can be rewritten as
| (14) |
where the constant E is equal to 1.43% and 1.25%, respectively, for soft tissues and bone tissues. Equation (14) shows that a 1% EDR relative deviation causes a 1% SPR relative deviation, while an absolute change of the EAN by 1 causes about a 1.37% SPR relative deviation.
Our next step was to study the uncertainties in the calculation of the EDR and EAN using the DECT algorithm. After performing differential derivative of equation (6), we obtained
| (15) |
The equation above shows that the calculation of the EAN depends only on the relative difference between two CT numbers. After performing the differential derivative of equation (7), we obtained
| (16) |
After substituting equations (15) and (16) into equation (14), the relationship between the differential change of the SPR and the differential change of the CT number can be expressed by
| (17) |
where RL = FuncA − E * FuncB, RH = FuncA − E * FuncC, . The SPR sensitivity ratio factors RL and RH can be calculated for each human tissue if the beam spectrum and the material compositions are known. The values of RL and RH can tell us how sensitive the SPR estimation is to CT number variation in general.
2.6. Error analysis
The relative deviation, termed ‘relative error,’ in the estimated SPR was calculated by . The distribution of relative errors in the estimated SPRs was presented in the form of histograms to facilitate the comparison. The root-mean-square (RMS) error was calculated as an indicator of the magnitude of the error distribution. The RMS error was defined as , where i and N are the index and the total number of samples.
3. Results
3.1. Comparison of the accuracy of the DECT calculations using all three x-ray pairs when tissue composition variations and partial volume effects were considered
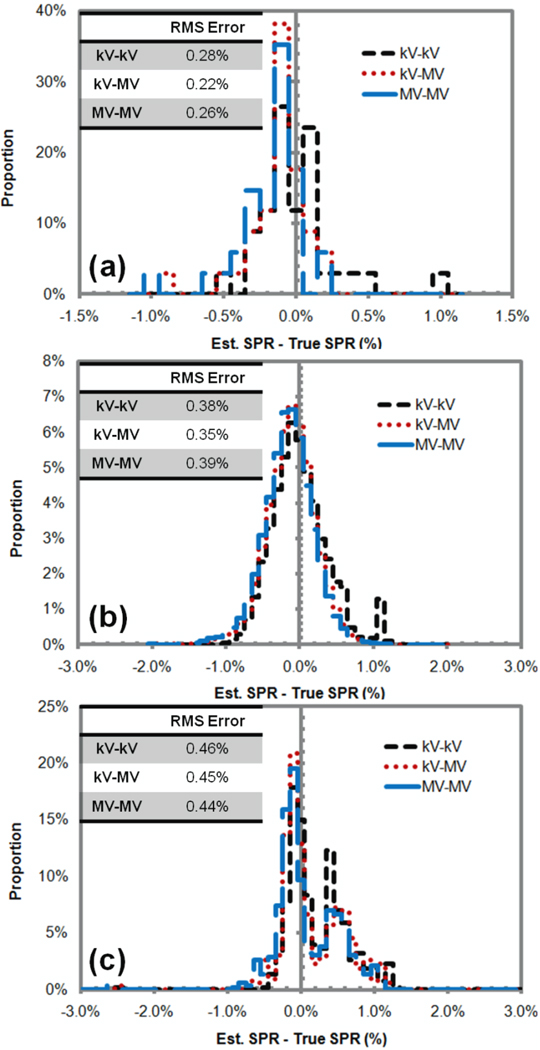
Figure 1(a) shows that the DECT with all three x-ray pairs had similar accuracy in deriving the SPRs of the standard human tissues. In addition, figure 1(b) and (c) show that the DECT with all three x-ray pairs achieved similar SPR accuracy even when tissue variation and the partial volume effect were considered. Here, the CT numbers were calculated directly based on the x-ray spectra without considering any artifact. In other words, the CT numbers fed to the DECT calculation fit the model assumed in the DECT calculation completely. When that condition was met, the selection of the x-ray pair was shown to have little impact on the accuracy of SPR estimation.
Figure 1.
Histograms of relative errors in the stopping power ratios (SPRs) of human tissues estimated using the kV-kV, kV-MV, and MV-MV dual-energy CT (DECT) for (a) standard human tissues, (b) nonstandard human tissues generated by introducing a small variation to the density and elemental composition values of standard human tissues, and (c) human tissues generated by mixing any two standard human tissues in equal volume in simulation of the partial volume averaging effect. The root-mean-square (RMS) error was calculated to describe the overall magnitude of error distribution. The results showed that under ideal conditions (i.e., without imaging artifacts) the DECT method was independent of the x-ray energy pairs.
3.2. Comparison of the accuracy of the DECT calculations using all three x-ray pairs when CT imaging artifacts (random noise and beam hardening effect) were considered
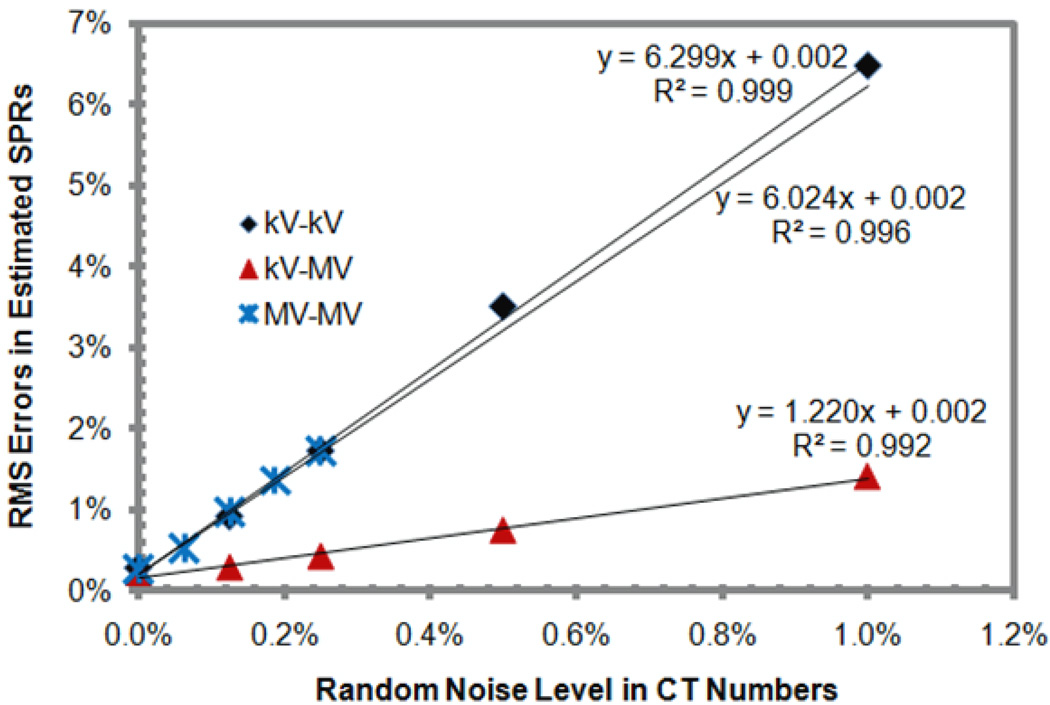
Figure 2 shows that the RMS errors in the derived SPRs increased with the random noise in a linear fashion for all three pairs. The slopes of the linear dependency (which was the sensitivity of RMS errors to the increase of random noise) were found to be 6.30, 1.22, and 6.02 for the kV-kV, kV-MV, and MV-MV pairs, respectively. The kV-MV pair was shown to be substantially less sensitive to random noise than were the other two pairs.
Figure 2.
The dependence of root-mean-square (RMS) errors in the stopping power ratios (SPRs) of standard human tissues derived using the dual-energy CT (DECT) method with different pairs of energy spectra on random noise in CT numbers.
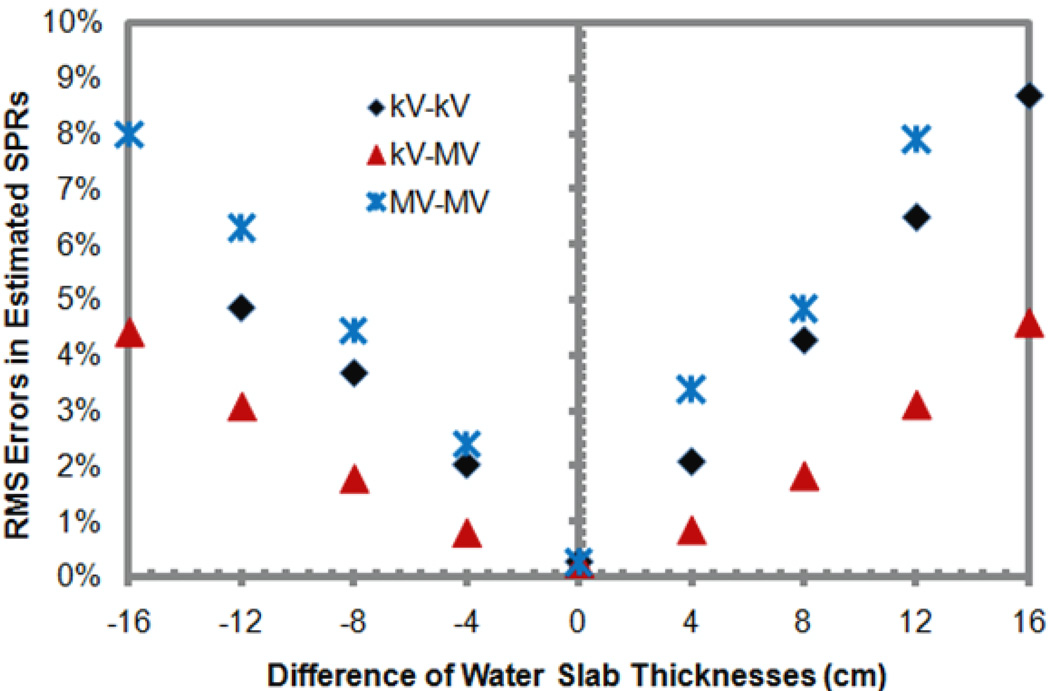
Figure 3 plots the relative errors in the estimated SPRs of the standard human tissues versus the difference between the thicknesses of the water slabs used to generate the x-ray spectra of non-standard beam ‘hardness’ and the average x-ray spectra of standard ‘hardness’ assumed in the DECT calculation. It was seen that the relative errors in estimated SPRs increase substantially with the difference of the x-ray spectra. Once again, the DECT using the kV-MV pair of x-ray beams was less sensitive to the spectra change, followed by the kV-kV DECT and then the MV-MV DECT.
Figure 3.
The relationship between the x-ray spectra difference and the root-mean-square (RMS) errors in the stopping power ratios (SPRs) of standard human tissues derived using the dual-energy CT (DECT) method for three pairs of energy spectra. Here, the x-ray spectra difference is represented by the difference between the thicknesses of the water slabs used to generate the x-ray spectra of non-standard ‘hardness’ and the average spectra of standard ‘hardness’. The thickness of the water slab used to generate the average spectra was 16 cm, while the thicknesses of the water slabs used to generate the x-ray spectra of non-standard ‘hardness’ ranged from 0 cm to 32 cm.
3.3. Error propagation
According to equations (15) and (16), we calcualted the ratios of absolute EAN variation (dZ) and relative EDR variation over relative CT number variation for all three x-ray beam pairs. We found that the ratios of soft tissues and bone tissues tend to have different values while remain relatively constant within each group. To demonstrate this effect, table 1 shows the average of all tissues within each tissue group. The EAN values of bone tissues were found to be much less sensitive to CT number variation than were the EAN values of soft tissues, while the EDR values of bone tissues were as sensitive as those of soft tissues except for the kV-kV DECT. Additionally, the EDR was seen to be less sensitive to the variation of a low-energy CT number than a high-energy CT number for all cases, especially for the kV-MV DECT. Overall, the calculation of the EDR and EAN using the kV-MV DECT was the least sensitive to CT number variation for both bone tissues and soft tissues.
Table 1.
The ratios of absolute effective atomic number variation (dZx) and relative electron density ratio variation over relative CT number variation in the dual-energy CT (DECT) calculation for different x-ray energy pairs. The ratios were calculated based on the error propagation, as shown in section 2.5. The values were averaged of all tissue types within each tissue group.
| Energy Pairs | Tissue Types | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| kV-kV | Soft Tissues | −2.81 | 3.81 | 70.86 | −70.86 | ||||
| Bone Tissues | −4.30 | 5.30 | 43.82 | −43.82 | |||||
| kV-MV | Soft Tissues | −0.06 | 1.06 | 19.77 | −19.77 | ||||
| Bone Tissues | −0.09 | 1.09 | 9.14 | −9.14 | |||||
| MV-MV | Soft Tissues | −1.09 | 2.09 | 369.52 | −369.52 | ||||
| Bone Tissues | −1.17 | 2.17 | 118.25 | −118.25 |
Based on equation (17), we calculated the ratios of relative SPR variation over relative CT number variation for all three x-ray beam pairs. The ratios of soft tissues and bone tissues are listed seperately in table 2 because of their different values. The kV-MV DECT was shown to be least sensitive to CT number variation; the ratio factors RL and RH of the kV-MV pair were at least 1/3 smaller than the ratio factors of the other two pairs. The MV-MV DECT was slightly more sensitive to CT number variation than was the conventional kV-kV pair. It was also seen that CT number variation of the high-energy beam caused greater SPR variation than did CT number variation of the low-energy beam. For the kV-MV pair, RL was less than 1/3 of RH. This suggests that it is more effective to reduce the uncertainties associated with high-energy CT imaging than uncertainties associated with low-energy CT imaging to reduce the overall uncertainties in SPRs.
Table 2.
The stopping power ratio (SPR) sensitivity ratio factors RL and RH calculated for all three x-ray beam pairs. The ratio factors were calculated based on the error propagation, as shown in section 2.5. The values were averaged of all tissue types within each tissue group.
| Energy Pairs | Tissue Types | ||||
|---|---|---|---|---|---|
| kV-kV | Soft Tissues | 3.82 | 4.82 | ||
| Bone Tissues | 4.85 | 5.84 | |||
| All Tissues | 4.19 | 5.18 | |||
| kV-MV | Soft Tissues | 0.34 | 1.34 | ||
| Bone Tissues | 0.21 | 1.21 | |||
| All Tissues | 0.30 | 1.30 | |||
| MV-MV | Soft Tissues | 6.36 | 7.35 | ||
| Bone Tissues | 2.63 | 3.63 | |||
| All Tissues | 5.38 | 6.34 |
Our error propagation analysis explained the linear ralationship between the RMS errors in SPRs and the random noise level in CT numbers observed in simulation results (figure 2). According to table 2, 1% of the random noise in the low-energy CT number translated to 4.19%, 0.30%, and 5.38% SPR errors for the kV-kV, kV-MV, and MV-MV DECT, respectively, while 1% random noise in the high-energy CT number translated to 5.18%, 1.30%, and 6.34%, respectively. By adding the errors quadratically, a 1% random noise in both CT numbers translated to a 6.67%, 1.33%, and 8.31% SPR error for the kV-kV, kV-MV, and MV-MV DECT, respectively. The corresponding values determined from simulation (figure 2) were 6.30%, 1.35%, and 6.02%, respectively. In general, the values determined by error propagation and simulation were in agreement, especially for kV-kV and kV-MV DECT. These findings validate our error propogation analysis. The difference between our theoretical prediction and the simulation for the MV-MV DECT suggests that the assumption used in our error propagation may not be completely valid for the MV-MV pair, possibly due to the fact that the approximation used in equation (4) is less accurate for Compton scatter dominated MV beams.
3.4. The relationship between SPR sensitivity to CT number variation in DECT calculation and the energy of the x-ray beam pairs used for the DECT scan
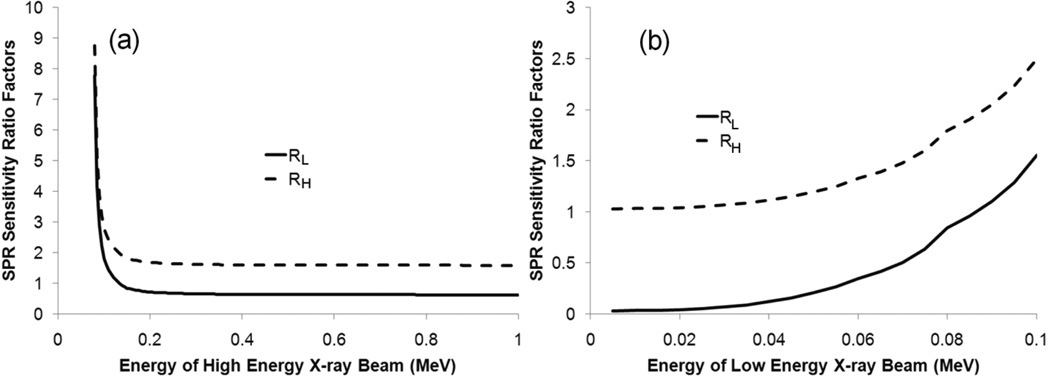
In order to find the optimal energy pair for DECT calculation, we calculated the SPR sensitivity ratio factors RL and RH for various monoenergetic x-ray pairs. The energy of monoenergetic x-ray beams investigated in this study ranged from 5 keV to 1 MeV, with an interval of 5 keV. In general, we found that the SPR sensitivity to CT number variation decreased as the spectra difference between the two beams increased. To illustrate how the sensitivity changed with the energy of each x-ray beam, we decided to vary the energy of one component at a time. Since the average energy of our 100-kVp beam was about 75 keV, we first set the energy of low-energy x-ray beam to be 75 keV and varied the energy of the high-energy x-ray beam from 80 keV to 1 MeV. Figure 4(a) shows that both SPR sensitivity ratio factors RL and RH decreased quickly as the energy of the high-energy x-ray beam increased shortly before it reached a plateau. Beyond 300 keV, the sensitivity ratio did not decrease much.
Figure 4.
The relationship between the stopping power ratio (SPR) sensitivity ratio factors (RL and RH) and the energy of (a) the high-energy x-ray beam and (b) the low-energy x-ray beam used for the dual-energy CT (DECT) scan. In (a), the energy of low-energy x-ray beam is 75 keV, and in (b), the x-ray energy of the high-energy component is 400 keV. Monoenergetic x-ray beams were assumed in this simulation.
Next, we wanted to see how the energy of the low-energy component affected the overall accuracy. This time, we chose the energy of the high-energy component to be 400 keV, which was about the average energy of our 1-MV beam, and varied the energy of the low-energy component from 5 keV to 395 keV. Figure 4(b) shows that both SPR sensitivity ratio factors RL and RH increased substantially with the energy of the low-energy component, i.e., RL increased more than 20% for every 5 keV increase from 25 keV to 75 keV. This finding indicates that it is important to make the energy of the low-energy x-ray beam as low as practically possible. In general, the energy of the low-energy x-ray beam is dominant in determining the lowest achievable sensitivity. The effective energy of the high-energy x-ray beam needs to be higher than a threshold value. The threshold value is observed to be about 200 keV higher than the effective energy of the low-energy x-ray beam. In addition, we noticed that the value of SPR sensitivity to the low-energy CT number was reduced to 0.03 at 5 keV while it was reduced to only 1.03 for the high-energy CT number. This finding indicates that the uncertainty in the SPR will become dominated by the uncertainty in the high-energy CT number as the energy of the low-energy x-ray beam decreases.
4. Discussion
4.1. Physical explanation to two interesting observations of the DECT calculation
In this section, we will discuss the reason behind two interesting observations of the DECT calculation: 1) the DECT calculation using the kV-MV pair is least sensitive to CT number variation and spectra variation; 2) the low-energy x-ray beam plays a major role determining the minimum value of the sensitivity ratio while the high-energy x-ray beam just needs to have sufficient energy to reach that minimum value.
The fundamental physical reason behind these two observations is that the sensitivity of the DECT calculation depends on the difference of two CT measurements of the same object. Each CT measurement contains the information of both EDR and EAN. The DECT calculation takes advantage of that by differentiating EDR and EAN from two CT measurements. Therefore, the more differences in the EDR and EAN values, the less sensitive the DECT calculation will be to the variation of each value. For example, if two spectra are extremely close to each other, the expected difference between two CT measurement will be small and any small CT number variation can cause large uncertainty in the calculated values for EDR or EAN.
The CT number is essentially the ratio of photon linear attenuation coefficients of the object relative to water. The photon linear attenuation coefficients include two major components for photons with energy below 1.02 MeV – photoelectric absorption and Compton scatter. The cross section of photoelectric absorption strongly depends on both EAN and x-ray energy while the cross section of Compton scatter doesn’t depend on EAN and only slightly depends on the x-ray energy. As the x-ray energy increases, the cross section of photoelectric interaction decreases dramatically while that of Compton scatter remains relatively constant. As a result, the major CT number difference between two energies depends on the lower energy, and the high-energy component just needs to be high enough to reach the dominating Compton interaction region. This explains our observed behaviors for the low-energy and high-energy x-rays. The information about EDR and EAN contained in the CT measurements using the kV-MV pair has the largest differential among all three pairs studied; therefore, it has the least sensitivity to CT number variations. For similar reason, the largest spectra difference offered by the kV-MV pair makes the DECT calculation least sensitive to spectra variation.
4.2. Selection of x-ray beam pairs for DECT calculation
There are two key questions we need to answer when using the DECT method to determine proton SPRs of human tissues: 1) what is the optimal x-ray beam pair, and 2) what is the total uncertainty in the estimated SPR with the optimal energy pair.
If we consider only the three beam pairs investigated in this study, it appears that the kV-MV pair is definitely the best because the SPRs determined using it have the least sensitivity to CT number variation. However, we must consider what the general principles are for selecting the optimal x-ray pairs for DECT calculation and whether we can find a better pair than our kV-MV pair to reduce the sensitivity further. Based on the results of section 3.4, we concluded that the energy of the high-energy x-ray beam needs to be at least 200 keV higher than that of the low-energy x-ray beam and that the energy of low-energy x-ray beam should be made as low as possible. In the kV-MV pair, the average energies of the 100-kVp and 1-MV beams were 75 keV and 400 keV, respectively. According to the calculation of the monoenergetic beam pairs (section 3.4), the sensitivity ratios RL and RH only decreased from 0.648 to 0.636 and from 1.616 to 1.603, respectively, as the energy of the high-energy x-ray beam increased from 400 keV to 1 MeV. Therefore, we are not gaining much if we replace the 1-MV beam with a beam with even higher energy, such as a 6-MV therapy beam.
The key is to reduce to the energy of the low-energy x-ray beam. However, we know we cannot make the energy of the low-energy x-ray beam too low. When x-ray energy gets too low, the CT number may start to vary substantially with such factors as position and patient size due to the beam hardening effect. The uncertainty in final SPR estimation depends on both the spectra differences in the energy pair and the individual uncertainty of the CT number measured by each energy. (equation (17)). Therefore, the increase of uncertainties in CT numbers can counter the reduction of the sensitivity ratio as the beam energy is decreased below a certain level. CT scanners used in current clinics normally have optional scanning beam energy from 80-kVp to 140-kVp. Further study needs to be done to estimate the CT number uncertainties associated with each beam and to determine which beam is the optimal one to pair with the 1-MV beam.
4.3. Comparison with the stoichiometric calibration method
The range uncertainty due to the uncertainty in proton SPR estimated from CT number using the stoichiometric calibration method is estimated to be 3.5% in current practice (Moyers et al., 2001; Moyers et al., 2009). Our ultimate goal is to reduce this range uncertainty by using the DECT method. But the intent of this study is not to compare the DECT method with the stoichiometric method, so the uncertainty values derived for the DECT in this study are not meant to be compared with that of the stoichiometric method − 3.5%.
One source of uncertainty in SPR estimation is tissue composition variation. Our previous study showed that the DECT method is much less sensitive than the stoichiometric method to tissue composition variations (Yang et al., 2010). The uncertainty in SPRs caused by tissue composition variations was shown to be less than 0.5% for all DECT beam pairs, as shown in figure 1. Another source of uncertainty is the uncertainties in CT number measurement. The CT number of an object is shown to vary with its position in the scan, its surroundings, the patient’s size, etc., due to the beam hardening effect. In general, the uncertainty in the CT number will be amplified by the DECT calculation and passed to the estimated SPR. For example, a 1% uncertainty in CT numbers of the 100-kVp and 140-kVp beams translates to about a 4% and 5% uncertainties in the SPR, respectively, as shown in table 2. Because of this, the kV-kV DECT is not a good candidate for achieving our goal. But the kV-MV DECT still has a good chance of achieving our goal for two reasons: first, the CT number variation of the 1-MV beam due to the beam hardening effect should be less than that of the kV beam, especially in bone tissues; and second, the uncertainty in the kV CT number is minimized in DECT calculation for the kV-MV DECT in that a 1% uncertainty in the kV CT number only translates to a 0.34% uncertainty in the SPR for soft tissues and 0.21% for bone tissues. Therefore, the kV-MV DECT does have the potential to reduce the uncertainties in SPR estimation. Our next task is to estimate the uncertainties associated with the MV CT number through experimental measurements. Based on that, we can estimate the overall uncertainties in the derived SPRs using our error propagation equation (equation (17)). Finally, we can determine if the DECT method is able to reduce the range uncertainty.
In our previous publication (Yang et al., 2010), we demonstrated the theoretical advantage of DECT over the stoichiometric calibration method. In this study, we found that uncertainties in the CT number could have an impact on the achievable accuracy of the DECT method. It would be interesting to perform a comprehensive analysis of uncertainties and achievable accuracies for both the stoichiometric calibration method and DECT method, which will be our future goal.
4.4. Metal artifact reduction by using 1-MV beam
Another benefit of using the 1-MV beam is the reduction of metal artifacts in patients with high Z material, such as dental inserts. In our previous study, the use of a 320-kVp beam substantially reduced the metal artifact caused by a Ti insert (Yang et al., 2008). The 1-MV beam should reduce the metal artifact even more, which will make it easier for physicians to draw contours in the artifact-affected area. In the artifact-affected area, the CT number of the kV beam may deviate substantially from its true value, which may cause errors in DECT calculation. If we use DECT, we can use just the MV CT number to estimate the SPR based on the calibration curve. This will minimize the imaging artifacts.
4.5. Radiation dose in DECT scan
The kV-kV DECT will deliver about twice the dose delivered in conventional single-CT treatment planning, and the kV-MV DECT will deliver an even higher dose. We have performed Monte Carlo simulations that show the 1-MV beam needs to deliver about 5 times the dose delivered by the 100-kVp beam to achieve the same level of imaging noise. The detector modeled in our simulation was a 0.6 mm cesium iodide (CsI) scintillator detector. For the kV-MV DECT, the SPR sensitivity ratio for the MV CT number is larger than that for the kV CT number. This indicates that it is more important to reduce the noise in the MV CT image, implying using a higher radiation dose. Although the dose in imaging for the treatment planning is negligible compared to the dose delivered by the radiation treatment itself, we would like to reduce the dose to the patient as much as possible. One way to accomplish this is to use a thicker detector. There have been several studies showing that the dose can be reduced substantially for the MV CT if a thicker segmented scintillator detector is used (Sawant et al., 2005; Monajemi et al., 2006; Wang et al., 2008; Wang et al., 2009). Based on our Monte Carlo simulation results, we found that the ratio of the dose needed for a 1-MV beam to that of a 100-kVp beam to achieve the same noise level can be reduced from 6 to 2 by increasing the detector thickness from 0.6 mm to 10 mm. Another way is to reduce the noise through software. Even if the random noise is high, the overall range uncertainty can still be low because of the averaging effect along the beam path (Chvetsov and Paige, 2010).
5. Conclusions
Our simulation showed that, when random noise and beam hardening effects are considered, the kV-MV DECT can improve the accuracy of SPR estimation substantially compared with kV-kV DECT. Our error propagation analysis on the DECT calculation confirmed that the DECT calculation using the kV-MV pair will be less sensitive to CT number uncertainty than that of the kV-kV pair in general. Further study needs to be done to estimate the uncertainties in both kV CT imaging and MV CT imaging in clinical situations, which will help determine the overall uncertainty in SPR estimation for the proposed kV-MV DECT method.
Our error propagation analysis also showed that the effective energy of low-energy x-ray beam needs to be as low as practically possible and the effective energy of high-energy x-ray beam needs to be about 200 keV higher than that of the low-energy x-ray beam to reach a plateau for the best combination of x-ray energy to reduce the sensitivity of the DECT method to imaging noise and beam hardening effects.
Acknowledgments
This work was supported in part by a sponsored research grant from Varian Medical Systems (Palo Alto, CA), the National Institutes of Health grant P01 CA021239-29A1, and the institutional core grant CA016672.
References
- Berger MJ, Hubbell JH, Seltzer SM, Chang J, Coursey JS, Sukumar R, Zucker DS. XCOM: Photon Cross Section Database (version 1.3) 2005 [Google Scholar]
- Chvetsov AV, Paige SL. The influence of CT image noise on proton range calculation in radiotherapy planning. Physics in Medicine and Biology. 2010;55 doi: 10.1088/0031-9155/55/6/N01. [DOI] [PubMed] [Google Scholar]
- Clayton J, Virshup G, Yang M, Mohan R, Dong L. Proceedings of SPIE - The International Society for Optical Engineering. San Diego, CA: 2009. Improvements in medical CT image reconstruction accuracy in the presence of metal objects by using X-rays up to 1 MeV. [Google Scholar]
- ICRU. Tissue substitutes in radiation dosimetry and measurement. ICRU Report. 1989;44 [Google Scholar]
- Kawrakow I, Mainegra-Hing E, Tessier F, Walters BRB. The EGSnrc C++ class library. 2009 [Google Scholar]
- Monajemi TT, Fallone BG, Rathee S. Thick, segmented CdWO4-photodiode detector for cone beam megavoltage CT: A Monte Carlo study of system design parameters. Medical Physics. 2006;33:4567–4577. doi: 10.1118/1.2370503. [DOI] [PubMed] [Google Scholar]
- Moyers MF, Miller DW, Bush DA, Slater JD. Methodologies and tools for proton beam design for lung tumors. International Journal of Radiation Oncology Biology Physics. 2001;49:1429–1438. doi: 10.1016/s0360-3016(00)01555-8. [DOI] [PubMed] [Google Scholar]
- Moyers MF, Sardesai M, Sun S, Miller DW. Ion Stopping Powers and CT Numbers. Medical Dosimetry. 2009;35:179–194. doi: 10.1016/j.meddos.2009.05.004. [DOI] [PubMed] [Google Scholar]
- Rogers DWO, Walters B, Kawrakow I. BEAMnrc users manual. 2005 [Google Scholar]
- Sawant A, Antonuk LE, El-Mohri Y, Zhao Q, Li Y, Su Z, Wang Y, Yamamoto J, Du H, Cunningham I, Klugerman M, Shah K. Segmented crystalline scintillators: An initial investigation of high quantum efficiency detectors for megavoltage x-ray imaging. Medical Physics. 2005;32:3067–3083. doi: 10.1118/1.2008407. [DOI] [PubMed] [Google Scholar]
- Schneider U, Pedroni E, Lomax A. The calibration of CT Hounsfield units for radiotherapy treatment planning. Physics in Medicine and Biology. 1996;41:111–124. doi: 10.1088/0031-9155/41/1/009. [DOI] [PubMed] [Google Scholar]
- Seltzer SM, Berger MJ. Evaluation of the collision stopping power of elements and compounds for electrons and positrons. International Journal of Applied Radiation and Isotopes. 1982;33:1189–1218. [Google Scholar]
- Wang Y, Antonuk LE, El-Mohri Y, Zhao Q, Sawant A, Du H. Monte Carlo investigations of megavoltage cone-beam CT using thick, segmented scintillating detectors for soft tissue visualization. Medical Physics. 2008;35:145–158. doi: 10.1118/1.2818957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Antonuk LE, Zhao Q, El-Mohri Y, Perna L. High-DQE EPIDs based on thick, segmented BGO and CsI:Tl scintillators: Performance evaluation at extremely low dose. Medical Physics. 2009;36:5707–5718. doi: 10.1118/1.3259721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White DR, Woodard HQ, Hammond SM. Average soft-tissue and bone models for use in radiation dosimetry. British Journal of Radiology. 1987;60:907–913. doi: 10.1259/0007-1285-60-717-907. [DOI] [PubMed] [Google Scholar]
- Williamson JF, Li S, Devic S, Whiting BR, Lerma FA. On two-parameter models of photon cross sections: Application to dual-energy CT imaging. Medical Physics. 2006;33:4115–4129. doi: 10.1118/1.2349688. [DOI] [PubMed] [Google Scholar]
- Yang M, Virshup G, Clayton J, Zhu RX, Mohan R, Dong L. Theoretical variance analysis of single- and double-energy computed tomography methods for measuring proton stopping power ratios of biological tissues. Physics in Medicine and Biology. 2010;55:1343–1362. doi: 10.1088/0031-9155/55/5/006. [DOI] [PubMed] [Google Scholar]
- Yang M, Virshup G, Mohan R, Shaw CC, Zhu XR, Dong L. Improving accuracy of electron density measurement in the presence of metallic implants using orthovoltage computed tomography. Medical Physics. 2008;35:1932–1941. doi: 10.1118/1.2905030. [DOI] [PubMed] [Google Scholar]