MDAnalysis: A Toolkit for the Analysis of Molecular Dynamics Simulations

Abstract

MDAnalysis is an object-oriented library for structural and temporal analysis of molecular dynamics (MD) simulation trajectories and individual protein structures. It is written in the Python language with some performance-critical code in C. It uses the powerful NumPy package to expose trajectory data as fast and efficient NumPy arrays. It has been tested on systems of millions of particles. Many common file formats of simulation packages including CHARMM, Gromacs, Amber, and NAMD and the Protein Data Bank format can be read and written. Atoms can be selected with a syntax similar to CHARMM’s powerful selection commands. MDAnalysis enables both novice and experienced programmers to rapidly write their own analytical tools and access data stored in trajectories in an easily accessible manner that facilitates interactive explorative analysis. MDAnalysis has been tested on and works for most Unix-based platforms such as Linux and Mac OS X. It is freely available under the GNU Public License from http://mdanalysis.googlecode.com.

INTRODUCTION

Molecular dynamics (MD) simulations generate a wealth of data. Deducing meaningful conclusions from simulations requires analysis of MD trajectories in terms of the individual positions (and possibly velocities and forces) of all atoms or a selected subset of atoms for each time frame of a trajectory. Users can often rely on a single tool or package for most of their analysis. For instance, the Gromacs¹ package contains a large number of individual programs (written in C) that each performs a particular analysis task such as calculating a root mean square deviation or a timeseries of some dihedral angles. Similarly, ptraj², Wordom³, MD-TRACKS⁴, and Simulaid⁵ provide interfaces to pre-defined analysis tools. Some large, monolithic programs such as CHARMM⁶ or VMD⁷ come with a scripting language that allows the use of a powerful atom selection languages and built-in or scripted analysis modules. A number of libraries such as MMTK⁸, MMTSB⁹, or pymacs¹⁰ also provide some analysis capabilities in addition to other functions such as simulation setup or execution.

Implementing new analysis algorithms can be difficult within the existing packages as it often requires an intimate knowledge of the internals of the software. Object-oriented libraries such as LOOS¹¹ or MDAnalysis (described here) encapsulate essential input/output (I/O) functionality in order to present a consistent interface to the data in a trajectory. They both emphasize enabling the user to create novel analysis tools easily without having to spend effort on reimplementation of standard functionality.

We developed the open source MDAnalysis toolkit to simplify the development of new analysis tools that specifically make use of the widely used Python language (www.python.org). It is available under the GNU Public License from http://mdanalysis.googlecode.com. MDAnalysis facilitates rapid code development by building on Python, which provides a powerful and extensible but easy to learn programming language that has been found particularly useful in the scientific community. MDAnalysis utilizes fast numeric/algebraic libraries such as ATLAS, LAPACK, or MKL to improve speed and powerful Python libraries such as NumPy and SciPy (www.scipy.org), which provide optimized classes and functions for important components of scientific code such as multidimensional arrays or linear algebra routines. A wide range of other high-quality libraries is freely available such as the NetworkX package¹² for the representation and analysis of network graphs. The seamless integration of these scientific libraries via NumPy arrays enables users, as we show below, to write non-trivial analysis code in a concise and almost symbolic manner.

In this paper we first introduce the basic philosophy and layout of MDAnalysis (Figures 1 and 2) and then show examples with Python code for solving a range of analysis tasks, ordered from simple to advanced. Code examples together with the required input are provided at the code download URL and as part of the package test suite.

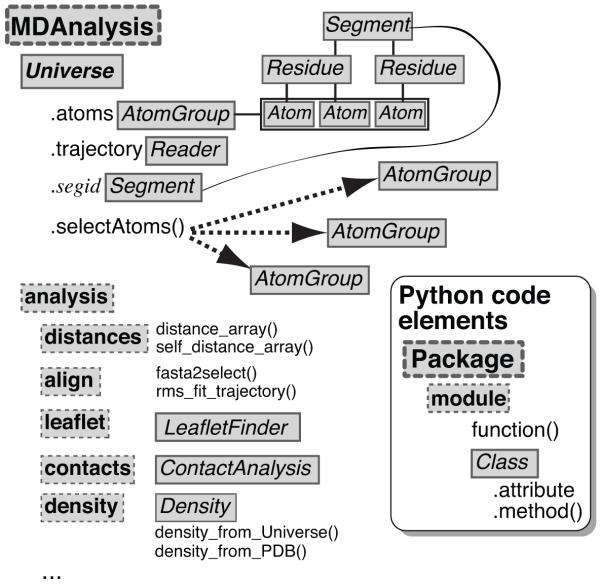
Figure 1.

Organization of the MDAnalysis Python library. The Universe class contains both topological and structural information and maintains a list of all atoms – an AtomGroup instance named atoms – in the system. The selectAtoms() methods provides an interface to the selection mechanism and returns an AtomGroup instance. A molecular dynamics trajectory is accessed through the trajectory attribute, which is an instance of a Reader class. MDAnalysis also contains an analysis sub-module, which collects a number of pre-defined classes and tools.

Figure 2.

Layout of important MDAnalysis classes. The Universe class contains an AtomGroup of all Atom instances that can be accessed through the attribute Universe.atoms. It also features a number of auto-generated AtomGroups, one for each segment identifier of the topology. Users can obtain information from the individual Atom instances and computed data from a whole AtomGroup by querying the instance attributes and methods. The Timestep class represents the current state of the system at a particular time frame of the trajectory. Trajectory Reader and Writer classes provide an abstract interface to trajectory I/O. They implement special methods that allow “Pythonic” access to the objects such as treating a Reader as an iterator over trajectory frames (via the __iter__() special method) or selecting individual frames by the indexing operation (implemented through a custom __getitem__() method).

METHODS

MDAnalysis, which was initially inspired by MDTools for Python (http://www.ks.uiuc.edu/Development/MDTools/Python/, J.C. Phillips, unpublished) and MMTK ⁸, is implemented as a Python package. It consists of a core library, which is exposed via the Universe class in the top-level name space and the analysis sub-module, which contains an expanding selection of functionality that make use of the core library (Figure 1). A number of performance critical or low-level input/output (I/O) routines are written in C (either directly or using Cython), and hence installation requires a working C-compiler. It has been tested successfully on Linux and Mac OS X platforms. Reading of CHARMM DCD trajectory files utilizes open source code from catdcd (part of VMD⁷) and PDB files are read with the Bio.PDB package¹³. For some analysis functions a fast linear algebra library such as LAPACK, ATLAS or the native vecLib framework on Mac OS X is needed. MDAnalysis depends on the NumPy package (http://numpy.scipy.org). The development process follows standard software engineering “best practice”¹⁴ by using a publicly accessible version-controlled source code repository with a bug tracker and a mailing list dedicated to the project. Importantly, individual code blocks are tested through an extensive unit test suite, ensuring that enhancements and bug fixes do not break old code or re-introduce bugs.

MDAnalysis is fully object-oriented and treats atoms, residues, segments and trajectories as objects. These objects are represented in Python as classes with appropriate functions (“methods”) and variables (“attributes”) defined on these objects. In the following we describe the overall architecture of the package and some of the most important classes to enable users to make best use of the library. A complete simulation system is represented by the Universe class (Figure 1). It is initialized from a topology file, which defines the atoms in the system, and a trajectory or coordinate file, which lists the position of each atom for a number of time frames or a single snapshot.

Universe contains the attribute atoms (an instance of an AtomGroup), which can be thought of as a list of all atoms that are represented as Atom instances. The Atom is the fundamental object in MDAnalysis. It contains data such as chemical type, partial charge, or its Cartesian coordinates. For convenience, atoms are grouped in residues (represented by a Residue class, which is a special AtomGroup); a list of residues can be referred to as a Segment (a ResidueGroup that inherits from AtomGroup). A segment can correspond to a chain in a PDB file or a whole multi-chain protein; similarly, a residue typically corresponds to a single amino acid in a peptide chain, water molecule, or lipid. Residues and segments are simply containers for Atom objects; an Atom records the Residue, Segment and Universe it belongs to. In this way it is possible to directly switch between structural hierarchies, depending on which level is the most convenient for a task at hand. Attributes of Atom instances can be read (and set) individually and thus provide fine grained control for specific analysis tasks. Python indexing and “slicing” of an AtomGroup returns an Atom or a list of Atoms; index operations on a Segment return Residue objects.

In many cases, the user is interested in a property of a group of atoms. Any AtomGroup has a number of methods predefined that provide properties of all atoms in the group (such as coordinates or masses) as NumPy arrays or aggregate properties of the whole group such as the center of mass, the total mass, or the principal axes (see Figure 2 and the documentation of the package, accessible from within Python via the help (Classname) command). Every AtomGroup (which includes Residue, ResidueGroup, Segment and SegmentGroup classes by inheritance) also has the attributes atoms, residues, and segments. They contain lists of those Atom, Residue, and Segment instances to which the atoms in the group belong; for instance, residues contains all residues of which the atoms are members so that one can quickly find all residues for which a certain atom-based selection criterion is true. Because such a consistent application programming interface (API) applies at all levels of the structural hierarchy, concise code can be written that processes segments, residues and arbitrary collections of atoms in the same manner. Additionally, managed attributes are automatically generated that simplify access to certain selections. For instance, any AtomGroup contains an attribute for each atom name that it contains (such as “CA” or “N”). Such an “instant selector” attribute provides a group of all atoms with the same name, e.g. all CA-atoms. Similarly, a Segment also contains instant selectors for residue names and residue numbers (the latter are prefixed with the letter “r” to make them valid Python identifiers). The Universe contains instant selectors for segment identifiers (prefixed with “s” if they start with a number).

A new AtomGroup can be generated from an instant selector or a selection via the selectAtoms() method. MDAnalysis contains a full selection language comparable to the one offered by CHARMM⁶ or VMD⁷. It includes selections by atom properties, connectivity, and geometry (such as distances). Selections can be grouped by Boolean operators to create arbitrarily complex expressions.

A simulation trajectory file consists of a sequence of coordinate frames. MDAnalysis provides a view or a “cursor” on the trajectory. A trajectory has a Timestep object associated with it (Figure 2). The Timestep contains the current frame number, the unitcell dimensions (if recorded in the trajectory file), and the coordinates of all atoms. Atom and AtomGroup coordinates always refer to the coordinates in the current time step; they update automatically. A trajectory Reader instance is responsible for reading the trajectory file and populating the Timestep whenever a new frame is read from the file. Reader classes can be used as Python iterators, they have a next() method to advance the trajectory cursor, and they typically also allow indexing to jump to a specific frame. A Writer class is used to write a Timestep to a file on disk. The design of the library is easily extensible; for instance, new trajectory readers and writers can be added through a common API by inheriting from the coordinates.base.Reader class and adding appropriate low-level code for the actual I/O.

The default units in MDAnalysis are the ångström (10⁻¹⁰ m) for length and the picosecond (10⁻¹² s) for time. Data from trajectories are automatically converted to these units, and data written to trajectories is converted to the native format (although this behavior can be changed using internal flags). The unit cell representation differs between trajectory formats. MDAnalysis always makes the unit cell available in the dimensions attribute as a tuple (a,b,c,α,β,γ) for the lengths and angles of the parallelepiped forming the simulation box.

RESULTS

Basic use of the library: Trajectory I/O and Selections

Once installed, MDAnalysis is imported in the standard Python fashion as:

import MDAnalysis

or

from MDAnalysis import *

For the following discussion and the examples we will assume that the second form has been used, which makes a number of useful classes and modules available in the top-level name space (Figure 1).

The most important class is Universe, which represents the complete simulation system. It is initialized from a topology file, which defines the atoms in the system, and a trajectory, which lists the position of each atom for a number of time frames:

universe = Universe(topology_file, trajectory_file)

MDAnalysis can read a range of popular file formats. This includes trajectories produced by CHARMM, NAMD, LAMMPS, Amber, and Gromacs and the generic XYZ format (also compressed with gzip or bzip2). It can write DCD (CHARMM/NAMD/LAMMPS) and XTC/TRR (Gromacs) trajectories. Furthermore, it can read and write a number of single frame formats such as Brookhaven PDB, CHARMM coordinates (CRD), GROMOS96 coordinates (GRO), and it can read PQR files as used in electrostatics calculations ¹⁵. Periodic boundary conditions are not automatically taken into account and hence trajectories should be appropriately preprocessed. In order to define the atoms in the system, a topology file is required. Typically this is a CHARMM/XPLOR PSF file or a Amber PARMTOP but it is also possible to use any of the single frame formats instead and make use of the information stored there. For instance, using a PQR file sets the charge attribute of each atom to the charge stored in the file. There are no restrictions on the type or number of atoms; for instance, PDB files with large numbers of atoms are handled gracefully and coarse grained simulations can be analyzed in the same way as atomistic ones.

The main purpose of Universe is to gather all atoms in the system in its Universe.atoms attribute and provide the Universe.selectAtoms() method to create arbitrary groupings of atoms (Figure 1). All such groups of atoms are instances of the AtomGroup class and a number of simple methods are automatically defined for such a group (Figure 2). For instance, AtomGroup.totalMass() computes the total mass of these atoms and AtomGroup.principalAxes() the principal axes by diagonalizing the tensor of inertia. Other examples of these types of functions include computing the center of mass, center of geometry, radius of gyration, or the total charge. Individual properties of all atoms in an AtomGroup can also be conveniently accessed in a fashion typical for Python (“Pythonic”) by calling methods that return lists or arrays of the property. For example, AtomGroup.coordinates() returns a NumPy array of the coordinates, which can be processed further in Python code:

from numpy import array
protein = universe.selectAtoms(‘protein’)
coords = protein.coordinates()
shifted = coords + array([10.,0,0])

The example above calculates the coordinates of all protein atoms shifted by the vector (10,0,0) along the x-axis. Other methods return lists of residue numbers, residue names, partial charges (if defined in the topology file), atom masses, or B-factors if loaded from a PDB file (Figure 2).

From an AtomGroup, one can also write different types of coordinate files such as trajectory or single coordinate files (Figure 2). A single coordinate file such as a PDB can be written with

universe.selectAtoms(“byres (resname SOL and around 3.5 protein)”).write(“solvationshell.pdb”)

The related write_selection() method writes selection commands to an output file; by loading these commands in an external program such as VMD or PyMOL one can visualize the MDAnalysis selection. It is also possible to use the selection commands as input for simulations in CHARMM or Gromacs.

To write trajectory files, one obtains a trajectory Writer and then writes every individual timestep, typically by iterating over an input trajectory. Coordinates can be manipulated before writing them, or only a selection of the whole system can be written. In the next example, a new trajectory in Gromacs XTC format is written, in which the whole system (universe.atoms) is rotated by 360° around an axis parallel to the z-axis that contains the center of geometry of residues 100 to 105:

writer = MDAnalysis.Writer(‘rotating.xtc’, \
            universe.atoms.numberOfAtoms())
for ts in universe.trajectory:
      angle = 360.*(ts.frame-1)/universe.trajectory.numframes
      universe.atoms.rotateby(angle, axis=(0,0,1), \
            point=universe.selectAtoms(“resid 100:105”))
      writer.write(ts)
writer.close()

The object-oriented design of the library allows the convenient use of selections (i.e. AtomGroups) in places where one could also provide an explicit Cartesian coordinate; if a point in space is required, the centroid of the AtomGroup is substituted. Vectors can be replaced by a tuple of two AtomGroups and the vector is calculated from the centroid of the first group to the second one.

Writing of selections and trajectories is also object-aware. For example, in order to write a C_α–only trajectory, the appropriate C_α–selection is passed to the write() method:

ca = universe.selectAtoms(‘name CA’)
writer = MDAnalysis.Writer(‘ca.dcd’, len(ca))
for ts in universe.trajectory:
      writer.write(ca)
writer.close()

Typical frame-based analysis of a trajectory follows the same simple iterator pattern: while looping through the frames of the trajectory, data are collected at each time step. In the next example, the end-to-end distance of a protein is calculated and printed at each time step:

from numpy.linalg import norm
protein = universe.selectAtoms(‘protein’)
nterm = protein[0].residue.N     # N atom of first residue
cterm = protein[−1].residue.C    # C atom of last residue
for ts in universe.trajectory:
      d = norm(cterm.pos - nterm.pos)
      print “End-to-end distance %f at frame %d” % (d,ts.frame)

The example also demonstrates the important fact that coordinates of selections or individual atoms change dynamically when the trajectory is moved to a different frame. The iterator approach is robust and because MDAnalysis only loads individual frames into memory when needed, it is possible to handle large systems. So far MDAnalysis has been tested successfully with systems up to 4.5 million particles (Daniel Parton, personal communication).

The MDAnalysis.analysis module and advanced usage

A typical approach to testing convergence of a property is to calculate the property of interest over blocks of a trajectory and analyze the standard deviation of the block averages as function of the block size ¹⁶. Accumulating block results can be almost trivially carried out in MDAnalysis by iterating over blocks and appending calculated observables to a list. The following example defines a function blocked() that takes a universe, the number of blocks, and a function operating on a universe as arguments:

def blocked(universe, nblocks, analyze):
    size = universe.trajectory.numframes/nblocks
    blocks = []
    for block in xrange(nblocks):
        a = []
        for ts in u.trajectory[block*size:(block+1)*size]:
            a.append(analyze(universe))
        blocks.append(numpy.average(a))
    blockaverage = numpy.average(blocks)
    blockstd = numpy.std(blocks)
    return nblocks, size, blockaverage, blockstd

In order to calculate the block average of the radius of gyration of a protein one would define an analysis function such as

def rgyr(universe):
      return universe.selectAtoms(‘protein’).radiusOfGyration()

that can be directly used with blocked() for a range of block numbers:

results = []
for nblocks in xrange(2,10):
      results.append(blocked(universe, nblocks, rgyr)

MDAnalysis already contains a number of analysis applications that are user-friendly “best-practice” examples for tool development (Figure 1). One example is the align module, which contains code to fit a trajectory to a reference structure by minimizing the root mean square deviation (RMSD) of a selection between the current frame and the reference. The implementation uses the fast QCP method for calculating the minimum RMSD between two structures ¹⁷ and determining the optimal least-squares rotation matrix ¹⁸.The rms_fitting() function can be used to re-center the trajectory based on an atom selection and/or to concatenate trajectories together while extracting an arbitrary subset of frames or atoms. An example for this tool, rmsfit_alignment.py, is located within the examples directory.

Time series analysis

A number of often-used geometric calculations over time series of atoms are predefined and written in C. Instead of looping over individual frames, the so-called Timeseries analysis functions directly operate on the underlying trajectory. First a collection is populated with the desired analysis tasks and then the analysis is carried out by passing the collection to the correl method of the trajectory object:

MDAnalysis.collection.addTimeseries(\
       Timeseries.Dihedral(atomselection))
data = universe.trajectory.correl(MDAnalysis.collection, skip=10)

The current implementation (for DCD only) includes functions for Angle, Bond, Dihedral, CenterOfGeometry, CenterOfMass, Atom, Distance, and WaterDipole moment.

An example is shown in Figure 3 where a KALP19 peptide in a lipid membrane is analyzed. The script below shows how to set up the calculation of a single ψ peptide backbone dihedral; Figure 3B shows values for all ψ_i:

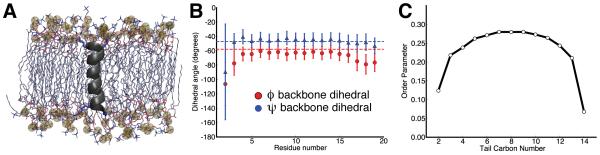
Figure 3.

Calculation of geometric parameters for a KALP19 peptide in a DMPC bilayer. (A) The alpha-helical KALP19 peptide (black) was simulated in a DMPC bilayer with 90 lipids with the CHARMM27 force field. (B) Backbone dihedral angles φ and ψ averaged over a 75 ns MD trajectory. Error bars indicate one standard deviation from the mean. The values for an ideal α-helix are shown as dashed lines (φ = −57° and ψ = −47°) for comparison. (C) Average deuterium order parameter profiles, S_CD, of DMPC lipid tails. S_CD converges slowly and only the average over the last 25 ns is shown.

psi_sel = universe.selectAtoms(“atom KALP 21 N”, \
      “atom KALP 21 CA”, “atom KALP 21 C”, \
      “atom KALP 22 N”)
a = collection.TimeseriesCollection()
a.addTimeseries(Timeseries.Dihedral(psi_sel))
data = universe.trajectory.correl(a, skip=10)*180./pi

The structure of a lipid bilayer can be analyzed by the average deuterium order parameter, S_CD = (3〈cos²θ〉 − 1)/2;¹⁹ θ is the angle between carbon-hydrogen bonds in the fatty acid tail and the bilayer normal. S_CD can range from −0.5 to 1.0, representing completely disordered chains to fully ordered chains. To analyze S_CD of DMPC lipid tails in the KALP system (Figure 3C), the C-H vectors for a given carbon on each aliphatic chain of every lipid molecule are extracted and stored in a NumPy array. The data can be extracted in different formats depending on the analysis – for example, the timeseries is generated in ‘afc’ format for ‘atom, frame, coordinate’. S_CD is then calculated using NumPy’s powerful arithmetic:

carbon = 3  # analyze the 3rd carbon
selection = “resname DMPC and (name C2%d or name H%dR or \
      name H%dS or name C3%d or name H%dX or name H%dY)” % \
      ((carbon,)*6)  # selects C23 H3R H3S C33 H3X H3Y
group = universe.selectAtoms(selection)
data = universe.trajectory.timeseries(group, format=“afc”, skip=skip)
cd = numpy.concatenate((data[1::3]-data[0::3], \
                        data[2::3]-data[0::3]), axis=0)
cd_r = numpy.sqrt(numpy.sum(numpy.power(cd,2), axis=−1))
cos_theta = cd[…,2]/cd_r
S_cd = −0.5*(3.*numpy.square(cos_theta)-1)
S_cd.shape = (S_cd.shape[0], S_cd.shape[1]/4, −1)
order_param = numpy.average(S_cd)

Distances

The distance package contains functions to calculate distances between atoms in selections. The versatile distance_array() function (implemented as a fast compiled library) can be used to rapidly calculate all distances d_ij between two groups of atoms. The following example shows how to use it in order to calculate the radial distribution function, g(r), of water molecules around the amino group of all lysine residues. In the example below, g(r) is stored in the variable rdf:

from MDAnalysis.analysis.distances import distance_array
group = universe.selectAtoms(“resname LYS and name NH*”)
water = universe.selectAtoms(“resname TIP3 and name OH2”)
dmin, dmax = 1.0, 5.0
rdf, edges = numpy.histogram([0], bins=100, range=(dmin, dmax))
rdf *= 0
for ts in universe.trajectory:
    box = ts.dimensions[:3]
    amino_coor = group.coordinates()
    water_coor = water.coordinates()
    dist = distance_array(amino_coor, water_coor, box)
    new_rdf, edges = numpy.histogram(numpy.ravel(dist), \
                        bins=100, range=(dmin, dmax))
    rdf += new_rdf
numframes = \
   universe.trajectory.numframes/universe.trajectory.skip
# Normalize RDF
density = 1.
vol = (4./3.)*numpy.pi*density*\
      (numpy.power(edges[1:],3) - numpy.power(edges[:−1], 3))
rdf = rdf/(vol*numframes)

Distances under periodic boundary conditions can be taken into account via a minimum-image convention by providing the unit cell information to the distance_array()function. At the moment this functionality is limited to cubic or orthogonal unit cells but additional periodic boundary processing will be implemented in the future. In the general case it is advisable to pre-process trajectories to center the system on the molecule of interest and remap solvent molecules into the primary unit cell using native tools.

Density

The density package contains functions to calculate a density of a selection of atoms. The following example shows how to use the density_from_Universe() function to calculate the three-dimensional (3D) density map for the oxygen atom for all water molecules in the system on a grid with spacing 1 Å:

from MDAnalysis.analysis.density import density_from_Universe

D = density_from_Universe(universe, delta=1.0, \
                          atomselection=“name OH2”)
D.convert_density(“water”) # measure relative to bulk water
D.export(“md_wat.dx”)

The resulting OpenDX file can be viewed in a molecular viewer such as VMD or PyMOL. The density object can be processed further and analyzed within a Python script.

Implementation of the LeafletFinder algorithm for lipid bilayer analysis

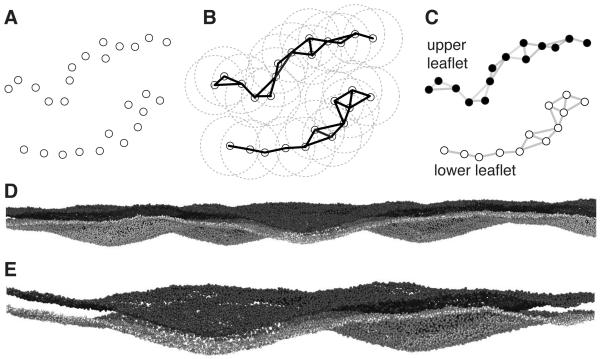
The tight integration between MDAnalysis and NumPy together with the availability of powerful specialized libraries enables one to express algorithms in a concise and efficient manner. As an example we present the LeafletFinder algorithm that returns the groups of atoms that make up the two leaflets of a bilayer. Such information is required for the automated analysis of lipid-protein interactions or lipid exchange between leaflets. For small, planar bilayer patches (e.g. with the bilayer normal assumed parallel to the z axis), it is not difficult to implement a simple algorithm that (1) collects specific head group atoms (for instance, phosphorous atoms for phospholipids), and then (2) assigns them to a leaflet, depending on the atom’s z coordinate being above or below the center of geometry of the bilayer. Such an approach breaks down when the bilayer shows strong undulations or if it is not planar, as is the case for vesicles. LeafletFinder follows a different approach, first building a network of neighbors and then using a graph-theoretic approach to analyze the network:

1. Build the network: Treat head group atoms as vertices of a graph (Figure 4A) and connect those that have a distance smaller than a set cut-off (Figure 4B).

2. Identify the connected subgraphs in the graph (Figure 4C).

3. Sort the subgraphs by decreasing size; the first and second subgraph are the leaflets.

Figure 4D shows the algorithm applied to a large coarse-grained bilayer system with 24,056 lipids and a total system size of over 1.5 million particles. Here, membrane undulations have amplitudes larger than the bilayer thickness, thus rendering the simple approach useless whereas LeafletFinder reliably distinguishes the two leaflets as shown in the closeup in Figure 4E.

Figure 4.

Defining membrane leaflets (MDAnalysis.analysis.leaflets.LeafletFinder). A-C: LeafletFinder algorithm (A) A graph is constructed that connects particles within a fixed cutoff (circles) such as lipid head group particles. (B) An algorithm implemented in the NetworkX package detects all disconnected subgraphs. (C) Typically, only two graphs are found that describe the two topologically disjoint leaflets. (D) View of a coarse grained bilayer with strong deformations. The bilayer contains ~24,000 lipids and the total simulation system size was ~1.5 million particles (J. Goose, personal communication). The phosphate particles in the head groups are shown and are colored black or white according to the LeafletFinder algorithm. (E) Close-up view of a deformation that is larger than the bilayer thickness itself.

The implementation in MDAnalysis starts with a selection of lipid head group atoms, e.g.

headgroup_atoms = universe.selectAtoms(“name P*”)
coord = headgroup_atoms.coordinates()

Step 1 of the algorithm takes the coordinates of the selected head group atoms and builds the adjacency matrix, which contains True for any distance smaller than the cutoff and False otherwise; this only requires a single line of code because distance_array() returns a NumPy array that can be directly transformed using NumPy’s powerful Boolean array constructors:

from MDAnalysis.analysis.distances import distance_array
adj = (distance_array(coord,coord) < cutoff)

Step 2 and 3 make use of the NetworkX¹² package. The networkx.Graph class can directly build a graph from an adjacency matrix and the networkx.connected_components() function returns the connected components of a graph, sorted by size. Thus only a single line of code is required to analyze the network of neighbors of all lipids:

import networkx as NX
leaflets = NX.connected_components(NX.Graph(adj))

leaflets[0] and leaflets[1] contain the indices of the two leaflets that can be mapped back to the atoms by indexing the selection; the corresponding residues (i.e. the lipids) are obtained from the residues attribute of the AtomGroup:

A_lipids = headgroup_atoms[leaflets[0]].residues
B_lipids = headgroup_atoms[leaflets[1]].residues

The “top” or “bottom” leaflet of a planar membrane can be assigned by, for instance, comparing the centers of mass of the leaflets; membrane normals can be computed via singular value decomposition of the head group coordinates, leaflet-resolved diffusion coefficients and order parameters can now be easily computed with standard techniques.

Native contacts analysis

Trajectories between known end states such as folding/unfolding or a macromolecular transition between “closed” and “open” conformations are frequently simulated. A useful metric to described the progression of such a trajectory is the fraction of native contacts q_M(t) at each time t.²⁰ A contact exists if a atom pair (i,j) has a distance d_ij < R_c, where R_c is a cut-off. A native contact relative to state M is said to exist if d_ij(t) < R_c and d_ij^M < R_c. The fraction of native contacts is the ratio between the total number of native contacts and the total number of contacts in state M.

The following example implements a “Q1-Q2” analysis²⁰, applied to the simulated transition of the enzyme adenylate kinase (AdK) from a closed to an open conformation²¹. Contacts are defined between C_α atoms with R_c=8 Å. q₁ is the fraction of contacts relative to the closed state (pdb:1AKE), the starting conformation of the trajectory, and q₂ is the fraction of native contacts relative to the open conformation (based on pdb:4AKE). The outline of the algorithm only requires a few lines of code; a full implementation can be found in MDAnalysis.analysis.contacts.ContactAnalysis. To calculate the fraction of native contacts q1 relative to a native structure with C_α coordinates native_coords_1:

from MDAnalysis.analysis.distances import self_distance_array
native_contacts_1 = (self_distance_array(native_coords_1) < Rcut)
ca = universe.selectAtoms(“name CA”)
for ts in universe.trajectory:
      contacts = (self_distance_array(ca.coordinates()) < Rcut)
      native_contacts = numpy.logical_and(contacts, native_contacts_1)
      q1 = native_contacts.sum()/native_contacts_1.sum()

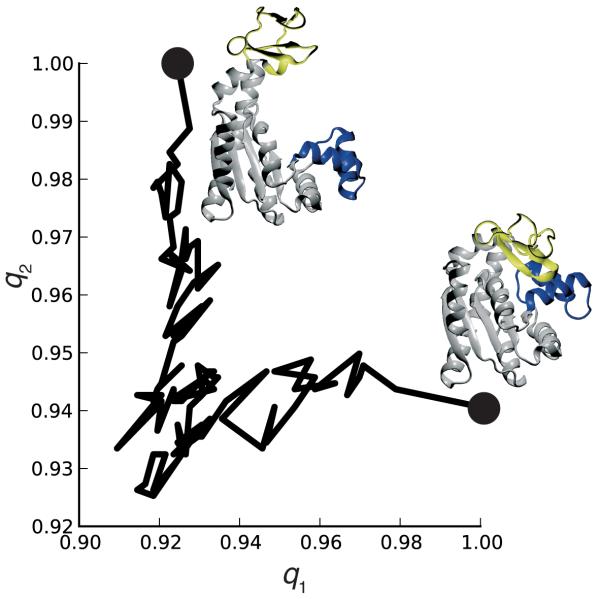
A plot of q₁ versus q₂ is shown in Figure 5, indicating that the transition progresses in a non-linear fashion and switches from a “closed”-like conformation to an “open”-like conformation^20,21.

Figure 5.

Native contacts analysis for the closed to open transition of adenylate kinase. q₁ is the fraction of native contacts relative to the closed state (PDB: 1AKE) and q₂ is relative to an open state structure (PDB: 4AKE).

Benchmark

Analysis of MD simulations can be time consuming and thus performance is a concern when using any analysis program. We benchmarked MDAnalysis together with three other software packages (CHARMM ⁶, VMD ⁷, and Gromacs ¹) on a number of representative tasks that are readily available in each package. For a 10-ns trajectory with 10,000 frames of fatty acid binding protein (pdb: 1IFC) in water (13,051 atoms) we computed time series for three distances, two dihedral angles, the RMSD relative to the starting conformation, and the radius of gyration of the protein. We also calculated the density of water oxygens around the protein from the same trajectory. The radial distribution of 3476 water oxygens in an urea solution was calculated from 2,000 frames of a trajectory with 11,492 atoms. MDAnalysis code used was similar to the examples shown above. Runs were timed on an Intel Xeon E5420 CPU at 2.5 GHz. Results are shown in Table 1.

Table 1.

Benchmark of standard analysis tasks using various analysis software packages

	MDAnalysis	VMD	CHARMM	Gromacs
Distances (3x)	1.04 s	4.81 s	2.22 s	14.71 s
Dihedrals (2x)	0.80 s	2.40 s	2.15 s	11.92 s
RMSD	29.10 s	4.29 s	5.09 s	32.18 s
Radius of Gyration	10.16 s	12.58 s	12.10 s	16.87 s
Radial Distribution	21 m 24 s	10 m 38 s	7 m 1 s	6 m 6 s
3-dimensional Density	1 m 32.31 s	5 m 52.37 s	– *	16.93 s

^*Currently not implemented within CHARMM as a stand-alone calculation.

In general, MDAnalysis performs fairly well and is even faster than most programs when performing simple calculations such as the analysis of distances, dihedrals, generating density maps, and the radius of gyration. Very computing intensive tasks that have to operate on large arrays such as the radial distribution function can be substantially slower. Profiling of the code with Python’s cProfile module revealed that in this case the drop in performance arose mostly from the NumPy histogram() function, which requires about three times as much time as the MDAnalysis distance calculation. If necessary, performance could likely be improved by implementing the whole analysis task in Cython or C without using NumPy, although requiring many more lines of code and hence implementation and testing time.

CONCLUSIONS

MDAnalysis is a Python framework that encapsulates access to atoms in molecular dynamics trajectories within a consistent, object-oriented framework. It hides details of the I/O operations from the user and enables the creation of analysis tools that are largely agnostic of the molecular dynamics code that was used to produce the trajectory. It features an expressive atom selection language and a rich interface to access atoms and groups of atoms in an object-oriented and “Pythonic” manner. Systems with millions of atoms have been successfully analyzed, with the only limitation that a single timestep must be able to fit into the main memory of the workstation. MDAnalysis comes with a suite of test cases (which are constantly used during development to verify that the code runs correctly), example scripts, and an expanding library of analysis modules for tasks that are not necessarily available in any other package we know of. Tight integration between MDAnalysis and NumPy makes it easy to immediately use a large number of scientific libraries, thus utilizing high quality and already tested code in preference to local implementations. The modular design of the Python language makes it easy to re-use analysis code by storing it in modules and packages that can be imported and subclassed as needed.

Several software packages exist that enable the user to analyze MD simulations (Tables S1 and S2, within the supporting information). Similar to pymacs ¹⁰, MMTK ⁸, mmLib ²², and Atomic Simulation Environment ²³, it utilizes Python libraries to perform a variety of functions. It has advanced, intuitive atom selections similar to programs such as CHARMM ⁶ or VMD ⁷. MDAnalysis is specifically tailored to the analysis of MD simulation as seen in examples mentioned above and on the MDAnalysis website, being able to handle many popular trajectory formats. MMTK ⁸ and MDAnalysis are both Python-based, object-oriented libraries dealing with MD simulations but they have rather different strengths. MMTK focuses on the development of MD simulation methods whereas MDAnalysis makes it easy to analyze MD trajectories by providing powerful selection commands, straightforward access to trajectory data at all levels of the atom/residue/segment hierarchy, and seamless integration with NumPy.

As MDAnalysis code can be very compact it is also possible to write short but powerful “throw-away” scripts. The library is also well suited for interactive work in a Python shell such as ipython (http://ipython.scipy.org). With the help of command completion features of the shell and the instant selection attributes it is possible to quickly analyze and explore a structure or simulation and immediately plot data (e.g. using matplotlib (http://matplotlib.sourceforge.net)). Such a rapid-prototyping approach to tool development and exploratory analysis is showing great promise in the authors’ labs.

MDAnalysis is available as open source code under the GNU Public License (version 2) from http://mdanalysis.googlecode.com. Documentation is available through the standard Python help system during interactive use and from the web site.