Abstract
Balanced steady-state free precession (bSSFP) is an attractive fMRI method at high fields due to minimal spatial distortion. To examine sensitivity and specificity of bSSFP fMRI at ultrahigh magnetic field of 9.4 T, we performed high-resolution pass-band high flip-angle (16°) bSSFP fMRI with four phase cycling (PC) angles at two repetition times (TR) of 10 ms and 20 ms and conventional gradient-recalled-echo (GRE) fMRI with TR of 20 ms on rat brain during forepaw stimulation. The sensitivity of bSSFP fMRI with TR of 20 ms was higher than that of GRE fMRI regardless of PC angle. Because of magnetic field inhomogeneity, fMRI foci were changed with PC angle in bSSFP fMRI, which was more prominent when TR was shorter. Within a middle cortical layer region where magnetic field inhomogeneity was relatively small, the homogeneity of bSSFP fMRI signals was higher at shorter TR. Acquisition of baseline transition-band bSSFP images helped to identify pass- and transition–band regions and to understand corresponding bSSFP fMRI signals. Fourier analysis of the multiple PC bSSFP datasets provided echoes of multiple pathways separately, and the main echo component showed lower sensitivity and better homogeneity than the free induction decay component. In summary, pass-band bSSFP techniques would have advantages over GRE-based fMRI in terms of sensitivity, and may be a good choice for fMRI at ultrahigh fields.
Keywords: balanced SSFP, fMRI, phase cycling, pass-band bSSFP, transition-band bSSFP, Fourier analysis, spatial specificity, high resolution, high fields
Introduction
Blood oxygenation level-dependent (BOLD) functional magnetic resonance imaging (fMRI) technique (Bandettini et al., 1992; Kwong et al., 1992; Ogawa et al., 1993) has made a wide impact on neuroscience, physiology, and psychology. The most commonly used pulse sequence for fMRI has been gradient-echo echo-planar imaging (EPI) because of its speed and high sensitivity to the BOLD contrast. However, this technique is also sensitive to image distortion and degradation caused by local field inhomogeneity, especially at high fields. To minimize distortion problems and enhance signal to noise ratio (SNR), balanced steady-state free precession (bSSFP) has been proposed as an alternative fMRI technique (Bowen et al., 2005; Lee et al., 2006; Lee et al., 2007; Lee et al., 2008; Miller et al., 2003; Miller et al., 2006; Miller et al., 2007; Scheffler et al., 2001; Wu et al., 2007; Zhong et al., 2007). Two distinctive methods have been proposed for bSSFP fMRI. One is pass-band bSSFP that is optimized for pass-band regions by employing high flip angle and the other is transition-band bSSFP that is optimized for transition-band regions by employing low flip angle. To minimize confusion, we will denote pass-band bSSFP and transition-band bSSFP by high flip-angle bSSFP (10°–20° at 9.4T) and low flip-angle bSSFP (1°–5° at 9.4T), respectively, throughout this article. Initial bSSFP fMRI studies have focused on improving the BOLD sensitivity by utilizing transition bands where both magnitude and phase signals change significantly with small frequency shifts (low flip-angle transition-band bSSFP) (Lee et al., 2006; Lee et al., 2007; Miller et al., 2003; Miller et al., 2006; Scheffler et al., 2001; Wu et al., 2007). Because low flip-angle bSSFP covers narrow spatial regions and is sensitive to B0 fluctuation, high flip-angle (pass-band-optimized) bSSFP has been recently adopted for fMRI studies (Bowen et al., 2005; Lee et al., 2008; Miller et al., 2007; Zhong et al., 2007).
Although high flip-angle bSSFP is a promising tool for high-resolution fMRI, its signal sources are unclear due to the existence of two distinctive frequency bands, i.e., phase-insensitive pass bands and phase-sensitive transition bands (Scheffler and Hennig, 2003). Various studies have been performed to understand contrast mechanism, tissue specificity, and contributions of multiple pathways of high flip-angle bSSFP fMRI. In some studies, sources of high flip-angle bSSFP fMRI signals have been reported as T2* at long repetition time (TR) (Miller et al., 2007; Zhong et al., 2007), T2 at short TR (Miller et al., 2007), and diffusion in the extravascular area (Bowen et al., 2006). Although the improvement of tissue specificity of high-flip-angle bSSFP fMRI has been found with computer simulations (Kim et al., 2007b; Miller and Jezzard, 2008; Patterson et al., 2008), it has not been clearly demonstrated experimentally, because the spatial resolution of fMRI for human studies is limited. Also contributions of multiple pathways in bSSFP fMRI have been implicated from multiple TE/TR studies (Lee et al., 2009; Zhong et al., 2007). Furthermore, bSSFP fMRI contrast will depend on the spatial location of the pass bands and transition bands, which will also depend on shimming conditions and anatomical structures within activation areas (e.g. large veins). Since it would be difficult that all activation pixels have frequency shifts within the pass-band domain especially at ultrahigh fields, it is more likely that both T2 and T2* characteristics reside with spatial heterogeneity in high flip-angle bSSFP fMRI map at ultrahigh fields. These effects have not been systematically investigated.
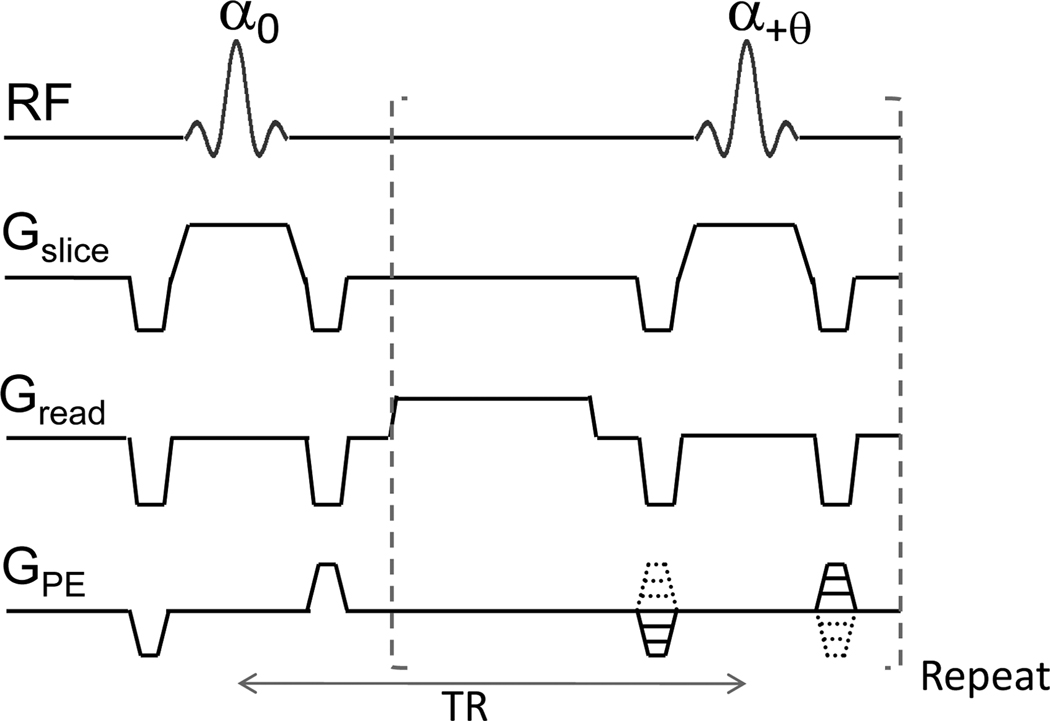
As shown in the pulse sequence diagram (Fig. 1), there is no accumulation of phases associated with gradients in bSSFP, because the zeroth moment is null over each repetition time (TR). The phase evolution per TR is spatially heterogeneous because of magnetic field inhomogeneity and can shift due to scanner B0 drift. The contribution of pass bands and transition bands to bSSFP images can be changed by incrementing the RF pulse phase in a constant amount for each TR period (which is often called phase cycling angle). Multiple datasets acquired at multiple phase cycling (PC) angles can virtually cover all cases of variations in pass bands and transition bands induced by magnetic field inhomogeneity. Furthermore, the bSSFP signal is summation of echoes of multiple pathways including the two major components of the free induction decay (FID) (often called as fast imaging with steady state precession, FISP) and the main echo (often called as reversed FISP, PSIF). The echoes of the multiple pathways of bSSFP can be separated from the multiple phase-cycled bSSFP data using Fourier analysis (Zur et al., 1990). If we acquire total M bSSFP datasets with PC angles of 2π (j –1) /M (j = 1 to M), the phase shift of n-th echo is 2π n(j –1) /M. Based on this, the M-point discrete Fourier transform of the M bSSFP datasets correspond to the individual M echoes of the multiple pathways including FID and main echo (see Zur et al for details, (Zur et al., 1990)). To this end, high-resolution multiple PC bSSFP fMRI with number of PC angles ≥ 4 (for Fourier transform) may overcome abovementioned limitations of bSSFP fMRI and provide new insights into contrast mechanism, tissue specificity, and contributions of multiple pathways of bSSFP fMRI.
FIG. 1. Pulse sequence diagram of balanced steady state free precession (bSSFP).
The sum of gradients along each of the three directions (Gslice, Gread, and GPE) is zero. Flip angle (α) of excitation RF pulse is optimized for maximizing signal at pass- or transition-band, and the phase of RF pulse is incremented by θ. TR: repetition time.
In this study, we performed high-resolution high flip-angle bSSFP fMRI at 4 phase cycling (PC) angles (0°, 90°, 180°, and 270°) and two different TR values (10 and 20 ms) in comparison with conventional gradient-recalled echo (GRE) fMRI on rat brains at 9.4T. The sensitivity and spatial specificity of fMRI maps were investigated in cortical surface, tissue, and middle layer regions separately, and the fMRI maps were visually compared with BOLD venogram (Park et al., 2008) and with baseline low flip-angle (transition-band-optimized) bSSFP images. In addition, we reconstructed two main components of bSSFP (i.e., FID and main echo) from the multiple phase-cycled bSSFP datasets using Fourier analysis (Zur et al., 1990) and then fMRI map from each component was obtained. Two additional methods developed for removing banding artifacts (maximum intensity projection and nonlinear averaging reconstruction (Elliott et al., 2007)) were also investigated for the multiple PC bSSFP fMRI datasets. Sensitivity and spatial specificity of all bSSFP and GRE fMRI data were compared to one another.
Methods
Computer simulation
Baseline magnitude and phase signals of 9.4T bSSFP were simulated as a function of precession angle per TR at four different PC angles of 0°, 90°, 180°, and 270°, which we will denote PC0, PC1, PC2, and PC3, respectively, throughout this article, and two TE/TR values of 10/20 ms and 5/10 ms with flip angle of 16°, based on the equations given by Scheffler and Hennig (Scheffler and Hennig, 2003) and tissue T1 = 2 s and T2 = 40 ms (Lee et al., 1999; Tsekos et al., 1998). The precession angle per TR represents the phase evolution during one TR period (−2π to +2π for TR of 10 ms and −4π to +4π for TR of 20 ms) in the range of resonance frequency shift of ±100 Hz. From the simulation results at the four different PC angles, magnitude and phase signals of the FID and main echo components were extracted at each TR value by applying Fourier analysis along the PC dimension (see below) (Zur et al., 1990). The four PC bSSFP fMRI datasets were reconstructed into two different datasets: maximum intensity projection (MIP) and the average of three highest values (i.e., (sum–minimum)/3) which will be called as nonlinear averaging (NLA) (Elliott et al., 2007) throughout this article. The NLA is based on the notion that the minimum intensity likely belongs to transition band, hence should be excluded to minimize banding artifacts while maintaining high SNR. To assess the contributions of aliasing effects from echoes other than the 4 echoes from the 4-point Fourier analysis, we additionally calculated intensities of total 21 echoes with the analytical solutions provided by Zur et al (Zur et al., 1990).
Animal preparation and forepaw stimulation
Six male Sprague-Dawley rats weighing 250–450 g (Charles River Laboratories, Wilmington, MA, USA) were used with approval from the Institutional Animal Care and Use Committee (IACUC) at the University of Pittsburgh. The rats were initially anesthetized with 5.0% isoflurane in an air:O2 mixture to attain a fraction of inspired oxygen of 30% within a small plastic box, and then intubated for mechanical ventilation (RSP-1002, Kent Scientific, CT, USA). The isoflurane level was reduced to 2.0% for surgical preparation. The femoral artery and femoral vein were catheterized for blood gas sampling and for fluid administration, respectively. Then the isoflurane level was reduced to 1.4%. The head of the animal was carefully secured to a home-built cradle by means of ear pieces and a bite bar. Rectal temperature was maintained at 37 ± 0.5 °C with a water-heating pad, controlled by a thermocouple and feedback unit. Five percent dextrose in saline was infused intravenously at 0.4 ml / h. Ventilation rate and volume were adjusted based on blood gas analysis results (Stat profile pHOx; Nova Biomedical, MA, USA).
Electrical stimulation was applied to either the right or left forepaw using two needle electrodes inserted under the skin between digits 2 and 4 (Silva et al., 1999). The electrodes were connected to a constant current stimulation isolator (A365D, World Precision Instruments, Inc., Sarasota, FL, USA), which was triggered by a pulse generator (Master 8, AMPI, Israel). Stimulation parameters for activation studies were: current = 1.2–1.6 mA, pulse duration = 1–3 ms, repetition rate = 6–8 Hz, stimulation duration = 15 s, and inter-stimulation period = 2–3 min, most of which were adopted from stimulus parameter optimization studies (Kim et al., 2007a; Kim et al., 2010; Masamoto et al., 2007).
MRI data collection
All experiments were carried out on a Varian 9.4 T / 31-cm MRI system (Palo Alto, CA) with an actively-shielded gradient coil of 12-cm inner diameter, which operates at a maximum gradient strength of 40 G / cm and a rise time of 130 µs. A homogeneous coil and a surface coil (Nova Medical, Wilmington, MA) were used for RF excitation and reception, respectively. Localized shimming was performed with point resolved spectroscopy (Bottomley, 1987) over a coronal slab (~12 × 6 × 6 mm3) covering forelimb somatosensory cortex to yield a water spectral linewidth of 20–30 Hz. To compare venogram with fMRI, BOLD microscopy was performed with a 3D RF-spoiled gradient-echo pulse sequence, as described previously (Park et al., 2008). Imaging parameters for BOLD 3D microscopy were: TR = 40 ms, TE = 20 ms, matrix size = 256 × 192 × 128, field of view = 2.4 × 2.4 × 1.2 cm3, number of averages = 2, and total scan time = 18.4 min.
For single-slice fMRI studies with matrix size = 256 (readout) × 192 (phase-encode), field of view = 2.4 × 2.4 cm2, and slice thickness = 2 mm, eight high flip-angle bSSFP and one GRE studies were performed. For GRE, no RF spoiling was used but contrast spoiling gradients were applied along slice-select and readout directions. The bSSFP studies were performed with four different PC angles of 0°, 90°, 180°, and 270° (PC0, PC1, PC2, and PC3, respectively), and TE/TR of 5/10 ms and 10/20 ms, while GRE fMRI was acquired with TE/TR = 10/20 ms. Spectral widths for all the fMRI studies with the short TR (10 ms) and long TR (20 ms) values were 64 kHz and 32 kHz, respectively. Flip angles for all the bSSFP studies and the GRE study were 16°and 8°, respectively, optimized based on simulation (data not shown). The number of averages for the datasets with TR of 10 ms and 20 ms was 2 and 1, respectively, to maintain the same temporal resolution of 3.84 s for all fMRI studies. These scan parameters are summarized in Table 1. Twenty four images were acquired for each ~92-s long fMRI run; eight during pre-stimulus baseline, four during stimulation, and twelve during the post-stimulus period. The resonance frequency was recalibrated before each fMRI run to minimize B0 drifting effects, which was measured to be 0.070±0.012 Hz/min (N=6). The amount corresponds to phase evolution per TR of 0.009 rad/min when TR=20ms, which is negligible within each fMRI scan. The nine fMRI studies of bSSFP and GRE composed one full set, and each full set was repeated 15 to 25 times.
Table 1.
Scan parameters of bSSFP and GRE fMRI studies.
| Scan Parameters |
Short TE/TR bSSFP | Long TE/TR bSSFP | GRE | ||||||
|---|---|---|---|---|---|---|---|---|---|
| PC0 | PC1 | PC2 | PC3 | PC0 | PC1 | PC2 | PC3 | ||
| TR (ms) | 10 | 20 | 20 | ||||||
| TE (ms) | 5 | 10 | 10 | ||||||
| PC angle | 0° | 90° | 180° | 270° | 0° | 90° | 180° | 270° | N/A |
| SW (kHz) | 64 | 32 | 32 | ||||||
| flip angle | 16° (2°) | 16° (4°) | 8° | ||||||
| NEX | 2 | 1 | 1 | ||||||
| Common parameters : matrix size = 256 (readout) × 192 (phase-encode), field of view = 2.4 × 2.4 cm2, and slice thickness = 2 mm | |||||||||
SW: spectral width; NEX: number of average, respectively. The flip angles for baseline low-flip angle transition-band bSSFP are given inside the parenthesis.
To understand signal characteristics of high flip-angle bSSFP fMRI, we acquired corresponding baseline low flip-angle bSSFP images (Lee et al., 2006; Lee et al., 2007; Miller et al., 2003; Miller et al., 2006; Scheffler et al., 2001; Wu et al., 2007). All the scan parameters were the same as the corresponding high flip-angle bSSFP fMRI, except flip angles of 2°and 4° at TR values of 10 ms and 20 ms (see Table 1), respectively, optimized with simulation (data not shown).
Post processing
Each 2D dataset acquired for fMRI and 3D dataset acquired with BOLD microscopy was zero-filled and Fourier-transformed to yield isotropic resolution of 93.75 µm in 2D and 3D, respectively. All repeated fMRI runs with the same imaging parameters were averaged. One FID and main echo components were extracted as new fMRI datasets from the four phase-cycled, high flip angle, pass-band bSSFP datasets for each TR value (Zur et al., 1990): the four points along the PC dimension were Fourier-transformed by sequentially applying MATLAB functions of “fft” and “fftshift” (MathWorks, Natick, MA, USA), and then the third and the second points were assigned to the FID and main echo components, respectively. Two additional datasets were reconstructed from the multiple PC bSSFP datasets with MIP and NLA, in the same way described in the “computer simulation” section. To reconstruct a 2D view from the 3D dataset acquired with BOLD microscopy, a 21-pixel (~2 mm) coronal slab corresponding to the position of fMRI studies was selected and vessel detection within the slab was improved by minimum-intensity projection (Reichenbach and Haacke, 2001) (see Fig. 2a).
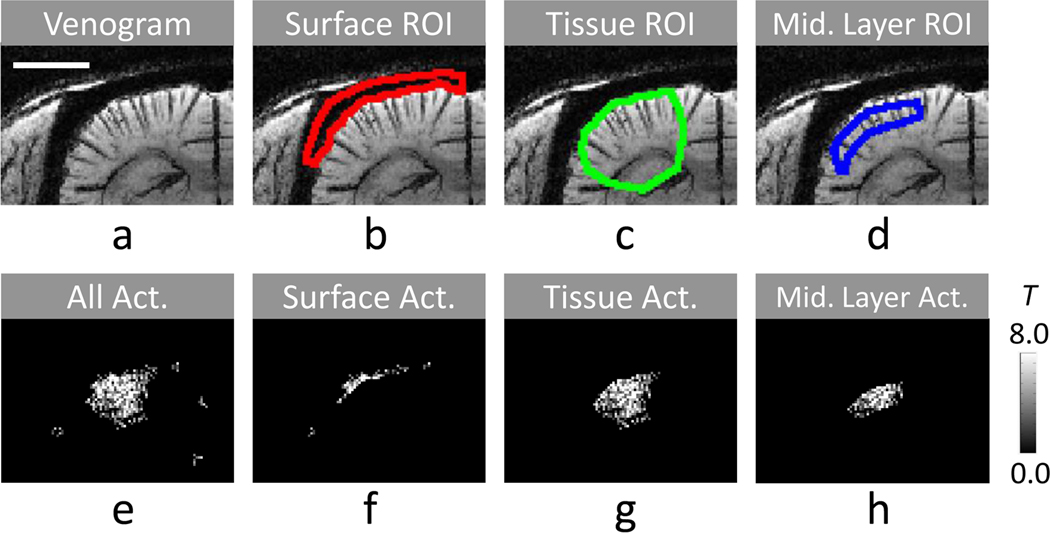
FIG. 2. Selection of ROIs and classification of functional activation pixels.
The cortical surface ROI (b), the tissue ROI (c), and the middle cortical ROI (d) were chosen based on venogram with minimum-intensity projection (a). Activation pixels were classified as cortical surface activation pixels (f), tissue activation pixels (g), and middle cortical ROI (h) from all activation pixels after cluster threshold (e). The fMRI map (e–h) was acquired from one representative animal with bSSFP at TR of 20 ms and phase cycling angle of 180°. The distance scale bar in a represents 3 mm.
A T-value functional map for each fMRI dataset (including those from FID, main echo, MIP, and NLA) was determined by performing T-test with significance level of ≤ 0.1 and the number of contiguous activated pixels > 6 (see Fig. 2e). For quantitative analyses, three regions of interest (ROI) were selected in functional activation areas; cortical surface ROI, tissue ROI, and middle cortical layer ROI. A cortical surface ROI (see Fig. 2b) was manually determined from hypointense cortical surface pixels in the venogram. A tissue ROI (see Fig. 2c) was manually drawn by including the whole functional activation regions, but excluding the cortical surface ROI. A middle cortical layer ROI (Fig. 2d) was defined between two manually-drawn curves along the cortical surface at ~0.3 and ~1.1 mm away from the cortical surface within the tissue ROI. Activation pixels within surface ROI (Fig. 2f), tissue ROI (Fig. 2g), and middle layer ROI (Fig. 2h) were separately grouped (Fig. 2b–d). In cortical surface and tissue ROI groups (see Fig. 2f,g), mean T value (Tmean) and number of activation pixels (Nact) were quantified, and a total fMRI sensitivity index was calculated as multiplication of Tmean with Nact (TN). To understand the spatial specificity of fMRI maps, a ratio of fMRI sensitivity index was calculated by dividing the total fMRI sensitivity index of the tissue ROI by that of the cortical surface ROI (TNtissue/TNsurf). To examine the homogeneity and potential source of fMRI signals, a normalized spatial variation of T values of activation pixels was calculated within the middle layer ROI (i.e., standard deviation divided by mean of T values, std(T)/mean(T)). Wilcoxon signed rank test was performed for comparison of two groups with significance level of 0.05.
Results
Simulation results
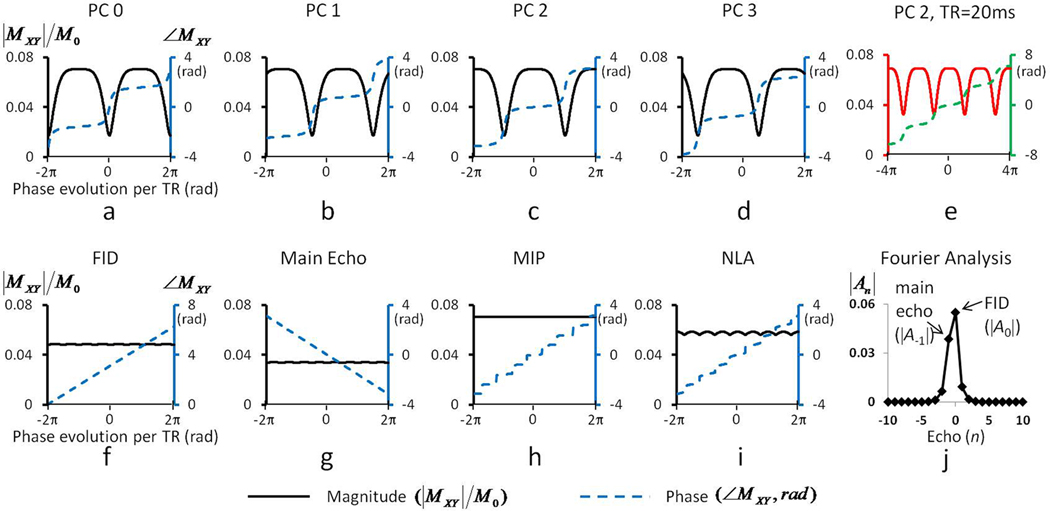
Figure 3 shows simulated magnitude and phase responses of bSSFP as a function of resonance frequency (phase) shift at four PC angles when TR = 10 ms (Fig. 3a–d), the responses at PC2 when TR = 20 ms (Fig. 3e), the responses of FID and main echo components extracted from the data in Fig. 3a–d with Fourier analysis (Fig. 3f,g), the responses of MIP and NLA of the data in Fig. 3a–d (Fig. 3h,i), and analytical solution of echo intensities of multiple pathways (Fig. 3j). Since our simulations were performed within a resonance frequency shift of ±100 Hz, the phase evolution induced by off-resonance frequency (horizontal axis) is twice larger at TR = 20 ms (Fig. 3e) than at TR = 10 ms (Fig. 3c). It should be noted that the magnitude response of bSSFP is related to T1 and T2 as well as flip angle and TR, but flip angle does not change the location of pass- and transition-bands. Both magnitude and phase responses shifted along the horizontal axis in the amount of the PC angle (Fig. 3a–d). At PC0, steep changes in magnitude and phase (indicating transition band) were observed near on-resonance frequency (phase evolution = 0 rad) (Fig. 3a), and the magnitude around on-resonance frequency was maximized at a low flip angle of 2° (i.e., transition-band bSSFP) (data not shown). At PC2, the constant magnitude and phase (indicating pass band) were detected near on-resonance frequency, and the magnitude around on-resonance frequency was maximized at this relatively high flip angle of 16° (i.e., pass-band bSSFP). In simulation data of bSSFP with TR = 10 ms (Fig. 3a–d), the phase changes were less flatter in the pass-band regions and less steeper in the transition-band regions than those simulated at TR of 3.6 ms for low fields (Scheffler and Hennig, 2003). This phenomenon became more severe at TR = 20 ms (Fig. 3e). The magnitude difference between pass-band and transition-band regions became smaller at the longer TR (Fig. 3e), implying that characteristics of bSSFP signals become closer to those of GRE which have constant magnitude and linearly-increasing phase responses with resonance frequency shift (i.e., phase evolution).
FIG. 3. Simulation results of 9.4T multiple phase-cycled balanced steady state free precession (bSSFP) signal.
(a–e) Magnitude and phase responses as a function of precession angle for pass-band bSSFP with TE/TR of 5/10 ms at 9.4T with phase cycling (PC) angles of 0° (PC0, a), 90° (PC1, b), 180° (PC2, c), and 270° (PC3, d), and for pass-band bSSFP with TE/TR of 10/20 ms with PC angle of 180° (PC2, e). Flip angle was 16°. The vertical axes on the left and right hand sides respectively represent magnitude and phase of transverse magnetizations, and the horizontal axis represents phase evolution per TR in radian unit. (f–i) Magnitude and phase responses of FID (f) and main echo components (g) extracted from the magnitude and phase responses in a–d with Fourier analysis, minimum intensity projection (h), and nonlinear averaging (i) obtained from a–d. The nonlinear averaging was performed as the average of three values after excluding the minimum intensity value, which has been used to reduce banding artifacts (Elliott et al., 2007). All the magnitude and phase responses are displayed in black and blue colors, respective, for TE/TR of 5/10 ms (a–d and f–i) and in red and green colors, respectively, for TE/TR of 10/20 ms (e). (j) Intensities of 21 echoes for TE/TR of 5/10 ms calculated with the analytical solution by Zur et al. (Zur et al., 1990) for examining the aliasing effects to FID and main echo data in f and g.
Magnitude responses of the FID and the main echo components (Fig. 3f,g) were almost constant regardless of phase evolution (frequency shift), but the FID intensity was higher than the main echo intensity. The phase of the FID and main echo signals was linearly changed with phase evolution angle (Fig. 3f,g). Note that the slope of phase changes of the two components was identical, implying their equal sensitivity to intravoxel functional susceptibility-induced frequency changes. Overall phase responses of MIP increased step by step and each step showed the flattest phase responses (Fig. 3h). Overall phase responses of NLA were similar to those of MIP, while phase responses in individual step of NLA were steeper than those of MIP (Fig. 3i). Although MIP provided the highest intensity (Fig. 3h), its functional sensitivity would not necessarily be higher than sensitivity of FID or NLA, because only one pixel point among the multiple PC points was chosen (rather than being averaged) in MIP.
According to the analytical solutions of Fourier analysis (Zur et al., 1990) with TR = 10 ms (Fig. 3j), the two highest intensities were observed at echo number 0 (A0, FID) and −1 (A−1, main echo), as expected. The next significant echoes were echo numbers 1 and −2 (A1 and A−2), which correspond to the two remaining points from the 4-point Fourier transform other than the two major points (FID and main echo). According to Zur et al (Zur et al., 1990), finite number of phase cycling angles (M = 4 in our case) may cause aliasing effects in an echo with echo number n from echoes with echo number n ± pM (p = ±1, ±2, ±3, etc). In our simulation studies, the signals quickly decreased in echoes with echo number ≤ −3 and those with echo number ≥ 2 (Fig. 3j), implying that there would be no significant aliasing effects under our experimental conditions. These characteristics at TR = 10 ms were similar to those at TR = 20 ms.
Functional MRI maps acquired at multiple phase cycling angles
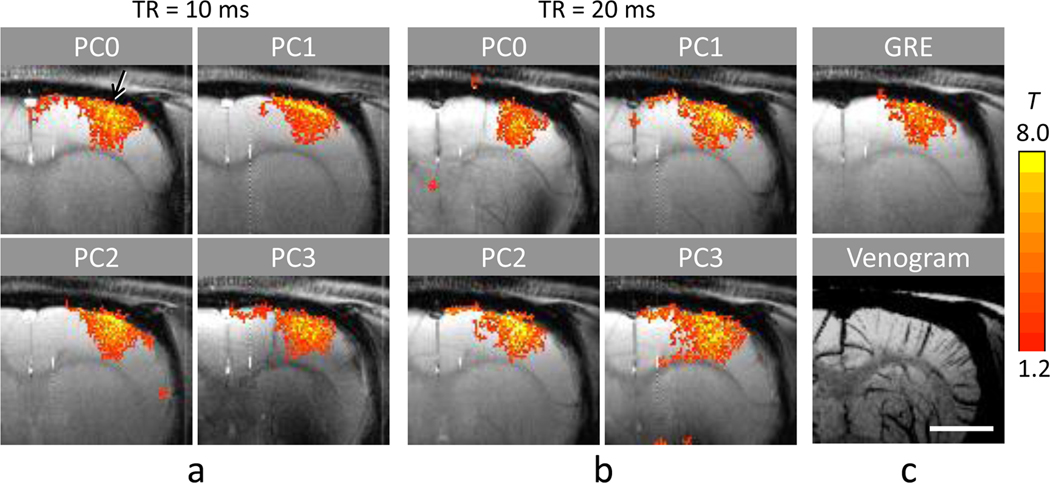
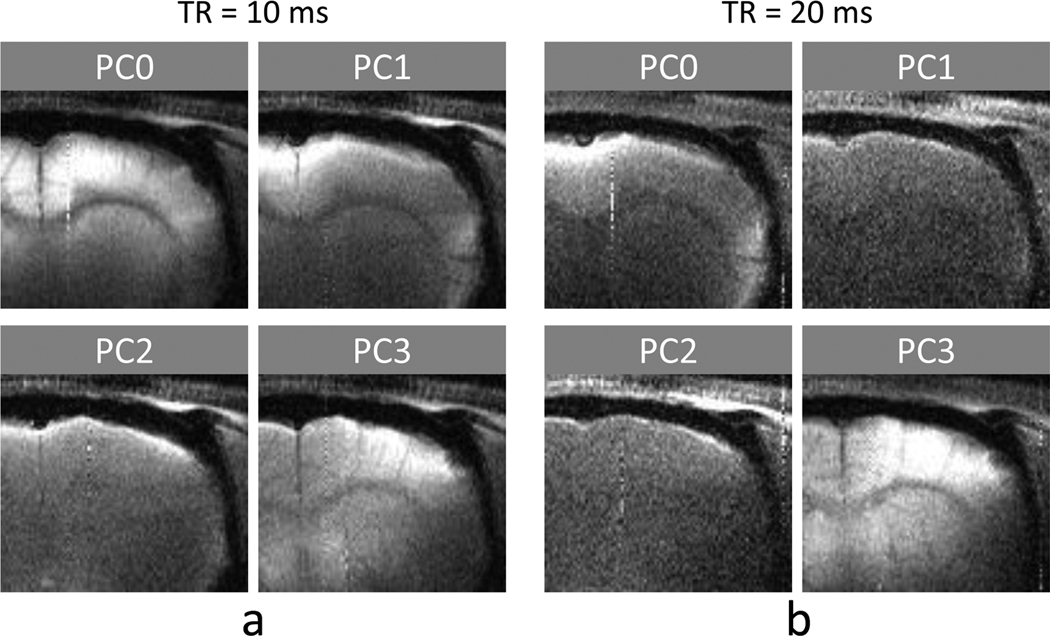
In multiple phase-cycled bSSFP fMRI maps at both TR values (Fig. 4), activation was observed at contralateral somatocortical areas. The activation foci (yellow pixels) were located around the cortical surface at some PC angles (mostly PC1 and PC2) and located in the middle cortical regions at the other PC angles (mostly PC0 and PC3), when TR = 10 ms (Fig. 4a). When TR = 20 ms, the activation foci moved in a similar manner to the case of TR = 10 ms but were more spread (Fig. 4b). In some cases, high activation areas were correlated with intracortical veins shown at the bottom of Fig. 4c (e.g., arrow in PC0 of Fig. 4a). It should be noted that the high surface signals in PC1 and PC2 could be from steep transition bands rather than flat pass bands and that magnetic fields are inhomogeneous in the brain and thus the on-resonance area varies with PC angle.
FIG. 4.
Four phase-cycled pass-band bSSFP and GRE fMRI maps at 9.4T overlaid on corresponding baseline images of a representative animal. The bSSFP fMRI datasets were acquired with flip angle = 16°, and TE/TR = 5/10 ms (a) and 10/20 ms (b). Phase cycling (PC) angles are indicated on top of each image. (c) Function MRI map acquired with GRE at TE/TR = 10/20 ms (top) and the BOLD venogram with minimum-intensity projection applied over the slab corresponding to the position of the fMRI maps (bottom). The images in c are for comparison reference to bSSFP fMRI maps shown in a and b. The distance scale bar in the bottom of c represents 3 mm.
Since low flip-angle (transition-band) bSSFP images have hyperintensities in transition bands, they can provide information as to how transition-band regions contribute to high flip-angle bSSFP fMRI maps. In the low flip-angle bSSFP images from this study (Fig. 5), hyperintensity was observed in either cortical surface regions at some PC angles (PC1 and PC2 in Fig. 5a and PC0, PC1, and PC2 in Fig. 5b) or middle cortical regions at other PC angles. In most cases, transition-band regions (determined by hyperintensity in the low flip-angle bSSFP images) showed high functional signals (Fig. 4a,b), as predictable from the steep magnitude and phase changes induced by frequency shift (i.e., phase evolution shift) (Fig. 3a–d). But not all activation foci corresponded to hyperintense regions in the corresponding low flip-angle bSSFP images (Fig. 5).
FIG. 5.
Four phase-cycled baseline transition-band bSSFP images acquired at 9.4T from the same animal shown in Fig. 4. The datasets were acquired with TE/TR = 5/10 ms and flip angle = 2° for (a), and 10/20 ms and flip angle = 4° for (b). Phase cycling (PC) angles are indicated on top of each image.
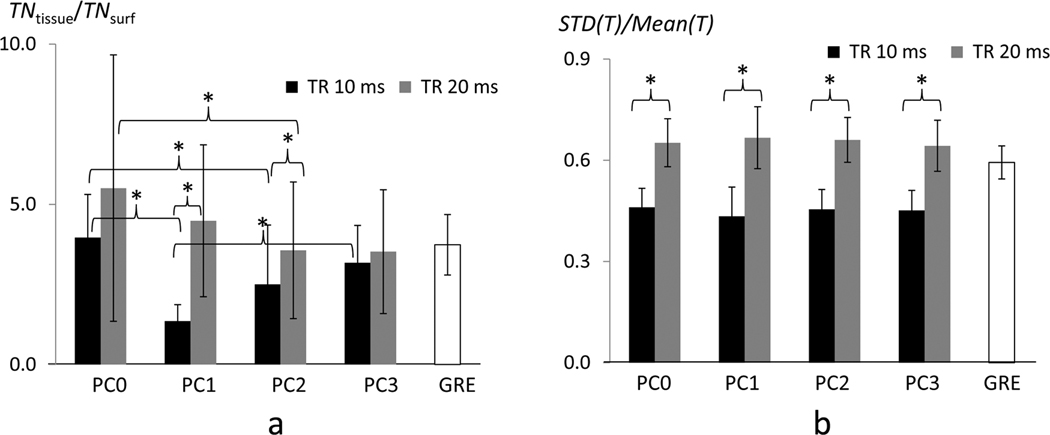
Quantitative ROI analysis is shown in Table 2 and Fig. 6. Generally, average T values of GRE in cortical area were lower than those of bSSFP with TR of 20 ms but higher than those of bSSFP with TR of 10 ms (Tmean in Table 2). Total number of activation pixels of bSSFP with TR of 20 ms was always higher than that of GRE (Nact in Table 2), implying that bSSFP has higher functional sensitivity than GRE of the matching parameters. When TR = 10 ms, average T values and Nact varied similarly with PC angle, while when TR = 20 ms no significant differences in the two sensitivity measures were observed between any PC angles for both ROIs (Table 2). The specificity measure of TNtissue/TNsurf (Fig. 6a) represented the sensitivity of the tissue region relative to the cortical surface region (i.e., large draining veins); hence a higher ratio indicated higher spatial specificity of the fMRI maps to the middle cortical regions. Another measure, normalized spatial variations of T values in the middle layer ROI (std(T)/mean(T), Fig. 6b), represented the blood vessel-induced pixel-by-pixel heterogeneity; hence a lower value indicated higher signal homogeneity. TNtissue/TNsurf values of bSSFP with TR = 20ms were higher (i.e., specificity was higher) and less heterogeneous among PC angles than those of bSSFP with TR = 10 ms, but similar to those of GRE fMRI (Fig. 6a). In contrast, std(T)/mean(T) was higher (i.e., homogeneity was lower) at TR = 20 ms than at TR = 10 ms. However, we could not observe variations in the index of std(T)/mean(T) across PC angles (Fig. 6b), in contrast to the variations in the other index (TNtissue/TNsurf) across PC angles (Fig. 6a).
Table 2.
Comparison of sensitivity and spatial specificity of functional signal changes in multiple phase-cycled bSSFP and GRE fMRI maps.
| Index | ROI | TE/TR = 5/10ms | TE/TR = 10/20ms | GRE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PC0 | PC1 | PC2 | PC3 | PC0 | PC1 | PC2 | PC3 | |||
| Tmean | Surf. | 3.5±0.5a | 4.1±0.7a,b | 3.7±0.8 | 3.2±0.2b | 4.6±0.8 | 5.0±0.7 | 5.3±1.0 | 5.2±0.9 | 4.9±0.7 |
| Tissue | 3.6±0.4 | 3.2±0.4 | 3.4±0.4 | 3.2±0.5 | 4.4±0.7 | 4.8±0.8 | 4.6±1.0 | 4.7±0.7 | 4.3±0.3 | |
| Nact | Surf. | 87±59 | 113±25c | 102±36d | 65±35c,d | 59±28 | 72±46 | 77±37 | 74±36 | 50±19 |
| Tissue | 278±105 | 192±60 | 225±70 | 190±80 | 235±20 | 263±49 | 264±61 | 252±110 | 195±49 | |
| TNtissue/TNsurf | 4.0±1.3e,f | 1.4±0.5e,g | 2.5±1.9f | 3.2±1.2g | 5.5±4.2h | 4.5±2.4 | 3.6±2.1h | 3.5±1.9 | 3.7±0.9 | |
| std(T)/mean(T) | .46±.06 | .43±.09 | .45±.06 | .45±.06 | .65±.07 | .67±.09 | .66±.07 | .64±.08 | .59±.05 | |
Average T values (Tmean), number of activation pixels (Nact), ratio of total fMRI sensitivities between tissue regions (Tissue) and cortical surface regions (Surf.) (TNtissue/TNsurf), and normalized standard deviation within a middle cortical layer (std(T)/mean(T)) are represented as mean ± standard deviation (n = 6) for GRE and bSSFP fMRI maps acquired at the four phase cycling (PC) angles of 0°, 90°, 180°, and 270° (PC0, PC1, PC2, and PC3, respectively) and the two TR values of 10 ms and 20 ms.
Statistically significant difference was observed between two values indicated by the same alphabetical superscript. Statistical test was performed among the four PC angles within the same TE/TR for each index and each ROI separately, with Wilcoxon signed rank test at the 0.05 level of significance. Statistical test between values from the two TE/TR conditions was performed for the indices of TNtissue/TNsurf and std(T)/mean(T). The results are shown in Fig. 6, but not in this Table for simplicity.
FIG. 6. Spatial specificity and homogeneity indices of four phase cycled bSSFP fMRI maps.
(a) Spatial specificity index determined as ratio of total fMRI sensitivities between tissue regions (Tissue) and cortical surface regions (Surf.) (TNtissue/TNsurf). (b) Homogeneity index determined as standard deviations divided by mean T values within the middle cortical ROI. The data are displayed for bSSFP fMRI maps with phase cycling (PC) angles of 0° (PC0), 90° (PC0), 180° (PC2), and 270° (PC3) and with TR = 10 ms and 20 ms, in comparison with GRE fMRI map. ‘*’ represents statistically significant difference (p < 0.05).
Functional MRI maps from FID, main echo, MIP, and NLA
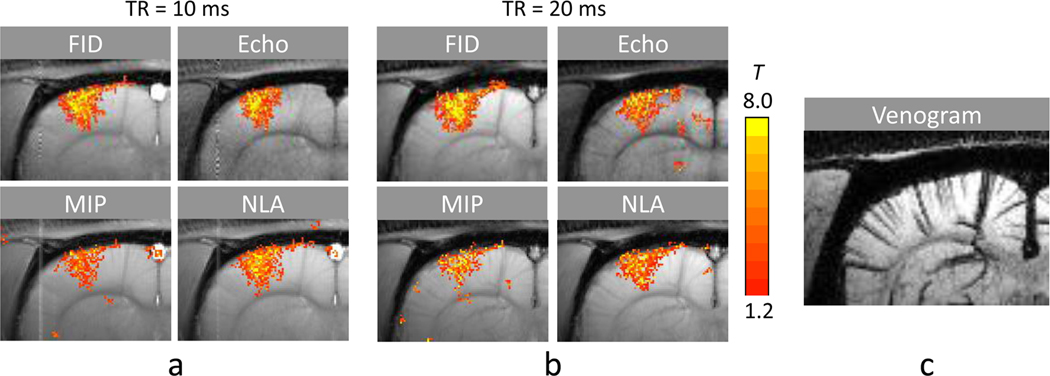
The multiple phase-cycled bSSFP datasets were reconstructed into images of FID and main echo components with Fourier analysis and also from MIP and NLA. The fMRI maps from the reconstructed images of a representative animal are shown in Fig. 7. The FID fMRI maps showed visually identifiable correlation with intracortical veins that was stronger than those from the main echo (Fig. 7) and bSSFP (Fig. 4a,b). These fMRI foci following the intracortical veins were visually less distinct in NLA and almost disappeared in MIP (Fig. 7).
FIG. 7.
Functional MRI maps of FID, main echo, maximum intensity projection (MIP), nonlinear averaging (NLA) signals extracted from the multiple phase cycled bSSFP fMRI datasets. The data were acquired with TE/TR = 5/10 ms (a) and 10/20 ms (b) from an animal different from those shown in Figs. 2 and 4–5. The FID and main echo components were extracted with Fourier analysis from bSSFP fMRI datasets acquired with phase cycling angles of 0°, 90°, 180°, and 270°. (c) BOLD venogram with minimum-intensity projection applied over the slab corresponding to the position of the fMRI maps for reference to fMRI maps shown in a and b.
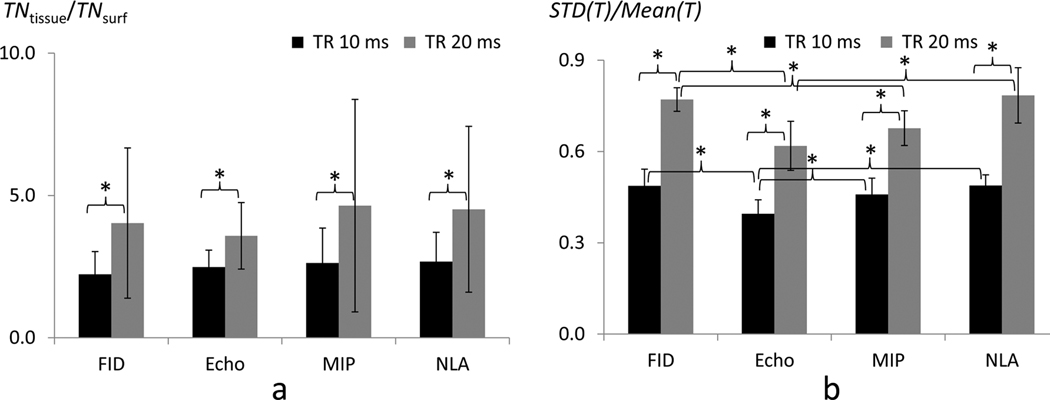
Average T values and number of activation pixels in the FID component were overall higher than those of the main echo component (Table 3). This demonstrates higher functional sensitivity of the FID component over the main echo component, which is consistent with theoretical baseline intensities (0.048 vs 0.034) shown in Fig. 3f,g. Functional sensitivity of NLA was similar to that of FID component, while that of MIP was between those of FID and main echo components (Table 3). For the specificity measure of TNtissue/TNsurf, no significant difference was observed across the fMRI maps from the four reconstruction methods (Fig. 8a). The normalized spatial variation (std(T)/mean(T)) of main echo component was generally lower (homogeneity was higher) than those of the other reconstructed images at both TR values (Fig. 8b and Table 3). The normalized spatial variation (std(T)/mean(T)) of MIP was also slightly lower than that of FID and NLA (Fig. 8b and Table 3).
Table 3.
Comparison of sensitivity and spatial specificity of functional signal changes in fMRI maps from FID and main echo components and from maximum intensity projection (MIP) and nonlinear averaging (NLA) reconstruction methods.
| Index | ROI | TR = 10ms | TR = 20ms | ||||||
|---|---|---|---|---|---|---|---|---|---|
| FID | Echo | MIP | NLA | FID | Echo | MIP | NLA | ||
| Tmean | Surf. | 4.2±0.8 | 3.5±0.5 | 3.8±0.5 | 4.5±0.8 | 5.1±1.2 | 4.2±0.8 | 5.2±1.0 | 5.6±1.3 |
| Tissue | 4.0±0.6a | 3.1±0.3a,b | 3.4±0.4 | 4.2±0.7b | 5.5±1.3 | 4.3±0.5 | 5.1±0.7 | 5.6±1.2 | |
| Nact | Surf. | 147±47c | 71±45c,d,e | 113±47d | 135±48e | 127±54f | 45±17f,g,h | 92±48g | 114±57h |
| Tissue | 320±58i | 194±64i,j,k | 291±74j | 348±65k | 393±80l | 163±77l,m,n | 315±67m | 397±71n | |
| TNtissue/TNsurf | 2.2±0.8 | 2.5±0.6 | 2.6±1.2 | 2.7±1.0 | 4.0±2.6 | 3.6±1.2 | 4.6±3.7 | 4.5±2.9 | |
| std(T)/mean(T) | .49±.05o | .40±.05o,p,q | .45±.05p | .49±.04q | .77±.04r,s | .62±.08r,t | .67±.06s | .78±.10t | |
The FID and main echo components are extracted with Fourier analysis from the bSSFP datasets acquired with the four phase cycling angles of 0°, 90°, 180°, and 270°. Average T values (Tmean), number of activation pixels (Nact), ratio of total fMRI sensitivities between tissue regions (Tissue) and cortical surface regions (Surf.) (TNtissue/TNsurf), and normalized standard deviation within a middle cortical layer (std(T)/mean(T)) are represented as mean ± standard deviation (n = 6).
Statistically significant difference (p < 0.05) was observed between two values indicated by the same alphabetical superscript. Statistical test was performed among the FID and main echo components, MIP, and NLA within the same TE/TR for each index and each ROI separately, with Wilcoxon signed rank test at the 0.05 level of significance. Statistical test between values from the two TE/TR conditions was performed for the indices of TNtissue/TNsurf and std(T)/mean(T). The results are shown in Fig. 8, but not in this Table for simplicity.
FIG. 8. Spatial specificity (a) and homogeneity (b) indices of FID, main echo, maximum intensity projection (MIP), and nonlinear averaging (NLA) signals.
Calculations for the two indices were performed in the same way as described in Fig. 6. ‘*’ represents statistically significant difference (p < 0.05).
Discussion
Sensitivity and Specificity of Pass-band (High Flip-Angle) bSSFP fMRI
The current study was to investigate signal characteristics of high flip-angle bSSFP fMRI maps at multiple PC angles. Sensitivity of high flip-angle bSSFP fMRI was higher than that of GRE fMRI of the matching parameters and the spatial distortion in these high-resolution bSSFP fMRI was minimal, indicating that high flip-angle bSSFP is a good alternative to EPI typically used for fMRI. Activation foci of bSSFP fMRI spatially shifted as a function of PC angle at both of the TR values, implying that signal sources of high-resolution high flip-angle bSSFP fMRI maps are spatially heterogeneous because of magnetic field inhomogeneity. Because of the dependence on the PC angle, the spatial heterogeneity of bSSFP fMRI signals is also expected to depend on shimming and local susceptibility effects, which are more severe at higher fields. However, the spatial heterogeneity might not be noticeable in the previous lower resolution fMRI studies at 3T (Miller et al., 2007; Zhong et al., 2007).
Although spatial shift of activation foci with PC angle was visually observable for bSSFP with both TR values, there were more significant PC-dependent variations in spatial specificity (TNtissue/TNsurf) at TR = 10 ms than at TR = 20 ms (Figs. 4 and 6a, Table 2). This might be due to flatter pass bands and steeper transition bands at TR = 10 ms than at TR = 20 ms (Fig. 3c,e). For instance, if functional activation induces a frequency shift of 20 Hz, the amount of phase shifts associated with the activation are 0.4π and 0.8π radian when TR = 10 and 20 ms, respectively. Associated with this phase shifts, magnitude changes of pixels in middle pass-band vs. middle transition-band (Fig. 3c,e) are 1.7% vs. 63% of the maximum baseline intensity at TR = 10 ms, and 32% vs. 53% at TR = 20 ms. This indicates that there will be much more significant spatial heterogeneity at TR = 10 ms than at TR = 20 ms and that stronger bSSFP fMRI signals will be observed in transition-band regions (than in pass-band regions) despite the lower baseline signal intensity, consistent with our experimental observations (Figs. 4–6 and Table 2). Using baseline transition-band bSSFP images, we may be able to choose a PC angle in high flip-angle bSSFP fMRI for minimizing signals of draining veins (cortical surface veins), at which the draining veins appeared as hypointense pixels in the corresponding baseline low flip-angle bSSFP images (e.g. PC3 in Fig. 5a,b). To find the appropriate PC angle, higher than 4 angular steps may be necessary depending on shimming and local susceptibility effects in regions of interest.
When magnetic field inhomogeneity is reduced by choosing a small middle cortical layer ROI, the homogeneity of bSSFP fMRI (std(T)/mean(T)) was better at shorter TR than longer TR. This result is opposite to that from the specificity index of TNtissue/TNsurf, but consistent with the implications from the previous bSSFP fMRI studies that T2 and T2* characteristics are dominant at shorter and longer TR values, respectively (Miller et al., 2007). The reason of small variations in std(T)/mean(T) across PC angles (Fig. 6b) is not clear. There were variations in std(T)/mean(T) across PC angles for individual animal, however, the correlation between the index and the baseline transition-band intensity across the PC angles was not significant (R < 0.3) (data not shown). We postulate that this may be due to the relatively small ROI, which results in a minimal variation of frequency shift among pixels at baseline and thus relatively homogeneous functional changes across PC angles.
In addition to the magnitude and phase responses of bSSFP, another factor that potentially affects spatial specificity of the bSSFP fMRI at ultrahigh field is short intravascular T2. Although it is often assumed that fractional BOLD fMRI signals linearly increase with TE, a previous study showed that the large-vessel intravascular signals can generate significant spin echo (T2 characteristics) fMRI signals at short TE at 9.4T (Jin et al., 2006). Our observation of relatively higher cortical surface signals in bSSFP fMRI at shorter TE/TR (T2 characteristics) might be partly attributed to contributions of the large-vessel intravascular signals in cortical surface regions. Since we used a single slice, inflow effects might also contribute to bSSFP fMRI signals. In bSSFP, inflow effects are complex but expected to be stronger at longer TR, because an inflow time is longer, while tissue intensity in pass-band regions does not change with TR (Fig. 3c,e). However, the cortical surface signals in bSSFP fMRI were lower at longer TE/TR, suggesting that contributions of inflow effects to the bSSFP fMRI signals at shorter TE/TR are minimal.
FID, Main Echo, MIP, and NLA of Multiple PC Pass-band (High Flip-Angle) bSSFP fMRI
To our knowledge, it is first time that bSSFP fMRI is performed at multiple PC angles and that Fourier analysis is performed for the multiple PC bSSFP fMRI to directly extract echoes of the multiple pathways. Multiple PC bSSFP fMRI enables us to extract various new fMRI maps. Contributions of FID component to bSSFP fMRI are dominant, which agrees with Zhong et al (Zhong et al., 2007), but contributions of main echo component are not negligible, which is consistent with Lee et al (Lee et al., 2009). The MIP and NLA visually reduced the fMRI signals in draining veins compared to FID component (Fig. 7), indicating that bSSFP fMRI of individual PC angle has certain tissue specificity and that there is room for manipulating sensitivity and specificity of bSSFP fMRI when acquired at multiple PC angles.
Conclusion and Implications for Human bSSFP fMRI studies
Magnetic field inhomogeneity in functional activation area would significantly affect the signal characteristics of bSSFP fMRI at high fields such as human 7T. The spatially heterogeneous signal characteristics of bSSFP fMRI induced by magnetic field inhomogeneity would be more prominent when TR is shorter, because of flatter pass bands and steeper transition bands. Acquisition of baseline transition-band bSSFP images helps to identify the location of pass and transition bands hence to understand corresponding bSSFP fMRI signals. Within a small middle cortical layer ROI where magnetic field inhomogeneity is relatively small, the homogeneity of bSSFP fMRI would be higher at shorter TR than longer TR. Multiple PC approach helps to understand signal characteristics of bSSFP fMRI in terms of magnetic field inhomogeneity and allows separating echoes from multiple pathways including FID and main echo. Many reconstruction methods for combination of multiple PC datasets also provide various fMRI maps, each of which can show slightly different sensitivity and specificity. Because of increased T1 / T2 ratio at high field, the optimal flip angle for pass-band-optimized bSSFP significantly decreased (~16° at 9.4T vs ~70° at 1.5T), in favor of reducing specific absorption rate which can be further reduced by employing longer TR values. In summary, high flip-angle (pass-band-optimized) balanced SSFP techniques would have advantages over the conventional EPI-based GRE fMRI techniques in terms of high sensitivity and minimal distortion.
Acknowledgments
The authors thank Drs. Kwan-Jin Jung and Timothy Q. Duong for discussion and Kristy Hendrich for 9.4T system management. This work was supported by NIH (EB003324, EB003375, and NS44589).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bandettini PA, Wong EC, Hinks RS, Tikofsky RS, Hyde JS. Time course EPI of human brain function during task activation. Magn Reson Med. 1992;25:390–397. doi: 10.1002/mrm.1910250220. [DOI] [PubMed] [Google Scholar]
- Bottomley PA. Spatial localization in NMR spectroscopy in vivo. Ann N Y Acad Sci. 1987;508:333–348. doi: 10.1111/j.1749-6632.1987.tb32915.x. [DOI] [PubMed] [Google Scholar]
- Bowen C, Mason J, Menon R, Gati J. High field balanced-SSFP fMRI: Examining a diffusion contrast mechanism using varied flip-angles. Proc Intl Soc Mag Reson Med. 2006:665. [Google Scholar]
- Bowen C, Menon R, Gati J. High field balanced-SSFP fRMI: a BOLD technique with excellent tissue sensitivity and superior large vessel suppression. Proc Intl Soc Mag Reson Med. 2005:119. [Google Scholar]
- Elliott AM, Bernstein MA, Ward HA, Lane J, Witte RJ. Nonlinear averaging reconstruction method for phase-cycle SSFP. Magn Reson Imaging. 2007;25:359–364. doi: 10.1016/j.mri.2006.09.013. [DOI] [PubMed] [Google Scholar]
- Jin T, Wang P, Tasker M, Zhao F, Kim SG. Source of nonlinearity in echo-time-dependent BOLD fMRI. Magn Reson Med. 2006;55:1281–1290. doi: 10.1002/mrm.20918. [DOI] [PubMed] [Google Scholar]
- Kim T, Hendrich KS, Masamoto K, Kim SG. Arterial versus total blood volume changes during neural activity-induced cerebral blood flow change: implication for BOLD fMRI. J Cereb Blood Flow Metab. 2007;27:1235–1247. doi: 10.1038/sj.jcbfm.9600429. [DOI] [PubMed] [Google Scholar]
- Kim T, Lee J, Pauly J. Analysis of the BOLD Signal Characteristics in balanced SSFP fMRI: a Monte-Carlo Simulation. Proc Intl Soc Mag Reson Med. 2007b:696. [Google Scholar]
- Kim T, Masamoto K, Fukuda M, Vazquez A, Kim SG. Frequency-dependent neural activity, CBF, and BOLD fMRI to somatosensory stimuli in isoflurane-anesthetized rats. Neuroimage. 2010;52:224–233. doi: 10.1016/j.neuroimage.2010.03.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwong KK, Belliveau JW, Chesler DA, Goldberg IE, Weisskoff RM, Poncelet BP, Kennedy DN, Hoppel BE, Cohen MS, Turner R, et al. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proc Natl Acad Sci U S A. 1992;89:5675–5679. doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee J, Fukunaga M, Duyn JH. Pass-Band Balanced SSFP FMRI at 7 Tesla. Proc Intl Soc Mag Reson Med. 2009;17:1553. [Google Scholar]
- Lee J, Santos JM, Conolly SM, Miller KL, Hargreaves BA, Pauly JM. Respiration-induced B0 field fluctuation compensation in balanced SSFP: real-time approach for transition-band SSFP fMRI. Magn Reson Med. 2006;55:1197–1201. doi: 10.1002/mrm.20879. [DOI] [PubMed] [Google Scholar]
- Lee J, Shahram M, Schwartzman A, Pauly JM. Complex data analysis in high-resolution SSFP fMRI. Magn Reson Med. 2007;57:905–917. doi: 10.1002/mrm.21195. [DOI] [PubMed] [Google Scholar]
- Lee JH, Dumoulin SO, Saritas EU, Glover GH, Wandell BA, Nishimura DG, Pauly JM. Full-brain coverage and high-resolution imaging capabilities of passband b-SSFP fMRI at 3T. Magn Reson Med. 2008;59:1099–1110. doi: 10.1002/mrm.21576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SP, Silva AC, Ugurbil K, Kim SG. Diffusion-weighted spin-echo fMRI at 9.4 T: microvascular/tissue contribution to BOLD signal changes. Magn Reson Med. 1999;42:919–928. doi: 10.1002/(sici)1522-2594(199911)42:5<919::aid-mrm12>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
- Masamoto K, Kim T, Fukuda M, Wang P, Kim SG. Relationship between neural, vascular, and BOLD signals in isoflurane-anesthetized rat somatosensory cortex. Cereb Cortex. 2007;17:942–950. doi: 10.1093/cercor/bhl005. [DOI] [PubMed] [Google Scholar]
- Miller KL, Hargreaves BA, Lee J, Ress D, deCharms RC, Pauly JM. Functional brain imaging using a blood oxygenation sensitive steady state. Magn Reson Med. 2003;50:675–683. doi: 10.1002/mrm.10602. [DOI] [PubMed] [Google Scholar]
- Miller KL, Jezzard P. Modeling SSFP functional MRI contrast in the brain. Magn Reson Med. 2008;60:661–673. doi: 10.1002/mrm.21690. [DOI] [PubMed] [Google Scholar]
- Miller KL, Smith SM, Jezzard P, Pauly JM. High-resolution FMRI at 1.5T using balanced SSFP. Magn Reson Med. 2006;55:161–170. doi: 10.1002/mrm.20753. [DOI] [PubMed] [Google Scholar]
- Miller KL, Smith SM, Jezzard P, Wiggins GC, Wiggins CJ. Signal and noise characteristics of SSFP FMRI: a comparison with GRE at multiple field strengths. Neuroimage. 2007;37:1227–1236. doi: 10.1016/j.neuroimage.2007.06.024. [DOI] [PubMed] [Google Scholar]
- Ogawa S, Menon RS, Tank DW, Kim S-G, Merkle H, Ellermann JM, Ugurbil K. Functional Brain Mapping by Blood Oxygenation Level-Dependent Contrast Magnetic Resonance Imaging. Biophys J. 1993;64:800–812. doi: 10.1016/S0006-3495(93)81441-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park SH, Masamoto K, Hendrich K, Kanno I, Kim SG. Imaging brain vasculature with BOLD microscopy: MR detection limits determined by in vivo two-photon microscopy. Magn Reson Med. 2008;59:855–865. doi: 10.1002/mrm.21573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patterson S, Beyea S, Bowen C. Quantification of the BOLD contrast mechanism, including its dynamic approach to steady state, for pass-band balanced-SSFP fMRI. Proc Intl Soc Mag Reson Med. 2008:2382. [Google Scholar]
- Reichenbach JR, Haacke EM. High-resolution BOLD venographic imaging: a window into brain function. NMR Biomed. 2001;14:453–467. doi: 10.1002/nbm.722. [DOI] [PubMed] [Google Scholar]
- Scheffler K, Hennig J. Is TrueFISP a gradient-echo or a spin-echo sequence? Magn Reson Med. 2003;49:395–397. doi: 10.1002/mrm.10351. [DOI] [PubMed] [Google Scholar]
- Scheffler K, Seifritz E, Bilecen D, Venkatesan R, Hennig J, Deimling M, Haacke EM. Detection of BOLD changes by means of a frequency-sensitive trueFISP technique: preliminary results. NMR Biomed. 2001;14:490–496. doi: 10.1002/nbm.726. [DOI] [PubMed] [Google Scholar]
- Silva AC, Lee SP, Yang G, Iadecola C, Kim SG. Simultaneous blood oxygenation level-dependent and cerebral blood flow functional magnetic resonance imaging during forepaw stimulation in the rat. J Cereb Blood Flow Metab. 1999;19:871–879. doi: 10.1097/00004647-199908000-00006. [DOI] [PubMed] [Google Scholar]
- Tsekos NV, Zhang F, Merkle H, Nagayama M, Iadecola C, Kim SG. Quantitative measurements of cerebral blood flow in rats using the FAIR technique: correlation with previous iodoantipyrine autoradiographic studies. Magn Reson Med. 1998;39:564–573. doi: 10.1002/mrm.1910390409. [DOI] [PubMed] [Google Scholar]
- Wu ML, Wu PH, Huang TY, Shih YY, Chou MC, Liu HS, Chung HW, Chen CY. Frequency stabilization using infinite impulse response filtering for SSFP fMRI at 3T. Magn Reson Med. 2007;57:369–379. doi: 10.1002/mrm.21138. [DOI] [PubMed] [Google Scholar]
- Zhong K, Leupold J, Hennig J, Speck O. Systematic investigation of balanced steadystate free precession for functional MRI in the human visual cortex at 3 Tesla. Magn Reson Med. 2007;57:67–73. doi: 10.1002/mrm.21103. [DOI] [PubMed] [Google Scholar]
- Zur Y, Wood ML, Neuringer LJ. Motion-insensitive, steady-state free precession imaging. Magn Reson Med. 1990;16:444–459. doi: 10.1002/mrm.1910160311. [DOI] [PubMed] [Google Scholar]