A Framework for Remediating Number Combination Deficits

Abstract

This article introduces a framework for the remediation of number combination (NC) deficits. Research on the remediation of NC deficits is summarized, and research program studies are used to illustrate the 3 approaches to remediation. The Framework comprises a 2-stage system of remediation. The less intensive stage implementing 1 of 3 intervention approaches hypothesized to be most productive for a student uses a validated protocol while monitoring student response. The more intensive stage, which is reserved for nonresponders, involves integrating the 3 intervention approaches within a skills-based diagnostic-prescriptive scheme for individualizing intervention.

Mathematics disability is widespread, affecting 5% to 9% of the school-age population (e.g., Shalev, Auer-bach, Manor, & Gross-Tsur, 2000), and the consequences associated with mathematics disability are serious. This is because mathematics competence accounts for variance in employment, income, and work productivity even after intelligence and reading have been explained (Rivera-Batiz, 1992). In the research literature, mathematics disability is operationalized as low mathematics performance and referred to as mathematics difficulty. In this article, we do the same, using the term mathematics difficulty (MD).

Because early mathematics skills are foundational as the mathematics curriculum advances, prompt remediation of key deficits is important to the treatment of MD. One critical aspect of mathematical cognition in the primary grades is simple arithmetic problems (e.g., 5 + 7= 12; 9 − 5 = 4), which are sometimes referred to as math facts or number combinations (NCs). Consensus exists that NC skill is essential (Kilpatrick, Swaf-ford, & Findell, 2001), and research shows that fluency with NCs is a significant path to procedural computation and word-problem performance (Fuchs et al., 2006). Moreover, difficulty retrieving NCs from long-term memory is one of the most consistent findings in the MD literature (e.g., Cirino, Ewing-Cobbs, Barnes, Fuchs, & Fletcher, 2007; Geary, Hoard, Byrd-Craven, Nugent, & Numtee, 2007; Jordan, Hanich, & Kaplan, 2003), prompting some to conclude that NCs represent a signature deficit for students with MD (e.g., Fleishner, Garnett, & Shepherd, 1982; Geary, Widaman, Little, & Cormier, 1987; Goldman, Pellegrino, & Mertz, 1988).

Given the salience of NC deficits for students with MD and the need for effective intervention, we propose a framework for considering die remediation of NC deficits. We begin by describing typical development and explaining how that breaks down for students with MD. We then introduce our Remediation Framework, explaining how it links conceptually to the development of NC skill in typical students and considering the hierarchical nature of the Framework's three approaches to intervention. Next, we summarize research on the remediation of NC deficits, using studies from our research program to illustrate the three approaches to remediation. After integrating study findings and drawing conclusions, we complete description of the Framework by incorporating a two-stage system of remediation.

DEVELOPMENT OF NC SKILL

In developing competence with NCs, typically developing children gradually gain efficiency with counting strategies. When adding, children initially count two sets (e.g., 2 + 3) in their entirety (i.e., 1, 2, 3, 4, 5). This is referred to as the sum counting strategy (or counting alt). As they discover the number-after principle reflected in counting, children realize that the sum of 5 + 1 is the number that occurs after 5 when counting (Baroody, 1995). Fluent number-after knowledge makes 1 + n/n + 1 NCs among die easiest to learn (Baroody, 1995). The rule for adding 1 provides developmental scaffold for more abstract, sophisticated counting-on strategies: Once children recognize that the sum of 5 + 1 is the number after 5 in the counting sequence, they understand that the sum of 5 + 2 cannot be 6 but instead is two numbers past 5: 6, 7 (Baroody, 1995). In this way, children discover the efficiency of counting up from the first addend. When the smaller addend occurs first, as in 2 + 3, they begin counting from the smaller addend (i.e., 2, 3, 4, 5), using the max strategy. Eventually, as they come to understand the commutative property of addition, they discover the most efficient min counting strategy—counting from the larger addend (i.e., 3, 4, 5), regardless of whedier the larger addend appears first or second.

As conceptual knowledge about number becomes more sophisticated, children discover the additive identity property of zero and can therefore answer NCs represented by n + 0/0 + n. Also, children learn that a whole can be decomposed into parts in different ways, and this big idea sets the stage for decomposition strategies to derive answers (e.g., 2 + 3 = [2 + 2 = 4] + 1 = 5). As increasingly efficient counting and decomposition strategies help students consistently and quickly pair problems with correct answers in working memory, associations become established in long-term memory, and children gradually favor memory-based retrieval of answers (Ashcraft & Stazyk, 1981; Geary et al, 1987; Goldman et al, 1988; Groen & Parkman, 1972; Siegler, 1987).

Eventually, in developing a formal part-whole understanding of addition, students discover the meaning of missing-addend expressions (e.g., for 2 + ? = 5, 2 is the known part; ? represents the unknown part; 5 indicates the whole, which must be larger than either part). This not only promotes skill with addition NCs, but also helps children discover the missing-addend counting strategy for subtraction (e.g., for 5 − 3 = ?, 3 is the known part; 5 is the whole; counting from 3 to 5, i.e., 4, 5, reveals how many are in the other, unknown part; Baroody, 1995). Also, as children develop understanding of the relationship between subtraction and addition (Baroody, 1999; Baroody, Ginsburg, & Waxman, 1983), knowledge of addition NCs facilitates knowledge of subtraction NCs.

Research (e.g., Ashcraft & Stazyk, 1981; Geary et al., 1987; Goldman et al., 1988; Groen & Parkman, 1972; Siegler, 1987) documents that competent NC performance involves a mix of strategies, with counting strategies and decomposition strategies serving as back-ups for primary reliance on memory-based retrieval. In fact, individuals, even adults, use varying strategies at different times to solve the same NC. Although the extent to which counting strategies, decomposition strategies, and memory-based retrieval are explicitly addressed in general education varies (Miller & Hudson, 2007), typical students nonetheless become relatively adept with NCs by the end of third grade (Cirino et al., 2007).

Students with MD, by contrast, fail to make the shift to memory-based retrieval (Fleishner et al., 1982; Geary et al., 1987; Goldman et al., 1988). This failure occurs because students with MD have compromised number sense (e.g., Geary, Hamson, & Hoard, 2000) and greater difficulty with counting (e.g., Geary, Bow-Thomas, & Yao, 1992; Geary et al., 2007). Perhaps as a result, they persist widi immature counting strategies (i.e., the sum and max strategies) and fail to develop decomposition strategies. When children with MD do retrieve answers from memory, they commit more errors and their retrieval speeds are less systematic than younger, typically developing counterparts (e.g., Geary et al., 2007; Geary, Brown, & Samaranayake, 1991; Ostad, 1997).

OUR FRAMEWORK FOR REMEDIATING NC DEFICITS

The course of typical development and the corresponding difficulty students with MD experience suggest some productive approaches for remediating NC deficits. Depending on the student's understanding of basic number concepts when remediation begins, typical development highlights the importance of integrating a foundational focus on number concepts within any approach to intervention, including number–after knowledge, the commutative property of addition, the additive identity property of zero, the notion that a whole can be decomposed into parts in different ways, and the relationship between subtraction and addition. Yet, given the difficulty students with MD experience with implicit approaches to instruction (Kroesbergen, Van Luit, & Maas, 2004), it is unlikely that an exclusive focus on foundational number concepts will result in students discovering efficient counting strategies or decomposition strategies that lead to reliance on automatic retrieval. Therefore, in addition to a focus on number concepts, typical development suggests three major approaches to the remediation of NC deficits.

One approach is instruction on counting strategies, which is linked to typical students' earliest achievements related to NC skill, whereby children become increasingly knowledgeable about counting and eventually derive and depend on the most efficient counting strategies for solving addition and subtraction NCs. Another approach to intervention is designed to build understanding of part-whole relationships and teach the decomposition strategies typically developing students eventually discover and use to supplement counting strategies. A third intervention approach addresses the most efficient strategy and the ultimate accomplishment related to NC skill, whereby typical children rely heavily on memory-based retrieval of answers. As discussed, memory-based retrieval is facilitated in typical development as increasingly efficient counting and decomposition strategies help children consistently and quickly pair problems with correct answers in working memory. This creates associations in long-term memory. The third approach to intervention therefore involves drill and practice. The goal of remedial drill and practice is for students with MD to rehearse correct pairings. In remediation, it is sometimes designed as an alternative path to automatic retrieval, circumventing typical students' route to representations in long-term memory via correct pairings that occur with counting and decomposition strategies.

In our Remediation Framework, we conceptualize these three intervention approaches as a hierarchy that reflects the sequence by which typical children acquire the three related strategies. The lowest rung of the hierarchy is counting strategies; typical children discover these before they develop decomposition strategies or automatic retrieval. Counting strategies may, therefore, be easiest for students with MD to learn, although it is unclear whether acquisition of counting strategies among students with MD will promote automatic retrieval (as students successfully pair question stems with answers) or more simply will improve accuracy and perhaps fluency. The next most demanding intervention approach according to the developmental sequence is decomposition strategies. Again, it is unclear whether decomposition strategies in students with MD contribute to automatic retrieval or simply improve accuracy. The most challenging approach according to the developmental sequence is to proceed directly to drill and practice, which requires students to commit NCs to long-term memory through the repeated pairings that the drill and practice fosters. In the next section, we review the literature on the remediation of NC deficits, while considering and illustrating the three intervention approaches that constitute our Framework.

RESEARCH ON THE REMEDIATION OF NC DEFICITS

In this review, we discuss studies on the remediation of NC deficits in relation to our proposed Framework. We describe studies, beginning with relatively early investigations and proceeding to our more recent four-study research program. For the early studies, which focus predominantly on drill and practice, we summarize findings and limitations. For the more recent studies, we provide more detail, illustrating the three approaches to remediation by describing the interventions tested in those efficacy studies.

Earlier Studies

In the literature, the major method for remediating NC deficits relies on the third and most demanding intervention approach within our Framework: drill and practice. The participants in these early studies were students with school-identified learning disabilities. Working with 160 students ages 7 to 14, Hasselbring, Goin, and Bransford (1988) showed that students who received computerized drill and practice improved NC performance over the control group, and maintenance was demonstrated over 4 months. It was unclear whether random assignment was used. Okolo (1992) and Christensen and Gerber (1990) contrasted computerized drill and practice in a game-like format against unadorned computerized drill and practice. Okolo found no significant differences between groups, but students in the Christensen and Gerber study were disadvantaged by the game-like format, perhaps due to its distracting nature. Neither investigation, however, incorporated a control group to assess whether computer-assisted instruction promoted better outcomes than might be expected via business as usual.

Also without a control group, this time with 8- to 10-year-old students, Tournaki (2003) moved beyond drill and practice to contrast two intervention approaches within our Framework: instruction on counting strategies versus drill and practice (this time, delivered via paper-pencil). Results favored counting strategies; however, the practice condition provided students feedback on a delayed schedule, without deliberately mixing known with unknown NCs and without systematic review of mastered NCs. By contrast, counting strategies instruction incorporated immediate corrective feedback and re-teaching whenever an error occurred. So it is unclear whether better outcomes were attributable to counting strategies or to generally stronger instruction.

This older research base is largely limited to the drill and practice approach in our Framework. Moreover, most studies fail to provide the basis for determining whether remediation promotes better progress than would be expected with business as usual. Also, because learning disabilities were school-identified, it is unclear whether effects apply specifically to students with MD; participants may have been identified as having learning disabilities primarily due to reading problems.

More Recent Research

Focus of Our Research Program

More recently, we undertook a four-study program of research to extend prior work by addressing a greater variety of approaches to remediation. In addition, we relied on random assignment, included control conditions, screened students into studies to confirm that participants in fact experienced MD, and incorporated multiple sites by which to judge the transportability of the remediations.

We were also interested in whether the efficacy of remediation differs as a function of whether MD occurs alone or in combination with reading difficulty (MDRD), a scheme proposed by Geary (1993) for subtyping MD. Because a key deficit among students with reading difficulty is phonological processing (e.g., Bruck, 1992) and because phonological processing is linked to automatic retrieval of NCs (Geary), MDRD students may have greater difficulty with NCs than students with MD. Research is, however, inconsistent. Fuchs et al. (2005) found support for phonological processing as a predictor of NC skill across first grade when initial reading skill was controlled. By contrast, Hecht, Torgesen, Wagner, and Rashotte (2001) found no evidence at Grades 4 and 5, and Swanson and Beebe-Frankenberger (2004) identified reading, not the phonological loop, as a correlate of calculation skill among first through third graders. Research does show that students with MD-only use more efficient counting strategies to answer NCs (Geary et al., 2000; Geary et al., 2007; Jordan & Hanich, 2000) and perform better on untimed (but not timed) NC tasks (Andersson & Lyxell, 2007; Hanich, Jordan, Kaplan, & Dick, 2001; Jordan & Montani, 1997). Yet, Micallef and Prior (2004) and Reikeras (2006) found comparable performance even when time was unconstrained. In our intervention research program, we adopted a different approach for studying this issue. Stratifying on MD subtype, we randomly assigned students to treatment and control conditions, and found only limited evidence that the subtypes respond differentially to intervention. In this article, we comment on this aspect of the research program only as it relates to the study where MD subtype mattered.

Commonalities Across Studies

Important methodological commonalities exist across the four studies, each of which was conducted in a separate year with a different sample. All participants were third graders. We focused on third grade because typical students are relatively adept with NCs by the end of third grade (Cirino et al., 2007); therefore, when students still manifest substantial difficulty with NCs at third grade, remediation is warranted.

Recruitment, testing, and remediation occurred in local public schools. Study entry criteria required students to perform below the 26th percentile on the Wide Range Achievement Test (WRAT; Wilkinson, 1993)-Arithmetic; when word problems were also targeted for remediation, students could also qualify based on low word-problem performance. We selected this cut-point for low math performance (< 26th percentile) because of its frequent use in the MD literature. Students who met the mathematics entry criterion were also screened on WRAT-Reading (Wilkinson) and on the two-subtest Wechsler Abbreviated Scale of Intelligence (WASI; Weschler, 1999). We excluded students who scored between the 25th and 40th percentiles on WRAT-Reading to create a buffer zone between students with and without reading difficulty. Students scoring below the 26th percentile on the reading measure were designated as MDRD. Those scoring at or above the 40th percentile on reading were classified as MD-only. We also excluded students with a T-score below 30 on both IQ subtests because our interest was not in mental retardation. Mean standard scores for Studies 1 to 4, respectively, were 86, 86, 88, and 85 for MD-only and 82, 79, 81, and 80 for MDRD on WRAT-Arithmetic; 105, 108, 105, 103 for MD-only and 82, 80, 78, and 78 for MDRD on WRAT-Reading; and 94, 97, 92, and 91 for MD-only and 87, 84, 85, and 84 for MDRD on WASI IQ.

Each year, approximately half the participants were recruited and received remediation in Nashville; the other half, in Houston. At each site, all remediation sessions were audiotaped. We sampled tapes to represent sites, conditions, MD subtypes, and tutors comparably and coded tapes to reflect the fidelity to the remediation protocols. In each study, fidelity was high (> 95% of elements implemented) at both sites, for all remediation conditions, and for both MD subtypes. In terms of outcomes, there were no interactions between remediation efficacy and site. Thus, if training occurs as in the research program (i.e., 1 to 2 full days of tutor training along with ongoing supervision to use the tutoring materials with fidelity), the remediations appear transportable.

The next commonality across studies concerns how students were assigned to study conditions. Blocking on site, MD status (MD-only or MDRD), and type of screening difficulty when applicable (word problems, calculations, or both), we randomly assigned students to conditions. In all studies, the only demographic and pretreatment skill differences between students with MD-only versus MDRD were expected based on prior work (e.g., MDRD students had more severe mathematics deficits or were more likely to repeat a grade or to receive special education). Students were comparable on demographics and on IQ, reading, and mathematics pretreatment performance as a function of treatment conditions.

Finally, for each construct, we used the same outcome measures in each study. This facilitated comparisons across studies. When remediation focused on NCs, the outcome measures involved NC fluency and procedural calculations (i.e., two-digit computation problems with and without regrouping). In later studies, where we simultaneously addressed the remediation of NC and word-problem deficits, we also included outcomes relevant to word-problem remediation (i.e., word-problem skill and algebraic cognition).

Overview of the Four Studies

Across the four studies, we investigated the three approaches to intervention comprising our Remediation Framework. In Study 1 (Fuchs et al., 2008), we examined the effects of drill and practice to instantiate NCs in long-term memory. In Study 2 (Powell, Fuchs, Fuchs, Cirino, & Fletcher, 2009), we explored whether conceptual instruction focusing on decomposition strategies might impart added value over drill and practice. In Study 3 (Fuchs, Powell, Seethaler, Cirino, Fletcher, Fuchs, et al., 2009), we turned our attention to counting strategies for deriving answers to NCs. In Study 4 (Fuchs, Powell, Seethaler, Cirino, Fletcher, Fuchs, Hamlett, et al., in press), we assessed the effects of counting strategies remediation with and without brief but deliberate practice. The remediation protocols also incorporated, to varying degrees, a focus on the number concepts foundational to NC skill. Table 1 presents remediation components by study condition; Table 2 provides a list of study conditions and a summary of major findings.

TABLE 1.

Study Descriptions of Remediations

Study	Major Focus	NCs Content/Organization	Computerized Practice	Flash Card Practicea	Conceptual Instruction on NCs	Counting Strategies	Paper-Pencil Review	Embedded in Word-Problem Remediation
Study 1	Practice	122 NCs in 31 families (4 facts to a family, excluding NCs with +/−0 or +/−1; first family 6/4/2), organized from easiest (smaller sums) to hardest (bigger sums, ending with a sum of 18).	Math Flash A; mastery determined coverage; each session mixed lowest non-mastered family plus mastered family that took fewest days to master.	Type 1: Traditional (2 min) Type 2 (after mastery of Type 1): Generate number sentences for visual representations of number lines (2 min)	Number line representations during computerized practice and Type 2 flash cards	No	15 NCs (2 min)	No
Study 2	Practice	See Study 1.	See Study 1.	Type 1	See Study 1.	See Study 1.	See Study 1.	No
	Conceptual instruction on decomposition strategies	Organized as sets (all NCs with the same sum/minuend) beginning with 10 and moving to NCs that can be decomposed in relation to the 10 set and in relation to doubles (11 set, 9 set, 8 set, 12 set, 13 set, etc.).	Math Flash B; predetermined sequence of families, aligned with conceptual instruction, determined coverage. 8 NCs assigned to each session.	Type 2	Lessons with number line and blocks to emphasize decomposition strategies in relation to the 10 set and in relation to doubles.	No	15 NCs (2 min) Generate number sentences within a family (1 min)
Study 3	Counting-up	200 NCs in sets organized for greater efficiency.	Math Flash C; mastery determined pace through NCs sets with automatic advancement to next set if not mastered after 4 sessions; 10 lesson-specific NCs and 10 mixed NCs (randomly sampled from 200).	Type 1: Traditional with sample of 200 NCs (2 min) Type 2: Lesson-specific NCs (1 min with another min to beat score)	Lessons with number line and manipulatives to correspond to NCset	Min strategy for +; Missing addend strategy for −; strategic instruction in each session; error correction is counting up for all activities except computerized practice.	15 lesson-specific NCs (1 min) 15 review NCs (1 min)	No
	Word problems with minimal focus on NCs	See Study 3 (counting-up).	None	Traditional with sample of 200 NCs (2 min)	None	Min/missing addend strategies; 1 session of instruction only; error correction is counring-up for flash cards, paper-pencil review, and within word problems.	10 NCs, 2 double-digit without regrouping and 2 double-digit with regrouping (2 min)	Yes
Study 4	Counting-up with practice in counting-up	See Study 3.	None	Traditional with sample of 200 NCs (1 min with another min to beat score)	None	Min/missing addend strategies; 1 session of instruction only; error correction is counting-up except for paper-pencil review where tutor demonstrates counting-up. Review of counting-up strategies in each session.	Algebraic equations and word problems	Yes
	Single counting-up lesson	Not applicable	None	None	None	Min/missing addend strategies; 1 instructional session; no review; error correction is provision of correct answer.	Algebraic equations and word problems	Yes

Note. NCs = number combinations.

^aTraditional is vertical presentation of problem; student says answers.

TABLE 2.

Research Program Study Conditions and Findings

Study	Conditions and Findings
Study 1	(1) NCs: drill and practice
	(2) Procedural calculations: regrouping concepts, algorithms, estimation
	(3) NCs plus procedural calculations
	(4) Control (word identification)
	Across MD and MDRD: on NCs, (1) = (3) > (2) = (4); no evidence of transfer
Study 2	(1) NCs: drill and practice
	(2) NCs: conceptual/decomposition strategies
	(3) Procedural calculations: regrouping concepts, algorithms, estimation
	(4) Control (no tutoring)
	For MD: on NCs, (1) = (2) > (3) = (4); no evidence of transfer
	For MDRD: on NCs, no differences
Study 3	(1) NCs: counting strategies plus drill and practice
	(2) NCs: counting strategies embedded within word-problem remediation
	(3) Control (no tutoring)
	Across MD and MDRD: on NCs, (1) = (2) > (3); evidence of transfer to procedural calculations; on word problems, (3) > (1) = (2)
Study 4	(1) NCs: counting strategies with brief but deliberate practice, embedded within word-problem remediation
	(2) NCs: counting strategies without deliberate practice, embedded within word-problem remediation
	(3) Control (no tutoring) Across MD and MDRD: on NCs, (1) > (2) > (3); evidence of transfer to procedural calculations; on word problems, (3) > (1) = (2)

Note. NCs = number combinations; MD = mathematics difficulty; MDRD = mathematics difficulty plus reading difficulty.

Study 1: Drill and Practice to Instantiate NCs in Long-Term Memory

In the initial study, our approach to remediation mirrored the approach that dominated earlier work—drill and practice—but differed from prior work in two ways. First, it incorporated a focus on number concepts. Second, instead of simply requiring students to answer NCs, we tried to increase the probability that students would practice responses that were correct. Toward this end, for each computerized drill and practice trial, students saw a complete NC “flash” briefly; stored the question stem with its answer in short-term memory; and then reproduced the complete NC from short-term memory. Our assumption was that repeated pairings of a question stem and its correct answer would help students commit the NC to long-term memory. Typically developing students commit NCs to long-term memory through repeated pairings, but those repeated pairings occur naturally with development of efficient counting and back-up strategies. Given the deficiencies of students with MD with counting and decomposition strategies, we tested the efficacy of the “direct route” for the reliable and efficient pairings just described, relying primarily on computerized practice. A tutor supervised all sessions, ensuring correct and attentive use of the software; the tutor also answered questions, provided encouragement, and conducted supplementary practice activities.

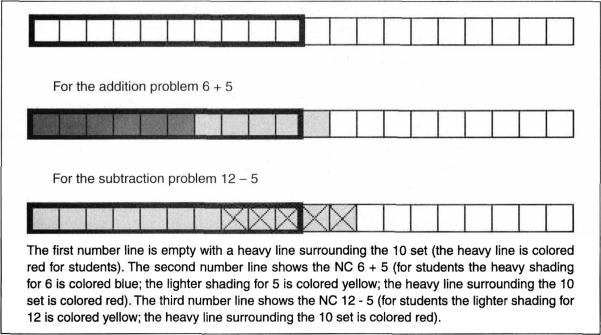
Three assumptions guided the design of our software, Math Flash (Fuchs, Hamlett, & Powell, 2007). The first assumption was that repeated pairings of a problem stem with its answer in short-term memory should help students commit NCs to long-term memory for automatic retrieval. Based on this assumption, the computer briefly “flashes” a complete addition or subtraction NC (with both operands and the answer) on the screen for 1.3 sec. The NC is presented vertically, because this represents the most frequent application to procedural calculations. When the NC disappears from the screen, the student types the complete NC from short-term memory; that is, the student has to remember both operands and the answer.

Our second assumption was that conceptual understanding would facilitate development of NC representations in long-term memory. We therefore displayed a number line depicting the NC at the top of the computer screen. This number line includes 20 uncolored boxes, with a red line denoting the perimeter of the first 10 boxes. As the student types the first addend, boxes on the number line automatically turn blue to represent the quantity; as the student types the second addend, boxes on the number line automatically shade yellow to signify that quantity. As the student types the minuend of a subtraction problem, boxes on the number line automatically turn yellow to represent the quantity; as the student types the subtrahend, black Xs are drawn through yellow boxes to represent the removal of that quantity. (We also included a flash card activity to reinforce the number line representations of NCs.)

Our third assumption was that reinforcing correct responses and providing performance feedback would motivate student interest and hard work, important because we targeted students who were experiencing failure with mathematics. We therefore incorporated the following features into Math Flash. If the student types the NC correctly, a numeral from 1 to 5 sparkles, and the student hears applause. After the first correct response, the numeral 1 sparkles; after the second correct response, the numeral 2 sparkles; and so on until five correct responses accumulate, at which point a picture of a “treasure” (e.g., a puppy or cake) drops into the “treasure box.” Then the count from 1 to 5 begins again, with a new “treasure” deposited into the treasure box after every five correct responses (no concrete rewards are provided). For an incorrect response, the NC reappears and remains on the screen while the student types the NC correctly (without sparkling numbers or applause). The session lasts 7.5 min. Applause sounds while the student's score for that session and the student's all-time high score are displayed.

The version of Math Flash used in the Year 1 study (Math Flash A) organized 122 NCs into 31 “families” to emphasize the conceptual relationships among numbers. A family comprised addition and subtraction NCs that involved the same three numbers. We excluded families with 1 or 0. Families with smaller sums/minuends were addressed first; those involving larger sums/minuends were covered later. For each family, the computer recorded (a) if the family was mastered and (b) how many days the student had worked on that family. At the start of each session, the computer selected (a) the easiest nonmastered family and (b) the mastered family on which the student had worked the fewest number of days. NCs from these families were randomly mixed for presentation. At the end of each session, mastery on the nonmastered family was determined and saved in the student's file. Mastery was defined as at least three of four NCs in the family learned. For a NC in a family to be deemed learned, the student had to attempt the NC at least twice. If the student had attempted the NC only twice, both attempts had to be correct. If the student had attempted the NC more than twice and made no more than one error, the NC was deemed learned. Mastery was also assessed on the already mastered family, and previously mastered families were returned to nonmastered status using the same criteria.

The major focus of Study 1's remediation was computerized drill and practice with a conceptual focus on number concepts embedded within that practice. Computerized practice lasted 7.5 min per session. To reinforce computerized practice, we also included 4 min of flash card practice with corrective feedback and 4 min of paper-pencil cumulative review with corrective feedback, for a total of 15 to 18 min per session. The tutor conducted these activities. Flash card practice included two types of flash cards. The first type showed traditional flash cards: NCs presented in vertical format, without answers. The student responded by saying answers, with 2 min to respond to as many cards as possible. The student graphed the number correct. After three consecutive sessions with at least 35 correct responses, practice with the second type of flash cards substituted for the traditional flash cards. The student was presented with a number line illustrating an NC (as represented on the Math Flash software screen). The student stated the NC represented by the number line, with 2 min to respond to as many cards as possible. The student graphed the number correct. With each type of flash card, the tutor corrected up to 5 incorrect responses. The final activity was paper-pencil cumulative review. The student had 2 min to complete 15 NCs on paper with corrective feedback.

In Study 1, we contrasted this drill and practice NC remediation to a word-identification control group and to competing remediation conditions that focused on different aspects of math: procedural calculations remediation and a combined drill and practice NC plus procedural calculations remediation. Each of the four conditions involved tutor-supervised computer-assisted instruction, followed by tutor-led activities. Word identification computerized practice was identical to Math Flash but the flashing stimuli were words; the follow-up activity was repeated reading of passages. With procedural calculations computer-assisted instruction, students focused on a single procedural calculation problem each session, completing three activities: the first to foster conceptual understanding about regrouping, the second to help students verbalize an efficient procedure for completing procedural calculations, and the third to foster estimation of procedural calculation problems. Follow-up involved manipulative activities and paper-pencil practice.

Remediation on word identification and on procedural calculations produced no benefit on NC outcomes. However, students who received NC remediation outperformed those in the procedural calculations condition and in the word identification condition. Effect sizes were moderate to large (0.69–0.78). We found no evidence that improvement in NC skill transferred to procedural calculation or to word-problem outcomes. We concluded that NC remediation that focused largely on drill and practice but also incorporated foundational focus on number concepts was efficacious for students with MD. This suggests that a focus on counting and decomposition strategies might be circumvented in instantiating NCs to long-term memory for automatic retrieval. Even so, we were concerned that the mastery criteria embedded in Math Flash A, which determined students' advancement through NCs, resulted in poor content coverage. Due to slow mastery, many students were exposed only to easy NCs. Also, we questioned whether a stronger focus on the conceptual underpinnings of NCs, as per our Remediation Framework, might enhance learning. With this concern and this question in mind, we reformulated remediation for Study 2.

Study 2: Conceptual Instruction Emphasizing Decomposition Strategies; Added Value?

In Study 2, we contrasted two approaches from our Remediation Framework. The first was similar to Study 1, where the major emphasis was on drill and practice in pairing question stems with answers—although, as in Study 1, students viewed number line representations during computerized practice. We refer to this condition as drill and practice, for which we made only one change from Study 1: We eliminated the number line flash card activity. In Study 1, we had hoped that students would discover decomposition strategies as a function of the number line representations on the computer and in the number line flash card activity. In Study 2's conceptual decomposition strategies plus drill and practice condition, tutors instead explicitly taught decomposition strategies in relation to the 10 set and in relation to doubles. Five activities comprised the conceptual decomposition strategies condition. Each session began with the same 2-min flash card warm-up as in the drill and practice condition.

Second (and more to the heart of the conceptual decomposition strategies condition), tutors conducted conceptual lessons using the number line and blocks to focus on number-after knowledge, the commutative property of addition, the additive identity property of zero, the notion that a whole can be decomposed into parts in different ways, and the relationship between subtraction and addition. The foci of the initial conceptual lessons were addition and subtraction concepts and adding/subtracting 0 and 1. Tutor-directed lessons accompanied the introduction of a new NC family (i.e., every third to sixth day). In these lessons, the tutor focused on how number sentences within the set were related. They used number lines and blocks superimposed on a mat with a red line denoting a set of 10 to teach strategies for decomposition in relation to the 10 set. Concrete manipulations mirrored the number line representation on the computer screen and in the flash card activity: Blue and yellow blocks along with a red box on a number line mat reflected the representation on the computer screen and in the flash card activity (see Figure 1). With tutor supervision, students experimented with constituting sets for a given NC in multiple ways. We also taught the commutative property, as well as the relationship between addition and subtraction. With introduction of the NC 10 set, the tutor drew the student's attention to the red box, emphasizing how all NCs of 10 fell exactly within the red box. The introduction of subsequent NC families (e.g., 11, 12, 9, 8, etc.) emphasized decomposition in relation to 10 (e.g., 11−3 = [10 + 1] − 3 = [10 − 3] + 1 = 8). We also addressed decomposition strategies in relation to the doubles sets (e.g., 2 + 3 = 2 +[2+1] = [2+ 2]+ 1=4 + 1 = 5) using similar methods to teach students strategies to capitalize on their knowledge of doubles. We limited decomposition strategies in relation to 10 and doubles to anchor these strategies to sets that were most familiar.

FIGURE 1.

Sample Number Lines Showing NCs in Relation to the 10 Set

The third activity was number-line flash cards, in which students had 2 min to derive equations for number-line depictions of NCs. The fourth activity was the Math Flash computerized drill and practice. The final activity was the same pencil-paper review as in the drill and practice condition. In the conceptual condition, however, we also included a task that required students to generate NCs for a given set within 1 min.

One other major difference distinguished the two remediation conditions in Study 2. For the conceptual decomposition plus drill and practice condition, we modified the manner in which the NCs were incorporated in computerized drill and practice. In Math Flash B, there were no decisions about when NCs were mastered. This addressed our concern from Study 1 that students spent too much time on easy NCs, receiving inadequate content coverage. Also, this allowed tutors to co-ordinate off-computer instruction better with computerized practice. Toward that end, Math Flash B used a predetermined list of NCs, widi eight NCs assigned to each session. These NCs represented NCs in the set the student was working on conceptually with the tutor. A set included the NCs that had the same number (e.g., 10) as the sum or the minuend (e.g., 9 + 1 = 10, 8 + 2 = 10, 10 − 1 = 9, 10 − 2 = 8, etc.). At the beginning of the session, the tutor entered the day number, and the computer retrieved that day's eight NCs.

In Study 2, there were four conditions: the two NC remediations just described (drill and practice; conceptual decomposition plus drill and practice); procedural calculations (as in Study 1); and control (no remediation). Interestingly, effect sizes comparing each NC remediation to the control condition were similar: 0.50 and 0.53. The same was true when comparing each NC remediation to the procedural calculations remediation: 0.31 and 0.37. The effect size comparing the two NC remediations was a minimal 0.08 but did favor conceptual. This suggests that explicit conceptual instruction to help students develop decomposition strategies for solving NCs (along with broader content coverage) does not impart added value over drill and practice for third graders with MD. Of course, this finding depends on the manner in which we operationalized decomposition strategies in this study, and additional research is warranted.

Even so, findings were not that straightforward. This was the only study in the four-study research program where remediation effects were moderated by MD status. MD-only students in the two NC conditions significantly outperformed MD-only students in the two contrast groups without NC remediation (procedural computations/estimation remediation and control). For MD-only students, effect sizes comparing practice or conceptual remediation against procedural computation/estimation remediation (which controlled for instructional time) were 1.11 and 0.96, respectively. When compared to the control group, effect sizes for the two NC conditions were 1.50 and 1.19. (There were no differences between the two NC remediations, again indicating that the conceptual treatment had no added value over the intensive drill and practice condition.) In contrast to the significant and large effects for MD-only students, there were no significant differences for MDRD students, regardless of which NC remediation they received. The lack of treatment efficacy for the MDRD students echoes Geary (1993) who hypothesized that because a key deficit in students with reading difficulties is phonological processing (Bruck, 1992) and because phonological processing deficits are linked to difficulty with automatic retrieval of NCs (Fuchs et al., 2005), MDRD students should experience greater difficulty with NCs compared to MD-only students.

To accommodate the special challenges MDRD students may face in acquiring NC skill, we designed the next iteration of our NC remediation to decrease demands. We relied on the remaining and most simple approach to intervention in our Framework: counting strategies. As previously discussed, counting strategies should represent the least demanding approach because typical children discover these strategies early, before they rely on decomposition or automatic retrieval. It is, however, unclear whether acquisition of counting strategies promotes automatic retrieval (as students successfully pair question stems with answers) or, more simply, improves accuracy and perhaps fluency.

Study 3: Emphasizing Counting Strategies

Disappointed with results for MDRD students, we revised the NC remediation dramatically for Study 3, this time emphasizing counting strategies for deriving answers, but combined with drill and practice and laced with work on number concepts. As discussed earlier, as typically developing students' understanding about number concepts grow, they naturally discover efficient counting strategies for solving NCs (Ashcraft & Stazyk, 1981; Geary et al., 1987; Goldman et al., 1988; Groen & Parkman, 1972; Siegler, 1987). This helps equip them to pair question stems witli answers successfully and quickly, thereby establishing representations in long-term memory. Students with MD fail to discover sound number concepts or to derive efficient counting strategies (Geary et al., 1987); they pair question stems with answers slowly, taxing short-term memory, and often producing incorrect answers. As a result, long-term representations for automatic retrieval fail to establish or are established incorrectly. This is thought to explain, in part, how students with MD accrue severe and chronic NC deficits. In line with Geary (1993) and as shown in Study 2, students with MDRD may have special difficulty committing NCs to memory, even with intensive drill and practice, with or without foundational instruction on number concepts. We hoped that explicitly teaching counting strategies would help students develop fluency with NCs, even if they remained incapable of automatic retrieval.

For the counting strategies instruction, we reorganized the presentation of NCs to emphasize key number concepts and to maximize learning efficiency. We addressed the 200 NCs with addends and subtrahends from 0 to 9. For the first two lessons, tutors addressed counting knowledge in relation to +1 and −1 NCs using manipulatives and the number line, while emphasizing the commutative property of addition and emphasizing that this property does not apply to subtraction. In the next two lessons, the identity property of addition was taught in relation to NCs of +0 and −0, again using manipulatives and the number line. In Lessons 5 and 6, tutors reviewed these concepts and NCs with +1, −1, +0, and −0. In Lesson 7, students began learning doubles from 0 through 6 (0 + 0, 0 − 0, 1 + 1, 2 − 1, etc.) using manipulatives and rehearsing “doubles chants.” At this point within computerized practice, we introduced mastery criteria: Students spent no more than 4 days on each lesson topic to avoid getting “stuck” on a topic and losing content coverage. After doubles, students learned NCs with +2 and −2 emphasizing counting knowledge with manipulatives and the number line.

Next, and most central to the Study 3 NC remediation, students learned efficient counting strategies to answer NCs. Students were taught that if they “just know” the NC, they “pull it out of their head.” If they do not know an answer immediately, they count up. Students were taught to count up using the number line and eventually fingers. For addition, counting involved the min strategy: Start with the bigger number and count up the smaller number on fingers; the answer is the last number spoken. For subtraction, counting involved the missing addend strategy: Count from the subtrahend to the minuend. For subtraction, students were taught that the minus number is the number directly after the minus sign and that the number you start with is the first number in the equation. Students started with the minus number and counted up to the number they started with; the answer is the number of fingers (or counts) used to count up. During each subsequent lesson, students were reminded to “know it or count up.”

Because students were now equipped widi efficient counting strategies for answering NCs, the tutor introduced additional NC sets, beginning with the 5 set (i.e., addition problems with 5 as the sum or subtraction problems with 5 as the minuend), and tutors used blocks to focus on part-whole relations involved in the 5 set. After mastering the 5 set, students progressed to the 6 set, then the 7 set, and so on through 18. Between the 12 set and the 13 set, students worked on doubles of 7 through 10. If a student mastered all sets before session 48, the remaining sessions were dedicated to review.

Each session comprised five activities, each of which emphasized counting strategies: flash card warm-up, conceptual and strategic instruction, lesson-specific flash card practice, computerized drill and practice with mastery assessment, and paper-pencil review. With flash card warm-up, tutors showed flash cards, one at a time, for 2 min. These cards were a random sample of the 200 NCs. Tutors placed correct cards in a pile on the table. When students answer incorrectly, tutors instructed them to “count up” to produce the correct answer, but placed the card in an incorrect pile. In this way, students were encouraged to count up as quickly as possible. At the end of 2 min, students counted the number answered correctly and graphed the score.

During conceptual and strategic instruction, tutors introduced or reviewed number concepts and counting strategies. Throughout conceptual and strategic instruction, tutors also emphasized the strategies for deriving answers (“know it or count up”); provided practice in counting up that encouraged quick, accurate counting; and required students to explain how to count up for addition and subtraction. Tutors then addressed that day's NC set using the number line and manipulatives.

After the tutor-led lesson, tutors conducted lesson-specific flash card practice for 1 min (i.e., NCs that were the focus of the day's lesson). Correctly answered flash cards were placed in the correct pile. When students erred, tutors required them to “count up,” encouraging quick, accurate counting up. These cards were returned to the card stack. After 1 min, the number of cards answered correctly was counted, but the score was not graphed. On the second, third, and fourth days of a lesson topic, students had the opportunity to beat their first score.

Next, students completed the computerized drill and practice to build fluency with NCs and to assess mastery with the day's NC set. The format of Math Flash C was consistent with Math Flash A and Math Flash B, although NCs within Math Flash C included 10 lesson-specific NCs and five mixed NCs. The mixed NCs were randomly selected from the entire pool excluding the lesson-specific NCs. Math Flash C ended after the student answered each of the 10 lesson-specifi c NCs correctly two times or after 7.5 min. The student then received feedback about correctly answered NCs for that day's session. Mastery on the lesson-specific NCs set was assessed automatically during computerized practice. If the student answered each of the 10 lesson-specific facts correctly two times before 7.5 min elapsed, mastered appeared on the screen. If not, repeat appeared on the screen. The tutor moved students to the next NCs set when mastery occurred or after the maximum number of days permitted on a given set. Finally, students completed paper-pencil review, similar to the other studies.

In Study 3, the contrasting active condition was a word-problem remediation that also incorporated counting strategies instruction. We incorporated a word-problem remediation at this point in the research program to address the word-problem deficits of students with MD and to assess the extent to which we might address both deficit areas (NCs and word problems) simultaneously. Each word-problem lesson lasted 20 to 30 min (see Fuchs et al., 2009, for information on other aspects of the word-problem remediation). The NC focus of each daily session was restricted to only 4 min and to the following activities. In an introductory unit, students were taught to “know it or count up,” as described. Next, each day, students did the 2-min flash card warm-up, which was identical to the flash card warm-up used for the NC remediation so that tutors required students to count up errors. Finally, in daily paper-pencil review, students had 2 min to complete 10 addition and subtraction NCs as well as four addition and subtraction double-digit computation items, two of which required regrouping. (We included double-digit calculations in the paper-pencil review and in the introductory lesson because double-digit calculations are foundational to success with word problems.)

So, Study 3 had three conditions: (a) a condition that combined counting strategies NC remediation with a focus on number concepts and with drill and practice, (b) a word-problem remediation (that also incorporated counting strategies but without supporting conceptual lessons or drill and practice), and (c) control, in which no remediation occurred. Interestingly, on NC outcomes, both remediations effected superior improvement compared to the control group, with effect sizes of 0.53 for NC remediation and 0.62 for word-problem remediation. There was no significant difference between remediation conditions. This is notable because NC remediation allocated dramatically more time to NCs over the course of the 16-week intervention. With NC remediation, each 20- to 30-min session was devoted entirely to NCs. By contrast, with word-problem remediation, tutors taught a counting strategy for deriving NC solutions in a single lesson, and then provided practice each session within the 2-min warm-up activity, within 2 min of paper-pencil review, and as NC errors occurred naturally within word problems. Thus, teaching efficient counting strategies, while providing frequent but small amounts of timed practice to gain efficiency in using these strategies and while applying the strategies in word problems, produces similar outcomes as an expanded remediation protocol that is devoted entirely to NCs and that incorporates a focus on number concepts and that incorporates more extended drill and practice.

On procedural calculations, both remediation conditions again effected superior outcomes compared to the control group, with effect sizes of 0.27 for NC remediation and 0.53 for word-problem remediation. The NC remediation therefore effected better outcomes on procedural calculations compared to the control group without any direct work on procedural calculations, indicating that transfer occurred (although not to word problems). Word-problem remediation allocated direct although limited time to procedural calculations (with one direct lesson in the introductory foundational skills unit; with 2 min of paper-pencil practice at the end of each session; and with students completing procedural calculations while solving word problems). The difference between tutoring conditions was not statistically significant, although the effect sizes suggest that with larger samples or with less variability, word-problem remediation might achieve differential efficacy compared to NC remediation.

We were also interested in whether the counting strategies remediation was effective for students with MDRD, who had proved unresponsive to Study 2's practice remediation and to Study 2's conceptual remediation. In Study 3, we found no evidence of differential responsiveness to the counting-up NC remediation as a function of MD status. On the one hand, this suggests that counting strategies may indeed represent a suitable approach for NC remediation, especially for students with MDRD. On the other hand, we remind readers that Study 1 findings suggested that intensive drill and practice was comparably effective for students with MD-only and with MDRD.

In any case, Study 3 results suggest promise for the counting strategies approach to remediating NC deficits. Moreover, it is interesting to consider the success of counting strategies without the conceptual number focus and without extensive drill and practice (as embedded within word-problem remediation). Effect sizes were almost identical to Study 3's more elaborate and time-consuming counting strategies remediation and were nearly the same as Study 1's intensive drill and practice remediation. We therefore wondered just how efficiently we could design counting strategies intervention, embedded within word-problem remediation, to produce similar NC outcomes.

Study 4: Utility of a Further Abbreviated Counting Strategies Remediation: Counting Strategies With and Without Deliberate Brief Practice

Toward that end, in the final study of the research program, we contrasted two counting strategies remediations, both embedded within word-problem tutoring. The first was Study 3's counting strategies remediation (i.e., a counting-up lesson, systematic review and timed practice of the counting strategy, as well as use of the counting strategies in word problems but without conceptual lessons or extensive drill and practice). This was contrasted to a further abbreviated version, limited to a single counting-up lesson (without systematic review or practice, either under timed condition or within word problems). In this way, we assessed the effects of the counting strategies with and without brief but deliberate practice.

For the counting strategies instruction with deliberate practice condition (similar to Study 3), students were taught the counting strategies in one lesson as part of a unit that was introductory to the word problem remediation. This introductory unit focused on skills that were foundational to success with word problems: counting up to derive answers to NCs, applying algorithms for answering procedural calculations, solving simple addition and subtraction algebraic equations, and using strategies for checking work within word problems. Following this introductory unit, we incorporated deliberate practice in counting up. The first activity in each session was flash card warm-up. Students had 1 min to answer NCs. If they responded incorrectly, the tutor required them to count up until they had the correct answer. At the end of 1 min, students counted correct cards and had another minute to beat their first score. Second, the tutor began each word-problem lesson by asking the student, “What are the two ways to find an answer to a math fact?” Students responded, “Know it or count up.” Then the tutor asked die student to explain how to count up an addition problem and how to count up a subtraction problem. Next the tutor asked students to count up two addition and two subtraction problems. Third, during the lesson, whenever students made an NC error, the tutor required them to count up. Finally, when checking die paper-pencil review (which focused on solving algebraic equations and word problems), the tutor corrected NC errors by demonstrating die counting strategies.

In counting strategies instruction without deliberate practice, tutors taught counting strategies using the same one-session lesson in the same introductory unit. However, after this introductory unit, instead of deliberate practice in counting strategies, the flash card warm up activity asked students to read numbers (0–9,999) aloud for 1 min. Also, there was no review of counting strategies at the beginning of lessons, and tutors corrected NC errors by simply giving correct answers. In addition, when checking the paper-pencil review (focusing on solving algebraic equations and word problems), tutors corrected NC errors by simply providing correct answers.

So in Study 4, we had three conditions: counting strategies instruction without deliberate practice, counting strategies instruction with deliberate practice, and control (no remediation). We found evidence that deliberate practice on the counting strategies was important for effecting strong outcomes on NCs as well as on procedural calculations. The remediation condition that included deliberate practice on counting strategies effected superior learning compared to the control condition (with effect sizes of 0.67 and 0.60 on NCs and procedural calculations, respectively). Also, students who received counting strategies instruction with deliberate practice significantly outperformed those without deliberate practice (effect size = 0.21 on NCs).

This supports the proposition that deliberate (albeit, in this case, brief) practice is a key component of effective remediation for students with MD. Yet, it is also interesting to consider that when students were taught counting strategies in a single lesson, without deliberate practice, effect sizes relative to the control were 0.44 on NCs and 0.39 on procedural calculations (the difference between groups was significant only on the former). This illustrates the power of the counting strategies for helping students with mathematics disabilities derive and apply solutions to NCs fluently and accurately.

We note that, as in Study 3, the counting strategies remediation with deliberate practice, which was embedded in word-problem remediation, produced strong outcomes not only on NCs and procedural calculations but also on word problems. For students who experience concurrent deficits with calculations and word problems, such efficiency is critical, because schools are reluctant to release students from general education for extended time. We conclude that counting strategies with deliberate practice, embedded in word-problem remediation, represent an efficacious and efficient approach for remediating NC deficits. It is possible, however, tiiat the efficacy of this relatively efficient remediation may depend on contextualizing it within word-problem remediation. Additional work will have to assess its efficacy as a stand-alone remediation.

Conclusions Across the Studies

Before drawing conclusions across the studies, we note some important limitations to our research program. First, although our research program addressed all three intervention approaches within our Remediation Framework, it did not systematically contrast each approach against each other. Also, the research program did not always isolate intervention approaches (e.g., Study 3's counting strategies remediation also focused on number concepts and incorporated drill and practice). Additional research is required that systematically (a) contrasts the different approaches; (b) isolates the effects of the intervention approaches; and (c) assesses effects of the intervention approaches with varying emphases on the number concepts related to NC skill. Also, a key limitation is that we failed to assess students' strategies for deriving NCs and therefore do not know which remediations promoted use of which strategies. For this reason, we can draw conclusions only about whether students' fluency with NCs improved, not the strategies students used to derive solutions. Future work is also needed to address this limitation. Finally, our remediations lasted no more than 30 min, three times per week for 15 to 16 weeks. The schools imposed this restriction because they opposed releasing students for mathematics tutoring for more extended periods. With greater intensity, effects may be larger as has been documented in reading (Torgesen et al., 2001), and future research might systematically vary the intensity of remediation.

Within the constraints imposed by these limitations, we tentatively draw the following conclusions. First, remediation can be efficacious. Across the four-study research program, remediation addressed each of the three intervention approaches in our Framework, with a focus on the number concepts underlying NC skill to varying degrees. We examined the effects of drill and practice to encourage automatic retrieval, conceptual lessons to promote decomposition strategies, and the teaching of efficient counting strategies. Regardless of intervention approach, effect sizes were of similar magnitude, suggesting the potential efficacy of all three approaches. On the basis of efficiency, however, we favor the counting strategies approach. It does not require the hardware and software needed for computerized drill and practice (and computerized practice still requires tutor supervision, without which students with MD use computers inappropriately and inattentively; Fuchs, Fuchs, Hamlett, & Appleton, 2002). In addition, counting strategies are more efficient than the conceptual decomposition lessons that require more training and closer supervision of tutors.

Due to the ease of implementation and the lower costs of the counting strategies approach to remediation, we relied on this approach to address participants' NC deficits as we moved toward word-problem remediation. In Study 3, we demonstrated that we could obtain comparable NC outcomes, either with a full counting strategies remediation that also incorporated conceptual lessons and drill and practice or with a substantially truncated counting strategies remediation that was embedded in word-problem remediation. Despite comparable NC outcomes, however, we cannot dismiss the possibility that the abbreviated counting strategies remediation must be contextualized within our word-problem remediation for benefits to accrue. Moreover, the conceptual lessons embedded in Study 3's full-blown NC remediation may promote superior math performance on other math outcomes, beyond the NC, procedural calculations, word-problem, and algebraic cognition outcomes we incorporated in our research program.

In Study 4, we pushed harder, further abbreviating the counting strategies remediation (while still embedding it in word-problem remediation). The final iteration of NC remediation was confined to a single counting strategies lesson. There was no deliberate practice. Tutors did not review strategies, did not demonstrate strategies after this initial lesson, did not provide practice to contextualize use of strategies, and did not ask students to use counting-up to correct errors. We contrasted this most-abbreviated version of the counting-up remediation against Study 3's truncated iteration, which included some, albeit limited, practice of the counting strategies. The counting strategies remediation with deliberate practice resulted in superior learning compared to the counting strategies instruction without deliberate practice, indicating the importance of deliberate practice for students with MD. Even so, the extent of that deliberate practice was substantially less than in our remediations that attempted to promote automatic retrieval via drill and practice or to develop decomposition strategies via conceptual instruction. This suggests the power of the counting strategies as a focus of remediation for helping students with MD derive solutions to NCs in a fluent and accurate manner.

The counting strategies remediation with deliberate practice resulted in superior learning compared to the counting strategies instruction without deliberate practice, indicating the importance of deliberate practice for students with MD.

In planning remediation for students with MD, it is also important to consider the extent of transfer expected from NC remediation to other aspects of mathematics. In Studies 1 and 2, there was no evidence of transfer from NC remediation (transfer could not be assessed in Study 4 because both remediations explicitly addressed procedural calculations and word problems). Transfer did however occur in Study 3, when students in the NC remediation showed superior performance on procedural calculations (effect size = 0.27). The issue of transfer from NCs to other aspects of mathematics is interesting in that NCs are viewed as a signature deficit, representing a bottleneck for students with MD (Fleishner et al, 1982; Geary et al., 1987; Goldman et al., 1988). If so, performance on procedural calculations and word problems should improve with NC remediation, just as decoding remediation has been shown to improve reading comprehension (e.g., Blachman et al., 2004; Torgesen et al., 2001).

We found support for this hypothesis in the transfer observed in Study 3 from NC remediation to procedural calculation outcomes, suggesting that NCs may in fact serve as a “bottleneck” deficit, at least with respect to procedural calculations. Yet, across Studies 1, 2, and 3, we found no evidence of transfer from NCs to word-problem outcomes (i.e., students continued to experience word-problem deficits unless the remediation directly addressed word problems). This suggests that difficulty with word problems is not due to students' struggle widi NCs, which diverts attention from the complex mathematics into which the NCs are embedded (cf. Ackerman, Anhalt, & Dykman, 1986; Goldman & Pellegrino, 1987), but that MD represents a more complicated pattern of difficulty involving language deficits (e.g., Fuchs et al., 2005, 2006). Assuming that MD involves more than NCs, it is unclear how pervasive the pattern of deficits may be. Future work should continue to explore differences in mathematics performance through die curriculum and examine which strengths and weaknesses on various aspects of the mathematics curriculum may characterize MD subtypes. Even so, as practitioners plan remediation programs, they cannot assume that successful remediation of NC deficits will result in enhanced performance on word problems.

INCORPORATING A TWO-STAGE SYSTEM OP REMEDIATION WITHIN THE REMEDIATION PRAMEWORK

Despite the statistically significant and practically important effects associated with each of three approaches in our Remediation Framework, we note that none of these approaches to remediation is universally effective. This is the case for all instructional methods, even those validated with randomized control studies as in the present research program. For example, at the Nashville site, although the Study 3 counting strategies remediation resulted in statistically significantly better improvement in NC fluency compared to the control group, with an effect size of one-half standard deviation, 3 of 21 students in this condition proved unresponsive. On the one hand, given the high percentage of responders to this research program's validated protocols and because personnel without high levels of professional training can implement these highly structured protocols if appropriately trained and supervised, efficiency demands that validated standard protocols be conducted as the first stage of remediation. On the other hand, because we must assume that validated protocols will not work for all students, schools must systematically monitor the effects of those protocols on individual learning. Thus, children who do not respond adequately can be identified promptly, and the special educator can individually tailor the remediation protocol to make it work for these students. But once we determine, via ongoing progress monitoring, that Stage 1 standard-protocol remediation is not working, how might individual tailoring occur in Stage 2?

One possibility is to rely on a skills-based diagnostic-prescriptive method. That is, for nonresponders, at the beginning of the individual tailoring process, conduct an assessment to determine the strategies a student uses to derive NC answers (e.g., Siegler & Shrager, 1984). Then, using the three approaches to intervention embedded in our Remediation Framework, the special educator matches the remediation approach to the student's profile of strategies. For example, if the assessment indicates that “Rita” primarily relies on the immature total counting strategy, then a counting strategies approach to remediation, with its focus on the more efficient counting strategies, might prove useful. Once Rita applies the min counting strategy accurately and fluently, the tutor might move to the decomposition strategies approach to remediation. After decomposition strategies are firm, the tutor might introduce intensive computerized drill and practice. By contrast, let's say that “Daniel's” strategy assessment reveals strong understanding of back-up (min counting as well as decomposition) strategies, but he nevertheless demonstrates an absence of automatic retrieval. For Daniel, the special educator might rely exclusively on drill and practice; for example, intensifying our repeated flash card activity, where students correct errors using the back-up strategies they have mastered efficiently, trying to beat previous scores (as in repeated reading) with correct and fluent responding. Furthermore, the teacher might systematically mix the repeated flash card activity with computerized drill and practice, requiring Daniel to apply his back-up strategies during Math Flash. Goldman et al. (1988) suggested a variation on this individualized approach when they documented clusters of students with different strategy patterns. Yet, to our knowledge, no research on its efficacy has been conducted. Experimental studies are needed to contrast such a Stage 2 diagnostic-prescriptive remediation against a Stage 2 standard protocol.

PRACTICAL IMPLICATIONS OF OUR REMEDIATION FRAMEWORK

Our Remediation Framework is designed to guide special educators as they design programs to remediate the NC deficits of students with MD. Depending on an individual student's understanding of basic number concepts at the time remediation begins, typical development highlights the importance of a foundational focus on number concepts within intervention, including number–after knowledge, the commutative property of addition, the additive identity property of zero, the notion that a whole can be decomposed into parts in different ways, and the relationship between subtraction and addition. Across the remediations of our research program, we integrated instruction on number concepts to varying degrees, with the most explicit instruction occurring in Study 2's conceptual decomposition condition. Nevertheless, given the difficulty students with MD experience with implicit approaches to instruction (Kroesbergen et al., 2004), it is unlikely that an exclusive focus on foundational number concepts will lead to students discovering efficient counting strategies or decomposition strategies or will translate into automatic retrieval. So, for example, even in Study 2's conceptual decomposition condition, we also incorporated intensive drill and practice.

The course of typical development suggests three major approaches to remediating NC deficits. These three major approaches to remediation are incorporated within our Framework in a hierarchy that is based on the development of NC skill among typical students. The least demanding rung of the hierarchy is counting strategies; this approach represents typical students' earliest achievements related to NC skill, whereby children become increasingly efficient in counting and eventually derive and depend on only the most efficient counting strategies. Counting strategies should, therefore, be easiest for students with MD to learn. The next most demanding intervention approach, according to the developmental sequence, is decomposition strategies, which typical children develop as their understanding of part-whole relationships grows. The third and most challenging approach to intervention, according to the developmental sequence, is drill and practice, which is related to the most efficient strategy and the ultimate accomplishment related to NC skill, whereby typical children rely heavily on memory-based retrieval of answers. Memory-based retrieval is made possible as typical children's increasingly efficient counting and decomposition strategies help them consistently and quickly pair problems with correct answers in working memory. This creates associations in long-term memory. The goal of remedial drill and practice is for students with MD to rehearse correct pairings that lead to long-term representations for automatic retrieval, which circumvents the time needed to build representations by first developing effective counting and decomposition strategies.

In this article, we described studies that illustrate how each of the three approaches to remediation might be operationalized. These studies also demonstrate that when any one of these approaches to remediation is combined with a foundational focus on number concepts and is designed and implemented using strong instructional principles, each produces important improvements in NC fluency among students with MD. Even so, as with any validated practice, we cannot expect universal response. Therefore, in our Framework, we recommend that special educators contextualize the three approaches to intervention within a two-stage system of remediation. The less intensive stage involves selecting an intervention approach, hypothesized to be most productive for a student, and implementing that approach via a validated protocol while monitoring student response. The more intensive stage, which is reserved for nonresponders, involves integrating the three intervention approaches within a skills-based diagnostic-prescriptive scheme for individualizing intervention.