Recent developments in imaging system assessment methodology, FROC analysis and the search model

Abstract

A frequent problem in imaging is assessing whether a new imaging system is an improvement over an existing standard. Observer performance methods, in particular the receiver operating characteristic (ROC) paradigm, are widely used in this context. In ROC analysis lesion location information is not used and consequently scoring ambiguities can arise in tasks, such as nodule detection, involving finding localized lesions. This paper reviews progress in the free-response ROC (FROC) paradigm in which the observer marks and rates suspicious regions and the location information is used to determine whether lesions were correctly localized. Reviewed are FROC data analysis, a search-model for simulating FROC data, predictions of the model and a method for estimating the parameters. The search model parameters are physically meaningful quantities that can guide system optimization.

Introduction

A frequent problem in imaging is assessing whether a new imaging system is an improvement over an existing standard [1]. The imaging system generally consists of several components, e.g., x-ray source, grid, x-ray detector, image processing algorithm, image display and the observer. Fourier measurements like modulation transfer function, signal to noise ratio, etc., are excellent tools for optimization of parts of the imaging chain, e.g., detector spatial resolution optimized by measurements of modulation transfer function. However, the effect on performance of the entire imaging chain, including the observer, requires different methods that fall under the rubric of observer performance methods or “ROC analysis” [2–4]. The receiver operating characteristic (ROC) analysis is widely used in this context but it has limitations that have led to research on alternate paradigms [5–8]. This paper reviews progress in the free-response paradigm [5].

ROC

The receiver operating characteristic (ROC) curve is the plot of true positive fraction vs. false positive fraction. A commonly used figure of merit is the area AUC under the ROC curve. AUC measures the ability of the observer/imaging system to correctly classify normal and abnormal images: AUC = 1 for perfect classification ability and 0.5 for chance level classification ability. The ROC curve is usually determined using the ratings method. The observer is shown an image, which could be normal (disease free) or abnormal (disease present), but the observer is “blinded” to this information. The observer reports a subjective confidence level that the image is abnormal. The confidence level is an ordinal variable, e.g., high confidence normal, low confidence normal, equally uncertain normal or abnormal, low confidence abnormal and high confidence abnormal, or the labels 1, 2, 3, 4 and 5 could be used to classify each image according to its confidence level. The ratings of a set of normal and abnormal images are used to calculate AUC [9], an objective measure of performance.

To compare two modalities one obtains AUC for each modality and the modality with the higher AUC is superior. Since the AUCs are subject to sampling variability, the result of the comparison is a p-value for rejecting the null hypothesis that the two modalities are identical. Let α denote the size of the test, i.e., the specified Type I error rate. If the p-value is sufficiently small, and typically one chooses α = 5% as “small enough”, then if p < α, the modalities are declared different at the α-significance level. In a multiple-reader multiple-case (MRMC) study a set of observers interpret a common case set in both modalities. The reader and case matching ensure that differences in expertise levels of readers and difficulty levels of cases do not obscure the modality effect that one is interested in detecting. Dorfman-Berbaum-Metz (DBM) MRMC software [10–12] is commonly used to analyze MRMC ROC data.

In ROC data collection the reader assigns a single rating to each image. When the signs of the disease are diffuse then the ROC rating captures the relevant information. An example is interstitial lung disease which is characterized by scarring of lung tissue. When the disease is manifested by the presence of localized lesions, such as lung nodules, pointing to the correction location informs the experimenter that the reader has actually seen the disease. Moreover the location is relevant as it may guide subsequent interventions (e.g., biopsy). Not collecting location information would introduce ambiguity since the experimenter cannot rule out that the reader missed the lesion and mistook a suspicious normal region for a lesion. For such tasks the ROC rating would represent the answer to the ambiguous question “what is your confidence level that there is at least one nodule somewhere in the image”.

FROC

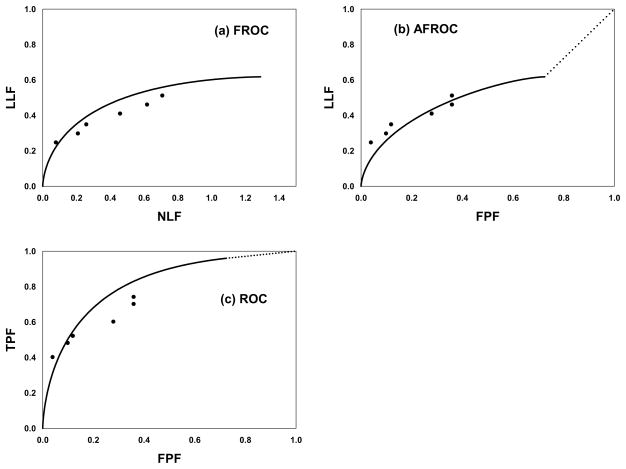
In free-response ROC (FROC) data collection the observer reports the locations and confidence levels of regions that are suspicious for disease [5, 13]. The unit of data is the mark-rating pair where the mark is the location and the rating is the confidence level that the reported region is actually a lesion. The experimenter decides whether a mark is close enough to a real lesion to qualify as a lesion localization (LL) and otherwise the mark is classified as a non-lesion localization (NL) [14]. The FROC curve is defined as the plot of lesion localization fraction (LLF) vs. non-lesion localization fraction (NLF), where the respective denominators are the total number of lesions and the total number of images [15]. Table 1 shows 6-rating FROC data, simulated by a model to be described later, for 50 normal images, 50 abnormal images with 98 lesions. It illustrates the procedure for calculating the operating points. For example, cumulating the counts in bins 3, 4, 5 and 6 one obtains NLF = (20+5+13+8)/100 = 0.46 and LLF = (6+5+5+24)/98 = 0.408. Note that while the total number of potential LLs is known, namely 98, the total number of potential NLs is unknown. The number of true negatives – normal regions that were examined by the observer but correctly rejected as possible lesions – is unknown.

Table 1.

This table illustrates a hypothetical FROC data set and the corresponding FROC operating points. It corresponds to a 6-rating FROC study where 1 = very low confidence in presence of lesion and 6 = definite lesion.

	TOTAL	BINS AND COUNTS
		Bin 1	Bin 2	Bin 3	Bin 4	Bin 5	Bin 6
NL	Unknown	9	16	20	5	13	8
LL	98	5	5	6	5	5	24
FROC		OPERATING POINTS
		Bins ≥ 6	Bins ≥ 5	Bins ≥ 4	Bins ≥ 3	Bins ≥ 2	Bins ≥ 1
NLF		0.080	0.210	0.260	0.460	0.620	0.710
LLF		0.245	0.296	0.347	0.408	0.459	0.510

If one assumes that the rating of the highest rated mark on an image is its ROC-equivalent rating, then one can infer ROC data from FROC data. If the image has no marks then its inferred rating is zero (or any number smaller than the smallest explicit rating, 1 in the present example). In Table 2 this has been done for the normal images and used to determine FP counts and FPFs. [By appropriate adjustment of bin-widths, the minimum number of counts in any bin has been constrained to be ≥ 5.] The values 32 and 48 under the 0 bin are the number of unmarked normal images and the number of unmarked lesions, respectively. The AFROC curve is the plot of LLF vs. FPF and this table illustrates the calculation of AFROC operating points.

Table 2.

This table illustrates the calculation of AFROC operating points. The zero bin represents unmarked normal images and unmarked lesions.

	TOTAL		BINS AND COUNTS
		Bin 0	Bin 1	Bin 2	Bin 3	Bin 4	Bin 5	Bin 6
FP	50	32	0	4	8	1	3	2
LL	98	48	5	5	6	5	5	24
AFROC			OPERATING POINTS
		Bins ≥ 6	Bins ≥ 5	Bins ≥ 4	Bins ≥ 3	Bins ≥ 2	Bins ≥ 1	Bins ≥ 0
FPF		0.040	0.100	0.120	0.280	0.360	0.360	1
LLF		0.245	0.296	0.347	0.408	0.459	0.510	1

Table 3 shows inferred-ROC counts and operating points. On normal images the highest rating is necessarily that of a NL, or zero, if there is no mark, but on abnormal images, the highest rating could be a LL or an NL, whichever is rated higher, or zero, if there is no mark.

Table 3.

This table illustrates the calculation of ROC operating points. The zero bin represents unmarked normal images and unmarked abnormal images.

	TOTAL		BINS AND COUNTS
		Bin 0	Bin 1	Bin 2	Bin 3	Bin 4	Bin 5	Bin 6
FP	50	32	0	4	8	1	3	2
TP	50	13	2	5	4	2	4	20
ROC			OPERATING POINTS
		Bins ≥ 6	Bins ≥ 5	Bins ≥ 4	Bins ≥ 3	Bins ≥ 2	Bins ≥ 1	Bins ≥ 0
FPF		0.040	0.100	0.120	0.280	0.360	0.360	1
TPF		0.400	0.480	0.520	0.600	0.700	0.740	1

Fig. 1(a–c) shows (a) FROC, (b) AFROC and (c) ROC operating points and the simulation predicted curves (not fitted curves), see Eqn. 1 below.

Fig. 1.

(a–c): shows (a) FROC, (b) AFROC and (c) ROC operating points and simulation parameter predicted operating characteristics (not fitted curves).

Analysis of MRMC FROC data

Analysis of observer performance data involves specification of a figure of merit quantifying performance and a method for assigning a significance value, or p-value, to the observed reader-averaged difference of figures of merit between two modalities. In DBM-MRMC analysis of ROC data one can use the area under the ROC curve as the figure of merit, estimate it using the proper ROC model [16], and the significance testing is performed by DBM analysis of variance [10–12]. In jackknife alternative FROC (JAFROC) analysis of FROC data the figure of merit is the area under the AFROC curve, currently estimated non-parametrically, and the significance testing is performed using DBM analysis of variance – the significant testing procedure is applicable to any scalar figure of merit. Software implementing the analysis is available at www.devchakraborty.com. Since it does not use location information one may suspect that ROC analysis is less precise than FROC and more prone to missing a true modality improvement, i.e., has less statistical power. For lack of statistical power a better algorithm design approach may be abandoned in favor of a suboptimal approach. In simulation studies JAFROC has been shown to have higher statistical power than ROC analysis [17–19].

The search model

The search-model assumes that each image yields a random number of decision sites - suspicious regions that are considered for marking - termed noise sites or signal sites if they correspond to normal anatomy or lesions, respectively. It is assumed that the number of noise-sites on an image is a sample from a Poisson distribution with mean λ. The number of signal-sites on an abnormal image is assumed to be a sample from a binomial distribution with mean sν and trial size s, where ν is the probability that a lesion is a decision site (it is “found”) and s is the number of lesions in the image. The decision variable (z-sample) or confidence level from a noise-site is sampled from N(0,1) and that from a signal-site is sampled from N(μ,1) where N(μ,1) is the normal distribution with mean μ and unit variance. The model can be used to simulate FROC data for a single reader. It is the free-response counterpart of the binormal model⁽²²⁾ used extensively in ROC analysis.

Operating characteristics

Expressions for operating characteristics predicted by the search model are [20–22]:

$$\begin{array}{l}\mathit{NLF}(\zeta )=\lambda [1-\mathrm{\Phi }(\zeta )]\hfill \\ \mathit{LLF}(\zeta )=\nu [1-\mathrm{\Phi }(\mu -\zeta )]\hfill \\ \mathit{FPF}(\zeta )=1-e^{\left(-\frac{\lambda }{2}+1/2\lambda \mathit{erf}(\frac{\zeta }{\sqrt{2}})\right)}\hfill \\ \mathit{TPF}(\zeta )=\sum _{s=1}^{s_{max}}{f}_s\left[1-{\left(1-\frac{\nu }{2}+\frac{\nu }{2}\mathit{erf}\left(\frac{\zeta -\mu }{\sqrt{2}}\right)\right)}^s{e}^{\left(-\frac{\lambda }{2}+1/2\lambda \mathit{erf}(\frac{\zeta }{\sqrt{2}})\right)}\right]\hfill \end{array}\}$$ Eqn. 1

Here Φ(ζ) is the cumulative normal distribution function, erf() is the error function, ζ is the reporting threshold, f_s is the fraction of abnormal images with s lesions, s_max is the maximum number of lesions per image in the data set and ${\displaystyle \sum _{s=1}^{s_{max}}}{f}_s=1$. TPF(ζ) is a weighted average over different values of s. The curves shown in Fig. 1 were generated using these equations with μ = 1.73, λ = 1.29 and ν = 0.617. This choice of parameters yielded AUC = 0.8.

The search-model fitted ROC curve does not extend continuously to (1,1). This is a direct consequence of the existence of a finite number of images with no decision sites. As the reporting threshold ζ is reduced decision sites with small (or large negative) z-samples will eventually satisfy z > ζ and be reported (marked), causing the operating point to move up the curve. However, since the total number of decision sites is finite there will come a point when all decision sites are reported and the operating point is at its upper limit. Further reduction of ζ will not result in further upward movement up the curve. A finite number of images will remain unreported (no marks). Only when the experimenter cumulates these images will the (1,1) point be reached discontinuously – this is shown by the dotted line in the figure. The area under the SM predicted ROC curve includes the portion under the straight-line portion. The straight line portion is inaccessible to the observer. If λ is large the end-point will be very close to (1,1).

Estimating the parameters of the model

Let (F_i, T_i) be the number of false positive and true positives, respectively, in ratings bin i defined by neighboring thresholds (ζ _i, ζ_i+1) where ζ→ ≡(ζ₀, ζ₁, ζ₂, …, ζ_R+1) is the cutoff vector, R is the number of FROC bins and ζ₀ = −∞ and ζ_R+1 = +∞. Here i = 0, 1, …, R and (F₀, T₀) are the number of normal images with no marks and the number of abnormal images with no marks, respectively. Ignoring combinatorial terms that do not depend on search model parameters the contribution to the likelihood function L_i from bin i is

$$L_i={[\mathit{FPF}({\zeta }_i)-\mathit{FPF}({\zeta }_{i+1})]}^{F_i}{[\mathit{TPF}({\zeta }_i)-\mathit{TPF}({\zeta }_{i+1})]}^{T_i}$$

The net likelihood L is the product of (R+1) terms like the one shown above, i.e.,

$$L=\prod _{i=0}^{i=R}{L}_i$$

and one maximizes the logarithm of the likelihood (LL) with respect to the 3+R parameters. The values of the parameters at the maximum are the maximum likelihood estimates. It was found that allowing all parameters to vary independently generally led to unrealistic parameter estimates. This is due to a near degeneracy of the likelihood function whereby the effect on LL of an increase in λ or ν can be almost cancelled by an increase in ζ₁. For example, increasing λ tends to increase F_i but increasing ζ₁ decreases F_i. The following constrained maximization algorithm was more successful. For given λ, ν, ζ→ the μ parameter was determined by minimizing the chi-square goodness of fit statistic and LL was calculated. This is the best value of μ, conditioned on the remaining parameters, that is consistent with the observed data. The parameters λ, ν, ζ→ were varied, μ was recalculated, etc., until LL was maximized. For comparison PROPROC analysis was also conducted on the ROC data [16, 23].

Application of estimation algorithm

The estimation method was applied to human observer data from a dual-modality FROC study in which 5 readers interpreted 96 normal and 89 abnormal cases. The two modalities were breast tomosynthesis and digital mammography. The total number of lesions was 95 and there were at most 2 lesions per abnormal case (s_max = 2). A 5-point rating scale was used (R = 5). The FROC data was reduced to ROC data by assigning the rating of the highest-rated mark on an image as its ROC-equivalent rating. If the image had no marks the default 0 rating was assigned to it. This resulted in ROC data on a 6-point scale. If necessary the data was re-binned to achieve F_i ≥ 5, T_i ≥ 5 by combining neighboring bins (this step is necessary for a meaningful calculation of the goodness of fit statistic).

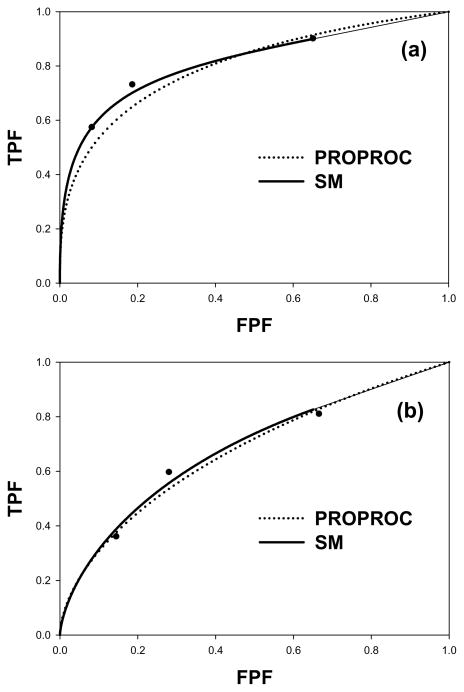
Fig. 2(a) shows the search-model fitted ROC curve (solid line) and the PROPROC-fitted ROC curve (dotted line) for a reader in the breast tomosynthesis modality. The search model parameters were μ = 2.05, λ = 1.06, ν = 0.698 and the PROPROC parameters were c = −0.132 and d_a = 1.2. The areas under the ROC curves were 0.815 for the SM fit and 0.799 for the PROPROC fit. Fig. 2(b) shows corresponding curves in the digital mammography modality; the parameter values were μ = 1.19, λ = 1.05, ν = 0.486 and the PROPROC parameters were c = −0.082 and d_a = 0.628. The areas under the ROC curves were 0.681 for the SM fit and 0.670 for the PROPROC fit.

Fig. 2.

(a–b): Proper ROC model (PROPROC) and search model (SM) fitted ROC curves to a radiologist operating points: (a) breast tomosynthesis and (b) digital mammography.

Discussion

Even though the shapes of the predicted ROC curves are quite different, e.g., the SM curve does not continuously approach (1,1), the area under the SM curve agreed with that predicted by PROPROC. The SM parameters have physical meanings. For example, the SM parameters for Fig. 2(a) indicate that in the breast tomosynthesis modality the radiologist is finding about 70% of the lesions (ν = 0.698) while also finding, on the average, about 1 normal region per image (λ= 1.06). The separation of the noise and signal distributions is about twice their common variance (μ = 2.05). For Fig. 2(b), digital mammography modality, the λ-parameter is about the same as for (a) but μ (= 1.19) and ν (=0.486) are smaller. The radiologist is finding more lesions in the tomosynthesis modality while holding the number of found normal regions about the same, and the radiologist is better at separating lesions from lesion-like normal regions in the tomosynthesis modality. For the digital mammography modality the smaller value of μ results is shallower rise of the ROC curve from the origin modality - at the origin the slope is infinite. For this observer both smaller μ and smaller ν contribute to poorer performance in the 2-dimensional digital modality. These results are for a specific reader and case-set and should not be used to make more general conclusions. Since the search model parameters have direct correspondences to different aspects of search-expertise they can be used to guide how to best improve performance of the observer and/or the modality.

An aspect of FROC analysis that has caused much confusion is how to deal with the true negatives, i.e., normal regions that were looked at but not marked. In general one does not know the total number of normal regions that were looked at – cell marked “unknown” in Table 1. Nevertheless, it is desirable to credit the observer for not marking normal regions. This is accomplished in JAFROC analysis because statistically an observer who does not mark normal regions will also tend to have small FPFs, which will tend to increase the area under the AFROC.