Global pattern of pairwise relationship in genetic network

Abstract

In recent times genetic network analysis has been found to be useful in the study of gene-gene interactions, and the study of gene-gene correlations is a special analysis of the network. There are many methods for this goal. Most of the existing methods model the relationship between each gene and the set of genes under study. These methods work well in applications, but there are often issues such as non-uniqueness of solution and/or computational difficulties, and interpretation of results. Here we study this problem from a different point of view: given a measure of pair wise gene-gene relationship, we use the technique of pattern image restoration to infer the optimal network pair wise relationships. In this method, the solution always exists and is unique, and the results are easy to interpret in the global sense and are computationally simple. The regulatory relationships among the genes are inferred according to the principle that neighboring genes tend to share some common features. The network is updated iteratively until convergence, each iteration monotonously reduces entropy and variance of the network, so the limit network represents the clearest picture of the regulatory relationships among the genes provided by the data and recoverable by the model. The method is illustrated with a simulated data and applied to real data sets.

1. INTRODUCTION

A gene regulatory network (also called a GRN or genetic regulatory network) is a collection of DNA segments in a cell which interact with each other (indirectly through their RNA and protein expression products) and with other substances in the cell, thereby governing the rates at which genes in the network are transcribed into mRNA. From methodology point of view, genetic networks are models that, in a simplified way, describe some biological phenomenon from interactions between the genes. They provide a high-level view and disregard most details on how exactly one gene regulates the activity of another. The gene-gene pair wise relationships provide a special insight of the network and are of interest in the study.

Our work is closely related to that of genetic network analysis, and we first give a brief review of the methods. Some methods are deterministic, such as differential (difference) equation models [1-3], which may not be easy to solve nor have unique solutions. Since the genetic network is a complex system, any artificial model can only explain part of its mechanism; the unexplained parts are random noises, so we prefer a stochastic model. Existing stochastic methods for this problem including the linear models [4,5] or generalized linear models [6], the Bayesian network [7,8] etc. All these methods have their pros and cons, but have the common disadvantage that the solution may not be unique and the results are not easy to interpret. Also, when the network size exceeds that of the data, these methods break down. In genetic work the pair wise regulatory relationships among the genes are important. For such data, it is of interest to investigate the underlying patterns that may have biologic significance, in particular those arising from pair wises regulatory relationships among the genes. Here we study this problem from a different point of view. Given a measure of pair wise gene-gene relationship, we compute the measures from the data, and use the technique of pattern recognition and image restoration to infer the underlying network relationships. The pair wise regulatory relationships among the genes are inferred according to the principle that neighboring genes tend to share some common features, as neighboring genes tend to be co-regulated by some enhancers because of their close proximity [9]. In this method, the solution is unique and computationally simple, the results are easy to interpret and the network can be of any size. In the following we describe our method, study its basic properties, and illustrate its application. This method is used to reveal the true relationships of structured high dimensional data array [10-12].

2. MATERIALS AND METHODS

The gene expression data are generally time dependent, as in Iyer et al. [14]. Let X_ij (t) (i = 1, …, m; j = 1, …, n;t; = 1, …k) be the observed gene expression response for subject i, gene j at time t. Denote x_i (t) = (x_i1(t), …, x_in (t))′ be the observations across all the genes for subject i, and we use x(t) to denote a general sample of the x_i(t)'s. Often for this type of data, m and k are in the low tens, and n in the tens to thousands.

The commonly used differential equation model for genetic network analysis is a set of first order homogeneous differential equations with constant coefficients, in the simple case, has the form

$$\frac{\mathit{dx}\left(t\right)}{\mathit{dt}}=\mathit{Wx}\left(t\right),$$

where W = (w_ij) is the n × n matrix of unknown regulatory coefficients to be solved. This type of models and its more specific and complicated variations characterize well the dynamic of the network over time. The base solution of the above equation set is the matrix exponential $e^{\mathit{tW}}≔{\displaystyle {\Sigma }_{r=0}^{\infty }}{t}^r{W}^r∕r!≔{(v_1\left(t\right),\dots ,v_n\left(t\right))}^{\prime }$, and the general solution of it has the form $x_i\left(t\right)={\displaystyle {\Sigma }_{j=1}^n}{c}_j{v}_j\left(t\right)\mathrm{x}\_\left\{\mathrm{i}\right\}\left(t\right)$, (i = 1, …,m), where the c_j's are constants to be determined by initial conditions from the data. So there are in total n² + n = n(n + 1) coefficients, n² of them from W and n from the c_j's, to be determined from a total of mnk data points. When mnk < n(n + 1) these coefficients can not be determined; when mnk ≥ n(n + 1) they may be uniquely or non-uniquely determined, or may still be not determined. For differential (difference) equation models more complicated than this, solutions are more difficult to get.

The commonly used stochastic model is the multivariate linear model

$$x_i(t+1)={\mathit{Wx}}_i\left(t\right)+{\epsilon }_i,E\left({\epsilon }_i\right)=0,(i=1,\dots ,m;t=1,\dots ,k-1)$$

where ε = (ε_i1, …, ε_in) ′ is the random deviations unexplained by the model. Denote X(t) = (x_ij (t)), if X'(t)X(t) is non-singular, the least-squares solution of the above model is W = X'(t + 1) X(t) (X'(t) X(t))⁻¹, and it may have multiple solutions for different t. For X'(t_r)X(t_r) to be non-singular, one must have n ≤ m. Even for n < m, X'(t_r)X(t_r) may not necessarily be non-singular. This puts an immediate restriction on the size of the network to be analyzed. Also, the solution of the above model may not be unique due to different time points.

For these reasons, we study the problem from a different point of view; by analyze the pair wise gene-gene relationships in the network. In the following we describe our model in which there is always an unique solution, the result is easy to interpret, and there is no restriction on the size of the network. Since the pattern in the genetic network is based on the principle of neighboring similarity, the order of the genes matters in the study, and generally we assume the genes are arranged in their chromosome order.

First we need a measurement for the relationship between any pair of genes, and the network can be represented by the matrix of the pair wise relationships. For large network, linear relationship is not adequate to use, as most of the coefficients will be very small. Also, as mentioned above, such model in this case has no solution because of the small sample size. Pearson's correlation is a good choice for this purpose, other choices including Kendal's tau and Spearman's rho, etc. Here we illustrate the method with Pearson's correlation, and our goal is to infer the triangular correlation matrix R = (r_ij)_1≤i<_j≤n from the observed data, where r_ij is the Pearson's correlation coefficient between genes i and j. As usually the number m of individuals is small (sometimes as few as 2), estimate the correlations using the data at each time point alone is inadequate. So we use all the data to estimate them. An empirical initial version of these correlations are

$${r_{\mathit{ij}}}^{\left(o\right)}=\frac{1}{\mathit{mk}}\underset{r=1}{\overset{m}{\Sigma }}\underset{s=1}{\overset{k}{\Sigma }}\frac{(x_{\mathit{ri}}\left(t\right)-x_i\left(t\right))(x_{\mathit{sj}}\left(t\right)-x_j\left(t\right))}{\sqrt{\mathit{Var}\left(x_i\left(t\right)\right)\mathit{Var}\left(x_j\left(t\right)\right)}},\left(\right(1\le i<j\le n)$$ (1)

where $x_i\left(t\right)=\frac{1}{m}{\displaystyle {\Sigma }_{r=1}^n}{x}_{\mathit{ri}}\left(t\right)$,

$$\mathit{Var}\left(x_i\left(t\right)\right)=\frac{1}{m}\underset{r=1}{\overset{n}{\Sigma }}{(x_{\mathit{ri}}\left(t\right)-x_i\left(t\right))}^2,(i=1,\dots ,n;s=1,\dots ,k).$$

here the x_ri (t)'s are not i.i.d. over the time t's, and the sample size mk is often not large, so the above empirical correlations are very crude evaluations of the true correlations r_ij's. The initial table R⁽⁰⁾ = (r_rj ⁽⁰⁾ :1≤i < j ≤ n) is used as the raw data for the next step analysis. For each fixed i the observations x_i(t) s at different time conditions reduced the common features in the data, this table is biased as an estimate of R. We need to restore their values according to the basic property of the genetic regulatory system. Many reports have shown that nearby genes tend to have similar expression profiles [13-16], thus nearby pairs of genes tend to have similar relationships, and their correlations tend to be close. This is just the same principle as used in image restoration of data arrays of any size. In the following we use this technique to reduce the bias and improve the estimate of R based on the observation R⁽⁰⁾ .

Meloche and Zammar [10] considered a method for image restoration of binary data, here we adopt their idea and revise their method to gene expression analysis for continuous data. We assume the following model

$${r_{\mathit{ij}}}^0=r_{\mathit{ij}}+{\epsilon }_{\mathit{ij}},{\epsilon }_{\mathit{ij}}~N(0,{\sigma }^2),(1\le i<j\le \mathrm{n})$$ (2)

for some unknown σ² > 0, where the ε_ij's represent the part of measurements unexplained by the true regulatory relationships in the model. Define the neighbor R_ij⁽⁰⁾ of r_ij⁽⁰⁾ to be the collection of the nine immediate members of R_ij⁽⁰⁾ of r_ij⁽⁰⁾ = {r_ab⁽⁰⁾ :|a − i|≤ 1, |b − j|≤ 1 }, which includes r_ij⁽⁰⁾ itself at the center. For r_ij⁽⁰⁾'s on the boundary of R⁽⁰⁾ the definition is modified accordingly. For example, R_1,2⁽⁰⁾ and R_n−1,n⁽⁰⁾ has only three members, R_{1, j}⁽⁰⁾ (3 < j < n−1) has six members, etc. Larger neighbors of different shapes can also be considered; here we only illustrate using the above neighbor systems. We assume the r_ij⁽⁰⁾'s only depend on their neighbors R_ij⁽⁰⁾'s. The aim is to provide estimates ȓ_ij's for the true r_ij's based on the records R⁽⁰⁾. WE assume the estimates have the form for some function h(·) to be specified. The performance of the estimates will be measured by the average conditional mean squared error.

$$r_{\mathit{ij}}=h\left({R_{\mathit{ij}}}^{\left(0\right)}\right),(1\le \mathrm{i}<\mathrm{j}\le \mathrm{n}),$$ (3)

$$\frac{2}{n(n-1)}\underset{1\le i<j\le n}{\Sigma }E[{({\stackrel{⌢}{r}}_{\mathit{ij}}-r_{\mathit{ij}})}^2\mid R^{\left(0\right)}]$$ (4)

The optimal set of estimates is the one which minimizes (4). Although r_ij is deterministic, we may view it as a realization of the random variable rIJ with (I, J) uniformly distributed over the integer set

S = {(i, j) :1 i ≤ j ≤ n}. So (4) can be rewritten as

$${\mathit{EE}}_{\mathit{IJ}}[{({\stackrel{⌢}{r}}_{\mathit{IJ}}-r_{\mathit{IJ}})}^2\mid R^{\left(0\right)}]=E[{({\stackrel{⌢}{r}}_{\mathit{IJ}}-r_{\mathit{IJ}})}^2\mid R^{\left(0\right)}]=E[{(h\left(R^{\left(0\right)}\right)-r_{\mathit{IJ}})}^2\mid R^{\left(0\right)}]$$

Thus by (3), the minimizer of (4) is achieved by

$${\stackrel{⌢}{r}}_{\mathit{IJ}}≔h^{\ast }\left({R_{\mathit{IJ}}}^{\left(0\right)}\right)=E(r_{\mathit{IJ}}\mid R^{\left(0\right)})=E(r_{\mathit{IJ}}\mid {R_{\mathit{IJ}}}^{\left(0\right)}),\text{and so}{\stackrel{⌢}{r}}_{\mathit{ij}}=h^{\ast }\left({R_{\mathit{IJ}}}^{\left(0\right)}\right)=E(r_{\mathit{IJ}}\mid R^{\left(0\right)}).$$

To evaluate the above conditional expectation, we need a bit more preparation. Note σ² is estimated by

$${\stackrel{⌢}{\sigma }}^2=\frac{2}{n(n-1)}\underset{(i,j)\in S}{\Sigma }{({r_{\mathit{ij}}}^{\left(0\right)}-\stackrel{-}{r})}^2,\stackrel{-}{r}=\frac{2}{n(n-1)}\underset{(i,j)\in S}{\Sigma }{r_{\mathit{ij}}}^{\left(0\right)}.$$

Denote φ(t | σ¹) the normal density function with mean 0 and variance σ². Denote S_ij as the collection of indices for R_ij⁽⁰⁾. Given R_ij⁽⁰⁾, for (I, J ) ∈ S_ij, view r_IJ⁽⁰⁾ as a random vector over indices (I,J). We define the conditional distribution of r_IJ⁽⁰⁾ as

$$P({r_{\mathit{IJ}}}^{\left(0\right)}={r_{\mathit{uv}}}^{\left(0\right)}\mid {R_{\mathit{ij}}}^{\left(0\right)})=\frac{\{\#\mathit{member}\dots \mathit{in}\dots {R_{\mathit{ij}}}^{\left(0\right)}={r_{\mathit{uv}}}^{\left(0\right)}\}}{\left|S_{\mathit{ij}}\right|}=\frac{1}{\left|S_{\mathit{ij}}\right|}$$

In the above we used the fact that the r_uv⁽⁰⁾ are continuous random variables, so the collection {members in R_ij⁽⁰⁾ = r_uv⁽⁰⁾} = {r_uv⁽⁰⁾} almost surely. The corresponding conditional probability is defined as

$$P((I,J)=(u,v)\mid {R_{\mathit{ij}}}^{\left(0\right)})=\frac{\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^2)P({r_{\mathit{uv}}}^{\left(0\right)}\mid {R_{\mathit{ij}}}^{\left(0\right)})}{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^2)P({r_{\mathit{uv}}}^{\left(0\right)}\mid {R_{\mathit{ij}}}^{\left(0\right)})},(\mathrm{u},\mathrm{v})\in S_{\mathit{ij}}$$

By (2), we deduce E(r_IJ | R_IJ⁽⁰⁾, (I, J) = (u, v)) = r_uv⁽⁰⁾, so we have

$$\begin{array}{cc}\hfill & {\stackrel{⌢}{r}}_{\mathit{ij}}=E(r_{\mathit{IJ}}\mid {R_{\mathit{ij}}}^{\left(0\right)})=\underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }E(r_{\mathit{IJ}}\mid {R_{\mathit{ij}}}^{\left(0\right)},(I,J)=(u,v))P((I,J)=(u,v)\mid {R_{\mathit{ij}}}^{\left(0\right)})\hfill \\ \hfill & =\frac{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}{r_{\mathit{uv}}}^{\left(0\right)}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^2)P({r_{\mathit{uv}}}^{\left(0\right)}\mid {R_{\mathit{ij}}}^{\left(0\right)})}{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^2)P({r_{\mathit{uv}}}^{\left(0\right)}\mid {R_{\mathit{ij}}}^{\left(0\right)})}\hfill \\ \hfill & =\frac{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}{r_{\mathit{uv}}}^{\left(0\right)}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^2)}{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^2)}\approx \frac{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}{r_{\mathit{uv}}}^{\left(0\right)}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\stackrel{⌢}{\sigma }}^2)}{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\stackrel{⌢}{\sigma }}^2)},(i,j)\in S_{\mathit{ij}}\hfill \end{array}$$ (5)

The matrix Ȓ = (ȓ_ij) is our one-step restored estimate of the genetic correlation network R, we also denote it by R = R⁽¹⁾ = (r_ij⁽¹⁾).

Denote F(·) the operator given in (5), as r_ij⁽¹⁾ = F(R_ij⁽¹⁾), and denote r_ij⁽¹⁾ = F(R_ij⁽¹⁾) R⁽¹⁾ = F(R⁽⁰⁾) = E(R | R⁽⁰⁾). We view F(·) as a filter for the noises, so R⁽¹⁾ is a smoothed version of R⁽⁰⁾ . Let R = r_IJ be the random variable of the r_ij's over the random index (I,J) and the variation of possible values of the r_ij's with density p(·), its uncertainty can be characterized by variance and entropy, which is defined as

$$H\left(p\right)=-E\left[\mathit{log}p\left(R\right)\right]=-\int p\left(r\right)\mathit{log}p\left(r\right)\mathit{dr}.$$

It is maximized or most uncertain when R is uniformly distributed, and has smaller value when the distribution of r is more certain. It has some relationship with variance. The former depends on more innate features, such as moments, of the distribution than the latter, which only measures the disparity from the mean. When p(·) is a normal density with variance σ², then $H\left(p\right)=1+\sqrt{2\pi {\sigma }^2}$. For many commonly used parametric distributions, entropy and variance agree with each other, i.e. an increase in one of them implies so for the other. But this is not always true and a general closed form relationship between variance and entropy does not exists. Variance is more popular in practice because of its simplicity.

Although generally, in the image restoration context, R is estimated by just applying F once, a natural question is what will happen if we use the operator F repeatedly? i.e. let R^(k+) = (r_ij^(k+)) = F(R^(k)) = E(R | R^(k)) for k ≥ 0. To investigate this question, we impose the model

$$r_{\mathit{ij}}^{\left(k\right)}=r_{\mathit{ij}}+{{\epsilon }^{\left(k\right)}}_{\mathit{ij}},{{\epsilon }^{\left(k\right)}}_{\mathit{ij}}~N(0,{\sigma }^{2\left(k\right)}),(1\le \mathrm{i}<\mathrm{j}\le \mathrm{n})$$ (6)

The estimators r_ij^(k)'s are obtained by minimizing

$$\frac{2}{n(n-1)}\underset{1\le i<j\le n}{\Sigma }E[{({\stackrel{⌢}{r}}_{\mathit{ij}}-r_{\mathit{ij}})}^2\mid R^{\left(k\right)}]$$

and are given by

$$r_{\mathit{ij}}^{\left(k\right)}=E(r_{\mathit{IJ}}\mid r_{\mathit{ij}}^{\left(k\right)}).$$

similarly σ^2(k) is estimated by

$${\stackrel{⌢}{\sigma }}^{2\left(k\right)}=\frac{2}{n(n-1)}\underset{(i,j)\in S}{\Sigma }{({r_{\mathit{ij}}}^{\left(k\right)}-{\stackrel{-}{r}}^{\left(k\right)})}^2,$$

$${\stackrel{-}{r}}^{\left(k\right)}=\frac{2}{n(n-1)}\underset{(i,j)\in S}{\Sigma }{r_{\mathit{ij}}}^{\left(k\right)}.$$

Since n is usually large, σ̑^2(k) is a good estimator of σ^2(k). Corresponding to (5), we have

$${r_{\mathit{ij}}}^{(k+1)}=E({r_{\mathit{IJ}}}^{\left(k\right)}\mid {R_{\mathit{ij}}}^{\left(k\right)})=\frac{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}{r_{\mathit{uv}}}^{\left(k\right)}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^2)}{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^2)}\approx \frac{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}{r_{\mathit{uv}}}^{\left(k\right)}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\stackrel{⌢}{\sigma }}^{2\left(k\right)})}{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\stackrel{⌢}{\sigma }}^{2\left(k\right)})},(i,j)\in S_{\mathit{ij}},\mathrm{k}\ge 1$$ (8)

In the above we do not replace the r_ij⁽⁰⁾'s by the r_ij^(k)'s in φ(·|·) but with σ²⁽⁰⁾ replaced by the step k estimator σ^2(k), only for the reason of simplicity in the proof of the Proposition below. Finally, σ^2(k) is replaced by σ̑^2(k) in actual computation.

Although few density functions are convex, many of them are log-convex. For example, the normal, exponential (in fact any quadratic exponential families), Gamma, Beta, chisquare, triangle, uniform distributions. But some are not, such as the T and Cauchy distributions. Condition A) does not require all the p^(k) (·)'s to belong to the same parametric family, nor even to be parametric. Condition B) is satisfied for almost all parametric families as few parametric families require more than the first two moments to determine. The only restriction we make is that all the p^(k) (·)'s belong to the same parametric family.

View r^(k) as a random realization of the r_ij^(k)'s and as of R⁽⁰⁾, let p^(k) (·) be the density function of r^(k). To study the property of the algorithm, we say a non-negative function f(·) is log-convex if log f(·) is convex, and assume the following conditions

• A) p^(k) (·) is log-convex for all k.

• B) All the p^(k) (·)'s belong to a parametric family which is determined by the fist two moments.

Our algorithm has the following desirable property (see Appendix for the proof)

Proposition.

• 1) Assume either A) or B), then H(p^(k+)) ≤ H(p^(k)), k≥0.

• 2) σ^2(k+1) ≤ σ^2(k), k≥0.

• 3) As k →∞, the table R^(k) converges in the component wise sense:

  $$R^{\left(k\right)}\to R^{\ast }$$

  for some stationary array R* = R* (R⁽⁰⁾, F).

This Proposition tells us that, if the assumption of neighboring similarity is valid for R⁽⁰⁾, then the estimates R^(k) become more and more clear (less entropy), and more and more accurate as an estimator of R (less variance). So R^(*) is the sharpest picture the data R⁽⁰⁾ provide and can be restored by the filter F, the innate regulatory relationships among the genes can be recovered by filter F and provided by the data R⁽⁰⁾ under the ideal situation of no noise. Intuitively, this picture has some close relationship with the haplotype block structures.

As of small sample size (mk) and large number (n(n−-1)/2) of parameters, there is no way of talking about the consistency of R to R. So in general R^(*) and R may not equal, however our algorithm enable us to do the best effort we can. Convergence of R^(k) can be accessed by the distance criteria: for a given > 0 (usually =1/100 or 1/1000)

$$d_1(R^{(k+1)},R^{\left(k\right)})=\frac{2}{n(n+1)}\underset{i<j}{\Sigma }|{r_{\mathit{ij}}}^{(k+1)}-{r_{\mathit{ii}}}^{\left(k\right)}|\le \epsilon$$

or

$$d_2(R^{(k+1)},R^{\left(k\right)})=\frac{2}{n(n+1)}{\left(\underset{i<j}{\Sigma }({r_{\mathit{ij}}}^{(k+1)}-{r_{\mathit{ii}}}^{\left(k\right)})\right)}^{1∕2}\le \epsilon .$$

Network at each time. We may also investigate the problem at each different time point t. In this case (1) is replaced by

$${r_{\mathit{ij}}}^{\left(o\right)}=\frac{1}{m}\underset{r=1}{\overset{m}{\Sigma }}\frac{(x_{\mathit{ri}}\left(t\right)-x_i\left(t\right))(x_{\mathit{rj}}\left(t\right)-x_j\left(t\right))}{\sqrt{\mathit{Var}\left(x_i\left(t\right)\right)\mathit{Var}\left(x_j\left(t\right)\right)}},(1\le i<j\le n)$$

where, $x_i\left(t\right)=\frac{1}{m}{\displaystyle {\Sigma }_{r=1}^m}{x}_{\mathit{ri}}\left(t\right)$,

$$\mathit{Var}\left(x_i\left(t\right)\right)=\frac{1}{m}\underset{r=1}{\overset{m}{\Sigma }}{(x_{\mathit{ri}}\left(t\right)-x_i\left(t\right))}^2,(i=1,\dots ,n;t=1,\dots ,k)$$

and R⁽⁰⁾ (t) = (r_ij⁽⁰⁾(t) : 1 ≤ i < j ≤n) be the corresponding initial table at each t, and the neighborhood for r_ij⁽⁰⁾(t) is R_ij⁽⁰⁾(t) = {r_ab⁽⁰⁾ : |a-i|≤1,|b-j|≤1}. In this case (6) is

$$r_{\mathit{ij}}^{\left(k\right)}\left(t\right)=r_{\mathit{ij}}\left(t\right)+{{\epsilon }^{\left(k\right)}}_{\mathit{ij}},{{\epsilon }^{\left(k\right)}}_{\mathit{ij}}\left(t\right)~N(0,{\sigma }^{2\left(k\right)}\left(t\right)),(1\le \mathrm{i}<\mathrm{j}\le \mathrm{n})$$

and ȓ_ij^(k)(t) = E(r_IJ^(k))(t) | R_ij^(k)(t)).

$$\text{let}{\stackrel{⌢}{\sigma }}^{2\left(k\right)}\left(t\right)=\frac{2}{n(n-1)}\underset{(i,j)\in S}{\Sigma }{({r_{\mathit{ij}}}^{\left(k\right)}\left(t\right)-{\stackrel{-}{r}}^{\left(k\right)}\left(t\right))}^2,$$

$${\stackrel{-}{r}}^{\left(k\right)}\left(t\right)=\frac{2}{n(n-1)}\underset{(i,j)\in S}{\Sigma }{r_{\mathit{ij}}}^{\left(k\right)}\left(t\right).$$

(8) is now

$${r_{\mathit{ij}}}^{(k+1)}\left(t\right)=E({r_{\mathit{IJ}}}^{\left(k\right)}\left(t\right)\mid {R_{\mathit{ij}}}^{\left(k\right)})=\frac{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}{r_{\mathit{uv}}}^{\left(k\right)}\left(t\right)\phi (r_{\mathit{uv}}^{\left(0\right)}\left(t\right)-r_{\mathit{ij}}^{\left(0\right)}\left(t\right)\mid {\sigma }^2)}{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}\phi (r_{\mathit{uv}}^{\left(0\right)}\left(t\right)-r_{\mathit{ij}}^{\left(0\right)}\left(t\right)\mid {\sigma }^2)}\approx \frac{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}{r_{\mathit{uv}}}^{\left(k\right)}\left(t\right)\phi (r_{\mathit{uv}}^{\left(0\right)}\left(t\right)-r_{\mathit{ij}}^{\left(0\right)}\left(t\right)\mid {\stackrel{⌢}{\sigma }}^{2\left(k\right)}\left(t\right))}{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}\phi (r_{\mathit{uv}}^{\left(0\right)}\left(t\right)-r_{\mathit{ij}}^{\left(0\right)}\left(t\right)\mid {\stackrel{⌢}{\sigma }}^{2\left(k\right)}\left(t\right))},(i,j)\in S_{\mathit{ij}},\mathrm{k}\ge 1$$

The matrix R^(k)(t) = (r^(k)_ij(t)) is the k-step restored estimate of the genetic correlation network R(t) = (r_ij(t)) at time t. The proposition is then hold for each fixed t.

3. SIMULATION STUDY

We simulate 40 genes over 12 time conditions at time (hour) points (t₁, …,t₁₂ ) = (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12) for 6 individuals by mimicking the setting of the data analyzed in Iyer et al. [17]. We simulate the genes from 6 clusters, the numbers of genes in each cluster are given by the vector (n₁, …,n₆) = (8, 6, 4, 4, 6, 12). The baseline values of the gene expressions over time t ∈ [0,12] in cluster k are generated by functions of the form

$$h_k\left(t\right)=a_{k1}\sin \left(t\right)+a_{k2}\sin (t∕2)+a_{k3}\sin (t∕3),(k=1,\dots .,6).$$

Let h(t) be the vector of length 40, with first n₁ components given by h₁(t), second n₂ components by h₂(t), …., last n₆ components by h₆(t). Denote a_k = (a_k1, a_k2, a_k3). We arbitrarily choose the a_k's as a₁ = (0.54, −0.18, 1.23), a₂ = (−0.12, −0.25, 0.45), a₃ = (1.0, −0.55, −0.15), a₄ = (−0.32, −0.15, −0.65), a₅ = (0.15, 0.25, 0.35) and a₆ = (−0.52, −0.45, −0.55). First we need to simulate the r_ij 's with coordinated patterns. We divide the 40 genes into the 6 clusters, and assume independence among the clusters.

Then for given a covariance matrix Ω = Ω₁ ⊕…⊕ Ω₆ we generate the data using this Ω and the time conditions, where Ω_k is the covariance matrix for the genes in cluster k. Directly specifying a high dimensional positive matrix is not easy, we let each Ω_k has the structure Ω_k = Q′_k Q_k, for some Q_k is positive definite. Note that the Q′_k Q_k's may not be correlation matrices, but they are covariance matrices, but they are covariance matrices, so is Ω . Let Q_k be upper diagonal with dimension n_k. The non-zero elements of Q₁ are drawn from U(0.5,0.8); those for Q₂ from U(0.2,0.4); those for Q₃ from U(0.2,0.6), those for Q₄ from U(−0.3, −0.1); those for Q₅ from U(0.6,0.9); and those for Q₆ from U(−0.8, −0.6). Then let Ω^½ = Q₁ ⊕ … ⊕ Q₆ . The 6 individuals are i.i.d, so we only need to describe the simulation of observation x₁ = {x_1j (t) : j = 1, …, 40;t 1, …,12}of the first individual. Note for each fixed t, x₁(t) = (x₁₁(t), …, x_1,40 (t)) has covariance matrix Ω . We first generate y = (y₁, …y₄₀) with the components i.i.d. N(0,1), then x₁(t) = (h(t) + Ω^½ y + ε(t) is the desired sample, where for each fixed t, ε(t) = (ε₁(t), …,ε₄₀(t)) is the noise, with the ε_i(t) 's i.i.d N(0,1) and independent over t. Convert the covariance matrix Ω = (ω_ij) to a correlation matrix R = (r_ij) as $r_{\mathit{ij}}={\omega }_{\mathit{ij}}∕\sqrt{{\omega }_{\mathit{ii}}{\omega }_{\mathit{jj}}}$ only for i < j. Using the data X = (x_ij(t)), we compute the R^(k) 's from (8) then use perspective plots to compare the restored correlations after convergence at step k, R^(k), the one-step restored R⁽¹⁾, the initial estimated R⁽⁰⁾ and the true simulated correlations R.

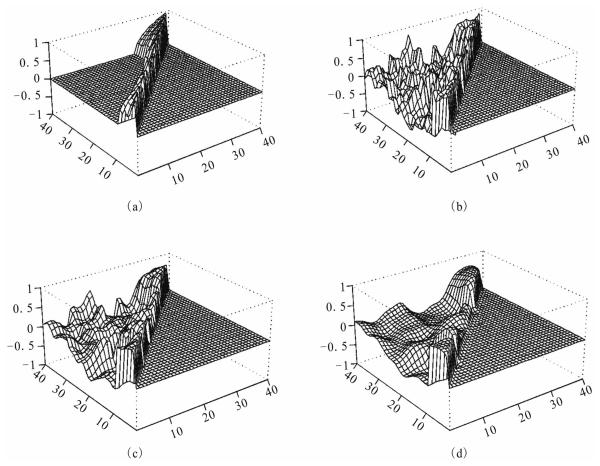
After computation, the algorithm meets the convergence criterion at iteration 14 with = 10⁻⁴. The distances between the observed, first step estimate and last step estimate are: d₁(R⁽⁰⁾, R) = 0.125, d₁(R⁽¹⁾,R) = 0.108 and d₁(R⁽¹⁴⁾, R) = 0.094. We see that the estimate after convergence is closest to the true correlations. The results are displayed in Figure 1 below. We only display the correlations r_ij for j > i. Those values for r_ij is 1′s, and those for r_ij (i > j) are set to zero's, which can be obtained by symmetry.

Figure 1.

Network Correlations: (a). Simulated R, (b) Initial R⁽⁰⁾, (c) One-step Restored R⁽¹⁾, (d) k-step Converged R^(k)

From this figure we see that the correlations computed from the raw data, panel (b), are very noisy, the true pattern, panel (a), in the network is messed up. The one-step estimate, panel (c), gives some limited sense, while the final estimates, panel (d), recover the true picture with reasonably well. Considering the large number of 40(40+1)/2 = 820 parameters and the small number of 15 individuals on 40 genes, the last step estimates are quite a success. Large number of simulations yield similar results, the convergence criterion is met with 10 to 15 iterations.

Note we only used networks of 40 genes, as large networks are not easy to display graphically. The computations of a network with n genes is in the order n(n−1)/2, so there should be no computational problem for ordinary computer using this method to restore even the whole genome.

4. RESULTS

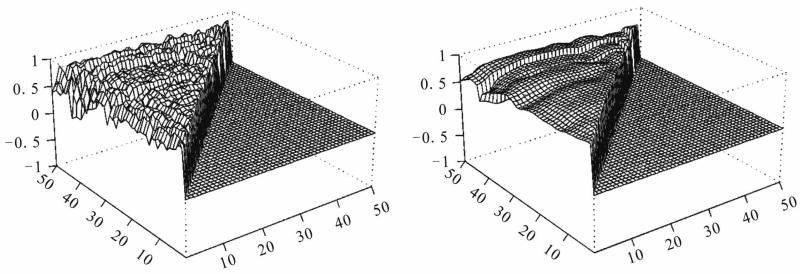
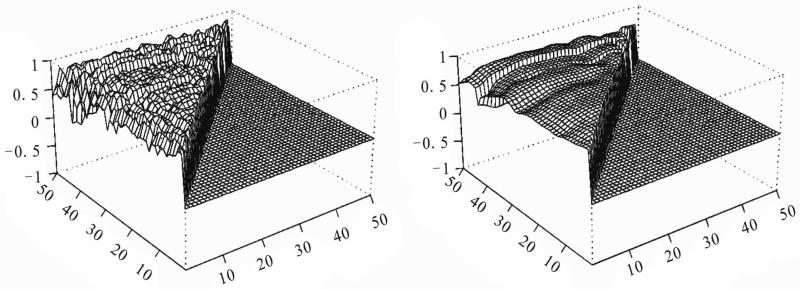
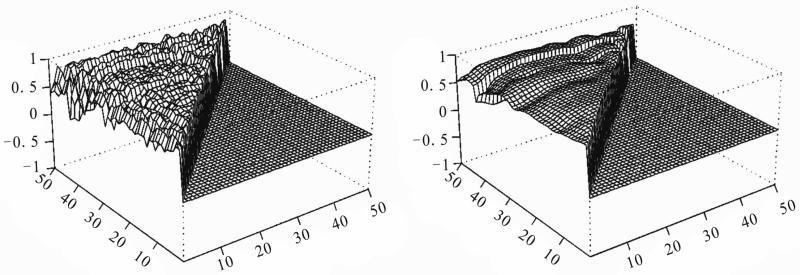
We use the proposed method to analyze the data with 30 microarray chips from the Stanford microarray database: http://smd.stanford.edu/cgi-bin/search/QuerySetup.pl. The Category is Normal tissue and the subcategory is PBMC, the following 30 files are the Raw data in the database: 19430.xls, 19438.xls, 19439.xls, 19446.xls, 19447.xls, 19448.xls, 19449.xls, 19450.xls, 19451.xls, 19500.xls, 19505.xls, 19506.xls, 19507.xls, 21407.xls, 21408.xls, 21409.xls, 21410.xls, 21411.xls, 21412.xls, 21413.xls, 21414.xls, 21415.xls, 21416.xls, 21424.xls, 21425.xls, 21426.xls, 21427.xls, 21428.xls, 21429.xls, 21430.xls. The data we used are the overall intensity (mean), the 67th column in the 30 excel files. We choose three subsets of genes on the 30 arrays: set I is genes 0-49, set II is genes 1000-1049 and set III is genes 5000-5049 from the original data set. There are 80 variable for each array. We choose the intensity from normal people for our analysis. The initial correlation coefficients among the genes computed from the raw data in each set, and those estimated after convergence by our algorithm are shown in Figures 2-4. Clearly the initial correlations are noisy and difficult to see any patterned relationships among the genes. In contrast, the restored pictures are quite clear. For set I, the coefficients are rather homogeneous with values around 0.5, but there is a clear boundary around gene 43, which suggests that most of the genes in this set have similar relationships, or functions. But gene 43 seems to have its own separate mechanism. Genes 38 and 29 also have weak relationships with the other genes. For set II, the relationships among the genes are not so homogeneous. The genes are moderately correlated with coefficients around 0.5, some genes around positions 10, 16, 24, 30, and 38 have weak interactions with the other genes. For set III, there is moderate coordinating pattern among the genes, but three genes, around positions 15, 29, and 40, appears to have relatively independent patterns of regulatory functioning.

Figure 2.

Real data I: initial (left panel) and restored (right panel) correlations.

Figure 4.

Real data III: initial (left panel) and restored (right panel) correlations.

5. CONCLUDING REMARKS

We considered a image restoration method for genetic network analysis. This method gives unique solution, the results are easy to interpret and computationally simple. We may implement the genetic distances among the genes into the updating system given in (8). The method is not confined to correlation coefficients among genes, other measures of gene-gene relationships can be considered analogously. Very large networks can be analyzed in principle, the only challenge is how to display the results. We found when the number of genes exceeds 50, the figure is difficult to distinguish visually. The computation for a network of size 40 takes about a couple of minutes using the Splus software. It will be much faster using the C program, and there should be no problem to analyze the whole genome by this method. The only requirement is that the data be arranged in their chromosomal order, otherwise the results may not easy to interpret.

The method can also be used for other analysis purposes and data types, such as cluster analysis. Cluster objects by pattern similarities, etc. It can be used to analyze qualitative data type such as haplotype analysis.

Figure 3.

Real data II: initial (left panel) and restored (right panel) correlations.

Appendix

Proof of the Proposition

Recall r^(k+1) = r_IJ^(k+1) = r_IJ^(k+1) (R^(k)) is random in (I,J) and R^(k); for fixed (I,J)=(i,j), r_ij^(k+1) = r_ji^(k+1) (R^(k)) is random in R^(k); r_IJ^(k+1) = r_IJ^(k+1) (R^(k) | R⁽⁰⁾) is random in (I,J) (discrete); also r^(k+1) = E(r^(k) | R_IJ^(k)) = E[r_UV^(k) | R_IJ^(k)] for random index (I,J) ∈S and random index (U,V)∈S_IJ.

1) We first prove the result under condition A). We have

$$E\log p^{(k+1)}\left(r^{(k+1)}\right)-E\log p^{\left(k\right)}\left(r^{(k+1)}\right)=\int p^{(k+1)}\left(r\right)\log \frac{p^{(k+1)}\left(r\right)}{p^{\left(k\right)}\left(r\right)}\mathit{dr}=D(p^{(k+1)}\parallel p^{\left(k\right)})\ge 0,$$

which is the relative entropy between p^(k+1)(·) and p^(k)(·). It is known that D(p^(k+1) ∥ p^(k)) ≥ 0 with “=” if and only if p^(k+1)(·) = p^(k)(·). Note log-convexity of p^(k)(·) imply, for each given R_IJ^(k),

$$\log p^{\left(k\right)}\left(E[r^{\left(k\right)}\mid {R_{\mathit{IJ}}}^{\left(k\right)}]\right)\ge E[\log p^{\left(k\right)}\left(r^{\left(k\right)}\right)\mid {R_{\mathit{IJ}}}^{\left(k\right)}].$$

Thus by the above two inequalities we get

$$\begin{array}{cc}\hfill & H\left(p^{(k+1)}\right)=-E\log p^{(k+1)}\left(r^{(k+1)}\right)\le -E\log p^{\left(k\right)}\left(r^{(k+1)}\right)\hfill \\ \hfill & =-E\log p^{\left(k\right)}\left(E[r^{\left(k\right)}\mid {R_{\mathit{IJ}}}^{\left(k\right)}]\right)\le E\left(E\left[\log p^{\left(k\right)}(r^{\left(k\right)}\mid {R_{\mathit{IJ}}}^{\left(k\right)})\right]\right)\hfill \\ \hfill & =-E\log p^{(k+1)}\left(r^{\left(k\right)}\right)=H\left(p^{\left(k\right)}\right).\hfill \end{array}$$

Under condition B), the result in Ebrahimi et al. [18] states that entropy and variance agree each other. i.e. one increase/decrease implies the other. Now the conclusion is immediate from 2).

2) By the total variance formula, we have

$$\begin{array}{cc}\hfill & {\sigma }^{\left(k\right)}=\mathit{Var}\left({r_{\mathit{UV}}}^{\left(k\right)}\right)\hfill \\ \hfill & =E\left[\mathit{Var}(r_{\mathit{UV}}\left(k\right)\mid R_{\mathit{IJ}}\left(k\right))\right]+\mathit{Var}\left(E(r_{\mathit{UV}}\left(k\right)\mid R_{\mathit{IJ}}\left(k\right)]\right)\hfill \\ \hfill & =E\left[\mathit{Var}(r_{\mathit{UV}}\left(k\right)\mid R_{\mathit{IJ}}\left(k\right))\right]+\mathit{Var}\left(r_{\mathit{IJ}}\left(k\right)\right)\hfill \\ \hfill & =E\left[\mathit{Var}(r_{\mathit{UV}}\left(k\right)\mid R_{\mathit{IJ}}\left(k\right))\right]+{\sigma }^{(k+1)}\ge {\sigma }^{(k+1)},\hfill \\ \hfill & (k=0,1,2,\dots ).=\hfill \end{array}$$

3) We only need to prove the convergence of the component r_ij^(k) for any fixed (i,j). In fact from (8), for any integer m and k we have

$$\begin{array}{cc}\hfill & {r_{\mathit{ij}}}^{(k+m)}=\frac{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}{r_{\mathit{uv}}}^{(k-1+m)}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^{2(k-1+m)})}{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}\phi (r_{\mathit{uv}}^{\left(0\right)}-r_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^{2(k-1+m)})}:\hfill \\ \hfill & =F\left({R_{\mathit{ij}}}^{(k-1+m)}\right),(i,j)\in S,k,m=0,1,2\dots \hfill \end{array}$$

Since σ⁽⁰⁾ ≺ ∞ and σ^(k) ≥ 0, by ii), we have σ^(k) → σ* for some 0 ≤σ* < ∞. So if we let

$$\begin{array}{cc}\hfill & {{\tilde{r}}_{\mathit{ij}}}^{(k+m)}=\frac{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}{{\tilde{r}}_{\mathit{uv}}}^{(k-1+m)}\phi ({\tilde{r}}_{\mathit{uv}}^{\left(0\right)}-{\tilde{r}}_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^{2\ast })}{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}\phi ({\tilde{r}}_{\mathit{uv}}^{\left(0\right)}-{\tilde{r}}_{\mathit{ij}}^{\left(0\right)}\mid {\sigma }^{2\ast })}:\hfill \\ \hfill & =\tilde{F}\left({R_{\mathit{ij}}}^{(k-1+m)}\right),(i,j)\in S,k,m=0,1,2\dots \hfill \end{array}$$

then r_ij^(k+m) = r̃_ij^(k+m) +o(1) as k →∞, thus we only need to prove the convergence of {r̃_ij^(k+m)}.

Note

$$\frac{\partial \tilde{F}\left({R_{\mathit{ij}}}^{(k-1+m)}\right)}{\partial {{\tilde{r}}_{\mathit{ij}}}^{(k-1+m)}}=\frac{\phi (0\mid {\sigma }^{2\ast })}{{\displaystyle \underset{(u,v)\in S_{\mathit{ij}}}{\Sigma }}\phi ({{\tilde{r}}_{\mathit{uv}}}^{\left(0\right)}-{{\tilde{r}}_{\mathit{ij}}}^{\left(0\right)}\mid {\sigma }^{2\ast })}≔C_{\mathit{ij}},$$

We have 0 < C_ij < 1, and for all m,

$$\begin{array}{cc}\hfill & |{{\tilde{r}}_{\mathit{ij}}}^{(l+1)}-{{\tilde{r}}_{\mathit{ij}}}^{\left(l\right)}|=C_{\mathit{ij}}|{{\tilde{r}}_{\mathit{ij}}}^{(k-1+m)}-{{\tilde{r}}_{\mathit{ij}}}^{(k-1)}|=\cdots ={C^k}_{\mathit{ij}}|{{\tilde{r}}_{\mathit{ij}}}^{\left(m\right)}-{{\tilde{r}}_{\mathit{ij}}}^{\left(0\right)}|\hfill \\ \hfill & \le {C^k}_{\mathit{ij}}\underset{l=0}{\overset{m-1}{\Sigma }}|{{\tilde{r}}_{\mathit{ij}}}^{(l+1)}-{{\tilde{r}}_{\mathit{ij}}}^{\left(l\right)}|\le {C^k}_{\mathit{ij}}\underset{l=0}{\overset{m-1}{\Sigma }}{C^l}_{\mathit{ij}}|{{\tilde{r}}_{\mathit{ij}}}^{\left(1\right)}-{{\tilde{r}}_{\mathit{ij}}}^{\left(0\right)}|\hfill \\ \hfill & \le \frac{{C_{\mathit{ij}}}^k}{1-C_{\mathit{ij}}}|{{\tilde{r}}_{\mathit{ij}}}^{\left(1\right)}-{{\tilde{r}}_{\mathit{ij}}}^{\left(0\right)}|\hfill \end{array}$$

thus {r̃_ij^(k+m)}_{k=1,2, …} is a Cauchy sequence, and the convergence follows.