Skip to main content
PMC home page
The Journal of Experimental Biology logoLink to The Journal of Experimental Biology
. 2011 Aug 15;214(16):2649–2653. doi: 10.1242/jeb.052985

High efficiency in human muscle: an anomaly and an opportunity?

Frank E Nelson 1,*, Justus D Ortega 2, Sharon A Jubrias 1, Kevin E Conley 1, Martin J Kushmerick 1
PMCID: PMC3144848  PMID: 21795559

Summary

Can human muscle be highly efficient in vivo? Animal muscles typically show contraction-coupling efficiencies <50% in vitro but a recent study reports that the human first dorsal interosseous (FDI) muscle of the hand has an efficiency value in vivo of 68%. We examine two key factors that could account for this apparently high efficiency value: (1) transfer of cross-bridge work into mechanical work and (2) the use of elastic energy to do external work. Our analysis supports a high contractile efficiency reflective of nearly complete transfer of muscular to mechanical work with no contribution by recycling of elastic energy to mechanical work. Our survey of reported contraction-coupling efficiency values puts the FDI value higher than typical values found in small animals in vitro but within the range of values for human muscle in vivo. These high efficiency values support recent studies that suggest lower Ca2+ cycling costs in working contractions and a decline in cost during repeated contractions. In the end, our analysis indicates that the FDI muscle may be exceptional in having an efficiency value on the higher end of that reported for human muscle. Thus, the FDI muscle may be an exception both in contraction-coupling efficiency and in Ca2+ cycling costs, which makes it an ideal muscle model system offering prime conditions for studying the energetics of muscle contraction in vivo.

Key words: muscle, efficiency, human

Introduction

A value of 0.68 for the efficiency of force production and activation (contraction-coupling efficiency) was recently reported for a human muscle (Jubrias et al., 2008). This value was calculated from the change in ATP per change in work over several work levels (so-called delta efficiency) (Gaesser and Brooks, 1975). Compared with other values, a contraction-coupling efficiency of 0.68 lies outside the range normally reported in skeletal muscle (Smith et al., 2005) and has recently been characterized as an anomalously high value (Barclay et al., 2010a). Here we evaluate how such a high value is possible and the implications of differences in the skeletal muscle efficiency between humans and small animals.

We examine four factors to understand the basis of this high efficiency value. First we examine two key factors of our system: (1) the biomechanical transfer of cross-bridge work to mechanical work and (2) the role of elastic energy transfer in the measured external work. Next we compare our efficiency estimate with those from in vitro experiments and other in vivo experiments in human muscle to determine the range of reported values and whether 0.68 lies outside these values. Finally, we explore the implication of a high contraction-coupling efficiency to Ca2+ activation costs in this muscle. In the end we find that the first dorsal interosseous (FDI) muscle of the hand represents an ideal muscle model system for measuring contraction-coupling efficiency in vivo as well as for studying mechanics and control of motor function.

Is the FDI a uniquely suited system for the study of contraction-coupling efficiency?

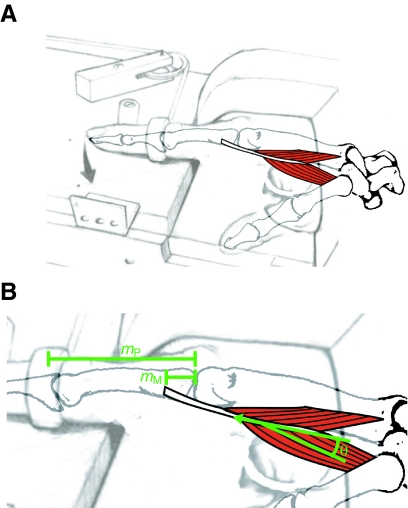
We employ a simple mechanical system that ensures a minimal loss of muscular work in the generation of mechanical work. Muscular work could be lost by transfer of work to another joint (Williams, 1985; Winter, 1990), co-contraction of an antagonist (Frost et al., 2002) or work on the muscle itself (Otten, 1988). These losses are minimized by the FDI muscle, which operates as a simple lever in a pinching motion involving the index finger and thumb. The FDI system achieves Wilkie's (Wilkie, 1949) four criteria for a simple mechanical system to measure exercise efficiency in human muscle: (1) it crosses a simple joint formed between the second metacarpal of the hand and the first phalange of the index finger (Fig. 1), (2) it is the only muscle that moves the index finger laterally (abduction), (3) it has a movement that is highly reproducible and often used for the study of motor control (Duchateau and Enoka, 2008), and (4) it can function while the hand is held in a rigid constraint. The FDI muscle also has a low pennation angle (Infantolino and Challis, 2010), which assures an efficient transfer of muscle work to mechanical work (Azizi et al., 2008; Otten, 1988). Thus a simple biomechanical system involving this hand muscle allows for efficient transfer of muscle work to the measuring device.

Fig. 1.

Fig. 1.

Open in a new tab

The orientation of the hand, first dorsal interosseous (FDI) muscle, and point of external force measurement. (A) The hand and FDI muscle oriented in our restraining apparatus used to make work and cost measurements. (B) The FDI muscle in greater detail, with its muscle moment arm (mM), phalange moment arm (mP), internal and external tendon (red) and pennation angle (θ).

Does recycling of energy via elastic storage do positive work and elevate efficiency?

Release of stored elastic energy during a contraction is an important source of error in measuring exercise efficiency (Hill, 1965). An example of how elastic energy can drastically reduce the muscular work required is hopping in a wallaby or kangaroo. In this system, elastic energy does half of the performed work at no additional energetic cost (Kram and Dawson, 1998). It operates by the gastrocnemius muscle contracting against the external force generated by the animal landing after each stride. The resulting stretch of the Achilles tendon stores elastic energy that is released as the animal is taking off from the ground. Under these conditions, twice as much work is measured externally as the work that the muscle alone produces because energy is stored and released from tendons.

Our system has been designed to remove the possibility that elastic energy recovery will add to the work generated by the FDI muscle. We have adopted Hill's (Hill, 1965) suggestion to use a lever system with small inertia. However, even after minimizing inertia there is some fluctuation in force (6.5–11 N) evident from our external measurement of force [fig. 1 in Jubrias et al. (Jubrias et al., 2008)]. The peak of this force fluctuation occurred at the same time muscle shortening stopped in our experiment, which prevents any stored elastic energy from generating mechanical work and artificially elevating the work accomplished in the experiment. Thus, we can eliminate mechanical energy recycling as a factor in our calculation of contraction-coupling efficiency.

How high is contraction-coupling efficiency?

Thermodynamic efficiency (η) is defined in terms of Gibbs free energy ΔG:

where w is mechanical work and ΔG is the free energy from ATP splitting. The free energy from ATP splitting is calculated from the extent of ATP splitting times its molar free energy (60 kJ mol–1). Jubrias and coworkers measured the work output and ATP splitting in a series of contractions done at several different workloads (Jubrias et al., 2008). The value of this ATP flux was multiplied by the value for the molar free energy of ATP to obtain data for chemical energy change at each incremental level of workload. The molar free energy of ATP was derived from measurements of intracellular pH and the concentrations of ATP, orthophosphate (Pi) and ADP. Contraction-coupling efficiency (ηcc) was determined directly from ATP because the predominant energy cost was cross-bridges doing work (Jubrias et al., 2008). The slope of regression analyses of work versus energy cost gave ηcc=(Δw/ΔΔGATP). This method for measuring η, termed `delta efficiency' by Gaesser and Brooks (Gaesser and Brooks, 1975), excludes not only resting ion pumping costs but also any changes in ion pumping costs with changes in work rate.

graphic file with name math001.jpg

However, most papers on muscular efficiency report results on the total energetic cost measured as the sum of the liberated heat and work output that is the total enthalpy change. Mechanical efficiency (ε) is:

where ΔH is the total change in enthalpy (Smith et al., 2005) as originally used by Hill (Hill, 1965) and subsequently by many authors cited in Smith et al. (Smith et al., 2005). ε and η are quantitatively related. For example, Smith and coworkers (Smith et al., 2005) illustrated the relationship between enthalpy and Gibbs free energy in the following equation:

graphic file with name math002.jpg

where T is the absolute temperature and ΔS is the change in entropy. Most of the measurements of ε are made such that net splitting of phosphocreatine (PCr) is the only significant reaction occurring, and thus the total enthalpy equals the extent of PCr change times the molar enthalpy of PCr splitting. Therefore:

graphic file with name math003.jpg

for ΔHPCr=34 kJ mol–1 and ΔGATP=60 kJ mol–1, ηε=ε/1.765. However, there are other differences in the conditions of these thermodynamic experiments leading to the calculations of thermodynamic and mechanical efficiencies (Barclay et al., 2010b). Thermodynamic quantities depend on intracellular conditions (e.g. pH, ionic strength and concentrations of metabolites), but these are not the source of variation among muscles and animal species. The temperature dependence of enthalpy and free energy can be calculated by the van 't Hoff relationship (Teague and Dobson, 1992), but empirical measurements of efficiency show it varies little with temperature (Barclay et al., 2010a). Therefore, the major consideration in comparing papers on efficiency is distinguishing between ε and η and converting one value to the other.

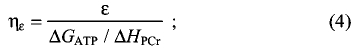graphic file with name math004.jpg

For brevity, we selected the highest four ε values reported for animals to compare with four papers reporting on η in human muscle (Table 1). The highest ε values come from four studies of different animal species and range from 0.33 to 0.77 (Barclay, 1994; Curtin and Woledge, 1993; Curtin et al., 1974; Woledge, 1968), which seems to suggest that Jubrias and colleagues' (Jubrias et al., 2008) value of 0.68 is not different from previous reports in animals. However, after we correct for the different denominators in the ε and η calculations, this range of efficiency values becomes 0.19 to 0.44, well below the 0.68 measured for the human FDI muscle. This clearly shows that estimated values for η in animal muscle in vitro are below 0.5 whereas the values measured in human muscle are higher.

Table 1.

Mechanical and thermodynamic efficiency studies with original and converted values using a common denominator

graphic file with name table001.jpg

Open in a new tab

For comparison to our recent estimate (Jubrias et al., 2008), the human studies require a complex adjustment to contemporary reference values because they measure energy costs by indirect or direct calorimetry (Table 1). In contrast to the animal studies, all of the human studies found efficiencies of 0.5 or greater; one of these studies even came very close to our estimate of 0.68 after corrections to common units (Table 1). All values listed in Table 1 are those as published followed by values recalculated using a common energetic parameter, mitochondrial efficiency (P/O), of 2.5 and a ΔGATP value of 60 kJ mol–1. A study using direct calorimetry in the quadriceps (Bangsbo et al., 2001) found a range of efficiencies during work isolated to this muscle group. Efficiency values were highest early in a sustained work bout and decreased by half at the end; the value given in Table 1 reflects the results over the initial 10 s of exercise. Another study (Gaesser and Brooks, 1975), using well-conditioned individuals, reported contraction-coupling efficiency in the range of 0.41–0.57 in steady state work on a bicycle; those values were adjusted in Table 1, as explained in the following paragraph. A third study found a contraction-coupling efficiency value of 0.49 based on an analysis of the series of efficiencies linking contraction-coupling, mitochondrial and exercise efficiency (Whipp and Wasserman, 1969).

Mitochondrial coupling has been found to be lower (ATP/O2=5, P/O=2.5) than classical values (ATP/O2=6) (Amara et al., 2007; Brand, 2005). Recent work from our laboratory shows a P/O of ∼ 2.5 in human and mouse muscle in vivo (Amara et al., 2007; Marcinek et al., 2004), which is indicative of well-coupled mitochondria (Brand, 2005). This value confirms the value found in the quadriceps (P/O=2.3) in an earlier study using independent methods [calculated from Conley et al. (Conley et al., 2000)] and values on isolated muscles (P/O=2.6) (Lou et al., 2000). The conversion of the P/O ratio from a stoichiometric to an efficiency value requires the use of Gibbs free energy (ΔG), which our measurements show is higher than previously thought (∼60 kJ mol–1 during exercise) (Barclay et al., 2010a; Jubrias et al., 2008). We use 60 kJ mol–1 to scale all reported values in Table 1. The total energy available per mole of O2, as used in indirect calorimetry (Scott and Kemp, 2005), is 258 kJ mol–1 and, with P/O=2.5, yields a value for free energy from ATP (ΔGATP) equal to 52 kJ mol–1, or 0.86 times our value of 60 kJ mol–1. Applying these adjustments decreases the adjusted η values from the results of Whipp and Wasserman [table 1 in Whipp and Wasserman (Whipp and Wasserman, 1969)]. The two cycling efficiency values (Gaesser and Brooks, 1975; Whipp and Wasserman, 1969) could have had some co-contraction or a lower mitochondrial coupling than we guessed, leading to an underestimate of contraction-coupling efficiency. The contraction-coupling efficiency values for one cycling study (Whipp and Wasserman, 1969) and the study of the quadriceps muscle group (Bangsbo et al., 2001) were calculated only at one workload, so they did not account for possible floating baselines. Nonetheless, there is an overall consistency in human contraction-coupling efficiency values, given the number of assumptions and complications of the mechanical systems and techniques. These reports of human muscle efficiency give high efficiency values, above 0.5, and considerably higher than found in animal muscles in vitro.

In summary, our value of 0.68 in the FDI muscle has been characterized as an `anomaly' relative to values in animal muscle (Barclay et al., 2010a). Our analyses show that there is a systematic difference between measurements of efficiency in human muscle in vivo (Table 1) and animal muscle in vitro [table 3 in Smith et al. (Smith et al., 2005)]. The reason for this difference remains to be discovered. One possibility is that this difference is due to scaling with body mass. For example, smaller animals tend to have lower efficiencies than larger animals during locomotion [table 3 in Heglund et al. (Heglund et al., 1982)]. Independent of these differences, this paper outlines how the FDI muscle can be used to advantage for studies of muscle efficiency. We argue that it is a useful model and exceptionally good system for studying muscle efficiency. For example, the FDI has a high and stable mitochondrial coupling (P/O=2.7) value up to late middle age (19–50 years old) in comparison with the large range of values found in the quadriceps [calculated from Conley et al. (Conley et al., 2000)] and tibialis anterior muscle (Amara et al., 2007). It also is uniquely able to exercise close to its aerobic capacity without the fatigue that is evident in leg muscles (Jubrias et al., 2003). Exceptional systems are highly sought after in comparative studies to provide insight into physiological limits and as means to explore underlying mechanisms that might not be apparent at the middle of the continuum (Krebs, 1975; Krogh, 1929). The exceptional contraction-coupling efficiency of the FDI muscle may qualify this muscle as a model system for investigating how high efficiency is possible.

Is the energetic cost of activation of cross-bridge cycling low in human muscle?

One factor that could account for a high contraction-coupling efficiency is a low cost for activating cross-bridge cycling. The cost of activation is typically attributed to Ca2+ cycling by the sarcoplasmic reticulum Ca2+ ATPase and has recently been estimated to be 0.25–0.40 of contraction-coupling costs in isometric contractions (Barclay et al., 2007). However, this value could decline in working contractions. Barclay and coworkers [fig. 1B in Barclay et al. (Barclay et al., 2010b)] illustrate that the energetic cost does not show the expected linear increase with shortening velocity in a working contraction. This non-linearity suggests that the relative activation costs may decrease with shortening velocity in a working contraction.

A decline may also occur for long-duration contraction trains such as the >40 s contraction train needed to measure ATP flux versus work in the FDI experiment. A good example of reduced costs during prolonged contractions is shown in fig. 1 of Crow and Kushmerick (Crow and Kushmerick, 1982). Their study shows that contraction-coupling costs per time-tension integral decline by half at longer stimulus trains in mouse extensor digitorum longus (EDL) muscle. The EDL has substantial levels of parvalbumin (Moerland et al., 1989), which act as a Ca2+ buffer in the muscle cell. In contrast, mouse soleus muscle lacks parvalbumin and does not show a change in contraction-coupling costs under the same conditions (Moerland and Kushmerick, 1994). Therefore, parvalbumin may act to reduce Ca2+ cycling costs in later contractions because it acts as a buffer that fills with Ca2+ in a series of contractions. Once the buffers are full or close to full, the amount of Ca2+ necessary is only that needed to be cycled for activation and deactivation. Evidence that this occurs in human muscle is the decrease in the fraction of the total cost with exercise duration in gastrocnemius muscle (Russ et al., 2002). Thus, one plausible explanation for the high contraction-coupling efficiency in human FDI is the intriguing possibility that the ATP cost for non-cross-bridge cycling is lower in this muscle. This lower activation cost may be apparent during working contractions and in the series of contractions that are needed to measure ATP flux in vivo.

Conclusions and integration

In this paper we examined two key factors that are responsible for contraction-coupling efficiency in human FDI: (1) efficient transfer of cross-bridge work to mechanical work and (2) the absence of elastic energy to do this external work. Comparison of our value with in vitro and other in vivo estimates from the literature reveals that a contraction-coupling efficiency of 0.68 is probably outside the range reported for animal muscles but on the upper end of published values in human muscle. This high value leads to the intriguing notion that non-cross-bridge energy costs during contraction may be lower in this muscle in a series of working contractions than in single isometric twitches typically used in isolated muscle studies. Thus, the unusually high contraction-coupling efficiency in the FDI muscle may provide a unique opportunity for exploring the limits of cross-bridge and Ca2+ cycling costs that underlie contraction in vivo in human muscle.

Acknowledgements

We would like to thank the reviewers and Daryl Monear for their suggestions and criticisms.

Glossary

Gibbs free energy (ΔG)

Total useable energy from a quantity of a substance at constant temperature and pressure (Gibbs, 1873), which can be used for mechanical work (Whipp and Wasserman, 1969).

Entropy (ΔS)

A measure of the energy not available for useful work in a thermodynamic process (Clausius, 1865; Whipp and Wasserman, 1969).

Enthalpy (ΔH)
graphic file with name math005.jpg
The heat content of the system at constant pressure, this includes the Gibbs free energy and the temperature of the environment times the entropy (Smith et al., 2005; Whipp and Wasserman, 1969).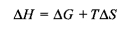
Mechanical efficiency (ε)
graphic file with name math006.jpg
Total mechanical work divided by the change in heat content, where the change in heat content is measured by changes in heat (Smith et al., 2005).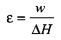
Thermodynamic efficiency (η)
graphic file with name math007.jpg
Total mechanical work divided by total free energy, where the total free energy is measured by the flux of ATP (Smith et al., 2005).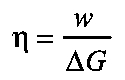
Delta efficiency (Δε or Δη)
graphic file with name math008.jpg
Total change in mechanical work divided by the change in total or total free energy across loads; ΔG is used in this equation but ΔH could also be used (Gaesser and Brooks, 1975).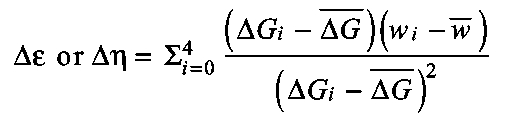
Exercise efficiency

Total mechanical work divided by energy expended in doing work, where the energy expended is measured by indirect calorimetry (Powers et al., 1984).

Mitochondrial efficiency (P/O)

The ratio of mitochondrial phosphorylation flux to mitochondrial oxidation flux divided by two (Amara et al., 2008).

Contraction-coupling efficiency

Total mechanical work divided by ATP flux (Whipp and Wasserman, 1969).

Footnotes

Funding for this work was provided by grants R01AR41928, F32AG029064 and 1RC2AG036606 from the US NIH. Deposited in PMC for release after 12 months.

References

  1. Amara C. E., Shankland E. G., Jubrias S. A., Marcinek D. J., Kushmerick M. J., Conley K. E. (2007). Mild mitochondrial uncoupling impacts cellular aging in human muscles in vivo. Proc. Natl. Acad. Sci. USA 104, 1057-1062 [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Amara C. E., Marcinek D. J., Shankland E. G., Schenkman K. A., Arakaki L. S., Conley K. E. (2008). Mitochondrial function in vivo: spectroscopy provides window on cellular energetics. Methods 46, 312-318 [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Azizi E., Brainerd E. L., Roberts T. J. (2008). Variable gearing in pennate muscles. Proc. Natl. Acad. Sci. USA 105, 1745-1750 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bangsbo J., Krustrup P., Gonzalez-Alonso J., Saltin B. (2001). ATP production and efficiency of human skeletal muscle during intense exercise: effect of previous exercise. Am. J. Physiol. Endocrinol. Metab. 280, E956-E964 [DOI] [PubMed] [Google Scholar]
  5. Barclay C. J. (1994). Efficiency of fast- and slow-twitch muscles of the mouse performing cyclic contractions. J. Exp. Biol. 193, 65-78 [DOI] [PubMed] [Google Scholar]
  6. Barclay C. J., Woledge R. C., Curtin N. A. (2007). Energy turnover for Ca2+ cycling in skeletal muscle. J. Muscle Res. Cell Motil. 28, 259-274 [DOI] [PubMed] [Google Scholar]
  7. Barclay C. J., Curtin N. A., Woledge R. C. (2010a). Is the efficiency of mammalian (mouse) skeletal muscle temperature dependent? J. Physiol. 588, 3819-3831 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Barclay C. J., Woledge R. C., Curtin N. A. (2010b). Inferring crossbridge properties from skeletal muscle energetics. Prog. Biophys. Mol. Biol. 102, 53-71 [DOI] [PubMed] [Google Scholar]
  9. Brand M. D. (2005). The efficiency and plasticity of mitochondrial energy transduction. Biochem. Soc. Trans. 33, 897-904 [DOI] [PubMed] [Google Scholar]
  10. Clausius R. (1865). The Mechanical Theory of Heat – with Its Applications to the Steam Engine and to Physical Properties of Bodies. London: John van Voorst; [Google Scholar]
  11. Conley K. E., Jubrias S. A., Esselman P. C. (2000). Oxidative capacity and ageing in human muscle. J. Physiol. 526, 203-210 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Crow M. T., Kushmerick M. J. (1982). Chemical energetics of slow- and fast-twitch muscles of the mouse. J. Gen. Physiol. 79, 147-166 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Curtin N. A., Woledge R. C. (1993). Efficiency of energy conversion during sinusoidal movement of red muscle fibres from the dogfish Scyliorhinus canicula. J. Exp. Biol. 185, 195-206 [DOI] [PubMed] [Google Scholar]
  14. Curtin N. A., Gilbert C., Kretzschmar K. M., Wilkie D. R. (1974). The effect of the performance of work on total energy output and metabolism during muscular contraction. J. Physiol. 238, 455-472 [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Duchateau J., Enoka R. M. (2008). Neural control of shortening and lengthening contractions: influence of task constraints. J. Physiol. 586, 5853-5864 [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Frost G., Bar-Or O., Dowling J., Dyson K. (2002). Explaining differences in the metabolic cost and efficiency of treadmill locomotion in children. J. Sports Sci. 20, 451-461 [DOI] [PubMed] [Google Scholar]
  17. Gaesser G. A., Brooks G. A. (1975). Muscular efficiency during steady-rate exercise: effects of speed and work rate. J. Appl. Physiol. 38, 1132-1139 [DOI] [PubMed] [Google Scholar]
  18. Gibbs J. W. (1873). A method of geometrical representation of the thermodynamic properties of substances by means of surfaces. Trans. Conn. Acad. Arts Sci. 2, 382-404 [Google Scholar]
  19. Heglund N. C., Fedak M. A., Taylor C. R., Cavagna G. A. (1982). Energetics and mechanics of terrestrial locomotion. IV. Total mechanical energy changes as a function of speed and body size in birds and mammals. J. Exp. Biol. 97, 57-66 [DOI] [PubMed] [Google Scholar]
  20. Hill A. V. (1965). Trails and Trials in Physiology. London: Edward Arnold Ltd. [Google Scholar]
  21. Infantolino B. W., Challis J. H. (2010). Architectural properties of the first dorsal interosseous muscle. J. Anat. 216, 463-469 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Jubrias S. A., Crowther G. J., Shankland E. G., Gronka R. K., Conley K. E. (2003). Acidosis inhibits oxidative phosphorylation in contracting human skeletal muscle in vivo. J. Physiol. 553, 589-599 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Jubrias S. A., Vollestad N. K., Gronka R. K., Kushmerick M. J. (2008). Contraction coupling efficiency of human first dorsal interosseous muscle. J. Physiol. 586, 1993-2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kram R., Dawson T. J. (1998). Energetics and biomechanics of locomotion by red kangaroos (Macropus rufus). Comp. Biochem. Physiol. 120B, 41-49 [DOI] [PubMed] [Google Scholar]
  25. Krebs H. A. (1975). The August Krogh principle: ``for many problems there is an animal on which it can be most conveniently studied''. J. Exp. Zool. 194, 221-226 [DOI] [PubMed] [Google Scholar]
  26. Krogh A. (1929). The progress of physiology. Science 70, 200-204 [DOI] [PubMed] [Google Scholar]
  27. Lou F., van Der Laarse W. J., Curtin N. A., Woledge R. C. (2000). Heat production and oxygen consumption during metabolic recovery of white muscle fibres from the dogfish Scyliorhinus canicula. J. Exp. Biol. 203, 1201-1210 [DOI] [PubMed] [Google Scholar]
  28. Marcinek D. J., Schenkman K. A., Ciesielski W. A., Conley K. E. (2004). Mitochondrial coupling in vivo in mouse skeletal muscle. Am. J. Physiol. Cell Physiol. 286, C457-C463 [DOI] [PubMed] [Google Scholar]
  29. Moerland T. S., Kushmerick M. J. (1994). Contractile economy and aerobic recovery metabolism in skeletal muscle adapted to creatine depletion. Am. J. Physiol. 267, C127-C137 [DOI] [PubMed] [Google Scholar]
  30. Moerland T. S., Wolf N. G., Kushmerick M. J. (1989). Administration of a creatine analogue induces isomyosin transitions in muscle. Am. J. Physiol. 257, C810-C816 [DOI] [PubMed] [Google Scholar]
  31. Otten E. (1988). Concepts and models of functional architecture in skeletal muscle. Exerc. Sport Sci. Rev. 16, 89-137 [PubMed] [Google Scholar]
  32. Powers S. K., Beadle R. E., Mangum M. (1984). Exercise efficiency during arm ergometry: effects of speed and work rate. J. Appl. Physiol. 56, 495-499 [DOI] [PubMed] [Google Scholar]
  33. Russ D. W., Elliott M. A., Vandenborne K., Walter G. A., Binder-Macleod S. A. (2002). Metabolic costs of isometric force generation and maintenance of human skeletal muscle. Am. J. Physiol. Endocrinol. Metab. 282, E448-E457 [DOI] [PubMed] [Google Scholar]
  34. Scott C. B., Kemp R. B. (2005). Direct and indirect calorimetry of lactate oxidation: implications for whole-body energy expenditure. J. Sports Sci. 23, 15-19 [DOI] [PubMed] [Google Scholar]
  35. Smith N. P., Barclay C. J., Loiselle D. S. (2005). The efficiency of muscle contraction. Prog. Biophys. Mol. Biol. 88, 1-58 [DOI] [PubMed] [Google Scholar]
  36. Teague W. E., Jr, Dobson G. P. (1992). Effect of temperature on the creatine kinase equilibrium. J. Biol. Chem. 267, 14084-14093 [PubMed] [Google Scholar]
  37. Whipp B. J., Wasserman K. (1969). Efficiency of muscular work. J. Appl. Physiol. 26, 644-648 [DOI] [PubMed] [Google Scholar]
  38. Wilkie D. R. (1949). Relationship between force and speed in the human muscle. J. Physiol. 108, Proc, 7 [PubMed] [Google Scholar]
  39. Williams K. R. (1985). The relationship between mechanical and physiological energy estimates. Med. Sci. Sports Exerc. 17, 317-325 [PubMed] [Google Scholar]
  40. Winter D. A. (1990). Biomechanics and Motor Control of Human Movement. New York: John Wiley and Sons; [Google Scholar]
  41. Woledge R. C. (1968). The energetics of tortoise muscle. J. Physiol. 197, 685-707 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from The Journal of Experimental Biology are provided here courtesy of Company of Biologists

RESOURCES