Abstract
Magnetic resonance elastography (MRE) is a non invasive phase-contrast based method for quantifying the shear stiffness of biological tissues. Synchronous application of a shear wave source and motion encoding gradient waveforms within the MRE pulse sequence enable visualization of the propagating shear wave throughout the medium under investigation. Encoded shear wave induced displacements are then processed to calculate the local shear stiffness of each voxel. An important consideration in local shear stiffness estimates is that the algorithms employed typically calculate shear stiffness using relatively high signal-to-noise ratio (SNR) MRE images and have difficulties at extremely low SNR. A new method of estimating shear stiffness based on the principal spatial frequency of the shear wave displacement map is presented. Finite element simulations were performed to assess the relative insensitivity of this approach to decreases in SNR. Additionally, ex vivo experiments were conducted on normal rat lungs to assess the robustness of this approach in low SNR biological tissue. Simulation and experimental results indicate that calculation of shear stiffness by the principal frequency method is less sensitive to extremely low SNR than previously reported MRE inversion methods but at the expense of loss of spatial information within the region of interest from which the principal frequency estimate is derived.
Keywords: shear modulus, shear stiffness, transpulmonary pressure, lungs, magnetic resonance elastography, elasticity
1. Introduction
Magnetic resonance elastography (MRE) is a phase-contrast MR imaging technique (Muthupillai et al., 1995) that is capable of spatially resolving the shear stiffness of biological tissues and has been shown to be a sensitive metric for detection of both benign and malignant processes in the breast (Sinkus et al., 2005b, Siegmann et al., , McKnight et al., 2002 , Plewes et al., 2000, Bercoff et al., 2003, Lorenzen et al., 2002), prostate (Dresner et al., 2003), heart (Kolipaka et al., 2009), skeletal muscle (Papazoglou et al., 2006 Dresner, 2001 #319, Bensamoun et al., 2007, Bensamoun et al., 2006) brain (Kruse and Ehman, 2003, Kruse et al., 2006, Kruse et al., 2008, Sack et al., 2007, Green et al., 2008), and liver (Yin et al., 2007, Huwart et al., 2007). However, each of these applications have been applied to organs in which the signal-to-noise ratio (SNR) is generally considered to be high, both in terms of the magnitude of the MRE signal as well as the phase into which the shear wave displacements are encoded. In contrast, MRE of the lung is uniquely challenging due in large part to the decreased SNR of both the magnitude and phase of conventional 1H MRE images. This decrease in SNR is due to the decreased physical density of lung which is approximately one third that of solid organs (Hachenberg et al., 1993)) and the ultra short T2* of lung parenchyma. Decreased physical density reduces the number of protons that contribute to the net MR signal within each voxel while the ultra short T2*, which is of the order of 1 to 2 msec (Hatabu et al., 1999), means that significant signal decay occurs during the typical echo time used to acquire the MR signal using conventional pulse sequences, resulting in further signal loss and SNR degradation. This decrease in SNR is further exacerbated with increasing inflation pressure resulting in decreased physical density and increased susceptibility-induced signal loss.
Many techniques to calculate shear modulus from MRE wave displacement data have been described (Manduca et al., 2001b), with perhaps the most commonly used being direct inversion of the Helmholtz equation (Romano et al., 2000, Romano et al., 2005, Oliphant, 2001, Sinkus et al., 2005a, Papazoglou et al., 2008). In moderate to high SNR data sets, various inversion methods have been shown to accurately calculate the shear stiffness of tissue like materials (Hamhaber et al., 2003, Ringleb et al., 2005). However, as the SNR of the MRE data decreases, direct inversion and other inversion methods can underestimate the value of the shear stiffness (Papazoglou et al., 2008, Manduca et al., 2001a), particularly in less elastic materials in which the shear wavelength becomes large compared to the object's dimensions. A common method to calculate the shear stiffness of biological tissue which is more robust to noise is local frequency estimation (LFE) (Manduca et al., 2001a). This method estimates the local spatial frequency and hence wavelength of the shear wave over a range of several frequency scales. These scales are selected by filtering the spatial frequency data with a bank of six log-normal filters in which the peak frequency of each filter is equal to wave numbers of one, two, four, eight, 16 and 32 waves / field of view (FOV) and a weighted average of these yields a spatial map of wave speed c (Manduca et al., 1996). The shear stiffness is then calculated based on the relationship μ = ρc2 where μ is the shear modulus of a purely elastic material and ρ it's density. The final estimate of μ is obtained from the average of all six filtered data sets. This formula assumes no attenuation, and hence the shear stiffness is an effective quantity - the stiffness of a purely elastic material that would give the observed wavelength. In this work LFE will be the standard inversion method against which the newly proposed inversion method will be compared because of its relative insensitivity to noise.
The problem of low SNR becomes particularly important in the case of the lung, a relatively inelastic organ in which the density is typically one third that of solid organs (nominally considered to be equal to approximately 1 g/cm3 or 1000 kg/m3) and varies throughout the respiratory cycle due to changes in tidal lung volume. The SNR of MRE lung data is very low, as noted above, due to its low physical density and ultra short T2*. Additionally, a decrease in SNR with increasing lung volume can introduce a pressure-dependent bias in the MRE estimate of shear stiffness, with shear stiffness being increasingly underestimated as lung volume and hence transpulmonary pressure (Ptp) increases. While it is generally appreciated that lung stiffness is a linear function of Ptp with a slope approximately equal to 0.7 (when Ptp is measured in centimeters of water (cm H2O)) (Hajji et al., 1979), underestimation of shear stiffness with increasing Ptp due to decreased SNR will in turn result in an underestimate of this slope. Deviation from the true value of the slope and hence shear stiffness will introduce errors which could be misinterpreted as being indicative of some disease process or affect the diagnostic sensitivity and specificity of MRE-based estimates of shear stiffness. In this work, a new method for estimating shear stiffness for very low SNR MRE data such as lung parenchyma based on the principal spatial frequency of the propagating shear wave field is presented. We hypothesize that this method is less sensitive to decreases in MRE phase contrast SNR compared to standard inversion methods such as LFE. The purpose of this work is to evaluate this hypothesis both theoretically and experimentally by finite element simulation and MRE imaging of ex vivo normal rat lung.
2. Experimental Procedure
2.1 Principal Frequency Estimation of Shear Modulus
In MRE, visualization of the propagating shear wave field is achieved by acquiring phase contrast MRE images at multiple time points. These time points are usually chosen so as to be offset by a fraction of the period of the shear wave in which the fraction is calculated to be the 1/n times the period and n the number of images. In this way the sequence of images are spaced equally throughout the wave cycle and represent a temporal sample of the propagating wave. Typically, a temporal Fourier transform (i.e. the one-dimensional Fourier transform of the phase offset information) is performed at each pixel to extract the motion at the excitation frequency which is also equal to the first spatial harmonic of the shear wave. After identification of the first harmonic the data is then used as input to the chosen inversion algorithm such as LFE.
In the proposed method, a region up to and including the entire image is filtered as above to extract the temporal excitation frequency. The temporally filtered data is then zero filled by a factor of two followed by two-dimensional spatial Fourier transformation. The data is zero padded in this way to improve the frequency resolution of the peak of the power spectrum when the wavelength approaches the dimensions of the object within the image. That is, when the spatial frequency is close to zero or the center of the spatial frequency spectrum. A thresholding procedure is then applied in which the peak amplitude of the spectrum is identified followed by zeroing of amplitude values that are less than some fraction of the peak value. The threshold value of 50% is chosen by default and was used throughout this study but can be modified to be any value within the range of zero to 100% of the peak power spectrum value. A weighted average of the radial spatial frequencies corresponding to spectrum amplitude values above this threshold is then calculated. This average, given in equation 1, involves the magnitude, M(f), of the spectrum at each spatial frequency above the threshold, multiplied by its corresponding radial frequency frad.
| (1) |
The radial spatial frequency identified as fcentroid is then used to calculate the wavelength λ (the inverse of the spatial frequency), shear wave speed c (c = fλ where f is the excitation frequency), and shear stiffness (μ = ρc2). This approach does not attempt to calculate local stiffness values, but rather a single average value over a large region.
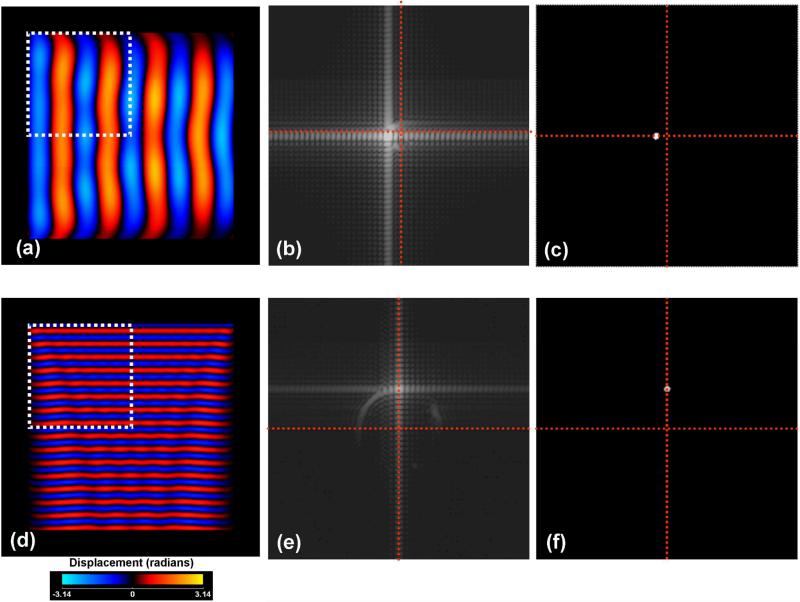
Figure 1 demonstrates this method in a simulation of a material of density equal to 1000 kg / m3 and shear modulus of 20 kPa in which two separate uniform shear waves are propagating at frequencies of 100 Hz (a) and 350 Hz (b) along the horizontal and vertical directions respectively. The material was simulated to have dimensions of 20 cm × 20 cm while the FOV containing the object was set to 25 cm × 25 cm. A total of eight phase offsets (45° apart) were simulated to represent the planar shear wave fronts. The two dimensional power spectrum of a region of interest approximately one quarter of the size of the object for both wave fronts is shown in figure 1 (b) and (e) respectively demonstrating that the majority of the power is located at wave numbers equal to 1.41 and 4.92 radians/centimeter, corresponding to shear stiffness estimates of 19.61 and 19.84 kPa respectively. Figures 1 (c) and (f) show the power spectrum after thresholding to identify the spectrum centroid from which the dominant wavelength is identified. The broadening of the principal frequency is due to the convolution with the Fourier transform of the window used to select the appropriate region of interest.
Figure 1.
Principal frequency based method of estimating shear modulus within a region of interest of the phase contrast shear wave displacement map for a simulated material of shear stiffness of 20 kPa. The FOV of the image is 25 cm × 25cm while the object is of dimension 20 cm × 20 cm. The square region of interest indicates the region over which the shear stiffness was estimated. Figures (a) through (c) show the simulated displacement field for a 100 Hz shear wave, the original and thresholded power spectrum of the displacement field within the identified region of interest, respectively. Figures (d) through (f) show the equivalent data as in (a) through (c) but at the higher frequency of 350 Hz. The red cross-hairs overlaying the power spectrum data identify the two frequency axes while their intersection marks the location of the zero or DC frequency term.
2.2 Finite Element Simulations
To evaluate the response of the proposed method to decreased MRE phase SNR and to compare it to LFE-based estimates of shear stiffness, shear wave fields within a uniform phantom were simulated using finite element modeling (COMSOL 3.5, Burlington, MA). The finite element model consisted of a rectangular cuboid with a cross section of side 3.75 cm × 1.6 cm with infinite length. These in-plane dimensions were chosen to approximate the size of a normal rat lung imaged with parameters comparable to the ex vivo data, thereby facilitating comparison of phantom and ex vivo data and effectively providing a two dimensional model. Time-harmonic waves were induced at one of the boundaries propagated uniformly within the model domain according to the simple Helmholtz wave equation
| (2) |
where ▽2 is the Laplacian operator, u is the displacement vector, k is the wave number and λ is the wavelength. To simulate the wave propagation based on a particular stiffness and frequency of interest, the wave number was input as k2 = ρω2 / μ where ρ is the tissue density and assumed to be the density of water or 1000 kg/m3, ω is the angular frequency and equal to 2πf where f is the frequency of vibration which in this case was set at 220 Hz to approximate the ex vivo experiments, and μ is the complex shear modulus, expressed as μ1 + μ2i, where the real part μ1 indicates the storage modulus and the imaginary part μ2 indicates the loss modulus. Wave displacement fields were simulated for ten stiffness values with μ1 set from 2.5 kPa to 25 kPa in intervals of 2.5 kPa. μ2 values were set at 0.1μ1. The wave source was simulated by setting that boundary condition to be n.(▽u) + iku = 2ik where n is the outward boundary normal vector. All the other boundaries were set to be n.(▽u) + iku = 0 for matched boundary conditions resulting in no wave reflection or interference. The finite element simulations had 16678 elements and 33889 degrees of freedom.
To test the robustness of the proposed principal frequency algorithm with respect to noise, increasing amounts of Gaussian noise were added to the data obtained for all the simulated stiffnesses so as to have median SNRs ranging from 9 to 2. Noise was added by first converting the displacement images to complex data sets with a magnitude of unity and phase equal to the displacement field in radians. These data were then normalized so that the simulated values were within the dynamic range of -π to π. Gaussian noise was added to the real and imaginary channels independently. Each noise added data set was then processed with both the LFE and principal frequency algorithms. The estimated stiffnesses were then compared to the input stiffness values. Unlike previous simulations involving LFE (Manduca et al., 1996) in which the wavelength of the shear wave was less than the dimensions of the simulated object, in this study at larger stiffness values this was not true. Under these conditions LFE will under estimate shear stiffness independent of the SNR of the image.
2.3 Ex Vivo Validation
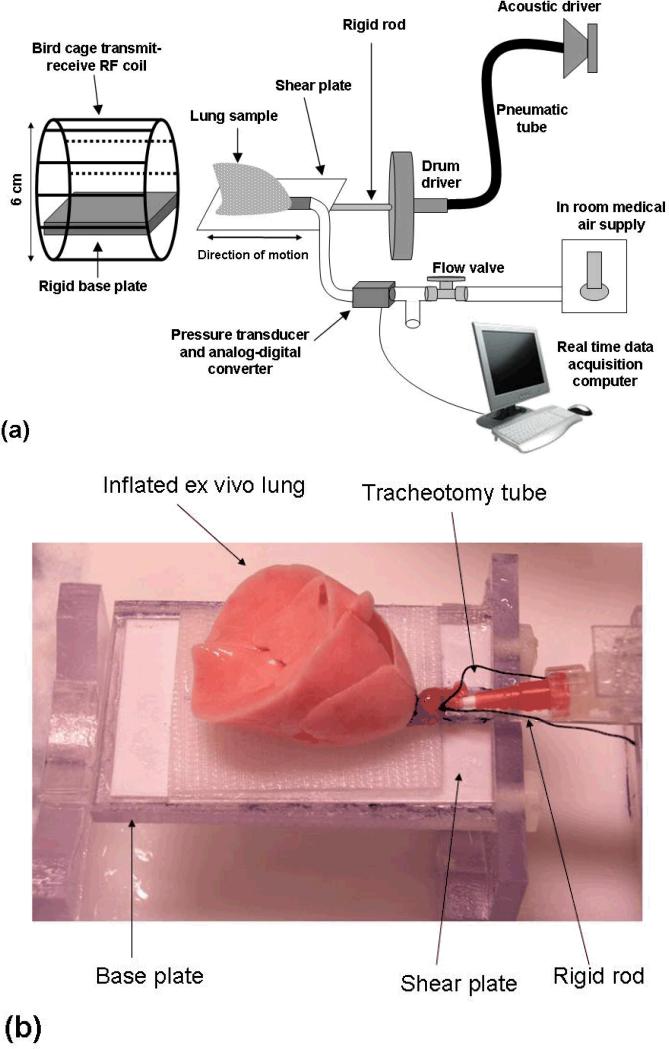
To evaluate the accuracy of the proposed principal frequency estimation method for estimating shear stiffness in low SNR biological tissue, a series of experiments were conducted on ex vivo rat lungs. Figure 2(a) shows the experimental setup which includes a pneumatic drum driver and shear plate, active driver system, six centimeter diameter RF transmit-receive coil and computer controlled air flow system for maintenance of constant inflation pressure. Lung specimens were placed on the driver shear plate that is mechanically tethered to the pneumatic drum driver by means of a rigid plexiglass rod as shown in figure 2(b). Shear waves were introduced within the lung specimen by cyclic motion on the driver plate/drum driver which was in turn attached to an active driver system that included an audio speaker, waveform generator and pneumatic tube. A positive air flow system, which included a needle valve (Cole Parmer, Vernon Hills, IL, USA) for pressure regulation, pressure transducer (Freescale Semiconductor model MPV7002DP, Austin, TX, USA), analog-to-digital converter (National Instruments model USB-9162, Austin, TX, USA) and computer controlled data acquisition and logging software (Measurement & Automation Explorer, National Instruments, Austin, TX, USA) was used to both regulate and monitor lung Ptp.
Figure 2.
(a) Schematic representation of the experimental set up for ex vivo rat lung MR elastography. (b) Ex vivo rat lung inflated to a pressure (Ptp) of 20 cm H2O. The lung is placed on the shear plate which in turn is connected to the rigid plexiglass rod and drum driver.
Whole lungs were harvested from a total of five adult female Sprague-Dawley rats. The lungs were obtained following expiration of the host by a fatal dose of anesthesia in accordance with institutional animal use and care protocols. After expiration, exsanguination was performed by administration of heprin followed by severing of the descending aorta. The rib cage was separated along the sternum after which the heart, thymus and lungs were removed en bloc. Shortly thereafter the left and right ventricles of the heart were removed followed by placement of a plastic tracheotomy tube into the severed trachea.
After excision the lungs were degassed to prevent air trapping upon reinflation. This was achieved by first placing the lungs and attached tracheotomy tube on a plastic sample dish within an in house glass bell jar and vacuum pump (Thomas Compressors & Vacuum Pumps, Model 2580B-01, Skokie, IL, USA) assembly. After placing the lung within the bell jar, the vacuum pump was turned on until the pressure within the jar was approximately 700 mm Hg below atmospheric pressure. This procedure lasted for approximately two minutes after which the pump was turned off and the pressure within the jar was allowed to slowly return to atmospheric pressure by means of a needle valve/pressure gauge assembly (Gast Manufacturing Corp., Benton Harbor, MI, USA) attached in line between the pump and bell jar. The lungs were immediately connected to the air system identified in figure 2 and inflated to a Ptp value of 20 cm H20. Once the lungs were fully inflated, they were transferred to the stage of the imaging apparatus described in figure 2. One such ex vivo rat lung inflated to a pressure of 20 cm H2O is shown in figure 2(b). The lungs were then deflated to a pressure of 3 cm H2O and imaged. To ensure that each lung experienced the same inflation history, following acquisition of MRE data at 3 cm H2O, the lungs were inflated to a pressure of 20 cm H20 for approximately one minute, after which they were deflated to the next inflation pressure. This procedure was then repeated for all inflation pressures that included 6, 9, 10, 12 and 15 cm H20.
Visualization of shear waves was performed by acquiring multi slice axial spin echo-based MRE images on a 1.5T MR scanner with Twinspeed gradients (Signa Excite, GE Healthcare, Milwaukee, WI) with the following parameters: FOV = 6 cm, slice thickness = 4 mm, TE = 21 msec TR = 200 – 300 msec, mechanical excitation frequency = 200 – 220 Hz, motion sensitivity direction = slice, kx/ky = 128/64, bandwidth = ±15.6 kHz, MRE phase offsets = 4-6. The spin echo pulse sequence was synchronized to the active (audio speaker) and passive (drum driver) shear wave generator by a timing pulse included within the pulse sequence that allows continuous waves to be present within the sample during imaging as well as timing of the appropriate delay times necessary to generate phase contrast images at given phase offsets throughout the shear wave period. After acquisition, the MRE data were processed off line using in house software to calculate both LFE and principal frequency based estimates of shear stiffness for each slice of each data set.
For each ex vivo lung sample, six to eight MRE transaxial slices were acquired at each of the previously stated inflation pressures. Each slice was processed by both the LFE and principal frequency inversion algorithms to produce estimates of lung shear stiffness. In both algorithms, directional filtering in the direction of shear wave propagation which was orthogonal to the plate motion and along the anterior-posterior direction of the lung was performed using a fourth order Butterworth low pass filter with cut-off parameters of 0.5 and 40 waves/FOV (Smith and Ehman, 2000). Slices that did not include lung tissue or lacked visual evidence of propagating shear waves were discarded. Of the total of 35 slices acquired for all five lung samples, 11 were discarded because the slice did not include lung while an additional five were discarded due to low wave amplitude resulting from lack of contact between the lung at that slice location and the shear driver plate. The remaining 19 slices were used for subsequent shear stiffness calculations. LFE-based estimates of shear stiffness involved first manually contouring the lung within each slice, specifically excluding non lung tissue such as the thymus and heart. The average estimate of shear stiffness within this region of interest was then calculated. In order to ensure that both methods included the same amount of lung tissue, the principal frequency method calculated the average shear stiffness within the region of interest that included the lung within each slice.
2.3.1 Lung density versus inflation pressure
Calculation of shear stiffness requires the estimation of the physical density ρ of the material under investigation. In most solid organs this value is assumed to be approximately 1000 kg/m3 or one g/cm3. However, within the lung, the physical density is typically considered to be approximately one third of that of solid organs and varies as a function of inflation volume as measured by Ptp (Mercer et al., 1987) and disease (Faffe and Zin, 2009). Without the appropriate values for lung densities, both LFE and principal frequency inversion algorithms will incorrectly estimate lung shear stiffness. To estimate lung density in the ex vivo experiments, a mono-exponential decay curve was fitted to values of physical density versus inflation pressure for both inspiration and expiration as reported by Mercer et al (Mercer et al., 1987). The exponential curve was then used to approximate the physical density of a rat lung for each inflation pressure. The specific density estimates were: 402, 303, 248, 236, 218 and 202 kg/m3 at Ptp values of 3, 6, 9, 10, 12, and 15 cm H2O respectively.
2.3.2 SNR Calculation
The SNR of MRE wave images depends on both the noise within the MR data and the amplitude of the harmonic displacement. It is calculated here by first measuring the standard deviation of the background regions of the magnitude image in both the real and imaginary channels of the complex data. This quantity is also the noise level of the magnitude signal and dividing it into the magnitude yields the conventional SNR of the magnitude data. If this SNR is high enough this is also a good estimate of the noise in the phase in radians. In MRE the signal is considered to be equal to the amplitude in phase of the first harmonic. This amplitude, divided by the phase noise and √2 to account for the positive and negative gradient acquisitions typically used to generate a single wave image, is the MRE phase-difference SNR. If the magnitude SNR is significantly less than three, the noise in the phase will deviate from a Gaussian distribution and will be underestimated by this approach. The rationale for this method of estimating the SNR and an explanation for the lower limit of this value is provided in the appendix. Using this approach the MRE SNR for all five ex vivo lungs within each slice at each inflation pressure were calculated.
2.3.3 Statistical Analysis
Evaluation of linear response to pressure
To determine which of the two MRE stiffness estimates was less sensitive to SNR variations induced by changes in inflation pressure, a least squares linear regression was performed (Origin V7, OriginLab Corporation, Northampton, MA) on both LFE and principal frequency shear stiffness estimates as a function of Ptp. Since it is well established that shear modulus is linearly related to Ptp, (Salerno and Ludwig, 1999, Stamenovic and Yager, 1988, Hajji et al., 1979) the inversion method that provided a higher correlation coefficient as measured by the R value was considered to be the more accurate method for estimating this relationship. In addition, the slope of the linear least squares fit was also calculated in order to allow comparison between MRE-based shear stiffness estimates and previously reported estimates of shear stiffness as a function of Ptp.
Evaluation of differences between groups
To determine at which pressure the differences in shear stiffness as estimated by both the LFE and principal frequency methods became statistically significantly different, hierarchical linear models (HLM) (Raudenbush and Bryk, 2002) were used to test for differences in shear stiffness estimated between the two methods. Specifically, the difference in shear stiffness in units of kPa between the two methods was computed for each image slice as well as the mean shear stiffness over all slices. The HLM model was specified such that the repeated measurements attributable to different experimental Ptp within each lung set (i.e. animal) were accounted for. This approach corrects for the incorrect variance estimates obtained if the shear stiffness for each pressure (within animal) were treated as statistically independent (Raudenbush and Bryk, 2002). Model-based estimated means were obtained for each experimental Ptp value along with a linear trajectory model that was used to test if the experimental pressures affected the difference between the LFE and principal frequency estimations.
3. Results
3.1 Finite Element Simulations
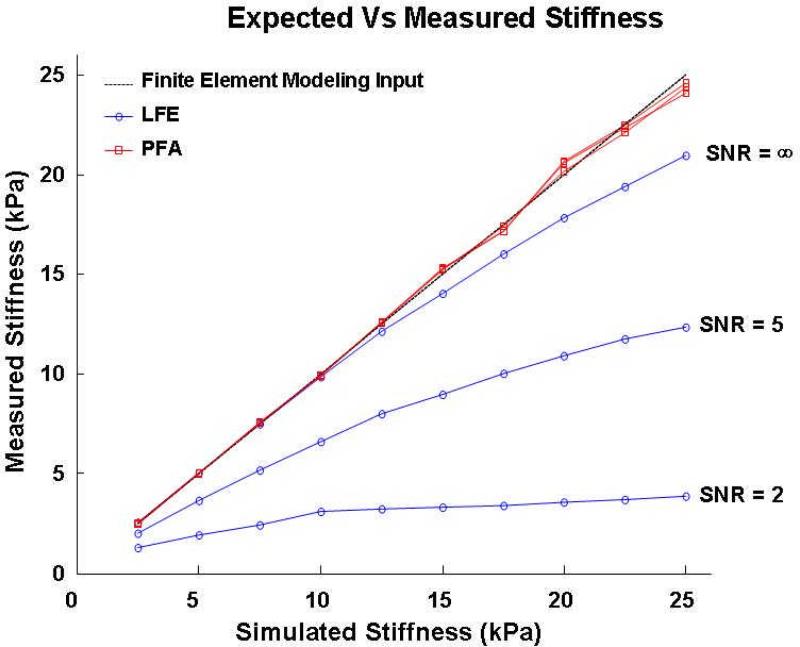
Figure 3 plots the calculated stiffness values using LFE (blue) and PFA (red) algorithms as a function of the input or expected stiffness used for the FEM simulation for the three SNR values of 2.5 kPa, 12.5 kPa and 25 kPa with the actual stiffness values plotted as the black line. The PFA results are observed to be very accurate at all noise levels. Conversely, LFE consistently underestimates shear stiffness as both actual shear stiffness and noise level increase. This is because LFE interprets both noise and edge discontinuities as evidence of high spatial frequency (i.e. soft material). Since high shear stiffness implies low spatial frequency, this bias gets progressively worse with both increased actual shear stiffness and increased noise.
Figure 3.
Stiffness estimates obtained from finite element simulation data at ten stiffness values ranging from 2.5 kPa to 25 kPa in intervals of 2.5 kPa processed using local frequency estimation (LFE, blue) and principal frequency (PF) estimation (red) algorithms at signal-to-noise values of infinity (i.e. no noise) five and two. PF-based estimates of shear stiffness track with their simulated values (fall along the solid line) independent of SNR level while LFE-based estimates demonstrate a high sensitivity (error) to the level of added noise.
3.2 Ex Vivo Validation
3.2.1 MRE-Based Estimates of Lung Shear Modulus
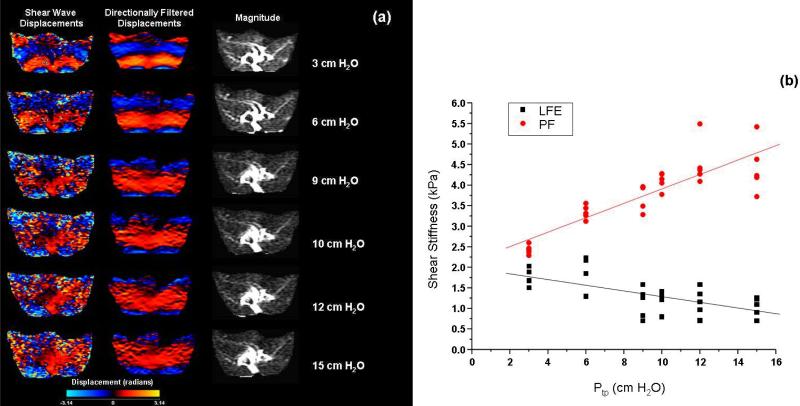
Figure 4 presents shear wave displacement, phase contrast SNR and shear stiffness data for rat lung data set five of this study. In the first two columns of figure 4(a) the raw and directionally filtered shear wave displacements at inflation pressures of 3, 6, 9, 10, 12 and 15 cm H2O for a single phase offset are shown. For comparison the third column shows the corresponding magnitude image. While the directionally filtered data more clearly shows the encoded shear wave, the effect of low phase-contrast SNR limits the ability to clearly visualize the shear wave throughout the lung. The phase-difference SNR was equal to 5.31, 3.70, 2.66, 2.39, 2.66 and 2.43 at Ptp values of 3, 6, 9, 10, 12 and 15 cm H20 respectively. For the purposes of illustration figure 4(b) is a plot of the LFE and principal frequency estimates of shear stiffness for the last lung data set used in this study. For the principal frequency data, the region of interest included all of the lung data within each slice. At each pressure point, five values of shear stiffness are plotted and represent the average value within each of the five MRE slices acquired at that pressure. While the principal frequency method shows the expected positive relationship between shear stiffness and inflation pressure, the density corrected LFE values demonstrate an opposite, negative trend with inflation pressure for this data set. As an estimate of the inter slice shear stiffness variability, the maximum and minimum values of the coefficient of variation (standard deviation / mean) calculated for each pressure ranged from 0.37 to 0.011 for the LFE and 0.24 to 0.014 for the principal frequency method respectively across all five animal data sets.
Figure 4.
(a) Shear wave displacement data before (first column) and after directional filtering (middle column) as a function of inflation pressure for data set 5. Note that despite directional filtering, the phase-difference data SNR visually decreases with inflation pressure. The magnitude images for the given slice are presented in the third column. (b) Plot of local frequency estimation (LFE) and principal frequency (PF) estimates of shear stiffness for each slice in this data set as a function of inflation pressure.
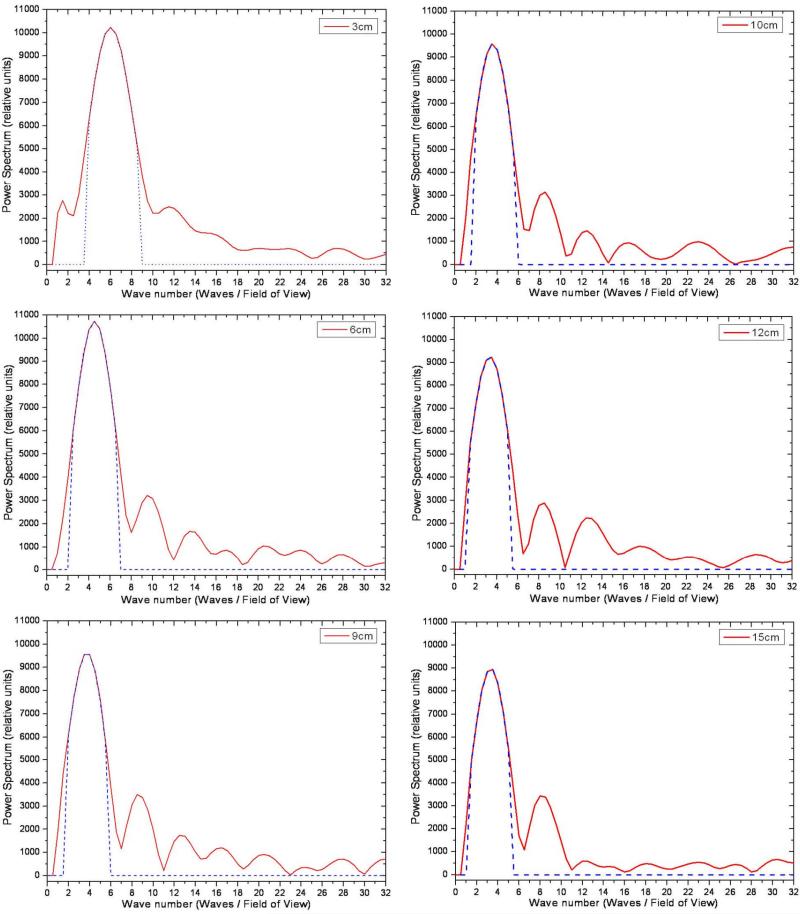
To gain a greater appreciation of the spatial frequencies of the shear waves visualized in the ex vivo rat lung samples of figure 4, one-dimensional profiles through the power spectrum of the spatial Fourier transform of the first harmonic wave data are shown in figure 5. The profiles include the spatial frequencies along the ordinate at the spatial frequency of zero along the abscissa. For each inflation pressure, the original (red) and thresholded (blue dash) power spectra are shown for a threshold of 50% of the peak spectral value. The corresponding values for fcentroid are 5.50, 4.02, 3.30, 3.10, 2.93, and 2.90 waves / FOV at inflation pressures of 3, 6, 9, 10, 12, and 15 cm H2O respectively. Before calculating the spatial Fourier transform, the first harmonic wave data were zero padded from a base resolution of 256 points to 512. Interpolation of the data in this manner improves the resolution of the power spectrum of the first spatial harmonic as the spatial frequency of the shear wave approaches the imaging FOV or a wave number of 1.0 waves/FOV or less.
Figure 5.
Power spectrum profiles before (red) and after thresholding (blue dash) for the ex vivo rat lung data set shown in figure 4. The profiles were obtained from the spatial Fourier transform of the first harmonic shear wave data at each of the six lung inflation pressures for a wave number of zero along the spatial frequency direction corresponding to the x-axis of the image. The value of fcentroid was 5.50, 4.02, 3.30, 3.10, 2.93, and 2.90 waves / field of view at inflation pressures of 3, 6, 9, 10, 12, and 15 cm H2O.
3.2.2 Statistical Analysis
Table 1 lists the slope of the least squares linear fit as well as the R value for all five animal sets for both the LFE and principal frequency shear stiffness estimation methods. For all five data sets, the principal frequency estimation method demonstrated a larger linear correlation coefficient (0.64 ≤ R ≤ 0.86) than the LFE estimates (-0.65 ≤ R ≤ 0.39). The slope of the least squares linear regression fit was larger for all principal frequency-based estimates than for the LFE-based estimates and the latter had a positive slope in only one of the five data sets. This suggests that principal frequency based estimates of shear stiffness versus Ptp match more closely with the accepted linear and positive slope relationship between these two parameters. The results of the HLM model estimating the difference between the LFE and principal frequency methods and projected means across all subjects for each pressure indicated that, for the fixed effect of pressure, there is strong evidence (p < 0.0001) of a relationship between pressure and difference between LFE and principal frequency shear stiffness calculations (numerator and denominator degrees of freedom = 5 and 18 respectively) with an F-value of 20.87. Further evidence is provided by examining the difference in residual variances between this model and the unconditional HLM model of the difference, which indicated that pressure explains about 81% of the variability in LFE/principal frequency difference measurements within rats.
Table 1.
Least squares linear regression correlation coefficient (R), intercept and slope for the principal frequency and LFE-based shear stiffness estimation inversion algorithms as a function of inflation (i.e transpulmonary (Ptp)) pressure. The R and slopes were calculated for each data set which consisted of between two to five points (slices) per Ptp value. Both LFE and principal frequency values represent the average shear stiffness within the lung within each slice with each point corresponding to a single slice.
| Principal Frequency-Based Shear Stiffness | Local Frequency Estimation (LFE)-Based Shear Stiffness | |||||
|---|---|---|---|---|---|---|
| Data Set | Intercept (kPa) | Slope | R | Intercept (kPa) | Slope | R |
| 1 | 1.42 | 0.720 | 0.642 | 1.36 | -0.169 | -0.264 |
| 2 | 1.72 | 1.35 | 0.856 | 1.76 | -0.0126 | -0.0186 |
| 3 | 1.67 | 1.14 | 0.777 | 1.69 | -0.225 | -0.256 |
| 4 | 1.66 | 1.93 | 0.825 | 1.70 | 0.392 | 0.384 |
| 5 | 2.15 | 1.79 | 0.855 | 1.98 | -0.705 | -0.649 |
Note: Before performing the least squares linear regression, Ptp values were converted from units of centimeters of H2O to kPa (1 cm H2O (at 4 °C) = 0.0981 kPa). Therefore the slope and R values quoted in this table are unit less.
Table 2 provides a list of model-based estimated means which indicate that the difference between LFE and principal frequency measurements increase with increased experimental pressure. Further t-tests of each mean indicate that the difference in LFE and principal frequency measurements of shear stiffness become significant beginning at pressure 6 cm H2O.
Table 2.
Model-based estimated difference between shear stiffness (μ) as calculated using local frequency estimation (LFE) and principal frequency analysis (PF) methods. At a pressure of 6 cm H20 and above, the difference becomes statistically significantly different.
| Ptp (cm H2O) | Est. diff. in μ [LFE-PF) (kPa) | Standard Error (kPa) | Degrees of Freedom | t-statistic | p |
|---|---|---|---|---|---|
| 3 | -0.65 | 0.33 | 18 | -1.99 | 0.0615 |
| 6 | -0.84 | 0.33 | 18 | -2.57 | 0.0194 |
| 9 | -1.49 | 0.32 | 18 | -4.67 | 0.0002 |
| 10 | -1.56 | 0.32 | 18 | -4.89 | 0.0001 |
| 12 | -1.95 | 0.32 | 18 | -6.11 | <.0001 |
| 15 | -2.11 | 0.32 | 18 | -6.60 | <.0001 |
4. Discussion and Conclusion
This work has described a new method for quantification of average shear stiffness in very low SNR MRE data based on estimation of the principal frequency of the propagating shear wave. These data indicate that the proposed principal frequency method is much less sensitive than LFE to decreases in phase-contrast SNR, particularly when wavelengths are long compared to the object's dimensions. This method appears to be well suited to estimating the shear stiffness of normal lung parenchyma as validated by least squares linear regression analysis and statistically significant differences between groups for estimates of rat lung shear modulus as a function of Ptp for values of greater than 6 cm H2O.
While this method has been tested only for lung MRE data, the approach is equally valid in other organs under conditions that produce low shear wave SNR. Such conditions arise when an external shear driver is used to create shear waves within an organ that is deep within the body such as the prostate and/or when the shear wave frequency is sufficiently high that viscous losses attenuate the shear wave and therefore decrease the SNR. Although not tested in this work, it is reasonable to assume that the outlined approach will have application beyond just the lung.
Comparison of the FEM simulation and ex vivo lung data reveals differences in the upper limit of shear stiffness between the two methods. This discrepancy is due to the density value used as input into the FEM simulation which was uniform and equal to 1 g/cm3. To perform a direct comparison between the simulation and ex vivo data, the FEM shear stiffness estimates must be corrected for the density values of the lung. In this study these values ranged from 0.4 to 0.2 g/cm3 for Ptp values of three and 15 cm H2O respectively. Correcting for these densities reduces the shear stiffness range simulated to between 1.0 to 5.0 kPa which is representative of the density corrected stiffness values reported for the ex vivo rat lungs evaluated in this study.
Although LFE has been well validated in many other organs and phantoms (e.g. Ringleb 2005), finite element modeling supports the experimental findings indicating that LFE is sensitive to the high levels of noise and long wavelengths (low spatial frequencies) encountered here. In contrast, the principal frequency estimation technique is less sensitive to very low MRE SNR, but loses all local information, providing a single estimate of shear stiffness. While this is useful for comparison with global estimates of lung stiffness, it allows only evaluation of those lung diseases in which the assumption of at least a regional homogeneous medium is valid (e.g. diffuse diseases such as pulmonary fibrosis). However, it is possible to achieve a compromise between the size of the region of interest over which the principal frequency estimation method is performed and the degree of regional information obtained. For example, rather than selecting a region that includes the entire lung, each lobe of each lung could be potentially divided into four quadrants over which the principal frequency estimation method would be applied to provide four separate regional estimates of shear stiffness. However, these regions must remain large enough that the convolution in frequency space with the Fourier transform of the window does not bias the weighted average used to calculate the principal frequency.
While the principal frequency method has been demonstrated to be less sensitive to decreased phase-difference SNR, the algorithm will be expected to produce stiffness estimates that deviate from the actual value as the wave number of the spatial shear wave is less than one and approaches zero. That is, when the wave length becomes larger than the imaging FOV. Without sufficient resolution, a wave number greater than zero but less than one wave/FOV is likely to be biased towards a value of zero. To reduce the potential for this effect, zero padding of the harmonically filtered data is performed by a factor of two, thereby increasing the effective spatial frequency resolution two-fold. While the potential for this type of error exists, the effect was not observed in this study as demonstrated in the power spectra of the ex vivo rat lungs as shown in figure 5. The lowest spatial frequency was approximately three waves/FOV, well above the wave number of one wave/FOV or the regime in which this error will begin to dominate. Under the experimental conditions for the ex vivo lungs and assuming a very low lung density of 0.1 g/cm3, at a wave number of one wave/FOV the shear stiffness would be equal to 17.4 kPa corresponding to an inflation pressure of greater than 178 cm H2O. While it may be technically feasible to inflate the rat lung to this pressure, it represents a pressure factor of three greater than what was used in this study and most likely a pressure beyond the total lung capacity of the rat lung.
It is somewhat difficult to compare the values of shear stiffness reported in this work with previously published data, as previous results are themselves inconsistent, measure different quantities, and are method-dependent. The slope of the relationship between shear stiffness and Ptp (average slope over five data sets = 1.38) reported here is higher than previously reported values derived from punch indentation testing. For instance, Stamenovic and Yager (Stamenovic and Yager, 1988) have reported a value of 0.5 for rabbit lungs while Stamenovic and Smith (Stamenovic and Smith, 1986) reported a similar value of 0.6. Hajji et al (Hajji et al., 1979) reported values of 0.66, 0.86 and 0.60 for dog, pig and horse lung respectively with a value of 0.7 which was independent of species. Similarly Ganesan et al (Ganesan et al., 1997) reported a value of 0.9 for in vivo pig lung based on the analysis of surface waves. For rat lung this ratio was reported by Salerno and Ludwig (Salerno and Ludwig, 1999) to be 0.96. Similarly, in this study, the shear stiffness averaged over all five ex vivo lung sets of deflated normal rat lung at 220 Hz would, by extrapolation, be equal to 1.72 and 1.70 kPa for the LFE and principal frequency estimates respectively. In contrast, previously reported values of shear modulus based on punch indentation testing for deflated lung were 0.29 kPa for sheep (Stamenovic and Yager, 1988), 0.34 kPa for rabbit (Stamenovic and Yager, 1988) and 0.26 kPa for rat lung (Salerno and Ludwig, 1999).
There are several potential reasons for these discrepancies. While degassing was performed to reduce regional air trapping, it is possible that some trapping and/or atelectasis could occur due to the fact that each lung pair underwent several cycles of inflation followed by deflation as shear stiffness was evaluated across the range of Ptp values. As indicated by Salerno and Ludwig (Salerno and Ludwig, 1999), regional air flow restriction increases shear stiffness estimates, suggesting that this may be a contributing factor. Another possibility is that since lung density was estimated rather than measured, there may be biases in this estimation that potentially account for the variation in MRE-derived estimates of slope. Also, shear stiffness by definition is simply an alternative way to express wave speed, which is affected by boundary conditions as wavelengths approach and exceed the object's dimensions, so the values obtained here, particularly at higher pressures, do not necessarily reflect the actual complex (viscoelastic) shear modulus. Most importantly, however, the quasistatic nature of punch indentation testing means that this method inherently provides a ‘DC’ estimate of shear stiffness. In contrast, the MRE experiments here employed shear waves at 220 Hz. The viscoelastic nature of lung parenchyma (Suki et al., 1994) implies that at these frequencies shear stiffness increases rapidly with frequency and will be significantly higher at 220 Hz than at DC due to the increasing dominance of viscous effects.
A more direct method of assessing the validity of the MRE-based estimates presented in this work is to compare MRE-based wave speeds to previously reported values. Under the assumption that lung density is equal to 1.0 g/cm3 at Ptp = 0, then the square root of the extrapolated MRE-based shear stiffness is equal to a shear wave speed or 1.31 and 1.30 m/s for the LFE and principal frequency estimates respectively averaged over all five ex vivo rat lung sets. In comparison, Jahed et al (Jahed et al., 1989) reported that the shear wave speed for the slow component (i.e. shear wave) of a stress wave within sheep lungs ranged from ~ 1.5 to 2.2 m/s at inflation pressures of 5 (0.49 kPa) and 10 cm (0.98 kPa) H2O with a speed of approximately 1.0 m/s at 0 cm H2O based on extrapolation. In a similar study based on the analysis of a 2 ms displacement impulse (Jahed et al., 1990), the shear wave speed in canine lungs ranged between 2.5 and 0.50 m/s depending upon lung density with shear wave speed decreasing with increasing lung density. Finally, Zhang et al (Zhang et al., 2009) using a laser vibrometer measured the wave speed of the slow component (i.e. shear) wave within an ex vivo pig lung and demonstrated a strong positive relationship with shear wave excitation frequency. Between 200 and 250 Hz or roughly the range of MRE-based measurements the wave speed was between 2.20 and 2.35 m/s at an inflation pressure of 0.392 kPa (~ 4cm H2O). The overall agreement in wave speed values indicates that MRE-based measurements accurately describe the mechanical properties of lung parenchyma and also indicate the need for caution when comparing data derived from inherently different methods.
In previously published data, a positive trend in lung shear stiffness with increasing inflation pressure was observed in post expiration porcine lungs in situ (Mariappan et al., 2010). This contrasts with the decrease in shear stiffness observed in both simulation and ex vivo MRE data when processed with the LFE inversion algorithm observed in this study. There are two reasons for this apparent discrepancy. The first is due to the difference in phase-contrast SNR as a result of the differences in image acquisition parameters including slice thickness (10 mm vs. 6 mm) and shear wave excitation frequency (220 Hz vs. 100 Hz). In the porcine data, the previously unreported phase-difference SNR values ranged between 10 and five for airway pressures between five and 20 cm H2O respectively. In contrast, the highest phase-difference SNR for the ex vivo data was approximately five at a pressure of 3 cm H2O. As demonstrated in table 2, LFE-based estimates of shear stiffness are statistically significantly different from principal frequency-based estimates at pressures greater than 3 cm or an SNR of less than five. Secondly, the values reported for the porcine lung were not corrected for decreases in density with inflation pressure. This was because of the inability to directly quantify this parameter in situ. Because lung density will decrease with inflation pressure, corrected LFE estimates will be correspondingly less than those reported. However, because of SNR differences, it is expected that the same positive trend would be observed.
In conclusion, this work describes a new method for calculating shear stiffness in low SNR MRE data such as the lung. This approach has been validated in both finite element modeling and ex vivo tissue samples, indicating that this method is more accurate than the LFE inversion algorithms under these long wavelength and low SNR conditions and yields shear stiffness values that are comparable to previously reported values obtained with other experimental techniques.
Acknowledgements
We would like to acknowledge the assistance of Rickey Carter, Ph.D., department of Biostatistics, Mayo Clinic in designing the statistical tests used in this study as well as Debora Rasmussen, Department of Pulmonary Research, Mayo Clinic for her help in the preparation and care of the animal lung tissue samples.
Support: NIH EB07593, NIH EB01981
Appendix. Calculation of MRE Signal-to-Noise Ratio (SNR)
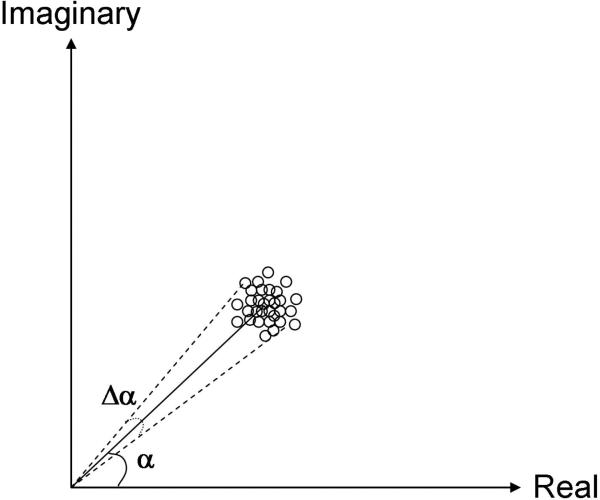
Figure A1 provides a graphical representation of the concept of calculating the phase-difference SNR. In this figure, the complex image data at one pixel is shown, and the length M of the complex vector represents the gray scale value of the pixel in the magnitude image while the angle α is the phase at that pixel (encoding the shear wave displacement). Data acquisition noise is attributed to resistive noise in the electrical components as well as digitization errors. Resistive noise will be randomly distributed and the material parameters governing noise (resistivity, temperature) will be the same for both in-phase and quadrature measurements, so it is reasonable to assume that the error in the real and imaginary components is equal but uncorrelated. The addition of noise into the complex data thus results in a circularly symmetric Gaussian distribution of values about the noise-free complex vector. Thus, the standard deviation in either the real or imaginary channel equals that in the magnitude value M and fully characterizes the uniform distribution of noise about M provided that M is sufficiently large compared to its standard deviation. The error in the phase angle α in radians is given by angle subtended by the width of the cloud normal to M. This is quantified by calculating the arc sine of the ratio of the standard deviation to M again provided that M is sufficiently large compared to its standard deviation. With this assumption, the phase angle divided by error in this value is the phase SNR.
Figure A1.
Graphical representation of the signal and noise values for a single pixel within a MRE image. The length of the vector represents the magnitude of the pixel while the angle α is the amplitude of the shear wave displacement that is encoded into the phase of the pixel. The amplitude of the noise both the real and imaginary channels of the complex signal are equal, resulting in a spatially invariant Gaussian cloud. Under these conditions, the noise in the phase or Δα is equal to the standard deviation of the cloud.
The first step in calculating the MRE SNR in practice involves estimating the noise within the air or the background region of the image. Segmentation of the image into regions that include the object and background can be achieved by histogram analysis of the gray scale magnitude data or by manually selecting a gray scale value where values below the threshold represent noise regions while those above the value are signal. The standard deviation of the Gaussian cloud can then be estimated from the background region as the average of the standard deviations of the real and imaginary channels, or as the standard deviation in the magnitude image divided by the Rician correction factor of 1.66. This is considered to be equal to the standard deviation of the noise in the phase image, as above. The pixel-by-pixel phase SNR is calculated by dividing the amplitude of the first harmonic fit across phase offsets at that pixel (taken to be the signal) by the standard deviation of the noise. An average estimate of the SNR within an object is obtained by averaging all of those values that include the object under interrogation. When the shear wave displacement is given by the subtracted phase of two images whose motion encoding gradients are of opposite polarity, the SNR increases by √2.
This method assumes that the noise is Gaussian in distribution in both the real and imaginary channels, uncorrelated between the channels, and spatially invariant. In general these assumptions hold when the B1 field of the RF coil used for signal reception is uniform over the volume of interest such as with transmit-receive whole body coils and dedicated smaller volume coils such as transmit-receive head and extremity bird cage coils such as the 6 cm diameter coil used in this study. This assumption begins to break down with the use of single coil surface or multi element phase array coils such as those used in large FOV imaging as in the abdomen. Also, the calculation above is accurate only when the magnitude SNR is sufficiently high which, based on empirical testing, occurs when the magnitude of the vector M is greater than three. Below this SNR, the method above will overestimate the true phase SNR, but at this point the data is sufficiently noisy that inversion is challenging and the SNR values obtained are still useful for comparing relative noise levels.
References
- Bensamoun SF, Ringleb SI, Chen QS, Ehman RL, An KN, Brennan M. J. Magn. Reson. Imaging. 2007;26:708–713. doi: 10.1002/jmri.21073. [DOI] [PubMed] [Google Scholar]
- Bensamoun SF, Ringleb SI, Littrell L, Chen Q, Brennan M, Ehman RL, An KN. J. Magn. Reson. Imaging. 2006;23:242–247. doi: 10.1002/jmri.20487. [DOI] [PubMed] [Google Scholar]
- Bercoff J, Chaffai S, Tanter M, Sandrin L, Catheline S, Fink M, Gennison JL, Meunier M. Ultrasound in Medicine and Biology. 2003;29:1387–1396. doi: 10.1016/s0301-5629(03)00978-5. [DOI] [PubMed] [Google Scholar]
- Dresner MA, Cheville JC, Myers RP, Ehman RL. 11th Scientific Meeting and Exhibition, Int. Society for Magnetic Resonance in Medicine; Toronto, Canada. 2003. p. 578. [Google Scholar]
- Faffe DS, Zin WA. Physiol Rev. 2009;89:759–75. doi: 10.1152/physrev.00019.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganesan S, Man CS, Lai-Fook SJ. Respir Physiol. 1997;110:19–32. doi: 10.1016/s0034-5687(97)00065-0. [DOI] [PubMed] [Google Scholar]
- Green MA, Bilston LE, Sinkus R. NMR in Biomedicine. 2008;21:755–64. doi: 10.1002/nbm.1254. [DOI] [PubMed] [Google Scholar]
- Hachenberg T, Lundquist H, Tokics L, Brismar B, Hedenstierna G. Acta Anaesthesiol Scand. 1993;37:549–55. doi: 10.1111/j.1399-6576.1993.tb03763.x. [DOI] [PubMed] [Google Scholar]
- Hajji MA, Wilson TA, Lai-Fook SJ. J Appl Physiol. 1979;47:175–81. doi: 10.1152/jappl.1979.47.1.175. [DOI] [PubMed] [Google Scholar]
- Hamhaber U, Grieshaber FA, Nagel JH, Klose U. Magn. Reson. Med. 2003;49:71–7. doi: 10.1002/mrm.10343. [DOI] [PubMed] [Google Scholar]
- Hatabu H, Gaa J, Tadamura E, Edinburgh KJ, Stock KW, Garpestad E, Edelman RR. Eur J Radiol. 1999;29:152–9. doi: 10.1016/s0720-048x(98)00167-3. [DOI] [PubMed] [Google Scholar]
- Huwart L, Sempoux C, Salameh N, Jamart J, Annet L, Sinkus R, Peeters F, ter Beek LC, Horsmans Y, Van Beers BE. Radiology. 2007;245:458–466. doi: 10.1148/radiol.2452061673. [DOI] [PubMed] [Google Scholar]
- Jahed M, Lai-Fook SJ, Bhagat PK. J Appl Physiol. 1990;68:2171–6. doi: 10.1152/jappl.1990.68.5.2171. [DOI] [PubMed] [Google Scholar]
- Jahed M, Lai-Fook SJ, Bhagat PK, Kraman SS. J Appl Physiol. 1989;66:2675–80. doi: 10.1152/jappl.1989.66.6.2675. [DOI] [PubMed] [Google Scholar]
- Kolipaka A, McGee KP, Araoz PA, Glaser KJ, Manduca A, Romano AJ, Ehman RL. Magn. Reson. Med. 2009;62:135–40. doi: 10.1002/mrm.21991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruse SA, Ehman RL. 11th Scientific Meeting and Exhibition, Int. Society for Magnetic Resonance in Medicine; Toronto, Canada. 2003. p. 1084. [Google Scholar]
- Kruse SA, Grimm RC, Lake DS, Manduca A, Ehman RL. 14th Scientific Meeting and Exhibition, Int. Society for Magnetic Resonance in Medicine; Seattle, Washington. 2006. p. 3385. [Google Scholar]
- Kruse SA, Rose GH, Glaser KJ, Manduca A, Felmlee JP, Jack CR, Ehman RL. NeuroImage. 2008;39:231–237. doi: 10.1016/j.neuroimage.2007.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lorenzen J, Sinkus R, Lorenzen M, Dargatz M, Leussler C, Roschmann P, Adam G. Fortschr Rontgenstr. 2002;174:830–834. doi: 10.1055/s-2002-32690. [DOI] [PubMed] [Google Scholar]
- Manduca A, Muthupillai R, Rossman PJ, Greenleaf JF, Ehman RL. In: Proceedings of the SPIE. Loew MH, Hanson KM, editors. Vol. 2710. SPIE - The International Society for Optical Engineering, Newport Beach; California: 1996. pp. 616–623. [Google Scholar]
- Manduca A, Oliphant TE, Dresner A, Greenleaf JF, Ehman RL. 9th Scientific Meeting and Exhibition, Int. Society for Magnetic Resonance in Medicine; Glasgow, Scotland. 2001a. p. 1630. [Google Scholar]
- Manduca A, Oliphant TE, Dresner MA, Mahowald JL, Kruse SA, Amromin E, Felmlee JP, Greenleaf JF, Ehman RL. Medical Image Analysis. 2001b;5:237–254. doi: 10.1016/s1361-8415(00)00039-6. [DOI] [PubMed] [Google Scholar]
- Mariappan Y, Kolipaka A, Ehman RL, McGee KP. 18th Scientific Meeting and Exhibition, Int. Society for Magnetic Resonance in Medicine; Stockholm, Sweden. 2010. [Google Scholar]
- McKnight AL, Kugel JL, Rossman PJ, Manduca A, Hartmann LC, Ehman RL. American Journal of Roentgenology. 2002;178:1411–1417. doi: 10.2214/ajr.178.6.1781411. [DOI] [PubMed] [Google Scholar]
- Mercer RR, Laco JM, Crapo JD. J Appl Physiol. 1987;62:1480–7. doi: 10.1152/jappl.1987.62.4.1480. [DOI] [PubMed] [Google Scholar]
- Muthupillai R, Lomas DJ, Rossman PJ, Greenleaf JF, Manduca A, Ehman RL. Science. 1995;269:1854–1857. doi: 10.1126/science.7569924. [DOI] [PubMed] [Google Scholar]
- Oliphant TE. Biomedical Imaging. Mayo Graduate School; Rochester: 2001. p. 336. [Google Scholar]
- Papazoglou S, Hamhaber U, Braun J, Sack I. Phys Med Biol. 2008;53:3147–58. doi: 10.1088/0031-9155/53/12/005. [DOI] [PubMed] [Google Scholar]
- Papazoglou S, Rump J, Braun J, Sack I. Magn. Reson. Med. 2006;56:489–497. doi: 10.1002/mrm.20993. [DOI] [PubMed] [Google Scholar]
- Plewes DB, Bishop J, Samani A, Sciarretta J. Phys. Med. Biol. 2000;45:1591–1610. doi: 10.1088/0031-9155/45/6/314. [DOI] [PubMed] [Google Scholar]
- Raudenbush SW, Bryk AS. Hierarchical Linear Models: applications and data analysis methods. Sage Publication, Ltd.; Thousand Oaks, CA: 2002. [Google Scholar]
- Ringleb SI, Chen Q, Lake DS, Manduca A, Ehman RL, An KN. Magn. Reson. Med. 2005;53:1197–1201. doi: 10.1002/mrm.20449. [DOI] [PubMed] [Google Scholar]
- Romano AJ, Abraham PB, Rossman PJ, Bucaro JA, Ehman RL. Magn. Reson. Med. 2005;54:893–900. doi: 10.1002/mrm.20607. [DOI] [PubMed] [Google Scholar]
- Romano AJ, Bucaro JA, Ehman RL, Shirron JJ. IEEE Transactions on Ultrasonics, Ferroelectronics, and Frequency Control. 2000;47:1575–1581. doi: 10.1109/58.883546. [DOI] [PubMed] [Google Scholar]
- Sack I, Beierbach B, Hamhaber U, Klatt D, Braun J. NMR in Biomedicine. 2007 doi: 10.1002/nbm.1189. [DOI] [PubMed] [Google Scholar]
- Salerno FG, Ludwig MS. J Appl Physiol. 1999;86:66–70. doi: 10.1152/jappl.1999.86.1.66. [DOI] [PubMed] [Google Scholar]
- Siegmann KC, Xydeas T, Sinkus R, Kraemer B, Vogel U, Claussen CD. Eur Radiol. 20:318–25. doi: 10.1007/s00330-009-1566-4. [DOI] [PubMed] [Google Scholar]
- Sinkus R, Tanter M, Catheline S, Lorenzen J, Kuhl C, Sondermann E, Fink M. Magn. Reson. Med. 2005a;53:372–387. doi: 10.1002/mrm.20355. [DOI] [PubMed] [Google Scholar]
- Sinkus R, Tanter M, Xydeas T, Catheline S, Bercoff J, Fink M. Magn. Reson. Imaging. 2005b;23:159–165. doi: 10.1016/j.mri.2004.11.060. [DOI] [PubMed] [Google Scholar]
- Smith JA, Ehman RL. Materials Evaluation. 2000;58:1395–1401. [Google Scholar]
- Stamenovic D, Smith JC. J Appl Physiol. 1986;60:1358–62. doi: 10.1152/jappl.1986.60.4.1358. [DOI] [PubMed] [Google Scholar]
- Stamenovic D, Yager D. J Appl Physiol. 1988;65:2565–70. doi: 10.1152/jappl.1988.65.6.2565. [DOI] [PubMed] [Google Scholar]
- Suki B, Barabasi AL, Lutchen KR. J Appl Physiol. 1994;76:2749–59. doi: 10.1152/jappl.1994.76.6.2749. [DOI] [PubMed] [Google Scholar]
- Yin M, Woollard J, Wang X, Torres VE, Harris PC, Ward CJ, Glaser KJ, Manduca A, Ehman RL. Magn. Reson. Med. 2007;58:346–53. doi: 10.1002/mrm.21286. [DOI] [PubMed] [Google Scholar]
- Zhang X, Qiang B, Urban MW, Kinnick R, Hubmayr R, Greenleaf JF. Ultrasonics Symposium (IUS), 2009 IEEE International. 2009. pp. 479–482.