Abstract
Nuclear resonance vibrational spectroscopy (NRVS) reveals the vibrational dynamics of a Mössbauer probe nucleus. Here, 57Fe NRVS measurements yield the complete spectrum of Fe vibrations in halide complexes of iron porphyrins. Iron porphine serves as a useful symmetric model for the more complex spectrum of asymmetric heme molecules that contribute to numerous essential biological processes. Quantitative comparison with the vibrational density of states (VDOS) predicted for the Fe atom by density functional theory calculations unambiguously identifies the correct sextet ground state in each case. These experimentally authenticated calculations then provide detailed normal mode descriptions for each observed vibration. All Fe-ligand vibrations are clearly identified despite the high symmetry of the Fe environment. Low frequency molecular distortions and acoustic lattice modes also contribute to the experimental signal. Correlation matrices compare vibrations between different molecules and yield a detailed picture of how heme vibrations evolve in response to (a) halide binding and (b) asymmetric placement of porphyrin side chains. The side chains strongly influence the energetics of heme doming motions that control Fe reactivity, which are easily observed in the experimental signal.
INTRODUCTION
Vibrational spectroscopic methods are widely applied to investigate all phases of matter.1 The enormous number of vibrational degrees of freedom in complex macromolecules presents a fundamental challenge to biological applications of vibrational spectroscopy.2 Methods such as resonance Raman3 or infrared difference spectroscopy4 reduce the spectral congestion by selecting vibrations coupled to an electronic resonance or to a reaction, respectively. However, selection rules may or may not allow observation of specific modes of interest among competing vibrational signals.
The sensitivity of molecular frequencies to small structural changes has been a primary motivation for vibrational spectroscopic investigations.2, 5, 6, 7, 8 However, vibrational properties can also provide information on the energetics of structural changes, especially those involved in chemical reactions. The latter opportunity has been exploited less, because of the increasing technical difficulty of detecting frequencies below 200 cm−1, which can be excited by thermal fluctuations and thus contribute to reaction activation.
Nuclear resonance vibrational spectroscopy (NRVS), is emerging as a powerful vibrational probe for metal sites in proteins.9, 10 NRVS reveals the complete vibrational spectrum of a Mössbauer probe nucleus, with no competing vibrational signal from the macromolecule or solvent.11, 12, 13 NRVS, also known as nuclear inelastic scattering, has been used to investigate the vibrational dynamics of 57Fe in protein active sites9, 14, 15, 16, 17, 18, 19, 20, 21, 22 and in small molecules.11, 23, 24, 25, 26, 27, 28, 29, 30
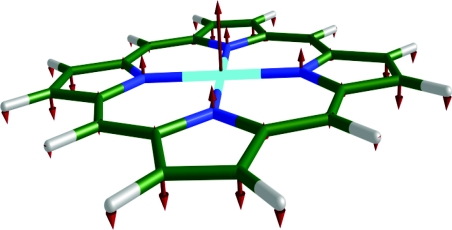
Since the use of NRVS to measure low frequency vibrations is restricted only by the experimental resolution (∼10 cm−1), it provides an important opportunity to characterize thermally excitable reactive modes. In particular, NRVS measurements have identified11, 23, 24, 25, 28 the doming mode of the heme (Fig. 1) long believed to control biologically important reactions in heme proteins, such as cooperative oxygen binding in hemoglobin.31, 32, 33
Figure 1.
Doming mode (γ9) in Fe(P). Color scheme: iron is cyan, carbon is green, nitrogen is blue, and hydrogen is white. In this and subsequent figures, each arrow is 50(mj∕mFe)1∕2 times longer than the zero-point vibrational amplitude of atom j.
Far infrared measurements find vibrational signals in the frequency range expected for heme doming in iron porphyrins34 and vibrational coherence spectroscopy (VCS) reveals low frequency molecular oscillations coupled to ligand binding reactions in heme proteins35, 36, 37, 38, 39, 40 and porphyrin model compounds.41, 42 However, these measurements do not exclude other vibrations that may appear in this frequency range, such as the FeCO distortion mode (in-phase bend∕tilt) in iron carbonyl porphyrins43, 44, 45 or other heme distortions that may control redox reactions.46, 47 The weak sensitivity of low frequencies to isotopic substitution presents a significant obstacle to associating specific atomic motions with observed frequencies. In contrast, NRVS measurements on oriented single crystals definitively identify Fe motion orthogonal to the heme plane associated with low frequency modes in model compounds.17, 25, 27, 28, 48, 49, 50
In addition, NRVS represents the ultimate limit in atomic selectivity, because it specifically reveals the vibrational spectrum of the probe nucleus, even in the presence of thousands of other vibrating atoms. Fe-ligand vibrations dominate the 57Fe NRVS signal. NRVS measurements on iron porphyrins reveal rich vibrational structure with unexpected sensitivity to the specific pattern of side chains attached to the periphery of the porphyrin core.25 Motion of the axial imidazole ligand contributes to multiple vibrations in six-coordinate iron carbonyl porphyrins.28 Although quantum chemical calculations accurately reproduce the observed 57Fe vibrations,19, 25, 27, 28 a more systematic approach is needed to interpret the predicted vibrational structure.
Here, we present NRVS measurements and density functional theory (DFT) calculations on halide complexes of iron porphine, Fe(P)(X), with X = Cl or Br, iron octaethylporphyrin Fe(OEP)(Cl), and the natural heme, iron protoporphyrin IX Fe(PPIX)(Cl). Porphine is the core of the porphyrin molecules found in heme proteins and in commonly studied model compounds. We find that removal of the peripheral substituents greatly simplifies the vibrational density of states (VDOS) of the Fe atom in comparison with those we reported for more complex porphyrins.11, 23, 24, 25, 26, 27, 28 A vibrational correlation method introduced here allows a simple description of the observed vibrations in terms of the mode nomenclature established for the four-coordinate Ni(P) molecule.51 Halide binding reduces the symmetry from D4h to C4v, and the loss of the symmetry plane allows modest mixing between nominally in-plane and out-of-plane modes. However, the Fe–halide stretch mixes significantly with totally symmetric out-of-plane vibrations of the porphyrin. The same correlation analysis relates the VDOS previously reported52 for Fe(OEP)(Cl) with the simpler Fe(P)(Cl) spectrum, establishing a systematic approach to understanding the spectra of molecules of increasing complexity.
These results also identify the response of the doming mode to molecular substitutions. Replacement of Cl with Br leads to an 18 cm−1 downshift of the doming frequency. Although a similar frequency shift is predicted for the Fe–halide tilting vibration, calculations clearly identify heme doming as the primary contributor to the 57Fe NRVS signal. Moreover, molecular substitutions on the edge of the porphyrin in Fe(OEP)(Cl) and Fe(PPIX)(Cl) perturb the doming and tilting frequencies and also alter the character of the doming modes. These results advance our program of identifying reactive modes by identifying molecular perturbations that will allow us to distinguish a specific reaction coordinate such as heme doming from other low frequency modes in multiple spectroscopic approaches.
MATERIALS AND METHODS
Preparation of samples
The 57Fe(P)(Cl) and 57Fe(P)(Br) powders were purchased from Frontier Scientific, 57Fe(OEP)(Cl) was purchased from Midcentury Chemicals, and 57Fe(PPIX)(Cl) was purchased from Sigma-Aldrich. 57Fe enrichment was >95% in all cases. To facilitate loading in the 20 μL well of the polyethylene sample cells, the powder was mixed with a minimal quantity of Apiezon M grease. Measurements on Fe(P)(Cl) and Fe(P)(Br) were performed at T = 18 K, on Fe(PPIX)(Cl) at T = 25 K, and on Fe(OEP)(Cl) at average T = 86 K.
NRVS measurements
The NRVS measurements on 57Fe-labeled samples were performed at sector 3-ID-D of the Advanced Photon Source. The experimental procedure and data analysis have been reviewed elsewhere in detail.10, 12 Briefly, the sample was mounted in a He-flow cryostat and exposed to the tunable monochromatic x-ray beam, with a bandwidth of ∼1 meV. The incident photon energy was scanned from −30 meV to +80 meV relative to the 14.4 keV Mössbauer resonance of 57Fe. Fluorescence from excited nuclei was distinguished from electronically scattered photons using a time discriminating circuit.12 The VDOS was obtained from the delayed fluorescence signal using the program PHOENIX.53 Experimental VDOS are presented below as a function of energy in units of cm−1 (1 meV = 8.066 cm−1), to facilitate comparison with other molecular spectroscopies.
Computational methods
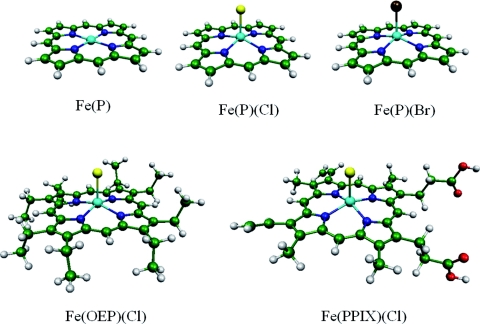
We performed gas phase DFT calculations on Fe(P), Fe(P)(Cl), Fe(P)(Br), Fe(OEP)(Cl), and Fe(PPIX)(Cl) (Fig. 2), as well as Ni(P), with GAUSSIAN 03 (Ref. 54) using the B3LYP functional.55, 56 The basis set for Ni, Fe, Cl, and Br atoms was Ahlrichs’ VTZ (Ref. 57) and the basis set for all other atoms was 6-31G*. Vibrational calculations were performed on equilibrium geometries optimized with S = 1 for Fe(P), S = 5/2 and 3/2 for the five-coordinate ferric compounds, and S = 0 for Ni(P). All calculated vibrational frequencies were real. The Fe(P) input geometry possessed D4h symmetry while Fe(P)(Cl) and Fe(P)(Br) geometries possessed C4v symmetry. These symmetries persisted during optimization. The conformations of the ethyl groups in Fe(OEP)(Cl) remained close to the structure reported in Ref. 58, which was used as the starting point for geometry optimization. Although crystalline Fe(PPIX)(Cl) consists of hydrogen bonded dimers,59 the calculation was performed on a monomer to reduce computational expense. Orientation of the protonated propionates above and below the plane (Fig. 2) in the starting structure prevented them from forming an intramolecular hydrogen bond during optimization.
Figure 2.
Optimized structures of Fe(P), Fe(P)(Cl), Fe(P)(Br), Fe(OEP)(Cl), and Fe(PPIX)(Cl). Halide complexes are domed, with Fe displaced towards the axial ligand, in contrast with the planar Fe(P). Color scheme: iron is cyan, carbon is green, nitrogen is blue, oxygen is red, chlorine is yellow, bromine is brown, and hydrogen is white. The geometry of Fe(P) is of D4h symmetry and the geometry of Fe(P)(Cl) and Fe(P)(Br) is of C4v symmetry.
Although experimental measurements indicate a sextet ground state for the halide complexes,60, 61, 62, 63, 64 predicted quartet state energies lie close to or slightly below the sextet energies, as found in previous calculations.65, 66, 67 The energies listed in Table 1 include the zero-point energies ∑αℏωα/2 calculated from the predicted normal mode frequencies ωα, which favor the sextet state. The small resulting sextet∕quartet energy splittings are on the order of energy differences resulting from minor variations in convergence criteria, and thus cannot be considered significant. For completeness, Table 1 includes predictions for both electronic states.
Table 1.
Optimized structural parameters and stiffness predicted from the DFT calculations for Fe(P), Fe(P)(Cl), Fe(P)(Br), Fe(OEP)(Cl), and Fe(PPIX)(Cl). Energies are given relative to the lowest lying sextet state and include zero-point energies determined from calculated vibrational frequencies. Fe–N, Fe–X, and Fe–p indicate distances from iron to nitrogen and halide (X = Cl or Br) ligands and to the mean plane of the four nitrogen ligands, respectively. The DFT calculations determine the stiffness ks (Eqs. 7) according to the predicted vibrational frequencies and mode composition factors appearing in Eq. 8.
| Electronic | Energy | Fe–N | Fe–X | Fe–p | ks | |
|---|---|---|---|---|---|---|
| state | Molecule | (kJ∕mol) | (pm) | (pm) | (pm) | (pN∕pm) |
| 3A2g | Fe(P) | 0 | 200.0 | 0 | 303 | |
| 6A1 | Fe(P)(Cl) | 0 | 208.3 | 227.9 | 47.3 | 228 |
| 6A1 | Fe(P)(Br) | 0 | 208.2 | 240.0 | 45.6 | 219 |
| 6A | Fe(OEP)(Cl) | 0 | 208.4 | 228.9 | 46.7 | 223 |
| 6A | Fe(PPIX)(Cl) | 0 | 208.4 | 228.5 | 46.8 | 222 |
| 4A2 | Fe(P)(Cl) | −2.59 | 201.2 | 233.7 | 20.1 | 302 |
| 4A2 | Fe(P)(Br) | −3.60 | 201.0 | 247 | 26.6 | 294 |
| 4A | Fe(OEP)(Cl) | −2.64 | 201.4 | 234.8 | 28.2 | 296 |
| 4A | Fe(PPIX)(Cl) | −2.24 | 201.4 | 234.3 | 28.1 | 296 |
Figure 2 displays optimized structures for the lowest lying triplet state of Fe(P) and sextet states of Fe(P)(Cl), Fe(P)(Br), Fe(OEP)(Cl), and Fe(PPIX)(Cl). As reported in other calculations,68 predicted nearest neighbor bond lengths (Table 1) are slightly longer than in the experimental structures reported for Fe(OEP)(Cl),58, 69, 70 Fe(TPP)(Cl),71, 72 Fe(TPP)(Br),73 and Fe(PPIX)(Cl).59 In contrast with the planar Fe(P) molecule, the halide complexes are domed with the Fe displaced 38 − 52 pm from the mean plane of the four nitrogens toward the halide ligand (Table 2). Crystal structures of Fe(OEP)(Cl) (Ref. 58) and Fe(PPIX)(Cl) (Ref. 59) reveal small additional asymmetric distortions of the porphyrin plane that are not reproduced in our vacuum calculations on the isolated molecules and may result from packing in the crystal lattice.
Table 2.
Structural parameters and stiffness determined experimentally for Fe(P), Fe(P)(Cl), Fe(P)(Br), Fe(OEP)(Cl), Fe(TPP)(Cl), Fe(TPP)(Br), and Fe(PPIX)(Cl). Structural parameters derive from sources cited in the reference column, and the stiffness is determined from the experimental Fe VDOS reported here (Fig. 3) according to Eqs. 7, 8.
| Fe–N | Fe–X | Fe–p | ks | ||
|---|---|---|---|---|---|
| Molecule | (pm) | (pm) | (pm) | Reference | (pN∕pm) |
| Fe(P)(Cl) | … | … | … | 192 ± 2 | |
| Fe(P)(Br) | … | … | … | 192 ± 2 | |
| Fe(OEP)(Cl) | 206.3 | 223.1 | 46 | 69 | 196 ± 6 |
| Fe(OEP)(Cl) | 207.1 | 223.1 | 49.4 | 58 | |
| Fe(OEP)(Cl) | 206.5 | 224.3 | 46.8 | 70 | |
| Fe(TPP)(Cl) | 204.9 | 219.2 | 38 | 71 | |
| Fe(TPP)(Cl) | 207.0 | 221.1 | 49 | 72 | |
| Fe(TPP)(Br) | 206 | 234.8 | 49 | 73 | |
| Fe(PPIX)(Cl) | 206.2 | 221.8 | 47.5 | 59 | 197 ± 4 |
The VDOS for the iron atom provides a natural basis for comparing vibrational DFT predictions with experimental results. The vectors
| (1) |
which describe the linear transformation from normal coordinates Qα to mass-weighted Cartesian displacements of atom j, determine the partial VDOS,
| (2) |
due to Fe motion along direction in an oriented ensemble of molecules.25 In Eq. 2 and subsequent expressions, we take j = Fe and suppress an explicit atomic index on (and on ks below) for notational simplicity, with the understanding that these quantities refer to the Fe atom. The mode composition factor determines the area contributed by mode α to the VDOS,
| (3) |
for unoriented samples.11 The line shape function is centered at mode frequency and normalized to ensure that
| (4) |
and
| (5) |
Calculations on an isolated molecule provide no predictions about vibrational lifetimes, and is thus chosen to have a width greater than or equal to the experimental resolution and a shape that facilitates comparison with the experimental VDOS. Because the mode composition factor measures the fraction of kinetic energy associated with motion of atom j in mode α,11 the mass mj and the predicted displacement of atom j in mode α determine the vector25
| (6) |
| (7) |
measures the force required to displace the Fe, with the positions of the surrounding atoms fixed, in terms of the second moment,
| (8) |
of the Fe VDOS, with . (Here, c is the speed of light in a vacuum.)
EXPERIMENTAL ANALYSIS OF PORPHINE HALIDE VIBRATIONS
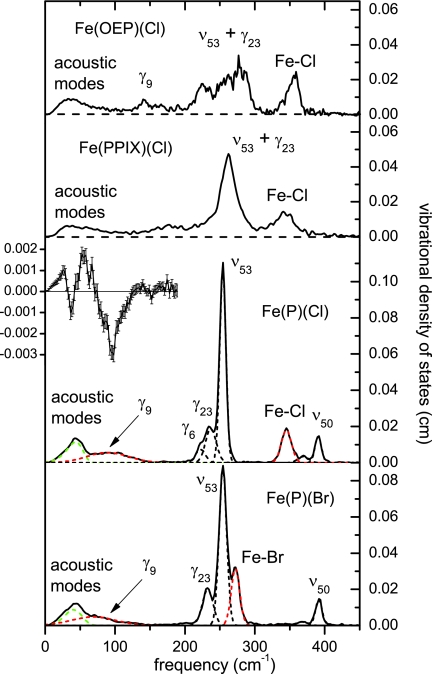
Figure 3 displays experimental VDOS for Fe(P)(Cl), Fe(P)(Br), Fe(OEP)(Cl), and Fe(PPIX)(Cl), together with individual peaks resulting from least squares fit of the Fe(P)(Cl) and Fe(P)(Br) results, using a Levenberg-Marquardt algorithm. We attribute the lowest frequency feature near 30 cm−1 to lattice vibrations. To account for the observed asymmetry, we fit it to a log normal function.77 The remaining peaks in the spectrum were fit to Gaussian functions. Their frequencies and areas are listed in Table 3.
Figure 3.
Measured VDOS for Fe(OEP)(Cl), Fe(PPIX)(Cl), Fe(P)(Cl), and Fe(P)(Br) compounds. Blue curves indicate fitted Gaussians attributed to the doming modes (89 cm−1 for Fe(P)(Cl) and 71 cm−1 for Fe(P)(Br)) and Fe–X stretching modes (345 cm−1 for Fe(P)(Cl) and 272 cm−1 for Fe(P)(Br)), which shift to lower frequency upon substitution of Br for Cl. Green curves indicate fitted log-normal curves attributed to lattice modes. Insert shows the difference between the Fe(P)(Br) data and rescaled Fe(P)(Cl) data in the region below 200 cm−1, as described in the text.
Table 3.
Correspondence of peaks fit to experimental VDOS with previously reported VCS frequencies (Ref. 42) and with predicted normal modes. Mode assignments are based on the frequency and area of predicted and measured peaks, as well as on symmetry considerations.
| Fe(P)(Cl) |
Fe(P)(Br) |
||||||
|---|---|---|---|---|---|---|---|
| VDOS |
VCS | VDOS |
VCS | ||||
| Symmetry | Frequency | Frequency | Frequency | Frequency | |||
| class | (cm−1) | (cm−1) | (cm−1) | (cm−1) | Assignment | ||
| A1, E | 44 | 0.34 | 41 | 0.27 | Lattice modes | ||
| A1 | 90 | 0.42 | 77a | 69 | 0.37 | 62a | γ9 (doming) |
| A1 | 222 | 0.13 | 219b | 162 | γ6 | ||
| A1 | 272 | 0.47 | 284 | Fe–Br stretch, γ6 | |||
| A1 | 345c | 0.33 | 343c | 341 | Fe–Cl stretch, γ7 | ||
| A1 | 369 | 0.06 | 376 | 368 | 0.04 | 375 | ν8 |
| E | 237 | 0.36 | 233 | 0.38 | γ23 | ||
| E | 254 | 1.17 | 254 | 1.18 | ν53 | ||
| E | 391 | 0.17 | 392 | 0.17 | ν50 | ||
The relative contributions of FeX (X = Cl or Br) tilting and γ9 to the VCS signal are undetermined.
Both γ6 and ν35 may contribute to the Fe(P)(Cl) VCS signal at 219 cm−1.
The observed Fe(P)(Cl) features at 345 cm−1 (NRVS) and 343 cm−1 (VCS) contain unresolved contributions from the predicted 338 cm −1 and 348 cm−1 vibrations.
Changes in Fe-ligand bond strength significantly affect the stiffness of the Fe environment in heme proteins.75, 76 In contrast, experimental stiffness values for Fe(P)(Cl) and Fe(P)(Br) determined from NRVS measurements (Table 2) are identical within uncertainty, suggesting that the vibrational differences seen in Fig. 3 primarily reflect the large increase in the mass of the bromide ligand. Comparison of the experimental VDOS for Fe(P)(Cl) and Fe(P)(Br) clearly points to candidates for doming (at 90 and 69 cm−1, respectively) and Fe-ligand stretching modes.
The feature at 345 cm−1 in Fe(P)(Cl) shifts to 272 cm−1 in Fe(P)(Br), qualitatively consistent with the behavior expected for the Fe–halide stretching mode. More quantitatively, a two-body oscillator model28 predicts a VDOS contribution with area
| (9) |
using the mass of Fe for m1. The areas 0.32 and 0.46 resulting from fitting the candidate features in the VDOS of Fe(P)(Cl) and Fe(P)(Br), respectively, are slightly smaller than the values 0.38 and 0.58 predicted by Eq. 9, using the masses of Cl or Br for m2. We use the appropriately averaged masses of two most abundant isotopes of Cl and Br: 35Cl, 37Cl, 79Br, and 81Br (all predictions for halide compounds considered in this paper depend very little on which of the above isotopes to use for halide). Similarly, the 0.79 frequency ratio observed for these features slightly exceeds the 0.65 ratio predicted78 for the two-body oscillator. The 272 cm−1 Fe(P)(Br) frequency lies within the range of values previously assigned to Fe–Br stretching in Fe(OEP)(Br),78, 79 while the 345 cm−1 Fe(P)(Cl) frequency is 12–33 cm−1 lower than Fe–Cl stretching frequencies reported for Fe(OEP)(Cl) (Ref. 78, 79) and Fe(TPP)(Cl).68 Given that the full (Fe)porphine-halide system is more complex than a simple two-body oscillator, the 345 cm−1 and 272 cm−1 features are quite well described as Fe–halide stretching.
The Fe VDOS also displays a broad feature at 90 cm−1 for Fe(P)(Cl) that shifts to 69 cm−1 for Fe(P)(Br). We expect that heme doming is likely to contribute to this feature. However, care must be taken to distinguish this broad feature from the lowest frequency feature (acoustic modes) with a maximum near 40 cm−1.
To better illustrate the low frequency mass sensitivity, we recall that acoustic modes contribute an area equal to 3mFe∕M11, 13 for a molecule of mass M. If we assume the same elastic constants for the Fe(P)(Cl) and Fe(P)(Br) lattices, then the frequencies of the acoustic modes are proportional to M−1/2. In this case, rescaling of both vertical and horizontal axes of VDOS of Fe(P)(Cl) by would produce an identical profile for the lattice modes. (Note that the area attributed to the acoustic modes depends on the product of the horizontal and vertical scaling factors.) In fact, subtraction of the rescaled Fe(P)(Cl) VDOS nearly cancels the lattice contribution and clearly reveals a difference feature near 80 cm−1 (see Fig. 3) that we attribute to the frequency shift of the doming mode. Small changes in the elastic constants of the Fe(P)(Cl) and Fe(P)(Br) lattices may account for incomplete subtraction of the lattice modes visible below 40 cm−1.
The Fe(P)(Cl) VDOS is remarkably simple in comparison with those observed for Fe(OEP)(Cl) (previously reported in Ref. 52) and Fe(PPIX)(Cl), as shown in the upper panels of Fig. 3. This facilitates the identification of the modes, as discussed in Secs. 4, 5. Despite their distance from the iron, the peripheral groups in Fe(OEP)(Cl) and Fe(PPIX)(Cl) introduce additional complexity that we will consider in Sec. 6.
COMPUTATIONAL DESCRIPTION OF PORPHINE HALIDE VIBRATIONS
The low frequency modes of Fe(P)(Cl) and Fe(P)(Br) molecules possessing C4v symmetry can be easily described in terms of the well-known porphyrin mode classification by Abe et. al.80 as adapted to Ni(P) in Ref. 51. In this section, we describe the quantitative decomposition of the modes of the five-coordinate species as combinations of the modes of Fe(P) with Fe–Cl tilting and stretching modes.
To establish a vibrational basis, we performed a DFT calculation on Fe(P) with D4h symmetry to reproduce the mode classification.80 Table S1 and Figs. S1 and S2 in the supplementary information81 describe the complete set of vibrational modes of Fe(P) below 450 cm−1. Calculated frequencies of Fe(P) (optimized to the 3A2g electronic state) agree within 12 cm−1 with those reported previously.82 All modes fall into ten D4h symmetry classes. The labels νi, with i = 1, ..., 53, denote modes with all atoms moving in the porphine plane and γi, with i = 1, ..., 26, denote modes with all atoms moving perpendicular to the porphine plane.
Mode correlation analysis
Consider two molecules with a large number of common atoms. The rows of the vibrational correlation matrix,
| (10) |
provide a useful decomposition of mode α of molecule A in terms of the modes β of molecule B. Equation 10 sums only over atoms that are common to both molecules and that are in equivalent locations. In the case of the porphyrins considered here, for example, these will include the Fe and the 24 atoms of the porphine core. In calculating vibrational correlations between porphyrin molecules below, we align the molecules to overlap the positions of the four pyrrole nitrogen atoms.
The orthonormal character,
of the transformation described by the vectors (Eq. 1) allows us to conclude that
As discussed in Refs.11, 28, the mode composition factors describe the kinetic energy distribution for mode α, such that is the fraction of mode energy associated with the motion of atom j. Thus, row α of the vibrational correlation matrix describes how the fraction of mode energy associated with the motion of shared atoms in mode α of molecules A is distributed among the vibrational modes of molecule B.
In the important special case where molecule B contains all atoms of molecule A,
| (11) |
for each row of the correlation matrix. This result is trivial if the two molecules are identical, when orthonormality ensures that Cαβ = δαβ, but also applies if A and B represent two isotopomers or two different electronic states of the same molecule. More generally, Eq. 11 holds if molecule A is a truncation of molecule B (for example, A = Fe(P) and B = Fe(P)(Cl)). In each of these cases, the vibrational correlation matrix provides a complete accounting of the contribution of the vibrational modes of molecule A to the vibrational motion of molecule B.
The use of mass-weighted coordinates is essential for modes involving significant Fe motion and distinguishes the correlation matrix in Eq. 10 from related approaches46 that neglect mass variations. The method presented here mirrors the vibrational projection analysis introduced by Grafton and Wheeler, who have elucidated the advantages of this approach.83, 84
As we will see, many elements of the correlation matrix vanish due to the high symmetry of the molecules considered here. We justify our adoption of the mode classifications identified for Ni(P) in Ref. 51 by using the correlation matrix to establish a one-to-one correspondence between the modes of Ni(P) and Fe(P). Correlations equal to 0.89 for γ6 and γ7 reflect a small degree of mixing between the corresponding modes in Fe(P). For the remaining 77 out of 79 modes, the correlation coefficient between the corresponding Fe(P) and Ni(P) modes is greater than 0.97.
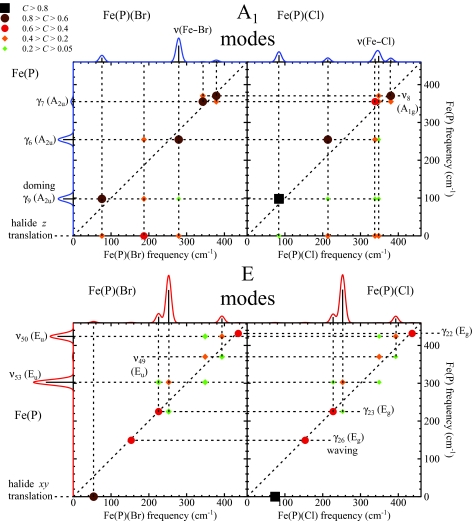
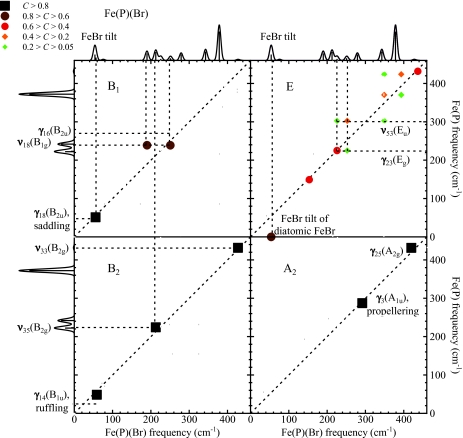
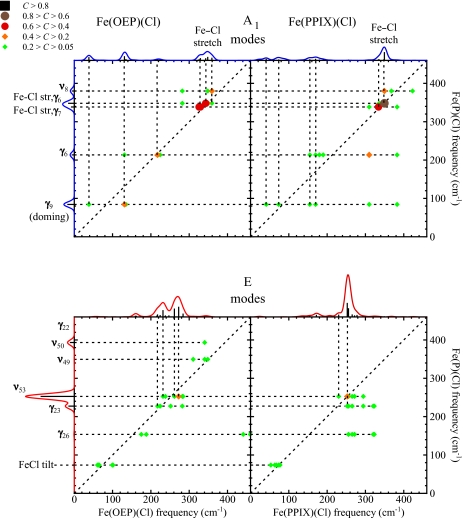
We thus proceed to describe the modes of Fe(P)(Cl) and Fe(P)(Br), using the vibrational predictions for Fe(P), supplemented by translation of the halide atom to complete the basis. Since the Fe atom lies on the C4 axis of these molecules, only modes of A1 and E symmetry contribute to the 57Fe NRVS signal. Figure 4 displays the correlations of low frequency modes of Fe(P) with A1 and E modes of Fe(P)(Cl) and Fe(P)(Br). Figure 5 displays correlations between low frequency modes of Fe(P) and the modes of Fe(P)(Br) belonging to additional symmetry classes. Table 4 summarizes mode descriptions established this way for Fe(P)(Cl) and Fe(P)(Br) below 450 cm−1. Note that by symmetry, the only nonzero correlations are the ones between A1 modes of C4v and A1g or A2u modes of D4h, A2 modes of C4v and A2g or A1u modes of D4h, B1 modes of C4v and B1g or B2u modes of D4h, B2 modes of C4v and B2g or B1u modes of D4h, E modes of C4v and Eg or Eu modes of D4h.
Figure 4.
Correlations between the low frequency modes of Fe(P) and the NRVS active low frequency modes of Fe(P)(Cl) and Fe(P)(Br). The upper (lower) panels display modes of A1(E) symmetry in the C4v point group of the five-coordinate Fe complexes. The color scale for C appears in the upper left part of the figure. Predicted VDOS for Fe(P) and for Fe(P)(Br) and Fe(P)(Cl) abut vertical and horizontal axes, respectively, for ease of reference. Red and blue traces indicate E and A1 contributions to the VDOS, respectively.
Figure 5.
Correlation between the low frequency modes of Fe(P) and modes of B1, E, B2, and A2C4v symmetry classes of Fe(P)(Br). Off-resonance Raman spectra predicted for Fe(P) and Fe(P)(Br) abut vertical and horizontal axes, respectively, for ease of reference.
Table 4.
The complete set of the DFT predicted vibrational modes of Fe(P)(Cl) and Fe(P)(Br) below 450 cm−1 with predicted values, symmetries, and decomposition with respect to Fe(P) modes.
| Fe(P)(Cl) |
Fe(P)(Br) |
||||
|---|---|---|---|---|---|
| Symmetry | (cm−1) | a | (cm−1) | a | Mode descriptionb |
| A1 | 0 | 0 | 0 | 0 | Rz |
| A1 | 0 | 0.166 | 0 | 0.147 | Tz |
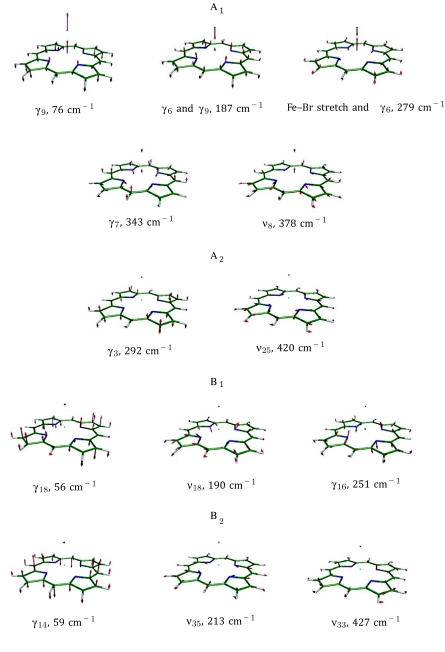
| A1 | 84 | 0.27 | 76 | 0.176 | γ9 (doming) |
| A1 | 213 | 0.107 | 187 | 0 | γ6c |
| A1 | 338 | 0.134 | 279 | 0.633 | Fe–Xd stretch, γ6 |
| A1 | 348 | 0.241 | 343 | 0.008 | γ7e |
| A1 | 380 | 0.101 | 378 | 0.049 | ν8 |
| A2 | 291 | 0 | 292 | 0 | γ3 (propellering) |
| A2 | 420 | 0 | 420 | 0 | ν25 |
| B1 | 55 | 0 | 56 | 0 | γ18 (saddling) |
| B1 | 189 | 0 | 190 | 0 | ν18 |
| B1 | 250 | 0 | 251 | 0 | γ16 |
| B2 | 57 | 0 | 59 | 0 | γ14 (ruffling) |
| B2 | 214 | 0 | 213 | 0 | ν35 |
| B2 | 428 | 0 | 427 | 0 | ν33 |
| E | 0 | 0.011 | 0 | 0.001 | Rx, Ry |
| E | 0 | 0.332 | 0 | 0.294 | Tx, Ty |
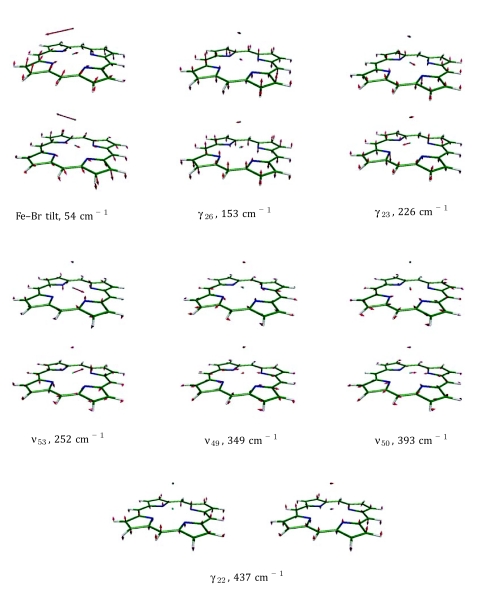
| E | 74 | 0.006 | 54 | 0.034 | Fe–Xd tilting |
| E | 154 | 0.008 | 153 | 0.01 | γ26 (waving) |
| E | 227 | 0.23 | 226 | 0.244 | γ23 |
| E | 253 | 1.272 | 252 | 1.256 | ν53 |
| E | 349 | 0.002 | 349 | 0.002 | ν49 |
| E | 393 | 0.174 | 393 | 0.178 | ν50 |
| E | 437 | 0.002 | 437 | 0.002 | γ22 |
Summation over degenerate mode pairs for E symmetry.
να and γα refer to the nomenclature established for Ni(P) in Ref. 51, Rj and Tj indicate rotation and translation of the entire molecule.
Significant mixing with γ9 for Fe(P)(Br).
X = Cl or Br.
Significant mixing with Fe–Cl stretching for Fe(P)(Cl).
Figure 5 shows that most modes of A2, B1, B2, and E symmetry in Fe(P)(Br) correlate with one particular mode of Fe(P) and show little or no correlation with other modes. Exceptions below 450 cm−1 include mixing of the ν53 and γ23 modes of Eu and Eg symmetry and the ν18 and γ16 modes of B1g and B2u symmetry in Fe(P), which takes place because these modes belong to the same symmetry class (E and B1, respectively) in the C4v symmetry of the five-coordinate molecule. In addition, FeCl and FeBr tilting modes (E) correlate strongly with halide translation parallel to the heme, but negligibly with Fe(P) vibrations.
The contribution of halide translation to A1 modes is more complex. In this case z-translation of the halide atom (Fig. 4, top panels) mixes with other modes of A1 symmetry (below 450 cm−1 those are γ9, γ6, γ7, and ν8). In order to analyze the contribution of Fe–halide stretching itself, we project Fe(P)(X) vibrations onto stretching of the fictitious diatomic FeX molecule. The mode composition factors
| (12) |
and
| (13) |
of the Fe–X stretching mode follow from energy conservation,11, 25 and the vectors and are oriented along the Fe–X bond and antiparallel to each other. Projection onto this two-body Fe–X oscillation according to Eq. 10 indicates that Fe–Cl stretching character is mainly distributed among modes at 338 cm−1 (37%), 348 cm−1 (52%), and 380 cm−1 (9%) for Fe(P)(Cl), while Fe–Br stretching character in Fe(P)(Br) is mostly distributed among modes at 187 cm−1 (15%), 279 cm−1 (81%), and 378 cm−1 (3%). The slightly more complex situation for Fe(P)(Cl) results from mixing with the γ7 mode, which is predicted to remain as a distinct vibration at 343 cm−1 for Fe(P)(Br).
ASSIGNMENT OF PORPHINE HALIDE VIBRATIONS
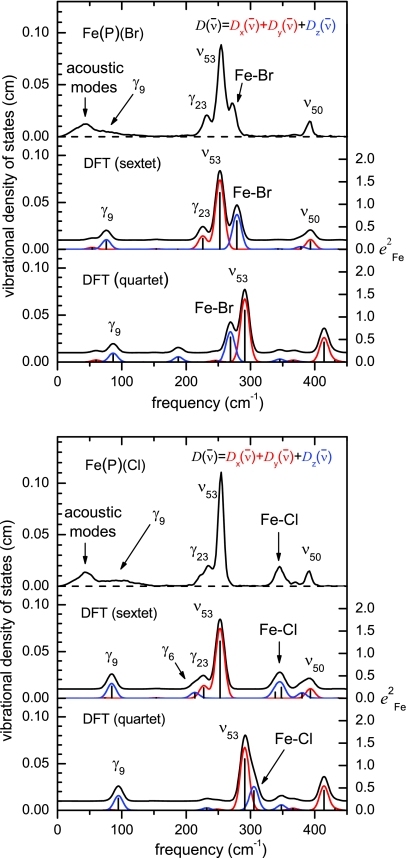
Figure 6 compares the Fe VDOS obtained from NRVS measurements on Fe(P)(Cl) and Fe(P)(Br) with predictions resulting from DFT calculations on both sextet and quartet states of these molecules. Based on its high degree of correspondence with the experimental results, we use the VDOS predicted for the S = 5/2 electronic state to describe the observed vibrational features.
Figure 6.
Measured (NRVS) and predicted (DFT) iron VDOS are compared for sextet and quartet states of Fe(P)(Br) (top) and Fe(P)(Cl) (bottom). A 16 cm−1 Gaussian was convoluted with the predicted VDOS to facilitate comparison with experiment. Sextet state predictions correspond very well with experimental results, while quartet state predictions clearly disagree. Black, red, and blue traces indicate total, E, and A1 contributions, respectively, to the predicted VDOS.
Modes of A1 and E symmetry, corresponding to Fe motion parallel and perpendicular to the molecular C4 axis, contribute to the predicted VDOS. Since the Fe atom lies on the C4 axis, its displacement vanishes for modes of other symmetries. Molecular translation and rotation take place at zero frequency in the gas phase calculations and are omitted from the predicted VDOS shown in Fig. 6. Nevertheless, both involve significant Fe motion (Table 4) and are expected to contribute to the experimental VDOS at nonzero frequencies because of interactions with the surrounding lattice.
The dominant feature of the NRVS signal for Fe(P)(Cl) appears at 254 cm−1 (Fig. 3). Based on its large area (), this cannot be a single mode. Consistent with this expectation, the degenerate (E −symmetric) ν53 modes (Fig. S2) at 253 cm−1 dominate the predicted VDOS, with area 1.272. Similarly, for Fe(P)(Br) the largest NRVS feature located at 254 cm−1 with area 1.18 corresponds to the predicted ν53 mode pair at 252 cm−1 with area 1.257 (Fig. 7).
Figure 7.
Vibrational modes of Fe(P)(Br) of E symmetry below 450 cm−1. Color scheme: iron is cyan, carbon is green, nitrogen is blue, bromine is brown, and hydrogen is white. For ease of visualization, each arrow is 50(mj∕mFe)1∕2 times longer than the zero-point vibrational amplitude of atom j.
The γ23 doublet of E symmetry (Fig. S2) is predicted at 227 cm−1 with area 0.231 for Fe(P)(Cl) and contributes to the observed 237 cm−1 band in NRVS with area 0.36, along with a shoulder at 222 cm−1, which can be attributed to the γ6 mode (Fig. S1) predicted by DFT at 213 cm−1 with area 0.107. Notice that γ23 cannot contribute to the VDOS for Fe(P) by symmetry, and contributes to the NRVS signal in Fe(P)(Cl) through mixing with ν53, when the symmetry lowers to C4v. The total area (1.61) predicted for ν53, γ23, and γ6 is close to the total area of the observed 222, 237, and 254 cm−1 bands (1.66). The γ23 in Fe(P)(Br) is predicted at 226 cm−1 with area 0.244 (Fig. 7) and contributes to the band observed at 233 cm−1 in NRVS with area 0.38. For both molecules, DFT overestimates the area of one E doublet and underestimates the area of the other. However, the total area predicted for ν53 and γ23 is very close to the total area of the observed 233/236 cm−1 and 254 cm−1 bands, about 1.5 in all cases. Thus, the small quantitative error in the predicted degree of mixing between ν53 and γ23 does not alter the qualitative description of the observed features at 254 cm−1 and 226 cm−1 as ν53 and γ23, respectively.
Three more significant features appear in the observed Fe(P)(Cl) VDOS at 345, 369, and 391 cm−1. The DFT predicts two modes with Fe–Cl stretching character and with significant Fe motion in this region at 338 cm−1 and 348 cm−1. The total area 0.377 accounts for the NRVS feature at 345 cm−1 (area 0.33). The NRVS peak at 391 cm−1 (area 0.17) corresponds to the DFT predicted ν50 mode doublet of E symmetry (Fig. S2) at 393 cm−1 of combined area 0.175.
The weaker experimental feature at 369 cm−1 corresponds to the ν8 mode predicted at 380 cm−1. Note that, in the D4h symmetry of the Fe(P) reference calculation, ν8 is an in-plane A1g vibration involving no Fe motion. Examination of the correlation diagram (Fig. 4) reveals that ν8 acquires a component of Fe motion perpendicular to the porphine plane through mixing with the A2u-symmetric γ7 vibration in the reduced C4v symmetry of the halide complexes. We observed a similar weak contribution of Fe motion to the ν8 vibration in reduced cytochrome c, which has an asymmetrically ligated and distorted heme group.76
The mode with the most significant predicted out-of-plane iron motion in Fe(P)(Br) is the one at 279 cm−1, which is a combination of Fe–Br stretch and γ6 (Fig. 8). It has area 0.635 and reproduces the Fe(P)(Br) NRVS peak at 272 cm−1 (area 0.47). In the region 300 − 400 cm−1 there are two significant Fe(P)(Br) NRVS peaks at 368 and 392 cm−1. These peaks are well reproduced by DFT predicted ν8 (which again acquires Fe motion in C4v) and the ν50 doublet of E symmetry at 393 cm−1 (Fig. 7).
Figure 8.
Vibrational modes of Fe(P)(Br) of A1, A2, B1, and B2 symmetry below 450 cm−1. Color scheme: iron is cyan, carbon is green, nitrogen is blue, bromine is brown, and hydrogen is white. For ease of visualization, each arrow is 50(mj∕mFe)1∕2 times longer than the zero-point vibrational amplitude of atom j.
The γ7 mode, predicted to appear at 343 cm−1 in Fe(P)(Br), has two features worthy of notice. The γ7 overtone is near coincidence with the ν7 fundamental at 736 cm−1, and energy transfer to the γ7 overtone has been identified as an important channel for vibrational relaxation of ν7 in porphyrins.85 The predicted Fe amplitude is small, and γ7 does not contribute significantly to the predicted 57Fe VDOS for Fe(P)(Br). However, γ7 indirectly influences the predicted Fe(P)(Cl) VDOS by mixing with the nearby Fe–Cl stretching and ν8 modes.
The Fe(P)(Cl) VDOS below 150 cm−1 is fitted with two peaks at 44 cm−1 (lattice modes) and 90 cm−1 (Fig. 3). The DFT predicts only one mode with significant iron amplitude below 150 cm−1, the γ9 (doming) mode of A1 symmetry at 84 cm−1. The area of the 90 cm−1 peak is 0.42 while the area of the DFT predicted 84 cm−1 peak is 0.27. The discrepancy can be explained by incomplete knowledge of the shape of the NRVS feature due to the lattice motions. Thus, it is natural to assign this peak to doming (γ9). In the case of the bromide complex, we observe doming at 69 cm−1 with area 0.37, while γ9 (Fig. 8) is predicted at 76 cm−1 with area 0.177.
From Table 3 summarizing all Fe(P)(Cl) and Fe(P)(Br) assignments for modes below 450 cm−1, it follows that NRVS confirms the assignments of A1 low frequency modes in Fe(P)(Cl) and Fe(P)(Br) made in Ref. 42 with the possible exception of γ9 (doming) modes in Fe(P)(Cl) and in Fe(P)(Br) (see below). One interesting special case is the predicted mode at 187 cm−1 in Fe(P)(Br) which is a superposition of γ9, γ6, and Fe–Br stretch such that the Fe atom practically does not vibrate (Fig. 4), consistent with the absence of NRVS signal corresponding to the 162 cm−1 coherence observed using VCS.
The γ9 (doming) frequencies identified in the Fe VDOS (Fig. 3) differ by 13 cm−1 and 7 cm−1 from robust VCS coherences reported for Fe(P)(Cl) and Fe(P)(Br), respectively. These are not large discrepancies, considering the width of the NRVS peaks and their overlap with acoustic modes. On the other hand, we must consider the possibility that γ14, γ18 (Figs. S1 and 8), and Fe–X tilting (Figs. S2 and 7) modes may also contribute to the VCS signal in the same frequency region. In particular, the DFT calculations on Fe(P)(Cl) and Fe(P)(Br) indicate that the largest contribution to the off-resonance Raman signal is coming from the Fe–X tilt and γ9 modes. Thus, it is possible that Fe–X tilting, heme doming, or both could contribute to the VCS features at 77 cm−1 in Fe(P)(Cl) and at 62 cm−1 in Fe(P)(Br). However, it must be noted that VCS signals are obtained under electronic resonant conditions, so correlation of the VCS signals to the off-resonance Raman calculations is unclear. Nevertheless, the fact that VCS peaks are located between the frequencies predicted for Fe–X tilt and doming modes (74 cm−1 and 84 cm−1 in Fe(P)(Cl) and 54 cm−1 and 76 cm−1 in Fe(P)(Br)) suggests that both motions may contribute to the VCS observations.
CORRELATION ANALYSIS OF PERIPHERAL SUBSTITUTIONS
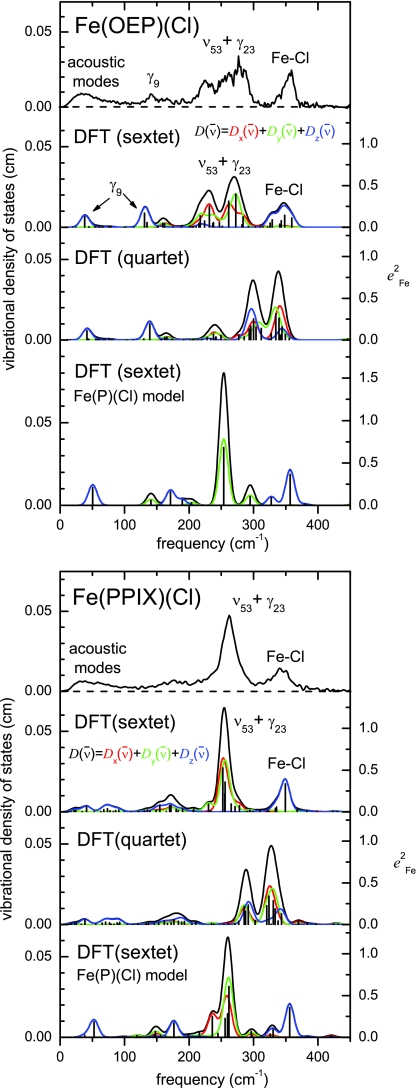
To gain insight into the vibrational properties of real heme systems, we investigated the effect of added side chains in the more complex molecules Fe(OEP)(Cl) and Fe(PPIX)(Cl). Again, the VDOS predicted for the sextet state of these models reproduces the experimental VDOS rather well (Fig. 9). We calculated correlations between Fe(P)(Cl) and Fe(OEP)(Cl) and between Fe(P)(Cl) and Fe(PPIX)(Cl), all in sextet states, to understand the effect of the additional side chains on the vibrational dynamics of Fe. Comparing Fig. 9 to Fig. 6, many more modes contribute to the 57Fe VDOS predicted for Fe(OEP)(Cl) and Fe(PPIX)(Cl) than for Fe(P)(Cl).
Figure 9.
Comparison of measured (NRVS) and predicted (DFT) iron VDOS for Fe(OEP)(Cl) (top) and Fe(PPPIX)(Cl) (bottom). Predictions include Fe(P)(Cl) sextet with hydrogen masses adjusted to those of the peripheral group as well as both sextet and quartet states of the complete molecule. A 16 cm−1 Gaussian was convoluted with the predicted VDOS to facilitate comparison with experiment. Sextet state predictions correspond very well with experimental results, while quartet state predictions clearly disagree.
Figure 10 shows predicted correlations of the low frequency modes of Fe(OEP)(Cl) and Fe(PPIX)(Cl) with those of Fe(P)(Cl). Unlike the case of axial ligand binding (which only affected A1 modes substantially), the introduction of the asymmetrically oriented side chains in Fe(OEP)(Cl) and Fe(PPIX)(Cl) leads to splitting of modes of all symmetry classes. We note that the splitting of a rather pure γ9 (doming) mode predicted at 84 cm−1 for Fe(P)(Cl) correlates (C > 0.1) with three modes at 38, 131, and 135 cm−1 for Fe(OEP)(Cl) and with six modes for Fe(PPIX)(Cl). The large ν53 mode of Fe(P)(Cl) contributes to Fe(OEP)(Cl) modes at 232, 238, 261, 273, 282, and 284 cm−1, while the ν50 mode observed at 391 cm−1 for Fe(P)(Cl) does not contribute substantially to the VDOS of either Fe(OEP)(Cl) or Fe(PPIX)(Cl). Similar splittings appear for modes of all symmetry classes, including the Fe–Cl stretching modes. Although the pair of Fe(OEP)(Cl) modes predicted at 159 and 162 cm−1 contribute noticeably to the VDOS, they mostly involve motion of side chain atoms and vibrational correlations with Fe(P)(Cl) do not exceed 0.02 (with ν53).
Figure 10.
Correlations of the low frequency modes of Fe(P)(Cl) with Fe(OEP)(Cl) and Fe(PPIX)(Cl). Modes of all symmetry classes split as a result of the reduced symmetry.
The degree to which modes remain localized on the porphine core varies considerably. The summation measures the extent to which mode α is localized on the atoms included in the sum. By this criterion, motion of Fe and Cl accounts for more than 95% of the energy of the Fe–Cl stretching mode in Fe(PPIX)(Cl). However, other iron modes () have less than 75% of mode energy localized on the 30 atoms of the iron porphine core (including iron, halide, and methine hydrogens). At least 50% of iron modes have more than 50% of mode energy involved with motion of peripheral atoms.
DISCUSSION
Electronic state
Quantum chemical calculations are now widely employed to model hemes and other protein active sites.86, 87 Difficulties in correctly predicting the relative energies of different spin states are a widely acknowledged shortcoming of DFT calculations.88, 89 Ferric porphyrin chlorides, in particular, have been cited as an illustration of this problem.65 The ground state is experimentally established as a sextet,60, 61, 62, 63, 64 but the lowest lying sextet and quartet states are predicted to lie close in energy.65, 66, 67 Even after correcting for the larger zero-point energy of the quartet state, our calculations predict comparable energies for the quartet and sextet states in all ferric porphyrin chlorides that we have considered (see Table 1).
The Fe−Npyr bond lengths reported in crystal structures of ferric porphyrin chlorides58, 59, 69, 70, 71, 72, 90 are 1 − 3 pm shorter than the 208 pm value predicted for the sextet state, but 4 − 6 pm longer than the 201 pm value predicted for the quartet (Tables 1, 2). Similarly, the stiffnesses that we measure for all halide complexes are about 10% lower than those predicted for the sextet state, but 50% smaller than those predicted for the quartet state. Overall, the observed Fe-ligand bond lengths, Fe displacements from the porphyrin plane, and stiffnesses are significantly closer to the values reported for the sextet state than for the quartet state (see Tables 1, 2). These results are consistent with previous measurements that indicate S = 5/2 for the ground state.62, 63, 64
It is particularly telling that the DFT predictions for the ground sextet correspond very well to NRVS observations for all molecules considered here. On the other hand, Fe(P)(Cl), Fe(P)(Br), Fe(OEP)(Cl), and Fe(PPIX)(Cl) vibrational predictions for the lowest quartet clearly disagree with observations (Figs. 69), in spite of a slightly lower optimized energy. This agrees with other experimental evidence for a sextet ground state62, 63, 64 and supports confident assignment of prominent features observed in the experimental VDOS.
Agreement with detailed predictions of vibrational frequencies and amplitudes thus provides compelling evidence for the electronic states of these molecules. The strong correspondence with the predicted VDOS lends theoretical guidance to interpreting the motions responsible for the observed vibrational features, which complements conclusions based purely on experimental observations, such as frequency shifts on halide substitution. In particular, the correlation analysis presented above relates predicted vibrations to the well-established vibrational nomenclature for porphyrins.51
Characterization of reactive modes
Displacement of the Fe relative to the plane of the porphyrin, coupled with porphyrin distortion, often accompanies binding of axial Fe ligands. This observation has long fueled speculation that heme proteins can influence ligand binding reactions by controlling Fe displacement,33, 71, 91, 92 but the absence of direct experimental information about the energetic cost of Fe displacement has limited attempts to assess the quantitative significance of this effect.31
Vibrational motions relevant to thermally driven reactions are likely to lie at low frequencies ( cm−1), where technological advances are beginning to provide experimental access.9, 34, 42, 93, 94 However, frequency shifts on the order of a few percent become increasingly difficult to detect at low frequencies, inhibiting the traditional use of isotopic labeling to reveal the contributions of individual atoms. As a result, the identification of observed vibrational features with reactive motions remains challenging.
For example, the enhanced far infrared intensity available at synchrotron IR beamlines facilitates low frequency measurements on biomolecules.34, 94 A vibrational feature observed at 53 cm−1 in Fe(OEP)(pyr)(CO), with pyridine (pyr) and CO as axial ligands, shifts with pressure and was attributed to a doming mode predicted by DFT at 39 cm−1.34 However, the reported observations do not exclude other possibilities. In particular, an FeCO distortion mode (in-phase tilt∕bend) is also predicted in the 73 − 84 cm−1 frequency region of carbonyl porphyrins,28, 43, 95 and its possible dependence on pressure has not been evaluated.
Advances in laser technology provide additional routes to the low frequency region.42, 93 In particular, VCS reveals oscillations below 200 cm−1 strongly coupled to ligand dissociation reactions in heme proteins.35, 37, 38, 39, 42 Some of these have been plausibly associated with heme doming, but there is no direct evidence for involvement of the Fe. The VCS measurements on porphine halides reveal a 77 cm−1 oscillation whose frequency downshifts by 15 cm−1 upon substitution of Br for Cl,42 similar to the 19 cm−1 shift of γ9 determined using NRVS. However, DFT predicts a Fe–halide tilting mode in the same frequency region (Table 4), and the observed frequency shifts are intermediate between the 8 cm−1 and 20 cm−1 shifts predicted for the doming and Fe–halide tilting modes, respectively.
NRVS not only provides experimental access to the low frequency region, but also yields definitive evidence for Fe motion, and previous NRVS measurements on powders and oriented single crystals have identified low frequency motions associated with Fe displacement from the porphyrin plane.23, 24, 25, 28, 96
The present measurements on Fe(P)(Cl) and Fe(P)(Br) reveal particularly simple vibrational spectra where the γ9 mode associated with doming of the heme provides the only intramolecular contribution to the NRVS signal below 200 cm−1. Although the observed features are relatively broad, halide substitution reveals an unmistakable frequency shift from ∼89 cm−1 for Fe(P)(Cl) to 70 cm−1 for Fe(P)(Br) and clearly distinguishes the γ9 signal from overlapping lattice mode contributions. The DFT calculations predict large frequency shifts both for γ9 and for the FeX tilting mode, but only γ9 contributes substantially to the NRVS signal (Table 4). Previous VCS investigations on the same compounds42 are unable to unambiguously distinguish the relative contributions of γ9 and the FeX tilting contributions.
Influence of peripheral substitution
A traditional approach to modelling vibrational dynamics in complex molecules is to model a fragment of the molecule containing modes of interest, in the expectation that vibrations of the complete molecule will resemble those of the truncated model, with the effect of added groups restricted to frequency changes.
However, previous NRVS measurements on a series of iron nitrosyl porphyrins revealed that variations in the chemical groups bonded to the methine carbons and pyrrole β carbons at the periphery significantly influenced the vibrational dynamics of the Fe, despite minimal variation in the local coordination of the five-coordinate Fe.25 Experimental results presented above also show significant vibrational variations among Fe(P)(Cl), Fe(OEP)(Cl), and Fe(PPIX)(Cl), although the structural information and stiffnesses suggest that the geometry and energetics of the immediate Fe coordination environment are similar. Correlation analysis of the quantum chemical calculations presented here (Fig. 10) provides useful insights into the vibrational consequences of molecular additions.
Addition of a halide ligand to the Fe provides a useful reference point. Correlation analysis (Figs. 45) reveals that the vibrational dynamics of the Fe atom in Fe(P)(Cl) are noticeably perturbed in comparison with the four-coordinate “parent” compound Fe(P), reflecting the altered nearest-neighbor bond strengths (Table 1). In particular, modes of ν53 or ν50 character, involving stretching of the equatorial Fe–N bonds, dominate NRVS measurements on heme proteins and on model compounds and provide useful markers for the spin state of the Fe. In comparison with Fe(P), the E-symmetric modes ν49, ν50, and ν53 in Fe(P)(Cl) mix significantly as well as shifting in frequency. In addition, Fe(P) modes involving Fe motion perpendicular to the heme plane (mainly γ6 and γ7) mix with halide translation to produce the Fe−halide stretching vibration (Fig. 4). However, the fourfold molecular symmetry is maintained upon halide binding and modes of other symmetries undergo frequency changes, with minimal change in mode character.
We also observe significant changes in the vibrational dynamics of the Fe when side chains are added (Fig. 3), but analysis of computational results reveals substantial changes in mode character independent of symmetry class. Other than Fe–Cl stretching, no Fe(OEP)(Cl) mode has a correlation coefficient larger than 0.4 with any mode of Fe(P)(Cl) in the frequency range considered here. Although the number of modes contributing to the Fe VDOS increases in general, the ν50 mode observed at 393 cm−1 in Fe(P)(Cl) no longer contributes significantly to the NRVS signal for either Fe(OEP)(Cl) or Fe(PPIX)(Cl).
Interestingly, an attempt to mimic the effect of side chains by substituting side chain masses for the hydrogen masses in the Fe(P)(Cl) calculation captures qualitative changes in the VDOS predicted for the full Fe(PPIX)(Cl) model, including the diminished contribution of ν50, the appearance of new vibrational features in the 150 − 200 cm−1 region, and reduced frequencies for the doming and FeCl tilting modes (Fig. 9), in comparison with the natural abundance Fe(P)(Cl) sextet calculation (Fig. 6). However, the full Fe(PPIX)(Cl) calculation displays greater vibrational complexity, particularly below 200 cm−1.
The failure of mass effects alone to capture the vibrational influence of the peripheral groups is more apparent for Fe(OEP)(Cl), where calculations on the full molecular model predict significant splitting of the ν53 feature. The “heavy hydrogen” calculation clearly underestimates this splitting, which exceeds the experimental resolution and is needed to reproduce analogous observations in the experimental VDOS.
Correlation analysis suggests that the increased vibrational complexity predicted and observed for Fe(OEP)(Cl) reflects significant mixing of porphyrin and side chain vibrations. On the other hand, predicted Fe stiffnesses vary by less than 3%, suggesting that the electronic influence of the side chains on Fe vibrations is minimal.
Accurate modelling of thermally activated motions
Low frequency reactive vibrations are particularly strongly perturbed. The rather “pure” doming (γ9) mode predicted for Fe(P)(Cl) contributes significantly to predicted Fe(OEP)(Cl) modes at 38 cm−1, 131 cm−1, and 135 cm−1 with correlations equal to 0.13, 0.36, and 0.11, respectively. Lattice modes impede experimental confirmation of the predicted 38 cm−1 mode. However, we expect that the modes with predicted 131 cm−1 and 135 cm−1 frequencies contribute to the experimental feature at 142 cm−1.
An earlier attempt to model the Fe(OEP)(Cl) data using an empirical potential function with adjustable parameters also indicated unresolved vibrational complexity even greater than the current DFT predictions.52 However, the detailed assignments of observed features differ. In particular, the experimental feature at 142 cm−1, which we predict to have the largest overlap with the porphine γ9 mode (Fig. 1) was instead attributed to in-plane Fe motion associated with the ν51 mode pair.52 It is interesting that far infrared measurements on Fe(OEP)(pyr)(CO) identified a feature at 140 cm−1 with out-of-plane Fe motion, although this was predicted to occur out of phase with the doming of the porphyrin, and denoted inverse doming (γ6).34
Other significant discrepancies include attribution of the broad experimental feature at 230 cm−1 to N–Fe–Cl bending in the empirical calculation on Fe(OEP)(Cl),52 in contrast with the much lower frequency and negligible Fe amplitude predicted by DFT for the FeCl tilting mode (Fig. 6). The ability of two vastly different models to reproduce the main experimental features underscores the underdetermined nature of empirical modelling of data on unoriented samples. Analysis of measurements on single crystals of Fe(OEP)(Cl) will provide a crucial test of competing assignments, particularly for the 142 cm−1 feature, and may help to discriminate experimental signal corresponding to the out-of-plane vibration predicted at 38 cm−1 from the competing signal due to lattice vibrations. Continuing investigations, including measurements on oriented single crystals, will address disagreements with an alternative model52 for Fe vibrations in Fe(OEP)(Cl).
Regardless of the detailed model, peripheral groups clearly influence both the frequency and the character of reactive modes. Systematic investigations of a series of related compounds with a range of experimental and computational techniques will not only resolve discrepancies among different calculations, but also help to evaluate the extent to which the peripheral groups affect the energetics of molecular distortion and its potential influence on molecular reactivity.
CONCLUSION
Comparison of experimental and computational results on simple heme models not only allows straightforward identification of the ground electronic state, but also paints a comprehensive picture of the vibrational dynamics of hemes. A mode correlation technique introduced here reveals how the vibrations of the heme core evolve in response to binding of halide ligands and addition of peripheral side chains. In particular, we find that asymmetric substitutions on biologically relevant protoporphyrins strongly influence thermally activated modes associated with ligand binding and dissociation.
Analysis of NRVS measurements on oriented single crystals of these and related compounds, now underway, will further clarify the vibrational dynamics of Fe in these molecules. We anticipate that systematic variation of reactive modes with side chains will allow us to assess their contribution to vibrational coherences induced by femtosecond pulses and to quantify their contribution to reactive energetics.
ACKNOWLEDGMENTS
We acknowledge financial support from the National Science Foundation (CHE-1026369 and MCB-0744738) and the National Institutes of Health (DK35090). Use of the Advanced Photon Source was supported by the U.S. Department of Energy, Basic Energy Sciences, Office of Science, under Contract No. DEAC02-06CH11357. We thank Dr. Weiqiao Zeng, Dr. Nathan J. Silvernail, and Professor W. Robert Scheidt for assistance during NRVS data collection.
References
- Handbook of Vibrational Spectroscopy, edited by Chalmers J. M. and Griffiths P. R. (Wiley, New York, 2002). [Google Scholar]
- Dyer R. B. and Woodruff W. H., in Applications of Physical Methods to Inorganic and Bioinorganic Chemistry, edited by Scott R. A. and Lukehart C. M. (Wiley, Chichester, 2007), pp. 489–512. [Google Scholar]
- Biological Applications of Raman Spectroscopy, edited by Spiro T. G. (Wiley-Interscience, New York, 1988). [Google Scholar]
- Barth A. and Zscherp C., Q. Rev. Biophys. 35, 369 (2002). 10.1017/S0033583502003815 [DOI] [PubMed] [Google Scholar]
- Badger R., J. Chem. Phys. 2, 128 (1934). 10.1063/1.1749433 [DOI] [Google Scholar]
- Badger R., J. Chem. Phys. 3, 710 (1935). 10.1063/1.1749581 [DOI] [Google Scholar]
- Green M. T., J. Am. Chem. Soc. 128, 1902 (2006). 10.1021/ja054074s [DOI] [PubMed] [Google Scholar]
- Morris D. E. and Woodruff W. H., in Spectroscopy of Inorganic-Based Materials , edited by Clark R. J. H. and Hester R. E. (Wiley, New York, 1987) pp 285–332. [Google Scholar]
- Sage J. T., Durbin S. M., Sturhahn W., Wharton D. C., Champion P. M., Hession P., Sutter J., and Alp E. E., Phys. Rev. Lett. 86, 4966 (2001). 10.1103/PhysRevLett.86.4966 [DOI] [PubMed] [Google Scholar]
- Zeng W., Silvernail N. J., Scheidt W. R., and Sage J. T., in Applications of Physical Methods to Inorganic and Bioinorganic Chemistry, edited by Scott R. A. and Lukehart C. M. (Wiley, Chichester, 2007), pp. 401–421. [Google Scholar]
- Sage J. T., Paxson C., Wyllie G. R.A., Sturhahn W., Durbin S. M., Champion P. M., Alp E. E., and Scheidt W. R., J. Phys.: Condens. Matter 13, 7707 (2001). 10.1088/0953-8984/13/34/315 [DOI] [Google Scholar]
- Sturhahn W., J. Phys.: Condensed Matter 16, S497 (2004). 10.1088/0953-8984/16/5/009 [DOI] [Google Scholar]
- Chumakov A. I., Rüffer R., Leupold O., and Sergueev I., Struct. Chem. 14, 109 (2003). 10.1023/A:1021677228507 [DOI] [Google Scholar]
- Keppler C., Achterhold K., Ostermann A., van Bürck U., Potzel W., Chumakov A. I., Baron A. Q., Rüffer R., and Parak F., Eur. Biophys. J. 25, 221 (1997). 10.1007/s002490050034 [DOI] [PubMed] [Google Scholar]
- Bergmann U., Sturhahn W., D. E.LinnJr., F. E.Jenney, Jr., Adams M. W., Rupnik K., Hales B. J., Alp E. E., Mayse A., and Cramer S. P., J. Am. Chem. Soc. 125, 4016 (2003). 10.1021/ja028767+ [DOI] [PubMed] [Google Scholar]
- Achterhold K. and Parak F. G., J. Phys.: Condensed Matter 15, S1683 (2003). 10.1088/0953-8984/15/18/302 [DOI] [Google Scholar]
- Zeng W., Silvernail N., Wharton D. C., Georgiev G. Y., Leu B. M., Scheidt W. R., Zhao J., Sturhahn W., Alp E. E., and Sage J. T., J. Am. Chem. Soc. 127, 11200 (2005). 10.1021/ja051052x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao Y., Wang H., George S. J., Smith M. C., Adams M. W.W., F. E.Jenney, Jr., Sturhahn W., Alp E. E., Zhao J., Yoda Y., Dey A., Solomon E. I., and Cramer S. P., J. Am. Chem. Soc. 127, 14596 (2005). 10.1021/ja042960h [DOI] [PubMed] [Google Scholar]
- Zeng W., Barabanschikov A., Zhang Y., Zhao J., Sturhahn W., Alp E., and Sage J., J. Am. Chem. Soc. 130, 1816 (2008). 10.1021/ja077823+ [DOI] [PubMed] [Google Scholar]
- Leu B. M., Ching T. H., Zhao J., Sturhahn W., Alp E. E., and Sage J. T., J. Phys. Chem. B 113, 2193 (2009). 10.1021/jp806574t [DOI] [PubMed] [Google Scholar]
- Tonzetich Z. J., Wang H., Mitra D., Tinberg C. E., Do L. H., Jenney F. E., Adams M. W.W., Cramer S. P., and Lippard S. J., J. Am. Chem. Soc. 132, 6914 (2010). 10.1021/ja101002f [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orzechowska A., Lipińska M., Fiedor J., Chumakov A., Zajac M., Slezak T., Matlak K., Strzałka K., Korecki J., Fiedor L., and Burda K., Biochim Biophys. Acta 1797, 1696 (2010). 10.1016/j.bbabio.2010.06.012 [DOI] [PubMed] [Google Scholar]
- Rai B. K., Durbin S. M., Prohofsky E. W., Sage J. T., Wyllie G. R.A., Scheidt W. R., Sturhahn W., and Alp E. E., Biophys. J. 82, 2951 (2002). 10.1016/S0006-3495(02)75636-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rai B. K., Durbin S. M., Prohofsky E. W., Sage J. T., Ellison M. K., Roth A., Scheidt W. R., Sturhahn W., and Alp E. E., J. Am. Chem. Soc. 125, 6927 (2003). 10.1021/ja028219w [DOI] [PubMed] [Google Scholar]
- Leu B. M., Zgierski M. Z., Wyllie G. R.A., Scheidt W. R., Sturhahn W., Alp E. E., Durbin S. M., and Sage J. T., J. Am. Chem. Soc. 126, 4211 (2004). 10.1021/ja038526h [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ronayne K. L., Paulsen H., Höfer A., Dennis A. C., Wolny J. A., Chumakov A. I., Schünemann V., Winkler H., Spiering H., Bousseksou A., Gütlich P., Trautwein A. X., and McGarvey J. J., Phys. Chem. Chem. Phys. 8, 4685 (2006). 10.1039/b610634j [DOI] [PubMed] [Google Scholar]
- Silvernail N. J., Barabanschikov A., Pavlik J., Noll B., Zhao J., Alp E., Sturhahn W., Sage J., and Scheidt W., J. Am. Chem. Soc. 129, 2200 (2007). 10.1021/ja066869k [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leu B., Silvernail N., Zgierski M., Wyllie G., Ellison M., Scheidt W., Zhao J., Sturhahn W., Alp E., and Sage J., Biophys. J. 92, 3764 (2007). 10.1529/biophysj.106.093773 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell C. B., Wong S. D., Xiao Y., Klinker E. J., Tenderholt A. L., Smith M. C., Rohde J.-U., Que L., Cramer S. P., and Solomon E. I., Angew. Chem., Int. Ed. Engl. 47, 9071 (2008). 10.1002/anie.200803740 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehnert N., Sage J. T., Silvernail N., Scheidt W. R., Alp E. E., Sturhahn W., and Zhao J., Inorg. Chem. 49, 7197 (2010). 10.1021/ic1010677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Šrajer V., Reinisch L., and Champion P. M., J. Am. Chem. Soc. 110, 6656 (1988). 10.1021/ja00228a009 [DOI] [Google Scholar]
- Perutz M. F., Wilkinson A. J., Paoli M., and Dodson G. G., Annu. Rev. Biophys. Biomol. Struct. 27, 1 (1998). 10.1146/annurev.biophys.27.1.1 [DOI] [PubMed] [Google Scholar]
- Hoard J. L. and Scheidt W. R., Proc. Natl. Acad. Sci. U.S.A. 70, 3919 (1973). 10.1073/pnas.70.12.3919 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klug D. D., Zgierski M. Z., Tse J. S., Liu Z., Kincaid J. R., Czarnecki K., and Hemley R. J., Proc. Natl. Acad. Sci. U.S.A. 99, 12526 (2002). 10.1073/pnas.152464699 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu L., Sage J. T., and Champion P. M., Science 226, 629 (1994). 10.1126/science.7939716 [DOI] [PubMed] [Google Scholar]
- Liebl U., Lipowski G., Négrerie M., Lambry J.-C., Martin J.-L., and Vos M. H., Nature (London) 401, 181 (1999). 10.1038/43699 [DOI] [PubMed] [Google Scholar]
- Rosca F., Kumar A., Ye X., Sjodin T., Demidov A., and Champion P. M., J. Phys. Chem. A 104, 4280 (2000). 10.1021/jp993617f [DOI] [Google Scholar]
- Rosca F., Kumar A. T.N., Ionascu D., Ye X., Demidov A. A., Sjodin T., Wharton D., Barrick D., Sligar S. G., Yonetani T., and Champion P. M., J. Phys. Chem. A 106, 3540 (2002). 10.1021/jp0129277 [DOI] [Google Scholar]
- Gruia F., Kubo M., Ye X., Ionascu D., Lu C., Poole R., Yeh S.-R., and Champion P., J. Am. Chem. Soc. 130, 5231 (2008). 10.1021/ja7104027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gruia F., Kubo M., Ye X., and Champion P., Biophys. J. 94, 2252 (2008). 10.1529/biophysj.107.122119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gruia F., Ye X., Ionascu D., Kubo M., and Champion P. M., Biophys. J. 93, 4404 (2007); 10.1529/biophysj.107.114736 [DOI] [PMC free article] [PubMed] [Google Scholar]; See URL http://www.sciencedirect.com/science/article/B94RW-4V9YVVB-14/2/46c6a2b81bf9606bc6b42da8f6efcbde.
- Kubo M., Gruia F., Benabbas A., Barabanschikov A., Montfort W., Maes E., and Champion P., J. Am. Chem. Soc. 130, 9800 (2008). 10.1021/ja800916d [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh A. and Bocian D. F., J. Phys. Chem. 100, 6363 (1996). 10.1021/jp953543h [DOI] [Google Scholar]
- Spiro T. G. and Kozlowski P. M., J. Am. Chem. Soc. 120, 4524 (1998). 10.1021/ja9732946 [DOI] [Google Scholar]
- Spiro T. G. and Kozlowski P. M., Acc. Chem. Res. 34, 137 (2001). 10.1021/ar000108j [DOI] [PubMed] [Google Scholar]
- Shelnutt J., Song X.-Z., Ma J.-G., Jia S.-L., Jentzen W., and Medforth C., Chem. Soc. Rev. 27, 31 (1998). 10.1039/a827031z [DOI] [Google Scholar]
- Roberts S. A., Weichsel A., Qiu Y., Shelnutt J. A., Walker F. A., and Montfort W. R., Biochemistry 40, 11327 (2001). 10.1021/bi0109257 [DOI] [PubMed] [Google Scholar]
- Pavlik J. W., Barabanschikov A., Oliver A. G., Alp E. E., Sturhahn W., Zhao J., Sage J. T., and Scheidt W. R., Angew. Chem. Int. Ed. Engl. 49, 4400 (2010). 10.1002/anie.201000928 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehnert N., Sage J. T., Silvernail N., Scheidt W. R., Alp E. E., Sturhahn W., and Zhao J., Inorg. Chem. 49, 7197 (2010). 10.1021/ic1010677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheidt W. R., Barabanschikov A., Pavlik J. W., Silvernail N. J., and Sage J. T., Inorg. Chem. 49, 6240 (2010). 10.1021/ic100261b [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spiro T., Kozlowski P., and Zgierski M., J. Raman Spectrosc. 29, 869 (1998). [DOI] [Google Scholar]
- Budarz T. E., Prohofsky E. W., Durbin S. M., Sjodin T. A., Sage J. T., Sturhahn W., and Alp E. E., J. Phys. Chem. B 107, 11170 (2003). 10.1021/jp027348w [DOI] [Google Scholar]
- Sturhahn W., Hyperfine Interact. 125, 149 (2000). 10.1023/A:1012681503686 [DOI] [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B.et al. , gaussian 03, Revision D.01, Gaussian, Inc., Wallingford, CT, 2004. [Google Scholar]
- Becke A. D., J. Chem. Phys. 98, 5648 (1993). 10.1063/1.464913 [DOI] [Google Scholar]
- Lee C., Yang W., and Parr R. G., Phys. Rev. B 37, 785 (1988). 10.1103/PhysRevB.37.785 [DOI] [PubMed] [Google Scholar]
- Schäfer A., Horn H., and Ahlrichs R., J. Chem. Phys. 97, 2571 (1992). 10.1063/1.463096 [DOI] [Google Scholar]
- Senge M., Acta Cryst. E 61, 399 (2005). 10.1107/S1600536805002461 [DOI] [PubMed] [Google Scholar]
- Koenig D., Acta Cryst. 18, 663 (1965). 10.1107/S0365110X65001536 [DOI] [PubMed] [Google Scholar]
- Dolphin D., Sams J. R., Tsin T. B., and Wong K. L., J. Am. Chem. Soc. 100, 1711 (1978). 10.1021/ja00474a011 [DOI] [Google Scholar]
- Marathe V. R. and Mitra S., J. Chem. Phys. 78, 915 (1983). 10.1063/1.444794 [DOI] [Google Scholar]
- Reed C. A. and Guiset F., J. Am. Chem. Soc. 118, 3281 (1996). 10.1021/ja954263i [DOI] [Google Scholar]
- Nishio T., Yokoyama S., Sato K., Shiomi D., Ichimura A., Lin W., Dolphin D., McDowell C., and Takui T., Synth. Met. 121, 1820 (2001). 10.1016/S0379-6779(00)01009-2 [DOI] [Google Scholar]
- Aziz E. F., Ottosson N., Bonhommeau S., Bergmann N., Eberhardt W., and Chergui M., Phys. Rev. Lett. 102, 068103 (2009). 10.1103/PhysRevLett.102.068103 [DOI] [PubMed] [Google Scholar]
- Ghosh A. and Taylor P. R., Curr. Opin. Chem. Biol. 7, 113 (2003). 10.1016/S1367-5931(02)00023-6 [DOI] [PubMed] [Google Scholar]
- Ghosh A., Persson B. J., and Taylor P. R., J. Biol. Inorg. Chem. 8, 507 (2003). 10.1007/s00775-002-0435-2 [DOI] [PubMed] [Google Scholar]
- Liao M.-S., Watts J. D., and Huang M.-J., J. Comput. Chem. 27, 1577 (2006). 10.1002/jcc.20458 [DOI] [PubMed] [Google Scholar]
- Paulat F., Praneeth V., Näther C., and Lehnert N., Inorg. Chem. 45, 2835 (2006). 10.1021/ic0510866 [DOI] [PubMed] [Google Scholar]
- Ernst J., Subramanian J., and Fuhrhop J.-H., Z. Naturforsch. 32A, 1129 (1977). [Google Scholar]
- Safo M. K., Buentello K. E., Oliver A. G., and Scheidt W. R., Acta Cryst. E 66, m733 (2010). 10.1107/S1600536810020015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoard J., Cohen G., and Glick M., J. Am. Chem. Soc. 89, 1992 (1967). 10.1021/ja00985a004 [DOI] [Google Scholar]
- Scheidt W. and Finnegan M., Acta Cryst. C 45, 1214 (1989). 10.1107/S0108270189000715 [DOI] [PubMed] [Google Scholar]
- Skelton B. and White A., Aust. J. Chem. 30, 2655 (1977). 10.1071/CH9772655 [DOI] [Google Scholar]
- Lipkin H. J., Phys. Rev. B 52, 10073 (1995). 10.1103/PhysRevB.52.10073 [DOI] [PubMed] [Google Scholar]
- Adams K., Tsoi S., Yan J., Durbin S., Ramdas A., Cramer W., Sturhahn W., Alp E., and Schulz C., J. Phys. Chem. B 110, 530 (2006). 10.1021/jp053440r [DOI] [PubMed] [Google Scholar]
- Leu B., Ching T., Zhao J., Sturhahn W., Alp E., and Sage J., J. Phys. Chem. B 112, 2193 (2009). [DOI] [PubMed] [Google Scholar]
- Malinovsky V., Novikov V., and Sokolov A., Phys. Lett. A 153, 63 (1991). 10.1016/0375-9601(91)90363-D [DOI] [Google Scholar]
- Kitagawa T., Abe M., Kyogoku Y., Ogoshi H., Watanabe E., and Yoshida Z., J. Phys. Chem. 80, 1181 (1976). 10.1021/j100552a012 [DOI] [Google Scholar]
- Ogoshi H., Watanabe E., Yoshida Z., Kincaid J., and Nakamoto K., J. Am. Chem. Soc. 95, 2845 (1973). 10.1021/ja00790a017 [DOI] [Google Scholar]
- Abe M., Kitagawa T., and Kyogoku Y., J. Chem. Phys. 69, 4526 (1978). 10.1063/1.436450 [DOI] [Google Scholar]
- See supplementary material at http://dx.doi.org/10.1063/1.3598473 for tabulated quantitative information on predicted vibrational modes of Fe(P) and for depictions of predicted normal modes of Fe(P) and Fe(P)(Cl) with frequencies below 450 cm-1.
- Kozlowski P. M., Spiro T. G., Bérces A., and Zgierski M. Z., J. Phys. Chem. B 102, 2603 (1998). 10.1021/jp973346d [DOI] [Google Scholar]
- Grafton A. K. and Wheeler R. A., J. Comput. Chem. 19, 1663 (1998). [DOI] [Google Scholar]
- Grafton A. K., J. Comput. Chem. 28, 1290 (2007). 10.1002/jcc.20642 [DOI] [PubMed] [Google Scholar]
- Zhang Y. and Straub J. E., J. Chem. Phys. 130, 095102 (2009). 10.1063/1.3086080 [DOI] [PubMed] [Google Scholar]
- Rovira C., Kunc K., Hutter J., Ballone P., and Parrinello M., J. Phys. Chem. A 101, 8914 (1997). 10.1021/jp9722115 [DOI] [Google Scholar]
- Ryde U., Curr. Opin. Chem. Biol. 7, 136 (2003). 10.1016/S1367-5931(02)00016-9 [DOI] [PubMed] [Google Scholar]
- Cohen A. J., Mori-Sanchez P., and Yang W., Science 321, 792 (2008). 10.1126/science.1158722 [DOI] [PubMed] [Google Scholar]
- Scherlis D. A., Cococcioni M., Sit P., and Marzari N., J. Phys. Chem. B 111, 7384 (2007). 10.1021/jp070549l [DOI] [PubMed] [Google Scholar]
- Scheidt W. R., “Inorganic, organometallic, and coordination chemistry,” in The Porphyrin Handbook, edited by Kadish M., Smith K. M., and Guilard R. (Academic, San Diego, 1996), Vol. 3, pp. 49–112. [Google Scholar]
- Perutz M. F., Nature (London) 228, 726 (1970). 10.1038/228726a0 [DOI] [PubMed] [Google Scholar]
- Perutz M. F., Fermi G., Luisi B., Shaanan B., and Liddington R. C., Acc. Chem. Res. 20, 309 (1987). 10.1021/ar00141a001 [DOI] [Google Scholar]
- Markelz A., IEEE J. Sel. Top. Quantum Electron. 14, 180 (2008). 10.1109/JSTQE.2007.913424 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dörr S., Schade U., and Hellwig P., Vib. Spectrosc. 47, 59 (2008). 10.1016/j.vibspec.2008.02.003 [DOI] [Google Scholar]
- Kozlowski P. M., Vogel K. M., Zgierski M. Z., and Spiro T. G., J. Porphyr. Phthalocyanines 5, 312 (2001). 10.1002/jpp.318 [DOI] [Google Scholar]
- Rai B. K., Durbin S. M., Prohofsky E. W., Sage J. T., Ellison M. K., Scheidt W. R., Sturhahn W., and Alp E. E., Phys. Rev. E 66, 051904 (2002). 10.1103/PhysRevE.66.051904 [DOI] [PubMed] [Google Scholar]