Ploidy and the evolution of parasitism

Abstract

Levels of parasitism are continuously distributed in nature. Models of host–parasite coevolution, however, typically assume that species can be easily characterized as either parasitic or non-parasitic. Consequently, it is poorly understood which factors influence the evolution of parasitism itself. We investigate how ploidy level and the genetic mechanisms underlying infection influence evolution along the continuum of parasitism levels. In order for parasitism to evolve, selective benefits to the successful invasion of hosts must outweigh the losses when encountering resistant hosts. However, we find that exactly where this threshold occurs depends not only on the strength of selection, but also on the genetic model of interaction, the ploidy level in each species, and the nature of the costs to virulence and resistance. With computer simulations, we are able to incorporate more realistic dynamics at the loci underlying species interactions and to extend our analyses in a number of directions, including finite population sizes, multiple alleles and different generation times.

1. Introduction

Understanding the complex ecological and evolutionary interactions between parasites and their hosts has long been a central focus in the biological sciences. This is largely owing to the important consequences that advances in this field have had on the development of new strategies for disease and pest management. The continued need for progress has led to high levels of communication between theoreticians and empiricists, which has helped propel research in both fields (e.g. [1,2]). Consequently, there are numerous theoretical models covering a wide range of topics, including the evolution of virulence (e.g. [1–3]), sex (e.g. [4,5]), recombination and mutation rates (e.g. [6,7]), the evolution of host resistance (e.g. [8,9]), and local adaptation (e.g. [10]).

One typical assumption of theoretical host–parasite models is their treatment of species as either parasitic or non-parasitic (e.g. [6,10–14]). In other words, models typically operate under the assumption that a species lives strictly as a parasite. While many species do fit this assumption (e.g. those for whom the very completion of their life cycle depends on the successful infection of a host, such as the plasmodium species that cause malaria), there are numerous examples of species for whom this assumption is not appropriate.

For example, a number of species from a range of taxonomic groups have been shown to be ‘facultatively parasitic’ (e.g. ciliates [15,16], flatworms [17], fungi [18], nematodes [19]). These species are parasitic if the opportunity arises, but are otherwise free-living and capable of reproduction without the aid of a host species. Levels of parasitism should thus be seen as distributed along a continuum in which ‘completely parasitic’ and ‘completely non-parasitic’ define the extreme cases. Two questions that then arise are: how does evolution occur along this continuum, and what are the main factors that determine whether evolution occurs towards higher or lower levels of parasitism?

Empirical work on a number of different host–parasite systems has uncovered a variety of genetic mechanisms employed by hosts and parasites to generate the phenotypic variation needed to defend against and invade one another [1]. For example, a single allele in flax (Linum usitatissimum) causes resistance to the fungal pathogen Melampsora lini, and a single virulent allele in the pathogen allows infection of both non-resistant and resistant strains of flax (a ‘gene-for-gene’ interaction [20–22]). Host–parasite interactions have also been shown to exert strong selection on the underlying genes that modulate species interactions (e.g. favouring changes in expression level [23] or ploidy level [14]). That there are many ways species can interact on a genetic level, and that these interactions have been shown to be under selection, suggests that the nature of the genetic interactions between species also exerts a selective force on the degree of parasitism. Here we ask how ploidy level—an important component of such genetic interactions—influences evolutionary transitions along the continuum from free-living to parasitic life histories.

Using a combination of analytical models and simulations, we examine evolution at a locus that modifies the amount of time a facultatively parasitic species spends parasitizing its host species. This is done in the context of each of the three models of host–parasite interactions that are thought to describe a large number of host–parasite systems [14].

2. Model summary

We consider two interacting species, denoted by H and P for hosts and parasites, respectively. The term ‘parasite’ is used loosely here, as the species in question can spend anywhere from 0 to 100 per cent of its time as a parasite. Species interactions are governed by a single locus (from here on referred to as the A-locus) with two alleles in each species (A_H and a_H in hosts, and A_P and a_P in parasites). We suppose that parasites spend a proportion of their life cycle parasitizing hosts, and the remaining proportion as free-living organisms. A second locus (from here on referred to as the M-locus, or the ‘modifier’ locus) determines how a parasitic individual partitions its time between these two strategies; individuals of genotype i spend a proportion f_i of their life cycle as parasites (see table 1 for a complete list of parameters and their descriptions).

Table 1.

Description of parameters.

parameter	description
fi	proportion of time spent as a parasite by genotype i
xi,j	frequency of genotype j in species of type i (i = H or P)
αP	fitness gained by a parasite that successfully infects a host
βP	fitness lost by a parasite that attempts but fails to infect a resistant host
αH	fitness lost by hosts when they are infected
ηi,j	indicator variable defined to equal 1 if parasites of genotype i can infect hosts of genotype j, and 0 otherwise
wi,j	fitness of genotype j in species of type i
cH	cost of the resistant allele in hosts (GFG only)
cP,c	conditional cost of the virulent allele in parasites (GFG only)
cP,u	unconditional cost of the virulent allele in parasites (GFG only)
ψi	proportion of species of type i that reproduce sexually
r	recombination rate in parasites
ΔM	effect size of the modifier (haploid parasites)
ΔMm	effect size of the modifier when present in heterozygotes (diploid parasites)
ΔMM	effect size of the modifier when present in homozygotes (diploid parasites)
δi	deviation from a frequency of 0.5 at the A-locus in species i
pM	frequency of the modifier in parasites
	marginal fitnesses of alleles M and m
	difference between marginal fitnesses (i.e. )
μ	mutation rate at the A-locus in both species (simulations only)

We consider here three models of host–parasite interactions. The matching-alleles model (abbreviated MAM) is based on a system of self/non-self recognition [24–27], as typically occurs in immune systems that develop via the elimination of self-compatible major histocompatibility complex (MHC) molecules. In this model, hosts are susceptible to parasites carrying only alleles that mimic or ‘match’ their own cell signals and are resistant to parasites possessing any non-matching alleles. The inverse-matching-alleles model (abbreviated IMAM) is essentially the opposite of the MAM: hosts can defend against parasites carrying any matching alleles and are susceptible to parasites carrying only non-matching alleles [25]. This model describes components of the vertebrate MHC system, where host alleles influence the array of antigen molecules that can be detected. Hosts can only defend against parasites whose antigens they can detect. In the gene-for-gene model (abbreviated GFG), avirulent parasite alleles produce signal molecules that bind to cell surface receptors on resistant host cells, triggering an immune response and thus unsuccessful invasion [28,29]. Virulent pathogens, however, are able to suppress the production of these elicitors and are, therefore, able to invade both resistant and non-resistant hosts. These systems are typically characterized by dominant resistance alleles and recessive virulence alleles [1]; we shall assume these dominance interactions throughout. Since their first discovery, GFG interactions have been shown to be quite common in plant–pathogen interactions [29].

Because we are interested in the effects of ploidy on species interactions, we will consider all combinations of haploid and diploid hosts and parasites. We let {x_H,1[t], …, x_H,k[t]} and {x_P,1[t], …, x_P,l[t]} denote the frequencies of the k host and l parasite genotypes at time t. As a free-living organism, each individual has some basal fitness, which we arbitrarily set to 1. Selection coefficients for other life stages are then measured relative to this fitness. Parasitic individuals that successfully infect hosts experience a fitness gain of α_P, while those that encounter resistant hosts experience a fitness loss of β_P. If a parasite attempts to find a host, but fails, and if it can no longer reproduce as a free-living organism, then fitness would be lower in both cases. Infection by a parasite is assumed to lower host fitness by α_H.

We define the indicator variable η_i,j to equal 1 if parasites of genotype i can infect hosts of genotype j, and 0 otherwise. Table 2 summarizes the infection patterns for each of the models considered here. The fitness of a genotype i parasite at time t is then given by

2.1

and the fitness of a genotype i host is given by

2.2

Table 2.

Invasion matrices. Each entry represents the outcome of interactions in the three models in the following order: {MAM, IMAM, GFG}. I is used to denote infection (η_i,j = 1 in equations (2.1) and (2.2)) and R resistance (η_i,j = 0). Both haploid and diploid hosts and parasites are included in the table.

		host
		AH or AHAH	AHaH	aH or aHaH
parasite	AP or APAP	{I,R,I}	{I,R,I}	{R,I,I}
	APaP	{R,R,R}	{I,R,R}	{R,R,I}
	aP or aPaP	{R,I,R}	{I,R,R}	{I,R,I}

The above ignores demographic fluctuations and assumes that each individual engages in at most one host–parasite interaction per time step.

Costs of resistance and virulence have been demonstrated in some GFG systems [30,31]. Without such costs, we would expect the resistant host alleles and/or virulent parasite alleles to spread to fixation. We therefore assume that both the virulent parasite allele and the resistant host allele are costly. In hosts we assume that the resistant allele (A_H) reduces the fitness of its carriers by an amount c_H. In parasites, we consider two types of cost: a conditional cost (c_P,c) that impacts only individuals involved in host–parasite interactions (e.g. reduces growth within a host), and an unconditional cost (c_P,u) that impacts all virulent individuals (e.g. reduces growth within and outside of hosts). The effects of these costs act additively, so that the fitness of a virulent individual of genotype i is reduced by (f_ic_P,c + c_P,u). The frequency of genotype i in species j (j = H or j = P) after selection may then be computed as:

2.3

where is the mean fitness of species j (the sum is taken over all genotypes).

While we largely focus on the effects of ploidy and the model of genetic interaction, it is worth mentioning that the above model also captures possible ecological changes in the opportunity for parasitism; if the environment clearly favours one life-history strategy over another (as may occur, for example, when a new host species becomes available), then parasitism would be expected to evolve, regardless of the genetic architecture underlying species interactions. This possibility would be captured by high values of α_P (large advantages of successful invasion) and potentially low values of β_P (weak host defences against the parasite). In cases where the environmental forces favouring parasitism are not absolute, however, our analysis will help predict how the underlying genetics shapes the course of evolution.

We let ψ_H and ψ_P denote the proportion of hosts and parasites, respectively, that undergo sexual reproduction at each time step, and we assume that the remaining individuals consist of surviving parents or asexual offspring. We let x″_H,i and x″_P,i denote the frequency of genotype i individuals in hosts and parasites, respectively, formed through random mating within the parental generation after selection. In both hosts and parasites, all sexual individuals contribute their gametes to a general gamete pool, out of which offspring are selected at random. Recombination between the modifier and the A-locus occurs during meiosis in parasites at rate r. After reproduction, genotype frequencies in species j are then given by

2.4

3. Analytical results

We make the assumption that selection is weak (α_H, α_P and β_P are all of the same order as some small term ɛ), and that most individuals are sexual in both species (ψ_H and ψ_P are of the order of 1 − ɛ; this assumption is relaxed in the electronic supplementary material). We also assume that the modifier has a small effect (i.e. we set f_M = f_m + Δ_M or f_Mm = f_mm + Δ_Mm and f_MM = f_mm + Δ_MM, and then assume that the Δs are also of order ɛ). Performing a change of variables allows us to describe the system in terms of the departure from a frequency of 0.5 at the A-locus in each species (δ_H[t] in hosts and δ_P[t] in parasites), the frequency of the modifier in parasites (p_M[t]), and several higher order association measures, such as the departure from Hardy–Weinberg equilibrium and linkage disequilibrium (as defined in [32]).

A quasi-linkage equilibrium analysis [32] showed that all genetic associations are of order ɛ² or higher, and that changes in allele frequency at the M-locus are governed largely by terms of order ɛ, which describe differences in fitnesses of the different genotypes. Specifically, a modifier M of parasitism level will spread only if the difference between the marginal fitnesses of alleles M and m, which we denote by , is positive. The expressions for for an allele that increases parasitism for the four combinations of host–parasite ploidy levels are given in table 3.

Table 3.

The fitness advantage of the modifier allele, , when genetic associations are weak. We have dropped a factor Δ_M from the haploid parasite cases and (p_M(Δ_MM − Δ_Mm) + (1 − p_M)Δ_Mm) from the diploid parasite cases; these terms can be interpreted as the average effect size of the modifier.

model	host ploidy	parasite ploidy
MAM	1	1	(αP − βP)/2 + (αP + βP)(2δHδP)
	1	2	(αP − 3βP)/4 + (αP + βP)(2δHδP + δP2)
	2	1	(3αP − βP)/4 + (αP + βP)(2δHδP − δH2)
	2	2	(5αP − 3βP)/8 + (αP + βP)(4δHδP(1 + δHδP) − 3δH2 + δP2)/2
IMAM	1	1	(αP − βP)/2 − (αP + βP)(2δHδP)
	1	2	(αP − 3βP)/4 − (αP + βP)(2δHδP − δP2)
	2	1	(αP − 3βP)/4 − (αP + βP)(2δHδP − δH2)
	2	2	(αP − 7βP)/8 − (αP + βP)(4δHδP(1 − δHδP) − δH2 − δP2)/2
GFG	1	1	(3αP − βP)/4 + (αP + βP)(δP − δH(1 − 2δP))/2 − cP,c(1 + 2δP)/2
	1	2	(7αP − βP)/8 + (αP + βP)(2(1 + 2δH)(1 − δP)δP − δH)/4−cP,c(3/4 + (1 − δP)δP)
	2	1	(5αP − 3βP)/8 + (αP + βP)(3δP + 2(1 − 2δP)(δH2 − δH))/4 − cP,c (1 + 2δP)/2
	2	2	(13αP − 3βP)/16 + (αP + βP)(δH2 (1 − 2δP)2 − δH (1 − 2δP)2 + 3(1 − δP)δP)/4 − cP,c (3/4 + (1 − δP)δP)

As is typical in models of host–parasite coevolution, dynamics at the A-locus are characterized by cyclical fluctuations (figure 1). In the MAM and the IMAM models, these cycles are symmetric about an allele frequency of 0.5 (equivalently, about δ_H = 0 and δ_P = 0). By assuming (for these cases) that these cycles are small (e.g. that both δ_H and δ_P are also of the order of the small term ɛ), we are able to find simple conditions under which selection favours increased levels of parasitism (table 4).

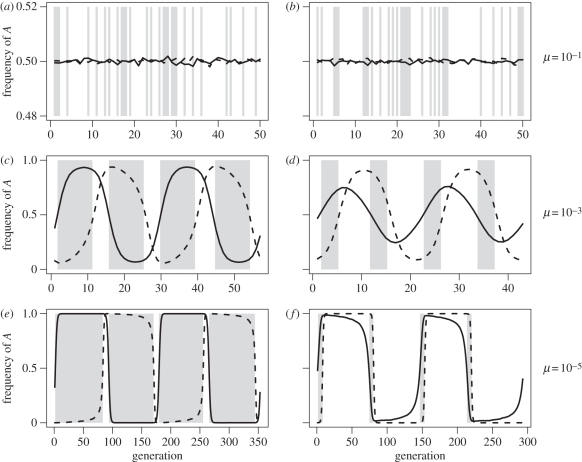
Figure 1.

Sample trajectories from simulations (after a burn-in period) in the MAM model with complete parasitism (f = 1). Left column is with haploid hosts and diploid parasites, right column is with diploid hosts and haploid parasites, and row labels indicate mutation rates. The background is coloured grey to indicate when the parasite is ‘losing’ the arms race with the host, and white when it is ‘winning’. Other parameters were α_P = 0.05, β_P =0.05, α_H = 0.05, ψ_H = ψ_P = 1 and r = 0.5, and population sizes were 10⁶ in both species. Solid line, host; dashed line, parasite.

Table 4.

Invasion condition for a modifier that increases the level of parasitism in MAM and IMAM, assuming small cycles around allele frequencies of 1/2 (or δ_H = δ_P = 0).

model	host ploidy	parasite ploidy	invasion condition
MAM	1	1	αP > βP
	1	2	αP > 3βP
	2	1	αP > βP/3
	2	2	αP > 3βP/5
IMAM	1	1	αP > βP
	1	2	αP > 3βP
	2	1	αP > 3βP
	2	2	αP > 7βP

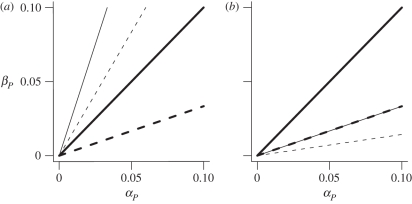
It is clear from the expressions in table 4 that the fitness effects of matching versus not matching the genotype of the host, α_P /β_P, must be sufficiently beneficial for parasites to adopt a less free-living life cycle in both MAM and IMAM. However, where this threshold occurs depends on both the model of genetic interactions and the ploidy level of each species (figure 2). In general, the MAM tends to favour parasitism more strongly than the IMAM (compare figure 2a with b), mainly because it is easier for a parasite to mimic hosts that are heterozygous diploid (MAM) than to evade detection by them (IMAM). In both MAM and IMAM, the transition to parasitism occurs over a broader range of parameters when the parasite is haploid, because such parasites express only one antigen allele (compare solid with dashed lines in figure 2). The role of host ploidy is more complicated, however. Diploidy allows for the appearance of heterozygous hosts that are infected by any type of parasite in MAM, but resistant to every type of parasite in IMAM. Thus, host diploidy favours (disfavours) the evolution of parasitism in MAM (IMAM; compare thick to thin lines in figure 2).

Figure 2.

Invasion conditions in the (a) MAM and (b) IMAM model. Solid (dashed) lines correspond to haploid (diploid) parasites, and thick (thin) lines to haploid (diploid) hosts. For a given case, parasitism is expected to evolve when selection is such that the point (α_P, β_P) lies below the corresponding line. The slopes of these lines can be inferred from the invasion conditions in table 4. Note that there are two lines with the same slope in (b).

Because cycles in the GFG model are not typically centred around 0.5, we take a slightly different approach in this case. We first solve for the equilibrium δ_H and δ_P, and then substitute these into the expressions for . Assuming weak selection, we are again able to simplify the expressions for . For all ploidy combinations, we find

3.1

where f denotes the resident parasitism level (f = f_m for haploid parasites and f_mm for diploid parasites). Unlike for MAM and IMAM models, there are no major effects of ploidy on the evolution of parasitism in the GFG. While qualitative dynamics at the A-locus differ between cases, parasitism is favoured for the same combinations of selection and cost parameters across all ploidy levels. This contrasting result for GFG is a consequence of our empirically motivated assumption of complete dominance. With both the resistant allele in hosts and the virulent allele in parasites completely dominant, the two species are essentially composed of only two types, and thus effectively interact as haploids.

In contrast to ploidy, the nature of costs of virulence is critically important to the evolution of parasitism in the GFG (figure 3). Consider setting c_P,u equal to zero. With just conditional costs (c_P,c), we find

3.2

and thus parasitism should evolve whenever the benefits to successful invasion, α_P, are greater than the conditional cost of the virulent allele c_P,c. In contrast, when c_P,c equals zero,

3.3

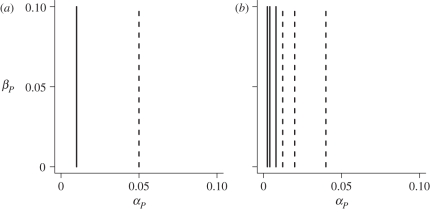
Figure 3.

Invasion conditions in the GFG model with (a) conditional (solid line, c_P,c = 0.01; dashed line, c_P,c = 0.05) and (b) unconditional (solid lines, c_P,u = 0.01; dashed lines, c_P,u = 0.05) costs. For a given case, parasitism is expected to evolve for all ploidy combinations when α_P lies to the right of the plotted line. The three curves for each unconditional cost in (b), from left to right, correspond to different initial parasitism levels of f = 0.9, 0.7 and 0.5. Other parameters were α_H = 0.05 and c_H = 0.01.

Here the cost term is weighted by 1/f². With lower resident parasitism levels (smaller f values), a larger selective benefit to parasitism (α_P) is required in order for selection to favour further increases in parasitism. This makes it exceedingly difficult for parasitism to evolve from initially low levels when costs are unconditional. Intuitively, because the unconditional cost is paid by all virulent individuals, it is unlikely that any fitness gains acquired through parasitism will sufficiently compensate for the costs of virulence when the chance of infecting a host is low.

4. Simulation model summary

We ran computer simulations to investigate the robustness of our model to violations of its assumptions, such as small cycles (electronic supplementary material, figures S1 and S2), weak selection (electronic supplementary material, figure S3), infinite population sizes (electronic supplementary material, figure S4) and high rates of sexual reproduction (electronic supplementary material, figure S5). We also investigated the effect of differences in generation times (electronic supplementary material, figure S6) and of multiple alleles (electronic supplementary material, figure S7) on the evolution of parasitism. In each case, we employed a Wright–Fisher model with constant and finite population size. Each time step consisted of selection followed by sex and recombination (with r = 0.5). Because population sizes were finite, mutation between alleles at the A-locus was necessary to ensure that allelic variation at this locus was not permanently lost. Mutation between alternative alleles at the A-locus occurred in both species at rate μ per generation.

In order to investigate the evolution of parasitism, we initialized populations with low levels of parasitism (f = 0.1) and tracked evolution at the modifier locus. We also ran simulations initialized with high levels of parasitism (f = 0.9), but because the final level of parasitism attained was typically similar, these results are not presented. Where this change did affect the final outcome, we provide a more detailed discussion. All individuals were initially identical at the modifier locus, and whenever fixation occurred a novel modifier allele was introduced at low frequency (we used 0.01) and in linkage equilibrium with the A-locus. The parasitism level (f) corresponding to the novel modifier was drawn from a Gaussian distribution centred on the current level of parasitism with a standard deviation of 0.1 (parasitism levels were redrawn if they fell outside the range [0,1]). While introducing a mutant allele into the population at linkage equilibrium is not biologically realistic, it eliminates unwanted artefacts that may result from biased initial associations between the modifier and the A-locus. It is also worth mentioning that the initial frequency of the new modifier and the standard deviation used to draw new mutants did not qualitatively affect the results, but they did affect the speed of the simulations.

We examined a number of extensions to our model (see electronic supplementary material). Most extensions had little effect on our results. Here we focus on only the simplest and most informative extensions. Unless specified otherwise, simulations were run for 10⁶ generations and initial frequencies at the A-locus in each species were drawn independently from a uniform distribution.

(a). Matching-alleles model and inverse-matching-alleles model simulation results

(i). Small cycles

We begin by examining the simpler case when cycles at the A-locus are small in amplitude. To constrain cycle size in the simulations, we increased the mutation rate, which pushes allele frequencies towards intermediate values and thus dampens cycles (exposure to multiple parasites per time step has also been shown to dampen cycles [33]). With intermediate to high mutation rates, cycles were characterized by smooth sinusoidal curves (figure 1c,d; note that for very high mutation rates cycles were absent altogether, as in figure 1a,b). When cycles were absent or small, increased levels of parasitism evolved as predicted in table 4 (columns 1 and 2 in electronic supplementary material, figure S1).

(ii). Large cycles

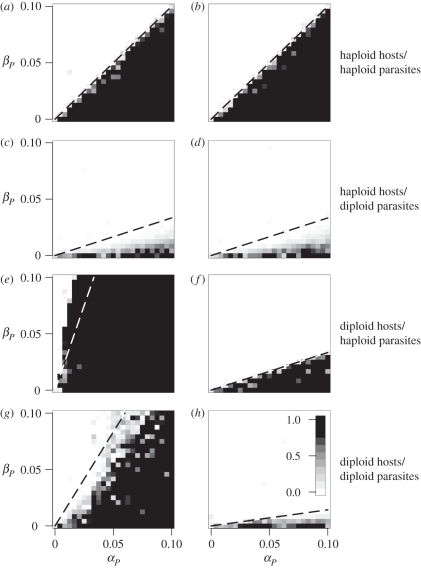
Large amplitude cycles were observed with lower mutation rates (figure 1e,f). Mutation to other serotypes in Borrelia hermsii has been estimated to occur at a rate somewhere between 10⁻³ and 10⁻⁴ per generation [34], and new variant surface glycoproteins arise in trypanosomes at a rate somewhere between 10⁻² and 10⁻⁶ per cell doubling time [35]. We thus set μ = 10⁻⁵ to investigate realistic mutation rates. With large amplitude cycles, a few cases did not match the small-cycle analytical approximations in table 4 (figure 4), although the large-cycle conditions in table 3 continued to hold, given the observed dynamics for δ_H and δ_P (results available upon request). We will describe these cases in turn.

Figure 4.

Evolutionarily convergent level of parasitism (f) as a function of the strength of selection in parasites under the (a,c,e,g) MAM and (b,d,f,h) IMAM. The mutation rate was μ = 10⁻⁵, and thus large cycles occurred in all cases except (f). Dashed lines denote the analytical invasion condition assuming small cycles (table 4). Cells are shaded based on the mean level of parasitism present in the population after 10⁶ generations of evolution in a single simulation (darker = higher; see shading scale in (h)). Initial frequencies at the A-locus were randomly drawn for each cell. Different ploidy combinations are indicated on the right-hand side. Other parameters were as in figure 1.

When parasites were diploid and hosts were haploid, large cycles led to a reduction in the size of the region where parasitism evolved (figure 4c,d). Because in MAM and IMAM heterozygous parasites could not invade either haploid host, parasites responded slowly to changes in allele frequency in the hosts. Consequently, the proportion of time parasites spent ‘losing’ the host–parasite arms race grew as cycle size increased (figure 1a,c,e), and thus the region where parasitism was favoured shrunk.

When parasites were haploid and hosts were diploid, the opposite scenario occurred. Here it was the diploid hosts that were slow to respond to allele frequency changes in the haploid parasites. Furthermore, because heterozygous hosts in IMAM are more resistant than homozygous hosts, cycles tended to dampen (remaining near δ_i = 0), whereas a slow coevolutionary response in hosts was observed in MAM (figure 1b,d,f). The region where parasitism was favoured thus grew slightly with MAM (figure 4e).

When both species were diploid, general conclusions could not be drawn about which species would lag behind in the arms race. Unlike the previous comparisons, whether the region where parasitism was favoured slightly grew or shrunk depended more sensitively on the strength of selection in hosts (α_H; see electronic supplementary material, figures S2 and S3).

(b). GFG simulation results

Because high mutation rates drive allele frequencies to 0.5, which is not generally the equilibrium in the GFG model, we only consider low mutation rates and thus large cycles in this case. With conditional costs, our simulations exactly matched our predictions, and parasitism evolved whenever the fitness benefit of successfully invading a host, α_P, was greater than the cost of the virulent allele, c_P,c (figure 3a and electronic supplementary material, figure S8). As predicted for unconditional costs, the initial level of parasitism present in the population strongly affected which parameter combinations favoured further evolution of parasitism (figure 3b and electronic supplementary material, figure S9). In large populations (n = 10⁶ individuals) and initially low levels of parasitism (f = 0.1), increased parasitism never evolved, as expected. With high initial levels of parasitism, however, evolution of a more parasitic life history was possible. In other words, the system exhibited bistability. Interestingly, in regions where the evolution of a free-living life cycle was expected, the GFG system would often converge to an M/m polymorphism fixed for allele a. That is, the initial mA/ma polymorphism involving a costly virulent allele and a sensitive allele was replaced with an Ma/ma polymorphism involving sensitive alleles with higher and lower levels of parasitism (explaining why the regions shown in electronic supplementary material, figures S8 and S9 were grey rather than white). With unconditional costs, the effect of initial conditions described above disappeared altogether in small populations (electronic supplementary material, figure S10). Stochastic fluctuations in allele frequency at the interaction locus, combined with drift at the modifier locus, allowed occasional excursions into the parameter space in which further evolution of parasitism became advantageous.

5. Discussion

We have used analytical and simulation methods to investigate the evolution of parasitism in a pair of coevolving species. Our results provide an initial characterization of how genetic architecture affects selection on life history in antagonistic species interactions.

By and large, the evolution of parasitism depends on the mean fitness of allelic variants at a locus governing how much time a species spends as a parasite and is not strongly influenced by genetic associations. By comparing mean fitness of these allelic variants, we were able to characterize the conditions under which high levels of parasitism were expected to evolve. While the fitness effects of matching or not matching the genotype of the host had to be sufficiently beneficial in order for parasites to adopt a more parasitic life cycle, the exact threshold depended on both the model of genetic interactions and, in most situations, the ploidy level of each species. In situations where hosts are only able to defend against parasites for which they have the correct allele, as with IMAM, hosts that carry a larger suite of alleles (diploids) or parasites that carry few alleles (haploids) tend to thrive. Thus, lower ploidy levels in either species tend to increase the benefits to parasitism. In contrast, in situations where parasites must match host genotypes in order to invade (e.g. MAM), diploid hosts can be infected by a greater number of parasite types, and thus diploidy in hosts tends to favour parasitism, while haploidy in parasites is again most conducive to further evolution of parasitism. With GFG interactions, ploidy had little impact on the evolution of parasitism because of the complete dominance assumed.

The above predictions were derived under a number of assumptions, the most significant being intermediate allele frequencies at the locus governing host–parasite interactions (i.e. small cycles). Using simulations we were able to investigate our model's behaviour when no such constraints were imposed on allele frequencies. The predictions based on small cycles were altered slightly under some conditions (figure 4c–e,g,h), although the main qualitative results continued to hold under all conditions. The differences from our predictions occurred mostly when host and parasite fluctuations were not 90° out of phase with one another (figure 1). Typically, this occurred when heterozygotes of one species had low fitness (e.g. hosts in MAM and parasites in IMAM). These low-fitness heterozygotes reduced the efficacy of selection in this species, as beneficial alleles, when rare, were found almost exclusively in the heterozygous form. As a result, this species responded slowly to changes in allele frequency in the other species. This meant that more time was spent in a population configuration that favoured the faster-responding species, and thus the region of parameter space where parasitism evolved was shifted in favour of that species. Violations of our other main assumptions (infinite population sizes, weak selection and primarily sexual populations) were also tested using simulations, and were shown to have only minor effects (see electronic supplementary material).

In nature, parasites typically have much shorter generation times than their hosts, and, furthermore, many host–parasite interactions are governed by more than two alleles (e.g. trypanosomes are known to possess hundreds of allelic antigen variants [36]). Using simulations, we investigated how these extensions changed our general conclusions. While neither led to any qualitative changes across ploidy combinations, more alleles at the interaction locus had significant and opposite effects in the MAM and IMAM models. Because higher genetic diversity among hosts with more alleles makes them resistant to a larger number of parasites in MAM, more alleles were less conducive to the evolution of parasitism. Similarly, with MAM, high diversity in parasites tends to help hosts recognize their parasites as genetically distinct. The opposite held true in IMAM, where greater genetic diversity in hosts allows parasites to invade a greater proportion of host genotypes and greater genetic diversity in parasites allows them to remain undetected by more host genotypes. Thus, the more alleles segregating at the genes mediating host–parasite interactions, the more conducive IMAM systems are to the evolution of parasitism.

Another factor found to have a large influence on the evolution of parasitism was the nature of the costs to virulence in the GFG models. Interestingly, conditional costs were much more conducive to the evolution of parasitism. When parasitism is rare, unconditional costs of virulence typically outweigh the benefits of being parasitic, and result in the spread of sensitive parasites and resistant hosts, which prevents the evolution of further parasitism. Had unconditional costs been weak enough to allow parasitism to increase when low, they would have been too weak to prevent the fixation of virulent alleles once parasitism levels were high. In the absence of factors such as strong genetic drift, which may stochastically shift parasitism levels upward, a predominantly free-living life history is thus expected with substantial unconditional costs of virulence.

Previous theoretical work has shown that transitions between haploidy and diploidy are expected as a consequence of host–parasite interactions [14]. In particular, haploidy is most favoured in parasites because of the advantage of reducing antigenic expression to a single allele, while diploidy is more often favoured in hosts because of the advantage (in many cases) of heterozygous hosts being able to recognize multiple parasites. In accordance with the above theoretical predictions, a survey of empirical data revealed an association between ploidy and life history [14]; parasitic protists are three to four times as likely as non-parasitic protists to be haploid. This pattern would, however, be consistent with either parasites evolving more haploid life cycles [14], or haploids evolving more parasitic life cycles (herein). Indeed, if transitions in parasitism occur more frequently than transitions in ploidy, transitions in parasitism may be more important in explaining the association between parasitism and haploidy.

Some groups of species today are almost wholly parasitic (e.g. Apicomplexa), while others contain a mixture of both free-living and parasitic individuals (e.g. dinoflagellates) [37,38], and many are wholly non-parasitic. In groups such as dinoflagellates, the ability to photosynthesize (and thus produce one's own food) may make the switch between parasitic and free-living life styles relatively easy, whereas in other groups it appears that the ability to regain a free-living lifestyle has been altogether lost (e.g. no Borrelia sp. proliferating in an environment outside a vertebrate or invertebrate host has been observed [39]). A comparative phylogenetic analysis of closely related groups of species that differ in their proportions of parasitic species would provide additional insight into exactly what sorts of traits facilitate acquisition or loss of parasitism and, furthermore, just how common such transitions have been.

There are a number of worthwhile extensions to our model. Ample empirical evidence suggests that many, if not most, host–parasite interactions are governed by more than a single locus [3]. For example, the brown planthopper (Nilaparvata lugens), a pest on rice in southeast Asia, was originally assumed to be engaged in a GFG interaction, but it has since been shown to contain several biotypes, each determined by different co-adapted gene complexes [40]. Extending our model to include multiple interaction genes would allow us to consider the build-up of the co-adapted gene complexes that facilitate life-history transitions. Furthermore, the model presented here assumes that some level of parasitism is already present, or that at least the genetic architecture is already in place for proper parasitic invasion of hosts. De novo evolution of parasitism realistically requires more than a single mutational event, perhaps mediated by intermediate stages involving mutualistic or trophic interactions. More detailed models on these early stages could provide insight into how parasitic lifestyles have evolved out of non-parasitic ones.