Bats are able to maintain long-term social relationships despite the high fission–fusion dynamics of their groups

Abstract

Elephants, dolphins, as well as some carnivores and primates maintain social links despite their frequent splitting and merging in groups of variable composition, a phenomenon known as fission–fusion. Information on the dynamics of social links and interactions among individuals is of high importance to the understanding of the evolution of animal sociality, including that of humans. However, detailed long-term data on such dynamics in wild mammals with fully known demography and kin structures are scarce. Applying a weighted network analysis on 20 500 individual roosting observations over 5 years, we show that in two wild Bechstein's bat colonies with high fission–fusion dynamics, individuals of different age, size, reproductive status and relatedness maintain long-term social relationships. In the larger colony, we detected two stable subunits, each comprising bats from several family lineages. Links between these subunits were mainly maintained by older bats and persisted over all years. Moreover, we show that the full details of the social structure become apparent only when large datasets are used. The stable multi-level social structures in Bechstein's bat colonies resemble that of elephants, dolphins and some primates. Our findings thus may shed new light on the link between social complexity and social cognition in mammals.

1. Introduction

How complex social systems function is a key question in biology, economics and social sciences. Answering it requires information about the structure and dynamics of the social network, which characterizes the relationships among group members [1,2]. One important aspect of social complexity is the presence of stable individual relationships despite frequent splitting and merging in groups of variable composition [3–5]. Despite a long tradition of analysing social structures [2], detailed long-term data on the individual relationships of wild mammals with high fission–fusion dynamics and fully known demography and kin structures are available for only a handful of species, all of which are assumed to have high socio-cognitive abilities [4–7]. Although comparative data suggest a relationship between social interaction and socio-cognitive abilities in mammals [8], it is unclear whether high socio-cognitive abilities are required for maintaining multiple long-term social bonds in a complex social environment, such as societies with high fission–fusion dynamics [9,10]. Many bats also show fission–fusion behaviour in their colonies [11] but little is known about their ability to maintain long-term individual relationships.

Very little is known about the socio-cognitive abilities of bats; thus detailed information on bat social networks may shed new light on how social complexity and dynamics affect social behaviour and cognitive abilities in mammals [4,7]. If bats are limited in their socio-cognitive abilities, species living in colonies with high fission–fusion dynamics should either form no long-term social relationships, or apply simple behavioural rules that do not require high cognitive abilities, such as aggregating according to size, age, reproductive status or relatedness [7]. Conversely, long-term social relationships between bats that differ in their morphological, demographical and genetic characteristics would be evidence that bats are capable of maintaining individualized relationships in highly dynamic societies, comparable to that of elephants, dolphins and some primates [4,6,7].

Here, we analysed the long-term relationships in two wild Bechstein's bat (Myotis bechsteinii) colonies of different sizes (the smaller named BS: 11–18 bats, the larger GB2: 33–42 bats), over a period of 5 years. In this 10 g species living up to 20 years, 10–45 females of various age, relatedness and reproductive status live each year from April to September in a colony that disintegrates over winter and reforms in spring (males are solitary) [12,13]. During the summer months, colony members switch between up to 50 communal roosts in tree cavities and bat boxes on an almost daily basis and also regularly split into two to six roosting groups spread over a forest area of 30–50 ha [12,13] (figure 1). Despite this fission–fusion behaviour, females are faithful to their natal colony and members of different colonies do not roost together [13]. Colony members profit from communal roosting through social thermoregulation [17]. Field experiments show that they coordinate their daily roosting behaviour via information transfer and group decisions about suitable roosts [18,19].

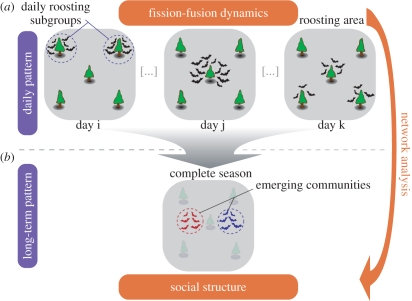
Figure 1.

Schematic of the fission–fusion dynamics of a representative Bechstein's bat colony and its social structure. (a) Typical roost occupation pattern for the colony (one to three roosting groups, occupying different roosts) on three randomly chosen census days (i, j, k). (b) Underlying social structure (with distinct communities) that may arise from this daily pattern, identified through a weighted network analysis [14–16] based on the roosting associations of the colony members over the entire season (five months). For details of the methods, see the electronic supplementary material.

2. Material and methods

(a). Study animals, sampling and roost monitoring

We monitored the day roosts of two wild Bechstein's bat colonies (BS and GB2) daily through the breeding seasons from 2004 to 2008. Since 1996, all bats in both colonies have been individually marked with individual microchips (PIT-tags) in their first year of life, a piece of their wing tissue collected, and their individual size as well as yearly reproductive status determined [20]. From 2004 onwards, between April and September, we checked daily for the presence of bats in the ca 150 bat boxes and five to 10 tree cavities located in the two colonies' home ranges [13]; BS was not monitored in 2005. If we observed bats, we installed an automatic PIT-tag reader that recorded date, time and PIT-tag numbers of ca 97 per cent of the bats passing by the antenna fixed in the roost entrance during the emergence in the evening [18].

(b). Association analysis

We obtained from the automatic PIT-tag readers 6655 and 13 845 individual roosting records for BS (11–18 bats) and GB2 (33–42 bats), respectively. We used the I_ij-index and χ²-statistics [12,21] to determine individual dyadic roosting associations within each study colony (BS, n = 20 females; GB2, n = 61 females; six additional females present for just a few weeks were excluded). The I_ij-index measures how often two animals roost together in relation to the days they are both observed in the study area [12]. The χ²-statistic allows for discrimination between a ‘passive’ association of two bats, if both are independently attracted to the same roost owing to shared roost preference, and an ‘active’ association, regardless of any shared roost preference [21]. Significant associations indicate individual preferences of two animals for each other. We tested differences between the expected distribution of association indices and the observed one using a two-sample Kolmogorov–Smirnov test.

(c). Network analysis

Based on these associations, we constructed weighted undirected networks of the bats' social links. Because the network of roosting interactions is fully connected (each bat has roosted at least once with each other bat), its topology per se is not informative. We therefore used the weight of the links connecting colony members in order to characterize the social structure of the two observed Bechstein's bat colonies. Previous studies on the social structure of animal groups used unweighted networks, sometimes built from weighted networks by keeping only links stronger than a certain threshold (usually the association rate expected by chance). Using such an approach would, while reducing the complexity of the study, have led to a loss of much of the information on the strength of social bonds, which is the focus of our study. Moreover, unweighted network metrics have been shown to yield misleading results when compared with their weighted counterparts [22]. We applied different network measures in Matlab v. 7.5.0 (assortativity [2], Q-modularity [14,15]) to analyse the structure of the weighted network. Matrix correlations were tested with two-tailed Mantel tests implemented in Matlab v. 7.5.0. The frequency of individuals switching between communities was compared with that of a Monte Carlo simulation (10 000 runs) in which individuals had no preference for a given community but community size was kept constant. The year-to-year stability of associations was assessed by constructing association matrices including only individuals found in two successive years and running Mantel tests on these matrices. Additional methods, including information on the colony pedigrees calculation and the null network model used, are available in the electronic supplementary material.

3. Results

(a). Distribution of individual roosting associations

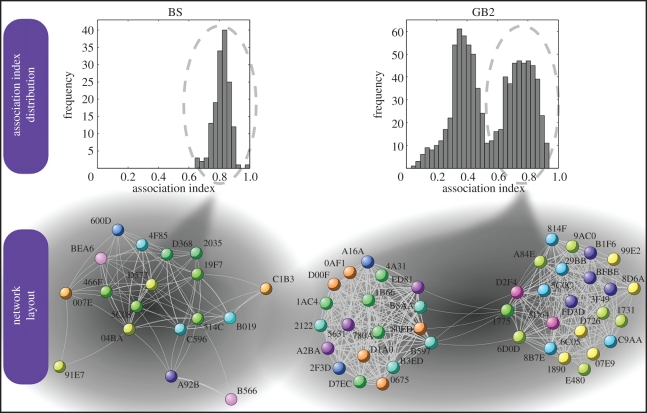
To quantify social relationships, we calculated for each year and colony, pairwise roosting associations (I_ij) that measure how often any two individuals share the same roost [12] (figure 1). The observed values of I_ij could not be explained in either colony by passive associations that would occur if bats were independently attracted to the same roost owing to shared roost preferences [21] (two-sample Kolmogorov–Smirnov test: n = 595–932 pairwise associations for GB2, n = 66–171 pairwise associations for BS: p < 0.001 for all years; see the electronic supplementary material for details). This shows that roosting associations are not a by-product of shared individual roosting strategies (compare [23]), but instead result from active preferences of bats for each other and thus measure social relationships among colony members [11,12,21,24]. The frequency distribution of individual roosting associations is shown in figure 2. For two different colony sizes, we found different distributions of I_ij: in the smaller colony, BS, we observed a unimodal distribution every year, whereas in the larger colony, GB2, I_ij always had a bimodal distribution. The latter reveals strong and weak links among the members of GB2. Thus, despite forming one colony, individuals clearly prefer to roost with some colony members, while keeping loose relationships with the rest of the colony.

Figure 2.

From pairwise association to social networks in two Bechstein's bat colonies. The upper graphs show the frequency distribution of the strength of associations (I_ij) in the colonies BS (left) and GB2 (right), in the year 2007. The lower graphs show the corresponding social networks in each colony. The social network is fully connected as all pairs of bats roosted together at least once. For clarity purposes, however, only links belonging to the upper mode of the distribution are included in the visualization (strong links), even though all (weak and strong) links are used for the calculations. Networks layouts were produced with Cuttlefish (http://cuttlefish.sourceforge.net). GB2 forms two distinct communities whereas no modular structure is visible in BS. The bats (nodes of the network) are identified by their printed PIT-tag numbers. Different colours of the nodes depict different matrilines within each colony. Members of a given matriline always belong to the same community in GB2.

(b). Social network structure

Our analyses on social networks—where the weight of the links [16] between bats is proportional to the strength of their roosting association—suggest that, in addition to the colony level, a second social structure exists. Applying a community detection algorithm [14–16] on the weighted network, we find in the larger colony, GB2, two distinct communities (range of the modularity-value Q_max: 0.125–0.249; comparison to an equivalent random network [25]: p < 0.001 for all 5 years) but no differentiation into communities in the smaller colony BS (Q_max = 0 for all years). Interestingly, the size of each of GB2's two communities (16–23 bats) is similar to the size of the entire colony BS, suggesting that social structure in Bechstein's bats depends on colony size. The decomposition of GB2 into two communities is particularly evident when we analyse only strong links between bats (in the upper mode of the bimodal distribution of I_ij, Q_max: 0.490–0.499). This shows that mainly the strong links are responsible for the formation of two communities in GB2 (figure 2). It is important to note that the bats' daily fission–fusion dynamics cannot directly explain the existence of two communities in GB2 as members of each community were also regularly found in several roosting groups.

We also analysed the emergence of the community structure within each year. We observed the onset of a modular pattern always around mid-May, the time when all bats had returned from hibernation. However, modularity values did not reach a stable plateau before August–September, the end of the breeding season (figure S2 in the electronic supplementary material). It is also only from this moment that the network structure remained largely unchanged (indicated by a stable distribution of I_ij). Consequently, increasing the temporal resolution of the analyses, for example by studying monthly patterns, would be insufficient to reveal the full network structure and the communities existing therein. This finding advocates against the use of datasets of a small size or covering limited time periods in the analysis of highly dynamic animal social networks.

The communities effectively play the role of social units and show a very different social structure than the whole colony. On the colony level of GB2, we found an assortative [2,26] and modular pattern of social links that is typical for social networks known from humans and dolphins [26,27]. The observed assortativity and modularity values are both significantly higher than in a corresponding random network [25] (p < 0.01 in all years) showing that bats with many social links roost preferentially with each other (Pearson's correlation coefficient between weighted degree and affinity [2]: r = 0.130–0.489, with the exception of 2008, where r = −0.031; n = 33–42 bats). By contrast, on the community level of GB2, as well as for the whole BS colony, the network is disassortative (r = −1.000 to −0.510) and non-modular, confirming the absence of further subunits and suggesting that communities resemble random networks (p = 0.001–1.000, in 23 out of 28 comparisons with random networks no significant difference was observed for assortativity and modularity values). In other words, within communities we found no consistent preference for certain roosting partners although this preference was pronounced at the colony level in GB2.

(c). Stability of individual relationships over time

The relationships of individuals in GB2 were strikingly stable over years. Community membership was largely constant: only in 10 out of the 124 cases when individuals returned after hibernation to GB2 in the following year had a bat switched community (Monte Carlo simulation: p < 0.001 for all years). Moreover, on the colony level, the strength of individual roosting associations (I_ij) was significantly positively correlated between successive years (Mantel test: r² = 0.355–0.784, p < 0.001 for each of the 4 year-to-year comparisons). Moreover, for the 17 individuals, which lived in all 5 years in GB2, the respective r²-value was 0.61 (p < 0.001) between 2004 and 2008. This shows that individuals keep their preferred roosting partners over a long time, although their colony disintegrates every year for six months during hibernation. This persistence contrasts with the findings on the community level, where I_ij was only weakly correlated between successive years (for GB2, r² = 0.003–0.114; two out of the eight correlations were significantly positive, p < 0.05; likewise, for BS: r² = 0.008–0.021, p = 0.184–0.374). Thus, bats indeed have the ability to distinguish between members of different communities over the years but appear not to keep track of individual relationships within communities. One reason for this could be that distinguishing between communities requires less cognitive abilities, e.g. if community membership is the result of bats aggregating according to size, age, reproductive status or relatedness [7].

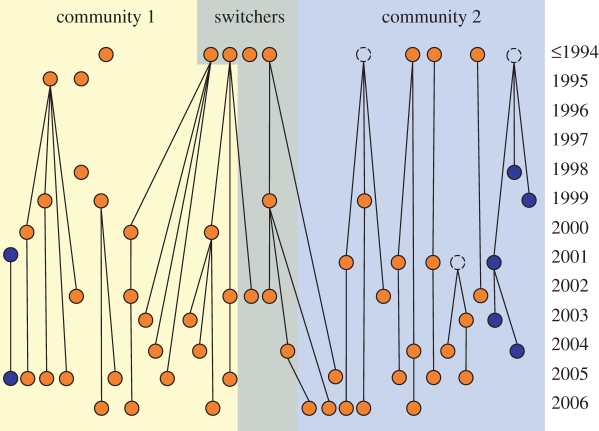
This hypothesis can be rejected, as age, size and reproductive status had no consistent influence on I_ij on the colony or community level in GB2, and in BS. At the same time, we found that in GB2, related bats had significantly stronger associations in each year, whereas no such pattern occurred in BS (table 1). In GB2, mothers and daughters were present in the same community in 231 out of 247 possible cases, and complete families belonged almost always to the same community (figure 3). Moreover, six of the eight females who had changed communities between years switched together with their mother or daughter. Persistent social bonds among kin also occur in other mammalian societies with fission–fusion dynamics [4,6,7], but so far kinship has not been shown to predict social structure in bat colonies with fission–fusion dynamics [11,28], as we find it. Kinship, however, did not fully explain the structure of GB2 as related and unrelated bats belonged to the same community, and had similar degrees of associations within their respective community (figure 3 and table 1).

Table 1.

Correlation between the bats' roosting associations and individual features for colonies BS and GB2. (For GB2 means (±s.d.) of r² and p-values of Mantel tests are given over 5 years, for the entire colony as well as for both of its communities separately. For BS, which was not monitored in 2005, the respective means are given over 4 years. Relatedness is the coefficient of genetic relatedness, whereas ‘genealogy’ is the coefficient of relatedness determined from pedigree analyses in each colony [13] (see figure 3 for GB2). p-values in bold denote consistantly significant correlations over all years.)

	GB2	GB2-community 1	GB2-community 2	BS
	(n = 33–42)a	(n = 15–22)a	(n = 17–23)a	(n = 11–18)a
age	r2 = 0.002 ± 0.002	r2 = 0.059 ± 0.066	r2 = 0.056 ± 0.059	r2 = 0.032 ± 0.026
difference	p = 0.416 ± 0.276	p = 0.267 ± 0.370	p = 0.042 ± 0.037	p = 0.157 ± 0.186
size	r2 = 0.001 ± 0.001	r2 = 0.004 ± 0.003	r2 = 0.046 ± 0.067	r2 = 0.005 ± 0.005
difference	p = 0.571 ± 0.263	p = 0.514 ± 0.263	p = 0.219 ± 0.288	p = 0.624 ± 0.192
lactation	r2 = 0.004 ± 0.005	r2 = 0.037 ± 0.064	r2 = 0.047 ± 0.045	r2 = 0.049 ± 0.065
statusa	p = 0.398 ± 0.388	p = 0.327 ± 0.227	p = 0.231 ± 0.438	p = 0.247 ± 0.196
relatedness	r2 = 0.043 ± 0.007	r2 = 0.019 ± 0.028	r2 = 0.023 ± 0.017	r2 = 0.016 ± 0.018
	all p < 0.001	p = 0.202 ± 0.213	p = 0.192 ± 0.232	p = 0.353 ± 0.223
genealogy	r2 = 0.055 ± 0.012	r2 = 0.015 ± 0.014	r2 = 0.022 ± 0.027	r2 = 0.008 ± 0.006
	all p < 0.001	p = 0.284 ± 0.336	p = 0.221 ± 0.131	p = 0.426 ± 0.267

^aThe reproductive status of all bats was not always known in all years, see table S1 in the electronic supplementary material for exact sample sizes.

Figure 3.

Genetic and social relationships in the Bechstein's bat colony GB2. The figure shows the genealogy and community membership of 61 adult female Bechstein's bats living in the colony GB2 during at least one year between 2004 and 2008. Broken circles symbolize three mothers that lived in the colony before 2004 but were not present during the study period. Bats born after 1995 (the year of birth is given on the right-hand side of the graph) are assigned to a specific mother or daughter using 11 polymorphic nuclear microsatellites [13]. In this colony two distinct mtDNA lineages occur [13], indicated by different colours (orange and dark blue). ‘Switchers’ are bats that have changed their community membership during the 5 years of the study.

Despite the presence of two distinct communities in all 5 years, GB2 never completely split into two separate colonies. Indeed, although members of different Bechstein's bat colonies do not share day roosts [13], even if living within roost-switching distance from each other (as the colonies RT, KAL and GB2 [29]), all members of GB2 continued to roost with each other in each year (on average 20–30% of the days). This indicates that certain individuals may play a crucial role in maintaining the links between communities.

Using a bridging index [30] normalized to community size (NBI), we are able to show that mainly older individuals were responsible for maintaining the cohesion of the colony, as revealed by a significant positive correlation between NBI and age (r² = 0.316–0.405, p = 0.008–0.047; n = 34–42 bats) in all years but 2008 (r² = 0.087, p = 0.631; n = 33 bats). As in elephants [31], older females may therefore play a crucial role in the bats' social interactions.

4. Discussion

Our study reveals a multi-level social structure in wild Bechstein's bats, which resembles that of elephants, dolphins and some primates, including humans, who keep social relationships despite their regular splitting and merging into a variable number of groups [4–7]. At the same time, we found that the social structure differed between colonies, and communities only occurred in the larger of the two colonies (GB2). This decomposition, while keeping the social structure of the whole colony intact, may help in maintaining the number of social links between bats in GB2 within the range where cooperation still works. Theoretical models show that cooperation in social networks is more likely to occur if the number of links between individuals is small [32]. Bechstein's bats show various cooperative behaviour, including information transfer, social thermoregulation and allogrooming [11,17,18,20]. Benefits from long-term social bonds [33] during cooperation and communal breeding could explain why bats have stable community membership despite high fission–fusion dynamics, which probably occur for ecological reasons [12,17]. Alternatively, constraints on cognitive abilities may limit the number of social relationships that individuals are able to maintain [8], thereby restricting community sizes to about 20 bats.

We found long-term relationships between bats that differ in their morphological, demographical and genetic characteristics, suggesting that Bechstein's bats are able to maintain individual relationships in a highly dynamic social environment over extended periods of time. While these relationships may be of a different nature to those found in groups of female-bonded elephants and primates (compare [9]), the multi-level structure of the bats' social network does resemble such species, which are believed to face high socio-cognitive demands [4,5,7–9]. The bats may even have to cope with socio-cognitive challenges that primates and elephants do not face, as their colonies not only show daily fission–fusion behaviour in summer, but also disintegrate each year during several months of hibernation. (During winter, Bechstein's bats roost solitarily or in clusters of just a few individuals while hibernating apart from their summer habitat in under-ground structures such as caves, cellars and mines [34].) In conclusion, our findings may suggest that the link between social complexity and social cognition in mammals is weaker than assumed by the various hypotheses [3,8–10] that explain the evolution of large brains in humans and other primates by high socio-cognitive demands in complex societies of cooperating individuals.