Nuclear Physics

Abstract

The internal workings of the nucleus remain a mystery. A list of component parts exists, and in many cases their functional roles are known for events such as transcription, RNA processing, or nuclear export. Some of these components exhibit structural features in the nucleus, regions of concentration or bodies that have given rise to the concept of functional compartmentalization—that there are underlying organizational principles to be described. In contrast, a picture is emerging in which transcription appears to drive the assembly of the functional components required for gene expression, drawing from pools of excess factors. Unifying this seemingly dual nature requires a more rigorous approach, one in which components are tracked in time and space and correlated with onset of specific nuclear functions. In this chapter, we anticipate tools that will address these questions and provide the missing kinetics of nuclear function. These tools are based on analyzing the fluctuations inherent in the weak signals of endogenous nuclear processes and determining values for them. In this way, it will be possible eventually to provide a computational model describing the functional relationships of essential components.

The nucleus has long been known to be functionally and spatially organized. Specific areas have been identified including the nucleolus, PcG bodies, nuclear speckles, Cajal bodies, Gems, cleavage bodies, perinucleolar compartments, the SAM68 nuclear body, PML bodies, etc. (for review, see Spector 2001), resulting in a patterned space. These structures can be stable for hours in live cells, justifying the long-held view of a nuclear space containing static subcompartments. This picture was challenged, however, when quantitative fluorescence microscopy techniques were first applied to probe the structure of the nucleus and the dynamics of nuclear factors (Phair and Misteli 2000). Approximately a decade later, it is now clear that dynamic processes are ubiquitous in the nuclear landscape: Most of the nuclear subcompartments are in a highly dynamic equilibrium, maintaining high fluxes of their components (Phair and Misteli 2000); factors shuttle between the nucleus and the cytoplasm (Whiteside and Good-bourn 1993; Vartiainen et al. 2007; Hill 2009), chromatin undergoes condensation and decondensation transitions (Hubner and Spector 2010); and genome-wide epigenetic signatures shift over time (Chang et al. 2008; Sharma et al. 2010). These processes cover a wide range of time scales (Hager et al. 2009), from the short time that factors bind to their cognate DNA sequences (typically a few seconds) (Darzacq et al. 2009) to the hours during which epigenetic changes remodel the expression profiles of cell subpopulations (Chang et al. 2008; Sharma et al. 2010). To complete this picture of factors constantly roaming around the nucleus, all measurements indicate that diffusion governs nuclear transport. As a consequence, gene expression cannot be the entirely deterministic process it was long thought to be: The nuclear interactions driving gene expression (e.g., the binding of a transcription factor to its promoter) are dependent on random collisions of diffusing factors. Consistent with this fact, recent studies have demonstrated how stochastic processes result in variability in gene-expression outcomes (Raj et al. 2006; Elf et al. 2007; Zenklusen et al. 2008; Larson et al. 2009). Tremendous efforts in biochemistry have identified a number of the players involved in gene expression and their interactions (Fuda et al. 2009). However, most of the information gathered from these measurements is static, and we are left with a few paradoxes: How can cells orchestrate synchronized, genome-wide responses, when all the components at the root of gene expression randomly collide with one another? How can a sustained transcriptional profile emerge from short-lived interactions between transcription factors and/or transcription machinery components? These questions and others will only be answered by building a consistent view of transcription in vivo, i.e., strongly coupled to the dynamic environment of the nucleus.

The constant progress in quantitative optical microscopy has provided multiple tools that can specifically probe fluorescently labeled factors of interest within live cells over time and thereby contribute to answers for these crucial questions. Fluorescence recovery after photobleaching (FRAP, or its variants based on either photobleaching or photoactivation) (Spector and Goldman 2005) provides a quantitative measure of the local mobility of a factor of interest. Fluorescence correlation spectroscopy (FCS) is a method that measures both the concentration and the mobility of fluorescent molecules. The ultimate resolution of light microscopy is set by diffraction to typically ~300 nm, two orders of magnitude above the distances involved in molecular interactions. A first method overcoming this limitation is FRET (fluorescence resonance energy transfer) (for review, see Jares-Erijman and Jovin 2003), which measures the distance between two known factors over very short distances (<10 nm), e.g., demonstrating that splicing factors interact even in the absence of transcription (Ellis et al. 2008; Rino et al. 2008). Other imaging techniques that break the diffraction barrier have recently appeared under the broad name of super-resolution (Patterson et al. 2010). Among these, a first family of methods exploits nonlinear quenching of emission states by stimulated emission (stimulated emission depletion [STED]) (Hell and Wichmann 1994; Hell 2003) or by modulation of the excitation light (Heintzmann and Ficz 2006; Gustafsson et al. 2008; Schermelleh et al. 2008). A second subset of related methods termed photoactivated localization microscopy (PALM), F-PALM, or STORM (Betzig et al. 2006; Hess et al. 2006; Rust et al. 2006; Egner et al. 2007) makes use of the dark states of specific fluorophores to keep the concentration of bright molecules low; as a result, the isolated single molecules are distinguishable from one another, and their positions can be determined with high precision (Thompson et al. 2002). Live-cell single-molecule studies have the potential to produce detailed kinetic information with high temporal resolution regarding a variety of players such as proteins or mRNA particles (Goulian and Simon 2000; Shav-Tal et al. 2004; Kubitscheck et al. 2005; Grunwald et al. 2006, 2008; Elf et al. 2007; Siebrasse et al. 2008; Speil and Kubitscheck 2010). Such techniques are still in their infancy in live cells and have so far been mostly limited to the study of one factor at a time, because detecting single molecules in two colors simultaneously is experimentally extremely challenging. Being able to observe individual interaction events between single molecules will represent a crucial step in our understanding of nuclear processes. Indeed, a technique termed “super-registration” microscopy has recently been developed to achieve simultaneous detection of single mRNA particles and single nuclear pores using a cell-inherent fiduciary marker to achieve cross-channel registration beyond the diffraction limit (Grunwald and Singer 2010). Interestingly, this approach revealed that the rate-limiting steps of mRNA export were the entry and the release from the pore rather than the passage through the narrow aperture.

The most exquisitely detailed images and movies of nuclear processes will remain useless unless we know how to analyze them and configure the results to a coherent model of nuclear dynamics. For example, gene expression is strongly influenced by both kinetics and abundance of factors: First, complex kinetics result from the large number of steps leading from an upstream protein effector (the concentration and spatial distribution of a transcription factor) to its downstream product (the number of a particular mRNA per cell); second, many factors and resulting mRNAs are present at low copy number, resulting in randomness and high levels of fluctuations (Taniguchi et al. 2010). We show here examples of analyses that capture these two essential aspects of gene expression (and nuclear processes in general). We first tackle the case of the elongating polymerase as an example of complex kinetic modeling. We use Monte Carlo simulations to make predictions of FRAP outcomes depending on which regulatory steps are present. We then introduce the general notion of fluctuation analysis as a technique that exploits the randomness of gene expression to yield mechanistic information. Although fluctuation analysis can potentially be applied to multiple situations, we restrict ourselves here to two important examples: the case of fluorescence fluctuation spectroscopy (FFS), in which fluctuations in the fluorescence signal yield information regarding concentration and mobility of the fluorescent species; and single mRNA counting, in which fluctuations in the number of mRNAs per cell over a population can lead to the details of transcription regulation.

KINETIC MODELING OF COMPLEX ENZYMATIC SCHEMES

So far, FRAP is perhaps the most used technique to study nuclear mobility and kinetics, because of its relative simplicity of use compared to other techniques, e.g., single-molecule tracking or FCS. In FRAP, a fluorescent marker is photobleached in a small volume of interest using a short pulse of a high-intensity, focused light source (for review, see Reits and Neefjes 2001). As the dark molecules from the photobleached volume exchange with the fluorescent molecules from the rest of the sample, fluorescence in the volume of interest gradually returns to equilibrium. It offers the advantage of studying the mobility of proteins in a spatially resolved manner; i.e., it is possible to study how a specific protein traffics in a given nuclear subcompartment (because these are usually larger than the diffraction limit, they can be selectively photo-bleached). Each experiment measures the kinetics of all the proteins that move through the bleaching spot during the acquisition time, which can be in the thousands for a factor with micromolar concentration. This averaging inherent to FRAP can be an advantage as it generates locally an ensemble measurement of mobility. However, it also sets some challenges: Individual proteins, although similar, might behave differently; alternatively, a given protein molecule might alternate between states (e.g., bound and free). Therefore, one usually needs to deconvolve multiple kinetically distinct populations from a given FRAP curve through quantitative analysis. For example, the presence of an immobile fraction in the population results in an incomplete fluorescence recovery. On the other hand, a transient immobilization of the photobleached factor slows down fluorescence recovery. Fitting the FRAP curve is a challenging task: First, technical details such as the size and shape of the beam or excessive photobleaching might affect the result (Mueller et al. 2010). Second, the molecules diffuse in the confined, highly anisotropic space of the nucleus, very far from the ideal case of free isotropic 3D diffusion for which analytical equations are well known (Bancaud et al. 2009). Third, the biochemistry involved is often complex and sometimes unknown. This opens the door to discrepancies in interpretations, especially when using complex models (Mueller et al. 2010). Despite such challenges, FRAP has been successful at describing dynamics within the nucleus, down to the dynamics of transcribing complexes. FRAP studies have been instrumental in reshaping our view of the nucleus as a highly dynamic diffusive environment (for review, see Hager et al. 2002, 2009). Even chromatin is highly plastic (Lever et al. 2000; Misteli et al. 2000; Nagaich et al. 2004), which means that the epigenetic-mark distributions observed using biochemical assays likely do not reflect static states but, rather, the most probable configurations of a highly dynamic landscape.

In addition to studying nuclear mobilities, FRAP has also been used to investigate transcription kinetics. In FRAP, labeling a global factor such as RNAPII presents a challenge: There are ~500,000 polymerases in a eukaryotic nucleus, some inactive, others engaged at potentially thousands of gene locations within the nucleus. How is it then possible to extract a specific signal amenable to kinetic modeling of a single gene? Using a gene-specific fluorescent factor also challenges the detection of one specific binding event over the background of freely diffusing proteins. To improve the signal by orders of magnitude over the background, various approaches have been developed. First, using an array in which multiple (~100–1000) copies of a given gene are present at the same genomic locus amplifies the signal by as much as a factor of a thousand. Such arrays occur naturally in genomes: For instance, the Drosophila salivary gland contains multiple copies of its entire genome (Yao et al. 2006); some gene families such as rRNA genes are organized as clusters (Gorski et al. 2008); finally, some genes naturally occur as tandem repeats, such as the copper response genes in yeast (Karpova et al. 2008). Alternatively, gene arrays can be synthetically generated and inserted using genetic engineering (McNally et al. 2000; Tsukamoto et al. 2000). Finally, it is also possible to label a given mRNA using the MS2 system (Bertrand et al. 1998): When repeated MS2 binding sites (MBS) are inserted in a gene of interest, the transcripts produced become fluorescent because they are bound by a fluorescent MS2 coat protein. Using this system, it has been possible to describe transcription kinetics quantitatively in vivo (Darzacq et al. 2007).

These approaches have contributed to animate our picture of transcription. Binding of a transcription factor at its cognate site in the case of the glucocorticoid receptor (GR) revealed surprisingly short dwell times (seconds), in comparison with the duration of transcription of a typical gene (minutes) (McNally et al. 2000). This observation suggests a model of transcription initiation as a series of sequential short-lived interactions. This might not be an absolute rule, as experiments on the heat shock promoter in Drosophila have shown that during heat shock response, the transcription factor (HSF) binds for minutes at the locus (Yao et al. 2006). FRAP has also been used to observe polymerases at one active locus to obtain the rates of assembly, initiation, and elongation. Various Pol I subunits displayed different recovery kinetics at their locus, indicating that the holoenzyme might assemble on the spot (Dundr et al. 2002; Gorski et al. 2008). Measured transcription rates are in the range of 0.5–5 kb/min (Mueller et al. 2010). Surprisingly, some of the proposed models so far indicate that transcription can be surprisingly inefficient (Darzacq and Singer 2008): Only 10% of the observed Pol I molecules are actively engaged in elongation (Dundr et al. 2002); Pol II is proposed to be ~1% efficient (one successful RNA transcribed out of 90 Pol II binding events) (Darzacq et al. 2007). However, efficiency might depend on the specifics of the gene: Drosophila heat shock response genes were shown to transcribe efficiently (Yao et al. 2007), with individual polymerases possibly undergoing multiple rounds of transcription through recycling at the locus; similarly, HIV-1 displayed efficient transcription (Boireau et al. 2007). Arrays are a useful tool, but because of their unusual structure, the results might be hard to generalize to the more common situation of a single-copy gene. The signal amplification inherent to the MS2 system has recently enabled researchers to image the recovery of a single gene construct (Yunger et al. 2010). The elongation rates measured are in agreement with previous results and emphasized the fact that different promoters resulted in different initiation rates, whereas the elongation rates were identical. Despite some degree of agreement (e.g., elongation rates within the same order of magnitude), separate FRAP studies have used different approximations to model transcription; for example, a process as central as elongation has never been treated explicitly. In one study, elongation was treated as a one-step process (Darzacq et al. 2007). This assumption has the advantage of considerably simplifying the modeling. However, in a one-step model, the most probable elongation time is zero; only a succession of processive elongation steps can yield the expected bell-shaped distribution of elongation durations (Fig. 1A). Other experimental studies tried to capture the processive nature of elongation by modeling it as a small number of discrete steps (10 steps) (Dundr et al. 2002) or used computer simulations to infer a linear fitting scheme (Boireau et al. 2007). Still lacking is an accepted, integrated model that could be used to compare experiments to reconcile the various observations. Although demanding, modeling the elongation process at nucleotide resolution is necessary, because some behaviors (RNAP traffic, pulsing) only emerge when explicitly treating all substeps involved (Dorbzynski and Bruggeman 2008; Ribeiro et al. 2009). In this section, we present simulations of transcription at single-nucleotide resolution and show how FRAP predictions can be made based on the regulatory steps involved.

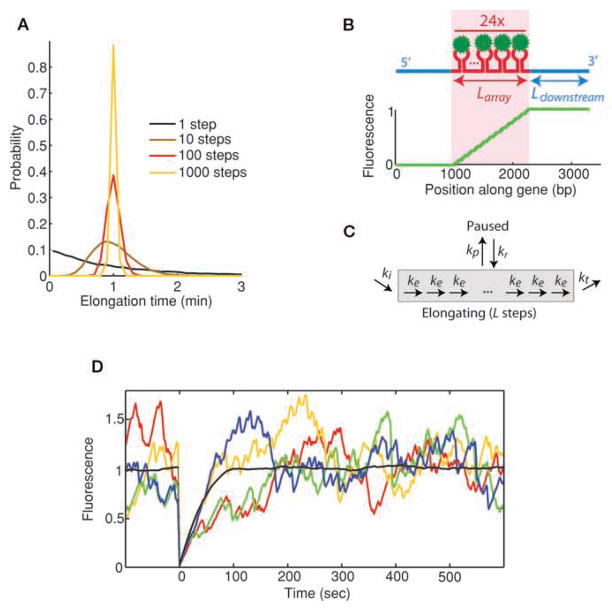
Figure 1.

(A) Distribution of elongation times depending on number of substeps involved. All models have the same average elongation time, but distributions narrow around the mean as the number of steps increases. Elongation of a kilobase-long gene involves at least 1000 steps. (B) MS2 system used in the simulations. Fluorescent proteins (green) bind to an array of hairpin loops (red) encoded within a specific mRNA (blue). (Bottom) Fluorescence of a nascent chain as a function of its position along the gene is plotted. (C) Schematic representation of kinetic model used in the simulations. Pausing and termination steps are separately added to the elongation pathway. (D) Individual Monte Carlo simulations (colors) are shown superimposed with the average of 300 photobleaching cycles (black). Because the number of polymerases present on the gene at a given time is low (~20), relative fluctuations observed in individual recovery curves become important. Initiation rate k_i = 0.2 s⁻¹, elongation rate k_e = 15 bp/s⁻¹, termination rate k_t = 15 s⁻¹, no pausing.

We used a gene that contains a 24x MBS array in its center (Fig. 1B) and assumed that diffusion and binding of the fluorescent MS2 coat protein occurs faster than the transcription timescales. Each polymerase initiates independently through a single-step random process, as suggested for yeast constitutive transcription (in addition, details of initiation including promoter escape might not appear in the MS2-based experiments, where the readout is the elongating nascent chain). Once initiated, elongation is simulated as a series of individual base-pair steps, each occurring as single-step processes at a rate of 1 kb/min (Fig. 1C). Polymerases engaged in elongation are hypothesized to be independent of one another.

When considering only elongation (i.e., excluding pausing and rate-limiting termination), the recovery curve displayed first a linear region as observed in Boireau et al. (2007), followed by a roundoff (Fig. 1D). The slope s of the linear part of the curve varies linearly as a function of the elongation rate k_e:

$$s=\frac{k_e}{\frac{L_{\mathit{array}}}{2}+L_{\mathit{downstream}}},$$ (1)

where L_array is the length of the region containing the MBS array and L_downstream the length of the region downstream from it (Fig. 2A,B). The denominator is not the length of the gene but, rather, an effective length of the gene, where each base is weighted by its fractional fluorescent intensity (0 before the MBS array, 1 after the array, and on average 0.5 within the array). We then examined how the influence of a rate-limiting termination step affected the recovery curves. The model hypothesizes that one of the postelongation steps is the bottleneck of transcript release, without requiring any assumption regarding the nature of this step. As seen in Figure 2C, the termination step adds an exponential component to the roundoff phase of the curve. Although the elongation rate is identical in all simulations, the slope of the linear region decreases with increased termination time; the slope value now convolves the effects of elongation and termination, according to the equation:

$$s=\frac{k_e}{\frac{L_{\mathit{array}}}{2}+L_{\mathit{downstream}}+\frac{k_e}{k_t}},$$ (2)

where k_t denotes the termination rate (Fig. 2D). The interpretation of the denominator is the same as before (the last term reflects the contribution of the increased concentration of transcripts at termination). Because the slope of

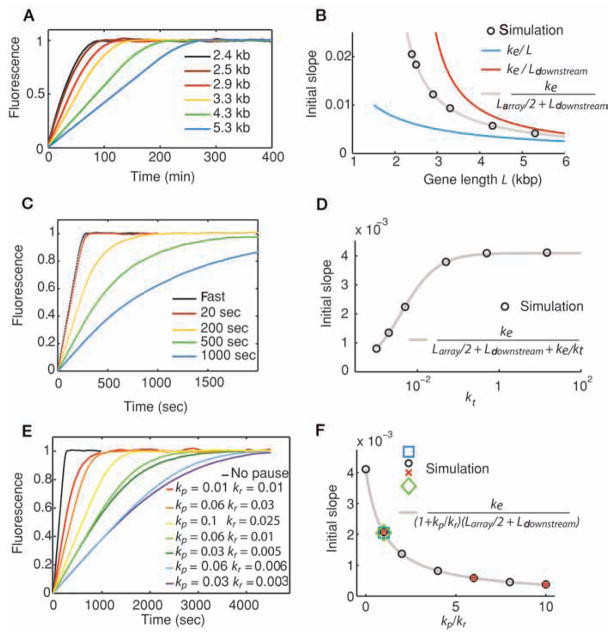
Figure 2.

Quantitative results from FRAP simulations. (A) Simulated FRAP recovery curves, in the absence of pausing or rate-limiting termination, for genes that vary in length of their downstream region L_downstream. Total length L of each gene is indicated. (B) Variation of the initial slope s of recovery curves from A (black circles) as a function of length L of the gene, overlaid with the theoretical predication (gray curve). (C) Influence of a rate-limiting termination on the shape of recovery curves. Termination step duration of each experiment is indicated. (D) Variation of initial slope s of recovery curves from C as a function of termination rate k_t. Fits of simulated data (black circles) are shown along with the prediction (gray curve). (E) Influence of pausing on shape of recovery curves. (F) Variation of initial slope s of recovery curves from E as a function of paused state occupation k_p/k_r (different symbol shapes represent different [k_p,k_r] pairs that yield the same [k_p/k_r] value). Theoretical prediction is shown in gray. In A–F, elongation rate k_e = 15 bp/s⁻¹; in C–F, the length of the gene is 5300 bp; no pausing in A–D; termination rate k_t = 15 s⁻¹ in A, B, E, and F.

the linear region combines two unknowns (elongation and termination rates), only a fit of the curve can provide the elongation rate unambiguously. We investigated the effects of pauses on the shape of the recovery curves, because pausing is progressively being recognized as an important postinitiation regulatory step (Margaritis and Holstege 2008). We used a simple model of pausing for many reasons: First, it is generic and does not make any assumption regarding the nature of the gene; second, it is consistent with the in vitro observations of ubiquitous pausing (for review, see Herbert et al. 2008); finally, it has already been used in the fitting of experimental in vivo FRAP curves (Darzacq et al. 2007). In this model, we assume that pauses occur randomly, independently of the sequence, with a one-step rate k_p, and that paused RNAPs return to the productive elongation pathway with a rate k_r. The effect of pausing on the recovery curves looks qualitatively similar to the one for termination. The initial slope of the recovery is decreased by more frequent and longer pauses, whereas the roundoff becomes more exponential (Fig. 2E). The variation of the slope as a function of the pausing rate constants once again corresponds to the elongation rate divided by the length of the gene weighted for fluorescence and occupancy (Fig. 2F):

$$s=\frac{k_e}{\left(1+\frac{k_p}{k_r}\right)\left(\frac{L_{\mathit{array}}}{2}+L_{\mathit{downstream}}\right)}.$$ (3)

A few lessons can be learned from these results. First, termination and pausing steps both have the effect of lowering the observed slope of the linear region. In the absence of any external mechanistic information, one only obtains a lower bound of the elongation rate by measuring the initial slope of the FRAP curve. Second, because different mechanisms yield qualitatively similar curves, the only way to unambiguously determine the mechanism and its associated kinetic constants seems to be to perform a series of experiments in which the most controllable parameter is varied: the length of the gene. Finally, simulations can model the challenge set by single genes in FRAP experiments. Because recovery curves are based on averaging the fluorescence from the molecules present at the gene, the more these molecules, the smoother the FRAP curve. When the number of nascent chains is small, separate experiments yield curves that significantly diverge from one another (~20 nascent chains on average) (Fig. 1D). As a result, the number of photobleaching cycles necessary to obtain a well-defined curve becomes experimentally challenging (here 300). The curves presented are noisy, not because of experimental imprecision, but as a consequence of the underlying molecular processes, namely, the irreducible randomness of chemical processes, in this case, initiation and elongation. Techniques that uncover the information hidden in these fluctuations are presented in the next section.

FLUCTUATION ANALYSIS

The fundamental principle of fluctuation analysis is to observe fluctuations around the mean value for a particular species—either protein or RNA—in time, space, or over a population. Such fluctuations carry information regarding the underlying kinetic processes and therefore help to define the roles of individual factors in modulating transcription. Fluctuations have a larger effect (and become easier to measure) as the number of molecules involved in the process decreases, making this approach ideal for the study of transcription factors (present at nanomolar concentrations) and mRNA (present at tens or hundreds of copies per cell). Here, we describe the application of two variations of fluctuation analysis for studying expression. First, we present fluorescence fluctuation spectroscopy (FFS), including the most widely used technique termed fluorescence correlation spectroscopy (FCS) (Magde et al. 1972), and then synthesize the results from existing FCS measurements for observing the reaction-diffusion behavior of DNA-binding transcription factors in the living nucleus. Second, we present mRNA counting experiments on more than 20 genes in yeast, measuring the mean and variation in fixed cells to infer transcription dynamics. From these data, we conclude that DNA-binding factors have an average dwell time of ~0.2 sec on chromatin, and that Saccharomyces cerevisiae genes exhibit a range of expression kinetics varying from fast turnover to stable binding of factors, depending on the gene.

FLUCTUATION-BASED MEASUREMENTS OF MOBILITY AND MOLECULAR INTERACTIONS

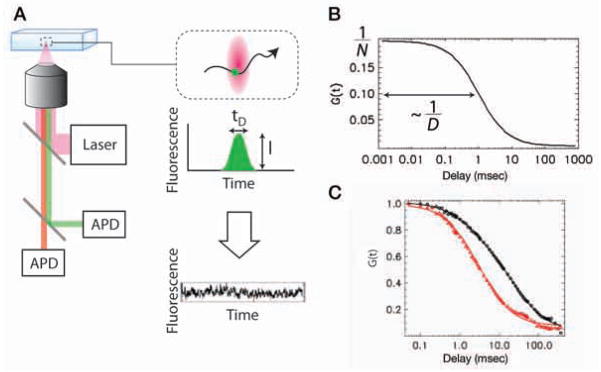
Measures of nuclear dynamics other than FRAP include FFS (FCS), single-particle tracking, and photoactivation (Wachsmuth et al. 2008). They are not as prevalent, likely because of the technical difficulties inherent in these approaches. FFS techniques exploit the fluctuating fluorescence signal from a very small observation volume created by two-photon or confocal microscopes to characterize the behavior of fluorescently labeled molecules (Fig. 3A). Each passage of a fluorescent molecule through the excitation volume leads to a short burst of detected photons. Collectively, these diffusing molecules give rise to a stochastic fluorescent signal. Statistical analysis tools are then applied to extract information regarding the fluorescent molecules, such as concentration, mobility, and interactions from the stochastic signals (Fig. 3B). Specifically, FCS uses the autocorrelation function to capture the temporal information in the fluorescence signal. The amplitude of the autocorrelation function is inversely proportional to the concentration of the fluorescent molecules. The decay time of the correlation function is the characteristic time of the fluctuating signal. For translational diffusion, the decay time is inversely proportional to the diffusion constant of the molecule. FCS is a powerful tool to study diffusion, transport, and chemical interaction both in vitro and in vivo (Bonnet et al. 1998; Kim et al. 2004).

Figure 3.

Dual-color fluorescence fluctuation spectroscopy. (A) Experimental setup (left). Excitation laser beam is focused by the microscope objective and creates a small observation volume (100 aL; top right, red volume). Fluorescence is collected by the same objective, spectrally separated, and detected by two avalanche photo diodes (APD). As each molecule passes through the focal volume, it generates a burst of fluorescence photons (center right). The properties of fluorescent molecules can be extracted from the stochastic photon counting signals (bottom right). (B) Autocorrelation function of fluorescence signal is calculated and fitted to a theoretical model, from which the concentration (number of molecules in the focal volume N) and diffusion constant D of the molecule is measured. (C) FCS measurement of molecular mobility. EGFP-RXR is transiently expressed in CV-1 cells. Laser is focused in the nucleus, and fluorescence is acquired for 1 min. Autocorrelation functions before (red triangles) and after (black circles) adding the ligand 9-cis retinoic acid are plotted together with the fit (solid lines). Diffusion time is changed from 2.9 msec to 11.6 msec after adding the ligand.

As an example of using FCS to measure the mobility of the molecules in living cells, we describe the nuclear receptor (NR), and specifically the retinoid X receptor (RXR). Nuclear receptors are transcription factors that regulate gene expression in a ligand-specific manner. RXR has a central role in NR signaling because it homodimerizes and heterodimerizes with other NRs as well. In the absence of ligand, RXR is associated with corepressors. Following ligand binding, it forms a homodimer and recruits coactivators and the transcription machinery to activate target genes. In Figure 3C, we plotted the auto-correlation function of EGFP–RXR before and after adding the ligand 9-cis retinoic acid. It is clear that the correlation function decays slower in the presence of ligand, indicating that RXR diffuses about four times more slowly when bound to its ligand (11.6 msec vs. 2.9 msec).

In addition to its potential for mobility measurements, FCS can also be applied to study chemical interactions, such as ligand binding to receptor or antigen binding to antibody. To distinguish species (such as bound and unbound), FCS relies on the difference in their mobility. However, in many biologically relevant interactions, the heterogeneity in mobility is difficult to resolve with FCS. For example, in a monomer/dimer equilibrium, the difference in diffusion time between monomer and dimer is only ~20%. This problem can be overcome by analyzing the fluctuations in terms of brightness rather than mobility. The brightness of a species is defined as the average photon count rate emitted by a single fluorescent particle. Therefore, the brightness of a homodimer is twice that of a monomer, which allows for an easy separation (Fig. 4A). Various techniques exist to measure brightness experimentally, such as building a photon counting histogram (Chen et al. 1999; Kask et al. 1999) or using a related technique based on moment analysis (Müller 2004; Wu and Müller 2005). Brightness analysis has been used to study the homodimerization of RXR (Chen et al. 2003). In Figure 4B, we plotted the brightness of the ligand binding domain (LBD) of RXR as a function of the concentration of RXR. The apparent brightness increases as the concentration of EGFP–RXRLBD increases and saturates at the dimer brightness. From each apparent brightness value, one can extract the fraction of monomer and dimer; the curve, therefore, provides a quantitative in vivo titration experiment of nuclear receptor dimerization.

Figure 4.

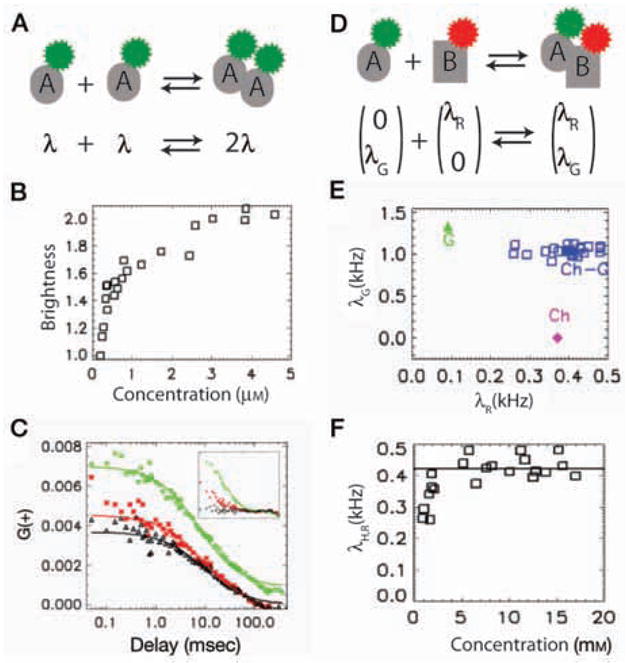
Application of FFS to study molecular interactions. (A) Monomer A carries a single fluorophore (brightness λ). Dimer A₂ is twice as bright (2λ). (B) Brightness analysis of homodimerization of RXR in CV-1 cells. Brightness of EGFP–RXRLBD is measured in the nucleus after adding the ligand 9-cis retinoic acid and is plotted as a function of concentration. For convenience, brightness is normalized to monomer EGFP brightness. (C) Application of FCCS to study interactions between EGFP–RXRLBD and mCherry–RARLBD. CV-1 cells are cotransfected with EGFP–RXRLBD and mCherry–RARLBD. Autocorrelation functions of the green (green diamonds) and red (red stars) channel are plotted along with the cross-correlation function (black triangles). Cross-correlation amplitude is comparable to that of the red channel correlation amplitude, indicating a strong interaction. (Inset) Correlation functions of a mixture of EGFP and mCherry in a CV-1 cell. Cross-correlation amplitude is close to zero because there is no interaction between EGFP and mCherry. (D) In a two-color experiment, brightness is represented as a two-dimensional vector: Green molecule A (0, λ_G) and red molecule B (λ_R, 0) form a complex with the resulting brightness (λ_R, λ_G). We can deduce oligomeric state of a species by comparing its brightness with that of corresponding monomers. (E) Application of HSP to study interaction displayed in D. Brightness data points of the heterospecies (blue squares) are clustered around the brightness expected for 1:1 EGFP:mCherry stoichiometry. (F) Averaged red channel brightness of heterospecies, which directly measures the fraction of EGFP–RXRLBD that binds mCherry–RARLBD, is plotted as a function of concentration of mCherry–RARLBD.

The desire to measure the interactions between two arbitrary proteins (rather than homodimers) motivated the introduction of dual-color FFS. To study an interaction between two factors, one needs to label each type of interacting molecules with specific color. The fluorescence is then spectrally separated and collected on two distinct detectors. If the colors are perfectly separated between the two channels, only the presence of hetero-interacting species leads to a coincident detection of fluorescence in both channels. Fluorescence cross-correlation spectroscopy (FCCS) (Schwille et al. 1997; Hwang and Wohland 2007) detects this coincidence by measuring the cross-correlation function of the two channel intensities (as well as the autocorrelation functions for both channels). Using these three correlation amplitudes, FCCS is able to determine the fraction of interacting species, provided that the interaction stoichiometry is known. We have studied the interaction between the ligand-binding domain of two nuclear receptors, retinoid X receptor (RXR) and retinoic acid receptor (RAR) using FCCS. It is known that RAR and RXR function as a heterodimer. In Figure 4C, we plotted the autocorrelation curves in both channels as well as the cross-correlation curves. High cross-correlation amplitude relative to the autocorrelation amplitude indicates a strong interaction between these two proteins. On the other hand, if there is no interaction, the cross-correlation should be close to zero (see inset).

A few technical challenges restrict the application of FCCS to relatively simple reactions with known stoichiometry. First, the emission spectrum of fluorescent proteins is very broad; the resulting spectral cross talk (fluorescence leakage of one fluorophore into the other detection channel) considerably complicates the analysis. In most cases, a single FCCS experiment is insufficient to resolve even a binary mixture (Chen et al. 2005). Second, similar to FCS, FCCS relies on mobility to distinguish high-order interactions (involving more than two molecules) and, hence, suffers from the same limitation in resolution. To overcome these issues, the brightness analysis can be generalized to a two-channel experiment (Chen and Müller 2007). In a dual-color experiment, brightness is represented as a two-dimensional (2D) vector. For example, if the brightness of a green monomer A is (0, λ_G) and that of a red monomer is (λ_R, 0), each oligomeric state A_mB_n displays a specific dual-color brightness vector (nλ_G, mλ_G) (Fig. 4D). This property provides a unique signature for each interacting species that should be easy to resolve experimentally. However, there is no general way to extract the concentration and individual brightness of each species from the dual-color fluctuation measurements. The recently introduced heterospecies partition (HSP) analysis solves this problem in the case of a chemical interaction A + nB ↔ AB_n (Wu et al. 2010). HSP combines all the hetero-interacting molecules into a single hetero-species, H = {A, AB, AB₂, …}, with an apparent brightness that is analytically related to the degree of binding. Using this approach, one can quantitatively measure molecular affinities between two endogenous interacting factors in vivo: As different cells usually express different levels of a given factor, one can obtain a titration curve using measurements from multiple cells (FFS yields a measurement of the absolute concentration of both factors in each cell). The brightness of the complex at saturation determines the stoichiometry.

To illustrate the application of HSP, we studied the heterodimerization interaction between EGFP–RXRLBD and mCherry–RARLBD. In Figure 4E, we show the brightness vectors of the heterospecies (blue), along with that of the corresponding monomers (green and red, respectively). In both channels, the brightness of the heterospecies is similar to that of the monomer, indicating that the complex is composed of one copy of each factor. To obtain the binding affinity, we plotted the red-channel brightness of the heterospecies (which is proportional to the binding fraction) as a function of the total concentration of the red monomer (mCherry–RARLBD) (Fig. 4F). The binding fraction grows with concentration and finally saturates at the value expected for the heterodimer. Note that, in contrast to FCCS, HSP yields the stoichiometry directly from data without any assumptions. The application of HSP to high-order interaction has been discussed in Wu et al. (2010).

TOWARD A GLOBAL MODEL OF NUCLEAR MOBILITY

After presenting how FFS techniques can be used to probe mobility and interactions between factors, we now compile and analyze within the same framework of FCS nuclear mobility measurements from the literature. We restrict ourselves here to FCS only for several reasons. This approach works well at low concentrations and thus should be applicable to transcription factors expressed at endogenous levels. The time resolution of FCS extends easily to the millisecond regime, enabling the observation of potentially fast interactions. FCS measurements probe a small well-defined focal volume in the nucleus, enabling comparison between experiments from different laboratories. In contrast to photobleaching studies, in which the bleaching geometry varies significantly between different studies, the typical FCS setup quite consistently uses an overfilled high numerical aperture objective to produce a diffraction-limited volume either through confocal excitation/detection or two-photon FCS. All theoretical treatments of FCS explicitly treat both the shape of the focal volume and diffusion of the probe, thus avoiding two of the major pitfalls leading to misinterpretation of FRAP data in previous studies (Beaudouin et al. 2006; Mueller et al. 2010). Finally, even though FCS has its own experimental artifacts, these artifacts are likely to be different from FRAP experimental artifacts.

We took data that were interpreted in the following primary studies as multicomponent diffusion or anomalous diffusion and reanalyzed it in terms of a general framework of binding and unbinding to DNA (Maertens et al. 2005; Pack et al. 2006; Yao et al. 2006; Mikuni et al. 2007; Slaughter et al. 2007; Tudor et al. 2007; Vámosi et al. 2008; Bancaud et al. 2009; Dross et al. 2009; Michelman-Ribeiro et al. 2009; Szymanski et al. 2009; Lidke et al. 2010; Porcher et al. 2010). In Michelman-Ribeiro et al. (2009), the original data were already interpreted using the approach presented here. Figure 5 shows the original curves grouped into three categories: probe diffusion of noninteracting monomeric species (blue); probe diffusion of noninteracting multimeric species (green); and reaction-diffusion of probes with DNA-binding activity (red). For comparison, the curves were generated using the reported parameter values but a uniform focal volume size (w_xy = 0.250 μm, w_z = 0.650 μm). This last group encompassed Fos-Jun (Vámosi et al. 2008), peroxisome proliferator-activated receptor (Tudor et al. 2007), glucocorticoid receptor (Mikuni et al. 2007), LEDGF/p75 (Maertens et al. 2005), heat shock factor (Yao et al. 2006; J Yao, pers. comm.), bi-coid (Porcher et al. 2010), and vitellogenin binding protein (Michelman-Ribeiro et al. 2009). For simplicity, we have left out studies on histone mobility. Although there is variation across these studies, several trends are evident. Monomeric species are closely grouped, despite being variously described as one-component diffusion (Mikuni et al. 2007; Michelman-Ribeiro et al. 2009; Lidke et al. 2010), two-component diffusion (Maertens et al. 2005; Pack et al. 2006; Porcher et al. 2010), or anomalous sub-diffusion (Wachsmuth et al. 2000; Slaughter et al. 2007; Tudor et al. 2007; Bancaud et al. 2009; Dross et al. 2009). As expected, multimeric species (green region) (Pack et al. 2006; Bancaud et al. 2009; Dross et al. 2009) diffuse more slowly in comparison to the monomers (blue region), but proteins with DNA-binding activity occupy a distinct dynamic regime in the autocorrelation (red region), with longer dwell times even than multimers of larger size. Therefore, the data are consistent with DNA binding having a consistent, measurable effect on mobility of each factor, as was pointed out in the initial studies.

Figure 5.

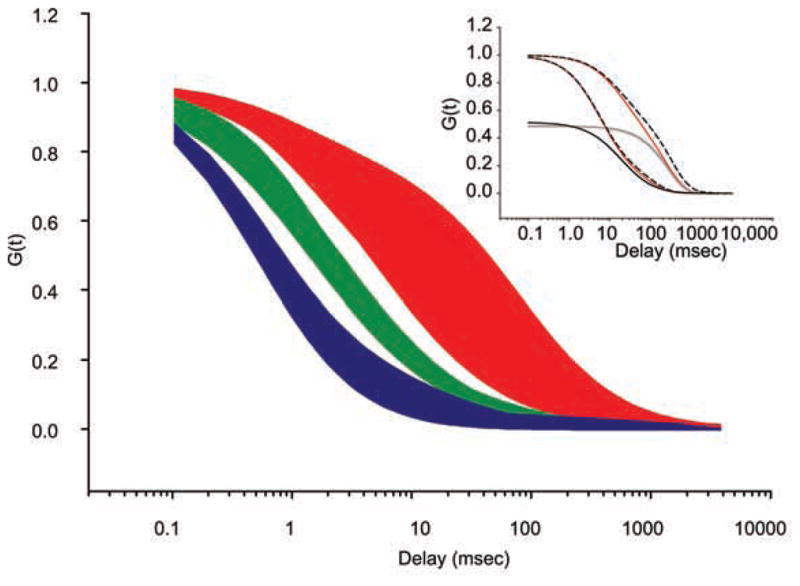
Compiled nuclear FCS data from previous studies. Reported fit parameters are used to calculate FCS curves by assuming standardized focal volume dimensions (w_xy = 0.250 μm, w_z = 0.650 μm). (Blue) Diffusion of noninteracting monomers (typically EGFP), (green) multimers, and (red) DNA-binding factors. (Inset) Theoretical fits to the data from the main panel. Boundaries of the red area are fit with a reaction-dominant approximation (Eq. 4, red solid lines) and compared to the full-theoretical solution with no approximation for the same parameters (black dashed lines). Individual components of the reaction-dominant approximation are shown separately: diffusion (black solid line) and reaction (gray solid line).

Rather than reporting an exhaustive representation of parameter space based on multiple models (which has already been treated in Sprague et al. 2004; Beaudouin et al. 2006; Michelman-Ribeiro et al. 2009), we use a specific model for the boundary of the autocorrelation region that is based on the reaction-diffusion model originally solved by Elson and Magde (1974) and adapted by Michelman-Ribeiro et al. (2009). This model posits a DNA-binding factor that is freely diffusing with diffusion constant D, binds DNA with a pseudo-first-order rate constant $k_{\text{on}}^{\ast }$, leaves DNA with an off rate k_off, and is immobile in the DNA-bound state. Because nonspecific binding sites are far more abundant than cognate binding sites, the binding is assumed to be nonspecific, which is one way that a factor might “scan” the genome by facilitated diffusion (Berg et al. 1981). This model has the benefit of having a straightforward comparison to in vitro biochemical rates while also recapitulating the dynamics in vivo. The lower envelope of the dynamic region for DNA-binding proteins (Fig. 5, red) corresponds to D = 2 μm²/sec, $k_{\text{on}}^{\ast }=1.7{sec}^{-1}$, and k_off = 9.4 sec⁻¹. The upper envelope corresponds to D = 0.6 μm²/sec, $k_{\text{on}}^{\ast }=3.5{sec}^{-1}$, and k_off = 3.7 sec⁻¹ (Fig. 5, inset, red solid lines). The resulting dwell times (1/k_off) of the factor bound nonspecifically to DNA therefore range between 0.1 sec and 0.3 sec. This regime corresponds to the reaction-dominant regime defined by Sprague et al. (2004), where $1/k_{\text{on}}^{\ast }\gg w_{xy}^2/4D$. Under these conditions, the average time the molecule spends diffusing around looking for a binding site ( $1/k_{\text{on}}^{\ast }$) is much greater than the time it takes the molecule to transverse the focal volume; thus, one can easily separate the reaction timescale (forming a complex with DNA) from diffusion. In this limit, the full solution (Elson and Magde 1974; Michelman-Ribeiro et al. 2009) is in good agreement with the approximation:

$$G(\tau )=\frac{1}{\left(1+\frac{k_{\text{on}}^{\ast }}{k_{\text{off}}}\right)\left(1+\frac{4D\tau }{w_{xy}^2}\right)\sqrt{1+\frac{4D\tau }{w_z^2}}}+\frac{e^{-k_{\text{off}}\tau }}{1+\frac{k_{\text{off}}}{k_{\text{on}}^{\ast }}},$$ (4)

where G(τ) is the autocorrelation amplitude as a function of the delay τ; D, $k_{\text{on}}^{\ast }$, and k_off are defined previously; and w_xy, w_z are the lateral and axial dimensions of the focal volume, which are particular to the microscope setup. The comparison between the complete theory and the approximation is shown in the Figure 5 inset (comparing red solid lines with black dashed lines). Note that in this limit, the reaction and diffusion timescales are decoupled. Furthermore, the characteristic timescale of the autocorrelation decay is only determined by the diffusion coefficient (D) and the off rate (k_off), with the on rate ( $k_{\text{on}}^{\ast }$) contributing to the relative partition between diffusion and reaction (Fig. 5, inset, black and gray solid lines, respectively).

This parameterization of the kinetic space results in diffusion coefficients that are lower than that observed for monomers in the nucleus (~1 μm²/sec compared to ~20 μm²/sec) (Fig. 5, cf. red and blue areas) and in dwell times that are shorter than observed by FRAP (~0.2 sec compared to 2 sec) (Mueller et al. 2008). For diffusion coefficients, caution must be exercised when comparing noninteracting probe molecules like GFP to macromolecules that, in addition to being larger in size, may interact with other proteins or with RNA in the nucleus. Thus, decreases in diffusive mobility may be independent of DNA binding (Slaughter et al. 2007). However, one can still experimentally recover the on/off rates of protein–DNA interactions when the timescales are as disparate as shown above in the reaction-dominant scenario. An alternative model seeks to recast these on/off rates within the more general framework of anomalous diffusion, which results from diffusion through a matrix of potential energy minima (i.e., bound states) (Wachsmuth et al. 2000; Wedemeier et al. 2009; Fritsch and Langowski 2010). For dwell times, the discrepancy between FRAP and FCS may be factor-specific and/or dependent on the relative spatial and temporal scales of these experimental approaches. In particular, long acquisitions with minimal photobleaching must be recorded to measure long dwell times with FCS, and these experimental conditions may be difficult to realize. However, we note that the range of variability for FCS measurements is surprisingly small across different laboratories and organisms, suggesting a consistent mechanism of genome scanning in which the factor is non-specifically bound ~15%–50% of the time to DNA for timescales on the order of ~0.2 sec.

FLUCTUATIONS IN mRNA COPY NUMBER REVEAL TRANSCRIPTION REGULATION

The questions of how a transcription factor finds a target, how nuclear structure may facilitate this process, and how long transcription complexes remain stable and active once assembled on DNA have direct bearing on the downstream levels of gene expression. In particular, if binding is stable and long lived or if transcription factors can be locally recycled in a subnuclear compartment, single stochastic events can have a profound effect on gene expression. This effect was first postulated by Ko (1991), who noted that stable binding of factors can lead to high levels of variation within a population as single stochastic binding events become locked in for a duration of time. On the other hand, for highly dynamic transcription complexes, these events become averaged out over time, and there is no memory in the expression levels of these individual stochastic binding events (Pedraza and Paulsson 2008). The phenomena of transcriptional bursting observed in some but not all genes may reflect a long-lived transcriptional active state induced by a single stochastic event (Zenklusen et al. 2008). These kinetic mechanisms—for example, bursting or nonbursting transcription—are evident in the fluctuations of mRNA levels in single cells. Whereas FCS records fluctuations over time, single mRNA counting in single fixed cells measures fluctuations over a population at a particular instance in time. The resulting population distribution is a record of the time-dependent process of transcription that occurred at the gene, which reflects the likely molecular dynamics of factors involved (Larson et al. 2009). Therefore, single mRNA counting is complementary to FCS in the nucleus: The latter measures the dynamics of the input (transcription factors), and the former reflects the dynamics of the output (mRNA distribution).

Using fluorescence in situ hybridization with single-molecule resolution, one is able to count the number of mRNAs per cell (Femino et al. 1998). Each mRNA appears as a diffraction-limited spot, and a bright spot in the nucleus is indicative of multiple nascent transcripts at the site of transcription (Fig. 6A). From these data, one can measure a frequency distribution directly, without the need for cell lysis, PCR, calibration, or normalization. More-over, in yeast, most mRNA (>80%) are present at fewer than five copies per cell (e.g., Fig. 6B) (Larson et al. 2009), which enables precise determination of both the mean and variance of mRNA levels from the full probability distribution (Fig. 6B).

Figure 6.

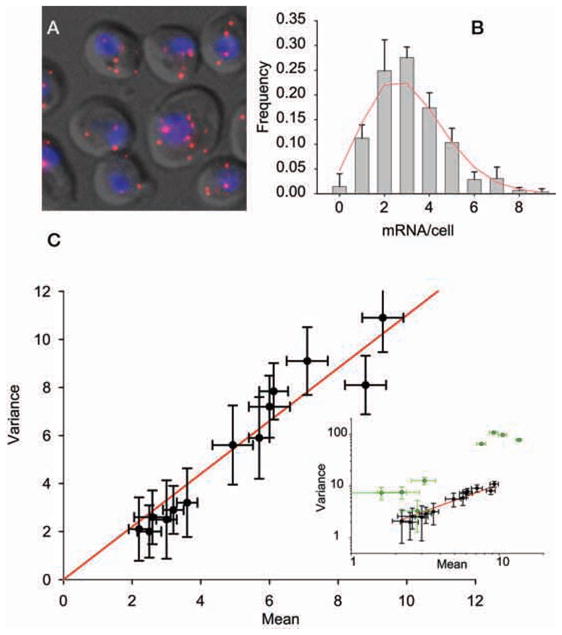
Single-molecule FISH for measuring cellular mRNA distributions. (A) Image of transcripts hybridized to multiple Cy-3-labeled DNA 50-mer oligos (red). (Gray) Differential interference contrast (DIC) image, (blue) nucleus. (B) Frequency distribution for PRP8 transcripts (gray bars) fit to a Poisson distribution (red solid line). (C) Variance of multiple endogenous housekeeping mRNA transcripts plotted against the mean. Fit has a slope of 1.1 ± 0.12. (Inset) In addition to housekeeping genes (black circles), cell-cycle-regulated genes and stress-response genes are also shown (green circles). Note that the inset is on a log–log scale. Error bars, S.E.M.

By developing an optimized protocol in S. cerevisiae, we have now quantified the expression distributions of 20 different genes (Zenklusen et al. 2008; Gandhi et al. 2011; Trcek et al., unpubl.). These genes encompass a broad range of observed expression behavior, including genes involved in transcription (RPB1, RPB2, RPB3, TAF5, TAF6, TAF12), protein degradation (PRE7, PRE3, PUP1, DOA1), ribosome biogenesis (MDN1), nuclear transport (KAP104), splicing (PRP8), cell-cycle-regulated genes (SWI5, CLB2, NDD1), and stress-response genes (GAL1, GAL7, GAL10) (Fig. 6C; Table 1). Plotting the mean versus variance for the housekeeping genes (Table 1, genes with asterisks) gives a line with a slope of 1.1 ± 0.12, which is indistinguishable from Poisson-distributed expression variation (Fig. 6C). This simple result enables a strong statement to be made regarding the nature of expression control of yeast housekeeping genes. The underlying process that generates a Poisson distribution is stationary, and the individual events are independent from one another. In biochemical terms, these data suggest that transcription complexes turn over fast enough such that no single stochastic event has any lasting effect. Interestingly, this turns out to be an efficient way to regulate mRNA levels. For an essential housekeeping mRNA present at three copies on average, there is only a 5% chance of having zero mRNA in a cell. Given the additional buffering capacity of protein levels, the cell can be successful by simply generating mRNAs randomly, at a low constant rate to ensure the continuing presence of sufficient quantities of mRNA and protein.

Table 1.

Mean and variance of mRNA/cell for selected S. cerevisiae genes

PUP1*	7.10	9.10
RPB1*	8.80	8.10
RPB2*	9.30	10.90
RPB3*	3.00	2.50
DOA1*	2.59	2.59
SWI5	1.60	7.40
CLB2	2.20	7.60
POL1	3.13	12.67
MDN1*	6.12	7.84
PRP8*	2.50	2.00
KAP104*	4.93	5.60
TAF6*	2.20	2.10
TAF12*	3.60	3.20
TAF5*	3.20	2.90
PRE7*	5.70	5.90
PRE3*	6.00	7.20

^*Constitutively expressed housekeeping genes.

For cell-cycle-regulated genes (SWI5, CLB2, NDD1) and induced genes (GAL1, GAL7, GAL10), expression is controlled in a much different manner. These genes have a variance that is several times greater than the mean (Fig. 6C, inset, green circles), indicating heterogeneity in gene expression or a nonstationary process. This super-Poisson variation in transcript levels results from transcriptional bursting—the case in which a single stochastic event such as binding of a transactivator results in many transcripts being produced from the active gene. This behavior arises from stable binding of the transcription factor from the promoter and has been observed for Gal4–promoter complexes (Nalley et al. 2006). One would predict, based on these data, that an FCS curve would demonstrate a long-lived kinetic component in the upstream transcription factor that binds the promoter (DR Larson et al., unpubl.).

CONCLUSIONS

During the last decades, intense research has focused on describing the nucleus as an ordered space: At least a dozen nuclear compartments have been identified, including the Cajal body (for review, see Morris 2008), nucleoli (for review, see Boisvert et al. 2007), nuclear speckles (Fu and Maniatis 1990), factories for transcription of multiple genes (Cook 2010), histone body loci (Nizami et al. 2010), and perinucleolar compartments (for review, see Pollock and Huang 2010), to name but a few. All these are composed of proteins that have implied or known functions in RNA metabolism. Up to a decade ago, the description of these components has been mainly phenomenological, and a quantification of their concentrations is lacking. Hence, a mechanistic understanding of gene expression has been elusive. However, the technologies and concepts described in some detail in this chapter have the intrinsic quality of quantification of the nuclear components and can derive functional information as well. They have provided results that invite us to rethink nuclear processes in terms of encounters between diffusing factors and their targets within a highly dynamic environment. Such processes are random in nature and give rise to potentially high fluctuations in their outcomes. We anticipate that the application of these approaches will do much to help us understand some of the most crucial questions, such as the emergence of long-term processes and order from short-lived interactions or the assembly of nuclear structures in relation to their function in gene expression.