Modeling diffusion-weighted MRI as a spatially variant Gaussian mixture: Application to image denoising

Abstract

Purpose: This work describes a spatially variant mixture model constrained by a Markov random field to model high angular resolution diffusion imaging (HARDI) data. Mixture models suit HARDI well because the attenuation by diffusion is inherently a mixture. The goal is to create a general model that can be used in different applications. This study focuses on image denoising and segmentation (primarily the former).

Methods: HARDI signal attenuation data are used to train a Gaussian mixture model in which the mean vectors and covariance matrices are assumed to be independent of spatial locations, whereas the mixture weights are allowed to vary at different lattice positions. Spatial smoothness of the data is ensured by imposing a Markov random field prior on the mixture weights. The model is trained in an unsupervised fashion using the expectation maximization algorithm. The number of mixture components is determined using the minimum message length criterion from information theory. Once the model has been trained, it can be fitted to a noisy diffusion MRI volume by maximizing the posterior probability of the underlying noiseless data in a Bayesian framework, recovering a denoised version of the image. Moreover, the fitted probability maps of the mixture components can be used as features for posterior image segmentation.

Results: The model-based denoising algorithm proposed here was compared on real data with three other approaches that are commonly used in the literature: Gaussian filtering, anisotropic diffusion, and Rician-adapted nonlocal means. The comparison shows that, at low signal-to-noise ratio, when these methods falter, our algorithm considerably outperforms them. When tractography is performed on the model-fitted data rather than on the noisy measurements, the quality of the output improves substantially. Finally, ventricle and caudate nucleus segmentation experiments also show the potential usefulness of the mixture probability maps for classification tasks.

Conclusions: The presented spatially variant mixture model for diffusion MRI provides excellent denoising results at low signal-to-noise ratios. This makes it possible to restore data acquired with a fast (i.e., noisy) pulse sequence to acceptable noise levels. This is the case in diffusion MRI, where a large number of diffusion-weighted volumes have to be acquired under clinical time constraints.

INTRODUCTION

Background: diffusion MRI

Diffusion weighted magnetic resonance imaging (DW-MRI) is the only technique that can image axonal fiber tracts in the brain in a noninvasive manner. DW-MRI produces images of biological tissue weighted by the local characteristics of water diffusion. Comparing a baseline T2-MRI scan with the MRI signal when a diffusion sensitizing gradient is added to the magnetic field in a certain direction, water diffusivity in that direction can be estimated. Repeating the procedure with different gradient directions, it is possible to reconstruct a diffusion profile at each spatial location. Due to the fact that water mainly diffuses along rather than across axonal fibers, the diffusivity information can be used to track the neural tracks in the brain white matter.

The continuous diffusivity profile, defined on the unit sphere, can be reconstructed from discrete measurements in different ways. The simplest approach is diffusion tensor imaging (DTI),^{1, 2} in which a zero-mean Gaussian probability distribution function (PDF) is fitted to the data measurements. At least seven samples are required for each voxel: six for the unique elements of the covariance matrix and one for the baseline MRI signal. DTI has shown great utility in imaging the fiber bundles in the brain because the architecture of the tissue can be inferred from the eigenstructure of the tensor: the major eigenvector gives the mean fiber direction at each location, whereas the anisotropy is a marker of fiber density. However, DTI has the limitation that it can only resolve one fiber direction in a voxel. When fibers cross or bifurcate within the voxel, which happens very often because voxels are from 100 to 1000 times wider than fibers, the monomodal Gaussian distribution fails to capture the diffusion profile.^{3, 4}

In order to resolve more complex fiber geometries, it is necessary to sample a higher number of directions. This approach is known as high angular resolution diffusion imaging (HARDI).^{4, 5, 6} Mathematical entities more complex than a Gaussian PDF can be fit to the measurements, overcoming the limitation that DTI uses a monomodal distribution. Among the most popular are spherical harmonics,^{7, 8} fourth-order tensors,^{9, 10} and mixture models.^{3, 11}

From the HARDI data, the PDF of the average spin displacement of water or a variant of this function can be computed. Several approaches have been proposed in the literature: the PDF of the fiber orientation distribution,¹² the diffusion orientation transform,¹³ the persistent angular structure of the PDF,¹⁴ and the orientation distribution function (ODF), which is the most popular. The ODF is the radial projection of the water diffusivity PDF, and is defined on a spherical shell. Much of the ongoing research in HARDI is focused on the computation of the ODF, because its maxima correspond to the most likely orientation of the underlying fibers, whereas the maxima of the raw attenuation data do not. In a first approach, Tuch¹⁵ used a numerical implementation of the Funk–Radon transform to approximate the ODF from the HARDI measurements. More recent work from different groups^{16, 17, 18} has converged to computing the Funk–Radon transform analytically from the spherical harmonic expansion of the HARDI data.

If the attenuation by diffusion of a scan (which depends of the pulse sequence and its parameter settings) is small, the directional information of the data can be enhanced by spherical deconvolution.¹² The ODF is assumed to be the convolution of a sharp fiber ODF (fODF) and a blurring kernel. Ideally, the fODF is zero for all directions except for those exactly corresponding to the orientation of fibers. The kernel can be estimated from highly anisotropic voxels, which are assumed to contain only one fiber population, and then inverted to compute the fODF from the ODF. It has been shown that using the fODF rather than smoother ODF in fiber tracking can improve the results.¹⁹

Background: denoising of diffusion MRI

Denoising strategies are very attractive in HARDI because acquiring a high number of gradient images under time constraints limits the signal to noise ratio (SNR). Denoising methods from the natural or medical image processing literature can be extended to HARDI by denoising each channel (gradient or baseline volumes) separately or by considering the HARDI data a vector-valued function. However, these extensions suffer from the same limitations as the methods they are based on.

Specifically, traditional image denoising algorithms based on (local or nonlocal) spatial smoothing^{20, 21, 22, 23} improve the SNR but also cause a loss of fine structures and increase partial volume error at the interfaces between different types of tissue. Techniques based on wavelets²⁴ preserve edges well but suffer from pseudo-Gibbs artifacts. This problem is solved by approaches based on variational calculus^{25, 26} and partial differential equations, but such methods still have the disadvantage that they cause loss of texture, leading to the well-known “staircase” effect. In general, all these methods perform satisfactorily when the noise level is moderate, but their limitations arise when the SNR decreases. Therefore, denoising of DW-MRI data remains an open, relevant problem, and algorithms that overcome the drawbacks of existing methods are necessary.

Contribution

In this study, we propose an approach to the DW-MRI denoising problem based on unsupervised learning. We take advantage of the relatively low variability in DW-MRI to learn the typical distribution of the data, which is fairly constant across subjects (except for cases with pathology). We then use this information to tailor a denoising method to DW-MRI and outperform the algorithms summarized in Sec. 1B.

We propose using a spatially variant Gaussian mixture model (GMM) to learn a relatively small dictionary of components that can accurately represent the diffusion data. GMMs, which have been successfully applied in many different problems in the literature, are very suitable to represent the signal attenuation of HARDI data, which is a weighted sum of contributions from different fiber populations. The number of components, whose predefinition is a limitation of GMMs in general, is automatically estimated using the minimum message length, a concept from information theory.

The mean and covariance of each component, which are learned from training data, are constant. This allows us to use a large number of different voxels to train the components. If the mean and covariances were spatially variant, if would be impossible to estimate them for each single voxel unless strong assumptions were made (as in DTI, for example). Each mixture component will typically correspond to isotropic profiles or fibers in a certain orientation, with some flexibility provided by their covariances. The mixing weights are allowed to vary across space such that different components are represented in different regions. Then, a smoothness prior is placed on top on these spatially variant weights to exploit the fact that neighboring voxels tend to be similar. This constraint is very flexible because it does not force neighboring voxels to have similar values, but similar statistical distributions, decreasing the spatial blurring (which can lead to spurious fiber crossings).

The trained model can be fitted to a (noisy) test case by maximizing the posterior probability of the underlying noiseless data in a Bayesian framework. The output is a denoised version of the image. A by-product is the set of mixture weights for each voxel, which can be used in image segmentation.

To summarize, the main contributions of this study are: (1) unsupervised learning of diffusion MRI attenuation data with a spatially variant mixture model for DW-MRI-tailored denoising; (2) rather than modeling the DW-MRI data in individual locations (as it is typically done in the DW-MRI literature), we exploit spatial regularities by modeling the diffusion data as a field; and (3) application of a spatially variant GMM to denoising.

It is important to note that this article is an extension of our own preliminary work³⁵ with the following differences: (1) we model the signal attenuation instead of the anisotropic diffusion coefficient, which is more principled; (2) the training stage has been improved; and (3) new experiments have been added, including fiber tracking, segmentation, and extended denoising experiments.

Further related literature

As explained above, mixture models in general suit DW-MRI very well because the attenuation by diffusion in a fiber crossing or bifurcation can be modeled as the sum of two or more mixture components. Therefore, they have been extensively used in the DW-MRI literature to model the diffusion signal for a given voxel. For example, Tuch et al.⁴ propose extending DTI to a mixture of ellipsoidal profiles. Assaf et al.³¹ use a mixture of hindered and restricted models of water diffusion. Behrens et al.^{11, 32} propose a partial volume model that mixes one isotropic (the background) and several anisotropic components (the fibers). A continuous mixture of diffusion tensors is proposed by Jian et al.³³ The ODF is modeled as the convolution of the fODF and a smoother response function in a number of other studies.^{12, 17, 19, 34} However, these estimation methods do not exploit the relations between neighboring voxels; they model the data for a single spatial location. Another key difference with our proposed method is that the distribution of the HARDI data is assumed to follow a specific model (mixture of tensors, convolution of fODF and a constant kernel), whereas in our approach, the distributions are learned from training data using a generic model (a GMM).

Spatially variant GMMs have been used in natural image processing by Nikou et al.³⁶ (extended by Sfikas et al.³⁷) and Rivera et al.³⁸ (the latter with some simplifications). These methods use the weights of the mixture components to segment the images. Peng et al.³⁹ also applied a similar method to segmentation of conventional (i.e., nondiffusion-weighted) MRI data into three different types of tissue. As opposed to our proposed method, the data in these three studies are scalar fields, the number of mixture components is fixed rather than learned, and no denoising is performed. Martin-Fernandez et al.⁴⁰ proposed a Gaussian Markov random field for simple denoising of DTI data, but their system cannot model multimodal distributions (and therefore HARDI). Finally, King et al.⁴¹ also described a system similar to ours in a general way, though without any mathematical formulation.

Outline

The rest of the paper is organized as follows. Section 2 describes the dataset utilized in the study. The image model, as well as the mechanisms to train it and to apply it to image denoising and segmentation, is described in Sec. 3. The proposed method is evaluated in Sec. 4. Finally, Sec. 5 includes the discussion.

MATERIALS

HARDI data from 100 different healthy subjects were acquired at the Center for Magnetic Resonance at the University of Queensland using a 4 Tesla Bruker Medspec scanner. A single-shot echo planar technique with a twice-refocused spin echo sequence was utilized. Ninety-four diffusion-sensitized gradient directions and 11 baseline images with no diffusion-sensitization were obtained for every subject. Imaging parameters were as follows: b-value = 1159 s∕mm², TE∕TR = 92.3∕8259 ms, voxel size = 1.8 mm × 1.8 mm × 2.0 mm, and image size 128 × 128 × 55 voxels. The acquisition time was approximately 15 min. The SNR, using the mean square of the foreground as signal power and the square of the first peak in the histogram as noise power (estimator for Rice distribution), was on average 24 dB for the baselines and 15 dB for the diffusion-attenuated images. The 11 baseline images were merged down to a single estimate of the reference using a method tailored for Rician data,⁴² increasing the SNR by approximately 10 dB up to 34 dB. The reference image was used to segment the brain using the BET algorithm.⁴³ The resulting mask was then applied to all the diffusion images to avoid including nonbrain matter in the model.

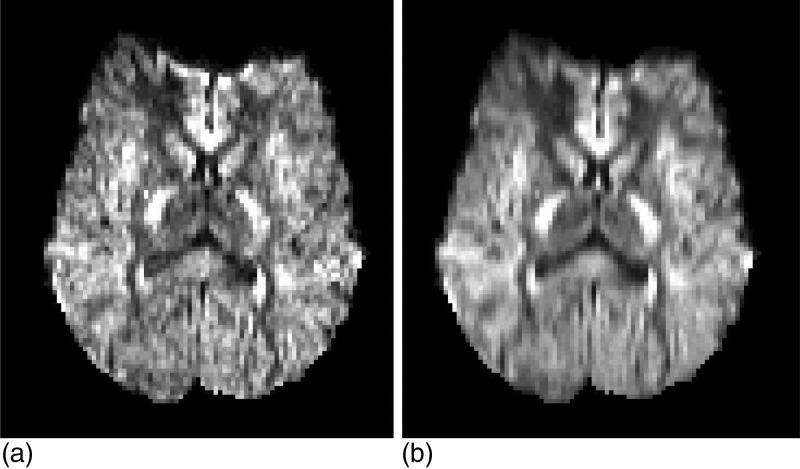
In order to evaluate denoising algorithms, it is necessary to a have ground truth that can be corrupted, subsequently restored and finally compared with the original. Hardware or software phantoms can be used as ground truth, but they are not a realistic approximation of the brain white matter. Ideally, one could use very long acquisition sequences (e.g., 24 or 48 h) to obtain very high SNR data that could be used as ground truth. However, these acquisition protocols are usually limited to ex-vivo scenarios due to motion artifacts. In this study, the original 94D data are too noisy to be directly used as ground truth [see Fig. 1a]. Instead, we propose to trade some angular resolution for redundancy that can be used to obtain a cleaner (though angularly coarser) pseudoground truth as follows.

Figure 1.

Axial slice (i.e., parallel to the ground) of the gradient image corresponding to direction (x,y,z)=(0,1,0) before (a) and after (b) angular downsampling. The downsampled images are the cleanest data that could be generated and were thus used as ground truth (i.e., SNR assumed to be ∞). Note that there is no spatial smoothing in (b).

First, the 94D DW-MRI data at each spatial location are downsampled to a new set of directions using a Laplace–Beltrami regularized spherical harmonic expansion of order six⁴⁴ (regularization coefficient λ=0.006). The fewer directions, the better the fit will be. On the other hand, the number of directions must remain high enough to be considered HARDI. We found 30 directions to be a good compromise. The 30 directions were computed with an electrostatic approach.⁴⁵ Henceforth, the 94D data are discarded, and the downsampled, smoothed (in angular domain) 30D data are assumed to be the noiseless (SNR = ∞) ground truth [see Fig. 1b]. A secondary advantage of the angular downsampling is that it lightens the computational load of the algorithms (denoising a volume with the proposed approach takes 25 min, see Discussion).

To evaluate the usefulness of the mixture weights in image segmentation, the second author made (under supervision of an expert radiologist) annotations of two brain structures (left and right ventricles and caudate nuclei) on the baseline images, which have higher SNR than the directional data because they are not attenuated by diffusion. Moreover, 25 of the test images were reannotated by the same author to estimate the intrauser variability in the annotations. These annotations can be used to train a supervised pixel classifier and evaluate its performance.

Finally, the 100 DW-MRI scans were randomly divided into two groups of 50 for cross validation. The first group was used to estimate the parameters of the model and to train the classifier. The images in the second group were artificially corrupted with noise and subsequently denoised to assess the performance of the proposed method.

METHODS

In this section, we first describe the image model in Sec. 3A. Then, the steps to estimate the parameters of the model from the data are detailed in Sec. 3B. Finally,the process to denoise diffusion MRI data is described in Sec. 3C.

Image model

A HARDI volume consists of a set of MRI images corresponding to a baseline and a set of different gradient directions. Since the diffusion is estimated by comparing the gradient images with the baseline, having a reliable estimate of the latter is very important. For this reason, it is usual that multiple (four or five) instances of the baseline volume are acquired and merged down into a reference with little noise. If this reference is denoted by S₀, the signal intensity S_k at a voxel location r when a gradient is applied in the direction (θ_k,ϕ_k) is given by the Stejskal–Tanner equation⁴⁶

$$S_k(\mathit{r})=S_0(\mathit{r})e^{-b_k\mathit{AD}{C}_k(\mathit{r})}\Rightarrow x_k(\mathit{r})=\frac{S_k(\mathit{r})}{S_0(\mathit{r})}=e^{-b_k\mathit{AD}{C}_k(\mathit{r})},$$

where θ∈[0,π] is the elevation, ϕ∈[0,2π] is the azimuth, ADC_k(r)≥0 is the apparent diffusion coefficient, x_k(r)∈[0,1] is the attenuation by diffusion and b_k is the Le Bihan’s factor, which groups several physical parameters from the image acquisition. ADC={ADC_k}, x={x_k} and S={S_k} have the property that they are symmetric because diffusion MRI cannot distinguish the two directions of each orientation, and hence, S_(θ,ϕ)=S_{(π-θ,ϕ±π)}.

The attenuation by diffusion in a voxel can be modeled with a multicompartmental model^{4, 32}

$$x_k(\mathit{r})\approx (1-\sum _{f=1}^{\mathit{NF}(\mathit{r})}{w}_f)e^{-b_k{\chi }_0}+\sum _{f=1}^{\mathit{NF}(\mathit{r})}{w}_f{e}^{-b_k{\mathit{\iota }}_k^t{\stackrel{-}{\stackrel{-}{}}\chi }_f(\mathit{r}){\mathit{\iota }}_k},$$ (1)

where NF is the number of fiber populations that coexist in the voxel, w_f≥0 is the weight of each population, χ₀ is the anisotropic diffusion, $\stackrel{-}{\stackrel{-}{}}\chi$ is the diffusion tensor corresponding to each fiber population, and ι_k is the unit vector in direction (θ_k,ϕ_k). The attenuation x_k (and thus the signal S_k=S₀x_k) is hence a mixture of an isotropic component (the first term in Eq. 1) plus a number of fiber components (the second half of the equation).

Rather than estimating NF for each voxel and then fitting the weights and diffusion tensors,⁴ we propose modeling the attenuation by diffusion x(r) as a generic mixture learned from training data.

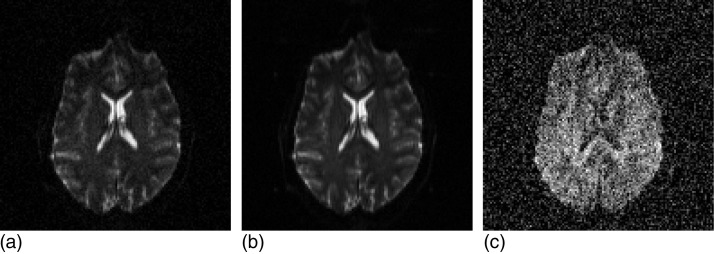
We assume that the baseline S₀(r) is a perfect estimate and only the gradient images S_k(r) are affected by noise (see Fig. 2). This is reasonable because, if we estimate $\stackrel{\wedge }{x_k}=S_k∕\stackrel{\wedge }{S_0}=S_k∕\sum _{i=1}^{11}{S}_{0,i}$ (where S_0,i are the signal intensities corresponding to the 11 acquired baseline images), the sensitivities of the estimate $\stackrel{\wedge }{x_k}$ with respect to S_k and S_0,i are

$$\begin{array}{c}\multicolumn{1}{c}{\left|\frac{\partial \stackrel{\wedge }{x_k}}{\partial S_k}\right|=\frac{1}{\stackrel{\wedge }{S_0}}\mathrm{and}\left|\frac{\partial \stackrel{\wedge }{x_k}}{\partial S_{0,i}}\right|=\frac{S_k}{11{\stackrel{\wedge }{S_0}}^2}=\frac{\stackrel{\wedge }{x_k}}{11\stackrel{\wedge }{S_0}}=\frac{\stackrel{\wedge }{x_k}}{11}\frac{\partial \stackrel{\wedge }{x_k}}{\partial S_k}\le \frac{1}{11}\left|\frac{\partial \stackrel{\wedge }{x_k}}{\partial S_k}\right|,}\end{array}$$

since $\stackrel{\wedge }{x_k}\in [0,1]$.

Figure 2.

Axial slice of a baseline volume (a), the corresponding average baseline (b), and one of the corresponding gradient images (c). We assume in this study that the noise of (b) is negligible compared with the noise of (c). The SNR of the original images was degraded 5 dB to better illustrate the difference between (b) and (c). Note that the intensity scales of (a–b) and (c) are different: the noise level is actually the same in (a) and (c).

Because the typical value of $\stackrel{\wedge }{x_k}$ is 1∕3 (9 dB attenuation, see Sec. 2), the sensitivity with respect to S_k is typically ~30 larger than with respect to S_0,i, and at least 11 times larger. In other words, the noise in S_k has to be at least 11 times larger than in S_0,i to have the same impact on $\stackrel{\wedge }{x_k}$.

Now, under the assumption that S_k is the only source of noise, the data for each voxel are uniquely characterized by the vector of attenuations x(r)=[x₁(r),x₂(r),…,x_D(r)]^t, where D is the number of probed directions. This assumption also simplifies the framework described in Sec. 3B

Next, we assume that the underlying “true” (i.e., not corrupted by noise) attenuation x(r) is a realization of a Gaussian mixture model (GMM)

$$p(\mathit{x}(\mathit{r}))=\sum _{c=1}^C{\pi }_c(\mathit{r})G(\mathit{x}(\mathit{r})|{\mathbf{\mu }}_c,{\mathit{\Sigma }}_c)$$ (2)

where G(x(r)|μ_c,Σ_c) is a Gaussian distribution with mean μ_c and covariance Σ_c, and each component plays a similar role as a fiber population in Eq. 1. While the means {μ_c} and covariance matrices {Σ_c} are independent of lattice locations, the weights of the mixture π(r)=[π₁(r)...π_C(r)]^t are allowed to be spatially variant, and they are constrained to lie in the probability simplex ${\sum }_{c=1}^C{\pi }_c(\mathit{r})=1$, with π_c(r)≥0. Most of the weights will be close to zero for a given voxel, which can be interpreted as a way of selecting NF(r).

Now, spatial coherence of the data is ensured by placing a Markov random field (MRF) on top of the mixture weights. Instead of laying a distribution on top of the data directly, laying it on top of another distribution (i.e., the GMM, which already has certain flexibility in the covariance matrices) gives an additional degree of freedom to the model³⁶

$$\begin{array}{c}\multicolumn{1}{c}{p(\mathit{\pi }({\mathit{r}}_1),\mathit{\pi }({\mathit{r}}_2),\dots ,\mathit{\pi }({\mathit{r}}_N))\propto \underset{d=1}{\overset{3}{\Pi }}\underset{c=1}{\overset{C}{\Pi }}{\beta }_{d,c}^{-N}\times \text{exp}[-\frac{1}{2}\frac{\sum _{i=1}^N{(2{\pi }_c({\mathit{r}}_i)-{\pi }_c({\mathit{r}}_i+{\mathit{u}}_d)-{\pi }_c({\mathit{r}}_i-{\mathit{u}}_d))}^2}{{\beta }_{d,c}^2}],}\end{array}$$ (3)

where N is the total number of voxels in the volume, ${\beta }_{d,c}^2$ is the variance of the mixture component c in the spatial directions d={1,2,3} (corresponding to the x,y,z axes), and u_d represents the unit vector along d. The variances ${\beta }_{d,c}^2$ are allowed to be direction dependent because the voxels are in general nonisotropic, and larger pixel spacings require larger variances in the model. The interpretation of the MRF prior is as follows: when one mixture component at one voxel is predicted as the average of the values of its neighbors in direction d, the error follows a zero-mean Gaussian distribution with variance ${\beta }_{d,c}^2∕2$.

Finally, the observed image data are a noise-corrupted version of x(r). The probability distribution of the noise in MRI is Rician

$$\begin{array}{c}\multicolumn{1}{c}{p({\mathit{x}}^{*}(\mathit{r})|\mathit{x}(\mathit{r}))=\underset{k=1}{\overset{D}{\Pi }}\frac{S_0(\mathit{r})x_k^{*}(\mathit{r})}{{\sigma }^2}{e}^{-\frac{S_0^2(\mathit{r})(x_k^2(\mathit{r})+{x^{*}}_k^2(\mathit{r}))}{2{\sigma }^2}}\times I_0\left(\frac{S_0^2(\mathit{r})x_k(\mathit{r})x_k^{*}(\mathit{r})}{{\sigma }^2}\right),}\end{array}$$ (4)

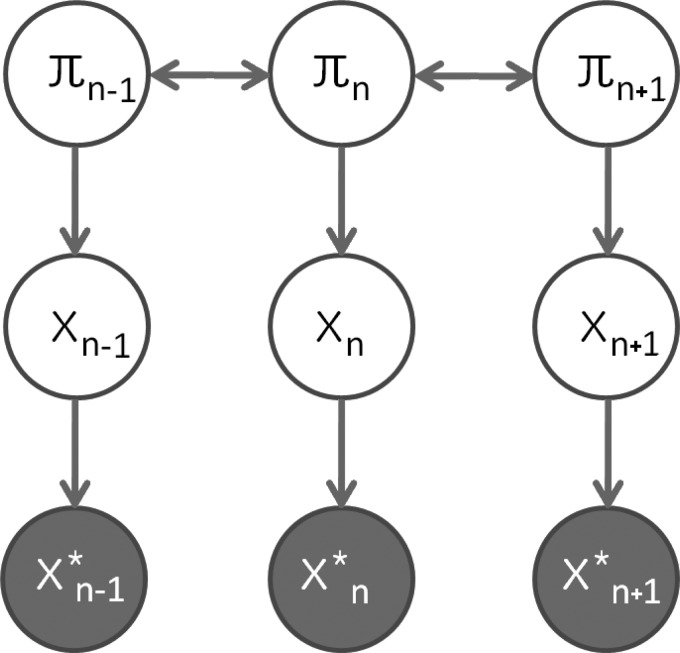
where x^*(r) represents the noise-corrupted observations, I₀ is the modified Bessel function of the first kind with order zero, and ${\sigma }_k^2$ is the noise power for gradient image in direction (θ_k,ϕ_k), typically constant across k, i.e., ${\sigma }_k^2={\sigma }^2,\forall k$. The complete graphical model of the data is depicted in Fig. 3.

Figure 3.

Graphical model for HARDI (in 1D, for the sake of simplicity): π represents the mixture weights, x represents the ADC data, and x^* represents the noise-corrupted observations.

Model training

Given some training data, the parameters of the model are estimated by maximizing the target function Q, which depends on {μ_c}, {Σ_c}, and {π_c(r)}

$$\begin{array}{c}\multicolumn{1}{c}{Q=\sum _{\mathit{r}}\sum _{c=1}^C{z}_c(\mathit{r})\{\log [{\pi }_c(\mathit{r})]+\log [G(\mathit{x}(\mathit{r})|{\mathbf{\mu }}_c,{\mathit{\Sigma }}_c)]\}-\frac{1}{2}\sum _{\mathit{r}}\sum _{c=1}^C\sum _{d=1}^3[\log ({\beta }_{d,c}^2)+\frac{[2{\pi }_c(\mathit{r})-{\pi }_c(\mathit{r}+{\mathit{u}}_d)-{\pi }_c(\mathit{r}-{{\mathit{u}}_d)]}^2}{{\beta }_{d,c}^2}],}\end{array}$$ (5)

where z_c(r) is the posterior probability that the voxel at r belongs to component c

$$z_c(\mathit{r})=\frac{{\pi }_c(\mathit{r})G(\mathit{x}(\mathit{r})|{\mathbf{\mu }}_c,{\mathit{\Sigma }}_c)}{\sum _{c\prime =1}^C{\pi }_{c\prime }(\mathit{r})G(\mathit{x}(\mathit{r})|{\mathbf{\mu }}_{c\prime },{\mathit{\Sigma }}_{c\prime })}.$$ (6)

The first term (first row) in Eq. 5 corresponds to the conditional likelihood of the GMM given the weights.⁴⁷ The second term accounts for the joint likelihood of the weights themselves, given by the MRF. The approach that was utilized to maximize Q is an expectation maximization (EM) algorithm inspired by the work by Nikou et al.,³⁶ with two major differences: the maximization step of the EM algorithm has been substantially improved and the number of components is not fixed but determined by the MML criterion.⁴⁸

Initialization: choice of C with minimum message length criterion (MML)

To initialize the algorithm, the problem can first be solved without the MRF term from Eq. 3 in the target function Q from Eq. 5. This amounts to the well-known problem of estimating the parameters of a GMM, which can be solved: with the EM algorithm. In turn, the EM can be initialized with the K-means algorithm, which is further initialized with random samples from the training data. The EM algorithm is prone to getting stuck in local maxima, and it is therefore beneficial to train the GMM with different initializations for K-means and then keep the instance with the highest final likelihood.

It is well known that one of the main limitations of mixture models is that the number of components C must be defined in advance. A possible way of tackling this problem is to select the value of C that minimizes the minimum message length (MML), a criterion from information theory. MML combines two terms: the inverse of the likelihood of the training data and a term that penalizes the complexity of the model. Higher values of C decrease the first term but also increase the second, so a compromise must be reached

$$\begin{array}{c}\multicolumn{1}{c}{\mathit{MML}(C)=-[\sum _{\mathit{r}}\sum _{c=1}^C{z}_c(\mathit{r})\{\text{log}({\pi }_c)+\text{log}[G(\mathit{x}(\mathit{r})|{\mathbf{\mu }}_c,\sum _c)]\}]+[\frac{D}{2}\sum _{c=1}^C\text{log}\frac{N{\pi }_c}{12}+\frac{C}{2}\text{log}\frac{N}{12}+\frac{C(D+1)}{2}],}\end{array}$$ (7)

where the weights π_c are location-independent at this point (the MRF prior is not considered yet).

Training the GMM for a wide range of values of C to find which one provides the minimal MML is computationally impractical. The following greedy algorithm was used instead: the parameters are estimated just once for a sole, high value of C, and then, components are merged down as long as the MML decreases.⁴⁹ At each step, all possible pairwise merges are considered. The merge that leads to a model with the lowest MLL is selected and proposed for acceptance. If this value of MML represents an improvement with respect to the MML of the current model, the merge is accepted and the process is repeated. If it does not, the algorithm terminates. The procedure is fast because, when a merge is considered, the terms corresponding to the C-2 components not being merged do not need to be reevaluated.

Optimization with EM algorithm

Once the number of components C is defined, the cost function from Eq. 5 can be maximized. This can be achieved through an EM algorithm. In the E step, the posterior probabilities z_c(r) are calculated using Eq. 6. In the M step, the estimates of the parameters $({\mathbf{\mu }}_c),\{\sum _c\},\{{\beta }_{d,c}^2\}$ and the mixture weights at each pixel π_c(r) must be updated to maximize Q. The update equations for the mixture model parameters are well-known⁵⁰

$$\begin{array}{cc}\multicolumn{1}{c}{{\mathbf{\mu }}_c\leftarrow \frac{\sum _{\mathit{r}}{z}_c(\mathit{r})x(r)}{\sum _{\mathit{r}}{z}_c(r)},}& \hfill {\sum }_c\leftarrow \frac{\sum _{\mathit{r}}{z}_c(\mathit{r})\left[(x(r)-{\mathbf{\mu }}_{\mathit{c}})\right]{[x(r)-{\mathbf{\mu }}_c]}^2}{\sum _{\mathit{r}}{z}_c(r)}\hfill \end{array}.$$ (8)

Updating the mixture weights in order to be able to update their variances $\{{\beta }_{d,c}^2\}$ is more complicated. Simultaneous optimization with respect to all the weights is very difficult and impractical. An alternative is to utilize coordinate ascent, in which voxels are visited in a random order and their weights are optimized under the assumption that the weights at all other locations are fixed. The algorithm typically converges after five or six passes over the volume.

In order to optimize the weights for a given spatial location r, Nikou et al.³⁶ compute the derivatives of the target function Q with respect to {π_c(r)}, set them to zero, and solve the resulting second degree equations. Because the weights are optimized in an unconstrained fashion, they must be projected back onto the probability simplex after each step. The problem with this approach is that the solution to the equations can yield a point arbitrarily far from the simplex, and the projected point is not guaranteed to increase Q (in practice, this often happens). Instead, we solve the problem exactly with the help of a Lagrange multiplier. If the terms in the target function that are independent from {π_c(r)} are disregarded, some algebraic manipulation of Eq. 5 yields the following optimization problem:

$$\begin{array}{c}\multicolumn{1}{c}{\underset{\{{\pi }_c(\mathit{r})\}}{\text{max}}\sum _{c=1}^C[w_c\text{log}{\pi }_c(\mathit{r})-\frac{1}{2}{({\pi }_c(\mathit{r})-a_c)}^2]\mathrm{subject}\mathrm{to}\sum _{c=1}^C{\pi }_c(\mathit{r})=1,{\pi }_c(\mathit{r})>0,}\end{array}$$ (9)

where

$$\begin{array}{cc}\multicolumn{1}{c}{w_c}& =\frac{z_c\underset{d=1}{\overset{3}{\Pi }}{\beta }_{d,c}^2}{4\sum _{d=1}^3\underset{\begin{array}{c}\multicolumn{1}{c}{d\prime =1}\\ \multicolumn{1}{c}{d^{\prime }\ne d}\end{array}}{\overset{3}{\Pi }}{\beta }_{d\prime ,c}^2}\hfill \end{array},$$

$$a_c(\mathit{r})=\frac{\sum _{d=1}^3\underset{\begin{array}{c}\multicolumn{1}{c}{d\prime =1}\\ \multicolumn{1}{c}{d\prime \ne d}\end{array}}{\overset{3}{\Pi }}{\beta }_{d\prime ,c}^2({\pi }_c(\mathit{r}+{\mathit{u}}_d)+{\pi }_c(\mathit{r}-{\mathit{u}}_d))}{2\sum _{d=1}^3\underset{\begin{array}{c}\multicolumn{1}{c}{d\prime =1}\\ \multicolumn{1}{c}{d\prime \ne d}\end{array}}{\overset{3}{\Pi }}{\beta }_{d\prime ,c}^2},$$

The corresponding Lagrangian is

$$\begin{array}{c}\multicolumn{1}{c}{L(\{{\pi }_c(\mathit{r})\},\lambda )=\sum _{c=1}^C[w_c\text{log}{\pi }_c(\mathit{r})-\frac{1}{2}{({\pi }_c(\mathit{r})-a_c(\mathit{r}))}^2]+\lambda [1-\sum _{c=1}^C{\pi }_c(\mathit{r})],}\end{array}$$

where the constraint π_c(r)>0 has been left implicit (it must be observed so that logπ_c(r)∈(R)) and λ is the multiplier corresponding to the explicit constraint. Now, setting the derivatives with respect to the weights equal to zero gives

$$\begin{array}{c}\multicolumn{1}{c}{\frac{w_j}{{\pi }_j(\mathit{r})}-{\pi }_j(\mathit{r})+a_j(\mathit{r})-\lambda =0\Rightarrow {\pi }_j(\mathit{r})=\frac{a_j(\mathit{r})-\lambda +\sqrt{{(a_j(\mathit{r})-\lambda )}^2+4w_j}}{2},}\end{array}$$ (10)

where the solution corresponding to the minus sign is discarded because it would yield π_j(r)≤0, since w_j>0. Finally, the value of the multiplier can be calculated by solving ${\sum }_{j=1}^C{\pi }_j(\mathit{r})-1=f(\mathit{r},\lambda )=0$. If f(r,λ) is expanded,

$$\begin{array}{c}\multicolumn{1}{c}{f(\lambda ,\mathit{r})=\sum _{j=1}^C\frac{a_j(\mathit{r})}{2}-\frac{C}{2}\lambda +\frac{1}{2}\sum _{j=1}^C\sqrt{{(a_j(\mathit{r})-\lambda )}^2+4w_j}-1=0.}\end{array}$$

There is no simple expression for the roots of this function. However, it is easy to check that df∕dλ<0 ∀λ. Since f is continuous and differentiable everywhere, this means that there is only one zero, which can be easily found with numerical methods; a bisection strategy was used in this study. Once the value of the multiplier λ has been determined, substitution in Eq. 10 provides the optimal mixture weights.

Finally, the EM iteration ends with calculating the new class variances from the updated mixture weights

$${\beta }_{d,c}^2\leftarrow \frac{1}{N}\sum _{\mathit{r}}{[2{\pi }_c(\mathit{r})-{\pi }_c(\mathit{r}+{\mathit{u}}_d)-{\pi }_c(\mathit{r}-{\mathit{u}}_d)]}^2.$$ (11)

The EM algorithm is summarized in Table TABLE I..

TABLE I.

EM algorithm to estimate the model parameters.

1.	Initialize the mixture model components {μc,Σc} with the results from Sec. 3B1.
2.	Initialize the mixture weights for every voxel with the weights of the MRF-free GMM from the same section.
3.	While the function Q from Equation 5 keeps increasing:
	a) Calculate the posterior probabilities zc(r) with Equation 6.
	b) Update the mixture model components with Equation 8.
	c) Visit all voxels in random order, updating their mixture weights πc(r) with the solution of the problem from Equation 9.
	d) Repeat step c) until convergence (typically 5–6 times).
	e) Update the class variances ${\beta }_{d,c}^2$ with Equation 11.

Application to image denoising

The model can be used for image denoising by fitting it to an image. In a Bayesian framework, the goal is to maximize the posterior probability of the underlying noise-free image given the noisy version. As it happened in the EM algorithm from the training stage (Sec. 3B2), direct optimization with respect to all variables is computationally very difficult. Once more, coordinate descent can be used. In this context, the algorithm is known as iterative conditional modes (ICM).⁵¹ In ICM, voxels are visited in random order, and their values are optimized by maximizing the conditional probability $p(\mathit{x}(\mathit{r})|{\mathit{x}}^{*}(\mathit{r}),\stackrel{\wedge }{\mathit{x}}(S\backslash \mathit{r}))$, where x^*(r) is the observed (noisy) attenuation at the given voxel and $\stackrel{\wedge }{\mathit{x}}(S\backslash \mathit{r})$ is the current restored value at all other locations. The algorithm typically converges (i.e., negligible change in x) after a few passes over the whole volume.

The joint conditional distribution of the mixture weights π(r) and the “real” attenuation x(r) at each voxel are given by Bayes’s rule [(Eq. 13]. Maximizing the joint probability p(x(r),π(r)) is much faster than maximizing the marginal p(x(r)) and yields good results (see Sec. 5). Under the assumptions in this study (namely the graphical model in Fig. 3), the following independence relationships hold:

• p(x^*(r)|x(r),π(r),π(S\r),x(S\r))=p(x^*(r)|x(r)),

• p(x(r)|π(r),π(S\r),x(S\r))=p(x(r)|π(r)),

• p(π(r)|π(S\r),x(S\r))=p(π(r)|π(ℵ_r)).

where ℵ_r represents the neighborhood of r. Substitution in Eq. 13 yields the final expression for the posterior likelihood of the “real,” underlying data

$$\begin{array}{c}\multicolumn{1}{c}{\mathit{POST}.L.\propto p(\mathit{x}(\mathit{r}),\mathit{\pi }(\mathit{r})|{\mathit{x}}^{*}(\mathit{r}),\mathit{\pi }(S\backslash \mathit{r}),\mathit{x}(S\backslash \mathit{r}))=\underset{\mathrm{NOISE}\mathrm{MODEL}}{\underbrace{p({\mathit{x}}^{*}(\mathit{r})|\mathit{x}(\mathit{r}))}}·\underset{\mathrm{GMM}}{\underbrace{p(\mathit{x}(\mathit{r})|\mathit{\pi }(\mathit{r}))}}·\underset{\mathrm{MRF}}{\underbrace{p(\mathit{\pi }(\mathit{r})|\mathit{\pi }({\aleph }_{\mathit{r}}))}}=F,}\end{array}$$ (12)

$$\begin{array}{c}\multicolumn{1}{c}{p(\mathit{x}(\mathit{r}),\mathit{\pi }(\mathit{r})|{\mathit{x}}^{*}(\mathit{r}),\mathit{\pi }(S\backslash \mathit{r}),\mathit{x}(S\backslash \mathit{r}))\propto p({\mathit{x}}^{*}(\mathit{r})|\mathit{x}(\mathit{r}),\mathit{\pi }(\mathit{r}),\mathit{\pi }(S\backslash \mathit{r}),\mathit{x}(S\backslash \mathit{r}))·p(\mathit{x}(\mathit{r}),\mathit{\pi }(\mathit{r})|\mathit{\pi }(S\backslash \mathit{r}),\mathit{x}(S\backslash \mathit{r}))=\dots \dots =p({\mathit{x}}^{*}(\mathit{r})|\mathit{x}(\mathit{r}),\mathit{\pi }(\mathit{r}),\mathit{\pi }(S\backslash \mathit{r}),\mathit{x}(S\backslash \mathit{r}))·p(\mathit{x}(\mathit{r})|\mathit{\pi }(\mathit{r}),\mathit{\pi }(S\backslash \mathit{r}),\mathit{x}(S\backslash \mathit{r}))·p(\mathit{\pi }(\mathit{r})|\mathit{\pi }(S\backslash \mathit{r}),\mathit{x}(S\backslash \mathit{r}))=F,}\end{array}$$ (13)

$$\begin{array}{cc}\multicolumn{1}{c}{p(\mathit{\pi }(\mathit{r})|\mathit{\pi }({\aleph }_{\mathit{r}}))}& =\underset{c=1}{\overset{C}{\Pi }}\underset{d=1}{\overset{3}{\Pi }}G(2{\pi }_c(\mathit{r})|{\pi }_c(\mathit{r}+{\mathit{u}}_d)+{\pi }_c(\mathit{r}-{\mathit{u}}_d),{\beta }_{d,c}^2)=\dots \hfill \\ \multicolumn{1}{c}{\dots }& =\underset{c=1}{\overset{C}{\Pi }}G[2{\pi }_c(\mathit{r})|\frac{\sum _{d=1}^3({\pi }_c(\mathit{r}+{\mathit{u}}_d)+{\pi }_c(\mathit{r}-{\mathit{u}}_d))\underset{\begin{array}{c}\multicolumn{1}{c}{p=1}\\ \multicolumn{1}{c}{p\ne d}\end{array}}{\overset{3}{\Pi }}{\beta }_{p,c}^2}{\sum _{d=1}^3\underset{\begin{array}{c}\multicolumn{1}{c}{p=1}\\ \multicolumn{1}{c}{p\ne d}\end{array}}{\overset{3}{\Pi }}{\beta }_{p,c}^2},\frac{\underset{d=1}{\overset{3}{\Pi }}{\beta }_{d,c}^2}{\sum _{d=1}^3\underset{\begin{array}{c}\multicolumn{1}{c}{p=1}\\ \multicolumn{1}{c}{p\ne d}\end{array}}{\overset{3}{\Pi }}{\beta }_{p,c}^2}],\hfill \end{array}$$ (14)

$$\frac{\partial \log (F)}{\partial {\pi }_c(\mathit{r})}=\frac{G(\mathit{x}(\mathit{r})|{\mathbf{\mu }}_c,{\mathit{\Sigma }}_c)}{\sum _{c\prime =1}^C{\pi }_{c\prime }(\mathit{r})G(\mathit{x}(\mathit{r})|{\mathbf{\mu }}_{c\prime },{\mathit{\Sigma }}_{c\prime })}-2\frac{\sum _{d=1}^3(2{\pi }_c(\mathit{r})-{\pi }_c(\mathit{r}+{\mathit{u}}_d)-{\pi }_c(\mathit{r}-{\mathit{u}}_d))\underset{\begin{array}{c}\multicolumn{1}{c}{d\prime =1}\\ \multicolumn{1}{c}{d\prime \ne d}\end{array}}{\overset{3}{\Pi }}{\beta }_{d\prime ,c}^2}{\underset{d=1}{\overset{3}{\Pi }}{\beta }_{d,c}^2},$$ (15)

$$\frac{\partial \log (F)}{\partial x_k(\mathit{r})}=\frac{S_0^2(\mathit{r})}{{\sigma }_k^2}[\frac{I_1\left(\frac{S_0^2(\mathit{r})x_k(\mathit{r})x_k^{*}(\mathit{r})}{{\sigma }^2}\right)}{I_0\left(\frac{S_0^2(\mathit{r})x_k(\mathit{r})x_k^{*}(\mathit{r})}{{\sigma }^2}\right)}{x}_k^{*}(\mathit{r})-x_k(\mathit{r})]+\frac{\sum _{c=1}^C({\pi }_c(\mathit{r})G(\mathit{x}(\mathit{r})|{\mathbf{\mu }}_c,{\mathit{\Sigma }}_c){[{\mathit{\Sigma }}_c({\mathbf{\mu }}_c-\mathit{x}(\mathit{r}))]}_k)}{\sum _{c=1}^C{\pi }_c(\mathit{r})G(\mathit{x}(\mathit{r})|{\mathbf{\mu }}_c,{\mathit{\Sigma }}_c)}.$$ (16)

The first term in Eq. 12 corresponds to the Rician noise model from Eq. 4. The second term in F is just the GMM from Eq. 2. The third term is a product of univariate Gaussians corresponding to the different mixture components and directions in the MRF. Each Gaussian term is the result of multiplying the conditional probabilities given by the neighbors in each of the three spatial directions [Eq. 14].

Maximizing the posterior F [(Eq. 12] is equivalent to maximizing its logarithm, which has a simpler expression. The derivatives of logF with respect to the mixture weights and attenuation values can be computed analytically [see Eqs. 15, 16, where [·]_k denotes the kth element of a vector, and I₁ is the modified Bessel function of the first kind with order one]. This makes it possibly to optimize logF efficiently using gradient ascent, i.e., taking small steps along the direction of the gradient at each point. After each step, it is necessary to project the mixture weights onto its constraint (i.e., the probability simplex). Unlike in Sec. 3B2, this now works well because the user-defined step is fixed and small. A simple and fast algorithm for projecting onto the probability simplex⁵² was utilized. It is also necessary to project x(r) onto its own constraint (x(r)∈[0,1]) after each step. This is accomplished by setting to zero any component below zero and setting to one any component over one.

EXPERIMENTS AND RESULTS

Training the model

The proposed model was trained with the 50 images from the training dataset. Rather than using all the available voxels, a random patch of size 25 × 25 × 20 voxels was extracted from each of them to lighten the computational load of the algorithm (in total N≈500,000 voxels). The patches were constrained to have at least two thirds of their voxels in the mask provided by the BET algorithm. A preliminary experiment evaluating the MML in Eq. 7 at C=5n,n=1,…,10, revealed that the minimum was achieved around C=25~30.

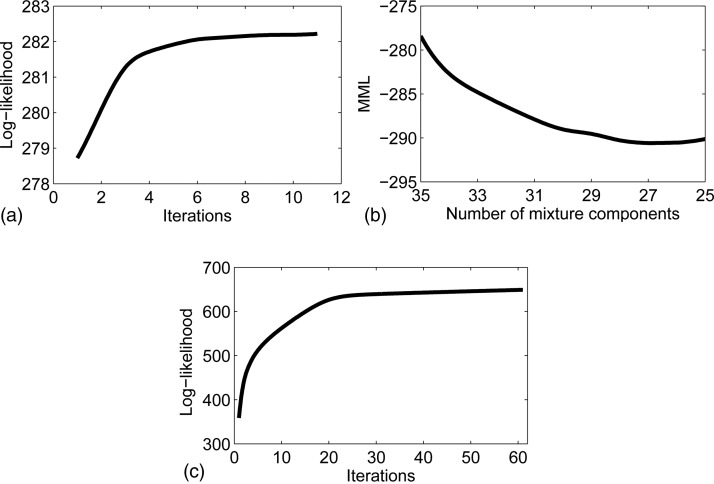
Because the algorithm that selects C can only decrease from an initial value C_ini by merging components, the initial GMM without the MRF term was first trained with C_ini=35 components. The training was repeated five times using EM with different seeds for the K-means algorithm, whose output initializes the EM. The model with the highest log-likelihood logQ was kept. The evolution of the metric logQ with the number of iterations for the best seed is displayed in Fig. 4a.

Figure 4.

Evolution of metrics in training: (a) GMM (best of 5), (b) MML, and (c) GMM-MRF.

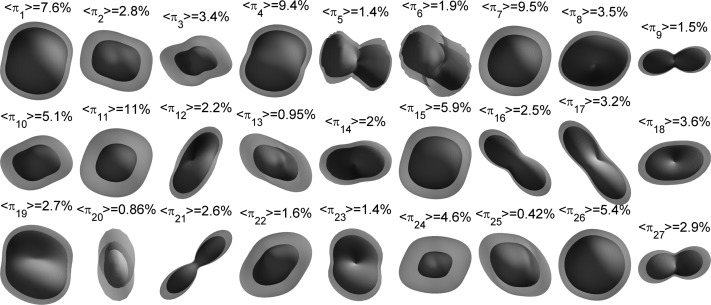
Once the GMM was trained with C_ini=35, components were iteratively merged until the MML did not decrease anymore, which happened at C = 27, as shown in Fig. 4b. The resulting GMM was used as initialization to train the GMM-MRF model [Fig. 4c]. The averages over all training pixels of the mixture weights (henceforth 〈π_c〉), which are useful in order to initialize the denoising algorithm (Sec. 4B), were saved along with the model. The model components, along with their weights and first mode of variation, are displayed in Fig. 5. The first mode depicts in most cases the scale of the diffusion. The second mode, displayed in Fig. 6, shows more variability in the orientations. From Figs. 56, we see that components such as {1,4,7,11,26} represent the isotropic part of the data, whereas the rest of the components display anisotropy in different directions.

Figure 5.

Mixture components after training. For each component, the first mode of variation (μ$\pm 2\sqrt{{\lambda }_1}{\mathit{e}}_1$, where {μ,λ₁,e₁} are the mean, first eigenvalue, and first eigenvector of the covariance matrix) and the average weights over the training data 〈π_c〉 are shown. The components were fitted to a (Laplace–Beltrami regularized) spherical harmonic expansion of order six and min-max normalized for display. The components are color-coded as follows: red indicates left/right direction, green is anterior/posterior, and blue is inferior/superior. Note that the components represent attenuation, so a toroidal shape implies a single fiber population along the axis.

Figure 6.

Mixture components after training: second mode of variation, $\mathit{\mu }\pm 2\sqrt{{\lambda }_2}{\mathit{e}}_2$ (see caption of Fig. 5).

Denoising

Rician noise was added to the 50 images in the test dataset, and the proposed method (as well as other three algorithms) was then utilized to restore them. Since the system was trained on the 50 other subjects in the training dataset, no bias was introduced in the evaluation. The RMS error in the attenuation data was used as evaluation metric

$$e=\sqrt{\frac{1}{N}\sum _{\mathit{r}}\Vert {\mathit{x}}_{\mathrm{denoised}}(\mathit{r})-\mathit{x}(\mathit{r}){\Vert }^2},$$

where x_denoised(r) represents the denoised attenuation data and x(r) is the ground truth.

In the denoising scheme proposed in this study, the restored data x_denoised(r) was initialized with the noisy version x^*(r), whereas the mixture weights π(r) were initialized with the average weights from the training data (Sec. 4A): π_c(r)=〈π_c〉 ∀r. The noise parameters {σ_k} are assumed to be known and constant across the gradient directions: σ_k=σ,∀k. This is a fair assumption in MRI because there is a large amount of background pixels in the data, so σ_k can be accurately estimated from them, for example, by studying their statistical moments⁵³ or histogram.⁵⁴

The proposed denoising algorithm was compared at different noise levels with the following strategies: a Gaussian smoothing filter, the classical anisotropic diffusion (AD) filter,⁵⁵ and a Rician-adapted, nonlocal means (NLM) filter.²¹ Rician bias correction was added to the first two in order to take advantage of the fact that the noise parameter σ is known; otherwise, the experiment would be biased against these two algorithms (the NLM filter already makes use of this information).

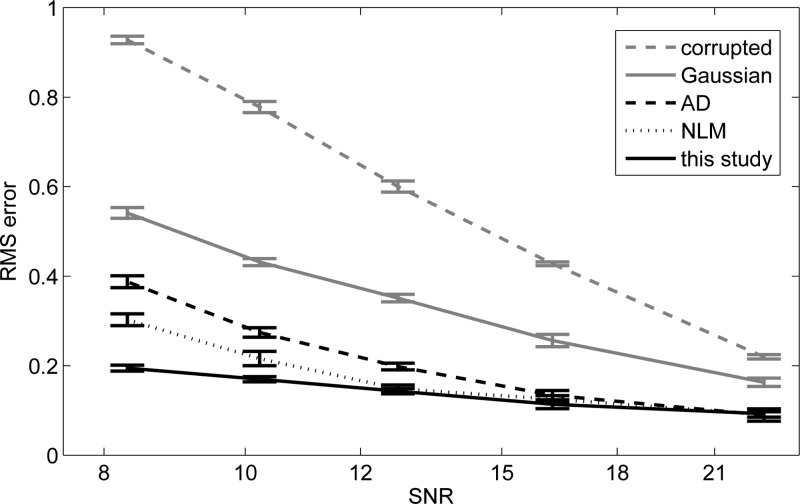
Figure 7 shows the performance of the different algorithms at different noise levels. The width of the Gaussian kernel and the conductance parameter of the AD filter were optimized to minimize the error at each noise level using the training data. Gaussian blurring is clearly worse than the other methods for every SNR. Regarding the other approaches, none of them is significantly better than the others at low noise levels. However, the performance of our method decreases slower with noise power than the others. The improvement with respect to AD and NLM is statistically significant (p<0.01) approximately when SNR<11 dB. The proposed method would for example allow for a very fast, noisy acquisition at SNR ≈8 dB that could be denoised to provide the same quality as an acquisition at SNR ≈22 dB restored with a Gaussian filter. At higher SNR, it would be more efficient to use AD or NLM due to their lower computational cost, unless image segmentation or analysis is to be carried out after the denoising. In that case, the features (probability maps) produced by our method can be worth the longer execution time (see Sec. 4C)

Figure 7.

Average RMS error from uncorrupted image to restored version at different noise levels. The 95% confidence interval, calculated at image level (rather than pixel level), is also displayed.

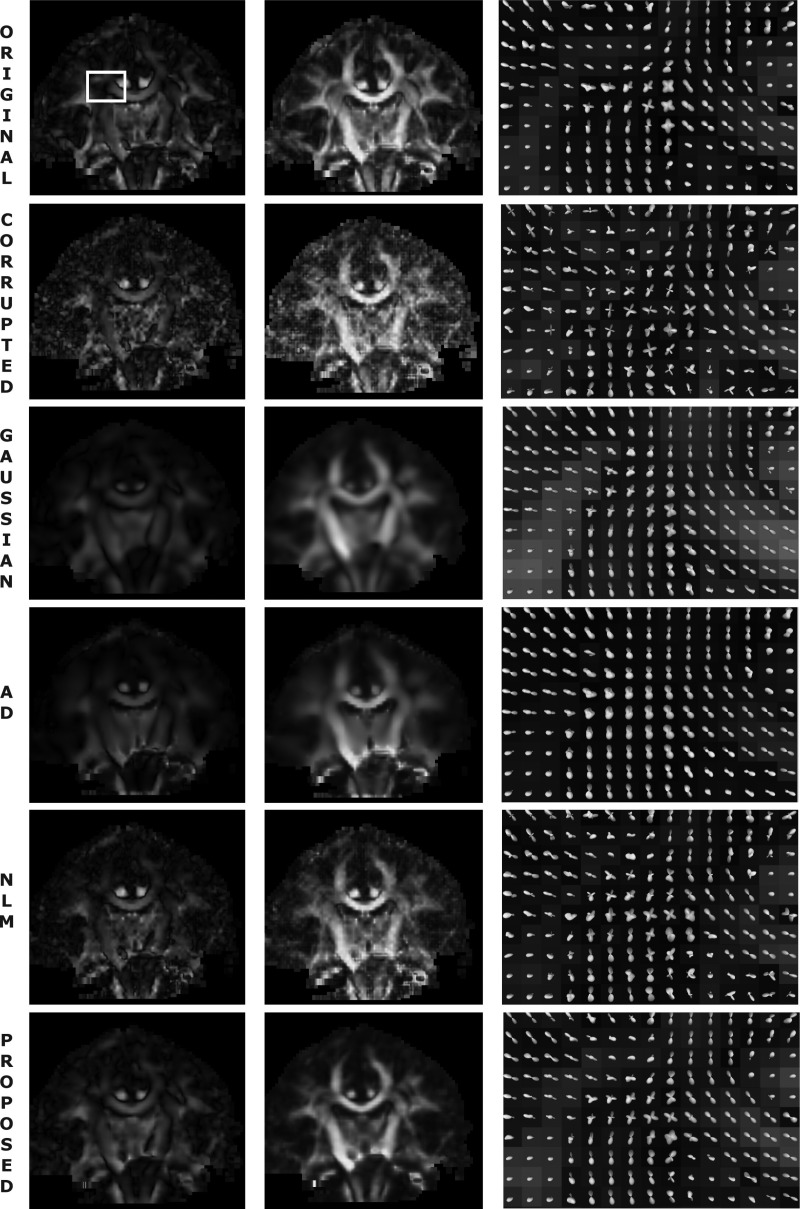
In Fig. 8, a slice of a diffusion-weighted image of a sample brain is displayed for the uncorrupted, corrupted (SNR = 10 dB), and denoised versions. The fODF field is also plotted for a region of interest (ROI) focused on the crossing between the corona radiata and the radiation of the corpus callosum. The ODF was estimated at 642 directions using a method by Descoteaux et al.¹⁶ with a spherical harmonic expansion of order six. The fODF was computed from the ODF in a nonparametric fashion using Tikhonov regularization.⁵⁶ The Gaussian filter requires a very wide kernel to eliminate the noise, which leads to oversmoothing. The anisotropic diffusion filter does preserve some edges slightly better (e.g., the callosal bundle on the right of the fODF field looks thinner) but also introduces too much blurring (e.g., the in the central region of the ROI, where the fiber crossing is smudged). The NLM filter respects the edges in some extent but does not eliminate as much noise as the other filters. Finally, the proposed method takes advantage of the learned diffusion distribution to remove most of the noise with less blurring and therefore less spurious crossings (these are especially noticeable in the output of the Gaussian filter).

Figure 8.

Color-coded coronal slice of a diffusion weighted scan (left column), corresponding fractional anisotropy (middle) and zoom-in of fODF field around the crossing between the corona radiata and the radiation of the corpus callosum (right). The corrupted version has SNR = 10 dB. The white square on the uncorrupted, color-coded slice marks the ROI for which the fODF field is displayed. AD stands for anisotropic diffusion and NLM for nonlocal means.

The ultimate goal of DW-MRI is fiber tracking. Figure 9 shows 3D reconstructions of the tractography output for a test subject given by a classic streamline tractography method very similar to Descotaux et al.¹⁹ From a number of points (1000) in a seed region, a step (0.5 mm) is taken in the direction of the global maximum of the fODF. Then, subsequent steps follow the orientation of the local maximum of the fODF that is closest to the direction of the previous step. The tracking ends if a point of low fractional anisotropy (<0.1) is reached or if the angle between two consecutive steps is above a threshold (60^∘).

Figure 9.

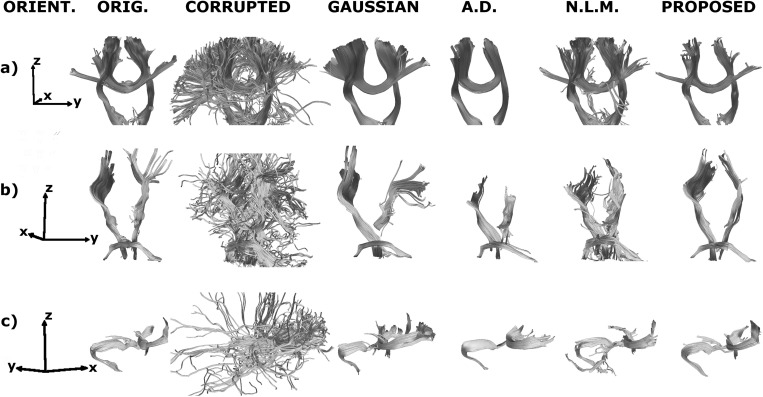
3D reconstruction of the fiber tracking output for the uncorrupted, corrupted (SNR = 10 dB) and denoised volumes of a sample test brain. The relative orientation of the reconstruction is displayed in the leftmost column: x represents posterior to anterior, y is right to left, and z is inferior to superior. The yellow spheres mark the seed regions. a) Corticospinal tract and corpus callosum b) Corticospinal tract and middle cerebellar peduncle. c) Corpus callosum, capsule fibers, and superior frontal gyrus fibers.

In Fig. 9a, one seed was placed on the corticospinal tract and another in the body of the corpus callosum to observe the behavior at the intersection of the corpus callosum and its radiation with the corona radiata. In Fig. 9b, the seeds are in corticospinal tract and in the middle cerebellar peduncle. The corticospinal tract crosses the peduncle on its way to the spinal cord. In Fig. 9c, there are three seeds: one to track the superior frontal gyrus fibers, one to track the capsule fibers, and one in the genu or the corpus callosum. The genu of the corpus callosum and the capsule fibers converge in the anterior∕posterior direction, whereas the superior frontal gyrus fibers bend toward the superior part of the brain. In all three cases, the corrupted version produces many false positives that lead to spurious tracts away from the bundles of interest. The Gaussian filter can partially recover the tracts, but the smoothing makes the bundles look thicker than they really are, especially at crossings. The anisotropic diffusion filter does a better job restoring the main tracts, but falters at the fiber intersections. The nonlocal means filter recovers the bundles to some extent but still displays some false positives. When the noisy data are fitted to our proposed model, the algorithm is able to track the bundles across the intersections as in the uncorrupted volumes.

Segmentation

Nikou et al.³⁶ and Rivera et al.³⁸ use a spatially variant mixture model for image segmentation: when the model is fitted to the data, the most likely mixture weights for each voxel π(r) are provided by the optimization algorithm, and these probability maps can be used as features in a segmentation algorithm. In our case, some of the probability maps correlate almost directly with anatomy (see the example in Fig. 10). It is interesting to test whether these probabilities can be used as features with classification purposes. The following experiment was set up: a support vector machine (SVM) was trained to classify the voxels as ventricle, caudate nucleus, or rest of the brain using the probability images; if the results are good, the mixing weights are good features.

Figure 10.

Probability maps for different mixture components (for which the second mode of variation, often more informative than the first, is displayed). (a) Sample saggital slice that shows high probability for a left/right component around the corpus callosum. (b) Coronal slice for a probability volume that displays high probability for a vertical component around the corticospinal tract. (c) Axial slice of the probability volume of an isotropic component that shows high probability around the ventricles.

The SVM was trained on the 50 training images and evaluated on the 50 test images. In the training stage, the model was first fitted to the training images. Then, all the positive voxels (i.e., annotated as ventricle or caudate) and an equal amount of randomly selected negative voxels (i.e., marked as background) were used to train the SVM. In the evaluation stage, the voxels in the test images were classified as ventricle, caudate, or background. This provides a mask for the ventricle and a mask for the caudate. These masks were morphologically closed with a spherical kernel (radius 3 mm), and then holes and islands were removed.

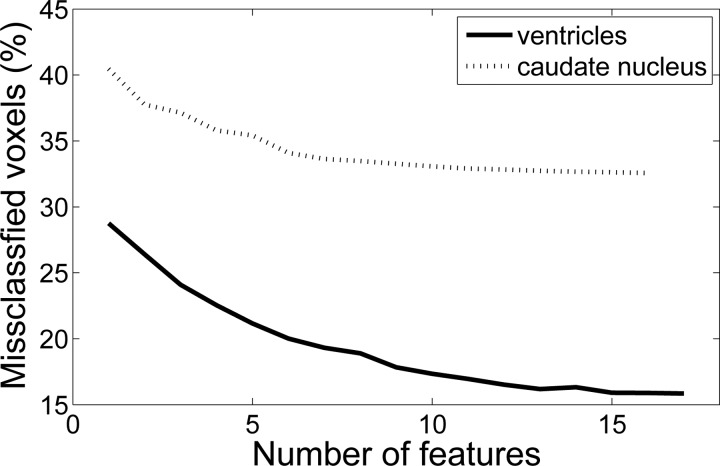
Rather than using the C = 27 weights as features for each voxel, a feature selection algorithm was used (“plus 3-take away 1”⁵⁷). Feature subsets were evaluated by cross-validation (ten folds with five images each) on the training data. The evolution of the error rate with the number of features is shown in Fig. 11. By visual inspection, the cut-off was set at 13 features for the ventricles and 8 for the caudate nucleus. Once the classifier was trained, its performance was evaluated with the 50 test images. The similarity indices (SI) of the gold standard and the automated segmentations are displayed in Table TABLE II.. The SI is defined as

$$\mathrm{SI}=\frac{2n(L_a\cap L_b)}{n(L_a)+n(L_b)}\in [0,1],$$

where L_a,b are the compared labels and n(·) is the number of voxels.

Figure 11.

Feature selection: error rate in cross-validation vs. number of selected features: (a) ventricles and (b) caudate nucleus.

TABLE II.

Segmentation results and intra-user variability.

Structure	SI auto	SI intrauser
Ventricles	0.75±0.05	0.85 ± 0.05
Caudate nucleus	0.61±0.06	0.75 ± 0.06

These SI values are not far from the intrauser variability (also in Table TABLE II.), which was determined using the 25 images that were reannotated. This variability defines the precision of the ground truth, and it is an intrinsic limit of the performance that an automated system can achieve. In absolute terms, the SI values are relatively low because of the low resolution of DW-MRI and the fact that the caudate is difficult to delineate in T2-weighted MRI, which is the modality of the baseline. For instance, a recent study using a multiatlas approach⁵⁸ reported SI values between 0.66 and 0.83 for the caudate.

DISCUSSION

A spatially variant mixture model for diffusion MRI has been presented in this article. The signal attenuation, which is inherently a mixture due to the coexistence of fiber populations, is modeled as a Gaussian mixture in which the mean vectors and covariance matrices are assumed to be independent of spatial locations, whereas the mixture weights are allowed to vary at different lattice locations. Spatial smoothness of the data is ensured by imposing a Markov random field prior on the mixture weights. The model is trained on clean pseudoground truth data using the expectation maximization algorithm. The number of mixture components is determined using the minimum message length criterion from information theory. The system has the advantage of not having any parameters to tune.

The main application of the model is image denoising: given the noisy data, the denoised image can be computed as the most likely explanation in a Bayesian framework. This poses an optimization problem that can be solved within a reasonable time with coordinate descent. The proposed approach was compared with some of the most popular denoising algorithms in the domain. Even though the presented methodology does not clearly outperform these approaches at typical SNR ratios, it is substantially superior at low SNR thanks to its prior knowledge on the data. This makes it possible to acquire the images using a fast (i.e., noisy) sequence and denoise them to acceptable noise levels. The denoised data were shown to be able to recover the tractography results from the uncorrupted version.

A possible improvement of the methodology would be to denoise the image by maximizing p(x(r)) rather than p(x(r),π(r)) (Sec. 3C). The problem is that the marginalization integral p(x(r))=∫_R^Cp(x(r),π(r))dπ(r) cannot be calculated analytically, so it would require statistical sampling, which is computationally taxing. Moreover, optimizing the joint probability has the advantage that it also provides the optimal mixture weights for each voxel, which can be used as features for subsequent image analysis.

Another possible improvement would be use a robust metric to penalize the differences between neighboring mixture weights. The proposed MRF uses a quadratic penalty corresponding to a Gaussian distribution. This might not be the most suitable approach when there exist discontinuities (e.g., edges) in the data. A possibility would be to use a Laplace distribution or generalization thereof, which penalizes the absolute difference rather than the squared difference.³⁷ This could help reduce the (on the other hand minimal) blurring introduced by the method, which can potentially introduce spurious crossings. However, this would greatly complicate the analysis and the optimization process.

One potential limitation of the model is the lack of a proper ground truth, which is required in the training stage. This is a recurrent problem in DW-MRI. Phantoms consisting of separate fibers embedded in a homogeneous background are commonly used in the literature, but this is not a realistic approximation of the brain white matter. Elaborating more sophisticated phantom remains an open problem (see Refs. ^{59, 60} for some recent efforts). Long image acquisition MRI sequences (24–48 h) can be used to obtain very high SNR data, but they typically require ex-vivo data from deceased subjects to avoid motion artifacts. In this study, the lack of ground truth is circumvented by downsampling the images in the directional domain to obtain relatively clean data.

The proposed algorithm makes two important assumptions about noise. First, that the noise in the baseline T2 data is negligible compared to the noise in the gradient images. And second, that the noise power is known exactly. Both assumptions are however reasonable: due to multiple acquisitions and the lack of attenuation by diffusion, the baseline images have indeed much higher SNR than the gradient images. The noise parameter σ can be accurately estimated as the mode of the background of the image, thanks to the large amount of background voxels that are typically present in a 3D scan.

Regarding the ability to generalize to other datasets, retraining should not be necessary as long as the new data are acquired in the set of directions in the dataset presented here and at the same spatial resolution. If the resolution was different, the class variances could be modified to account for the difference in voxels size. If the gradient directions were different, the data could be resampled to the set of directions used here. Correction for different Le Bihan’s constant is immediate. Evaluating the performance of the algorithm on a different dataset and exploring the impact of these adjustments when necessary remains as future work.

Another interesting aspect is the application of the algorithm to cases displaying pathology. In that case, the learned statistical distributions might not hold anymore. If a certain pathology is expected to be present in the test set, it should be possible to ensure that subjects with that particular disease are present in the training dataset. However, if there is no knowledge on potential conditions present in the test data, a very comprehensive training dataset might be necessary to obtain good results. Evaluating the method in these situations also remains as future work.

Finally, it is important to discuss the execution speed of the algorithm. All the described algorithms were implemented in java and run in an Intel Core i7 desktop. The training stage takes 3 h, which is not a problem because it must be executed only once. Denoising an image takes approximately 25 min. This is longer than the execution time of the other approaches discussed here (Gaussian filtering, NLM, and AD). However, given that the code was not optimized for speed and that java is an interpreted language, it should be possible to reduce the execution time to the order of ~10 min, which is completely acceptable given the dimensionality of the data (i.e., 128 × 128 × 128 voxels × 94 directions∕voxel).