A quality assurance protocol for diffusion tensor imaging using the head phantom from American College of Radiology

Abstract

Purpose: To propose a quality assurance procedure for routine clinical diffusion tensor imaging (DTI) using the widely available American College of Radiology (ACR) head phantom.

Methods: Analysis was performed on the data acquired at 1.5 and 3.0 T on whole body clinical MRI scanners using the ACR phantom and included the following: (1) the signal-to-noise ratio (SNR) at the center and periphery of the phantom, (2) image distortion by EPI readout relative to spin echo imaging, (3) distortion of high-b images relative to the b = 0 image caused by diffusion encoding, and (4) determination of fractional anisotropy (FA) and mean diffusivity (MD) measured with region-of-interest (ROI) and pixel-based approaches. Reproducibility of the measurements was assessed by five repetitions of data acquisition on each scanner.

Results: The SNR at the phantom center was approximately half of that near the periphery at both 1.5 and 3 T. The image distortion by the EPI readout was up to 7 mm at 1.5 T and 10 mm at 3 T. The typical distortion caused by eddy currents from diffusion encoding was on the order of 0.5 mm. The difference between ROI-based and pixel-based MD quantification was 1.4% at 1.5 T and 0.3% at 3 T. The ROI-based MD values were in close agreement (within 2%) with the reference values. The ROI-based FA values were approximately a factor of 10 smaller than pixel-based values and less than 0.01. The measurement reproducibility was sufficient for quality assurance (QA) purposes.

Conclusions: This QA approach is simple to perform and evaluates key aspects of the scanner performance for DTI data acquisition using a widely available phantom.

INTRODUCTION

Diffusion tensor imaging (DTI)¹ is increasingly being used clinically for quantitative assessment of white matter integrity in normal maturation, aging, and disease states^{2, 3, 4, 5, 6} and may be affected by numerous technical factors.⁷ Quantitative results derived from single center and multicenter studies using DTI may be biased by technical issues unrecognized in the absence of a rigorous quality assurance (QA) program. Thus far, such QA procedures are not supported by commercial MR vendors. Although many if not most clinical sites in the United States maintain certification of MR units by American College of Radiology (ACR), the ACR quality control procedure by itself is not adequate to ensure high-quality DTI studies. Many sites use MRI phantoms provided by the manufacturers for DTI QA scans, but the QA phantoms from different vendors vary in size, shape, and chemical content. This makes direct comparison difficult for multicenter studies. Furthermore, these phantoms do not contain internal structures which are extremely valuable for assessing image distortions.^{8, 9} We propose a QA procedure for DTI using the widely available ACR head phantom. It contains both a uniform section ideal for signal-to-noise ratio (SNR), fractional anisotropy (FA), and mean diffusivity (MD) measurements and sections with internal structures which can be exploited for assessing image distortions.

MATERIALS AND METHODS

Image acquisition

The ACR MRI phantom for head coils is available for purchase from J. M. Specialty Parts, Inc. (San Diego, CA). The phantom diameter is 190 mm, the length is 148 mm, and it is filled with a solution of 10 mM NiCl₂ and 75 mM NaCl. The phantom was brought to the scanner room for at least 24 h to reach thermal equilibrium and then placed in the eight channel SENSE head coil as specified by ACR [for a description of the phantom and the standard scanning protocol, see “Site Scanning Instructions for Use of the MR Phantom for the ACR^™ MRI Accreditation Program,” December 2002 (Ref. ³⁴)]. The DTI QA scan protocol consisted of a survey scan, a SENSE reference scan, the standard axial spin echo (SE) T1 scan as specified by ACR (ACR T1 scan), and a DTI scan using a protocol for clinical imaging. Details of the parameters are listed in Table TABLE I.. MRI data were acquired at 1.5 and 3.0 T (Achieva, Philips HealthCare Systems, Cleveland, OH). Scanner room temperature was recorded during the study. To estimate the reproducibility, the entire measurement procedure was carried out five times consecutively at both 1.5 and 3.0 T. Between repetitions, the phantom was removed from the coil and repositioned.

TABLE I.

Image acquisition parameters at 1.5 and 3.0 T. The survey scan and SENSE reference scan were performed first but not included in the table.

Image sequence	1.5 T	3.0 T
Spin echo (ACR axial T1 sequence)	TR/TE = 500/20 msfov = 250 mm, 11 slicesslice thickness = 5 mm, gap = 5 mmacquisition matrix = 256 × 256phase-encoding direction = APbandwidth = 109.3 Hz/pixelNSA = 1SENSE = no	TR/TE = 601/20 msfov = 250 mm, 11 slicesslice thickness = 5 mm, gap = 5 mmacquisition matrix = 256 × 256phase-encoding direction = APbandwidth = 207.8 Hz/pixelNSA = 1SENSE = no
Spin echo DTI with single shot EPI readout (a clinical scan protocol)	TR/TE = 8802/110 ms, b = 1000 s/mm2 Fov = 256 mm, 56 slicesslice thickness = 2 mm, gap = 0 mmacquisition matrix = 128 × 128encoding scheme: Jones30a phase-encoding direction = APfat shift direction = Pbandwidth (phase-encoding direction) = 18.9 Hz/pixelbandwidth (frequency-encoding direction) = 1786.7 Hz/pixelHalfscan factor = 0.806NSA = 1, b = 0 average = 5SENSE reduction (AP) = 2.0clear = yes	TR/TE = 8000/74 ms, b = 1000 s/mm2 Fov = 256 mm, 72 slicesslice thickness = 2 mm, gap = 0 mmreadout acquisition matrix = 128 × 128encoding scheme: Jones30a phase-encoding direction = APfat shift direction = Pbandwidth (phase-encoding direction) = 26.5 Hz/pixelbandwidth (frequency-encoding direction) = 2742.3 Hz/pixelHalfscan factor = 0.889NSA = 1, b = 0 average = 5SENSE reduction (AP) = 2.5clear = yes

^aJones 30 is a gradient-encoding scheme for DTI with 30 encoding directions (see Ref. 13 for details).

Image analysis

The DTI data were registered using vendor proprietary software¹⁰ [Philips Research Imaging Development Environment (pride)] simultaneously applying rotation, translation, shear, and scale corrections to high-b (diffusion weighted) image volumes and aligning them to the b = 0 image volume, thereby correcting small drifts in phantom position that occurred during scanning and removing some eddy current distortions in the high-b-value images without changing the b = 0 image. Image registration is a standard step for DTI processing for all vendors, although software may differ in details. Further analyses focused on the position of slices 5 and 7 (not to be confused with the fifth and seventh slices of DTI) defined in “Phantom Test Guidance.”³⁴ Data analyses were carried out with internally developed software using idl 8.0 (ITT, Boulder, CO) described in the following sections.

Signal-to-noise ratio

Due to the use of the phased array head coil and parallel imaging, the noise level in the image is not uniform, and the noise in the background is not the same as that on the object.¹¹ Consequently, noise levels need to be assessed in multiple areas across the phantom.¹²

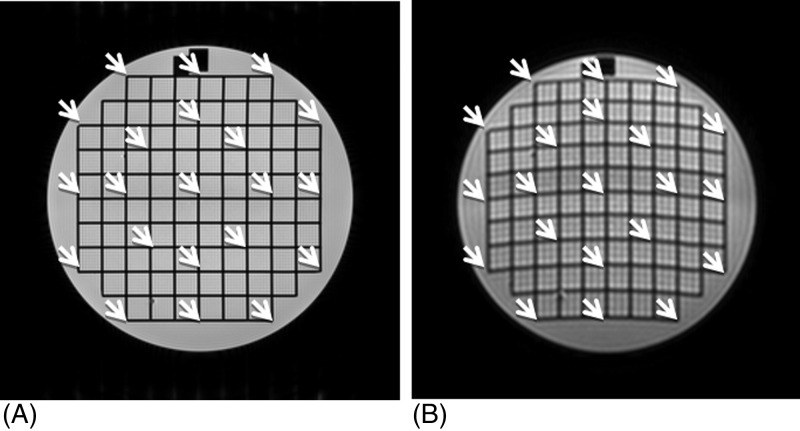
The SNR analysis was performed on the registered data at the location of ACR slice 7, where the phantom is uniform. The noise level was measured from the high-b-value images. The DTI protocol employed the Jones30 scheme,¹³ a commonly used diffusion-encoding scheme with 30 directions determined by applying the theory of electrostatic repulsion forces to obtain “optimal” gradient directions.¹⁴ We divided the 30 registered high-b images into two groups, with each group containing images of 15 encoding directions. The images within each group were summed, and the subtraction of the two group sums was divided by $\sqrt{30}$ to obtain a noise image for one NSA. The SNR of nine circular regions of interest (ROIs), each with a radius of 10 mm, were measured. There was an ROI placed at the center of the phantom and eight periphery ROIs with the same size. The eight periphery ROIs were distributed evenly on the horizontal and vertical axes or at 45° angles, with equal distance of 65 mm from the center of the ROIs to the center of the phantom [Fig. 1A]. For each ROI, the SNR was obtained as average signal in b = 0 image divided by the standard deviation of the noise over the ROI. The SNR for the central ROI and the median and range of the periphery ROIs were reported.

Figure 1.

SNR was quantified from circular ROIs at slice 7. (A) The b = 0 image was used for signal measurement. (B) The noise image was generated from 30 high-b-value DW images as described in the text.

EPI readout geometry distortions

Image distortion in DTI b = 0 image was assessed relative to the ACR SE T1 image at 21 grid points at slice 5 [Fig. 2A]. The ACR SE image of slice 5 and DTI b = 0 image were both displayed on a computer monitor. The operator used a land-marking technique to read the x and y coordinates of the crossing grid points. Both DTI and SE images were interpolated to 512 × 512 matrix size, allowing the grid position to be determined with approximately 0.5 mm step size. The range and median value of the relative displacement along the phase-encoding direction (AP) were obtained.

Figure 2.

Locations of 21 grid points where the relative shift in EPI and SE images was measured at slice 5. (A) T1 weighted SE image. (B) DTI b = 0 image.

Image distortion caused by eddy current induced by diffusion-encoding gradients

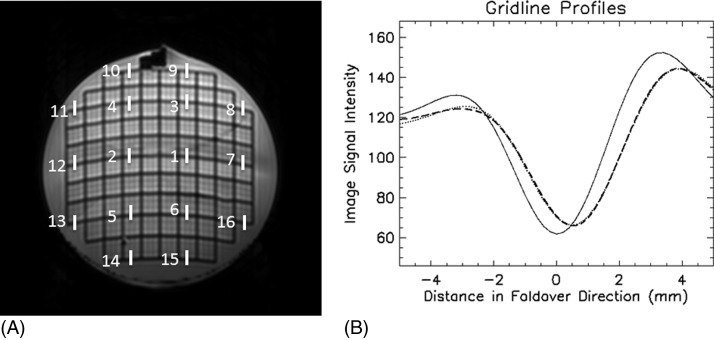
Distortion from eddy currents associated with diffusion-encoding gradients was assessed by quantifying the shift and broadening of the grid line profile along the phase-encoding direction (AP) on the high-b image relative to the b = 0 image at 16 points on gridlines in ACR slice 5 [Fig. 3A]. With one acquisition of the DTI data, SNR on one diffusion weighted image may not be sufficiently high for reliably measuring the gridline profile, especially if the b-value is large, TE is long, and B₀ is 1.5 T. Therefore, for the chosen slice, the DW images for all encoding directions were averaged to enhance the SNR. Furthermore, the AP-profile at each location was obtained by averaging over nine consecutive vertical lines on both b = 0 and high-b images for data at 1.5 T (see ). For each diffusion-encoding step, the gridline position may be shifted on the high-b image relative to the b = 0 image. These distortions may change the center position of the gridline on the averaged high-b profile, broaden the width of the downward valley, and reduce the depth of the valley. We assume the shift in gridline position due to encoding gradient can be modeled by a Gaussian distribution, and the averaged high-b profile is the b = 0 profile convoluted by this Gaussian distribution:

$$F_b^{\mathit{av}}(y)=A\int F_0(y-y\prime )·\text{exp}\left(\frac{-(y\prime -y_b){}^2}{2{\sigma }^2}\right)\mathit{dy}\prime$$ (1)

where A is a proportional constant, $F_b^{\mathit{av}}$ is the profile of the gridline along phase-encoding direction (we use y for this direction although different vendors may have different conventions) on the averaged high-b image, F₀ is the gridline profile along y on the b = 0 image, y_b is the average shift of the gridline position, and σ is standard deviation of the Gaussian distribution. The parameters, A, y_b, and σ, in the above equation are determined by a nonlinear least squares curve fit routine. The center position y_b and the standard deviation σ of the Gaussian were quantified at the 16 locations shown in Fig. 3A. The DTI data before and after registration were both analyzed. The median and range of y_b and σ were reported.

Figure 3.

Evaluation of distortion by diffusion-encoding gradient at 3 T. (A) The segments indicate the locations where the gridline profile was compared between the B₀ and average of high-b-value images. (B) The grid profile for a segment in (A). The solid line was the gridline profile on b = 0 image, the dashed line was the profile of the averaged high-b images, and dotted line was fit by Eq. (1). The intensity of the high-b-value profile was multiplied by 7.5.

FA and MD measurements

Using registered DTI data, FA and MD measurements were done at the ACR slice 7. Because the solution contained in the phantom is isotropic, the true FA value is zero. The diffusivity of water is also known as a function of temperature.¹⁵ These measurements assess the bias and uncertainty in the measured FA and MD. Image data inside a circular ROI at the center of the phantom with a radius 70 mm was used for analysis.

Both pixel-based and ROI-based FA and MD measurements were done. The pixel-based measurements mainly demonstrate the effects of random noise on the pixel-wise FA and MD values. The ROI-based measurements are more sensitive for testing systematic bias caused by factors not related to randomness of noise. For example, a small miscalibration of diffusion-encoding gradients may be revealed by increased FA or altered MD value in the ROI-based tests.

In pixel-based measurement, the FA and MD values of each pixel inside the circular ROI in the image slice were obtained. The mean and standard deviation of pixel-wise FA and MD were reported. In the ROI-based measurements, the average signal intensity within the circular ROI for the b = 0 image and each diffusion weighted high-b image was measured first. Using these values, a diffusion tensor was calculated, and FA and MD values were obtained. The reference MD value was extracted from Table TABLE I. of Holz et al.¹⁵ by a second order polynomial interpolation. The experimental error of the reference MD values is less than 1%.¹⁵

Reproducibility assessment

The average value and standard deviation (SD) of the five scans were obtained for each measurement location. The SD averaged over all locations was reported as the uncertainty or error bar of the measurement.

The radio frequency heating¹⁶ will increase the phantom temperature and the MD value; therefore, the SD of repeated MD measurement does not reflect the true uncertainty of each MD measurement. To estimate the uncertainty of MD measurement, the MD values over repeated scans were fitted by linear regression. The standard error of the linear fit is considered as the uncertainty of individual MD measurement. The intercept to the first measurement was reported as “average” MD value corresponding to the scanner room temperature.

RESULTS

Figure 1B shows the noise image of diffusion weighted images obtained at 1.5 T. Figure 2 shows both the SE image and DTI b = 0 image at slice 5, and the distortion in Fig. 2B is typical of EPI images. The horizontal curves will bend in the opposite direction if the fat shift direction is changed from P to A (not shown). Figure 3B shows the AP-profile of one segment in Fig. 3A for both b = 0 and averaged high-b image, together with the results of fitting by Eq. (1) at 3.0 T.

The results of testing on the two scanners are summarized in Table TABLE II.. The SNR measurements showed a large variability from the center to peripheries of the image slice at both 1.5 and 3 T. The uncertainty of SNR measurement was approximately 10% at the center and 7%–9% at peripheries at 1.5 T. This became 4% at the center and 11%–15% at peripheries at 3.0 T. The median value of image distortion on the DTI b = 0 image was 5 mm at 1.5 and 7 mm at 3 T, with measurement uncertainty of 0.4 and 0.6 mm, respectively. Gridline shifts caused by diffusion-encoding gradients were characterized by a mean (y_b) and SD (σ) of the shift distribution for all encoding directions before and after image registration. The median and range of these distribution parameters for locations in Fig. 3A are listed in Table TABLE II.. Imaging registration decreased the y_b values at both 1.5 and 3 T. The SD of the shift distribution σ decreased after image registration at 1.5 T but increased at 3 T. The uncertainty of y_b measurements was no more than 4% of the imaging acquisition pixel size, and the uncertainty of σ was below 7% of the pixel size. The average value derived from pixel-based FA was below 0.1 and 0.05 at 1.5 and 3 T, respectively. The ROI-based FA was less than 0.01 at both 1.5 and 3.0 T. The uncertainties of these FA measurements were on the order of 0.001. The difference between ROI-based and pixel-based MD quantification was 1.4% at 1.5 T and 0.3% at 3 T. The ROI-based MD values were in close agreement with the reference values (0.5% and 2.0% differences at 1.5 and 3.0 T). The uncertainty of MD quantifications was 0.05%–0.1% of the measured values.

TABLE II.

Measurement results in two MRI scanners. Values are average of five repetitions.

	1.5 T scanner	3.0 T scanner
SNR
Phantom center	20.7	60.2
Uncertainty	2.1	2.5
Phantom periphery
Median (minimum, maximum)	37.9 (34.0, 42.0)	106.7 (87.2, 125.7)
Uncertainty	3.0	13.3
EPI readout distortion along phase-encoding direction (mm)
Median (minimum, maximum)	−4.6 (−6.9, −0.4)	−7.1 (−10.0, −0.5)
Uncertainty	0.4	0.6
Image distortion from diffusion-encoding gradient in  phase-encoding direction (mm)
Median (minimum, maximum)
yb, before registration	0.06 (0.01, 0.16)	0.09 (−0.20, 0.41)
σ, before registration	0.49 (0.27, 0.77)	0.40 (0.08, 0.69)
yb, after registration	0.04 (−0.04, 0.11)	0.00 (−0.20, 0.11)
σ, after registration	0.58 (0.41, 0.81)	0.33 (0.08, 0.53)
uncertainty of yb	0.08	0.06
uncertainty of σ	0.13	0.13
FA
Pixel-based, mean ± SD	0.098 ± 0.037	0.044 ± 0.017
Uncertainties in mean ± SD	0.001 ± 0.001	0.001 ± 0.001
ROI-based	0.0083	0.0098
Uncertainty	0.0008	0.0007
MD (10−3 mm2/s)
Pixel-based, mean ± SD	2.025 ± 0.065a	2.038 ± 0.039b
Uncertainties in mean ± SD	0.001 ± 0.002	0.001 ± 0.002
ROI-based	1.998	2.033
Uncertainty	0.001	0.002

^aTemperature = 19.3 °C, reference MD value 1.988 × 10⁻³ mm²/s.

^bTemperature = 19.4 °C, reference MD value 1.993 × 10⁻³ mm²/s.

DISCUSSION

The need for specific DTI QA scan

DTI is technically demanding, requiring magnet stability, excellent B₀ homogeneity and eddy current compensation, and adequate SNR to achieve reliable diffusion tensor quantification. The ACR quality control measures are necessary but not sufficient for acquiring high-quality DTI data. For example, a miscalibration of enhanced gradient, which is mainly used for diffusion encoding for Philips scanners, does not affect routine imaging but may affect both FA and diffusivity in DTI. Many centers are therefore moving to QA protocols specific for DTI.

Considerations on action criteria based on the phantom DTI QA scan

After the QA results are obtained, on what criteria is scanner performance deemed to be acceptable? The establishment action criteria, or the standards for minimally acceptable scanner performance, may be based on many practical considerations and should also depend on the specific aims of the study or examination. One utility of a QA procedure is to track the scanner performances over a long period of time. For this purpose, a site may perform the QA procedure over a period of time when the DTI image quality are satisfactory and determine the range of acceptable variations. When a measured parameter is beyond 2 or 3 SD from the average value, service will be required.¹⁷ In addition, the measurement results from the QA scan could also be used to help determine whether the scanner performance is sufficient for specific tasks. Some considerations are discussed in the following.

SNR considerations

In DTI studies, acquiring images with high SNR is very important. It has been shown that high noise level will introduce uncertainty and bias in the measurement of FA, and fiber tracking is also less reliable.^{18, 19, 20} Therefore, SNR assessment is always an important component of QA for DTI scans.

In this study, the QA data was collected when the scanner was performing normally. Based on our experience, a 20% decrease in the SNR will not substantially impact the image quality. However, a 50% decrease is associated with very grainy images. A 30% decrease in SNR should prompt corrective intervention by service engineers.

This QA approach is based on scanning the phantom using clinical DTI protocol. With different vendors and the different protocols in use, the acceptable minimum SNR at the center and peripheries will need to be established based on the scanning protocol for site specific DTI QA. If the minimum SNR for human studies can be specified based on requirement of accuracy and precision needed for the study, the phantom scan SNR requirement can be calibrated against human subjects for establishing the minimum SNR required for the QA test.

In a multicenter study, a standard scanning protocol may be used by all participating sites. The central site may specify the SNR requirement for sites with similar scanners based on the local experience.

Distortion of EPI relative to SE images

Routine brain DTI scans employ single-shot EPI readout and is susceptible to susceptibility artifacts. The distortion depends on the homogeneity of the B₀ field, also depends on the acquisition parameters including acceleration factor in parallel imaging, receiver bandwidth, phase-encoding direction and fat shift directions, etc. The distortion is mainly along the phase-encoding direction. These distortions cause misregistration between DTI and anatomical images and are undesirable. Efforts have been made to correct these distortions using B₀ maps.^{21, 22, 23, 24} Although these distortions are unavoidable due to intrinsic properties of the head, they should be consistent in both cross-sectional and longitudinal studies. If automated image analysis method such as Tract Based Spatial Statistics²⁵ is used for voxel-wise whole brain analysis of all subjects, inconsistent fat shift direction may increase the difficulty for aligning the brain structures and increase the nonlinear transform displacement. Inconsistency in the fat shift direction is obvious on the phantom image.

Since the image distortion on b = 0 images is related to the sensitivity of EPI readout to susceptibility effects, this test contains information similar to that in B₀ mapping. With the DTI parameters in Table TABLE I., a 5 mm pixel shift in the EPI phase-encoding direction corresponds to 0.5 ppm B₀ field at 3 T and 0.7 ppm at 1.5 T. Consequently, the action criteria for EPI distortion need to be established in conjunction with practically achievable B₀ homogeneity within the image volume.

Distortion caused by eddy current induced by diffusion-encoding gradients

In DTI, the need to minimizing distortion due to eddy current is well appreciated. The eddy current distortions for different diffusion-encoding directions are different, introducing relative image misregistration of brain structures. For uniform phantoms, this effect only manifests itself on the edge of the phantom through the width of the annulus. Using slice 5 of the ACR phantom, the relative distortion can be assessed throughout the object at both the center and periphery areas. Our results showed the image registration decreased y_b, the average position shift of the gridline. However, it is not effective for decreasing σ, the variation of the shifts (Table TABLE II.). This underlines the need for regular preventative maintenance in order to minimize the eddy current effects.

Ideally, the pixel shift of high-b images relative to the b = 0 image caused by the diffusion-encoding gradient should be much smaller than the acquisition pixel size. For our two scanners in Table TABLE II., the standard deviation of the gridline shift distribution is typically on the order of several tenths of 1 mm, and the mean of gridline shift is typically about 0.1 mm. Hence, the size of a typical relative pixel shift is a substantial fraction of a 2 mm acquisition pixel and cannot be neglected. This distortion mainly affects thin fibers running along the EPI readout direction but have little effects on structures along the phase-encoding direction. Further studies correlating image quality and the size of distortion measured by the QA test may be needed. With current technology, it may not be practical to reduce this distortion to much less than reported here.

Deviation of FA from zero

Higher mean FA from pixel-based measurement is associated with deterioration of SNR. The ROI-based FA should be close to zero because the effects of random noise have been averaged out. If the encoding gradient along one direction is miscalibrated, the effects should be readily detectable from ROI-based FA value. Technically, keeping ROI-based FA value near or below 1% should not be difficult. However, our experience is only limited to scanners from one vendor presently.

Deviation of MD from the reference value

Mean diffusivity is an important index for characterizing pathology. Two factors may cause the measured MD value to deviate from the reference value, i.e., bias in MD caused by low SNR and deviation of the actual b-value from the nominal value. Acceptable MD values need to be established after the encoding gradient is carefully calibrated and when the SNR is at an acceptable value. Measurement at a lower b-value (e.g., b = 700 s/mm²) may help to check agreement between the actual and nominal b-values with smaller bias caused by low SNR. Technically, it should not be difficult to keep the deviation of the average actual b-value from the nominal value within 1%.

Practical aspects

The ACR head phantom is widely available in clinical settings for accreditation and routine QA purposes as required by ACR. The built-in structures in the phantom effectively dampen the flow inside after handling and positioning on the MR table. This QA protocol requires collecting one DTI and one SE data set in typically 8 min. This short data acquisition time is easy to accommodate for routine use. This QA procedure evaluates key aspects of scanner performance that are directly relevant to DTI data quality. Further analysis may be added to what have been demonstrated here. For example, ghosting analysis can be done for both b = 0 and high-b images. Other scans, such as an EPI stability and interference tests,²⁶ may be added to the protocol using the ACR phantom. Although we employ the Jones30¹³ encoding scheme, the method should be applicable for other schemes as well.

The DTI phantom image may have some SENSE artifacts, as can be seem in Fig. 3A. These artifacts arise because the reconstruction algorithm is optimized for human studies and may not be optimal for the ACR phantom. In our case, the artifacts are not present in human scans and have no impact for clinical studies. The artifacts do not seem to interfere with the analysis of the QA data.

Note that the TE of the DTI pulse sequence at our 3.0 T scanner is substantially shorter than that at 1.5 T, due to the availability of “enhanced gradient” for diffusion encoding. Enhanced gradient is an optional upgrade for Philips scanners which doubles the gradient strength, thus shortening the diffusion-encoding time and TE of the pulse sequence.

Limitations

The phantom used for DTI QA ideally should have built-in anisotropy. Much work has been devoted to design and construct such phantoms.^{27, 28, 29, 30, 31} However, such phantoms have not been available for routine use. Another limitation is that the diffusivity of the ACR head phantom is higher than that of human brain tissues. Phantoms with diffusivity closer to human brain have also been described,³² but these lack internal structures and are not readily available. These deficiencies may be overcome by including periodic scanning of human volunteers as part of a quality assurance procedure.³³

CONCLUSION

A QA approach is demonstrated to address key issues in DTI data quality using the ACR MRI head phantom. This procedure may be used for routine DTI quality assurance for both single center and multicenter studies.

APPENDIX: signal averaging for the gridline profile

The SNR of high-b images are lower at 1.5 T than at 3.0 T. Therefore, in the analysis of Sec. 2B3, additional signal averaging was done at 1.5 T for obtaining the gridline profile along the phase-encoding (y) direction. Nine adjacent y-profiles were averaged. Before taking the average, the lines were sinc-interpolated to a resolution of 0.1 mm and were aligned to yield a minimum valley on the b = 0 profile. The same alignment was applied to high-b image profile with the parameters determined from the b = 0 image. The resulting b = 0 and average high-b profiles were used in Eq. (1) to calculate the mean shift y_b and the standard deviation σ.