Perfusion systems that minimize vascular volume fraction in engineered tissues

Abstract

This study determines the optimal vascular designs for perfusing engineered tissues. Here, “optimal” describes a geometry that minimizes vascular volume fraction (the fractional volume of a tissue that is occupied by vessels) while maintaining oxygen concentration above a set threshold throughout the tissue. Computational modeling showed that optimal geometries depended on parameters that affected vascular fluid transport and oxygen consumption. Approximate analytical expressions predicted optima that agreed well with the results of modeling. Our results suggest one basis for comparing the effectiveness of designs for microvascular tissue engineering.

INTRODUCTION

Above a certain thickness and cellularity, engineered tissues require vascular networks to provide oxygen and nutrients for survival.¹ To date, studies of vascularization have focused primarily on the biochemical aspects of the process (e.g., how the release of growth factors promotes angiogenesis^{2, 3}). Assessment of the resulting vascular networks is morphological (e.g., by measuring capillary density^{4, 5, 6}) or functional (e.g., by measuring viability or gross perfusion of the surrounding tissue⁶). Little is known about whether these engineered vascular networks are optimal for perfusion. Given that recent methods^{7, 8, 9, 10, 11} have opened the possibility of precisely controlling the size and geometry of vessels within a scaffold, it would be helpful to understand which vascular arrangements are better than others and why.

Studies of optimality in vascular design have typically considered two classes of performance characteristics: those that involve fluid transport (e.g., pumping power¹²) and those that involve solute transport (e.g., oxygen extraction efficiency¹³). For instance, minimizing the metabolic cost of pumping blood while holding the total flow rate constant leads to Murray’s law, which relates the radii and angles at a bifurcation.^{14, 15} Related work in the design of hollow-fiber bioreactors has also examined similar parameters.¹⁶ Often, the design objective in these devices is to maximize the number of cells per reactor under the constraint of a given perfusion pressure or flow profile.¹⁷

Previous work by Baskaran and colleagues used computational methods to maximize the surface area of the vasculature in a model scaffold while holding the total vascular volume constant.¹⁸ This study effectively treated the oxygen transport rate to the surrounding scaffold as diffusion-limited and thus proportional to vascular area. Optimization yielded vascular lengths, widths, and spacings for networks of a given number of branching generations. The authors intended for their results to inform how best to design vascular networks for engineered tissues.

In the current study, we use a different metric—the fraction of the total volume that is occupied by vessels or the vascular volume fraction—for optimization of perfusion. Unlike Baskaran et al., we did not hold the vascular volume fraction constant, and we included the effect of convective transport of oxygen. We required that any region of an engineered tissue be maintained at or above a threshold oxygen concentration, and assumed that a maximum pressure head is available to drive perfusion. Given this constraint, we used computational models to isolate the vascular designs that minimize vascular volume fraction.

This study has four main objectives. First, this work determines the size scale of the optimal designs. In particular, we want to know whether the optimal designs fall within a size range that is achievable experimentally. Second, this work determines how sharp the optima are (i.e., how flexible the optimal designs are). Third, this work determines how various changes in the perfusion parameters or material properties affect the optimal design. The parameters that are considered are the available perfusion pressure, the oxygen consumption rate per volume, the thickness and hydraulic conductivity of the scaffold, and the viscosity and oxygen solubility of the perfusate. Fourth, this work provides analytical approximations that may simplify the elucidation of optimal designs, and compares the predictions of these formulas with the results of computational modeling.

For simplicity, this study only considers hexagonal arrays of parallel vessels (the standard Krogh geometry¹⁹). In this configuration, the vascular volume fraction is a function of the vessel diameter and the spacing between vessels only.

THEORY AND NUMERICAL METHODS

Features of model constructs

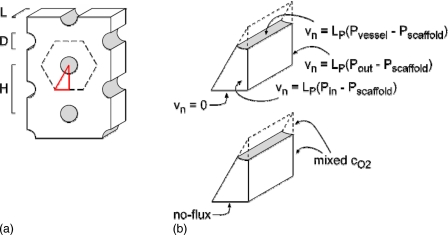
Each model represented a scaffold of thickness L, which contained a hexagonal array of open, parallel channels. All surfaces—those of the channels as well as the outer surfaces of the scaffold—were assumed to be covered by endothelium; such configurations can be realized experimentally.⁷ Endothelialized channels (“vessels”) had identical diameters D and were separated by a center-to-center distance H [Fig. 1a]. Scaffolds were assumed to contain a homogeneous distribution of oxygen-consuming cells.

Figure 1.

Schematic diagrams of (a) the model construct and (b) the computational domain. (a) The construct of thickness L contained vessels of diameter D and spacing H. Dashed black lines indicate planes of symmetry and red lines denote the computational domain. (b) The domain consisted of a wedge with indicated boundary conditions.

Governing equations

Fluid flow in the scaffold and vessels was coupled by filtration across the endothelium. Flow in the scaffold obeyed Darcy’s law,

$${\mathbf{v}}_{\text{scaffold}}=-K\nabla P_{\text{scaffold}},$$ (1)

where v_scaffold is the interstitial fluid velocity, K is the hydraulic conductivity of the scaffold, and P_scaffold is the interstitial fluid pressure. As in previous work,²⁰ we assumed that K was independent of interstitial pressure. Flow in the vascular lumen obeyed the Navier–Stokes equation,

$$\rho \left({\mathbf{v}}_{\text{vessel}}\cdot \nabla \right){\mathbf{v}}_{\text{vessel}}=\eta {\nabla }^2{\mathbf{v}}_{\text{vessel}}-\nabla P_{\text{vessel}},$$ (2)

where ρ is the density of perfusate, v_vessel is the vascular fluid velocity, η is the viscosity of perfusate, and P_vessel is the vascular pressure. Intra- and extravascular flows were coupled by Starling’s law of filtration,²¹

$$v_n=L_P\left(P_{\text{vessel}}-P_{\text{scaffold}}\right),$$ (3)

where v_n is the filtration velocity normal to the vessel wall and L_P is the endothelial hydraulic conductivity. We modeled perfusion with a protein-free medium or particulate suspension. Oncotic forces were not included in the analysis, and changes in viscosity of perfusate were assumed not to affect the viscosity of interstitial fluid.

These fluid flows resulted in convective transport of oxygen, which interacted with diffusive transport in both scaffold and vessels and with oxygen consumption in the scaffold. In the scaffold, oxygen concentrations satisfied the reaction-convection-diffusion equation,

$${\mathbf{v}}_{\text{scaffold}}\cdot \nabla c_{\text{scaffold}}=D_{\text{O}2}{\nabla }^2{c}_{\text{scaffold}}-q_{\text{O}2}.$$ (4)

Here, c_scaffold is the oxygen concentration in the scaffold, D_O2 is the oxygen diffusivity, and q_O2 is the oxygen consumption rate per volume. In the vessel lumen, the reaction term was absent,

$${\mathbf{v}}_{\text{vessel}}\cdot \nabla c_{\text{vessel}}=D_{\text{O}2}{\nabla }^2{c}_{\text{vessel}},$$ (5)

where c_vessel is the oxygen concentration in the vessel. At the vessel wall, oxygen fluxes were equated,

$$c_{\text{vessel}}{\mathbf{v}}_{\text{vessel}}-D_{\text{O}2}\nabla c_{\text{vessel}}=c_{\text{scaffold}}{\mathbf{v}}_{\text{scaffold}}-D_{\text{O}2}\nabla c_{\text{scaffold}},$$ (6)

and the partial pressures of oxygen were equated,

$$c_{\text{vessel}}=\frac{k_{\text{O}2}}{k_{\text{O}2}^{\ast }}{c}_{\text{scaffold}},$$ (7)

where k_O2 and k_O2^∗ are the oxygen solubilities in the perfusate and interstitial fluid, respectively.

We set the pressure difference between the inlet side (z=0) and the outlet side (z=L) of the tissue to be ΔP, and the oxygen partial pressure at the inlet to be 150 mm  Hg. At the outlet side of the tissue, we applied a flow-averaged concentration, as in previous work by Vunjak-Novakovic and colleagues;²² such a configuration describes a setup in which the perfusate and interstitial fluid are well-mixed after they exit the vessels and scaffold. The oxygen solubility in the scaffold was taken to be 1.2 nmol∕cm³ mm Hg; the endothelial hydraulic conductivity, 10⁻¹⁰ cm³∕dyn s (Ref. ²³). Given the extensive symmetry planes of the model geometry, we reduced the computational domain to a wedge, in which no-flux boundary conditions were applied to the bounding planes of symmetry [Fig. 1b].

Computational optimization of vascular design

Table 1 indicates the ranges examined for the six parameters of interest (driving pressure difference ΔP, perfusate viscosity η, scaffold thickness L, scaffold hydraulic conductivity K, oxygen consumption rate q_O2, and perfusate oxygen solubility k_O2). For each set of values (ΔP,η,L,K,q_O2,k_O2), we determined the optimal design for perfusion by first selecting an initial guess for the optimal vascular diameter D and spacing H, and solving for the minimum oxygen concentration c_min in the scaffold.

Table 1.

Design parameters and their values.

Parameter	Definition	Values
ΔP	Perfusion pressure difference	4–50 cm H2O
η	Viscosity of perfusate	0.7–4 cP
L	Thickness of scaffold	1–5 cm
K	Scaffold hydraulic conductivity	10−12,10−10,10−8 cm4∕dyn s
qO2	Oxygen consumption rate in scaffold	10−9−10−7 mol∕cm3 s
kO2	Oxygen solubility of perfusate	1.2×10−9−2.7×10−8 mol∕cm3 mm Hg
Constants
LP	Vascular hydraulic conductivity	10−10 cm3∕dyn s
DO2	Oxygen diffusion coefficient	3×10−5 cm2∕s
kO2∗	Oxygen solubility of interstitial fluid	1.2×10−9 mol∕cm3 mm Hg
ρ	Density of perfusate	1 g∕cm3

The value of c_min was obtained by solving Eqs. 1, 2, 3, 4, 5, 6, 7 with finite-element method software (COMSOL MULTIPHYSICS 3.5A; Comsol, Inc.) and the PARDISO algorithm. For models of greater than ∼1.5×10⁶ degrees of freedom, we first solved Eqs. 1, 2, 3 and then used the resulting flow profile to solve Eqs. 4, 5, 6, 7. Models ranged up to 4.7×10⁶ degrees of freedom; the largest models required overnight solution on parallel-processing workstations (Whitaker Computational Facility, Department of Biomedical Engineering, Boston University).

Once we obtained c_min for a trial vascular geometry (D,H), we increased H while holding D constant, until c_min was within 5×10⁻¹² mol∕cm³ of the desired critical oxygen concentration of 4.56×10⁻⁸ mol∕cm³ (equivalent to 5% O₂). We then scaled D and H in steps of 1.001× while holding their ratio constant, until c_min reached a maximum. The overall effect of this two-step procedure was to decrease vascular volume fraction while maintaining c_min at or above the threshold value. We then repeated both steps until c_min converged to a value between 4.5595×10⁻⁸ and 4.5605×10⁻⁸ mol∕cm³. This search strategy yielded an optimized (D,H) for each set of (ΔP,η,L,K,q_O2,k_O2); obtaining one optimum typically required solving ∼20 models. Vascular volume fraction was calculated as $\pi D^2∕2\sqrt{3}{H}^2$.

To check the mesh independence of the optimal (D,H), we found optima using meshes that were formed using two different sets of meshing parameters that yielded at least a twofold difference in degrees of freedom. If the two optimal values of D for the pair of mesh types differed by <0.1 μm, and if the two optimal values of H differed by <0.5 μm, then we considered the result to be independent of mesh fineness. All plots display optima obtained with the finer meshes.

RESULTS

Basic features

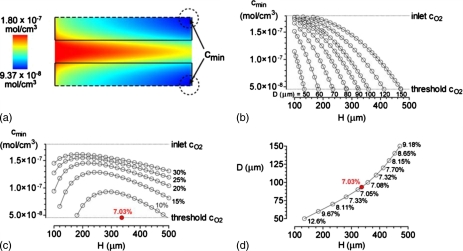
All models showed that oxygen concentration reached a minimum value c_min near the “lethal corner,” the location furthest from the inlet and vessel wall [Fig. 2a]. Because we treated the space adjacent to the downstream side of the scaffold as a well-mixed compartment, the point of minimum concentration resided slightly away (typically ∼0.5 mm) from the corner.

Figure 2.

Optimization for the case of ΔP=20 cm H₂O, η=0.7 cP, L=2 cm, K=10⁻¹⁰ cm⁴∕dyn s, q_O2=10⁻⁸ mol∕cm³ s, and k_O2=1.2×10⁻⁹ mol∕cm³ mm Hg. (a) Color map of oxygen concentration for D=100 μm and H=300 μm. The minimum oxygen concentration c_min in this model is 9.37×10⁻⁸ mol∕cm³. Flow is from left to right. (b) Plots of c_min vs vascular spacing H for various vascular diameters D. (c) Plots of c_min vs H for various vascular volume fractions. (d) Plot of D vs H for models in which c_min=4.56×10⁻⁸ mol∕cm³. Vascular volume fractions are noted as percentages. The optimal D and H (red dots) are 93.6 and 336.2 μm, respectively.

As expected, increasing the vascular spacing H while holding vascular diameter D constant led to decreased c_min [Fig. 2b]. Likewise, decreasing D while holding H constant decreased c_min. These two trends implied that attempting to decrease the vascular volume fraction by decreasing vascular diameter and∕or by increasing vascular spacing would eventually cause oxygen concentration to decrease below the set threshold (4.56×10⁻⁸ mol∕cm³) somewhere in the scaffold. Holding vascular volume fraction constant while changing the scale of the geometry led to decreased oxygen concentrations both at small and large scales [Fig. 2c]. Hence, an optimal design exists that minimizes vascular volume fraction while maintaining all oxygen concentrations above threshold [Fig. 2d, red dot].

Effect of parameters that affect fluid transport on optimal design

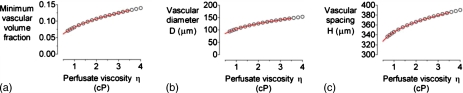
Increasing the perfusing pressure difference ΔP shifted the optimal design to smaller vascular volume fractions [Fig. 3a]. The resulting changes in optimal D and H were nearly identical [Figs. 3b, 3c]. Even at the highest value examined (50 cm H₂O), however, vascular volume fraction was still nearly 5%. Conversely, increasing the viscosity of perfusate η led to larger optimal vascular volume fractions [Fig. 4a]. Again, changes in optimal D and H were well-matched [Figs. 4b, 4c].

Figure 3.

(a) Plot of minimum vascular volume fraction vs axial pressure difference ΔP. [(b) and (c)] Plots of vascular diameter D and spacing H vs ΔP for the optimized models in (a). For all models, η=0.7 cP, L=2 cm,K=10⁻¹⁰ cm⁴∕dyn s, q_O2=10⁻⁸ mol∕cm³ s, and k_O2=1.2×10⁻⁹ mol∕cm³ mm Hg.

Figure 4.

(a) Plot of minimum vascular volume fraction vs perfusate viscosity η. [(b) and (c)] Plots of vascular diameter D and spacing H vs η for the optimized models in (a). For all models, ΔP=20 cm H₂O, L=2 cm, K=10⁻¹⁰ cm⁴∕dyn s, q_O2=10⁻⁸ mol∕cm³ s, and k_O2=1.2×10⁻⁹ mol∕cm³ mm Hg. Red curves denote data from Fig. 3 in which η is scaled by 20 cm H₂O∕ΔP.

These results suggested that changes in vascular flow rate, rather than in ΔP or η per se, were responsible for changes in optimal design. Indeed, scaling viscosity by 1∕ΔP led to near-superimposed plots (Fig. 4, red curves). For vascular flow rate to exert a dominant role in oxygen profile, interstitial flow must play a correspondingly minor role. Changes in scaffold hydraulic conductivity K over four orders-of-magnitude caused insignificant changes in optimal design: for K=10⁻¹² and 10⁻⁸ cm⁴∕dyn s, the optimal (D,H) were (93.6 μm, 336.2 μm) and (93.6 μm, 336.1 μm), respectively. These data confirmed that interstitial flows can be largely neglected.

Increasing scaffold thickness L induced changes in optimal design that were qualitatively similar to those of increasing perfusate viscosity (Fig. 5). We found, however, that these changes could not be entirely accounted for by changes in vascular flow rate. A doubling of scaffold thickness from 2 to 4 cm led to an increase of optimal vascular volume fraction, diameter, and spacing to 12%, 139 μm, and 377 μm, respectively. A doubling of viscosity from 0.7 to 1.4 cP yielded a smaller increase in the corresponding parameters to 9%, 114 μm, and 355 μm, respectively. Scaling of L by η∕ΔP isolated the residual effect that could be attributed to geometric, rather than flow-based, changes (Fig. 5, red curves).

Figure 5.

(a) Plot of minimum vascular volume fraction vs scaffold thickness L. [(b) and (c)] Plots of vascular diameter D and spacing H vs L for the optimized models in (a). For all models, ΔP=20 cm H₂O, η=0.7 cP, K=10⁻¹⁰ cm⁴∕dyn s, q_O2=10⁻⁸ mol∕cm³ s, and k_O2=1.2×10⁻⁹ mol∕cm³ mm Hg. Red curves denote data from Figs. 34 in which L is scaled by (η∕0.7 cP)×(20 cm H₂O∕ΔP).

Effect of parameters that affect oxygen consumption on optimal design

Increasing the oxygen consumption rate q_O2 led to large changes in optimal design (Fig. 6). An order-of-magnitude increase from 10⁻⁸ to 10⁻⁷ mol∕cm³ s, a value appropriate for highly metabolically active tissues like engineered liver,²⁴ resulted in an optimal vascular volume fraction of nearly 40%. An order-of-magnitude decrease in q_O2 to 10⁻⁹ mol∕cm³ s, on the other hand, led to <1% optimal volume fraction and vascular spacings in excess of 0.7 mm.

Figure 6.

(a) Plot of minimum vascular volume fraction vs oxygen consumption rate q_O2. [(b) and (c)] Plots of vascular diameter D and spacing H vs q_O2 for the optimized models in (a). For all models, ΔP=20 cm H₂O, η=0.7 cP,L=2 cm, K=10⁻¹⁰ cm⁴∕dyn s, and k_O2=1.2×10⁻⁹ mol∕cm³ mm Hg.

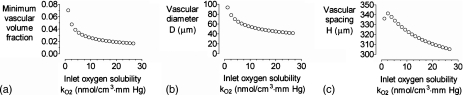
Increasing the perfusate oxygen solubility k_O2 mostly resulted in decreases in optimal vascular volume fraction, diameter, and spacing (Fig. 7). We found a nonmonotonic dependence of vascular spacing on k_O2 near k_O2=1.2×10⁻⁹ mol∕cm³ mm Hg. The origin of this behavior is not entirely clear, but small increases in oxygen solubility near this value may lead to such an improvement in oxygenation that the optimal spacing increases.

Figure 7.

(a) Plot of minimum vascular volume fraction vs inlet oxygen solubility k_O2. [(b) and (c)] Plots of vascular diameter D and spacing H vs k_O2 for the optimized models in (a). For all models, ΔP=20 cm H₂O, L=0.7 cP,L=2 cm, K=10⁻¹⁰ cm⁴∕dyn s, and q_O2=10⁻⁸ mol∕cm³ s.

DISCUSSION

Main findings

This computational study shows that, under a constraint of a given pressure difference for perfusion, an optimal vascular diameter and spacing exist that minimizes the vascular volume fraction. Changes that caused an increase in optimal vascular volume fraction were accompanied by an increase in optimal diameter and, in most cases, by an increase in vascular spacing. Increases in tissue oxygen consumption rate, however, caused vascular spacing to decrease while vascular volume fraction and diameter increased.

Implications for vascular design

The optimal vascular volume fractions ranged from ∼1% to nearly 40%. Even for our standard case, which was chosen to represent a scaffold of moderate oxygen consumption and thickness, the optimal fraction was 7%. This value is greater than the 1%–5% vascular volume fractions observed in vivo for many tissues.^{25, 26, 27} Thus, whether optimal designs based on a parallel array of vessels are appropriate for an engineered tissue will depend on how the magnitude of the vascular fraction affects the design objective. For instance, having a large fraction of a tissue consist of open vessels may compromise the mechanical stability of the tissue. At the same time, one should keep in mind that most of our models considered perfusates with an oxygen solubility of 1.2×10⁻⁹ mol∕cm³ mm Hg (representative of culture media²⁸); perfusates with greater oxygen carrying capacities (e.g., perfluorocarbons²⁹) enabled smaller optimal vascular volume fractions (Fig. 7).

The optimal diameters and spacings fell in ranges of 50–150 μm and hundreds of micrometers, respectively. Such scales are well within the reach of current experimental techniques for microfabrication in scaffolds,³⁰ and imply that the ability to attain capillary-sized vessels (5–10 μm in diameter) may not be required in engineered tissues for efficient perfusion. Moreover, we found that the optima are relatively broad, in that simultaneous changes in diameter and spacing up to ∼20% did not greatly affect the minimum oxygen concentration in the scaffold [Fig. 2d]. Thus, the experimentalist should have a fair amount of latitude in realizing (nearly) optimal vascular systems for perfusion.

To illustrate the application of these ideas, we analyzed the geometry studied by Vunjak-Novakovic and co-workers.²² One of the models they considered was a square array of vessels with a vascular diameter of 330 μm, a vascular spacing of 700 μm, a scaffold thickness of 2 mm, and an oxygen consumption rate of 9 nmol∕cm³ s; the available pressures for perfusion were not provided. This vascular design results in a vascular volume fraction of ∼17%, which appears to be far greater than necessary. Extrapolation from our plots (Figs. 56) indicated that an optimal vascular design only requires ∼2% of the total volume, given a modest perfusion pressure of 1 cm H₂O. Indeed, explicit optimization with this perfusion pressure and the parameters in their study yielded optimal vascular volume fraction of 2.8%, diameter of 58 μm, and spacing of 328 μm.

Comparison with an approximate analytical solution

Although we varied six parameters independently, not all of these variations led to independent changes in optimal design. For instance, the effects of changes in perfusion pressure difference ΔP and perfusate viscosity η could be effectively bundled into changes in vascular flow rate, as given by ΔP∕η. Changes in scaffold hydraulic conductivity, on the other hand, had essentially no effect on optimal design. These results suggested that a reasonable approximation to our models is one that neglects interstitial flow. When posed in a cylindrical geometry, this approximate model can be solved analytically (see the Appendix0) to yield expressions that relate the optimal geometric parameters,

$$\frac{\alpha }{2}-\frac{2\beta L}{\alpha }\left[{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2-1\right]\left\{\beta \gamma \left[{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2-1\right]+\delta \left[{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2\text{ln}{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2-{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2+1\right]\right\}=0,$$ (8)

$$R_{\text{vessel}}{}^2=\frac{2\beta L}{\alpha }\left[{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2-1\right],$$ (9)

where the constants α, β, γ, and δ depend on the prescribed values (ΔP,η,L,K,q_O2,k_O2), as given in the Appendix0.

Table 2 compares the results of computational versus analytical optimization for a randomly selected set of cases. We found that Eqs. 8, 9 were remarkably effective in predicting the computational results; the analogous lengths of the analytical solution (2R_vessel and 2R_scaffold) generally underestimated the computationally optimized diameter and spacing, respectively, by ∼5%. These expressions provide a practical alternative to computational modeling when designing vascular systems that minimize vascular volume fraction.

Table 2.

Predicted optimal geometries from Eqs. 8, 9 and computationally determined optima for selected cases.

Parametersa						Computedb		Predictedb
ΔP	η	L	K	qO2	kO2	D	H	2Rvessel	2Rscaffold
20	0.7	2	10−10	10−8	1.2×10−9	93.6	336.2	90.4	326.4
50	0.7	2	10−10	10−8	1.2×10−9	72.3	314.1	70.2	306.9
20	3	2	10−10	10−8	1.2×10−9	141.0	379.7	135.4	365.3
20	0.7	4	10−10	10−8	1.2×10−9	138.6	376.8	132.8	363.2
20	0.7	2	10−10	10−7	1.2×10−9	108.9	171.7	101.9	162.0
20	0.7	2	10−10	10−8	1.3×10−8	50.5	318.3	50.7	332.6
1	0.7	0.2	10−10	9×10−9	1.2×10−9	57.9	327.7	57.7	306.3

^aUnits: ΔP (cm H₂O); η (cP); L (cm); K (cm⁴∕dyn s); q_O2 (mol∕cm³ s); k_O2 (mol∕cm³ mm Hg).

^bAll optimal values are given in units of micrometers.

CONCLUSIONS

This study suggests that optimization of vascular systems on the basis of vascular volume fraction provides optimal geometries and size scales that can be readily achieved experimentally. Our work implies that although the parallel vascular geometry of the Krogh model may only exist in vivo in a limited number of tissues (e.g., skeletal muscle), it may be a reasonably efficient geometry for perfusion of engineered tissues. One caveat is that the optimal vascular volume fractions are somewhat higher than those observed in vivo. We have obtained analytical expressions for optimal designs and have validated their predictions against computational results; the agreement is very good (to within ∼5% for both vascular diameter and spacing). This study thus provides a straightforward method to obtain optimal vascular designs that minimize vascular volume fraction while maintaining oxygen concentration in a scaffold above a threshold value.

Practical microfluidic implementation of the optimized geometries will likely require coupling of branching networks to the vascular inlets and outlets of the array. One possible approach is to use this study to determine the optimal dimensions of an array and to use Murray’s law to merge the open ends pairwise into larger vessels. In this respect, our work can provide an absolute size scale that Murray’s law (which only provides the ratios of vascular radii) does not.

We note that interstitial flow played a negligible role in our models of oxygen transport. Thus, the same optima should apply to models in which oncotically active solutes are present in the perfusate, the endothelial hydraulic conductivity is spatially heterogeneous (e.g., due to a flow-dependent vascular phenotype³¹), or the scaffold is passively drained.²⁰

Other optimization functions (e.g., oxygen extraction efficiency) are certainly valid, and the choice of function will depend on the external constraints imposed on the engineered tissue. We expect lower vascular volume fractions to generally correlate with greater extraction efficiencies; thus, optimal designs based on this and possibly other functions may not differ substantially from those based on volume fractions.

Nomenclature

D

Diameter of vessels

H

Axis-to-axis distance between vessels

L

Length of vessels; thickness of scaffold

K

Hydraulic conductivity of scaffold

L_P

Hydraulic conductivity of vessel wall

P_vessel,P_scaffold

Hydrostatic pressures in vessel and scaffold

v_vessel,v_scaffold

Fluid velocities in vessels and scaffold

v_n

Velocity of interstitial fluid normal to vessel wall (i.e., filtration velocity)

c_vessel,c_scaffold

Oxygen concentrations in vessel and scaffold

q_O2

Volumetric oxygen consumption rate in scaffold

k_O2,k_O2^∗

Oxygen solubilities in perfusate and interstitial fluid

η

Viscosity of perfusate

ρ

Density of perfusate

c_min

Minimum oxygen concentration in scaffold

APPENDIX: DERIVATION OF ANALYTICAL EXPRESSIONS FOR OPTIMAL VASCULAR GEOMETRIES

This appendix derives Eqs. 8, 9, which describe an approximate analytical solution to the optimization of vascular geometry for perfusion. The volume-of-interest in this analysis is essentially identical to that used originally by Krogh, that is, a cylindrical scaffold of radius R_scaffold that contains a vessel of radius R_vessel. The axis of symmetry points in the z-direction with the vascular inlet at z=0 and outlet at z=L. We treated the lumenal flow as parabolic,

$$v\left(r,z\right)=v_{\text{max}}\left(1-\frac{r^2}{R_{\text{vessel}}{}^2}\right).$$ (A1)

We looked for steady-state solutions and neglected the axial diffusion of oxygen, so the convection-diffusion equation in the lumen simplified to

$$v\left(r\right)\frac{\partial c_{\text{vessel}}}{\partial z}=\frac{D_{\text{O}2}}{r}\frac{\partial }{\partial r}\left(r\frac{\partial c_{\text{vessel}}}{\partial r}\right).$$ (A2)

Following Lightfoot,³² we separated the concentration profile into radial and axial components,

$$c_{\text{vessel}}\left(r,z\right)=c_{\text{vessel}}\left(0,0\right)+c_1\left(r\right)-Az,$$ (A3)

where A is a constant and c₁(0)=0. Solving Eq. A2 with this concentration profile yielded

$$c_{\text{vessel}}\left(r,z\right)=c_{\text{vessel}}\left(0,0\right)-\frac{A{v}_{\text{max}}}{D_{\text{O}2}}\left(\frac{r^2}{4}-\frac{r^4}{16R_{\text{vessel}}{}^2}\right)-Az.$$ (A4)

The constant A was determined by noting that convective oxygen flux in the vessel decreases axially as oxygen is consumed within the scaffold,

$$-2\pi {\int }_0^R\frac{\partial c_{\text{vessel}}}{\partial z}v\left(r\right)rdr=q_{\text{O}2}\cdot \pi \left(R_{\text{scaffold}}{}^2-R_{\text{vessel}}{}^2\right).$$ (A5)

Since ∂c_vessel∕∂z=−A and v_max=R_vessel2ΔP∕4ηL by Poiseuille’s law, Eq. A5 yielded

$$A=\frac{8q_{\text{O}2}\eta L}{\Delta P}\frac{R_{\text{scaffold}}{}^2-R_{\text{vessel}}{}^2}{R_{\text{vessel}}{}^4}.$$ (A6)

To determine the concentration profile in the scaffold, we used the Krogh–Erlang equation³³ with an additional axial term and neglected the convective transport,

$$c_{\text{scaffold}}\left(r,z\right)=\frac{q_{\text{O}2}}{4D_{\text{O}2}}{r}^2-\frac{q_{\text{O}2}}{2D_{\text{O}2}}R_{\text{scaffold}}{}^2\text{\hspace{0.17em}ln}r-\frac{k_{\text{O}2}^{\ast }Az}{k_{\text{O}2}}+B,$$ (A7)

where B is a constant. The concentrations in the lumen and scaffold are related at the vessel wall by

$$c_{\text{vessel}}\left(R_{\text{vessel}},z\right)=\frac{k_{\text{O}2}}{k_{\text{O}2}^{\ast }}{c}_{\text{scaffold}}\left(R_{\text{vessel}},z\right).$$ (A8)

Combining Eqs. A4, A7, A8 yielded

$$c_{\text{scaffold}}\left(r,z\right)=\frac{k_{\text{O}2}^{\ast }}{k_{\text{O}2}}{c}_{\text{vessel}}\left(0,0\right)-\frac{3A{v}_{\text{max}}{k}_{\text{O}2}^{\ast }}{16D_{\text{O}2}{k}_{\text{O}2}}R_{\text{vessel}}{}^2-\frac{q_{\text{O}2}}{4D_{\text{O}2}}\left(2R_{\text{scaffold}}{}^2\text{\hspace{0.17em}ln}\frac{r}{R_{\text{vessel}}}-r^2+R_{\text{vessel}}{}^2\right)-\frac{k_{\text{O}2}^{\ast }Az}{k_{\text{O}2}}.$$ (A9)

To find the optimal R_scaffold and R_vessel, we sought to minimize the vascular volume fraction,

$$f\left(R_{\text{scaffold}},R_{\text{vessel}}\right)={\left(\frac{R_{\text{vessel}}}{R_{\text{scaffold}}}\right)}^2,$$ (A10)

subject to the constraint that the oxygen concentration everywhere (particularly at the lethal corner of r=R_scaffold and z=L) is greater than or equal to the threshold concentration c_crit,

$$g\left(R_{\text{scaffold}},R_{\text{vessel}}\right)=c_{\text{scaffold}}\left(R_{\text{scaffold}},L\right)-c_{\text{crit}}=0.$$ (A11)

Equations A6, A9, A11 yielded the following form for the constraint:

$$g=\alpha -\beta \frac{R_{\text{scaffold}}{}^2-R_{\text{vessel}}{}^2}{R_{\text{vessel}}{}^4}\left(\gamma R_{\text{vessel}}{}^4+L\right)-\delta \left(2R_{\text{scaffold}}{}^2\text{\hspace{0.17em}ln}\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}-R_{\text{scaffold}}{}^2+R_{\text{vessel}}{}^2\right)=0,$$ (A12)

where the constants α, β, γ, and δ are given by

$$\alpha =\frac{k_{\text{O}2}^{\ast }}{k_{\text{O}2}}{c}_{\text{vessel}}\left(0,0\right)-c_{\text{crit}},$$ (A13)

$$\beta =\frac{8k_{\text{O}2}^{\ast }{q}_{\text{O}2}\eta L}{k_{\text{O}2}\Delta P},$$ (A14)

$$\gamma =\frac{3\Delta P}{64D_{\text{O}2}\eta L},$$ (A15)

$$\delta =\frac{q_{\text{O}2}}{4D_{\text{O}2}}.$$ (A16)

To perform the constrained optimization, we used the method of Lagrangian multipliers,³⁴

$$\frac{\frac{\partial f}{\partial R_{\text{scaffold}}}}{\frac{\partial f}{\partial R_{\text{vessel}}}}=\frac{\frac{\partial g}{\partial R_{\text{scaffold}}}}{\frac{\partial g}{\partial R_{\text{vessel}}}}.$$ (A17)

Substituting Eqs. A10, A12 into Eq. A17 yielded a remarkably simple expression after straightforward but tedious algebra,

$$R_{\text{vessel}}{}^2=\frac{2\beta L}{\alpha }\left[{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2-1\right].$$ (A18)

Substituting Eq. A18 into Eq. A12 yielded an implicit equation for the ratio of the optimal R_scaffold and R_vessel,

$$\frac{\alpha }{2}-\frac{2\beta L}{\alpha }\left[{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2-1\right]\left\{\beta \gamma \left[{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2-1\right]+\delta \left[{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2\text{ln}{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2-{\left(\frac{R_{\text{scaffold}}}{R_{\text{vessel}}}\right)}^2+1\right]\right\}=0.$$ (A19)

For each case, we used Eqs. A13, A14, A15, A16 to calculate the constants α, β, γ, and δ, solved Eq. A19 numerically to obtain the optimal R_scaffold∕R_vessel, and used Eq. A18 to obtain the optimal R_vessel and R_scaffold.