Transport and shear in a microfluidic membrane bilayer device for cell culture

Abstract

Microfluidic devices have been established as useful platforms for cell culture for a broad range of applications, but challenges associated with controlling gradients of oxygen and other soluble factors and hemodynamic shear forces in small, confined channels have emerged. For instance, simple microfluidic constructs comprising a single cell culture compartment in a dynamic flow condition must handle tradeoffs between sustaining oxygen delivery and limiting hemodynamic shear forces imparted to the cells. These tradeoffs present significant difficulties in the culture of mesenchymal stem cells (MSCs), where shear is known to regulate signaling, proliferation, and expression. Several approaches designed to shield cells in microfluidic devices from excessive shear while maintaining sufficient oxygen concentrations and transport have been reported. Here we present the relationship between oxygen transport and shear in a “membrane bilayer” microfluidic device, in which soluble factors are delivered to a cell population by means of flow through a proximate channel separated from the culture channel by a membrane. We present an analytical model that describes the characteristics of this device and its ability to independently modulate oxygen delivery and hemodynamic shear imparted to the cultured cells. This bilayer configuration provides a more uniform oxygen concentration profile that is possible in a single-channel system, and it enables independent tuning of oxygen transport and shear parameters to meet requirements for MSCs and other cells known to be sensitive to hemodynamic shear stresses.

INTRODUCTION

Microfluidic devices have emerged as powerful tools for controlling the cellular microenvironment^{1, 2, 3, 4} and for assembling tissuelike structures,^{5, 6} as well as enabling high-throughput analysis.^{7, 8, 9, 10} A notable advantage of microfluidic cell culture is the potential to control concentrations of nutrients, growth factors, and other soluble cellular regulatory molecules both spatially and temporally. Microfluidic culture systems are particularly suited to controlling concentration gradients of soluble factors by generating defined gradients and eliminating undesirable gradients.^{11, 12, 13, 14, 15}

An enduring challenge in many in vitro culture formats including microfluidic cultures is the relatively poor solubility of oxygen in culture medium compared to its solubility in blood. This low solubility results in very rapid depletion of oxygen compared to other low molecular weight nutrients, and can result in gradients of oxygen along the flow path in microscale culture devices.¹⁶ Although gradients are in some cases desirable, when they are induced by cellular consumption, the magnitude of the gradients can be difficult to control.^{17, 18} Gradients can be reduced by increasing the flow rate of culture medium, but doing so increases the magnitude of shear stress experienced by cells exposed directly to flow, potentially exceeding physiological values. Shear stress is well known to govern the phenotype of endothelial cells,^{19, 20, 21, 22} and shear is emerging as an important regulator of behavior in other cell types. For example, shear stresses have been shown to regulate activation of signaling pathways, gene expression, proliferation, and osteogenesis in mesenchymal stem cells (MSCs).^{23, 24, 7, 25, 26} Several approaches have been developed to uncouple oxygen transport and fluid shear stress on cells cultured in microfluidic reactors, including culturing cells in biologically inspired microchannels which shield them from fluid flow,¹³ in bilayer constructs,²⁷ and in recessed grooves.¹²

In addition to oxygen, cells consume and produce numerous growth factors that regulate survival, growth, differentiation, and migration. Convective flow enhances the molecular transport of such factors to a greater degree than oxygen due to their larger size and lower diffusion coefficients.²⁸ While it is possible to control the concentrations of exogenous factors such as insulin, it is difficult to control the gradients of autocrine factors in the presence of significant flow.^{29, 30, 31}

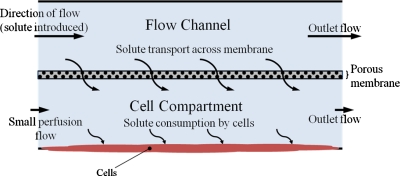
A two-compartment microfluidic device (Fig. 1), in which the cell culture region is separated from a high-flow channel by a semipermeable membrane, offers the possibility of uncoupling oxygen and molecular transport from the shear stress imparted to the cells. Such a design is similar to macroscale hollow fiber reactor platforms used for industrial protein production.³² The flow rate in the upper channel (Fig. 1) is set at a relatively high rate, determined by minimizing the concentration drop of oxygen or other components along the length of the flow channel. Modulation of the transmembrane pressure and membrane permeability enables precise control of local concentrations in the culture chamber. Devices incorporating semipermeable membranes with low hydraulic conductivity and tailored molecular weight cutoffs are expected to minimize effects of convective transport between the chambers, enabling fluxes of nutrients and macromolecules to the cell layer to be governed by the membrane permeability coefficients. High molecular weight autocrine factors can be retained in the cell compartment without significant restriction on oxygen transport by restricting the flux through the membrane by the appropriate choice of molecular weight cutoff.

Figure 1.

Schematic of a two-compartment microfluidic device operating in a monoculture mode. A high flow rate is used in the upper channel, providing nutrients to cells cultured on the substrate in the lower channel by a combination of diffusion and convection across the porous membrane separating the channels.

These design considerations derive from a growing interest in illuminating the role of oxygen and other soluble factors in regulating the survival, growth, and differentiation of stem cells.^{33, 34, 35, 36, 37, 38, 39} Very low oxygen concentrations are often reported to foster greater retention of desirable stem cell behaviors, for instance, proliferation. However, culturing cells at low oxygen concentrations exacerbates the rapid depletion from flowing culture medium. We therefore analyze the design of two-compartment membrane devices to determine operating parameters that will enable a uniform, low oxygen concentration to be achieved at the cell layer shown in Fig. 1, and evaluate the consequences for molecular transport of other species important in regulating cell behavior.

ANALYTICAL MODEL OF FLUID SHEAR AND MOLECULAR TRANSPORT IN A TWO-COMPARTMENT BILAYER DEVICE

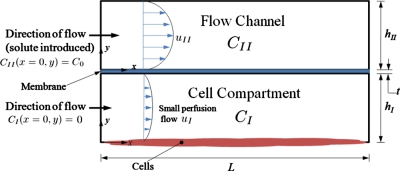
A cross-section depicting the flow geometry under consideration is illustrated in Fig. 2, which also defines the parameters governing the flow and transport. The general case allows for flow in both channels (as shown in the figure), but in practice, it may be favorable to eliminate flow in the lower channel for some culture scenarios. For the limiting case of negligible convective flow across the semipermeable membrane separating the flow channels, and for high aspect ratio flow channels (L⪢h), steady state velocity profiles in either channel can be described by fully developed Poiseuille flow, as shown in Fig. 2. Convective transport across the membrane will be low for membranes with small pores and low porosity, such as PDMS or track-etched polymer membranes.²⁷ In the limit of negligible membrane permeability to fluid, oncotic effects will vanish. In channels with aspect ratios w∕h∼10, a common experimental situation,^{40, 41, 42, 43} the two-dimensional assumption is valid across middle 85% of the channel to an error of 1; for w∕h=4, the approximation still holds for the central 62% of the channel (Supplementary Information, Fig. 2).⁴⁴

Figure 2.

Cross-sectional geometry of bilayer-membrane microfluidic device designed for cell culture in the bottom channel, indicating definitions of geometric and concentration parameters. Channels are of width w (not shown), w∕h⪢1.

A comparison of the relative diffusive and convective transport time scales in the x direction along the channel, captured by the Peclet number Pe=u₀L∕D, indicates that molecular transport of oxygen (or other solutes) in the x direction (along the length of the channel) is dominated by convection. For typical values of L (0.1–1 cm), u₀ (1×10⁻² cm∕s), and D (1–30×10⁻⁶ cm²∕s), values of Pe are between 16 and 1×10⁶. In this configuration, convection dominates where Pe>10.

With these considerations, the equations governing diffusion and convection of solute in the two different regions are identical in form and are simplified to the following:

$$u_i\frac{\partial C_i}{\partial x}=D_i\frac{{\partial }^2{C}_i}{\partial y^2},i=I,II,$$ (1)

where the solute concentrations in the upper and lower channels are C_II and C_I, respectively, and u_i is the velocity of the fluid in the horizontal (x) direction. The Poiseuille velocity profile in terms of the device geometric parameters is given by

$$u_i\left(y\right)=\frac{h_i}{2{\mu }_i}{\left(-\frac{dp}{dx}\right)}_i\frac{y}{h_i}\left(1-\frac{y}{h_i}\right),i=I,II,$$ (2)

with the shear imparted on the walls by this flow field given by τ_i=μ_i[∂u_i(y)∕∂y]_y=0,hi. The corresponding flow rates are $Q_i=w{\int }_{y=0}^{h_i}{u}_{i}dy$, where w is the width of the channel.

Fluid enters each channel (x=0) at a defined concentration C₀, and there is no flux of solute across the upper wall of the top chamber. This latter condition does not strictly hold true for devices made from PDMS due to the high oxygen solubility in PDMS;¹⁶ it is a reasonable assumption for alternate less-permeable materials now being employed for devices.²⁸ Cells consuming oxygen along the lower wall in the lower chamber create a diffusive flux of oxygen across the central membrane separating the two channels. Defining D_membrane as the effective diffusion coefficient of the solute in the membrane, and t the thickness of the membrane, the boundary conditions in the upper chamber may be summarized as

$$\phantom{\{}\begin{array}{c}{C}_{II}\left(x=0,y\right)=C_0\\ D_{II}{\phantom{|}\frac{\partial C_{II}}{\partial y}|}_{y=h_{II}}=0\\ D_{II}{\phantom{|}\frac{\partial C_{II}}{\partial y}|}_{y=0}=\frac{D_{\text{membrane}}}{t}\left[C_I\left(x,y=h_I\right)-C_{II}\left(x,y=0\right)\right]\end{array}\}.$$ (3)

In the lower chamber, we take the inlet concentration of solute is zero. Solute diffuses into the lower chamber from the upper chamber across the membrane. The rate of diffusive flux at the upper boundary (membrane) is balanced by the flux at the lower boundary, where cells consume the solute. Solute consumption generally follows Michaelis–Menten kinetics, allowing the boundary conditions for the lower channel to be summarized as

$$\phantom{\{}\begin{array}{c}{C}_I\left(x=0,y\right)=0\\ D_I{\phantom{|}\frac{\partial C_I}{\partial y}|}_{y=h_I}=D_{II}{\phantom{|}\frac{\partial C_{II}}{\partial y}|}_{y=0}\\ D_I{\phantom{|}\frac{\partial C_I}{\partial y}|}_{y=0}=V_{\text{max}}{\rho }_{\text{cells}}\frac{C_I\left(x,y=0\right)}{K_M+C_I\left(x,y=0\right)}\end{array}\},$$ (4)

where V_max is the maximum rate of consumption of solute, K_M is the Michaelis–Menten constant, and ρ_cells is the area density of the cells. Michaelis–Menten parameters have been reported for oxygen consumption by a wide variety of cell types including mesenchymal stem cells.^{33, 45, 35, 36} A particular application focus for the device design described herein is culture of MSCs under very low oxygen tensions, such as those that might obtain during embryonic development³⁷ or in the marrow or a wound environment. In response to a low oxygen tension, MSCs upregulate hypoxia-induced factors that then control cell behaviors such as proliferation and differentiation (e.g., into osteoblasts or chondrocytes).^{38, 39} For oxygen consumption by mammalian cells, a wide range of values have been reported for K_M, the critical parameter that governs the transition between zero-order (at high solute concentrations) and first-order (low solute concentrations) kinetic regimes, but values in the 5%–30% of air saturation are typical.^{33, 35} Thus, for culture at target oxygen tensions in the range of <20% of air saturation, it is reasonable to presume the first-order limit of the Michaelis–Menten kinetic expression applies. This allows the boundary condition at the lower boundary of the lower channel to be simplified to

$$D_I{\phantom{|}\frac{\partial C_I}{\partial y}|}_{y=0}\approx \frac{V_{\text{max}}{\rho }_{\text{cells}}}{K_M}{C}_I\left(x,y=0\right).$$

Typical parameter values for microfluidic cell culture, where oxygen is the solute of interest, are summarized in Table 1. Table 2 summarizes three combinations of parameter values of interest, ranging from low (Case 1) to high (Case 3) uptake rates (given by the ratio V_max∕K_M), as well as varying cell seeding densities, ranging from sparse (Case 1) to confluent (Case 3).

Table 1.

Parameters chosen for study. Parameters are appropriate for culturing MSCs in a microfluidic device, based on values reported in the literature.

Parameter	Value	Note
DII,DI	3×10−5 cm2∕s	Diffusion coefficient for oxygen in water
Dmembrane	1×10−5 cm2∕s	Diffusion coefficient for oxygen in polymeric membranea
t	10 μm	Thickness of membrane
μ	1×10−2 dyne s∕cm2	Viscosity of water
hI,hII	50 μm	Height of channelb
w	200 μm	Width of channelb
L	1.5 cm	Length of channelb
KM	1×10−7 mol∕cm3	Michaelis–Menten parameter for oxygenc
Csat	2.15×10−7 mol∕cm3	Oxygen concentration at saturationd
C0	2.15×10−9 mol∕cm3	0.01×Csat, 1% saturationd
τ	0.3 dyne∕cm2	Shear, determined by initiation of osteogenic differentiation in MSCse

^aReference ⁴⁰.

^bReferences 41, 42.

^cReference ¹⁶.

^dReference ³³.

^eReferences 25, 46.

Table 2.

Values of V_max∕K_M and ρ_cells for three separate cases, representing varying cell uptake rates and cell seeding densities.

	Case 1	Case 2	Case 3
Vmax∕KM	5×10−5 cm3∕106 cells∕s a	1×10−4 cm3∕106 cells∕s	2×10−4 cm3∕106 cells∕s b
ρcells	1×103 cells∕cm2c	1×105 cells∕cm2d	1×106 cells∕cm2e

^aReference ¹⁶.

^bReference ⁴⁷.

^cReferences 16, 47, 48, 49.

^dReferences 16, 50.

^eReference ⁵⁰.

The range of suitable flow rates in the cell compartment, should flow be desired, can be determined by considering threshold values that have been reported to affect MSC cell phenotypes. In this regard, proliferation and osteogenic differentation are affected by shear in a range between 0.3 and 2.7 dyne∕cm².^{25, 46} We therefore take as an upper threshold value for the shear in the lower compartment, should flow be included during operation, of τ=0.3 dyne∕cm². This constraint sets the maximum allowable volumetric flow rate in the lower channel at a level Q_I=2.5 nL∕s. Flow rates of this order have been used to culture stem cells in work that has successfully sustained cells over a sustained period of time and removed metabolic waste products.^{25, 46} There are no corresponding maximum limits on flow in the upper channel, Q_II, because it can be modulated without affecting the shear imparted to the MSCs due to the shielding effect of the membrane. A channel height of 50 μm and a channel length of 1.5 cm are selected based on experimental values for comparable devices.^{41, 42}

RESULTS

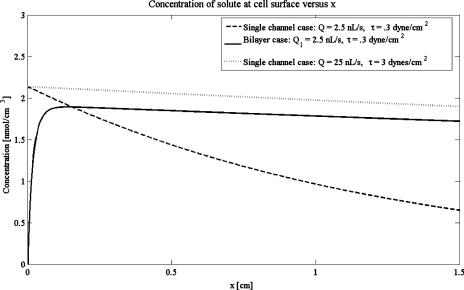
In Fig. 3, model results for oxygen concentration at the cell surface for the bilayer and single channel case are shown. The least stringent set of culture conditions for maintaining oxygen concentrations invariant down the length of the devices involves sparse cells respiring at the lower end of the reported ranges of consumption rates (Case 1, Table 2). For flow rates Q_I=2.5 nL∕s (governed by maximum allowable shear on the cell layer) with Q_II=10 nL∕s in the upper channel (solid black line), the oxygen concentration profile is almost invariant along the length of the cell compartment except for a small zone of depletion in the initial region, due to the assumption of zero concentration in the inlet. If, instead of using a bilayer membrane device, where the membrane protects cells from high shear flow required to deliver oxygen by diffusion, cells were cultured in a single channel configuration with a low flow rate (given by Q=2.5 nL∕s), to protect them from shear (i.e., τ=0.3 dyne∕cm²), the oxygen concentration falls rapidly along the length of the channel (dashed black line). The concentration profile for increasing flow to 25 nL∕s (comparable to the flow in the upper channel in the bilayer device) in this single channel comparative situation diminishes this drop, but at the cost of an unacceptable increase in shear stress (to 3 dyne∕cm²).

Figure 3.

Concentration at cell surface as a function of x, in units of nmol∕cm³: single channel (dotted and dashed lines) vs bilayer (solid black line). For the bilayer, the cell compartment flow rate is given by Q_I=2.5 nL∕s (τ=0.3 dyne∕cm²), while the flow channel flow rate is given by Q_II=25 nL∕s. For the single channel, we have flow rates given by Q=2.5 nL∕s, corresponding to τ=0.3 dyne∕cm² (dashed black line) and Q=25 nL∕s, corresponding to τ=3.0 dyne∕cm² (dotted blue line). For the single channel case corresponding to τ=0.3 dyne∕cm², note the decaying concentration profile, while the bilayer concentration profile is, except for a small depletion zone at the beginning of the channel, nearly uniform. Other parameters are those for Case 2.

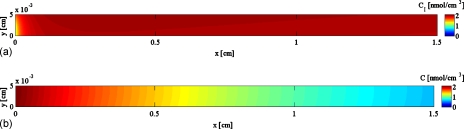
The concentration profiles themselves can be visualized using color maps over the domain of interest. We see in Fig. 4a that, with Q_I=2.5 nL∕s and Q_II=25 nL∕s, the concentration field in the cell compartment for the bilayer case is nearly uniform. For the single channel configuration operating at a flow rate of Q=2.5 nL∕s [Fig. 4b], there exists considerable nonuniformity in the concentration profile along the length of the channel.

Figure 4.

Concentration fields for (a) bilayer and (b) single channel, in units of nmol∕cm³. In (a), we see the concentration field in the cell compartment of the bilayer construct with Q_I=2.5 nL∕s and Q_II=25 nL∕s. In (b), we have the concentration field for the single channel construct with Q=2.5 nL∕s. The bilayer case demonstrates a far more uniform profile for a given flow rate and shear, while for the single channel configuration, the concentration of solute is depleted for much of the length of the channel. Other parameters are those for Case 2.

Increasing the cell density and respiration parameters (corresponding to Cases 2 and 3) for these same flow rates (2.5 nL∕s the lower chamber and 25 nL∕s in the upper chamber) results in development of oxygen concentration profiles down the length of the device for Case 3 but a near-constant linear profile is maintained for Case 2 [Fig. 5a]. The concentration profile can be flattened for Case 3 by increasing the volumetric flow rate in the upper compartment by a factor of 5, so that Q_II=125 nL∕s [Fig. 5b]. This increase in flow rate has no consequence on the shear stress experienced by the cells, as they are shielded by the semipermeable membrane.

Figure 5.

Concentration at cell surface as a function of x for cases 1, 2, and 3, in units of nmol∕cm³ with (a) Q_I=2.5 nL∕s and Q_II=25 nL∕s, and (b) Q_I=2.5 nL∕s and Q_II=125 nL∕s. By increasing the flow rate in the upper chamber by a factor of 5, the concentration profile becomes more uniform. In particular, for the high uptake rate and confluent seeding case (Case 3), increasing the flow rate in the upper chamber prevents depletion along the length of channel caused by high uptake of oxygen. For both (a) and (b), the shear imparted on the cell culture is the same (τ=0.3 dyne∕cm²).

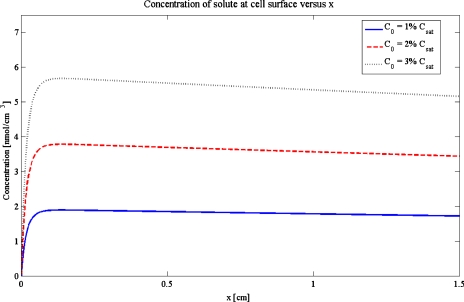
In Fig. 6, we see the effect of simply increasing the concentration of solute introduced into the flow channel. As expected, the concentration increases along the length of the channel.

Figure 6.

Concentration at cell surface as a function of x for Cases 1, 2, and 3, in units of nmol∕cm³: C₀ varied as 0.01×C_sat (solid blue line), 0.02×C_sat (dashed red line), and 0.03×C_sat (dotted black line). Q_I=2.5 nL∕s and Q_II=25 nL∕s, while other parameters are those for Case 2.

Discussion

The results presented in Figs. 3456 describe the range of operating parameters that enable a bilayer membrane microfluidic device to provide uniform, tailored levels of oxygen to various densities of cultured MSCs, while shielding cells from shear stresses induced by the volumetric flow rates necessary to deliver oxygen. In the bilayer case, however, it is possible to achieve controlled levels of oxygen delivery without an unacceptable increase in the shear stress to which the cells are exposed. Significantly, we see in Figs. 3456 that the concentration and delivery profiles are, except for the entry zone, nearly uniform.

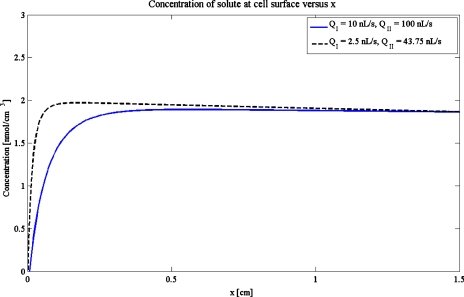
In the analysis presented in Figs. 3456, an extreme boundary condition of zero inlet oxygen was employed, although in practice, the inlet oxygen concentration could be tailored to whatever value is desired. This use of this extreme boundary condition, however, provides an estimate of the length scale over which effects of the lower inlet oxygen concentration persist before diffusion from the upper chamber reaches a fully developed state. Intuitively, it is anticipated that the entry zone effects for the extreme boundary condition (zero inlet oxygen in the lower flow channel) will be diminished for lower flow rates in the lower channel. For example, if Q_I is decreased from 10 nL∕s to 2.5 nL∕s with the flow channel flow rate Q_II decreased from 100 nL∕s to 43.75 nL∕s, the entry zone depletion region is reduced by a factor of 4 (Fig. 7, blue line and dashed black line, respectively).

Figure 7.

Reduction of the depletion zone in the bilayer construct. The solid blue curve is the concentration profile in the bilayer construct if Q_I=10 nL∕s and Q_II=100 nL∕s. The depletion zone, which extends approximately 0.25 cm, may be reduced in extent if we choose Q_I=2.5 nL∕s and Q_II=43.75 nL∕s (dashed black curve). The subsequent reduction is by a factor of about 4. Other parameters are those for Case 2.

Implications for device design

One aspect that has been assumed in this analysis is the fully developed nature of the fluid flow. In practice, it is often useful to ensure that the fluid flow within the operational portions of the device is both laminar and fully developed. With fully developed flow, the velocity field is assumed to be the same along the operating length of the device. Other device configurations designed to shield cells from stress, such as those featuring grooves¹³ or complex channel geometries,¹² may introduce mixing and other effects that could interfere with the dynamic measurement of quantities of interest, such as oxygen concentration, and which would introduce complex flow and concentration fields under the high flow conditions required to maintain a relatively constant concentration field along the length of the device. In order to characterize the entry length for the fluid, we may refer to one of the several correlations that describe the entry length for a fluid, e.g.,51

$$L_{\text{entrance}}=D_h\left[\left(\frac{0.6}{1+0.035{\text{Re}}_L}\right)+0.056{\text{Re}}_L\right],$$ (5)

where D_h is the hydraulic diameter of the channel, given by 2hw∕(h+w), and Re_L is the Reynolds number for the flow, given by ρ_fluidu₀L∕μ. For the values given in Table 1, we have Re_L=4.2, D_h=80 μm, and L_entrance=60 μm, while the delivery profile (i.e., the depletion zone) may be tuned as above to extend beyond this range.

CONCLUSION

We have constructed an analytical model that demonstrates the transport profile in a membrane bilayer cell culture device that enables tunable modulation of transport and fluid shear. We have shown that the bilayer configuration allows us to maintain nearly uniform concentration profiles along a length of channel while subjecting cultured cells to minimal shear. This represents an improvement over conventional microfluidic cell culture devices comprising a single channel configuration, in which uniformity in solute concentration along the length of the channel is achieved only by increasing flow rate, which increases shear imparted to cells. We have shown the potential for tuning the oxygen delivery profile within a model cell culture system. The model presented here may be used as a baseline for device design and parameter selection in the construction of a microfluidic device for tissue culturing, bioassay, and drug delivery systems. Furthermore, the basic physics of this model may be extended to consider more complex systems involving the interaction of several soluble factors in devices comprised of varying cell populations and types.

APPENDIX: SOLUTION TO THE TRANSPORT EQUATION FOR A MEMBRANE BILAYER

Solution

This section describes the method used to arrive at the solution. In order to make the solutions more broadly applicable, the equations are cast in nondimensional form. A characteristic fluid velocity $u_{i,0}\equiv {(-dp∕dx)}_i{h}_i^2{\left(8{\mu }_i\right)}^{-1}$ is defined for each region, depending on the given pressure gradient and height. Additionally, the characteristic concentration is C₀, corresponding to the inlet concentration which is being introduced at the left of the upper region. Scale x and y against the height of the lower channel h_I, and let Ω_II and Ω_I denote the flow channel and cell compartment, respectively. Then the dimensionless transport equation is, for the upper channel,

$$\frac{4y}{\beta }\left(1-\frac{y}{\beta }\right)\frac{\partial C_{II}\left(x,y\right)}{\partial x}=\frac{1}{{\text{Pe}}_{II}}\frac{{\partial }^2{C}_{II}\left(x,y\right)}{\partial y^2},x∊\left[0,L∕h_I\right]\text{\hspace{0.5em}\hspace{0.5em}and\hspace{0.5em}\hspace{0.5em}}y∊\left[0,\beta \right],{\Omega }_{II}\equiv \left[0,L∕h_I\right]\times \left[0,\beta \right],$$ (A1)

and for the lower channel,

$$4y\left(1-y\right)\frac{\partial C_I\left(x,y\right)}{\partial x}=\frac{1}{{\text{Pe}}_I}\frac{{\partial }^2{C}_I\left(x,y\right)}{\partial y^2},x∊\left[0,L∕h_I\right],\text{\hspace{0.5em}\hspace{0.5em}and\hspace{0.5em}\hspace{0.5em}}y∊\left[0,1\right],{\Omega }_I\equiv \left[0,L∕h_I\right]\times \left[0,1\right]$$ (A2)

where β≡h_II∕h_I, and Pe_II≡u_0,IIh_I∕D_II and Pe_I≡u_0,Ih_I∕D_I are the Peclet numbers for each channel. u_0,II is equal to ${\left(-dp∕dx\right)}_{II}{h}_{II}^2{\left(8{\mu }_{II}\right)}^{-1}$ and u_0,I equal to ${\left(-dp∕dx\right)}_I{h}_I^2{\left(8{\mu }_I\right)}^{-1}$ In terms of flow rates Q_I and Q_II in Ω_I and Ω_II, respectively, we may write the Peclet numbers,

$${\text{Pe}}_I=\frac{3Q_I}{2w{D}_I},$$

$${\text{Pe}}_{II}=\frac{3Q_{II}}{2\beta w{D}_{II}}.$$

The shear along the walls τ_i is given by

$${\tau }_i={\mu }_i{\phantom{|}\frac{\partial u_i}{\partial y}|}_{y=0,h_i},i=I,II.$$

A separation of variables methodology may be used to derive the general solutions for Eqs. A1, A2. Writing C_i(x,y)=ξ_i(x)η_i(y) (i=I,II) and separating, we have in Ω_I,

$$\frac{4{\text{Pe}}_I{\xi }_I^{\prime }\left(x\right)}{{\xi }_I\left(x\right)}=\frac{{\eta }_I^{″}\left(y\right)}{y\left(1-y\right){\eta }_I\left(y\right)}=-{\lambda }_I^2,$$

and in Ω_II,

$$\frac{4{\text{Pe}}_{II}{\xi }_{II}^{\prime }\left(x\right)}{{\xi }_{II}\left(x\right)}=\frac{{\eta }_{II}^{″}\left(y\right)}{\frac{y}{\beta }\left(1-\frac{y}{\beta }\right){\eta }_{II}\left(y\right)}=-{\lambda }_{II}^2,$$

where ${\lambda }_I^2$ and ${\lambda }_{II}^2$ are some constants to be determined. The left sides may be integrated to give

$${\xi }_i\left(x\right)=A_i\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_i^2}{4{\text{Pe}}_i}x\right),$$

where A_i is a constant of integration. The equations to solve for η_i(y) are given by

$$\{\begin{array}{c}{\eta }_I^{″}\left(y\right)=-{\lambda }_I^{2}y\left(1-y\right){\eta }_I\left(y\right)\\ {\eta }_{II}^{″}\left(y\right)=-{\lambda }_{II}^2\frac{y}{\beta }\left(1-\frac{y}{\beta }\right){\eta }_{II}\left(y\right).\end{array}\phantom{\}}$$

These may be solved for by a method of power series, where η_i is expanded in powers of y as ∑_na_nyⁿ and η_II in powers of y∕β as ∑_na_n(y∕β)ⁿ. If we do this, we may write the general solutions to the separated equations as

$$C_I\left(x,y\right)=A_I\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_I^2}{4{\text{Pe}}_I}x\right)\left[\sum _{n=0}^{\infty }{a}_{I,n}^0{y}^n+a_{1,I}\sum _{n=0}^{\infty }{a}_{I,n}^1{y}^n\right]=A_I\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_I^2}{4{\text{Pe}}_I}x\right){\eta }_I\left(y\right)$$

and

$$\begin{array}{l}{C}_{II}\left(x,y\right)=A_{II}\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_{II}^2}{4{\text{Pe}}_{II}}x\right)\left[\sum _{n=0}^{\infty }{a}_{II,n}^0{\left(\frac{y}{\beta }\right)}^n+a_{1,II}\sum _{n=0}^{\infty }{a}_{II,n}^1{\left(\frac{y}{\beta }\right)}^n\right]\\ =A_{II}\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_{II}^2}{4{\text{Pe}}_{II}}x\right){\eta }_{II}\left(y\right),\end{array}$$

where the coefficients $a_{I.n}^0$, $a_{I.n}^1$, $a_{II.n}^0$, and $a_{II.n}^1$ are given in Appendix0, subsection 03 and a_1,I and a_1,II are to be determined.

Application of boundary conditions to solution

The boundary conditions may be nondimensionalized as well, so that we now have in the upper channel

$$\phantom{\{}\begin{array}{c}{C}_{II}\left(x=0,y\right)=1\\ {\phantom{|}\frac{\partial C_{II}}{\partial y}|}_{y=\beta }=0\\ {\phantom{|}\frac{\partial C_{II}}{\partial y}|}_{y=0}=\text{Sh}\left[C_{II}\left(x,y=0\right)-C_I\left(x,y=1\right)\right],\text{Sh}\equiv \frac{D_{\text{membrane}}{h}_I}{t{D}_{II}}\end{array}\},$$ (A3)

where Sh is the Sherwood number, and in the lower channel,

$$\phantom{\{}\begin{array}{c}{C}_I\left(x=0,y\right)=0\\ {\phantom{|}\frac{\partial C_I}{\partial y}|}_{y=1}=\alpha {\phantom{|}\frac{\partial C_{II}}{\partial y}|}_{y=0},\alpha \equiv \frac{D_{II}}{D_I}\\ {\phantom{|}\frac{\partial C_I}{\partial y}|}_{y=0}=\text{Da}\frac{C_I\left(x,y=0\right)}{K_M∕C_0},\text{\hspace{0.5em}\hspace{0.5em}Da}\equiv \frac{V_{\text{max}}{\rho }_{\text{cells}}{h}_I}{D_I{C}_0}\end{array}\},$$ (A4)

where Da is the Damkohler number.

For Ω_II, the no-flux boundary condition on the top surface gives

$$a_{1,II}=-\sum _{n=0}^{\infty }{a}_{II,n}^0∕\sum _{n=0}^{\infty }{a}_{II,n}^1.$$

In Ω_I, the lower boundary condition gives a_1,I=Da. If we apply the membrane boundary conditions, we have

$${\phantom{|}\frac{\partial C_I}{\partial y}|}_{y=1}=A_I\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_I^2}{4{\text{Pe}}_I}x\right){\eta }_I^{\prime }\left(1\right)=\text{Sh}\left[A_{II}\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_{II}^2}{4{\text{Pe}}_{II}}x\right)-A_I\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_I^2}{4{\text{Pe}}_I}x\right){\eta }_I\left(1\right)\right],$$

so that

$$\frac{A_{II}}{A_I}\text{exp}\left(-\frac{{\lambda }_{II}^2}{4{\text{Pe}}_{II}}x+\frac{{\lambda }_I^2}{4{\text{Pe}}_I}x\right)=\frac{\text{Sh\hspace{0.5em}}{\eta }_I\left(1\right)+{\eta }_I^{\prime }\left(1\right)}{\text{Sh}}$$

and

$${\phantom{|}\frac{\partial C_{II}}{\partial y}|}_{y=0}=A_{II}\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_{II}^2}{4{\text{Pe}}_{II}}x\right)a_{1,II}=A_I\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_I^2}{4{\text{Pe}}_I}x\right){\eta }_I^{\prime }\left(1\right)$$

so that

$$\frac{A_{II}}{A_I}\text{exp}\left(-\frac{{\lambda }_{II}^2}{4{\text{Pe}}_{II}}x+\frac{{\lambda }_I^2}{4{\text{Pe}}_I}x\right)=\frac{{\eta }_I^{\prime }\left(1\right)}{a_{1,II}}.$$

Setting the two expressions equal gives

$$\frac{\text{Sh\hspace{0.5em}}{\eta }_I\left(1\right))+{\eta }_I^{\prime }\left(1\right)}{\text{Sh}}-\frac{{\eta }_I^{\prime }\left(1\right)}{a_{1,II}}=0.$$ (A5)

Since the quantity

$$\frac{A_{II}}{A_I}\text{exp}\left(-\frac{{\lambda }_{II}^2}{4{\text{Pe}}_{II}}x+\frac{{\lambda }_I^2}{4{\text{Pe}}_I}x\right)$$

is equal to constants, the additional constraint

$$\frac{{\lambda }_{II}^2}{{\text{Pe}}_{II}}=\frac{{\lambda }_I^2}{{\text{Pe}}_I}$$ (A6)

must be satisfied. Solving Eqs. A5, A6 will give a number of possible values for λ_II and subsequently λ_I. The linear combinations

$$C_{II}\left(x,y\right)=\sum _{i=1}^{\infty }{C}_{II,i}=\sum _{i=1}^{\infty }{A}_{II,i}\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_{II,i}^2}{4{\text{Pe}}_{II}}x\right){\eta }_{II,i}\left(y\right),$$ (A7)

$$C_I\left(x,y\right)=\sum _{i=1}^{\infty }{C}_{I,i}=\sum _{i=1}^{\infty }{A}_{I,i}\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_{I,i}^2}{4{\text{Pe}}_I}x\right){\eta }_{I,i}\left(y\right)$$ (A8)

form the general solution, where each C_I,i and C_II,i is a set of solutions characterized by the linked characteristic values ${\lambda }_{I,i}^2$ and ${\lambda }_{II,i}^2=\Gamma {\lambda }_{I,i}^2$, where we define Γ≡Pe_II∕Pe_I.

Since we have $A_{I,i}=A_{II,i}\left[a_{1,II}∕{\eta }_I^{\prime }\left(1\right)\right]$, it may be shown that

$$A_{II,i}=\frac{{\int }_{y=0}^{\beta }\frac{4y}{\beta }\left(1-\frac{y}{\beta }\right){\eta }_{II,i}dy}{{\int }_{y=0}^{\beta }\frac{4y}{\beta }\left(1-\frac{y}{\beta }\right){\left|{\eta }_{II,i}\right|}^{2}dy+\frac{1}{\Gamma }{\left[\frac{a_{1,II}}{{\eta }_I^{\prime }\left(1\right)}\right]}^2{\int }_{y=0}^{1}4y\left(1-y\right){\left|{\eta }_{I,i}\right|}^{2}dy},$$ (A9)

$$A_{I,i}=A_{II,i}\left[\frac{a_{1,II}}{{\eta }_I^{\prime }\left(1\right)}\right].$$ (A10)

Equations A9, A10 allow us to complete our description of the solution to Eqs. A1, A2. Nondimensionally, the consumption may be given by

$$\text{Consumption}\left(x\right)=\frac{Da}{K_M∕C_0}\sum _{i=1}^{\infty }{A}_{I,i}\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_{I,i}^2}{4{\text{Pe}}_I}x\right).$$

Expansion coefficients

The coefficients for the expansions given for the solution are given in the tables below. We must divide by β² for the flow compartment.

a1=0
	Coefficient $a_n^{\left(0\right)}$	Value(∕β2)
	$a_0^{\left(0\right)}$	1
	$a_1^{\left(0\right)}$	0
	$a_2^{\left(0\right)}$	0
	$a_3^{\left(0\right)}$	−λ2∕6
	$a_4^{\left(0\right)}$	λ2∕12
	$a_5^{\left(0\right)}$	0
	$a_6^{\left(0\right)}$	λ4∕180
	$a_7^{\left(0\right)}$	−λ4∕168
	$a_8^{\left(0\right)}$	λ4∕672
	$a_9^{\left(0\right)}$	−λ6∕12960
	$a_9^{\left(0\right)}$	16λ6∕125131

a0=0
	Coefficient $a_n^{\left(0\right)}$	Value(∕β2)
	$a_0^{\left(1\right)}$	0
	$a_1^{\left(1\right)}$	1
	$a_2^{\left(1\right)}$	0
	$a_3^{\left(1\right)}$	0
	$a_4^{\left(1\right)}$	−λ2∕12
	$a_5^{\left(1\right)}$	λ2∕20
	$a_6^{\left(1\right)}$	0
	$a_7^{\left(1\right)}$	λ4∕504
	$a_8^{\left(1\right)}$	−λ4∕420
	$a_9^{\left(1\right)}$	λ4∕1440
	$a_{10}^{\left(1\right)}$	−λ6∕45360

Solution

The final expressions for the concentrations in the flow chamber and cell compartment read, respectively,

$$C_{II}\left(x,y\right)=C_0\sum _{i=1}^{\infty }{A}_{II,i}\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_{II,i}^2{D}_{II}}{4u_{0,II}}\frac{x}{h_I^2}\right){\eta }_{II,i}\left(y∕h_{II}\right),$$ (A11)

$$C_I\left(x,y\right)=C_0\sum _{i=1}^{\infty }{A}_{I,i}\text{\hspace{0.17em}exp}\left(-\frac{{\lambda }_{I,i}^2{D}_I}{4u_{0,I}}\frac{x}{h_I^2}\right){\eta }_{I,i}\left(y∕h_I\right),$$ (A12)

where u_0,II is equal to ${\left(-dp∕dx\right)}_{II}{h}_{II}^2{\left(8{\mu }_{II}\right)}^{-1}$ and u_0,I equal to ${\left(-dp∕dx\right)}_I{h}_I^2{\left(8{\mu }_I\right)}^{-1}$, and ${\lambda }_{II,i}^2$ and ${\lambda }_{I,i}^2$ are given by the solutions to Eqs. A5, A6. Finally, consumption is given by

$$\text{Consumption}=D_I{\phantom{|}\frac{\partial C_I}{\partial y}|}_{y=0}=\frac{V_{\text{max}}{\rho }_{\text{cells}}}{K_M}{C}_I\left(x,y=0\right).$$